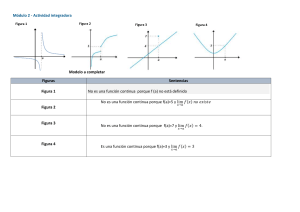
ÁLGEBRA
FACTORIZACIÓN I
DESARROLLO DEL TEMA
I.
B. Método de agrupación de términos
DEFINICIÓN
La factorización es un proceso que consiste en
Generalmente agrupamos los términos de 2 en 2
transformar un polinomio en el producto indicado de
sus factores primos.
o de 3 en 3 convenientemente buscando factores
comunes en cada grupo.
Ejemplos:
II. FACTORES PRIMOS
P = ax + bx + ay + by
Son aquellos factores que se les conoce por:
P = x(a + b) + y(a + b)
1. Presentar coeficientes racionales.
P = (a + b)(x + y)
2. Ser divisibles solo por sí mismos y por la unidad.
3. Contener por lo menos una variable.
Nota:
III. CONTEO DE FACTORES PRIMOS
1. Se factoriza al máximo el polinomio dado.
2. Se cuenta el número de "factores basales", es
decir, los factores que se encuentran como base
de una potencia y que contengan a la variable.
x 2 – y 2 = x + y x – y
•
x 3 + y 3 = x + y x 2 – xy + y 2
•
x 3 – y3 = x – y x 2 + xy + y 2
C. Método de las identidades
Ejemplos:
•
•
1. Diferencia de cuadrados
P(x) = 3x2y (x + y)7
Factores primos = { x, y, x + y}.
a2 – b2 = (a + b)(a – b)
# de factores primos = 3.
•
Ejemplo:
A = x4 – y6 = (x2 + y3)(x2 – y3)
P(x) = (x – 1)4(x + 3)5
Factores primos = { x – 1, x + 3}.
# de factores primos = 2.
x 2 y3
IV. MÉTODOS DE FACTORIZACIÓN
2. Trinomio cuadrado perfecto
A. Método del factor común
a2
Se utiliza cuando todos los términos del polinomio
tienen un factor común.
2ab + b2 = (a
b)2
Ejemplos:
Ejemplos:
1. A = x2 + 2x + 1 = (x + 1)2
A = 36x3y2 – 12x4y + 24x5y3
A = 12x3y (3y – x + 2x2y2)
UNI SEMESTRAL 2013 - III
x
1
. 2
. 1 = 2x
ÁLGEBRA
TEMA 1
FACTORIZACIÓN I
Exigimos más!
2. B = 4x2 + 12xy + 9y2 = (2x – 3y)2
Observación:
2x
. 2
.
3y = 12xy
*
Todo polinomio de primer grado es primo.
3. Suma y diferencia de cubos
VI. CRITERIOS DE FACTORIZACIÓN
a3 + b3 = (a + b)(a2 – ab + b2)
a3 – b3 = (a – b)(a2 + ab + b2)
A. Factor común
Ejemplos:
Se denomina así al factor repetido en varios términos, para lo cual se eligen las bases comunes afec-
1. P = 125x6 – y9 = (5x2–y3)(25x4+5x2y3+y6)
3
3
5x2
tadas del menor exponente.
Ejemplo:
y3
Factorizar:
3
2
2. A = x + 8 = (x + 2)(x – 2x + 4)
3
f(x;y) 4x3y4 + 5x2y5 + 7x4y7
Se observa: x2y4 como factor común.
3
x
Luego factorizando tenemos:
2
f(x; y) x2y4 (4x – 5y + 7x2y3)
Nota:
• En P(x) si la suma de coeficientes es 1 entonces
(x – 1) es factor de dicho polinomio.
B. Identidades
Es la aplicación inmediata de algunos productos
• Si el trinomio no es cuadrado perfecto entonces
se su ma y rest an los termin os necesario s.
Finalmente se llega a una diferencia de cuadrados.
notables como:
– Diferencia de cuadrados:
A2 – B2 = (A + B) (A – B)
Es un proceso mediante el cual, un Polinomio se expresa
como la multiplicación de otros Polinomios llamados factores.
Ejemplo:
Factorizar
V. FACTOR PRIMO
Reconocemos : P(x) (3x)2 – (4)2
Son aquellos polinomios literales que no se pueden
literales.
– Diferencia de cubos
Ejemplo:
*
*
: P(x) (3x + 4) (3x – 4)
Luego
expresar como una multiplicación de otros polinomios
*
: P(x) 9x2 –16
A 3 – B3 = (A – B) (A 2 + AB + B2)
2
f(x) x – 4 no es primo, por que se puede expresar como (x – 2)(x + 2).
Ejemplo:
f(x) x – 2 es primo, por que no se puede
Factorizar
factorizar.
Reconocemos : P(x) (3x)3 – (2)3
f(x) 3x – 6 si es primo porque al obtener 3(x – 2)
Luego
: P(x) 27x3 – 8
: P(x) (3x – 2)(9x2 + 6x + 4)
percatese que 3 es de grado cero.
– Suma de cubos
A3 + B3 = (A + B) (A2 – AB + B2)
Se dice que la factorización se realiza en cuando los
factores primos obtenidos presentan únicamente coeficientes enteros; mientras no se indique alguna acla-
Ejemplo:
ración la factorización solo se realiza en .
Factorizar
UNI SEMESTRAL 2013 - III
2
: f(x) 8x6 + 1
ÁLGEBRA
TEMA 1
FACTORIZACIÓN I
Exigimos más!
2 3
Reconocemos : f(x) (2x ) + (1)
8
3
8
Factor Repetido: (x – y )
: f(x) (2x2 + 1) (4x4 –2x2 + 1)
Luego
Luego: f(x;y) (x8 – y8) (x2 + y2)
– Trinomio cuadrado perfecto
Continuamos:
A2 + 2AB + B2 = (A + B)2
f(x;y) (x4 + y4) (x2 + y2) (x + y) (x – y) (x2 + y2)
A2 – 2AB + B2 = (A – B)2
Se uso repetidas veces diferencia de cuadrados:
Ejemplo
f(x;y) (x4 + y4) (x2 + y2)2 (x + y) (x – y)
4
2
Factorizar : f(x) 9x + 6x + 1
Notese
: f(x) (3x2)2 + 2(3x2)(1) + (1)2
Luego
: f(x) (3x2 + 1)2
D. Aspa simple
Se utiliza para factorizar particularmente Polinomios
de la forma: P(x) ax2n + bxn + c ó que se amolden a dicha forma.
C. Agrupación de términos
Consiste en seleccionar convenientemente los términos de tal manera que se genere algún factor
común o alguna identidad.
Proceso
*
Descomponer los extremos.
*
Verificar que la suma de productos en aspa sea
igual al término central.
Ejemplo:
Factorizar:
Ejemplo:
f(x;y) x10 – x2y8 + x8y2 – y10
Nos percatamos que no existe factor común en
todos los términos, pero si agrupamos de dos en
dos obtenemos:
Luego los factores se forman:
f(x;y) x2 (x8 – y8) + y2 (x8 – y8)
Horizontalmente: (x – 3) (x – 4)
problemas resueltos
Problema 1
Problema 2
Resolución:
Factorizar:
Factorizar:
10x2+21y2+29xy
5r(p4+q)–p2(r2+25q)
A) (rp2–5q)(5p2–r)
B) (rp–5q)(5p4–r)
Agrupando los términos indicados
y factorizando parcialmente
2
2
= 5p (rp –5q)–r(rp –5q)
B) (5x+7y)(2x+4y)
= (rp2–5q)(5p2–r)
C) (5x+7y)(2x+3y)
C) (rp4–5q)(5p3–r)
D) (5x+7y)(3x+3y)
D) (rp3–5q)(5p2–r)
E) (rp2–5q)(5p4–r)
UNI SEMESTRAL 2013 - III
A) (6x+7y)(2x+3y)
2
Respuesta: A) (rp2–5q)(5p2–r)
3
E) (4x+7y)(2x+3y)
ÁLGEBRA
TEMA 1
FACTORIZACIÓN I
Exigimos más!
Resolución:
2
10x +29xy+21y
2
Problema 3
Resolución:
Factorizar e indicar la suma de sus
factores primos.
Ordenando y aplicando el criterio
de aspa doble
2
2
12a -7ab - 10b - 15a - 59b - 63
5x
2x
7y
3y
14xy +
15xy
29xy
4a
3a
12a2–59b–63–7ab–10b2+15a
A) 7a–3b+4
B) 7a–3b+3
–5b
2b
–7
9
Finalmente (4a–5b–7)(3a+2b+9)
luego facto res primos : 7a–
Finalmente: (5x+7y)(2x+3y)
C) 7a–4b+2
3b+2
D) 7a–5b+2
Respuesta: C) (5x+7y)(2x+3y)
UNI SEMESTRAL 2013 - III
Respuesta: E) 7a–3b+2
E) 7a–3b+2
4
ÁLGEBRA
TEMA 1
ÁLGEBRA
FACTORIZACIÓN II
DESARROLLO DEL TEMA
CRITERIO DE EVALUAR (DIVISORES
BINÓMICOS)
Proceso:
Se usa básicamente para factorizar polinomios de grado
mayores o iguales a 3.
*
Traza dos aspas simples
*
Verificación final con los extremos, veamos en
un ejemplo:
Factorizar:
Proceso:
Consiste en evaluar usando la regla de Ruffini.
P(x;y) 15x2 – xy – 6y2 + 34x + 28y – 16
como se encuentra ordenado.
1.er Aspa
Luego:
f(x) = (x – a) q (x)
2.O Aspa
Al valor de "a” se denomina cero del polinomio.
Por ejemplo:
P(x) = x3 – x2 – 4; si evaluamos en x = 2, tenemos:
Verificación final
(Los términos estan descompuestos)
Luego: x3 – x2 – 4 se puede expresar como:
P(x)= (x – 2) (x2 + x + 2)
Luego, en un esquema se tiene:
(Nótese que esta factorizada)
A.
Aspa doble
Se usa en forma particular para polinomios de la forma:
P(x;y) ax2m + bxmyn + cy2n + dxm + eyn + f
UNI SEMESTRAL 2013 - III
P(x;y) = (5x + 3y –2) (3x – 2y + 8)
5
ÁLGEBRA
TEMA 2
FACTORIZACIÓN II
Exigimos más!
B.
Aspa doble especial
Ejemplo:
Se emplea para factorizar polinomios de 5 términos
con la forma:
P(x) Ax4n + Bx3n + Cx2n + Dxn + F
Factorizar:
Proceso:
*
Se descomponen los términos extremos en 2
factores cada uno.
*
P(x) (x2 5x 1)(x2 x 1)
Se hace el balanceo
problemas resueltos
Problema 1
Problema 2
Problema 3
¿Cuántos factores primos tiene el polinomio:
Determine la suma de los factores primos del polinomio:
Reconocer un factor de:
3
P(x; y) x 7 y 2x 6 y 2 x 5 y 3 ?
B) 2
C) 3
D) 4
UNI
P(x) x x x 1
UNI
A) 1
P(x) x5 x 1
2
UNI
A) 2x + 1
C) 3x – 1
E) 2x
E) 5
B) 3x + 2
D) 3x + 1
A) x2 – x – 1
B) x2 – x + 1
C) x3 – x – 1
D) x3 – x2 + 1
E) x3 + x2 + 1
Resolución:
Resolución:
Por agrupación de términos tenemos:
De acuerdo con el criterio del factor
común tenemos:
2
P(x; y) x 5 y (x
2xy
y2)
Dando uso de los productos notables
tenemos:
5
P(x; y) x y (x y)
2
P(x) x3 x 2 (x 1)
P(x) x2 (x 1) (x 1)
N de factores primos 3
de cubos sumamos y restamos x2.
5
P(x) x
x2 x2 x 1
P(x) (x 1) (x21)
P(x) x 2 (x3 1) x2 x 1
Por diferencia de cuadrados tenemos:
2
2
P(x) x2(x 1) (x
x 1) (x
x 1)
P(x) (x 1) (x 1) (x 1)
P(x) (x 1)2 (x 1)
Aquí reconocemos que los factores
primos son: (x + 1) y (x – 1)
Por el criterio del factor común:
P(x) (x 2 x 1) x 2(x 1) 1
P(x) (x2 x 1)(x 3 x 2 1)
de f .p 2x
Respuesta C) 3
UNI SEMESTRAL 2013 - III
Con la finalidad de formar una diferencia
Por el criterio del factor común:
Finalmente los factores primos son:
x, y (x y)
Resolución:
Respuesta E) 2x
6
Respuesta D) x3 – x2 + 1
ÁLGEBRA
TEMA 2
ÁLGEBRA
ECUACIONES I
DESARROLLO DEL TEMA
I.
ECUACIÓN
Por ejemplo la igualdad x – y = z, podemos
sumar “y” a ambos miembros, con lo que resulta
x = y + z.
Es una igualdad entre dos expresiones matemáticas
en la que al menos esté presente una variable que
ahora recibirá el nombre de incógnita.
•
Si se restan miembro a miembro varias igualdades, se obtiene otra igualdad. Por ejemplo,
en la igualdad x + 5 = 7, podemos restar 5 a
ambos miembros con lo que se obtiene x = 2.
•
Si se multiplican miembro a miembro varias
igualdades se obtiene otra igualdad.
Notación:
A(x;
y;...z)
Primer miembro
B(x;
y;...z)
Segundo miembro
Donde: x; y; ...; z: incógnita
Una ecuación que sólo se verifique para ciertos valores
de las incógnitas recibe el nombre de ecuación condicional o, simplemente, ecuación.
Por ejemplo, si se multiplican por 3 los dos
miembros de la igualdad: 1 y 5x2 .
3
Se obtiene: y = 15x2
Por ejemplo:
• x – 1= 3 se verifica solo para x = 2; es una ecuación
condicional.
• x2 – 1 = (x + 1) (x – 1) se verifica para todos los
valores de x; es una identidad.
Análogamente, si los dos miembros de:
9 C k – 492
5
se multiplican por:
Para representar una identidad se emplea el símbolo
en lugar del símbolo =.
Se obtiene: C 5 (k – 492)
9
A. Soluciones de una ecuación
•
Las soluciones de una ecuación son los valores de
las incógnitas que transforman la ecuación en una
identidad, es decir, se igualan ambos miembros. Las
soluciones satisfacen a la ecuación. Resolver una
ecuación es hallar todas sus soluciones.
Por ejemplo:
x = 2 es una raíz, o solución de la ecuación x + 3 = 5,
ya que sustituyendo x = 2 en esta se obtiene
2 + 3 = 5, es decir, los dos miembros se hacen
iguales y la ecuación se convierte en una identidad.
a F
m
Fórmula:
La fórmula es una ecuación que expresa un
hecho general, una regla o un principio.
Si se suman miembro a miembro varias igualdades, se obtiene otra igualdad.
UNI SEMESTRAL 2013 - III
Si se dividen miembro a miembro varias igualdades se obtiene otra igualdad siempre que
no se divida por cero.
Por ejemplo, si se dividen los dos miembros de
la igualdad 3x = 6 por 3, se obtiene x = 2.
Análogamente, en la igualdad F = ma se puede
dividir los dos miembros por m(m 0) obteniéndose:
B. Operaciones aplicadas en la transformación
de ecuaciones
•
5
9
7
ÁLGEBRA
TEMA 3
ECUACIONES I
Exigimos más!
II. ECUACIÓN LINEAL O DE PRIMER GRADO CON UNA INCÓGNITA
Forma General:
Aplicando el teorema:
a2 = b2 a = b a = –b
(x – 1)2 2 x – 1 2 x – 1 – 2
ax + b = 0 ; a 0 ; en donde a y b
x 1 2 x 1–
son constantes arbitrarias.
Como primer paso para la resolución de esta ecuación
transponemos “b” al segundo miembro obteniéndose
así la ecuación equivalente.
2
C.S. {1 2;1 – 2}
Observación:
ax = b
La aplicación de este teorema nos conduce a la
demostración de la fórmula de las soluciones o
raíces de una ecuación de se-gundo grado.
Después dividimos ambos miembros entre “a”, obteniéndose otra ecuación equivalente que es la solución
de la ecuación dada:
B. Fórmula general
x–b
a
Sea: ax2 + bx + c = 0
Donde: a 0
Si este valor de “x” se sustituye en ax + b = 0 obtendremos la identidad:
Para encontrar las soluciones necesitamos seguir
los siguientes pasos:
a – b b 0
a
Factorizamos el coeficiente de x2:
–b + b = 0
ax 2 bx c 0 x 2 b x c 0
a
a
Teorema:
La ecuación lineal con una incógnita
ax + b = 0, a 0
x2 b x c 0
a
a
Tiene solución única:
Sumar y Restar la mitad del coeficiente de x:
2
1 b b
b
elevado
al
cuadrado:
2 a 2a
2a
x–b
a
III. ECUACIÓN DE SEGUNDO GRADO CON
UNA INCOGNITA
x2
A. Método de completar cuadrados
Raíces x
Consiste en completar el cuadrado de un binomio
y está basado en la aplicación del siguiente teorema.
2
2
b
2a
2
2
2
x b b 2 – c b – 4ac
2a
a
4a
4a2
a 2 b2 a b a –b
Ejemplo:
Hallar la solución de: x2 – 2x – 1 = 0
Dar como respuesta la menor raíz.
Si: b2 – 4ac 0, las soluciones son:
x b
2a
Solución:
Como es difícil de factorizar, usamos el método de
completar cuadrados, los pasos a seguir son:
b2 – 4ac
2a
2
o x+ b – b – 4ac
2a
2a
2
x – b b – 4ac
2a
2a
x2 – 2x – 1 = 0
2
x –b b – 4ac
2a
Sumar y restar la mitad del coeficiente de x:
12 –2 –1
o x=– b –
2a
b2 – 4ac
2a
2
o x –b – b – 4ac
2a
Finalmente; las raíces de la ecuación
ax2 + bx + c = 0, están dadas por:
2
Elevado al cuadrado: (–1) = 1, nos queda en 1.
2
x
–
2x
12 – 12 – 1 0
2
x –b b – 4ac
2a
(x –1)2 2
UNI SEMESTRAL 2013 - III
2
b
b b
c
b
b2 c
x – 0 x
–
0
a
a
2a
2a 2a
4a2 a
8
ÁLGEBRA
TEMA 3
ECUACIONES I
Exigimos más!
–12 0
3
–
8
2
Ejemplo:
Resolver aplicando la fórmula general:
a) x2 – 3x + 2 = 0
En este caso: a = 1, b = – 3 , c = 2
–12 0
8
t1,2
–12 – 0
8
–
8
3
Sabiendo que:
x1,2
Luego: x1,2
C.S. –3
2
–b b2 – 4ac
2a
c) 9x2 + 18x –17 = 0
–(–3) (–3)2 – 4(1)(2)
2(1)
Tenemos: a = 9, b = 18, c = –17
Luego:
31
2
2
x1,2
es una raíz doble.
x1,2
31
2
–(18) (18)2 – 4(9)(–17)
2(9)
x1,2 –18 936
18
3– 1
1
2
–3 26
3
C.S.{1, 2}
x1,2
2
b) 4t + 12t + 9 = 0
–18 6 26
18
–3 – 26
3
En este caso: a = 4, b = 12, c = 9
Luego: t1,2
–(12) (12)2 – 4(4)(9)
2(4)
C.S. –3 26 ; –3 – 26
3
3
problemas resueltos
Problema 1
Si {x1; x2} es el conjunto solución de:
3
x 1
x
3x = 1
x 0
Tenemos: –x – 1 = 1
3 1 3 2
Resolución:
Si: 3
Reduciendo: 3–x–1 = 3
x
entonces la suma de x1 y x2 es:
UNI 2008-I
Nivel fácil
A) –4
B) –2
C) 2
D) 4
E) 0
x 1
Tenemos:
De donde:
Si: – 1 x 0
Eliminando los valores absolutos:
3x+1 + 3x – 1 = 3x + 2
Respuesta: B) –2
Tenemos: x + 1 = 1
De donde: x = 0
Eliminando los valores absolutos:
3x+1 – (3x – 1) = 3x + 2
Reduciendo:
3x . 3 –2 . 3x – 1 = 0
UNI SEMESTRAL 2013 - III
Piden: –2 + 0 = –2
Reduciendo: 3x+1 = 3
– 3x – 1 3x 2
Si: x 0
x –2
C.S. {–2;0}
0 1 x 0
Si: x < –1
Eliminando los valores absolutos:
3–x–1 3 x – 1 3
9
x
2
Problema 2
Las raíces de la ecuación x x 2 4
son:
UNI 2008-I
Nivel intermedio
A) Solo x = 6
B) Solo x = 3
C) x = 3, x = 6
D) x 6 , x = 3
E) No existen soluciones
ÁLGEBRA
TEMA 3
ECUACIONES I
Exigimos más!
Resolución:
x x 2 4
x 2 4 x
A)
2 5 17
2
Elevando al cuadrado y teniendo en
cuenta que:
B)
2 5 17
2
x 2 0 4 x 0
C)
2 5 17
2
D)
3 5 17
2
E)
3 5 17
2
Tenemos: x2 – 9x + 18 = 0
(x – 3)(x – 6) = 0 de donde la que
verifica solo será x = 3.
Reemplazando :
m2 7m 10 0
(m 2)(m 5) 0
m 2 m 5
Reemplazando:
x2 x 1 2 x2 x 1 5
x 2 x 1 0 x2 x 4 0
Utilizando la fórmula general:
x
Respuesta: B) x = 3, x = 6
Resolución:
Problema 3
La suma de todas las soluciones positivas de la ecuación:
10
1 x x2
6 x x2
10
7 m
m
1 5
1 17
x
2
2
como x > 0:
Piden: x > 0
x1
Llamemos a:
x2 + x + 1 = m; m > 0
1 5
1 17
x2
2
2
x1 x 2
2 5 17
2
Del dato:
es:
UNI 2009-II
Nivel difícil
UNI SEMESTRAL 2013 - III
10
1 x x2
7 (1 x x 2)
10
Respuesta: B)
ÁLGEBRA
2 5 17
2
TEMA 3
ÁLGEBRA
ECUACIONES II
DESARROLLO DEL TEMA
I.
Se cumple:
ECUACIÓN DE SEGUNDO GRADO (CUADRÁTICA)
• Suma: s x1 x 2 –
A. Forma general
• Producto: p x1 . x 2 c
a
ax 2 bx c 0
b2 4ac
;a 0
a
Para determinar la diferencia de raíces se recomienda
utilizar la equivalencia de Legendre, veamos:
(x1 + x2)2 – (x1 – x2)2 = 4(x1 x2)
donde: x incógnita, asume dos valores
a;b ; c /a 0
• Diferencia: | x1 x 2 |
B. Fórmula de Carnot
Si: x1; x2 son las raíces de la ecuación:
ax2 + bx + c = 0; a 0
Estas se obtienen a partir de la relación:
x1;2
A. Casos particulares
Dada la ecuación cuadrática en "x": ax2 + bx + c = 0
2
–b b – 4ac
2a
De raíces x1 ; x2, si estas son:
1. Simétricas, se cumple: x1 + x2 = 0.
2. Recíprocas, se cumple: x1 . x2 = 1.
1. Discriminante
dada la ecuación cuadrática en "x":
ax2 + bx + c = 0; a 0
se define como:
B. Reconstrucción de la ecuación cuadrática en "x"
b2 – 4ac
2. Propiedad del discriminante
El discriminante de una ecuación cuadrática permite decidir qué clase de raíces presenta, es
decir:
1. Si: 0 , la ecuación tiene raíces reales y
diferentes.
2. Si: 0, la ecuación tiene raíces reales e
iguales (raíces dobles).
3. Si: 0, la ecuación tiene raíces imaginarias y conjugadas.
II. RELACIÓN ENTRE LAS RAÍCES Y LOS COEFICIENTES (PROPIEDADES DE LAS RAÍCES) DE UNA ECUACIÓN CUADRÁTICA
Si x1 ; x2 son las raíces de la ecuación cuadrática en "x"
Siendo "s" y "p", suma y producto de raíces, respectivamente, toda ecuación cuadrática en "x" se
determina según la relación:
x 2 – sx p 0
C. Ecuaciones cuadráticas equivalentes
ax2 + bx + c = 0
Siendo:
a1x2 + b1 x + c1 = 0
Se cumple:
a b c
a1 b1 c1
D. Ecuaciones cuadráticas con una raíz común
ax2 + bx + c = 0
a1 x2 + b1 + c1 = 0
Sean:
Se cumple:
(ab1 – a1b)(bc1 – b1c) (ac1 – a1c)2
ax 2 + bx + c = 0
UNI SEMESTRAL 2013 - III
b
a
11
ÁLGEBRA
TEMA 4
ECUACIONES II
Exigimos más!
problemas resueltos
Problema 1
Sea la ecuación 4x2 – 2x + 3 = 0, cuyas
raíces son a y b. Halle otra ecuación
cuadrática que tenga por raíces (2a – 1)
y (2b – 1)
UNI 2008 - I
Nivel fácil
A) y2 – y + 1 = 0
B) y2 – y – 2 = 0
C) y2 + y + 3 = 0
D) y 2 1 y 2 0
2
1
E) y 2 y 3 0
4
Resolución:
Dada la ecuación:
4x2 – 2x + 3 = 0 de raíces {a;b}
1. Si cambiamos: "x" por " y "
2
2
entonces: 4 y 2 y + 3 = 0
2
2
tenemos: y2 – y + 3 = 0
de raíces {2a; 2b}
2. Si cambiamos: "y" por "y+1"
Entonces: (y + 1)2 – (y + 1) + 3 = 0
Tenemos: y2 + y + 3 = 0 de raíces
{2a – 1, 2b – 1}
UNI SEMESTRAL 2013 - III
Respuesta: C) y2 + y + 3 = 0
Problema 2
Las raíces de la ecuación x x 2 4
son:
Problema 3
Una ecuación cuadrática tienen como
raíces a 4 y 2. Halle la suma de
las cifras del producto de estas raíces,
siendo el discriminante de la ecuación.
UNI 2007 - II
Nivel intermedio
A) solo x = 6
B) solo x = 3
A) 10
C) x = 3, x = 6
E) 14
UNI 2006 - II
Nivel difícil
B) 11
D) 13
C) 12
D) x 6 , x = 3
E) No existen soluciones
Resolución:
Suma de Raíces S 2 2
Producto Raíces P 2 2 8
Resolución:
Luego la ecuación será:
x x 2 4
x2 4x
Elevando al cuadrado y teniendo en
cuenta que
x– 2 0 4– x 0
tenemos x2 – 9x + 18 = 0
(x – 3)(x – 6) = 0 de donde la que
verifica solo será x = 3
x 2 (2 2)x 2 2 8 0
Luego calculando el discriminante:
2
(2 2) 4( 2 2 8)
36
Luego:
Producto de Raíces = (40)(34) = 1360
cifras 10
Respuesta: B) Solo x = 3
12
Respuesta: A) 10
ÁLGEBRA
TEMA 4
ÁLGEBRA
ECUACIONES III
DESARROLLO DEL TEMA
I.
DEFINICIÓN
en general, tiene exactamente n raíces y P(x) puede
Dado un número entero n 3, un polinomio en variable
x con coeficientes en k de grado n, es una función de
la forma:P(x) anxn + an–1xn–1 + ........ + a1x + a0, con
an 0.
A la cual llamaremos polinomio de grado superior, donde:
• x = es la variable independiente.
• ai K, son los coeficientes de las x y son constantes
que pueden ser cualesquiera números.
• K es un conjunto.
• an= coeficiente principal
• ao= término constante
• n = [P]° es el grado del polinomio P(x)
ser expresado en la forma P(x)=an(x – r1) (x – r2)... (x
Observación:
III. POLINOMIOS CON COEFICIENTES
REALES
A. Teorema (paridad de las raíces imaginarias)
Si un polinomio P(x) con coeficientes reales tiene
como raíz el número imaginario Z, entonces Z también es raíz de P(x).
Observaciones
•
El estudio de todo polinomio:
P(x) anxn + an–1xn–1 + ... + a1x + a0
con an 0, a 0 0 radica en el tratamiento de sus
coeficientes a i K y en particular de an y a0.
•
II. EL TEOREMA FUNDAMENTAL DEL ÁLGEBRA
La paridad de raíces imaginarias, refiere lo
siguiente, si Z = a + bi, con b 0 es raíz de
un polinomio P(x) entonces Z = a – bi también es raíz de P(x).
Si Z = a + bi es raíz del polinomio P(x), entonces
(x – Z) (x – Z ) será un factor de P(x).
Propiedad
Un polinomio con coeficientes reales puede escribirse como el producto de un número real, multiplicado por factores cuadráticos irreductibles con
coeficientes reales y factores lineales con coeficientes reales.
Todo polinomio P(x) de grado n > 0 con coeficientes
complejos en general, tiene al menos una raíz generalmente compleja.
Colorario:
Todo polinomio P(x) de grado n > 0, tiene exactamente "n" raíces.
Por ejemplo P(x) = x5 + x – 1 tiene en total 5 raíces
entre reales e imaginarias, asimismo podemos decir que
F(x) x 4 tiene en total 4 raíces (cada una es igual a
cero).
Propiedad
Todo polinomio: P(x) = anxn + an–1xn–1 + ... + a1x + a0 de
grado n > 0, n Z , an 0; con coeficientes complejos
UNI SEMESTRAL 2013 - III
– rn) y ri es raíz de P(x).
13
B. Teorema (paridad de raíces irracionales)
Si un polinomio P(x) con coeficientes racionales tiene
como raíz a b, donde b es irracional, a y b son
racionales; entonces a b también es raíz de P(x).
Sea P(x) un polinomio con coeficientes racionales.
Si ( a b) es raíz del polinomio P(x), donde a,
b , ab son irracionales, entonces a b,; a b ,
a b también son raíces de P(x).
Si la raíz ( a b) es de multiplicidad K, las otras
raíces también son de multiplicidad K.
ÁLGEBRA
TEMA 5
ECUACIONES III
Exigimos más!
IV. RELACIONES ENTRE LAS RAÍCES Y
LOS COEFICIENTES
Dado el polinomio de grado n > 0:
P(x) = anxn + an–1xn–1 + ....... + a0
•
an 0 (con coeficientes reales o complejos) y cuyos n
raíces son r1, r2, r3, ..., rn (reales o complejas, incluidas
tantas veces como se repiten las raíces múltiples), entonces existen relaciones entre los coeficientes de P(x)
y las raíces ri.
Dichas relaciones se obtienen del siguiete modo:
• an xn an 1x n1 ... a0 0
xn
•
Como P(x) = 0 an(x – r1)(x – r2)....(x – rn)=0,
an 0 (x – r1)(x – r2)....(x – rn) = 0
(2*)
Pero son idénticos (1*) y (2*):
a
a
a
xn n 1 x x 1 n2 x n2 ... 0
an
an
an
(x r1)(x r2 )...(x rn) xn r1 r2 ... rn x n 1
n
r1r2 r1r3 ... x n1 ... 1 r1r2r3...rn
a
r1 r2 r3 ... rn n 1
an
a
r1r2 r1r3 ... rn1rn n2
an
a
r1r2r3 r1r2r4 ... rn2rn 1rn n3
an
n a
r1r2r3r4...........rn 1 0
an
a
an1 n1 an2 n2
x
x ... 0 0 an 0
an
an
an
(1*)
Como r1, r2, ..., rn son las n raíces de P(x), entonces
el polinomio P(x) se puede escribir como:
P(x) = an(x – r1) (x – r2) .... (x – rn)
problemas resueltos
Problema 1
La función polinomial:
3
2
F(x, y, z) (x y)(y z 3)
4
[(Z y)(y x 3)] (x y z 3)
2
tiene N raíces (x, y, z). Entonces N es
igual a:
UNI 2008 - I
Nivel fácil
A) 0
B) 1
C) 2
D) 3
E) 4
Resolución:
2
(x y)(y z 3) (z y)(y x 3)
0
4
0
2
(x
y
z
3) 0
0
Se genera un sistema de ecuaciones:
x y 0 y z 3 0
z y 0 y x 3 0
x y z 3 0
De donde:
1
2
x y 0
z y 0
x y z 3 0
C.S. (1,1,1)
x y 0
y x 3 0
x y z 3 0
C.S.
UNI SEMESTRAL 2013 - III
4
y z 3 0
C.S.
z y 0
x y z 3 0
y z 3 0
y x 3 0 C.S. (2; 1, 2)
x y z 3 0
N es igual a 2
Respuesta: C) 2
Problema 2
Determine el polinomio mónico de menor grado de coeficientes enteros que
tenga como raíces a los números reales
2 3 y 3 2. Dar como respuesta
la suma de sus coeficientes.
UNI 2007 - II
Nivel intermedio
A) 28
B) 42
C) 56
D) 70
E) 84
Resolución:
Por el teorema de la paridad de raíces
irracionales: Si una raíz es 3 2 la otra
será (3 2) la cual origina el polinomio
cuadrático x2 + 6x + 7.
Análogamente: Si la otra raíz es 2 3
la otra será 2 3 que origina el
polinomio: (x2 + 4x + 1).
Por lo tanto el polinomio mónico será:
P(x) = (x2 + 6x + 7)(x2 + 4x + 1)
Nos piden: P(x) (14)(6) 84
Problema 3
Dados los siguientes polinomios: P(x)
de grado 2 y término independiente
uno; y Q(x) = (x – 1) P(x) + 3x + 1.
Si Q(2) = 7 y P(1) = 2, halle la suma
de raíces de Q(x).
UNI 2004 - II
Nivel intermedio
A) 0
B) 8/3
C) 10/3
D) 4
E) 5
Resolución:
De los datos: P(x) = ax2 + bx + 1
Q(x) = (x – 1) (ax2 + bx + 1) + 3x + 1
Pero:
Q(2) 7; (1)(4a 2b 1) 7 7
4a 2b 1......(1)
P(1) 2 ; a b 1 2
a b 1...(2)
de (1) y (2) = a 3 / 2;b 5 / 2
De donde:
Q(x) 3 x 3 4x 2 3 x
2
2
se pide:
x1 x 2 x 3
Respuesta: E) 84
14
4 8
3 / 2 3
Respuesta: B) 8/3
ÁLGEBRA
TEMA 5
ÁLGEBRA
NÚMEROS REALES
DESARROLLO DEL TEMA
I.
DEFINICIÓN AXIOMÁTICA DE LOS
NÚMEROS REALES
(M4) a : !1 / a 1 1 a a
(Existencia y unicidad del elemento neutro)
El sistema de los números reales, es un conjunto provisto
de dos operaciones internas (adición y multiplicación) y
una relación de orden y otra de igualdad.
Notación
Denotamos por al conjunto de los números reales.
(M5) a – {0} : !a 1 / a a –1 a –1 a 1
(Existencia y unidad del elemento inverso)
C. Axioma distributiva
Distributividad de la multiplicación respecto de la
adición.
A. Axiomas de adición
(D1) a, b, c : a(b c) ab ac
(A1) a, b : a b
(D2) a, b, c : (b c)a ba ca
(Clausura o cerradura)
D. Relación de orden
(A2) a, b : a b b a
Es una comparación que se establece entre 2 elementos de un conjunto que pertenece al campo
de los números reales, el campo real es un campo
(Conmutatividad)
(A3) a, b, c : a (b c) (a b) c
ordenado.
(Asociatividad)
Símbolos de la relación de orden:
(A4) a : !0 / a 0 0 a a
> : "mayor que"
: "menor o igual que"
< : "menor que"
: "mayor o igual que"
(Existencia y unidad del elemento neutro)
II. DESIGUALDAD
(A5) a : !(–a) / a (–a) (–a) a 0
Es una relación de orden que se establece entre dos
números reales de diferente valor.
(Existencia y unidad del elemento inverso)
Existen tipos de desigualdades.
B. Axiomas de multiplicación
(M1) a, b : ab
6>1
(Desigualdad verdadera)
5 < –2
(Desigualdad falsa)
(Clausura)
A. Axioma de tricotomia
(M2) a, b : ab ba
Si a b , entonces una y solamente una
(Conmutatividad)
de las siguientes relaciones se cumple:
(M3) a, b, c : a(bc) (ab)c
(Asociatividad)
UNI SEMESTRAL 2013 - III
15
ÁLGEBRA
TEMA 6
NÚMEROS REALES
Exigimos más!
B. Axioma de transitividad
•
Si: a x b ab 0 entonces:
Si: (a b) (b c) (a c); a, b, c
0 x 2 Max(a2 ,b2 )
C. Otros axiomas y teoremas de la desigualdad
a, b, c, d , se cumple:
•
•
•
Si: 0 a b entonces a a b b
2
•
Si: 0 a b entonces a ab b
a b ac bc
a bc dac bd
D. Propiedades de desigualdades entre medias
•
Si: a b c 0 ac bc
•
Si: a b c 0 a b
c c
•
Si: a b –a –b
Si: x1; x2; ... xn son números positivos, se define:
•
Media aritmética de x1; x2; ... ; xn
n
MA (x1; x2; ...; xn) = 1 x i
n i 1
•
Media geométrica de x1; x2; ...; xn
n
•
Si: 0 a b 0 c d 0 ac bd
•
a ;a2 0
MG (x1; x2; ...; xn) = n xi
i 1
•
Media armónica de x1; x2; ...; xn
n
MH (x1; x2; ... xn) =
•
ab 0 {(a 0 b 0) (a 0 b 0)}
•
ab 0 {(a 0 b 0) (a 0 b 0)}
n
1
x
i1
•
i
Media potencial de x1; x2; ...; xn
n
MP (x1; x2; ...; xn) =
•
a y 1 tienen el mismo signo a – {0}
a
•
Si a y b tienen el mismo signo y a b 1 1
a b
•
Si: ab 0 a x b 1 1 1
a x b
k
x ki
i 1
n
Entonces:
MP MA MG MH
Para dos números: a b, K
k
•
a b a2n–1 b2n–1 , n
•
0 a b a2n b2n, n
•
a b 0 a2n b2n; n
ak bk
a b
2
ab
2
2
1 1
a b
E. Recta numérica real
UNI SEMESTRAL 2013 - III
Es la recta geométrica donde se puede ubicar los
números reales, es decir, existe una correspondencia biunivoca entre el conjunto de los números
reales y esta recta.
16
ÁLGEBRA
TEMA 6
NÚMEROS REALES
Exigimos más!
, – son símbolos ideales, no son números rea-les, son simples representaciones.
problemas resueltos
UNI 2008 - II
Problema 1
Luego:
Sean a, b, c y d cuatro números reales
1 (c d) 1 (a b)
c
a
positivos tal que a – b = c – d y a < c.
Decir la verdad o falsedad de las siguientes afirmaciones:
I.
1
a c , si a b
b
d
II.
c a , si c d
d
b
III.
c a
b
d
Nivel fácil
n
d
b
1
c
a
A)
bd, ac
a c b d
a1n
(V)
ai
i1
n
n
ai
i 1
B)
a1
C)
a1 ai an
n
II. Si c < d a < b
UNI 2004 - I
Nivel fácil
A) FFV
B) FVV
C) FVF
III.
an
n
ca
d
ann
(F)
b
i1
a c
bd
D)
na
1
n
ai
na
n
i1
ab cd
ca
b d
(F)
E)
n
a1
a
ai n
n i1
n
D) VFV
Respuesta: E) VFF
E) VFF
Resolución:
Para un grupo de datos no todos iguales:
Resolución:
Problema 2
I.
Sean los números racionales a1, a2, ...,
Si a < c
1 1 ; si a b a b 0
c a
UNI SEMESTRAL 2013 - III
an tales que a1< a2 < ... < an–1 < an.
Entonces se cumple que:
17
a1
a1 a2 a3 ... an
an
n
ÁLGEBRA
TEMA 6
NÚMEROS REALES
Exigimos más!
n
•
ai
a1
i1
n
an
a, b números enteros,
es un número racional.
•
n
Si k y k2 es par, entonces k es
par.
ai
Respuesta: B) a1
ab
1 a2
i1
n
Número A / A Z B Z 0
racional B
b) Solución del problema
•
Es falso, cuando b = 0.
•
Es verdadero, porque en:
UNI 2009 - I
an
Nivel difícil
A) FVV
B) FFV
Problema 3
C) VFV
D) VFF
Clasifique como verdadero (V) o falso
E) FFF
ab
1 a2
•
Es verdadero:
o
2
K
2. K Z
(F) cada una de las siguientes afirmaciones:
•
a, b números enteros, a/b es un
número racional.
UNI SEMESTRAL 2013 - III
2
; (1 a 0)
o
Resolución:
a)
K 2
Aplicación de teorema
Recordar:
18
Respuesta: A) FVV
ÁLGEBRA
TEMA 6
ÁLGEBRA
INECUACIONES I
DESARROLLO DEL TEMA
I.
INECUACIONES DE SEGUNDO GRADO
Son aquellas inecuaciones de la forma:
I. ax2 + bx + c > 0
II. ax2 + bx + c > 0
III. ax2 + bx + c < 0
IV. ax2 + bx + c 0
D. Método de los puntos de corte
Donde: a 0 ;b, c
Sea: ax 2 + bx +c 0
A. Método de resolución de inecuaciones de segundo grado con una incógnita
P(x)
I. Método de completar cuadrados.
II. Método de la ley de signos de la multiplicación.
III. Método de los puntos de corte.
B. Método de completar cuadrados
Sea: ax2 + bx + c 0
1. El coeficiente de x2 debe ser 1, si no lo fuese
entonces se divide a ambos miembros entre a.
bx c
x2
0
a a
2. El término independiente se pasa al segundo
miembro.
x2 b x
c
a a
3. Se busca obtener un trinomio cuadrado perfecto,
sumando a ambos miembros la mitad del coeficiente de x elevado al cuadrado.
2
2. Aplicar uno de las teoremas siguientes:
I. ab 0 (a 0 b 0) (a 0 b 0)
II. ab 0 (a 0 b 0) (a 0 b 0)
III. ab 0 (a 0 b 0) (a 0 b 0)
IV. ab 0 (a 0 b 0) (a 0 b 0)
2
x 2 2(x) b b c b
a 2a
2a 2a
4. Escribiendo el primer miembro como un binomio
al cuadrado y reduciendo el segundo miembro.
Consideraciones previas
• En la resolución de una inecuación cuadrática
se transpone, si es necesario, todos los términos
a un sólo miembro de la desigualdad.
1. Factorizar la expresión cuadrática si es posible;
si no se puede factorizar aplicar la fórmula cuadrática.
2. Hallar los puntos de corte (valor de x) igualando
a cero el factor o los factores.
3. Ubica los puntos de corte en la recta numérica real.
4. Denotar las zonas o regiones determinadas por los
puntos de corte colocando los signos intercalados
empezando por la derecha con signo positivo.
5.
I. Si: P(x) > 0, el conjunto solución es la unión
de intervalos positivos (abiertos).
II. Si: P(x) 0 , el conjunto solución es la unión
de intervalos positivos (cerrados).
II. Si: P(x) < 0, el conjunto solución es el intervalo negativo (abierto).
IV. Si: P(x) 0 , el conjunto solución es el intervalo negativo (cerrado).
2
5. Finalmente:
x b b2 4ac
2a
4a2
Teorema
Sea: ax2 + bx + c > 0; a > 0
Si: b2 4ac 0
b
Se verifica para todo x diferente de
2a
C.S. : x b
2a
Teorema
Sea: ax2 + bx + c < 0; a > 0
Si: b2 4ac 0
No se verifica para ningún valor real "x".
C.S. : x
Teorema
x 2 m x m x m;m 0
x 2 m x m x m;m 0
C. Método de la regla de signos de multiplicación
Sea: ax2 + bx + c 0
1. Se factoriza el trinomio (factor común, diferencia de cuadrados, aspa simple)
UNI SEMESTRAL 2013 - III
19
ÁLGEBRA
TEMA 7
INECUACIONES I
Exigimos más!
Teorema
Sea: ax2 + bx + c > 0; a > 0
Si: b2 – 4ac < 0
Se verifica para todo valor real “x”.
C.S. : x
donde todos los ai son diferentes entre sí, para
luego aplicar: el método de los puntos de corte.
III. INECUACIONES FRACCIONARIAS
Son aquellas inecuaciones que reducida a su mas simple
expresión asume la siguiente forma general:
P(x)
0
Q(x)
Donde:
P(x) Q(x) son polinomios no nulos con coeficientes
reales.
Teorema
Sea: ax2 + bx + c < 0; a > 0
Si: b2 – 4ac < 0
La inecuación no se verifica para ningún valor real “x”.
C.S. : x
II. INECUACIONES POLINOMIALES
Resolución:
Son aquellas que presentan la siguiente forma general:
P(x) a0 xn a1xn-1 a2 xn-2 ... an-1x an 0
Se tiene: P(x)
0
Q(x)
Multiplicamos a ambos miembros por:
x Variable
a0; a1; a2; ... an Coeficientes
Q2 (x)
n Z n 2
• Reducir el polinomio mediante factorizaciones obteniendo la forma equivalente siguiente:
P(x) Q2(x)
0
Q(x)
Expresión reducida:
P(x) Q(x) > 0; no olvidando: Q(x) 0
Para luego utilizar el método de los puntos de corte.
x a1 x a2 ... x an 0
problemas resueltos
Problema 1
Halle el valor de a , para que la inecuación (a2 14) x 2 4x 4a 0 , tenga
como solución el conjunto [–2; 4].
UNI 2010-II
A) –6 B) –4 C) –2 D) –1 E) –1/2
De donde: 2 x x 2x x 0; x 0
Resolución:
(a2 – 14)x2 – 4x + 4a 0
Se debe cumplir que:
4
4a –8
2
2
2
a
–
14
a –14
De donde:
3x log3 x 3x log3 x 0; x 0
a 4 a –4
a 7 a –4
2
Por tanto: a = –4
Resolución:
Analizando:
x 2 2bx c 0
Resolviendo:
(2x–x)(3x–log3x)(x+3)(x–3)(3x–9) > 0
C.V.A. = Si: log3x R x > 0
x x
2
-x
x
3 (x 3)(3x 9) 0
3 -log3x
Respuesta: B) –4
Problema 2
Si el conjunto solución de la inecuación:
(2x – x) (3x – Log3x)(x2 – 9)(3x – 9) > 0
es de la forma: S a; b c; . Halle a + b + c.
UNI 2009-I
A) 0 B) 1 C) 2 D) 3 E) 5
Resolución:
(2x – x)(3x – log3x)(x2 – 9)(3x – 9) > 0
Resolviendo:
Luego: C. S.: C. V. A S1
S = 0; 2
3 ; +
a b
a+ b+c =5
x 3;5
Operando:
a) Aplicación de fórmula o teorema
•
•
Suma de raíces: x1 + x2 = b
a
c
Producto de raíces: x1x2
a
Reduciendo:
(x – 3)(3x – 9) > 0
(x 3 0 3x 9) (x 3 0 3x 9)
(x 3 x 2) (x 3 0 3 x 9)
x > 3 x < 2..... S1
c
Respuesta: E) 5
20
b) Solución del problema
–3 5 serán raíces de la ecuación:
x2 – 2bx – c = 0
Entonces:
x1 x 2 2 b 1
2b
x1 x 2 15 c 15
c
Problema 3
La inecuación x2 – 2bx – c < 0 tiene como
conjunto solución 3; 5 . Halle b + c.
UNI SEMESTRAL 2013 - III
UNI 2008 - II
A) 16 B) 18 C) 20 D) 22 E) 24
Conclusión
b + c = 16
Respuesta: A) 16
ÁLGEBRA
TEMA 7
ÁLGEBRA
INECUACIONES II
DESARROLLO DEL TEMA
I.
INECUACIONES IRRACIONALES
3°
Se denomina así a aquellas inecuaciones donde la
incógnita se encuentra bajo signo radical, los casos más
usuales son:
Luego: C.S. = S1 S2 S3
C.S.: [–2; 2>
A. Caso I
2n1 P(x)
Q(x)
C. Caso III
Donde P(x), Q(x) son polinomios; n N se resuelve:
2n+1
P(x)
Q(x)
Ejemplo:
(1) Resolver:
x + 2 < 6 –x
2x < 4
x<2
... (3)
3
x 2 1
P(x) Q(x)
Se resuelve el sistema construido a partir de:
P(x) 0
... (1)
Q(x) > 0
... (2)
P(x) < Q2(x) ... (3)
finalmente: C.S. S1 S2 S3
Resolución:
Se obtiene: x – 2 > 1
x>3
Ejemplo:
Resolver:
x 2 3
B. Caso II
2n P(x) 2n Q(x)
Es equivalente a resolver un sistema constituido a
partir de:
0 2n P(x) 2n Q(x)
Resolución:
1° x – 2 0
x 2
... (1)
2° 3 > 0
x R
... (2)
3° x – 2< 32
x < 11
... (3)
Así:
P(x) 0
Q(x) 0
P(x) Q(x)
... (1)
... (2)
... (3)
Luego: C.S. S1 S2 S3
C.S. = [2; 11>
D. Caso IV
finalmente: C.S. S1 S 2 S 3
P(x) Q(x)
Ejemplo:
(1) Resolver: x 2 6 x
Resolución:
1° x + 2 0
x –2
... (1)
2° 6–x 0
–x –6
x6
... (2)
UNI SEMESTRAL 2013 - III
Se resuelve:
P(x) 0
S1 P(x) 0 Q(x) 0 P(x) Q(x)
S2 P(x) 0 Q(x) 0
Finalmente: C.S. S1 S 2
23
ÁLGEBRA
TEMA 8
INECUACIONES II
Exigimos más!
problemas resueltos
Problema 1
Sea la igualdad:
i) x 0 : 0 1
C.S.i 0;
x a b x a b .....(*)
entonces la proposición verdadera es:
UNI 2009 - I
Nivel fácil
A) (*) si y solo si x 0 a2 b2
B) (*) si y solo si x = a = b
C) (*) si y solo si x 0 a b
D) (*) si y solo si x 0 a b
E) (*) si y solo si x = a = –b
Resolución:
a) Aplicación de fórmula o teorema
x y x y x y
b) Solución del problema
ii) x 0 : x - (-x) 1
B)
C)
D)
2x 1
1 2x 1
1
1
x pero x 0
2
2
II. Calculando el conjunto B (de la inecuación)
1
Como x A ;
2
i)
1
x 0 : 2x 1 1
2
1 2x 1 1
(x a b) x a b x a b (x a b)
2b 2a
2x 0
0 x 1 , pero
1
x 0
2
Conclusiones
ab x0
C.S.i
Otra solución
A)
E)
Resolución:
Ubicación de incógnita
Encontrar la gráfica de la relación.
Análisis de los datos o gráficos
y y x x
yx y x
Operación del problema
Si: x 0 y 0 y x y x
ii) x 0 : 1 1
Tenemos:
1 1
x ab x ab
(2x) (2b – 2a) = 0
C.S.ii 0;
x=0 a =b
C.S. C.S.i C.S.ii 0;
Recuerda: x y (x y)(x y) 0
B 0;
Problema 2
Sean los conjuntos:
A x / x x 1 y
Si: x 0 y 0 y x y x
2y 0 y 0
y
Calculando A–B
x
Si: x 0 y 0 y x y x
2x 0
B x A / x x 1 1
y
Entonces podemos decir que A\B es:
UNI 2009-II
Nivel intermedio
A)
1 1
B) ,
2 2
C)
1 , 0
2
1
D) 2 ;0
E)
0;
A B 1 ; 0
2
Si: x 0 y 0 y x y x
xy
y
Respuesta: D) 1 ;0
2
Problema 3
Dada la siguiente relación:
Resolución
B x A /
x
A x / x – x 1
y y x x
x – x –1 1
Operando:
I. Calculando el conjunto A (de la inecuación).
UNI SEMESTRAL 2013 - III
diga cuál de las siguientes gráficas es la
que le corresponde:
UNI 2010 - I
Nivel difícil
24
x
y
Luego:
x
y
Respuesta: D)
ÁLGEBRA
TEMA 8
x
ÁLGEBRA
INECUACIONES III
DESARROLLO DEL TEMA
I.
DEFINICIÓN
–
Generalizando:
|abc... n| = |a||b||c|...|n|
–
Estas dos propiedades antes mencionadas nos permiten
hacer lo siguiente:
– |3(x – 4)| = 3|x – 4|
Sea a , el valor absoluto se denota por |a|, el cual
se define por:
a;a 0
a =
–a;a 0
Ejemplos:
1. |4 – 2| =|2| = 2
2. |3 – 5| =|–2| = –(–2) = 2
II. PROPIEDADES
1. El valor absoluto de todo número real siempre es
un número no negativo. a 0
2. El valor absoluto de todo número real siempre es
igual al valor absoluto de su opuesto. a = – a
3. El valor absoluto de la multiplicación de dos números
reales es igual a la multiplicación de los valores
absolutos de los números en mención.|ab| = |a||b|
4. El valor absoluto de la división de dos números reales
(divisor es diferente de cero) es igual a la división
de los valores absolutos.
–
2|x + 2| = |2x + 4|
–
–2|x + 2| = –|2x + 4|
–
x +1 = x +1
3
3
–
x +2
x+2
= –
–3
3
Comentario
Esta propiedad va a ser de gran utilidad en el
trabajo de una ecuación e inecuación con un valor
absoluto.
7. Desigualdad triangular:
|a + b| |a| + |b|
I. Si|a + b|<|a| + |b|, entonces ab < 0.
II. Si|a + b| = |a| + |b|, entonces ab > 0.
a
a
=
;b0
b
b
5. Todo número al cuadrado, siempre es igual al valor
absoluto de la base elevado al cuadrado.
a2 = |a|2
6. La raíz cuadrada de todo número elevado al
cuadrado, siempre es igual al valor absoluto del
número.
a2 = a
a2n+1 = |a|2n.a
–
¡Tenga cuidado!
Teoría de exponentes
Números Reales
x2 = x
x
Generalizando:
|a + b| = |–a –b| ; |a – b| = |b – a|
UNI SEMESTRAL 2013 - III
a2n = |a|2n
x2 = x
x0
Nota:
– Hagamos la siguiente generalización:
x – a; x – a 0
x–a =
– x + a; x – a<0
–
Nota:
– Generalizando si n o:
321
ÁLGEBRA
TEMA 9
INECUACIONES III
Exigimos más!
III. ECUACIONES CON VALOR ABSOLUTO
A.
IV. INECUACIONES CON VALOR ABSOLUTO
Caso 1
A.
Caso 1
|x| = 0 x = 0
|x| a: a 0 (–a x a)
Ejemplo:
|x – 3| 5: 5 0 (–5 x – 3 5)
–2 x 8
Ejemplo:
• |x – 3|=0 x – 3 = 0 x = 3
B.
Caso 2
B.
|x| = a (a 0) (x = a a = –a)
Ejemplo:
• |x – 3| = 5
Si 5 0
x – 3 = 5 x – 3 = –5
x=8
x = –2
|x – 3| = –4
Si –4 0 (Falso)
C.S. =
Caso 2
|x| a: x a x –a
Ejemplo:
|x – 2| 3:
x – 2 3 x – 2 –3
x 5 x –1
C.
Caso 3
|x|
|y| (x – y)(x + y)
0
Ejemplo:
|x – 2| |2x – 3| (–x + 1)(3x – 5) 0
(x – 1)(3x – 5) 0
C.
Aplicando P.C.
Caso 3
|x| = |a| x = a x = –a
Ejemplo:
|x – 3| = |2x + 2|
x – 3 = 2x + 2 x – 3 = –2x –2
–5 = x
3x = 1
x=
5
x –;1 ;+
3
1
3
problemas resueltos
Problema 1
Resolución:
Resolución:
Resolver:
Aplicando el teorema:
Aplicando el teorema:
|x| a (a 0) (–a x a)
|2x + 6| = |x + 8|
Nivel fácil
|x| = a a 0 (x = a
x = –a)
Entonces:
2x–3 0 (3x+5=2x–3 3x+5=–2x+3)
3
(x = –8 5x = –2)
x
2
Resolución:
Aplicando el teorema:
x= –
|a|=|b| a = b a = –b
Entonces:
x+10 0 (–x –10 3x + 4 x + 10)
x –10 (–x–10 3x+4 3x+4 x+10)
–14 4x
2
5
7
x –10 – x
2
2x + 6 = x + 8 2x + 6 = –x–8
x= 2
3x = –14
14
x =–
3
2x 6
x 3
Como:
–8
3
(F)
2
7
x –10 – x 3
2
– 2 3 (F)
5 2
Intersectando:
14
Respuesta: C.S.= – ;2
3
Respuesta: C.S. =
Problema 3
Resolver: |3x + 4| x + 10
Problema 2
–
–7
2
–10
3
+
Resolver: |3x + 5| = 2x – 3
Nivel intermedio
Nivel intermedio
UNI SEMESTRAL 2013 - III
322
7
Respuesta: x – ; 3
2
ÁLGEBRA
TEMA 9
ÁLGEBRA
FUNCIONES I
DESARROLLO DEL TEMA
Por el diagrama del árbol
La palabra función se escuchará muy a menudo en la misma
vida diaria por ejemplo en las siguientes frases:
1.
2.
A
Los precios están en función a la oferta y la demanda.
El volumen de una esfera está en función del radio de
la misma.
Y así podría escucharse otras frases que nos dan una idea
intuitiva del concepto de una función, el concepto intuitivo
de función. "Es la relación de 2 ó más conjuntos bajo una
regla o ley".
El objetivo es esquematizar el concepto intuitivo en una
definición formal, pero antes daremos algunos conceptos
previos.
I.
m
n
B
AxB
p
(m,p)
q
(m,q)
r
(m,r)
p
(n,p)
p
(n,p)
q
(n,q)
r
(n,r)
Por el diagrama sagital o de Ven
PAR ORDENADO
A
B
m
p
q
Es un conjunto de 2 elementos denotado así: (a;b)
Donde:
a: se llama 1.a componente.
b: se llama 2.a componente.
Que formalmente se define así:
(a,b) = {{a}, {a, b}}
n
r
A B m,p , m,q , m,r , n,p , n, q , n,r
Por el diagrama cartesiano
Teorema:
(a,b) = (m,n) a = m b = n
II. PRODUCTO CARTESIANO
Dados 2 conjuntos A y B no vacíos el producto cartesiano de A y B denotado por A x B se define:
A xB
AB
a,b / a A b B
Ejemplo:
Sean A = m, n , B p, q,r
A x B = {(m,p), (m,q), (m,r), (n,p), (n,q), (n,r)}
B x A = {(p,m), (p,n), (q,m), (q,n), (r,m), (r,n)}
m,p , m, q , m,r , n,p , n,q , n,r
III. RELACIONES
Dados 2 conjuntos no vacíos, A y B se llama relación R
de A en B a todo subconjunto de A x B.
Ejemplo:
Sea A = {m, n}, B = {p, q,r}
Vemos que:
A xB B x A A B
UNI SEMESTRAL 2013 - III
A xB
25
m, p , m, q , m,r , n,p , n, q , n,r
ÁLGEBRA
TEMA 10
FUNCIONES I
Exigimos más!
Ejemplo:
Se citan las relaciones:
m,p , n,p , n,r
R 2 m,q , n,p , n,q
R 3 m, q
R1
f
A
IV. DEFINICIÓN DE FUNCIÓN
Una función f es una correspondencia entre 2 conjuntos A y B tales que a cada elemento a A le co-
B
m
1
n
2
p
3
q
7
Df = A m, n, p, q , Rf 1, 3
rresponde un único elemento de B.
Se llama función f al conjunto de pares ordenados
(a,b) que:
Observación:
Para cada a A, ! b B / a, b f asimismo:
Si: x, y f función de A en B
se denota, y = f(x), se dice:
a,b f (a, c) f b = c
y: es imagen de x bajo f.
Ejemplo
x: es la preimagen de x bajo f.
x: variable independiente.
y: variable dependiente.
C. Cálculo del dominio y el rango
El dominio se halla ubicando los posibles valores que
f
puede asumir la variable independiente. El rango,
3,a , 4, a , 5,b
dependiendo del dominio considera los valores de
Cumple la definición, por tanto f es una función.
la variable dependiente.
Ejemplo:
Ejemplo:
A
f
f
B
3
m
7
n
9
p
Halle el dominio y el rango en:
f x
3, m , 3,n , 7,p , 9,n
–
No se cumple la condición de unicidad.
–
No es función.
I)
25 x 2
x2 7
Df = x R / 25 x 2 0 x 2 7 0
2
= x R / x 5 x 5 0 x 7 0
x 5,5 x , 7
"No deben existir 2 o más pares ordenados con el
x 5 , 7
mismo primer elemento".
7;
Df = x 5 , 7
A. Dominio de una función
7 ,
7 ,5
Se llama así al conjunto de todas las primeras compoII)
nentes que coinciden con los elementos del conjunto de partida denotado por Df (dominio de f).
Df = { x A / !b B a,b f}}
Rf = R+0
D. Gráfica de una función
Se define como el conjunto de los pares (x,y)
x, y R x R / x Df Rf
B. Rango de una función
Es el conjunto de todas las segundas componentes
de todos los pares ordenados de f, denotado por
Así:
Rf (Rango de f ). Rf b B / a A a,b f
Sea: f
UNI SEMESTRAL 2013 - III
26
A
B
C
D
E
3,5 , 2, 2 , 1,2 , 4,3 , 5, 4
ÁLGEBRA
TEMA 10
FUNCIONES I
Exigimos más!
•
Si los pares son continuos la gráfica obtenida
es una línea.
E. Propiedad de las funciones reales
f es una función real de variable real si y solo si cada
recta vertical corta a lo más en un punto a su gráfica.
Ejemplo:
Observación:
•
Si tanto la variable independiente "x" y la variable
dependiente "y" son reales se llama función real
en variable real.
problemas resueltos
Problema 1
El rango de la función f : 0
definida por: f(x) x 1 es:
x
UNI 2008 - I
A)
UNI 2007 - II
A)
2, 2
B)
2, 2
C)
1, 1
D)
1, 1
E)
0
Restando 2:
Halle el rango de f .
13 ; 7
5
5
Por 5:
13 7
5 ; 5
C)
7 13
5 ; 5
x 2 7
13 5
f (x)
D) [7;13
Luego:
E)
7 f(x) 13
7;13]
Rg f 7;13
Sabemos:
Resolución:
x1 2; x 0
x
Piden: Rango de
f(x) 2 f(x) 2
Ranf = ; 2 2 ; 2;2
Respuesta: A) 2, 2
13
7
x2
5
5
B)
Resolución:
x 1 2 ; x 0
x
32x2 32
5
5
f .
Respuesta: D) 7;13
Siendo:
f(x)
5x2 7x 6
3
x
5
Tenemos:
f(x)
5(5x 3)(x 2)
5x 3
Problema 3
En la figura adjunta se muestra las gráficas de las funciones f y g definidas
por:
f(x) = ax2 + bx + c
g(x) = mx2 + nx + p
Reduciendo:
Problema 2
Dada la función:
2
f(x) 5x 7x 8
x3/5
definida sobre 3 , 3 .
5 5
UNI SEMESTRAL 2013 - III
f(x) 5(x 2)
3 3
Si: x ; , entonces:
5 5
3 x 3
5
5
27
ÁLGEBRA
TEMA 10
FUNCIONES I
Exigimos más!
De las siguientes relaciones:
I.
II.
n2 4mp
a b
m n
III. abc mnp
¿Cuáles son verdaderas?
A) Solo I
B) Solo II
C) Solo III
D) I y II
E) II y III
UNI SEMESTRAL 2013 - III
Resolución:
xb
b2 4ac
b3 4abc
Del gráfico: f y g tienen raíces reales e
iguales.
I.
0 para g n2 – 4mp = 0
2
n 4mp
xn
n2 4mp
n3 4mnp
De la segunda proposición se deduce:
a mb n
II. Como tienen vértices iguales entonces:
– b – n a b
2a
2m m n
b3 n3 es decir abc mnp
Solo I y II son verdaderas.
III. a > m, ya que f es más cerrada
Respuesta: D) I y II
que g. Siendo:
28
ÁLGEBRA
TEMA 10
ÁLGEBRA
FUNCIONES II
DESARROLLO DEL TEMA
I.
FUNCIONES ESPECIALES
A. Función identidad
E. Función signo (sig.x)
1 x 0
y Sig x 0 x 0
1 x < 0
B. Función constante
F. Función máximo entero
C. Función valor absoluto
f x x n n x n 1,n Z
x x 0
f x x 0 x 0
x x < 0
2 2 x 1
1 1 x 0
f x x 0 0 x 1
1 1 x 2
2 2 x 3
y
2
1
-2
D. Función escalón unitario
-1
O
0, x a
U x
1, x a
UNI SEMESTRAL 2013 - III
1
-1
-2
29
ÁLGEBRA
2
3
Df=R
Rf=z
TEMA 11
FUNCIONES II
Exigimos más!
G. Función inverso multiplicativo
f x 1
x
I. Función potencial
f x xn / n N
/ x 0 ; f x 1/ x; x 0
II. TRAZADO DE GRÁFICAS ESPECIALES
H. Función polinomial
En esta sección veremos una forma rápida de construir
1. Función lineal
las gráficas de algunas funciones definidas a partir de
f x ax b ; a 0
otras cuyas gráficas se asumen conocidas. En este sentido, dada la gráfica de una función de base y = f(x)
veremos primero la forma de construir rápidamente las
gráficas de las funciones siguientes:
1. g(x) = f(x) + k; g(x) = f(x - h); g(x) = f(x-h)+k
2. g(x) = -f(x);
g(x) = f(-x);
g(x) = -f(-x)
3. g(x) = af(x);
g(x) = f(ax); ( a 0 )
4. g(x) = |f(x)|;
5. g(x) = f(x)
y
[Todas en base a la gráfica y = f(x)]
2. Función cuadrática a 0
f x ax 2 bx c; de raíces x1, x2
(1a) La gráfica de g x f x k se obtiene despla-
Discriminante: = b2 – 4ac
zando verticalmente la gráfica de y = f(x) en |k| unidades:
i) Hacia arriba, si k > 0
ii) Hacia abajo, si k < 0
y
g(x) = f(x)+2
y = f(x)
2
h(x) = f(x)-2
O
x
-2
3. Función cúbica
f x ax 3 bx 2 cx d
Reemplazando x por x b se transforma en:
3a
k x 3 px q
(1b) La gráfica de g x f x h se obtiene desplazando horizontalmente la gráfica de y = f(x) en h uni-
dades:
i) Hacia la derecha, si h > 0
ii) Hacia la izquierda, si h < 0
f1 x x 3 px q , de raíces x1, x 2, x 3 llama-
mos discriminante:
2
q p
2 3
3
pues si f(x) = x2, entonces:
f(x – 4) = (x – 4)2 = g(x)
f(x + 3) = (x + 3)2 = j(x)
Donde en el caso de: j(x) = (x + 3)2 [x – (–3)]2 se
tiene que: h = –3 (<0). Tenemos la gráfica correspondiente a continuación:
UNI SEMESTRAL 2013 - III
30
ÁLGEBRA
TEMA 11
FUNCIONES II
Exigimos más!
Ejemplo:
Como ilustración de los resultados anteriores. Hallaremos
la gráfica de: y = g(x) = –(x – 2)2 + 1
Resolución:
Sean f(x) = (x + 2)2 – 1, entonces:
f(–x) = [(–x) + 2]2 – 1 = (x – 2)2 – 1
–f(–x) = –x(x – 2)2 + 1
Luego y = g(x) = –f(–x):
(1c) La gráfica de g x f x h k se obtiene com-
y
binando (1a) y (1b) en cualquier orden.
3
y
2
y=f(-x+2)-1
2
f(x)=(x+2)-1
-2
-4 -3
2
y=(x-7)
y=f(x)=x2
2
1
-1
0
1
=(x-2)-1
1
2 3
4
7
O
x
2
x
-3
g(x)=-(x-2)+1=-f(-x)
2
g(x) = (x-7)-3
y=x2-3
Note que pudimos haber graficado esta parábola di-3
rectamente, claro.
(7;-3)
(2a) La gráfica g x f x se obtiene por reflexión
(3a) La gráfica de y a f x . a 0 , se obtiene:
de la gráfica de y = f(x) sobre el eje x. Considerando a
i)
Estirando la gráfica de y = f(x) verticalmente en
un factor a, si a > 1, con base en el eje X.
este eje como doble espejo.
Todo lo que está encima del eje X pasa abajo, y viceversa.
y
ii) Si: 0 < a < 1, escogiendo la gráfica de: y = f(x)
verticalmente en un factor a.
(3b) La gráfica de y f ax , a > 0, se obtiene:
-f
y=-f(x)
i)
en un factor a, si a > 1, con base en el eje Y.
x
O
f
Encogiendo horizontalmente la gráfica de y = f(x)
ii) Estirando horizontalmente la gráfica de y = f(x) en
y=f(x)
un factor a, si 0 < a < 1.
(2b) La gráfica
y f x
se obtiene por reflexión
Gráfica de: y = |f(x)|
de la gráfica de y = f(x) sobre el eje y considerando a
Desde que:
este eje como doble espejo.
Todo lo que está encima del eje y, pasa abajo y viceversa.
f x , si f x 0
y f x
f x 0
f(x), si f x 0
y
y=f(x)
f(x)=f(-x)
y=-f(x)
Entonces la gráfica de: y f(x) se encontrará completamente en el semiplano superior y 0 y se obtiene a
-x
O
x
partir de la gráfica de la función y = f(x); reflejando
x
hacia arriba del eje x todo lo que este debajo de este
eje, quedando intacta la parte de la gráfica de: y = f(x)
(2c) La gráfica de
y f x se obtiene combinado
que originalmente ya se encontraba arriba o en el mismo
eje x (es decir, en la zona y 0).
(2a) y (2b).
UNI SEMESTRAL 2013 - III
31
ÁLGEBRA
TEMA 11
FUNCIONES II
Exigimos más!
problemas resueltos
Problema 1
Sea P(x) = x3 – 3ax2 – a2x + 3a3, donde
a > 0 y Q(x) = –P(x – a). Diga cuál de
las siguientes afirmaciones es correcta:
UNI 2009 - II
Nivel fácil
A) Q(x) P(x); x 0
Problema 2
B) Q(x) P(x); x 0; a
A)
[0;
C) P(x) Q(x); x a;2a
B)
[1;
D) Q(x) P(x); x 2a; 3a
C)
0;
E) P(x) Q(x); x 3a
D)
[4;
Resolución:
Graficando la función P(x):
E)
1;
Sea f una función tal que:
f x 2 x 2 x 4 x ;x 4
B)
entonces Dom(f) Ran(F) es igual a:
Nivel 2009 - II
Nivel intermedio
C)
D)
Resolución:
Esbozando la gráfica de: x 2 x
(por álgebra de funciones)
2
E)
2
P(x) (x a )(x 3a)
P(x) (x a)(x a)(x 3a)
Resolución:
Tenemos:
La expresión:
x 2 x es inyectiva.
Graficando la función: Q(x) = –P(x – a)
Dom(f ) = 0;
Analógicamente la expresión:
2 x 4 x
De donde:
es inyectiva:
2 x 4 x 4;
Esbozando ambas gráficas:
Ran(f ) =
4;
Dom(f )nRan(f) = 0;
Respuesta: A) 0;
Luego:
Problema 3
Indique la gráfica que mejor representa a:
g(x)
x2 4 3 , x
Para x 2a; 3a la gráfica de la función
UNI 2008 - II
Q(x) está en la parte superior del P(x).
Q(x) P(x); x 2a; 3a
Nivel difícil
Respuesta:
D) Q(x) P(x); x 2a; 3a
UNI SEMESTRAL 2013 - III
Respuesta: D)
A)
32
ÁLGEBRA
TEMA 11
ÁLGEBRA
FUNCIONES III
DESARROLLO DEL TEMA
I.
Son funciones impares:
a) f(x) = x3
b) f(x) = sen x
c) (x) = 1/x
FUNCIONES PARES, IMPARES Y PERIÓDICAS
A. Función par
Una función f se llama función par si:
i) x Domf x Dom f
Una función que es a la vez par e impar es, por
ejemplo:
f(x) = 0, x 5 , 2 2 ,5 .
ii) f (–x) = f(x)
En este caso la regla de correspondencia y = f(x)
no varía si se reemplaza x por –x. Geométricamente,
la gráfica es simétrica respecto al eje y.
y
-5
-2
0
2
5
x
C. Funciones periódicas
Una función f, en R, se denomina función periódica
si existe un número real T 0, tal que:
i)
x Domf x T Dom f
ii) f (x + T) = f(x) . x Dom f
Así tenemos que las funciones f(x) = x2, f(x) = Cosx,
f(x) = x4, son funciones pares.
Tal número T es llamado un periodo de T.
y
B. Función impar
Una función f se llama función impar, si:
i) x Domf x Dom f
ii) f (–x) = –f(x)
f(x)
0
Aquí la regla de correspondencia y = f(x) no varía si
se reemplaza simultáneamente tanto x por – x como
y por – y. Por lo tanto, su gráfica es simétrica respecto al origen.
y
f
f(x)
-x
0
x
x
x+T
T
x+2T x+3T
x
Note que f(x+T) = f(x)
Toda función periódica con periodo T tiene su gráfica de modo tal que la misma forma que tiene en
un intervalo de longitud T se repite horizontal y
periódicamente en el siguiente intervalo consecutivo de longitud T.
Note que si T es un periodo de f, entonces 2T, 3T...
también son periodos de f.
Las funciones seno y coseno tienen periodo T = 2 :
Sen(x + 2 ) = Senx . Cos(x + 2 ) = Cosx; x R
f(-x)=-f(x)
UNI SEMESTRAL 2013 - III
x
33
ÁLGEBRA
TEMA 12
FUNCIONES III
Exigimos más!
También vemos que: 2 . 4 . 6 ... 2k
2. Multiplicación "f . g"
con k entero 0, son periodos de seno y coseno,
siendo 2 el menor periodo positivo.
i) Dom (fg) = Dom f Dom g
ii) (f . g)(x) = f(x) g(x)
Definición
Se llama periodo mínimo de una función periódica
f g x, f x g x / x Dom f Dom g
II. ÁLGEBRA DE FUNCIONES
A. Igualdad de funciones
Notación
Dos funciones f y g son iguales si:
i)
f g x f x g x / x Dom f Dom g
al menor de sus periodos positivos.
La multiplicación de una función por sí misma:
Dom f = Dom g
f 2 f : f : f n f.f...f (n veces), n
ii) f(x) = g (x), x Dom f
Donde:
En tal caso se denota f = g.
Dom(fn) Dom f Dom f ... Domf Dom f
Así tenemos que las funciones:
Por lo tanto: el dominio de cualquier potencia
f(x) = x2 –x, x 0, 4 ; g(x) x 2 x, x 0,5
entera positiva de f tiene el mismo dominio de
la función f.
No son iguales, pues aunque tienen la misma regla
Así:
de correspondencia, sus dominios no coinciden.
f2
B. Adición de funciones
x, f x .f x / x Dom f
Asimismo:
Recordemos que una función está completamente
c .f
definida cuando se especifica su dominio y su regla
x,c f x / x Dom f
para cualquier constante real c.
de correspondencia.
C. División de funciones
Definición: si f y g tienen dominios Dom f y Dom g,
Si f y g son funciones con dominios Dom f y Dom g,
se define una nueva función llamada.
se define la nueva función "cociente" denotada por
"f/g", tal que:
Función Suma
i)
Dom (f/g) = Dom f x Dom g / g(x) 0
"f + g", tal que:
i)
= Dom f Dom g x Dom g / g(x) 0
Dom f g Domf Domg
ii) (f + g)(x) = f(x) + g(x)
ii)
C. Sustracción y multiplicación de funciones
Si f y g tiene dominios Dom f y Dom g, se definen
f x
f / g x g
x
, x Dom (f / g)
La condición (i) exige que el dominio de f/g no
las funciones:
debe contener los valores de x que hagan que
g(x) = 0.
1. Diferencia "f – g"
Es así, que:
i) Dom f g Dom f Dom g
f x
f / g x,
/ x Dom f / g
g x
ii) (f – g)(x) = f(x) – g(x)
UNI SEMESTRAL 2013 - III
34
ÁLGEBRA
TEMA 12
FUNCIONES III
Exigimos más!
problemas resueltos
Problema 1
III. F par: F(–x) = F(x)
Indique la secuencia correcta después
G par: G(–x) = –G(x)
de determinar si la proposición es ver-
(F G)(x) F(x) G(x)
dadera (V) o falsa (F):
I.
La composición de una función par
(F G)(x) F( x) G( x)
con una función impar es una fun-
(F G)(x) F(x) G(x)
ción par.
(F G)(x) (F G)(x)
Resolución:
Ubicación de incógnita
Determinar f + g
Análisis de los datos o gráficos
f : y f(x) x 2 2
II. El producto de dos funciones im-
y f(x)
F G es par _ _ _ _ _ _ _ (V)
pares es una función impar.
g y g(x) x2 2
III. La suma de dos funciones pares
Respuesta: A) VFV
es una función par.
Operación del problema
UNI 2011 - I
A) VFV
B) VV V
x2 x 2 ; x 2
2
x x 2 : x 2
y f(x) g(x)
Problema 2
C) FVV
Dadas las funciones f, g: , de-
D) FFV
finidas por:
f(x) x 2 2 y g(x) = –(x2 + 2)
E) VFF
Determine f + g.
Resolución:
A)
2
x 1 7 , x 2
2
4
2
1
9
x 2 4 , x 2
B)
x
x
Valor de verdad
Operación del problema
F par : F(x) F(x)
G impar : G(x) – G (x)
(FoG)(x) F(G(x))
Ahora:
(FoG)(x) F(G( x))
(FoG)(x) (FoG)(x)
2
1
1
,x 2
2
4
C)
G impar: G(–x) = –G(x)
D)
(F.G)( x) F( x) G( x)
(F.G)(x) – F(x) – G(x)
(F.G)(x) F(x) G(x)
(F.G)( x) (F.G)(x)
F . G es par _ _ _ _ _ _ _ _ _ (F)
UNI SEMESTRAL 2013 - III
9
; x 2
4
2
1
7
x
;x 2
2
4
Respuesta: A)
2
1
9
x 2 4 ; x 2
Problema 3
Sea f una función tal que:
f(x 2 x ) 2(x 4 x ), x 4
2
1
5
,x 2
2
4
2
1
x
2
2
1
x 2
entonces Dom(f) Ran(f) es igual a:
A)
9
,x 2
4
7
,x 2
4
II. F impar: F(–x) = –F(x)
(F.G)(x) F(x) G(x)
7
; x 2
4
UNI 2009 - II
(FoG)(x) F(G(x))
F o G es par _ _ _ _ _ _ _ _ _ (V)
1 2
x 2
y f(x) g(x)
1 2
x 2
UNI 2010 - II
Ubicación de incógnita
I.
xx; x4 ; x 22
E)
x 1 2 7 , x 2
4
x 1 2 1 , x 2
4
2
1
1
x , x 2
2
4
2
1
7
x 2 4 , x 2
35
B)
0;
1;
C)
0;
D)
4;
E)
1;
Resolución:
Ubicación de incógnita
Dom(f); Ran(f)
Análisis de los datos o gráficos
x
f x
2
x 2
4;x 4
Rango
Do min io
ÁLGEBRA
TEMA 12
FUNCIONES III
Exigimos más!
Operación del problema
La expresión:
x 2 x
Esbozando la gráfica de: x 2 x
(por álgebra de funciones)
es inyectiva.
2 x 4 x 4;
Ran(f ) =
4;
Dom(f ) = 0;
Analógicamente la expresión:
Dom(f)nRan(f ) = 0;
2 x 4 x ,
Respuesta: A) 0;
es inyectiva:
UNI SEMESTRAL 2013 - III
36
ÁLGEBRA
TEMA 12
ÁLGEBRA
FUNCIONES IV
DESARROLLO DEL TEMA
I.
COMPOSICIÓN DE FUNCIONES
Ejemplo:
Dadas 2 funciones f y g la función composición deno-
f(x) 4x 3 , x 15, 22
tado por fog se define así:
•
fog = {(x;y)|y = f(g(x))}
g(x) 3x 1, x 7,14
•
Dfog = x Dg g(x) Df
•
(fog)(x) = f(g(x)) = 4(3x – 1) + 3 = 12x – 1
•
Dfog x 7,14 3x 1 5,22
Esquematizando con el diagrama sagital:
x 16 , 23
3 3
x 7, 23
3
fog(x) 12x 1 / x 7, 23
3
Propiedades de la composición de funciones
Dadas las funciones f, g, h, I (identidad)
Ejemplo:
f = {(3;5), (4;3), (5;2)}
I.
(fog)oh = fo(goh) [asociativa]
II.
Si I es la función identidad: función f:
g = {(5;3), (3;5), (7;2)}
foI = f Iof = f
III. (f + g)oh = (foh) + (goh)
IV.
(fg)oh = (foh) . (goh)
V.
fog goh, en general
VI. InoIm = Inm; n,m, Z+
VII. Ino(f + g) = (f + g)n, n Z+
1
VIII. I n oIn | I |, para n par Z+
1
IX.
fog = {(5;5), (3;2)}
UNI SEMESTRAL 2013 - III
37
1
I n o In In o I n I , n Z+, impar
ÁLGEBRA
TEMA 13
FUNCIONES IV
Exigimos más!
B. Función suryectiva (epiyectiva)
II. FUNCIÓN INVERSA
Definiciones previas.
Sobreyectiva o sobre. Se dice suryectiva si el conjunto de llegada queda cubierto por el rango de ese
A. Función inyectiva
modo coincidiendo el rango y el conjunto de llegada.
Llamada también univalente o uno a uno, se dice
inyectiva si a cada elemento del rango le corresponde
un único valor del dominio.
Formalmente: f es inyectiva si para:
x1; x 2 Df
x1 x 2 f(x1) f(x 2 )
Equivalentemente:
f(x1 ) f(x 2 ) x1 x 2
Ejemplo:
Ver f(x) x 1 es inyectiva.
x 1
C. Función biyectiva
Una función se dice que es biyectiva si es inyectiva
Resolución:
y suryectiva a la vez.
Sean x1 ; x 2 Df
III. DEFINICIÓN DE FUNCIÓN INVERSA
Si: f(x1) = f(x2)
x1 1 x 2 1
x1 1 x 2 1
Dada una función f x, y / y f x inyectiva se
x1 x 2
define la función inversa denotado por f* como lo que:
f*
f es inyectiva.
y; x / y f(x) x Df
De donde:
Teorema
Df* = Rf, Rf* = Df
f es inyectiva si todo vector horizontal corta su
gráfica a lo más en 1 punto.
Ejemplo:
Ejemplo:
Halle la inversa de f(x) x 1 si existe.
x 1
Resolución:
Se ha visto que es inyectiva, es a su vez suryectiva.
su inversa
Para hallar la inversa se despeja "x".
x
f x 1
f x 1
f x x
f x x 1
x 1
Df* = R – {1} ; Rf* = R – {1}
IV. GRÁFICA DE LA FUNCIÓN INVERSA
Conociendo la gráfica de la función f(x) la gráfica de
f*(x) se obtiene reflejando en el eje de la función
identidad, así:
UNI SEMESTRAL 2013 - III
38
ÁLGEBRA
TEMA 13
FUNCIONES IV
Exigimos más!
Propiedades:
x, y / y f x , x Df y f x
f* y, x / y f x , x Df x f * y
f
y f x
I.
f * y x
x DF
f * f x x; x Df
II.
III. (fog)* = g* o f*
f f * y y; x Df* Rf
IV. (f*)* = f
problemas resueltos
Problema 1
Resolución:
Problema 2
Sean A y B conjuntos no vacíos, señale
I.
Verdadero
Dadas las funciones:
De acuerdo a la condición de unici-
f = {(3, 1); (2, –3); (5, 0); (4, –4);
la alternativa que presenta la secuencia
correcta, después de determinar si la
proposición es verdadera (V) o falsa (F):
I.
(1, 1)}
dad esta proposición es perfectamente válida.
g = {(–4, 3); (–2, 7); (0, 0); (1, 5);
Si:
(2, 1)}
(x, y);(x,z) f {(x, y)/x A, y B} AxB
implica que y = z, entonces podemos decir que f es una función
h = {(1, –4); (3, –2); (5, 0); (7, 2)}
II. Falso
No necesariamente, por ejemplo:
F : 1; 2 0; 4
de A en B.
II. Toda función sobreyectiva f:A B
es inyectiva.
y F(x) x2
Determine la función compuesta f o g
o h.
Es una función sobreyectiva, pero
UNI 2010-I
no es inyectiva.
Nivel intermedio
III. Toda función inyectiva f: A B es
A) {(1, 0); (5, 1)}
sobreyectiva.
III. Falso
A) VV V
B) {(3, –3); (5, –4)}
No necesariamente, por ejemplo:
B) VFV
F : 1; 3 2; 4
C) VFF
y F(x) 2x 1
Es una función inyectiva, pero no
D) FFV
C) {(1, 1); (7, 1)}
D) {(1, 1); (2, –3)}
E) {(3, –1); (7, 1)}
es sobreyectiva.
E) FFF
Resolución:
UNI 2010-I
Nivel fácil
UNI SEMESTRAL 2013 - III
Respuesta: C) VFF
39
f={(3;1), (2;–3), (5;0), (4;–4), (1;1)}
ÁLGEBRA
TEMA 13
FUNCIONES IV
Exigimos más!
g={(–4;3), (–2;7), (0;0), (1;5), (2;1)}
Halle todos los valores que puede
h={(1;–4), (3;–2), (5;0), (7;2)}
tomar K para que la gráfica de la función f y de su inversa sea la misma.
Calculando goh:
UNI 2010-I
goh = {(1;3), (3;7), (5;0), (7;1)}
Nivel difícil
f = {(3;1), (2;–3), (5;0), (4;–4), (1;1)}
fo(goh) = {(1;1), (7;1)}
Respuesta: C) {(1;1), (7;1)}
A)
1;2
B)
0 ;1
C)
1 ;1
D)
0 ;
f(x) K
1 ; x K
x K
UNI SEMESTRAL 2013 - III
E)
y K
1
; x K
x K
x K
1 x K 1 ; y K
y K
y K
f * (x) K
1 ; x K
x K
f(x) f * (x)
Lo cual se cumple para cualquier valor
Problema 3
Dada la función:
Resolución:
real de K, es decir: K ; .
Respuesta: E) ;
;
40
ÁLGEBRA
TEMA 13
ÁLGEBRA
LOGARITMOS EN
DESARROLLO DEL TEMA
I.
TEOREMA DE EXISTENCIA DEL LOGARITMO
•
Para todo par de números reales "a" y "b" tales que
a 0; a 1 y b 0 , existe un único número real x, que
cumple ax = b.
3 2
Log
3
2
2
1
2
IV. TEOREMAS SOBRE LOGARITMOS
Sea la base real a, tal que a 0 a 1
1. Sea A y B reales, tal que: AB > 0:
II. DEFINICIÓN DE LOGARITMO
Sean los números reales "a" y "b", si a 0, a 1 y b 0,
el número real x se denomina logaritmo del número b
en base a y se denota por Logab si y solo si ax b .
De la definición se tiene:
Loga AB Loga A Logb B
2. Sea A y B reales, tal que: A 0
B
x Logab a x b
Loga A Loga A Logb B
B
Donde:
a: base del logaritmo
b: número del logaritmo
c: logaritmo de b en la base a
3. Sea A real, tal que n N An 0 .
Loga An nLoga A
4. Sea A real, tal que n N, n 2. Si A 0
Ejemplos:
Loga n A 1 Loga A
n
1. Log264 x 64 2x 26 2 x x 6
Luego: Log2 64 6
5. Sea A real, tal que: A 0, m n
x
2. Log 1 729 x 729 1 36 3x x 6
3
Log n Am m Loga A ; n 0
a
n
3
Luego: Log 1 729 6
Colorario
Si se eleva a un exponente "m" y se extrae raíz
n-ésima a la base y número del logaritmo el valor
de logaritmo no se altera.
3
3. Calcular el valor de "x" si cumple la igualdad:
Log1 /2 1024 3 x
1024 1
2
x 13
3 x
210 2x 3 10 x 3
Loga A Log
2LOg23 3
(m 4)
Logab
10, m 4 m 5
UNI SEMESTRAL 2013 - III
A ; A0
7. Cambio de base:
Sea la base "c" donde c 0 c 1.
Ejemplos:
•
n
a
Loga A LogaB A B
Si a 0; a 1 b 0 se cumple: aLogab b
Logm 410
An Logn
6. Si: A 0 B 0
III. IDENTIDAD FUNDAMENTAL DEL LOGARITMO
•
an
41
ÁLGEBRA
Logc b
Logc a
TEMA 14
LOGARITMO EN R
Exigimos más!
Demostración:
Por identidad: c
logc b
1. Sistema decimal o de Briggs
Es aquel sistema de logaritmos en la cual la base
es 10.
b (1)
Por identidad: aloga b b (2)
Además: c logc a a (3)
Reemplazando (3) en (2) se obtiene:
c
logc a
loga b
Notación: Log10N LogN
Se lee: Logaritmo de "N". En general:
c logc b logc a loga b logc b
LogN
logc b
loga b
; Logb a Logab 1
logc a
Parte
;
entera
(característica)
Parte
decimal
(mantisa)
A. Propiedad
Logba ( Logba) 1
2. Sistema hiperbólico o Neperiano
Es aquel sistema cuya base es el número trascendental:
1
loga b
1
1 1
1
...
0! 1! 2! 3 !
e 2, 7182....
e
B. Regla de la cadena
Si: a 0; a 1; b 0; b 1; c 0; c 1 d 0 se
cumple:
Notación: LogeN LnN
loga b logb c logc d loga d
Teorema
Sea todo N > 1 el número de cifras es igual a la
característica más uno. Es decir:
C. Sistemas de logaritmos
Cada base de logaritmos determina un sistema de
logaritmos, en consecuencia existen infinitos sistemas de logaritmos para una base positiva y diferentes de 1; los sistemas más importantes son:
# de
N
cifras
característica 1
problemas resueltos
Problema 1
Calcular el logaritmo de 8 en base 4.
A) 1/2
B) 2
C) 3/4
D) 3/2
A) {1}
B)
34
E)
52
D)
C)
12
E) 5/2
Resolución:
Según teorema tenemos:
Resolución:
x 1 1 x
2x 2
x 1
Sea "" el logaritmo pedido, luego:
Log4 8 =
Según la definición:
Pero según definición de base x > 0;
x 1.
4 8
22 23
2 3
3
2
A)
B) 10
10
C) 100
E)
D)
1000
10 2
Resolución:
Según propiedad tenemos:
LogxLog(x) Log(x) 2
2
[Log(x)] Log(x) 2 0
Con el auxilio del aspa simple conseguimos:
[Log(x) – 2] [Log(x) + 1] = 0
CS
Log(x) = 2 log(x) = –1
Respuesta: C)
Respuesta: D) 3/2
xLogx (x 1) 1 x
Problema 3
Determine el mayor valor de x en:
LogxLog( x) = Log(x) + 2
UNI 2007 - I
Nivel difícil
UNI SEMESTRAL 2013 - III
42
Problema 2
Resolver:
x = 102 x = 10–1
1
x = 100 x =
10
Mayor valor de x = 100
Respuesta: C) 100
ÁLGEBRA
TEMA 14
ÁLGEBRA
FUNCIÓN EXPONENCIAL
Y LOGARITMOS
DESARROLLO DEL TEMA
I.
FUNCIÓN LOGARÍTMICA
y
x y=Log 2 x
A. Definición
+1/4
1/2
1
2
4
8
Dado un número real b (b 0; b 1) llamamos
función logarítmica de base b a la función de f de
R+ en R que asocia a cada x el número de Logbx.
En símbolos:
F : | y f(x) logb (x)
4
3
2
1
-2
+1
0
1
2
3
(8,Log28)
(5,Log25)
Log 5 Log28
2
1 2 3 4 5 6 7 8 9
-1
-2
-3
-4
x
Ejemplos:
A) f(x) = Log2x
B) g(x) Log1 x
Nótese que: 5 < 8 y Log25 < Log28
En general si b > 1 la gráfica tiene la forma
siguiente:
2
C) h(x) = Logx
D) p(x) = Ln x
Observaciones
a) y Logbx x by
y=Log x
b
De donde concluimos que las funciones exponenciales y logarítmicas son inversas una de
la otra.
Log r Logbs
b
m
b) Para la función y f x Logbx
1
Log m
Dominio Df 0, x 0
b
r
es una
función
creciente
s
Rango Rf R y Logbx R
Propiedades
1. f(1) = Logb1 = 0, es decir el par ordenado
(1,0) pertenece a la función.
2. Si: r < s entonces Logbr < Logbs.
3. Si: r > 1 entonces Logbr > 0.
4. Si: 0 < m < 1 entonces Logbm < 0.
B. Gráfico de la función logaritmo
1. Caso I
Si b > 1.
Ejemplos:
A) f(x) = Log2x
2. Caso II
Si 0 < b < 1.
B) g(x) = Logx
C) h(x) = Log4x
D) p(x) Log 2 x
Ejemplos:
A) f(x) Log1 x
Graficaremos:
B) g(x) Log
1
2
C) h(x) Log 3 x
y f x Log2 x
UNI SEMESTRAL 2013 - III
4
43
ÁLGEBRA
x
3
D) p(x) Log1 (2x)
5
TEMA 15
FUNCIÓN EXPONENCIAL Y LOGARITMOS
Exigimos más!
Graficaremos:
•
y f x Log1 x
•
2
El dominio de esta función es todos los reales,
es decir: Df , R .
Por propiedad: si x R y a 0 .
entonces: a x > 0, por tant o el rang o es:
Rf 0,
B. Gráfico de la función exponencial
x y=Log 2 x
8
4
2
1
1/2
1/4
1. Caso I
Si a > 1.
-3
-2
-1
0
1
2
Ejemplos:
x
A) f(x) 2
B) g(x) 3x
C) h(x) ( 3)
E) q(x) 3
2
En general: si 0 < b < 1, la gráfica tiene la forma
siguiente:
x
x
D) p(x) 10
x
5
F) r(x)
4
x
Graficaremos: y = f (x) = 2x
y
x
-3
-2
-1
0
1
2
3
Logbm
r
m 1
s
Logbr
x
Log s
b
y= Logbx
y=2
y
8
7
6
5
4
3
2
1
x
1/8
1/4
1/2
1
2
4
8
y=2
-4 -3 -2 -1 01 2 3 4
es una función
decreciente
x
x
En general
Si a > 1 la gráfica tiene la forma siguiente:
Propiedades
1. f(1) = Logb1 = 0, es decir el par ordenado
(1,0) pertenece a la función.
x
y=a (a1)
y
2. Si: r < s entonces Logbr > Logbs.
Es una función
creciente
3. Si: r > 1 entonces Logbr < 0.
4. Si: 0 < m < 1 entonces Logbm < 0.
II. FUNCIÓN EXPONENCIAL
A. Definición
Dado un número real a, tal que 0 a 1; se llama
función exponencial de base a la función que asocia
a cada x real el número ax . y = f(x) = ax.
m
am
B) g(x) 1
2
C) h(x) 3x
D) p(x) 10x
E) q(x) ( 2)
x
UNI SEMESTRAL 2013 - III
x
1
F) r(x)
3
as
1
a
0
r s
x
Propiedades
1. f(0) = a° = 1, es decir el par ordenado (0,
1) pertenece a la función.
2. Si r < s entonces ar < as, ó si s > r entonces
as > ar.
3. Si r < 0 entonces ar < 1.
4. Si m < 0 entonces am < 1.
Ejemplos:
A) f(x) 2 x
r
x
2. Caso II
Si 0 < a < 1.
44
ÁLGEBRA
TEMA 15
FUNCIÓN EXPONENCIAL Y LOGARITMOS
Exigimos más!
Ejemplos:
A) f(x) 1
2
x
B) g(x) 1
10
C) h(x) 1
3
Propiedades
1. f(0) = a0 = 1, es decir el par ordenado (0, 1)
pertenece a la función.
2. Si r < s entonces ar > as, ó si s > r entonces
as < ar.
3. Si r < s entonces ar > 1.
4. Si m > s entonces am < 1.
x
x
D) p(x) (0, 8) x
x
Graficaremos: y f(x) 1 2 x
2
1
x y
2
-3
-2
-1
0
1
2
3
x
1
y
2
x
C. La función exponenciaL de Base "e"
•
y
x
y=2
8
•
8
4
2
1
1/2
1/4
1/8
4
e 1
•
1
-4 -3 -2 -1 0 1 2 3 4
y
La gráfica de y = ex es:
y
y=a ; 0 a 1
x y=e
Es una función
creciente
-3
-2
-1
0
1
2
3
r
s
El valor de "e" con siete decimales de aproximación es: e = 2,7182818...
r
a
1
r s
0 m
1
1
1
1
1
1! 2! 3! 4 !
n!
x
En general
Si 0 < a < 1 la gráfica tiene la forma siguiente:
a
La función y = ex donde "e" es número irracional
trascendente juega un rol muy importante en
las matemáticas.
Las aproximaciones del número "e" se pueden determinar con la expresión:
x
y=e
x
0,05
0,14
0,37
1
2,72
7,39
20,09
4
-3 -2 -1 0 1 2 3
problemas resueltos
Problema 1
Sea S el conjunto solución de la ecuación, en R:
x 3 7x 2 15x 9
1
logx 3
5
Halle la cantidad de elementos de S.
UNI 2010 - I
Nivel fácil
A) 0
B) 1
C) 2
D) 3
E) 4
Operando:
3
También: g(x) = Log 3 x
5
2
x
7x
15x
9 Log 3 x
f(x)
5
Cuya gráfica:
g(x)
Tenemos: f(x) = x3 – 7x2 + 15x – 9
Factorizando: f(x) = (x – 1)(x – 3)2
Cuya gráfica:
Luego:
Resolución:
Analizando:
x3 7x2 15x 9
1
;x 0 x 1
logx 3
5
UNI SEMESTRAL 2013 - III
45
x
8
ÁLGEBRA
TEMA 15
x
FUNCIÓN EXPONENCIAL Y LOGARITMOS
Exigimos más!
Número de soluciones de la ecuación se encuentra a partir del número
de intersecciones de las gráficas de f(x)
y g(x) no encontrándose intersecciones
entre estas dos gráficas.
Respuesta: A) 0
Problema 2
Determine el conjunto solución de la
inecuación: 4x – 4–x < 1.
UNI 2008 - II
Nivel intermedio
A)
1 5
0;Log4
2
B)
; 0
C)
1 5
;Log4
2
D)
;
E)
;Log4 5 1
2
m2 m 1 0; m 0
m
Reduciendo:
3
V.C. 1 5 ; 1 5
2
2
x 1
– 3x – 1 3x 2
Si: x 0
Eliminando los valores absolutos:
3x+1 – (3x – 1)= 3x + 2
Reduciendo: 3x 3 2 3x 1 0
Tenemos: 3x = 1 x 0
Entonces:
Si: –1 x 0
m 0
Eliminando los valores absolutos:
3x+1 + 3x – 1 = 3x + 2
0 m 1 5
2
Reduciendo: 3x+1=3
Luego:
Resolución:
Piden: 4x = m; m > 0
Tenemos:
4 x 4 x 1
4x
A) –4
D) 2
Resolución:
m2 m 1 0
m 1 5 ; 1 5
2
2
1 5
2
UNI 2008 - I
Nivel difícil
B) –2
C) 0
E) 4
Efectuando:
4x
1 5
log4
2
4
x log4 1 5
2
Respuesta: C)
-; log4 1 5
2
1
1
4x
Reemplazando el cambio de variable:
m 1 1
m
UNI SEMESTRAL 2013 - III
Tenemos: x + 1 = 1 de donde: x = 0
0 1 x 0
Si: x < –1
Eliminando los valores absolutos:
x
3–x–1 3 x – 1 3 2
Reduciendo: 3–x–1 = 3
Tenemos: –x – 1 = 1
De donde:
Problema 3
Si {x1; x2} es el conjunto solución de:
Piden: –2 + 0 = –2
3 x 1 3x 1 3x 2
entonces la suma de x1 y x2 es:
46
x –2 \ C.S. {–2;0}
Respuesta: B) –2
ÁLGEBRA
TEMA 15
ÁLGEBRA
LÍMITES I
DESARROLLO DEL TEMA
I.
II. DEFINICIÓN
NOCIÓN INTUITIVA DE LÍMITES
El número L se llama límite de la función real de una
Consideremos una función real de variable real:
variable real f en el punto x0 (x0 no pertenece necesa-
3
f(x) x x ; x 0
x
riamente al Dom(f ); si para cada 0 , es posible hallar un que depende de , tal que:
Se observa que el equivalente será:
0 ; 0 / x Domf 0 x x 0 f(x) L
f(x) x2 1; x 0
Se dice que L es el límite de f(x), cuando x tiende a x0
y se escribe como:
¿Qué sucede si x asume valores muy cercanos a cero?
f(x) asumirá valores muy cercanos a 1, dándole un
enfoque geométrico:
Y
lim f(x) L
x x 0
f
III. INTERPRETACIÓN GEOMÉTRICA
Y
f
L
f(x)
L
1
0
(valores por
la izquierda)
x
f(x)
L
X
(valores por
la derecha)
Se observa que, a medida que x se acerca a 0, ya sea
por la derecha o por la izquierda, entonces f(x) se
acerca a 1. Es decir: Si x tiende a 0, entonces f(x)
tiende a 1. Simbolizando:
X 0 X X 0
X
X 0
IV. TEOREMA DE UNICIDAD DEL LÍMITE
Sea A una función real de una variable real y x0 no
lim f(x) 1
x 0
pertenece necesariamente al Dom A.
o en forma equivalente:
lim A(x) L1 lim A(x) L 2 L L
1
2
xx
x x
lim (x 2 1) 1
0
0
x 0
Para obtener el valor de 1 se ha reemplazado en
f(x) = x2 + 1 el valor x = 0, así:
A. Teoremas
Sean: f g dos funciones reales de variable real y
además "a" un punto que no pertenece necesaria-
lim f(x) f(0) 02 1 1
x 0
UNI SEMESTRAL 2013 - III
mente a: Domf Domg =
47
ÁLGEBRA
TEMA 16
LÍMITES I
Exigimos más!
Si:
lim f(x) A
4.
Entonces:
x a
Si c R
lim cf (x) c A
x a
lim (f g)(x) A + K
1.
lim (f g)(x) A K
3.
lim g(x) K
x a
x a
x a
5.
Si K 0:
f
A
lim (x)
K
x a g
lim (f g)(x) A K
2.
x a
problemas resueltos
Problema 2
Calcular:
Problema 1
Calcular:
6
2
Lim
x 1
x 1 x3 1
3 x 3
Lim
x
x 0
1
B)
2 3
1
3
C)
D)
1
3
A) -2
B) –1
C) 2
D) 1
E) x
2 3
7
2
B)
2
4
C)
5
2
D)
3
2
E)
2
7
Resolución:
Tenemos:
Resolución:
Tenemos:
2
E)
Nivel intermedio
2
3
A)
UNI
UNI
Nivel fácil
A)
UNI
Nivel intermedio
Lim x 2 x 5 x
x
6
2
Lim
x 1
x 1 x3 1
Resolución:
Evaluamos:
2 x 5
Tenemos:
Evaluamos:
3 x 3
Lim
x
x 0
Luego:
6 2
0 1 1
Evaluamos:
x5 2x4 5
Lim ax2 bx c
0
x3 1
x
Luego:
x 2 x 5 x
x 2 x 5 x
2(x 2 x 1)
Lim 36
x 1 x 1
(x 1)(x 2 x 1)
3x 3 0
0
0
Luego:
Efectuando:
Efectuando:
( 3 x 3) ( 3 x 3)
Lim
x
x
x 0
( 3 x 3)
Lim
2(x 2)(x 1)
Lim
x 1 (x 1)(x2 x 1)
(x 2)(x 5) x 2
x
(x 2)(x 5) x
Reduciendo:
Efectuando:
Simplificando:
x
Lim
x 0
2(x 2) 2(1 2)
Lim
2
2
x 1 x 2 x 1
1 1 1
x( 3 x 3)
Lim
x
7x 10
x2 7x 10 x
x(7 10 )
x
x 1 7 102 x
x x
Simplificando:
Lim
x 0
1
3 x 3
1
1
3 3 2 3
Respuesta: A) -2
Lim
Problema 3
Evaluar:
Respuesta: A)
UNI SEMESTRAL 2013 - III
1
2 3
10
)
7
x
2
7 10
1
1
x x2
(7
x
Lim x 2 x 5 x
x
Respuesta: A) 7/2
48
ÁLGEBRA
TEMA 16
ÁLGEBRA
LÍMITES II
DESARROLLO DEL TEMA
I.
Teorema:
LÍMITES LATERALES
lim f(x) lim f(x) L lim f(x) M
x a+
x a
xa
A. Definición 1
Se dice que L es el límite lateral de f(x) cuando x
tiende hacia "a" por la derecha y se denota por:
Es decir existe el límite de una función, sí y solo si
existen los límites laterales y son iguales.
lim f (x) L
x a+
II. TEOREMA SOBRE LÍMITES INFINITOS
Geométricamente:
1.
2.
lim
1
x
lim
1
x
x 0
x 0
3. Si "n" es un entero positivo, entonces:
1
xn
; sin es impar
1
b) lim
x 0 x n
; si n es par
a) lim
x 0
B. Definición 2
Se dice que "m" es el límite lateral de f(x) cuando
x tiende hacia "x" por la izquierda y se denota por
4. Sean f y g dos funciones tales que:
lim f(x) M
x a
lim f (x) lim g (x)
x
x
Geométricamente:
entonces:
lim f(x) g(x)
x
A lim f(x) g(x)
;
x
Generalmente, al calcular el Lim f(x) es necesario
x a
calcular los límites laterales de f(x) cuando la función tiene diferentes reglas de correspondencia para
x < a y x > a.
UNI SEMESTRAL 2013 - III
49
ÁLGEBRA
TEMA 17
LÍMITES II
Exigimos más!
Es decir, usando los siguientes símbolos, podríamos resumir así:
I. () ()
II. () ()
III. () ()
B. Forma indeterminada
Sea:
L lim
Nota:
Cuando se tienen funciones racionales, el análisis del
comportamiento en . Se realiza dividiendo el numerador y el denominador por la mayor potencia de la
función racional.
Entonces de acuerdo al valor de los grados n y m
de los polinomios se tiene:
; si n m
a
L 0 ; si n m
b0
0 ; si a n m
() ()
IV. () ()
V.
; n 0 (par)
n
VI. ()
; n 0 (impar)
IV.TEOREMA SOBRE LÍMITES AL INFINITO
Si n es un entero positivo cualquiera, entonces:
lim 1 0
lim 1 0
n
n
x x
x x
; K 0
VII. K()
; K 0
; K 0
VIII. K()
; K 0
Sea : f : R R definida por f(x) = 1+ 1
x
x
III.CÁLCULOS DE LOS LÍMITES
entonces : lim 1+ 1 e 2, 71828...
x
x
A. Forma indeterminada 0
0
Para las formas indeterminadas ; 0 se trata de
transformarlas a una de las dos formas:
Si se reeemplaza x por el valor del x0 correspondiente se obtiene la expresión 0/0, efectuaremos
ciertas operaciones algebraicas para levantar la indeterminación.
UNI SEMESTRAL 2013 - III
a0 xn a1 xn 1 a2 xn 2 ... an
b0 x m b1 xm 1 b2 x m 2 ... bm
0
0
50
ó
.
ÁLGEBRA
TEMA 17
ÁLGEBRA
DERIVADAS I
DESARROLLO DEL TEMA
Dada la ecuación y = f(x), generalmente, si cambiamos el
valor de x es lógico pensar que cambie el valor de y. Trataremos de hallar una relación que nos permita, de alguna
manera, medir estos cambios.
Esta idea será sumamente fructífera ya que muchos problemas reales (físico y/o geométricos) requieren analizar la relación entre las variaciones de dos magnitudes.
Veamos algunas consideraciones elementales que nos van
a permitir tener una visión más clara de esta idea.
Consideremos una función "f" real de variable real continua
en el intervalo a; b tal que y = f(x). Sea x 0 a;b , es
decir a < x0 < b. Si al punto x0 le sumamos una cantidad
pequeña x llamada incremento, encontramos el punto
x x 0 x, supondremos que el punto x a; b .
El incremento que experimenta la función al pasar del punto x0 a x x 0 x, lo representaremos por y , siendo por
tanto y f(x) f(x0 ) , tal como se observa en la figura adjunta:
De donde:
Tan()
y f(x) f(x0 )
x
x x0
y f(x) mx b
y 0 f(x 0) mx 0 b
Entonces:
Tan()
(mx b) (mx 0 b)
m
x x0
Luego:
tg m
m Tan () se le llama "pendiente" de la recta
.
Se observa además que la pendiente de la recta
:
y = mx + b
Luego el cociente de los dos incrementos se llama "cociente
incremental", entonces:
es el coeficiente principal.
I.
y f(x) f(x 0)
x
x x0
Se denomina derivada de la función f a la función denotada por f' cuya regla de correspondencia es:
f '(x) Lim f(x h) f(x)
h0
h
Si trazamos una recta
que pase por los puntos (x0, f(x0))
y (x, f(x)) cuya ecuación es: y = mx + b, se tiene:
UNI SEMESTRAL 2013 - III
DERIVACIÓN DE UNA FUNCIÓN
51
ÁLGEBRA
TEMA 18
DERIVADAS I
Exigimos más!
Donde su dominio está formado por los valores de x
del dominio de f, para los cuales el límite dado existe.
En este caso decimos que f es derivable o diferenciable.
Y ahora haciendo que h 0, la pendiente de la
recta (que ahora es tangente) es:
f(x h) f(x)
ms Lim
h
h0
Otras notaciones
Además de la notación f(x) para la derivada de y = f(x)
se utilizan:
y' ;
Y es lo que hemos definido como la derivada de f.
En conclusión:
dy df(x)
;
; D ,y
dx
dx
Se lee: “Derivada de f con respecto a x”.
II. REGLA GENERAL PARA HALLAR LA DERIVADA DE UNA FUNCIÓN
f(x h) f(x)
f(x x) f(x)
f(x) Lim
Lim
h
x
h0
x 0
•
•
•
f'(x) representa geométricamente (en caso de existir) a la pendiente de la recta tangente (de la gráfica de f) en el punto (x, f(x)), con x Domf y donde Domf ' Domf .
Se suma a la variable x un incremento x 0 y se
calcula f(x x).
Se forma el incremento y de la función correspondiente al incremento x de la variable x, es
decir, se calcula y f(x x) f(x) .
Se divide ambos miembros por el incremento x
es decir:
IV. DERIVADAS LATERALES
Dada la función f real de variable real definidos y denotamos:
y f(x x) f(x)
x
x
•
A. Derivada por la derecha de f en el punto x0
f' (x0 ) Lim
Se calcula f(x) lim y
x 0 x
h 0
f(x 0 h) f(x 0 )
h
Si tal límite existe.
B. Derivada por la izquierda de f en el punto x0
III. INTERPRETACIÓN GEOMÉTRICA DE
LA DERIVADA
f' (x 0 ) Lim
Consideremos al gráfico de la función f, representada
por la curva y = f(x), tomemos los puntos A y B, el
punto B muy próximo al punto A cuyas coordenadas
son (x, f(x)) como se muestran en la figura:
h 0
f(x 0 h) f(x0 )
h
Si tal límite existe.
Observación
Es consecuencia inmediata de la definición de límite que f(x) existe sí y solo sí las derivadas laterales existen y son iguales.
f '(x )=f ' (x ) f ' (x )
0
+
0
0
Por lo tanto f es diferenciable en x0.
•
•
Teorema
Si la función f es diferenciable en x0 entonces f es
continua en x0.
En este caso hemos supuesto un h > 0. Observamos que B es un punto de la gráfica de F que se
desliza a través de ella a medida que variamos h. Si
hacemos que h se aproxime a cero, la recta AB inicialmente secante se convierte en tangente.
Observamos que antes de hacer esta aproximación de h a cero, la pendiente de la recta AB era:
ms
Observaciones
•
•
f(x h) f(h)
h
UNI SEMESTRAL 2013 - III
52
Si la función no es continua en x0, entonces
f no es diferenciable en x0.
Si f es continua en x0, no se puede afirmar
que f sea diferenciable en x0.
ÁLGEBRA
TEMA 18
DERIVADAS I
Exigimos más!
Corolario
Si la función f es diferenciable sobre el intervalo I,
entonces f es continua sobre I.
2. c f es diferenciable en I y
Observación
3. f g es diferenciable en I y
(cf) '(x) c f '(x); x I
(f g) '(x) f '(x) g(x) f(x) g '(x); x I
Sea f una función definida en [a; b]; a < b diremos que f es diferenciable en todo el intervalo
[a; b] si lo es en a; b y además existen f' (a) y
f' (b).
4. f/g es diferenciable en I, si g(x ) 0 , x I y
f '(x) g(x) f(x) g '(x)
f '
g (x)
2
g(x)
V. DERIVADA DE ALGUNAS FUNCIONES
ELEMENTALES
VII.DERIVADAS DE LAS FUNCIONES TRIGONOMÉTRICAS
A. Teoremas
1. Sea "c" una constante. Si f(x) = c, entonces
1. Si f(x) = Senx, entonces f'(x) = Cosx; x
f '(x) 0; x .
2. Si f(x) = Cosx, entonces f'(x) = –Senx; x
2. Si f(x) = x, entonces f '(x) 1; x .
3. Si f(x) = Tanx, entonces f '(x) = Sec2x:
3. Sea "n" . Si f(x) = xn, entonces f '(x) nxn 1,
x (2k 1) ,k
2
x .
4. Si f(x) = Cotx, entonces f'(x) = Csc2x; x k ,
VI. ÁLGEBRA DE LAS DERIVADAS
k
5. Si f(x) = Secx, entonces:
A. Teorema
Sean f y g diferenciables en un intervalo I y c es
f '(x) Secx Tanx ; x (2k 1) ,k
2
una constante, luego.
6. Si f(x) = Cscx, entonces:
1. f g es diferenciable en I y
f '(x) Cscx Cotx ; x k, k
(f g) '(x) f '(x) g '(x); x I
problemas resueltos
Problema 1
Dato:
Largo: 50 m
Si deseas cercar un jardín rectangular
2x + 2y = 200 x + y= 100
Ancho: 50 m
y si tienes 200 metros de cerca, ¿cuá-
y = 100 – x
Respuesta: A) 50
les son las dimensiones del jardín más
grande que puedes cercar?
A) 50
B) 60
C) 70
D) 80
E) 200
Resolución:
Tenemos:
Maximizando el área: f(x) = xy
Problema 2
Hallar los valores extremos de:
f(x) = 3x2 – x3
Entonces:
f(x) = x(100 – x)
Resolución:
f(x) = 100x – x2
f'(x) = 100 – 2x = 0
Tenemos:
f(x) = 3x2 – x3
f'(x) = 6x – 3x2 = 3x(2 – x)
Luego:
x = 50; y = 50
Puntos críticos:
x=0
Dimensiones:
UNI SEMESTRAL 2013 - III
x=2
f''(x) = 6 – 6x
53
ÁLGEBRA
TEMA 18
DERIVADAS I
Exigimos más!
Luego:
64
9
B) 5 , 80
9
es un mínimo relativo.
16
C) 6 ,
3
32
D) 7 ,
9
f''(2) = –6 < 0 entonces f(2) = 4
E) 8 , 16
9
A) 4 ,
f''(0) = 6 > 0 entonces f(0) = 0
es un máximo relativo.
•
Problema 3
VOA
Vcilindro r2(16 16r) Derivando
9
2
32r 48r 0 r 6
9
En un cono de altura 16 cm y radio 9 cm
se inscribe un cilindro de radio r. Determine el radio y la altura del cilindro
de mayor volumen si sabemos que tiene
radio entero.
H 16
3
UNI
Respuesta: C) 6 , 16
3
Nivel difícil
UNI SEMESTRAL 2013 - III
9
r
16r
H 16
16 16 H
9
•
Resolución:
VO’B
54
ÁLGEBRA
TEMA 18
ÁLGEBRA
DERIVADAS II
DESARROLLO DEL TEMA
C.
APLICACIONES DE LA DERIVADA
A.
Si C un punto crítico de f si existe un intervalo [a; b]
donde f es continua y C a;b , entonces:
Valores extremos
Se llaman valores extremos de una función a todos sus
máximos y mínimos relativos.
Si f '(x) existe y si f '(x0) es un valor extremo entonces
la recta tangente en este punto debe ser horizontal,
esto equivale a que: f '(x0) = 0.
Teorema
Si una función f satisface las siguientes 3 características:
• f tiene un valor extremo en el punto x = a.
• f esta definida en un entorno N(a) de a.
• Existe f'(a).
B.
f(c) es un máximo
f '(x) 0; x a;c
1. y
relativo de f
f '(x) 0; x c;b
f '(x) 0; x a; c
2. y
f '(x) 0; x c;b
D.
f(c) es un mínimo
relativo de f
Concavidad y puntos de inflexión
Sea f una función continua sobre un intervalo a;b al
cual pertenece x0 tal que f''(x0) = 0.
f ''(x) 0; x a; x 0
1. f ''(x) 0; x x ;b (x 0 ; f(x 0))
0
Teorema de L' Hospital
Es un punto de inflexión
f(x)
L
x a g(x)
Si: Lim
sea de la forma:
Criterio de la primera derivada
2. f ''(x) 0; x a; x 0 x0 ; f(x 0)
f ''(x) 0; x x0 ;b
0
ó
0
Es un punto de inflexión
Se puede considerar el límite pero con las correspondientes derivadas:
E.
Dado un polinomio P(x) de grado no menor que dos.
Si X0 es una raíz de P(x) cuya multiplicidad es k, se
cumple:
f(x)
f '(x)
f ''(x)
Lim
Lim
..... L
x 0 g(x)
x 0 g '(x)
x 0 g ''(x)
L Lim
UNI SEMESTRAL 2013 - III
Raíz de multiplicidad
55
ÁLGEBRA
TEMA 19
DERIVADAS II
Exigimos más!
problemas resueltos
Problema 1
De este modo:
Calcular:
lim
1
2
f '(x)
cos2 x
4
lim cos x lim
lim
1
g'(x)
senx
cos2 x senx
senx
x
x
x
x
2
2
2
2
cos2 x
lim
tgx 8
sec x 10
x
2
Al ser f y g son derivables en un en
torno de
podemos aplicar la regla
2
de L'Hôpital y se tiene que:
Resolución:
tgx 8
lim
sec x 10
x
f(x)
f '(x)
tgx 8
lim
lim
lim
1
g(x)
g'(x)
sec x 10
x
x
x
2
2
Da lugar a una indeterminación del tipo
. Llamemos:
f(x) = tgx – 8 y
g(x) sec x 10
1 10
cos x
2
Problema 2
Res olver apli cando el teorema de
L'Hôpital:
1
1
lim
x 0 Ln(1 x) x
domino de definición (en particular en
y en un entorno suyo):
2
x 0 Ln(1 x)
g '(x)
1
cos2 x
(senx)
senx
cos2 x
UNI SEMESTRAL 2013 - III
1
lim
x 0
Ln(1 x) (1 x)
lim
1
1
Ln(1 x) 2 2
lim
1
1
1
1 x
Problema 3
Res olver apli cando el teorema de
L'Hôpital:
lim
Entonces f y g son derivables en su
1
y
cos2 x
0
(L'Hôpital)
0
x 0
Resolución:
f '(x) sec 2 x
2
x
1 x
x 0 (1 x)Ln(1 x) x
1 x
x
lim
x 0 (1 x)Ln(1 x) x
lim
x senx
x
x 0 1 cos
1
x
Resolución:
x Ln(1 x) 0
lim 1
1 lim
x0 Ln(1 x) x x0 x Ln(1 x) 0
1
1
1x
(L'Hôpital) lim
x 0
Ln(1 x) x
56
lim
x senx 0
(L'Hôpital)=
x 0
lim
senx x cos x 0
(L'Hôpital)=
senx
0
x 0 1 cos
x 0
1
1 x
lim
x 0
cos x cos x (senx) x 2
2
cos x
1
ÁLGEBRA
TEMA 19
ÁLGEBRA
FUNCIÓN POLINOMIAL
DESARROLLO DEL TEMA
I.
DEFINICIÓN
Propiedades
Una función polinomial es una expresión algebraica
racional entera, cuya forma general es:
Sea y = F(x) una función polinomial de grado no menor
que tres ([F]° 3) cuya gráfica aproximadamente es:
F(x) a 0x n a1x n1 a2x n2 ... an1x an ;n
Donde:
x = variable o indeterminada
a0, a1, a2, ... y an son los coeficientes, todos ellos son
números reales
a0xn es el término dominante siempre que an 0
a0 = Coeficiente principal
an = Término independiente de x, es un número real,
también se le llama término constante.
1. Cada punto que corresponde a la gráfica de la
función de modo que la gráfica de y = F(x) cruza al
eje x indica la presencia de una raíz simple o de
multiplicidad impar.
De la gráfica: x1 y x2 pueden ser raíces simple o
raíces de multiplicidad impar de la función.
2. Cada punto que corresponde a la gráfica de la
función de modo que la gráfica de y = F(x) es
tangente al eje x indica la presencia de una raíz de
multiplicidad par.
De la gráfica: x3 es una raíz de multiplicidad par de la
función y = F(x).
Observación: Las funciones constante, lineal y cuadrática que se obtienen cuando n = 0; n = 1 y n = 2
respectivamente son casos particulares de una función
polinomial.
II. CERO DE UNA FUNCIÓN POLINOMIAL
También llamado raíz, sea y = F(x) una función polinomial no constante, es decir [F]° 1, un cero de la
función es el valor que asume su variable de modo
que la función se anule. Matemáticamente:
F(x0 ) 0 x x 0 es un cero de F(x)
III. TEOREMAS DE TRANSFORMACIÓN DE
RAÍCES
Teorema: Si x = x0 es un cero de F(x), entonces un
factor de F(x) será el binomio (x – x0).
Ejemplo: Dado el polinomio F(x) x5 – 2x + 1 fácilmente podemos notar que F(1) = 0, luego afirmamos
que x = 1 es un cero de F(x) y por tanto (x – 1) es un
factor de F(x).
Sea y = F(x) una función polinomial de grado no menor
que dos, luego para la ecuación F(x) = 0, tenemos:
1. F 1 = 0, es la ecuación que tiene por raíces a
x
los recíprocos de las raíces de F(x) = 0.
2. F(x + h) = 0, con h , es la ecuación que tiene
como raíces a las raíces de F(x) = 0 disminuidas en
"h".
3. F(x – h) = 0, con h , es la ecuación que tienen
como raíces a las raíces de F(x) = 0 aumentadas
en "h".
4. F(k . x) = 0, con k , es la ecuación que tiene
como raíces de F(x) = 0 divididas por "k".
Observación
El cero o raíz de una función polinomial F(x) de grado
mayor o igual que dos, puede ser simple o múltiple.
1. Es simple si x = x0 solo determina al factor (x – x0)
no se repite en F(x).
2. Es múltiple si x = x0 determina el factor (x – x0)m,
con m N/m 2, es decir (x – x0) es un cero de
multiplicidad "m".
UNI SEMESTRAL 2013 - III
57
ÁLGEBRA
TEMA 20
FUNCIÓN POLINOMIAL
Exigimos más!
B. Teorema de Gauss
5. F x = 0, con k , es la ecuación que tiene
k
como raíces de F(x) = 0 multiplicadas por "k".
Permite analizar la existencia de alguna raíz racional
de la función F(x), cuyo grado es n 2 y término
independiente distinto de cero.
Sea la función polinomial:
F(x) a0xn + a1xn–1 + a2xn–2 + ... + an–1x + an
Donde: a0, a1, a2, ... an
Si x0 es una raíz racional de F(x) = 0 ésta será de la
IV. TEOREMAS ADICIONALES
A. Teorema de Descartes
Frecuentemente llamado Regla de los signos de
Descartes, esta referido a la cantidad de raíces positivas
o negativas que puede tener una función polinomial
F(x) de grado n 2 con coeficientes reales.
1. El número de raíces positivas de la ecuación F(x) = 0,
será igual al número de variaciones de signos
que presente los coeficientes de F(x), o, es
menor que esta cantidad en un número par.
2. El número de raíces negativas de la ecuación F(x) = 0
será igual al número de variaciones de signos que
presenten los coeficientes de F(–x), o, es menor
que esta cantidad en un número par.
p
, donde p y q son primos entre si, de
q
modo que p es un divisor del término independiente
de x en F(x) y q es divisor del coeficiente principal
en F(x).
forma x0 =
C. Teorema de Bolzano
Consideremos una función polinomial F(x) cuyo
grado es n 2 y de coeficientes reales. Si a < b
y F(a) • F(b) < 0, entonces existe al menos una
raíz real de F(x) que pertenece al intervalo a;b (o
en general un número impar de raíces reales).
Ejemplo: Para: F(x) x3 + 2x – 4
Se observa que: F(1) = –1 y F(2) = 8
Por lo que: F(1) • F(2) < 0
Luego por el teorema de Bolzano existe una raíz
real x0 que pertenece al intervalo 1; 2 , es decir:
1 < x0 < 2
Observación:
Llamaremos variación de signos de los coeficientes
de un polinomio ordenado en forma decreciente al
paso de un coeficiente positivo, a un coeficiente
negativo o viceversa.
problemas resueltos
Problema 1
La función polinomial:
2
F(x, y, z) (x y)(y z 3)
[(Z y)(y x 3)]4 (x y z 3)2
tiene N raíces (x, y, z). Entonces N es igual a:
A) 0
B) 1 C) 2 D) 3 E) 4
y z 3 0
4. y x 3 0 C.S. (2; 1, 2)
x y z 3 0
N es igual a 2
Respuesta: C) 2
Resolución:
2
4
(x y)(y z 3) (z y)(y x 3)
0
0
2
(x
y
z
3) 0
0
Se genera un sistema de ecuaciones:
x y 0 y z 3 0
z y 0 y x 3 0
x y z 3 0
De donde:
x y 0
1. z y 0
2.
x y z 3 0
C.S. (1,1,1)
x y 0
y x 3 0
x y z 3 0
C.S.
y z 3 0
C.S.
3. z y 0
x y z 3 0
UNI SEMESTRAL 2013 - III
Problema 2
Determine el polinomio mónico de menor grado de coeficientes enteros que
tenga como raíces a los números reales
2 3 y 3 2. Dar como respuesta
la suma de sus coeficientes.
A) 28 B) 42 C) 56 D) 70 E) 84
Resolución:
Por el teorema de la paridad de raíces
irracionales: Si una raíz es 3 2 la otra
será (3 2) la cual origina el polinomio cuadrático (x2 + 6x + 7).
Análogamente:
Si la otra raíz es 2 3 la otra será
2 3 que origina el polinomio:
(x2 + 4x + 1)
Por lo tanto el polinomio mónico será:
P(x) = (x2 + 6x + 7)(x2 + 4x + 1)
58
Nos piden: P(x) (14)(6) 84
Respuesta: E) 84
Problema 3
Dados los siguientes polinomios: P(x)
de grado 2 y término independiente
uno; y Q(x) = (x – 1) P(x) + 3x + 1.
Si Q(2) = 7 y P(1) = 2, halle la suma
de raíces de Q(x).
A) 0 B) 8/3 C) 10/3 D) 4 E) 5
Resolución:
De los datos: P(x) = ax2 + bx + 1
Q(x) = (x – 1) (ax2 + bx + 1) + 3x + 1
Pero:
Q(2) 7;(1)(4a 2b 1) 7 7
4a 2b 1......(1)
P(1) 2 ; a b 1 2
a b 1...(2)
de (1) y (2) = a 3 / 2;b 5 / 2
de donde: Q(x) 3 x 3 4x 2 3 x
2
2
4
se pide: x1 x 2 x 3
8
3 / 2 3
Respuesta: B) 8/3
ÁLGEBRA
TEMA 20
ÁLGEBRA
SUCESIONES
DESARROLLO DEL TEMA
I.
DEFINICIÓN
Lim X n L 0, un entero n0 0, tal n que
Una sucesión es una función cuyo dominio es y
rango un subconjunto de .
entero n no : x n L .
Observación:
Notación:
x :
n X(n)
También:
•
El entero n0 depende de 0.
•
Lim x n L ó Lim x n L.
n
x n x n xn
x n : x1; x 2 ,..., xn ,...
Ejemplo:
x n es el elemento n-ésimo de x n
Si x n 2n 1 , calcular Lim xn.
3n 2
Ejemplos:
1.
x n : 2, 4, 6,...,2n,... ó xn 2n
2.
x n : 1, 3, 5,...,2n – 1,... ó x n 2n – 1
3.
x n :
4.
x n : 21! ,
5.
x n : 11 2 , 21 3 , 3 1 4 ,...,
1,
Resolución:
xn 2n 1
3n 2
21
2n 1
n
Lim x n Lim
Lim
3n 2 n 3 2
n
1 1
1
1
, ,..., ,... ó x n
2 3
n
n
1
22 , 23 ,..., 2n ,... ó x 2n
n n!
2! 3!
n!
2
3
A. Teorema
Si r 1 Lim r n 0
1
,...
n n 1
n
n
Por ejemplo: Lim 0
4
II. LÍMITE DE UNA SUCESIÓN
B. Definiciones
Sea {xn} una sucesión y sea L , decimos que L es el
límite de {xn} si los términos xn n n0 de la sucesión
se aproximan a L. Es decir:
Sea {xn} una sucesión:
1. {xn} es acotada superiormente, si existe k1 ,
tal que n : x n k1.
2. {xn} es acotada inferiormente, si existe k 2 ,
tal que n : x n k 2.
3. {xn} es acotada si existe k > 0, tal que n :
xn k.
UNI SEMESTRAL 2013 - III
59
ÁLGEBRA
TEMA 21
SUCESIONES
Exigimos más!
Ejemplo:
3. La
La sucesión
sucesión {x
{xn} = {(–1)n} no es convergente, en
1. La sucesión {xn}, tal que x n
1
es acotada supen
1 ; n es par
n
efecto: Lim 1
1 ; n es impar
riormente e inferiormente: 0 x n 1, luego es
el límite no es único, entonces Limxn no existe.
acotada.
Teoremas
III. SUCESIONES MONÓTONAS
Sea {xn} una sucesión, diremos que {xn} es monótona
1. Toda sucesión monótona y acotada es convergente.
si es uno de los 4 tipos de sucesiones siguientes:
2. Toda sucesión convergente es acotada. Lo contrario
no necesariamente se cumple.
1. Sucesión creciente
3. Toda sucesión monótona no acotada es divergente
a ( o ).
Si: x n x n 1 ; n
2. Sucesión decreciente
Si: x n x n1 ; n
V. CRITERIOS DE CONVERGENCIA
3. Sucesión no decreciente
Si: x n x n 1 ; n
A. Criterio de la razón
4. Sucesión no creciente
Si: xn xn1 ; n
Sea {xn} una sucesión en , tal que si:
xn 1
1 lim x n 0
xn
n
Lim
Ejemplo:
1. La sucesión x n 1 es decreciente.
n
i.e. la sucesión converge a cero.
En efecto, n : 1 1
n n 1
Observación:
2. La sucesión xn = n2 es creciente.
2
En efecto, n : n (n 1)
Si lim
2
n
xn 1
1, no se puede decidir nada acerca
xn
de la convergencia.
IV. CONVERGENCIA DE UNA SUCESIÓN
Si lim
n
La sucesión {xn} es convergente si existe un único
L / Limx n L .
x n 1
1, entonces la suceción diverge.
xn
Ejemplos:
Observación:
n
1. Calcular: lim x n , siendo x n a y a 0
n!
n
Si Limxn no existe ó es ó , entonces decimos que {xn} es divergente.
Resolución:
n
n1
a 0; x n a ; x n 1 a
n!
n
1 !
Ejemplos:
1. La sucesión
xn
1
n
Apliquemos el criterio de la razón:
es convergente.
a
x n 1
a
n!
n 1 n
xn
n 1! a
n 1
En efecto: Lim 1 0.
n
n1
2. La sucesión x n 2 1 es convergente, en
3
n 1
1
efecto: Lim2
n
lim
n
UNI SEMESTRAL 2013 - III
0 1 lim xn 0
1
lim 1 x e e 2,7182818...
x
n
Lim
a
n 1
21
2
0 0
3 3
3
n
60
ÁLGEBRA
TEMA 21
SUCESIONES
Exigimos más!
VI. TEOREMA DEL ENCAJE
1
lim 1 x x e
Sean las sucesiones {an}, {bn} y {cn},
n
tales que an bn cn para todo n .
n
lim 1 1 e
n
n
Lim an Lim Cn L , entonces Lim bn L
n
2. Analizar la convergencia de: xn n!
nn
n
n
VII.TEOREMA DE LA MEDIA ARITMÉTICA
Resolución:
xn
Sea la sucesión convergente {an}n1,
n 1 !
n!
x n1
n
n 1
n
n 1
si:
a a2 ... an
Lim {an} a Lim 1
a; a
n
n
x
n 1 ! nn
nn
n 1
n
1
xn
n ! n 1 n
n 1
1
1 1
n
n
n
1
1
e
lim x n lim
VIII.TEOREMA DE LA MEDIA GEOMÉTRICA
Sea la sucesión convergente {an}n1;
n!
nn
si:
0
Lim {an} a Lim
xn es convergente.
n
n
n a1.a2.a3...an a; a
problemas resueltos
Problema 1
Sea la sucesión:
De la sucesión recurrente:
2an+2 – an+1 – an = 0
a1 0, a2 1, a3 1 , a 4 3 , a5 5 ,
2
4
8
Tenemos:
entonces la sucesión {an} converge a:
UNI 2010 - I
A)
7
12
a7
x1 1 x2 1
2
Problema 2
Llevamos a la sucesión correspondiente:
Dada la sucesión 2, 6, 12, 20, 30, 42, ...
n
1
n
determine la suma de los 100 primeros
términos de la sucesión anterior.
UNI 2009 - I
n 1 a1 0
2
n 2 a2 1
4
Resolución:
1
3
5
11
;a ;a ;a
;
2 4 4 5 8 6 16
21
43
;a
32 8 64
De donde: an 2
an1 an
; n IN
2
UNI SEMESTRAL 2013 - III
2
3
Respuesta: C) 2/3
Para
a1 0; a2 1; a3
2x 1 x 1 0
D) 1
E)
2x x 1 0
an 1
2
5
B)
8
2
C)
3
n
23
La sucesión converge a
2
a 6 11 , a7 21 , a8 43 ,...
16
32
64
Lim an Lim 2 4 1
3
2
n
n 3
Entonces: 4 2
3
3
Luego: an 2 4 1
3 3
2
n
A) 10100
B) 294880
C) 323400
D) 333300
E) 343400
Resolución:
La sucesión:
1 x 2; 2 x 3; 3 x 4; ... ; 100 x 101
Nos piden: convergencia {an}
t100
Calculamos:
61
ÁLGEBRA
TEMA 21
SUCESIONES
Exigimos más!
Recordar:
n(n 1)(n 2)
1 2 2 3 3 4 ... n (n 1)
3
y 9 respectivamente, obtenemos una
progresión geométrica. Hallar el producto de esos números.
n(n 1)(n 2)
n (n 1)
3
= 343400
Respuesta: E) 343400
gresión aritmética y además su suma
es 21. Si a esos números añadimos 2, 3
UNI SEMESTRAL 2013 - III
(7 – r + 2); (7 + 3); (7 + r + 9)
A) 231
9 – r; 10; 16 + r
B) 264
(9 r)(16 r) 102
P.G.
C) 273
D) 308
Conclusiones
E) 420
r=4
los 3 términos son: 3; 7 y 11
Problema 3
Tres números positivos forman una pro-
a = 7
Dato:
UNI 2008 - III
S100 1 2 2 3 3 4 ...
Dato: (a – r) + (a) + (a + r) = 21
el producto 3 7 11 231
Resolución:
Sean los 3 términos de la P.A.: a – r, a,
Respuesta: A) 231
a + r. Piden: (a – r) a(a + r)
62
ÁLGEBRA
TEMA 21
ÁLGEBRA
SERIES Y PROGRESIONES
DESARROLLO DEL TEMA
Teoremas
Sea {an} una sucesión en .
n
a1 a2 a3.......an ........
Si:
Entonces a la expresión: a1 a2 a2 .... an ...., se llama
serie infinita de números reales.
La sucesión:
an
es convergente, entonces: lim an 0
n
n 1
Si: lim an 0 , entonces: la serie infinita
Sn s1, s 2 ,....., s n,....
n
tal que:
an
es
n 1
divergente.
s1 a1
Son sumas
parciales
de la serie
sn a1 a 2 .... an
n
s2 a1 a 2
s3 a1 a2 a 3
n
ak
k 1
Si:
k 1
cak
k 1
n
c ak
k 1
n
II.
III.
ak siendo Sn la
C . Entonces:
k 1
n
I.
A la sucesión Sn n1, se denomina sucesión de sumas parciales de la serie infinita
n
ak , bk y
n
k 1
k 1
k 1
n
n
n
ak bk ak bk
k 1
n-ésima suma
k 1
n
ak bk ak bk
k 1
k 1
II. CRITERIOS DE CONVERGENCIA
parcial de la serie.
A. Criterio de la razón
I.
DEFINICIÓN
Consideremos una serie infinita
de sumas parciales Sn
ak
y una sucesión
k 1
.
Sea la serie
an y nLim
n 1
Si: L < 1, entonces
n1
Si: L > 1, entonces
Si el Lim Sn S existe, entonces diremos que:
n
La serie infinita
an es
convergente y converge a S.
convergente.
divergente.
Si la serie infinita
converge o no.
Ejemplo:
n1
Averiguar si la serie
an es convergente, se puede esSn = S
an nlim
Sean las series
n 1
Al cual llamaremos suma de la serie infinita. Si la serie
ak es divergente, carece de suma.
k 1
UNI SEMESTRAL 2013 - III
converge.
B. Criterio de la comparación
cribir de la siguiente forma:
3
kk !
k 1
n 1
an
an
Si: L = 1, entonces no podemos afirmar si la serie
infinita
an 1
L
an
63
an , bn
de términos no negati-
vos, tal que an bn; n mayor que un "k"
entero positivo suficientemente grande, entonces:
ÁLGEBRA
TEMA 22 - 23
SERIES Y PROGRESIONES
Exigimos más!
I. Si
bn
converge an converge.
II. Si
an
diverge
bn
a n y bn
diverge.
n=1
n=1
de términos positivos, entonces:
C. Criterio de la raíz
an
= k > 0 ambas series convergen
bn
o divergen.
I. Si: Lim
n
Sea la serie
an y
n 2
Lim n an L
n
Si: L < 1, entonces
an converge.
Si: L > 1, entonces
an
an
= 0 y bn converge an es
n bn
n=1
n=1
convergente.
II. Si: Lim
diverge.
Si: L = 1, entonces no podemos afirmar si la serie
an
= + y bn es divergente La
n bn
n=1
III. Si: Lim
converge o no.
D. Criterio de comparación por límite
serie
Sean las series:
an
es divergente.
n=1
problemas resueltos
Problema 1
La suma de la siguiente serie:
27 + 9 + 3 + 1 + ... es:
UNI 2009 - II
A) 38,5
B) 39,5
C) 40,5
D) 41,5
E) 42,5
a)
Aplicación de fórmula o teorema
Teorema:
Problema 3
Determine el valor de:
n
Lim bn1 Lim bn L
n
n
k 1
Suma límite:
S
Resolución:
t1
; q 1
1q
b) Solución del problema
Del dato:
A)
n
2n 1
B)
n
2n 2
C)
n 1
2n 1
D)
2n
2n 1
E)
n
2n 1n
Aplicando suma límite:
S
27
81
40,5
1
2
1
3
Resolución:
Tenemos:
n
S
Respuesta: C) 40,5
Luego:
S
n
1
bn1 bn ,n
3
Donde:
S
2
Luego : bn1 b1 1 1 ... 1
3 3
3
n
2
Tenemos : Lim bn1
n
1 1 1
...
2
3
3
SUMA LÍMITE
Resolución:
Lim bn1
Lim bn 1
n
n
Tenemos:
1
2
1
3
1
1 n
2
2 k 1 2k 1 2k 1
1 n 1
1
2 k 1 2k 1 2k 1
Propiedad telescópica:
b
f(k) f(k 1) f(a) f(b 1)
k a
Entonces:
1
3
1 1
Lim bn1 0
2 2
n
b1 1
2
S 1 1 1 n
2 1 2n 1 2n 1
n
bn 1 bn 1 ;n
3
UNI SEMESTRAL 2013 - III
1
2k 1 2k 1
k 1
Problema 2
Sea la sucesión definida por:
Donde: b1 1
2
Entonces la sucesión converge al valor:
A) –1/2
B) 0
C) 1/3
D) 1/2
E) 1
1
2k 1 2k 1
Respuesta: A)
Respuesta: B) 0
64
ÁLGEBRA
n
2n +1
TEMA 22 - 23
ÁLGEBRA
MATRICES I
DESARROLLO DEL TEMA
I.
DEFINICIÓN
Una matriz es el arreglo u ordenamiento rectangular de
elementos que podrán ser números reales, números
complejos, etc., en filas (horizontal) y columnas (vertical) encerrados entre corchetes o paréntesis.
Ejemplo:
La igualdad:
x y 2z w 3 5
x y z w 1 4
es equivalente al siguiente sistema de ecuaciones:
Representación:
x y 3
x y 1
2z w 5
z w 4
La solución del sistema es:
x = 2, y = 1, z = 3, w = –1
III. CLASES DE MATRICES
Donde aij representa el elemento de la fila "i" y la
columna "j".
Notación:
A. Matriz cuadrada
Una matriz cuadrada es aquella que tiene el mismo
número de filas que de columnas. En este caso una
matriz n n es de orden n y se le asigna el nombre
de matriz n-cuadrada.
Ejemplo:
i = 1, ..., m ; j = 1 , ... , n
Además: m n representa el tamaño, orden o dimensión
de la matriz A.
Ejemplo:
Traz(A) = 9 + 8 + 0 = 17
Nota:
Se debe destacar que una matriz es un arreglo y como
tal no tiene un valor numérico.
1. Tipos de matrices cuadradas
Las matrices cuadradas pueden ser:
II. IGUALDAD DE MATRICES
Dos matrices A y B son iguales, escrito A = B, si tiene
la misma forma y sus elementos correspondientes coinciden. Así la igualdad de dos matrices m x n equivale a
un sistema de m x n igualdades, una por cada par de
componentes.
UNI SEMESTRAL 2013 - III
65
a. Matriz diagonal
Es aquella matriz cuadrada en la cual al menos
un elemento de la diagonal principal es no nulo,
y los demás, si lo son.
ÁLGEBRA
TEMA 24
MATRICES I
Exigimos más!
Ejemplos:
1 0 0
A 0 7 0
0 0 7
Ejemplo:
A = [1 0 –3 2]
;
23 0
B
0 0
b. Matriz columna o vector columna
Si la matriz presenta una sola columna.
Ejemplo:
2
A5
1
b. Matriz escalar
Es una matriz diagonal que presenta elementos no nulos e iguales en la diagonal
principal.
Ejemplos:
5 0 0
A 0 5 0
0 0 5
C. Matriz nula
Es aquella matriz en la cual todos sus elementos son
nulos. Ejemplos:
6 0
B
0 6
;
0 0
A
0 0
c. Matriz identidad
Es una matriz escalar cuyos elementos de la
diagonal principal son no nulos e iguales a uno.
1 0 0
I 3 0 1 0
0 0 1
;
;
0 0 0
B 0 0 0
0 0 0
IV. OPERACIONES CON MATRICES
A. Adición de matrices
0
I2 1
0 1
Sea A = (aij) y B = (bij) dos matrices mn, entonces
la suma de A y B es la matriz m n, A + B dada por:
d. Matriz triangular
Existen dos clases:
A B aij bij
a11
a21
am1
• Superior:
Es una matriz cuadrada en donde todos los
elementos bajo la diagonal principal son
iguales a cero, y del lado opuesto al menos
un elemento no lo es.
b11
b21
a12 b12
a22 b22
bm1
am2 bm2
a1n b1n
a 2n b2n
a
b
mn
mn
Es decir, A + B es la matriz que se obtiene al sumar
las componentes correspondientes de A y B.
• Inferior:
Análogamente, es cuando los elementos sobre
la diagonal principal son todos nulos y del
lado opuesto al menos uno no lo es.
Advertencia:
La suma de dos matrices está definida sólo cuando
las matrices son del mismo tamaño.
Ejemplo:
Ejemplos:
1 2 4
3 5 8
A
; B
0 2 8
1 7 2
1 3 2 5 4 8 4 7 12
A B
0 1 2 7 8 2 1 5 6
B. Multiplicación de matrices
B. Matriz rectangular
1. Multiplicación de un escalar por una matriz
Si A = (aij) es una matriz de m n y si es un
escalar, entonces la matriz m n, A está dada por:
Son aquellas matrices en donde el número de filas
es distinto al número de columnas.
Ejemplos:
3 2
A 1 0
5 9 32
;
a11
a
A (aij ) 21
am1
B 17 9 5
0 4 2 23
1. Tipos de matrices rectangulares
a. Matriz fila o vector fila
Cuando una matriz está formada por una sola fila.
UNI SEMESTRAL 2013 - III
a12
a 22
am2
a1n
a 2n
a
mn
en otras palabras A = ( aij) es la matriz obtenida
al multiplicar cada componente de A por .
66
ÁLGEBRA
TEMA 24
MATRICES I
Exigimos más!
Ejemplo:
Sean las matrices:
Ejemplo:
Multiplicar a la matriz:
3 5 7
por el escalar 2.
4 2 1
0 5
A 2 4
y B 4
3 1 22
1 3 2 23
2 3 5
7
4 2 1
3(2)
4(2)
La matriz C producto de A y B será de orden
2 3 de la siguiente manera.
5(2)
7(2) 6 10 14
(1)2 8 4 2
2(2)
C
C 11
C21
C12
C22
C13
C23 23
Hallando cada uno de los elementos:
2. Multiplicación de una matriz fila por una matriz columna
Al tomar este producto es necesario que las matrices tengan el mismo número de componentes.
En este caso se tiene:
C11 2 4 4 2 4 4 1 C11 12
1
0
C12 2 4 2 0 4 3 C12 12
3
5
C13 2 4 2 5 4 2 C13 18
2
C 21 3 1 4 3 4 1 1 C21 13
1
0
C 22 3 1 3 0 1 3 C22 3
3
5
C 23 3 1 3 5 1 2 C23 17
2
n
Es decir: A B
Teoremas:
Sean A, B y C matrices para las cuales están definidas las operaciones de adición y multiplicación
i k y son escalares.
a. K(A + B) = KA + KB
akbk
k 1
Ejemplo:
A [1 9 7]
;
8
B 3
1
b.
c.
•
•
•
•
A .B (1 8 9 3 7 1) 42
3. Multiplicación de dos matrices
Dados dos matrices A (aij)m n y B (bij)n p.
Entonces el producto de A y B es una matriz:
C (Cij)mp , en donde:
(K + )A = KA + A
K( A) = (K )A
A (BC) = (AB) C
A (B + C) = AB + BC
AB = 0 no implica que A = 0 ó B = 0
AB = AC no implica que B = C
Definiciones:
• Si AB = BA, se dice que las matrices A y B
son conmutables.
• Si AB = –BA, se dice que las matrices A y B
son matrices anticonmutables.
Cij = (fila i de A) . (columna j de B)
es decir: Cij = ai1 b1j + ai2 . b2j + ... + bin . bnj
Para ilustrar esto, se consideran las siguientes
matrices: A, B y C.
4. Potenciación de matrices
Sea A una matriz cuadrada y n | n 2 , se
define:
An A
A A .... A
"n " veces
V. TRAZA DE UNA MATRIZ
Es la suma de elementos de la diagonal principal de
una matriz cuadrada.
UNI SEMESTRAL 2013 - III
67
ÁLGEBRA
TEMA 24
MATRICES I
Exigimos más!
D. Matriz idempotente
Teorema sobre traza
•
Traz (A ± B) = Traz(A) ± Traz(B)
•
Traz (KA) = KTraz(A)
•
Traz (A B) Traz(B A)
Una matriz cuadrada A es idempotente si y sólo si es
igual a su cuadrado (A2 = A).
Ejemplo:
1
¿La matriz A 2
1
2
Donde A y B son matrices del mismo orden y K un escalar.
VI. TRANSPUESTA DE UNA MATRIZ
Sea A = (aij) una matriz de m n. Entonces la transpuesta de A, que se escribe AT , es la matriz de n m
obtenida al intercambiar las filas por columnas de A,
AT = (aji). Ejemplo:
5 6 8
A
3 2 1
1
A A A 2
1
2
2
5 3
A T 6 2
8 1
1
2 es idempotente?
1
2
1 1
2 2
1 1
2 2
1
1
2 2
1
1
2
2
1
2 A
1
2
como A2 = A, entonces la matriz A es idempotente.
E. Matriz nilpotente
Se dice que una matriz A diferente de cero es
nilpotente si existe un número entero K tal que AK = 0.
El índice de nilpotencia se define como el entero
más pequeño para el que AK = 0.
Teorema
T
T
T
•
(A ± B) = A ± B
•
(AB)T = BT AT
•
(AT )T = A
•
( A)T = AT ; es un escalar
•
n
Ejemplo:
+
I = I; n Z
1 3 4
¿La matriz A 1 3 4 es nilpotente?
1 3 4
VII.OTROS TIPOS DE MATRICES
A. Matriz simétrica
1 3 4 1 3 4 0 0 0
A A A 1 3 4 1 3 4 0 0 0
1 3 4 1 3 4 0 0 0
Se dice que una matriz cuadrada es simétrica si cumple
la siguiente condición: AT = A. Ejemplos:
2
4 0 7
3 4
A
; B 0 3 1
4 5
7 1 9
entonces, A es nilpotente.
F. Matriz hermitania
B. Matriz antisimétrica
Dada una matriz cuadrada de componentes com-
Una matriz cuadrada será antisimétrica si y sólo si
es igual al negativo de su transpuesta (A = –AT ).
Ejemplos:
plejos será hermitania si y sólo si cumple lo siguiente:
A T
Ejemplo:
0
4 1
0 2
A
;
B
4
0 9
2 0
1 9 0
3
3
2 i 4 1
2 i 4 1
T
A 2 i 5
7 A 2 i 5
7
4 1 7
4 1 7
4
4
C. Matriz involutiva
G. Matriz ortogonal
Una matriz es involutiva si y sólo si su cuadrado es
igual a la matriz identidad (A2 = I).
Ejemplo:
Una matriz A se llama ortogonal, si verifica:
A . AT = AT . A = I
¿La matriz A 1 0 es involutiva?
0 1
Ejemplo:
A 2 A A 1 0 1 0 1 0 I
0 1 0 1 0 1
Cos Sen 0
A Sen Cos 0
0
0
1
como A2 = I entonces A es involutiva.
UNI SEMESTRAL 2013 - III
A.
68
ÁLGEBRA
TEMA 24
MATRICES I
Exigimos más!
problemas resueltos
Problema 1
Calcule Q(A), si:
Q(x) = (1 + x)(1 – x)
1 2
siendo: A
2 1
1 0
0 1
B)
1 1
1 1
C)
1 1
2
1 1
E)
2 7 1
Q 1 1
1 , P = Q101
1 4 4
a 0
b a
donde a 0, b , entonces los valores x1, x2, x3, x4 tales que:
x2
x4
Sabiendo que:
1 0
0 1
8
8
Q 3 3
5
5
son (en ese orden).
UNI 2007 - II
Nivel fácil
1 1
4
1 1
1 1
14
1 1
Resolución:
Piden:
Q(A)
Dato:
Q(x) = (1 + x) (1 – x)
Evaluando:
Q(A) = (1 + A)(1 – A)
Efectuando: Q(A) = I – A + A – A2
Tenemos:
Problema 3
Sean las matrices:
Sea la matriz:
a 0 x1
b a x 3
A)
D)
UNI 2008 - I
Nivel fácil
Problema 2
Q(A) = I – A2 ...
A)
1
b
1
,
, 0,
a
a
a2
B)
1 b
1
,
,0 ,
a a2
a
C)
1 b
1
,
,0,
a a2
a
D)
1
b 1
, 0,
,
a
a2 a
E)
1
b 1
, 0,
,
a
a2 a
1 2
Nos dan: A
2 1
tonces, el vector u y el número a tales
que Pu u son:
Resolución:
a 0 x1 x2
b a x 3 x 4
A
donde es un cierto número real. En-
B
A)
8
3 , 0
5
B)
1
1 , 1
1
C)
0
0 ,1
1
D)
8
3 , 1
5
E)
8
3 ,0
5
1 0
0 1
I
Tenemos:
2 1 2
AB = I; donde: B = A–1
Si: A A A
2 1
1 2 5 4
Entonces: A
4 5
2 1
A2
x1 x2
1 a 0
2
x 3 x 4 a b a
Reemplazamos: A2 en
1 0 5 4
Q(A)
0 1 4 5
4 4
1 1
Q(A)
4
4
4
1 1
1 1
Respuesta: D) 4
1 1
UNI SEMESTRAL 2013 - III
Por condición:
igualando:
x1
x3
1
x2 a
x4 b
a2
0
1
a
x1 1 ; x2 = 0; x b , x 4 1
a
3
a
a2
Respuesta: D) 1 , 0 , b , 1
a
a2 a
69
2 7 1
1
1 1
1 4 4
8
8
3
3
5
5
0 8
0 3 0
0 5
También: P = Q101
y además: pu u
ÁLGEBRA
TEMA 24
MATRICES I
Exigimos más!
Si 0 la igualdad sería absurda.
Luego: 0
Pu
Q100 Q u
como Q100
m
Qu ;u n
p
UNI SEMESTRAL 2013 - III
2 7 1
1
1 1
1 4 4
m 0
n 0
p 0
2m 7n p 0
m n p 0
m 4n 4p 0
Resolviendo: m = – 8
70
n =3
8
u 3 ; 0
5
8
Respuesta: E) 3 , 0
5
p=5
ÁLGEBRA
TEMA 24
ÁLGEBRA
MATRICES II Y III
DESARROLLO DEL TEMA
I.
DEFINICIÓN DE DETERMINANTE
Sea A = (aij)n una matriz cuadrada, el determinante de
A es un operador (función) que aplicado a la matriz A,
le hace corresponder un único valor numérico.
Notación: |A| o det(A) o detA
Pero el criterio de asignación de ese valor (número real
o complejo) a cada matriz cuadrada no es sencillo en el
caso general. Vamos a definir el determinante para una
matriz de orden 1; 2 y luego de orden 3.
A. Cálculo de determinantes
De orden 1
A (a11) A a11 a11
a11
a21
a12
a22
a31
a11
a32
a12
a21
a22
a13
a23
a11 a12
a33 o a 21 a 22
a13
a 31 a 32
a23
a13 a11 a12
a23 a21 a22
a33 a31 a32
Ejemplo:
2 2
2 2 3
1 1
A 1 1 0 A 1 2
1 2 1
2 2
1 1
3
0
1
3
0
|A|= –2 + 6 + 0 – 3 – 0 – 2 = –1
El determinante coincide con el valor del único elemento de la matriz.
B. Matrices singulares y no singulares
De orden 2
a
a
a
a
A 11 12 | A | 11 12
a21 a22
a21 a22
a11a22 a21a12
Sea A = (aij) una matriz cuadrada. Si |A| = 0 decimos
que A es una matriz singular, en caso contrario
(|A| 0) decimos que A es una matriz no singular..
1. Propiedades
Ejemplo:
3 2
3 2
A
3 4 1 2 10
| A |
1 4
1 4
(Sólo para matrices cuadradas)
a. |AB| = |A| |B|
b. I: matriz identidad |I| = 1
: matriz nula | | = 0
De orden 3
a11 a12
A a21 a22
a
31 a32
a13
a11
a23 A a21
a33
a31
a12
a22
a32
c. |A| = |AT |
a13
a23
a33
d. Si se intercambian 2 filas (o 2 columnas) de
una matriz, el determinante cambia de signo.
e. Si una matriz tiene 2 filas (o 2 columnas)
iguales su determinante es cero.
= a11a22a33+a12a23a31+a13a32a21–a31a22a13–a21a33a12–
a32a11a23
Para recordar fácilmente éste resultado vamos a
recurrir a una regla práctica, llamada la regla de Sarrus
que consiste en repetir las dos primeras filas (o
columnas) debajo (o a la derecha) de todos los elementos de la matriz, así:
UNI SEMESTRAL 2013 - III
71
3 7
• A
| A | 0
3 7
1 1 1
• B 3 5 7 | B | 0 (verifique)
1 1 1
ÁLGEBRA
TEMA 25 - 26
MATRICES II - III
Exigimos más!
f. Si una matriz tiene una fila nula (o columna
nula) su determinante es cero.
A la primera fila le sumamos
fila f1 1 f2 .
3
1 2 1
• A 0 0 0 | A | 0
4 5 3
5 10
B
| B | 15
3 9
k. El determinante de una matriz diagonal o triangular (inferior o superior), es igual al producto
de multiplicar los elementos de su diagonal
principal.
g. Si en una matriz, todos los elementos de una
fila (o columna) son multiplicados por una escalar , su determinante queda multiplicado
por .
1
0
• A
0
0
a b
a
b
• A
; B
c d
c d
|B| = ad – bc = (ad–bc)
|B| = |A|
| B | 4 5 1 10
2
Multiplicamos la segunda fila de A por 3,
queda:
• El determinante de una matriz antisimétrica
de orden impar es cero.
1 1 2
B 9 3 12 | B | 3 | A | 48
0 2 5
2. Menor complementario y con factor de un
elemento de una matriz
Sea A = (aij)n una matriz cuadrada:
h. Si una matriz A de orden n es multiplicada
por una escalar (es decir, todos los elementos de A son multiplicados por ), el determinante de A queda multiplicado por n.
Es decir:
a11 a12
a21 a22
A a11 a12
a
a
n1
n2
n
A A
i. Si dos filas (o dos columnas) de una matriz
tienen elementos respectivamente proporcionales, su determinante vale cero.
a1j
a2j
...
aij
... a1n
... a2n
... ain
... ann
...
anj
Columna j
Fila i
a. El determinante |Mij| se llama menor (menor
complementario) del elemento aij de la matriz A.
y 2y
x y y
u 2u 2 z u u 2 0 0
1 0
...
...
y sea Mij la matriz cuadrada de orden (n–1) que
resulta de eliminar la fila i y a columna j de A,
entonces:
x y 2y
A z u 2u
1 0 0
x
0 0 0
2 0 0
| A | 4 ! 24
0 3 0
0 0 4
4 0
6
• B 0 5
3
0 0 1 / 2
1 1 2
• A 9 3 12 | A | 16
0 2 5
| A | z
1
de la segunda
3
0
b. El cofactor del elemento aij, que se denota
por Aij, se define por Aij=(–1)i+j|Mij|.
1 0 0
Ejemplo:
Los menores complementarios y cofactores de
los elementos de la matriz.
j. Si una fila (o columna) de una matriz se le suma
(o resta) un múltiplo o submúltiplo de otra fila
(o columna, su determinante no se altera.
1 2 3
A 1 3 4
1 4 3
4 7
A
| A | 15
3 9
UNI SEMESTRAL 2013 - III
72
ÁLGEBRA
TEMA 25 - 26
MATRICES II - III
Exigimos más!
Son los siguientes:
Ejemplo:
Calcule el determinante de la matriz:
• Menores complementarios:
3 4
7
4 3
M11
M13
1 3
1 4
1
1 3
0
1 3
M22
M31
M33
2 3
3 4
1
M12
M21
M23
3 6 9
A 0 2 1
3 1 2
1 4
1
1 3
2 3
4 3
6
Resolución:
Calculemos el determinante, realizando el desarrollo
1 2
2
1 4
M32
1 3
1 4
por la segunda fila (a21= 0; a22 = 2; a23 = 1) luego:
|A| = a21A21 + a22A22 + a23A23
1
como:
1 2
1
1 4
A21 = (–1)2+1|M21|=
• Cofactores:
A11 = (–1)1+1 M11 = 1(–7) = –7
A12 = (–1)1+2 M12 = (–1)(–1) = 1
A13 = (–1)1+3 M13 = 1(1) = 1
A21 = (–1)2+1 M21 = (–1)(–6) = 6
6
9
1
2
3
A22 = (–1)2+2|M22|=
3 9
33
3 2
A23 = (–1)2+3|M23|=
3 6
21
3 1
Entonces:
|A| = 0(–3) + 2(33) + 1(21) = 87
A22 = (–1)2+2 M22 = 1(0) = 0
A23 = (–1)2+3 M23 = (–1)(2) = –2
A31 = (–1)3+1 M31 = 1(–1) = –1
Ahora, calculemos el determinante realizando el
desarrollo por la primera columna (a11 = 3; a21 = 0;
A32 = (–1)3+2 M32 = (–1)(1) = –1
a31 = 3). Luego: |A| = a11A11 + a21A21 + a31A31
A33 = (–1)
3+3
M33 = 1(1) = 1
Como:
Observación:
A11=(–1)1+1 |M11| =
El menor complementario |Mij| y el cofactor Aij de
un elemento aij de la matriz A, sólo se diferencian
en el signo.
Como Aij=(–1)i+j |Mij| Aij = |Mij|
II. DESARROLLO DE UN DETERMINANTE
POR COFACTORES
2
1
1 2
5
A21=(–1)2+1 |M21| =
6 9
3
1 2
A31=(–1)3+1 |M31| =
6 9
24
2 1
B. Determinante de Van Der Monde
A. Teorema
El determinante de una matriz cuadrada A = (aij)n
es igual a la suma de los productos de los elementos
de una fila (o columna) por sus respectivos cofactores. Para aplicar este teorema es necesario elegir
una fila (o una columna) y proceder a efectuar el
desarrollo por dicha fila (o columna).
•
•
1. Si elegimos la fila i, el desarrollo de determinante
(por filas) está dado por:
1
x
1
y
1
z z x z y y x
x2
y2
z2
1
x
1
y
1
z
1
w
x2
y2
z2
w2
x3
y3
z3
w3
w x w y w z
z x z y y x
|A| = ai1Ai1ai2Ai2 +... + ainAin
Ejemplos:
2. Si elegimos la columna j, el desarrollo del determinante (por columnas) está dado por:
•
|A| = a1jA1j + a2jA2j +... + ainAnj
UNI SEMESTRAL 2013 - III
73
1 1 1
3 4 5 5 3 5 4 4 3 2
9 16 25
ÁLGEBRA
TEMA 25 - 26
MATRICES II - III
Exigimos más!
Resolviendo el sistema:
•
1
1
1
1
2
3
5
7
22
32 52 72
23
33 53 73
x 5; y 6; z 4; w 3
9
9
9
9
7 2 7 3 7 5 5 2
5 3 3 2 2
Por tanto:
A
5 4 2 3 2 1 240
C. Matriz inversa
5
9
4
9
6
9
1 5 6
9 4 3
3
9
es la matriz inversa de A.
Sea A = (aij)n una matriz no singular, diremos que A
tiene inversa (o que es inversible) si existe otra matriz
B = (bij)n del mismo orden, tal que AB = BA = In (In
matriz identidad). B es llamada la matriz inversa de
A, y se denota por A–1.
1. Teorema
Si A = (aij)n es una matriz no singular, su inversa
es única.
2. Cálculo de la matriz inversa
Prueba
A es inversible A–1, luego A A1 1 (tomamos
determinantes):
A A 1 I A
De orden 1
A a11 A 1 1
a11
A 1 1
De orden 2
De aquí ninguno de los determinantes es cero.
Por tanto
1
A 0. Así A es no singular..
a b
1 d b
1
A
A | A |
c d
c a
Ejemplos:
Ejemplo:
2 3
• A
es inversible, pues |A| = 1 0.
3 5
4 2
A
; | A | 4
10 6
2 3
• B
no es inversible, pues |B| = 0.
4 6
A 1
Ejercicio:
3 6
Halle la inversa de A
4 5
3
2 2
1 6
4 10 4 5
2
1
2
1
De orden n 3
x y
1
Sea A 1
inversa de A, luego A A I2
z w
Aquí aplicamos un procedimiento conocido como
el método de Gauss-Jordan, donde a partir de la
matriz ampliada (A I) por medio de operaciones
elementales fila, se puede obtener una nueva
matriz ampliada (I B) y se concluye que B = A.
es decir:
Es decir:
Resolución:
O.E. fila
I A 1
A I
3 6 x y 1 0
4 5 z w 0 1
Ejemplo:
Entonces:
Halle la inversa de:
3x 6z 1
3y 6w 0
4x 5z 0
4y 5w 1
UNI SEMESTRAL 2013 - III
1 1 1
A 1 2 1
1 1 2
74
ÁLGEBRA
TEMA 25 - 26
MATRICES II - III
Exigimos más!
Resolución:
3 1 1
A 1 1 1 0
1 0 1
Aplicamos el método de Gauss-Jordan:
1 1 1
2 1
1 1 2
A I 1
f2 f1
f3 f1
1 0 0
0 1 0
0 0 1
1 1 1
0 1 0
0 0 1
Propiedades:
Sean A y B matrices cuadradas no singulares.
1
0 0
1 1 0
1 0 1
1 0 1
f1 f2
0 1 0
0 0 1
2 1 0
1 1 0
1 0 1
1 0 0
f1 f3
0 1 0
f3 f1
0 0 1
3
1
1. (A )
1
A
2. (AB)–1 = B–1A–1
3. (AT )–1 = (A–1)T
1 1
1 1
0 I A 1
1 0 1
1
4. |A–1| = | A |
5. A
1
1 A 1 ( escalar)
problemas resueltos
Problema 1
Operación del problema
Resolución:
Si A y B son matrices 3 x 3 y r 0 un
número real, indique la secuencia correcta después de determinar si la pro-
I.
Con los cambios:
posición es verdadera (V) o falsa (f).
I.
(V)
II. det(A + B) det(A) + det(B)
(F)
III. det(rA) = r3det(A)
(F)
C1 C2 ; C2 C3 ; C1 C2
en ese orden; tenemos:
1 a a2
det(aB) = det(A) det(B)
Respuesta: D) VFF
II. det(A + B) = det(A) + det(B)
F 1 b b2
1 c c2
III. det(rA) = rdet(A)
UNI 2008 - II
Nivel fácil
Problema 2
El valor del determinante de:
F = – (b – a) (c – a) (c – b)
A) VV V
a2
a
1
B) VVF
F b2
b
1
C) FVV
c2
c
1
D) VFF
UNI 2004 - II
Nivel intermedio
A) (a – b)(b – c)(c – a)
B) (a – b)(c – b)(a + c)
Aplicación de fórmulas o teoremas
Tenemos:
•
det (AB) = det (A) det (B)
•
det (rA) = rn det (A)
UNI SEMESTRAL 2013 - III
ó F = (a – b) (a – c) (b – c)
Respuesta: E) (a – b)(b – c)(a – c)
es:
E) FFF
Resolución:
por ser un determinante de Vandermonde:
Problema 3
Considere la ecuación matricial:
X 1 3 4 0
2 7 1 2
C) (b – a)(b + c)(a – c)
donde X es una matriz, calcule det(X)
D) (a + b)(b – c)(a – c)
UNI 2010 - I
Nivel intermedio
E) (a – b)(b – c)(a – c)
75
ÁLGEBRA
TEMA 25 - 26
MATRICES II - III
Exigimos más!
A) 6
B) 7
Resolución:
Operación del problema
Ubicación de incógnita
Tomando determinante
Det(x) = |x|
C) 8
Análisis de los datos o gráficos
D) 11
E) 19
UNI SEMESTRAL 2013 - III
| x | 1 3 4 0
2 7
1 2
| x | 1 8
| x | 8
x. 1 3 4 0
2 7 1 2
76
Respuesta: C) 8
ÁLGEBRA
TEMA 25 - 26
ÁLGEBRA
SISTEMA DE ECUACIONES I Y II
DESARROLLO DEL TEMA
I.
CONCEPTO
C.S. (3,2) (3, 2) (2,3) (2, 3)
Es un conjunto de dos o más ecuaciones que se verifican simultáneamente para un mismo conjunto de valores atribuidos a sus letras o incógnitas.
IV. CLASES DE SISTEMAS
A. De acuerdo a su solución
3x y 7
Ejemplo:
5x 2y 8
Vemos que se verifica simultáneamente para = 2, y = 1.
x 2 y 2 13
Ejemplo:
xy 6
Estas ecuaciones se verifican cuando:
(x = 3, y = 2) ó (x = –3, y = –2) ó (x = 2, y = 3) ó
(x = –2, y = –3) es decir se verifican para 4 pares de
valores de sus incógnitas.
1. Compatible
Es aquel sistema que tiene solución que a su vez
puede ser:
• Compatible determinado: Cuando su conjunto solución tiene un número finito de soluciones.
x y z 5
x y z 3
x 2y z 0
Dicho sistema sólo se verifica si: x = 1, y = 1,
z = 3. En tal caso: C.S. (1,1,3), por tener
x 2 y 2 2
Ejemplo en :
x y 5
una solución se dirá compatible determinada.
No existe "x" e "y" alguno en que verifique simultáneamente.
• Compatible indeterminada: Cuando su
conjunto solución tiene un número infinito
de soluciones, así:
II. CONJUNTO SOLUCIÓN DE UN SISTEMA DE ECUACIONES
x 3y 6 (1)
2x 6y 12 (2)
Es el conjunto de todas las soluciones de un sistema.
III. RESOLUCIÓN DE UN SISTEMA DE
ECUACIONES
Estas 2 ecuaciones se simplifican a una sola
ecuación de donde resulta: y
Consiste en hallar el conjunto solución.
Ejemplo:
x 6
3
x 3y 9
Resolver
x y 3
C.S. (0.2),(3,1), (6.0),....
Vemos que sólo se verifica para x = 0, y = 3.
Vemos que tendrá infinitas soluciones.
C.S.:
(0, 3)
2. Incompatible
So n aquello s s ist emas qu e n o p res ent an
solución, su conjunto solución es el vacío. Así:
Ejemplo:
x 2 y 2 13
Resolver
xy 6
3x 2y 7
6x 4y 1
Su conjunto solución está integrado por 4 pares ordenados, debido a que se tiene 4 soluciones, así:
UNI SEMESTRAL 2013 - III
77
ÁLGEBRA
TEMA 27 - 28
SISTEMA DE ECUACIONES I - II
Exigimos más!
•
No existe x, y alguno que verifique simultáneamente a las ecuaciones.
En tal caso se dirá que el sistema no tiene solución. Entonces: C.S.
ó C.S.
B. De acuerdo al grado de las ecuaciones
1. Sistemas lineales
Son aquellos sistemas donde cada una de las
ecuaciones son de primer grado, así:
Usando matrices
El sistema:
a11x1 a12 x 2 a13 x3 ........a1nxn b1
a21x1 a22x 2 a23x 3 ........a2n xn b2
am1x1 am2 x2 am3 x3 ......amnx n bn
es equivalente al sistema matricial:
a11 a12 .... a1n x1 b1
a 21 a22 .... a 2n x 2 b2
am1 am2 ... amn x n bn
2x 3y 16.......(1)
8x 2y 36.......(2)
Cuyo conjunto solución es: ((5,2))
X
A
2. Sistemas no lineales
Son aquellos sistemas donde al menos una de
las ecuaciones no es lineal.
AX B
Si m n A no es una matriz singular..
Se puede definir A–1 (matriz inversa de A), luego:
x 2 y 2 25 .....(1)
x y 7 .......(2)
X A 1 B
cuyo conjunto solución es {(3; 4), (4; 3)}
Ejemplo:
V. ESTUDIO DEL SISTEMA LINEAL
2x 5y 4
Resolver
3x 2y 13
En forma general: Consideramos un sistema lineal de
"m" ecuaciones con "n" incógnitas.
Solución:
Es equivalente al sistema matricial:
a11x1 a12 x 2 a13x 3 .......am xn b1
a21x1 a22 x 2 a23x 3 .......a2n xn b2
am1x1 am2 x 2 am3x 3 .......amn xn bm
2 5 x 4
3 2 y 13
Donde:
Donde los a1 son coeficientes y x1 x 2 x 3..... x n son las
incógnitas.
En tal caso el conjunto solución es:
2 5
1 2 5
1
A
A 19
3 2
3 2
2 5
A 1 1
19 3 2
C.S. (x1 x 2 x 3.......x n)
Para la resolución del sistema utilizaremos los si-guientes
métodos:
•
4
como: X A1
13
Método de Gauss
Conocido como los métodos de eliminación, sustitución, igualación consiste en ir eliminando incógnitas hasta llegar a una ecuación de una sola incógnita.
Así, resolver:
2 5 4 1 57
X 1
19 3 2 13 19 38
3
X
2
Luego: x = 3, y = –2
2x y 2z 10.....(1)
3x 2y 2z 1.....(2)
5x 4y 3z 4.....(3)
•
(2) – 2(1): –x + 6z = –19......... (1')
(3) – 4(1): –3x + 11z = –36........ (2')
2' – 3(1'): –7z = 21 z = 3 z 3
C.S. (1, 2 3)
UNI SEMESTRAL 2013 - III
B
78
C.S.(3, 2)
Método de los determinantes
Se utiliza cuando el sistema es determinado.
Sea el sistema:
a11x1 a12x2 a1n xn b1
a 21x1 a22x 2 a2nx n b2
....(*)
am1x1 am2x 2 amnx n bn
ÁLGEBRA
TEMA 27 - 28
SISTEMA DE ECUACIONES I - II
Exigimos más!
Llamaremos:
– Determinantes del sistema
a11 a12
a21 a22
a
a
n1 n2
–
Dicho sistema siempre es compatible donde una de
sus soluciones es la trivial {(0, 0, 0 … 0)}.
... ... a1n
... ... a2n
... ... amn
Así mismo puede tener otras soluciones las llamadas
no triviales.
TEOREMA
Un sistema homogéneo (**) tiene soluciones aparte
a la trivial, si y sólo sí:
Determinante con respecto a alguna incógnita
Se conseguirá a partir del determinante anterior
reemplazando los elementos de la columna de
coeficientes de la incógnita en referencia por los
términos independientes.
a11 a12 ... b1 ... a1n
a 21 a22 ... b2 ... a 2n
0
a
n1 a12 ... bn ... amn
a11 a12 ... b1 ... a1n
a21 a22 ... b2 ... a2n
a
n1 an2 ... bn ... amn
Ejemplo 1: Resolver 3x + 2y = 0
5x – y = 0
Solución:
3 2
3 10 13
5 1
TEOREMA DE CRAMER
implica que la solución seria única, la solución trivial (0,0).
La solución del sistema (*) puede determinarse hallando cada incógnita como sigue:
x1
i
2x 5y 0
Ejemplo 2: Resolver
6x 15y 0
, i 1...n
Ejemplo: Resolver: 2x 5y 4
Solución:
3x 2y 13
2 5
Como
30 30 0
6 15
Solución:
Calculando los determinantes:
La solución del sistema no sólo es la trivial (0,0); si
2 5
4 15 19
3 2
no que tendrá infinitas soluciones.
4 5
x
8 65 57
13 2
sola 2x – 5y = 0.
Veamos que ambas ecuaciones se reducen a una
y 2x
5
Asi: Si x = 5t, y = 2t
2 4
y
26 12 38
3 13
De donde:
x x 57 x 3
19
y
(x, y) (5, 2)t / t
VI. ANÁLISIS DE LAS SOLUCIONES
y
38 y 2
19
Sea el sistema:
C.S. (3, 2)
•
a11x1 a12x1 ... a1nx1 b1
a 21x1 a22x 2 ... a2nx n b2
an1x1 an2x2 ... amnxn bn
Sistema homogéneo
Es un sistema de ecuaciones lineales se llamará
homogéneo si todos los términos independientes
son nulos, así:
Sabemos que la solución viene dado por:
a11x1 a12x 2 ... a11x1 0
a 21x1 a22x 2 ... a12x1 0
...( )
an1x1 an2x2 ... amnxn 0
UNI SEMESTRAL 2013 - III
xi
79
i
determinante del sistema
i determinante respecto a x
ÁLGEBRA
TEMA 27 - 28
SISTEMA DE ECUACIONES I - II
Exigimos más!
Ejemplo 2:
Diremos que el sistema tendrá:
3x 4y 5
A. Solución única
6x 6y 10
Esto sucede si y sólo si 0 .
Como: 3 4 5
6 8 10
B. Infinitas soluciones
Si y sólo si 0 i 0, i 1, 2, ...n
Entonces el sistema tiene infinitas soluciones.
C. No tiene solución
Ejemplo 3:
Si y sólo si 0 1 0 para algún i.
Ejemplo 1:
3x y 2
2x 3y 3
3
1
2 3
2x 5y 7
6x 15y 30
9 2 11 0
Como:
El sistema tiene solución única.
2
5
7
el sistema no tiene solución.
6 15 30
problemas resueltos
Problema 1
Al resolver el siguiente sistema:
3
x y 2 2x 3y 7 3
23 x y 2 3 2x 3y 7 14
se obtiene que el valor de (x + y) es:
UNI 2008 - II
Nivel fácil
A) –2 B) –1
C) 0 D) 1
E) 2
Resolución:
Ubicación de incógnita
Piden: x + y
Análisis de los datos o gráficos
Llamemos:
3
Problema 2
Determinar k de manera que el sistema tenga solución no trivial, dar como
respuesta la suma de los valores de K.
(1 k)x y z 0
2x ky 2z 0
x y (1 k)z 0
UNI
Nivel intermedio
A) 4
B) 5
C) 0 D) 6
E) 1
Problema 3
Dado el sistema de ecuaciones:
Resolución:
Tenemos:
(1 k)x y z 0
2x ky 2z 0
x y (1 k)z 0
Resolución:
Haciendo un cambio de variable:
1
1
a
b
x y1
2x y 3
Dato: Sistema homogéneo con solución trivial se cumple:
x y 2 m
2x 3y 7 q
Operación del problema
3 x y 2 2x 3y 7 3
3
2 x y 2 3 2x 3y 7 14
1k
2
1
1
k
1
2
0
(1 k)
m q 3
... I
2m
3q
14
...
II
(1 – k)(– k)(– k –1) –2 + 2 – k + 2 (k + 1)
+ 2(k – 1) = 0
Luego: k3 – 4k = 0
3
x y 2 1
x + y = –1
De donde: k1 0 k 2 2 k 3 2
k1 k 2 k 3 0
Respuesta: B) –1
UNI SEMESTRAL 2013 - III
3
1
7
x y 1 2x y 3
5
El valor de x + y es igual a:
A) –1 B) 0
C) 1 D) 2 E) 3
UNI 2007 - II
Nivel difícil
Reemplazando en cada ecuación:
5
4a 5b 2 ... ()
3a b 7 ... ()
5
Sumando + 5
19
Tenemos 19a
2
1
de donde: a b 1
2
10
x y 1 2 ...(I)
Luego
2x y 3 10 ...(II)
Reemplazando el cambio de variable:
De: 3
+
Tenemos: 5m = 5
De donde: m = 1
Reemplazando:
4
5
5
x y 1 2x y 3
2
Sumando:
I II
3x + 2 = 8
x = 2 y = –3
Piden x + y = –1
Respuesta: C) 0
80
Respuesta: A) –1
ÁLGEBRA
TEMA 27 - 28
ÁLGEBRA
NÚMEROS COMPLEJOS I
DESARROLLO DEL TEMA
I.
B. Adición entre números complejos
DEFINICIÓN
El sistema de los números complejos es el conjunto C de
Para hallar la suma entres dos números complejos, se
todos los pares ordenados, de componentes reales,
sumarán las partes reales y también las partes imagina-
z = (x,y) y dos operaciones llamadas adición y multipli-
rias.
cación tales que para cualesquiera dos elementos que
Así:
pertenezcan a C, como por ejemplo: z1 = (x1;y1) y z2 =
(x2;y2) se definen:
–
z1 + z2 = (x1 + x2; y1 + y2)
–
z1 z2 = (x1x2 – y1y2; x1y2 + x2y1) … (multiplicación)
(x1 y1i) (x 2 y 2i) (x1 x2 ) (y1 y 2)i
… (adición)
C. Multiplicación entre números complejos
II. FORMA CARTESIANA O BINÓMICA DE
UN COMPLEJO
Para hallar el producto de multiplicar 2 números
complejos, para la parte real se multiplicaran las
partes reales menos el producto de las partes ima-
Teorema
ginarias. Y para la parte imaginaria se multiplicará la
Todo número complejo z de la forma z = (x;y) será
parte real con la segunda parte imaginaria au-
posible expresarlo como z = x + yi tal que i 1 se
mentando en el producto de multiplicar la primera
parte imaginaria con la segunda parte real.
denominará unidad imaginaria.
Es decir z (x; y) x yi ; i
Así:
1
(x1 y1i) (x2 y2i) (x1x 2 y1y2) (x1y2 x2y1)i
Ejemplo:
z (2; 3) 2 3i
III. REPRESENTACIÓN GEOMÉTRICA (PLANO DE GAUSS)
w (0; 3) 0 3i 3i
Si:
Re(z)....(Parte Real de z)
z x yi
I m(z)....(Parte Imaginaria de z)
En el plano cartesiano denominaremos al eje Y como
eje imaginario y al eje x como eje real.
Sea: z a bi / a 0 b 0
A continuación vamos a definir para los números complejos "x + yi" la relación de igualdad y las operaciones
de adición y multiplicación del siguiente modo:
Entonces su representación en el plano de "Gauss"
será como sigue:
A. Igualdad de números complejos
Dos complejos son iguales, si y sólo si sus partes
reales y sus partes imaginarias son iguales respectivamente. Así:
x1 y1i x 2 y 2i x1 x 2 y1 y 2
UNI SEMESTRAL 2013 - III
81
ÁLGEBRA
TEMA 29
NÚMEROS COMPLEJOS I
Exigimos más!
IV. CANTIDADES IMAGINARIAS
i8 i4 i4 1
Son aquellos números que resultan de extraer una raíz
de índice par a un número real negativo.
Así por ejemplo:
1;
i9 i4 i i
i10 i8 i2 1
i11 i8 i3 i
2; 4 5; 2n 16
i12 i8 i4 1
Donde: n
Se observa que las potencias enteras de "i" se re-
De todos estos el más importante es 1 ; al cual de-
piten cada cuatro veces y sólo toman uno de los
nominaremos unidad imaginaria, cuya notación univer-
cuatro valores i; –1; –i; 1; esto merece una espe-
sal es i 1 .
cial atención.
Aplicación:
Propiedades
16 16(1) 16 1 4i
Se observa principalmente que:
i4 1 ; i8 1 ; i12 1 ; etc.
5 5( 1) 5 1 5i
A. Unidad imaginaria
Esto implica que la unidad imaginaria elevado a un
El número complejo (0; 1) es la unidad imaginaria;
múltiplo de cuatro es igual a la unidad.
tiene la particular notación i = (0;1).
Por lo tanto i4 = 1
Teorema
o
En general
2
i 1; i (0;1)
i4 1
Luego deducimos que:
Prueba
i2 (0;1)(0;1) (0 1; 0 0)
(1; 0) 1
o
o
o
i4 1 i ; i4 2 1; i4 3 i
i2 1
Generalizando:
Teorema
o
i4 k ik ; k
y ; (0; y) yi
Luego se deduce:
Prueba
o
4 k
i– – ik ; k
yi (y; 0)(0;1)
(0 0; y 0) (0; y)
(0; y) yi
Teorema
ik (1)k ik ; k
B. Potencias enteras de la unidad imaginaria
Estudiaremos el comportamiento del número in ;
Propiedades
n ; teniendo en cuenta la siguiente definición:
Sea i
i0 1 ; i1 i
1 la unidad imaginaria:
1. i i2 i3 i4 0
i1 i
2. i4k i4k 1 i4k 2 i4k 3 0 ; k
i2 1
3. in in 1 in 2 in 3 0 ; n
3
2
i i i i
V. TIPOS DE NÚMEROS COMPLEJOS
i4 i2 i2 (1)(1) 1
i5 i4 i i
A. Complejo real o puramente real
i6 i4 i2 1
Es aquel número complejo que carece de la parte
imaginaria; es decir su parte imaginaria es cero.
i7 i4 i3 i
UNI SEMESTRAL 2013 - III
82
ÁLGEBRA
TEMA 29
NÚMEROS COMPLEJOS I
Exigimos más!
Notación:
5. z z 2i Im(z)
z x 0i x ; z
6. z1 z2 z1 z2
7. z1z2 z1z2
B. Complejo imaginario puro
Es aquel número complejo que carece de la parte
z
8. 1 z1 ; z2 (0;0)
z2 z2
real; es decir su parte real es cero; además su parte
imaginaria es diferente de cero.
n
9. zn z ; n
Notación:
z 0 yi yi ; y 0
10.
C. Complejo nulo
z
n
n
z ; n
VI. DIVISIÓN DE NÚMEROS COMPLEJOS
Es aquel número complejo que presenta la parte
Sean los números z1 , z2 z2 (0,0) para efectuar la
z1
habrá que multiplicar a z1 y z2 por z2 con lo
z2
cual se obtiene:
real e imaginaria igual al número cero; es decir las
dos componentes son nulas.
Notación:
z1 a bi;z2 c di
z 0 0i 0
z1
a bi (a bi)(c di)
z2
c di (c di)(c di)
1. Definición
• Dado el complejo z = x + y; se define el
complejo conjugado de z, denotado por z,
como:
(ac bd) (bc ad)i
c 2 d2
a bi ac bd bc ad
c di c 2 d2 c 2 d2
z x yi
VII.MÓDULO O VALOR ABSOLUTO DE UN
COMPLEJO
Representación geométrica de z = x + yi;
( x 0 y 0 ) de su conjugado y su opuesto.
Dado z = a + bi ; el módulo o valor absoluto de z es un
número real no negativo denotado por
z
z ; tal que
a2 b2 .
Propiedades
z; z1;z2
1. z z z es complejo real .
Observación
2. z z
3. z z z* z es complejo imaginario .
a;b z a | z | | a |
4. z z 2 Re(z)
UNI SEMESTRAL 2013 - III
z bi | z | | b |
83
ÁLGEBRA
TEMA 29
NÚMEROS COMPLEJOS I
Exigimos más!
Propiedades
9.
z1 z2 z1 z2
De la definición de módulo se desprende las siguientes
10. z1 z2 z1 z2
propiedades; sean Z; Z1; Z 2 entonces:
1.
z 0 ; z 0 z (0;0)
2.
z z z*
3.
z
4.
(z) z ; Im(z) z
5.
z1z2 z1 z2
6.
z
z1
1 ; z2 (0;0)
z2
z2
7.
zn z
n
8.
2
VIII.POTENCIACIÓN
La potenciación en forma binómica tiene muchas limitaciones; por ello se utiliza cuando las potencias son
zz
z
n
n
pequeñas.
Resultados importantes
(1 i)2 2i
; (1 i)2 2i
(1 i)3 2i(1 i) ; (1 i)3 2i(1 i)
(1 i)4 4
; n
; (1 i)4 4
1i
i
1i
z ; n n 2
;
1i
i
1i
problemas resueltos
Problema 1
Calcular: x y
y x
Reducir:
i2 + i4 + i6 + .... + i102
A)
A) i
B) –i
C) 1
Resolución:
10
3
C)
5
3
i4K 2 i4K 0; K
10
Respuesta: A)
3
Problema 3
Calcular z
D)
5
3
E)
15
2
Recordemos que:
10
3
10
3
B)
D) –1
E) 0
K
siendo:
z (2 i)(3 i)(1 i)
A) 2 10
B)
10
C) 10
Resolución:
En el problema:
2
4
6
98
100
102
E i
i i
... i i i
se anulan cada dos
E 0 i102 i4K 2 i2
Elevando al cuadrado ambos miembros
de la igualdad tenemos:
2
E) 2 5
2
5 – 3i = x – y + 2xyi
Resolución:
Por igualdad de complejos:
Por propiedad se plantea:
x 2 y2 5 xy 3
2
E 1
Se pide calcular el valor de:
Si 5 3i x yi; x, y .
UNI SEMESTRAL 2013 - III
z 2 i 3i 1i
z 5 10 2 100
Respuesta: D) –1
Problema 2
D) 10 2
2
y x y
K x
y x
xy
84
z 10
2
Respuesta: C) 10
ÁLGEBRA
TEMA 29
ÁLGEBRA
NÚMEROS COMPLEJOS II Y III
DESARROLLO DEL TEMA
I.
FORMA POLAR O TRIGONOMÉTRICA
DE UN NÚMERO COMPLEJO
Teorema
Sea z = a + bi un número complejo diferente del nulo.
z z (Cos iSen)
w w (Cos iSen)
Dados los números complejos no nulos:
Es decir z 0
Se verifican:
1. zw z w (Cos( ) Sen( )
2.
z
z
(Cos( ) iSen( ))
w
w
Observaciones:
Para multiplicar complejos en la forma polar se multiplica los módulos y se suma los argumentos.
De la figura x z Cos, y z Sen
y
Donde: Tan
x
Entonces: z x yi z Cos z Seni
arg(z w) arg(z) arg(w)
Para dividir complejo en la forma polar se dividen
los módulos y se resta los argumentos.
z z (Cos iSen)
arg z arg(z) arg(w)
w
Es la representación trigonométrica o polar de un complejo; donde el ángulo se le denomina el argumento de
Teorema (de De Moivre)
Dados z z (Cos iSen); z (0;0) n
z denotado por Arg(z); es decir: Arg(z)
Se observa que puede tomar infinitos valores como:
Se tiene zn z
Corolario
1 ; 2 2 ; 3 4
III. RAÍCES "n-ésimas" DE LA UNIDAD
Se pide hallar: x k n 1
De todos los valores de ; elegimos aquel que se encuentra en el intervalo 0; 2 ; es decir 0 2; a dicho se
le denomina argumento principal, cuya notación es:
z 1
Donde: z 1 oi
0
Arg(z)
Conociendo el argumento principal de z denotado por
Arg(z) podemos generar otros cuya notación es:
UNI SEMESTRAL 2013 - III
(Cos iSen )
arg(zn) n arg(z); n
III. ARGUMENTO PRINCIPAL DE UN NÚMERO COMPLEJO
arg(z) Arg(z) 2k
n
Luego : x k Cis 2k
n
k 0,1, 2,..........,n 1
K 0; 1; 2; 3; ...
85
ÁLGEBRA
TEMA 30 - 31
NÚMEROS COMPLEJOS II Y III
Exigimos más!
Donde:
x 0 w0 1
Donde:
e es el número de Euler e = 2,718281
argumento en radianes; i = (0; 1)
Entonces tenemos una nueva representación para el
complejo. z z (Cos iSen) z e
x1 w
x 2 w2
z z e i ...(*)
xn 1 wn1
Entonces: Las "n" raíces de la unidad serán:
V. RAÍZ DE UN NÚMERO COMPLEJO
1, w,w , w ,....., w
2
3
n 1
Una raíz n - ésima del número complejo z = x + yi es
número complejo W, tal que wn = z.
Es decir: n z w w n z
Teorema:
Si w es una raíz enesima de la unidad y w 1 ,
Entonces: 1 + w + w2 + ......+ wn-1 = 0
wk
IV. FORMA EXPONENCIAL DE UN COMPLEJO
n
Teorema de Euler
2k
2k
z Cos
iSen
n
3
Donde: k = 0, 1, 2, ......., n – 1
Son las raíces de z = x + yi
ei Cos iSen
problemas resueltos
Problema 1
Dadas las siguientes proposiciones:
I. Las raíces de ein – 1 = 0, pertenecen a un polígono regular de n lados, n .
3
;
II. Si e i a bi y
, enton4 4
Asi mismo b
Pues b sen().
III. Verdadero
cos() cos() 2k
2
2
2
;
yb
;1 .
2
2
2
III. Dados , 0; 2 , tales que ,
si cos() cos(), entonces e
1.
UNI 2010 - I
Indique cuáles son correctas:
A) Solo I
B) Solo II
C) Solo III
D) I y II
E) II y III
Resolución:
I. Falso
Las raíces n-ésimas de la unidad al
ser llevadas al diagrama de Argan'd
están generan un polígono regular si: n n 3.
II. Falso
5 18
2 Cis
a bi
3
Elevamos a la 18 a ambos miembros:
3
Entonces:
18
3
5
2 Cis
3
18 a bi
26 Cis(30
) a bi
e i() 1
1
ces a
i()
2
;1
2
Respuesta: C) 1
Problema 2
La raíz cúbica del número complejo z = –2
de mayor argumento principal, es también raíz 18-ésima de otro complejo
u = a + bi con a y b números reales.
Determine a + b.
UNI 2009 - II
A) 25 ( 3 1)
B) 26
C) 27 ( 3 1)
D) 28
E) 29
Resolución:
Determine: a + b, a partir de: V = a + bi
Analizando:
Z 2 Z 2Cis
Calculando:
Luego: 36 + oi = a + bi
a 26 b 0
Respuesta: B) a + b = 26
Problema 3
Sabiendo que 1, W y W2 son las tres
raíces cúbicas de la unidad real. Calcular:
2
3
50
R (.....((W W )W )W .....)W
A) W 2
B) 1
D) W
E) –W2
C) –W
Resolución:
La expresión dada es:
2
3
50
R (W) W W W .... W
1 2 3... 50
3
2
2
;
De donde: a
2
2
a cos().
UNI SEMESTRAL 2013 - III
2k
Z 3 2 Cis
3
donde: k = 0, 1, 2
Siendo el de mayor argumento, si:
5
K 2 Z2 3 2 Cis
3
La cual también es una de las raíces de:
; pues
18
U 18 a bi
86
R (W)W
R (W)W
3K
W1
R W
Respuesta: D) W
ÁLGEBRA
TEMA 30 - 31
ÁLGEBRA
PROGRAMACIÓN LINEAL
DESARROLLO DEL TEMA
I.
RESOLUCIÓN GRÁFICA DE UN SISTEMA DE ECUACIONES LINEALES
II. PROGRAMACIÓN LINEAL
A. Concepto
Dado un sistema de inecuaciones lineales conformado
por dos o más inecuaciones, la solución gráfica de dicho
sistema es la región que se determina al intersectar
todos los semiplanos originados por las inecuaciones
que conforma el sistema.
Ejemplo:
Resolver:
2x y 4 ... (1)
3x y 6 ... (2)
Resolución:
Inicialmente graficamos los semiplanos que correspondan a cada inecuación del sistema:
(1) 2x y 4 y 4 2x; semiplano ubicado por encima de la recta y = 4 – 2x, incluyendo a ésta.
y
Es un modelo matemático mediante el cual se
resuelve un problema indeterminado, formulado por
ecuaciones lineales, optimizando la función objetivo,
también lineal.
La programación lineal consiste en optimizar (minimizar o maximizar) una función lineal, que llamaremos función objetivo, de tal forma que las variables de dicha función estén sujetas a una serie de
restricciones que expresamos mediante un sistema de inecuaciones lineales.
B. Función objetivo
Es una función lineal en dos variables que debemos
maximizar o minimizar. La función objetivo presenta
la siguiente forma:
F(x; y) ax by c
donde a, b y c son constantes y x, y se llaman
variables de decisión.
4
x
C. Conjunto de restricciones
2
(2) 3x y 6 3x y 6
y 3x 6
semiplano ubicado por debajo de la recta y = 3x – 6,
incluyendo a ésta.
y
D. Soluciones factibles
x
2
Es el sistema de inecuaciones lineales con dos
incógnitas que expresan un conjunto de limitaciones
que presenta el problema propuesto.
Aquí también se consideran a las variables de decisión
como valores no negativos, es decir x 0 y 0 .
Son cada una de las soluciones que verifican al conjunto de restricciones, cada solución factible se
representa por un punto del plano cartesiano.
–6
E. Región factible
Finalmente el conjunto solución del sistema viene dado
por la intersección de los semiplanos hallados, veamos:
y
(1)
CS
4
x
Se llama así al conjunto convexo formado por todos
los puntos que representan a las soluciones factibles,
en una región poligonal.
La región factible puede, o no, ser acotada, la primera incluye los puntos de su frontera y la otra no.
Observación: Sólo las regiones factibles acotadas presentan siempre solución, en las otras
puede o no existir solución.
2
–6
(2)
UNI SEMESTRAL 2013 - III
87
ÁLGEBRA
TEMA 32
PROGRAMACIÓN LINEAL
Exigimos más!
F. Solución óptima
III. MÉTODO ANALÍTICO O MÉTODO DE
LOS VÉRTICES
Es el punto cuyas coordenadas hacen de la función
objetivo un valor máximo o mínimo.
La solución óptima, en caso de existir, se alcanza
en un vértice de la región factible.
A. Descripción
Se determina la región factible calculando las coordenadas de todos sus vértices, luego cada punto
que corresponde a un vértice se reemplaza en la
función objetivo esperando obtener con alguno de
ellos un valor máximo o mínimo según corresponda
a la optimización.
y
B
C
B. Teorema
S
A
D
x
Si la función objetivo asume el mismo valor óptimo
en dos vértices de la región factible, también asume
el mismo valor en los puntos del segmento limitado
por dichos vértices.
S = región factible
A, B, C y D son posibles puntos de organización.
problemas resueltos
Problema 1
Determine el valor mínimo que toma la
función objetivo, P(x, y) = 10x + 20y
sujeta a las restricciones:
xy2
x 2y 2
yx
Resolución:
Ubicación de incógnita
Valor mínimo de la función objetivo P
Análisis de los datos o gráficos
x y 2
P(x;y) 10x 20y x 2y 2
yx
Operación del problema
x=y
2
1
A(1;1)
x - 2y = 2
-1 2
B(2;0) x + y = 2
Para A (1;1)
P = 10(1) + 20(1) = 30
Para B (2;0)
P = 10(2) + 20(0) = 20
Respuesta: 20
Problema 2
En relación a un programa lineal, indique la secuencia correcta, después de
determinar si la proposición es verdadera (V) o falsa (F):
I. Las condiciones de no negatividad
significan que todas las variables de
decisión deben ser positivas.
II. El número de puntos extremos de
la región admisible es finito.
III. En un programa lineal pueden
variarse los coeficientes de la funUNI SEMESTRAL 2013 - III
ción objetiva y aún mantenerse la
solución óptima.
UNI 2010 - I
Resolución:
Ubicación de incógnita
Valor de verdad
Operación del problema
I. FALSO
Tal condición establece que las
variables de recisión deberan ser
mayores o iguales que cero, es
decir: x 0 y 0 .
II. FALSO
En el caso de que el polígono sea
no acotado los puntos extremos
no se podrían determinar.
III. VERDADERO
De acuerdo con la Regla de Permutación esta proposición es perfectamente válida.
Respuesta: FFV
Resolución:
Ubicación de incógnita
* n° de peces de la especie S1: x;
peso promedio (S1) = 4 kg.
* n° de peces de la especie S2: y;
peso promedio (S2) = 2 kg.
Análisis de los datos o gráficos
Función objetivo: F(x; y) = 4x + 2y
S1(x)
S2(y)
F1
1x
2y
F2
3x
1y
Operación del problema
x 2y 500
3x y 900
x, y 0
Graficando:
Problema 3
Un lago se llena de dos especies de
peces S1 y S2. La especie S1 proporciona un peso promedio de 4 kg de carne y la especie S2 un peso promedio
de 2 kg.
Dos tipos de comida F1 y F2 están disponibles en el lago. El requerimiento
promedio de la especie S1 es 1 unidad
de F1 y 3 unidades de F2, mientras que
el requerimiento de S2 en 2 unidades
de F1 y 1 unidad de F2 cada día. Si se
dispone diariamente de 500 unidades
de F1 y 900 unidades de F2, determine
el número total de peces en el lago
que maximice el peso total de carne
de pescado.
UNI 2011 - I
88
y
900
(0;250)
(260;120)
500
0
(300;0)
x
I. F(0,250) = 500
II. F(260;120) = 1280 (máximo)
III. F(300,0) = 1200
El número de peces que maximiza
es: 260 + 120 = 380
Respuesta: 380
ÁLGEBRA
TEMA 32
ÁLGEBRA
INTRODUCCIÓN A LA POTENCIACIÓN
- POTENCIACIÓN DE UN POLINOMIO
DESARROLLO DEL TEMA
I.
FACTORIAL DE UN NÚMERO Z+
Luego: x – 4 0 x – 1 1
Llamamos así al producto que resulta de multiplicar
todos los números enteros y positivos de manera
consecutiva desde la unidad hasta el número indicado.
x 4
x 5
3. Si: a! = b! a = b
* a; b 0; 1
Ejemplo:
(x – 5)! = 6
(x – 5)! = 3!
x–5=3
x=8
Notación: n! ó n
Se lee: Factorial de "n".
Así: 2 ! 1 2 2
3! 1 2 3 6
4. Todo factorial contiene en su desarrollo a otro
factorial menor.
4 ! 1 2 3 4 24
5! 1 2 3 4 5 120
(n 2)!
n! n (n
1)
(n
2)...3
2
1
6 ! 1 2 3 4 5 6 720
(n1)!
En general:
n! = n(n – 1)!
n! = n(n – 1) (n – 2)!
n! 1 2 3... (n – 2)(n – 1)n
II. NÚMERO COMBINATORIO
o también: n! n(n – 1)(n – 2)...3 2 1
Representa el número de combinaciones de "n" elementos tomados de "k" en "k".
Observaciones:
1. (a b) ! a! b!
2. (ab) ! (a !) (b !)
Notación: Cnk n Ck n Ck
3. a ! a!
b!
b
n!
Definición: Cnk
; nk
k !(n k) !
Propiedades
Donde: n k o
1. n! existe n zo
Ejemplo:
Luego:
• (–5)! No existe
• –5! Si existe
• (2/3)! No existe
• 7! Si existe
C52
Regla práctica:
2. Por definición 1! = 1.
Por acuerdo 0! = 1.
Ejemplo: Hallar "x" en: (x – 4)! = 1
UNI SEMESTRAL 2013 - III
5!
120
10
2!(5 2) ! 2 6
Cnk
n!
k !(n – k) !
"k
" factores
n(n – 1)(n – 2)...(n – k 1) (n – k) !
1 2 3...k (n – k) !
" k " factores
89
ÁLGEBRA
TEMA 33 - 34
INTRODUCCIÓN A LA POTENCIACIÓN - POTENCIACIÓN DE UN POLINOMIO
Exigimos más!
Propiedades
5. Reglas de degradación
1. Cnk Existe n z
Cnk
•
k zo
kn
n n 1
C
k k 1
10 9
Ejemplo: C10
C
3
3 2
2. Propiedad complementaria
Cnk n – k 1 Cnk –1
k
•
Cnk Cnn–k
Ejemplo: C58 8 5 1 C84 C85 4 C84
5
5
Ejemplo:
50
C50
48 C2
Cnk
•
50 49
1 225
2 1
n
Cn–1
n–k k
9
C8
9–4 4
9
C 94 C84
5
Ejemplo: C 94
3. Propiedad de igualdad
Cnp Cnq
1.a Posibilidad: p = q
III. BINOMIO DE NEWTON
2.a Posiblidad: p + q = n
(Para exponente entero y positivo)
Ejemplo:
n
Definición: (x a)n Cnk x n–k ak
Hallar la suma de valores de "n" en:
k 0
10
C10
n C6 .
Donde: x; a 0 n
1.a Posibilidad: n1 = 6.
Así:
2.a Posibilidad: n + 6 = 10 n2 = 4.
(x + a)2 = x2 + 2 x a + a2
(x + a)3 = x3 + 3x2a + 3xa2 + a3
Luego n1 + n2 = 10.
(x + a)4 = x4 + 4x3a + 6x2a2 + 4xa3 + a4
(x + a)5 = x5 + 5x4a + 10x3a2 + 10x2a3 + 5xa4 + a5
4. Suma de combinatorios
Cnk Cnk 1 Ckn 11
Nos damos cuenta:
(x a)5 c50 x 5 c15 x 4a c 52 x3a2 c53x 2a3 c 54 xa4 c 55a5
Ejemplo:
Hallar: S C40 C15 C62 C73
Luego:
(x a)n c n0 xn c1n xn 1a cn2 x n 2a2 c n3 xn 3a 3 ... Cnn an
Luego: S C50 C15 C62 C73
Desarrollo o expansión del binomio
S C16 C62 C73
Propiedades
S C72 C73
1.
N. de términos Exponente " n " 1
de (x a)n
S C83
S
87 6
3 2 1
Hallar el nº de términos en el desarrollo de: (x + 3y)7.
56
UNI SEMESTRAL 2013 - III
N.º de términos = 7 + 1 = 8.
90
ÁLGEBRA
TEMA 33 - 34
INTRODUCCIÓN A LA POTENCIACIÓN - POTENCIACIÓN DE UN POLINOMIO
Exigimos más!
2. Si: x = a = 1; se obtiene la sumatoria de coeficientes:
4. Término central ("n" exponente del binomio)
Si "n" par existe un sólo T central:
c n0 c1n c 2n cn3 ... cnn 2n
Tc Tn
1
c 50 c15 c 25 c 35 c54 c 55 25 32
2
Si "n" impar existen 2 términos centrales:
n–2
c n–2
c1n–2 c 2n–2 ... c n–2
2n–2
0
1.er Tc Tn 1
Hallar la suma de coeficientes en el desarrollo de:
(5x2 + y4)40
2
2.do Tc Tn 1
Luego: x = y = 1 (5(1)2 + (1)4)60 660
2
3. Término de lugar general:
Siendo: (x + a)n.
En su desarrollo:
1
5. Suma de exponentes
Siendo B(x,a) = (xp + aq)n
Tk 1 c kn xn–kak
Exponentes
Donde: "k + 1" es el lugar.
Ejemplo:
Hallar el T61 en el desarrollo de:
2
(p q)n(n 1)
2
Ejemplo:
Hallar la suma de exponentes en el desarrollo de:
3 90
B(x; y) = (3x + 2y )
2 30
3 60
T61 c 90
60 (3x ) (2y )
3
x 4
39
Luego: p = 1/3; q = 1/2; n = 39.
30 60
60 180
T61 c 90
60 3 x 2 y
1 1
3 2 39(39 1)
exponentes
Exp 650
2
30
60 60 180
T61 c 90
60 3 2 x y
problemas resueltos
Problema 1
Resolución:
Problema 2
Si "x" es un número real tal que el
término central en el desarrollo de:
Sabemos que:
Hallar el valor de "n" de modo que:
2 – 3x
3
2
12
TK 1 Ckn xn–k ak
n
n
(2r 1) 2n 4
r 0
r
TC T12 T7
1
Nivel difícil
2
12–6
T7 C12
(–3x 2)6 924
6 (2 3)
Es 924, hallar el valor de:
1 + x 2 + x4 + x6
12.11.10.9.8.7 26 36 x 6 924
6.5.4.3.2.1
36
26
x=1
Nivel intermedio
A) 18
B) 16
C) 17
D) 15
E) 20
A) 4
B) 8
C) 6
Resolución:
Entonces:
1 + 12 + 14 + 16 = 4
D) 16
Respuesta: A) 4
E) 2
UNI SEMESTRAL 2013 - III
91
Sabemos:
n n
2n
r 0 r
ÁLGEBRA
n n
r n 2n–1
r 0 r
TEMA 33 - 34
INTRODUCCIÓN A LA POTENCIACIÓN - POTENCIACIÓN DE UN POLINOMIO
Exigimos más!
Entonces:
Determinar el valor de:
n
n n n
2r 2n– 4
r 0 r r 0 r
2 n 2n1 2n 2n 4
(n 1) 2n 2n 24
n = 15
Respuesta: D) 15
Problema 3
n! (n! 3)
Si:
18.
n! 4
UNI SEMESTRAL 2013 - III
K
n2 3n 7
Nivel intermedio
A)
47
B)
17
(n!)2 – 21(n!) – 72 = 0
(n! – 24 )(n! + 3) = 0
n! = 24 ;
n! = -3
n=4
Entonces:
C) 3 3
D)
35
E)
61
K
42 4 3 7
K 35
Resolución:
Tenemos:
(n!)2 – 3(n!) = 18(n!) + 18 4
92
Respuesta: D)
ÁLGEBRA
35
TEMA 33 - 34