introducc-edp

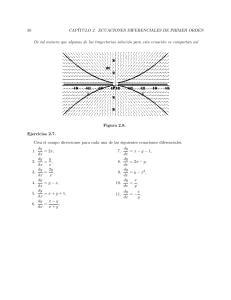
Capı́tulo 8
Introducción a las ecuaciones en
derivadas parciales
En la última parte del temario de la asignatura Métodos Matemáticos de la Fı́sica V vamos
a realizar un estudio introductorio y bastante elemental de las ecuaciones diferenciales en
derivadas parciales (en lo sucesivo abreviadas como edp), una vez que ya se han analizado
con suficiente amplitud en los capı́tulos precedentes las ecuaciones diferenciales ordinarias.
8.1
Comentarios generales
Al igual que se hizo anteriormente para las ecuaciones diferenciales ordinarias, el enfoque
que se ofrecerá en esta presentación de las edp será eminentemente práctico (no se tarta de
efectuar aquı́ un análisis del más alto rigor matemático), insistiendo sobre todo en mostrar
los métodos más usuales de los que se dispone para la resolución de algunas de las edp más
relevantes para un fı́sico. Se obviarán, por tanto, la mayor parte de los detalles técnicos más
delicados que, siendo muy importantes, forman un campo de estudio amplı́simo y sumamente
interesante. Estos vastos territorios necesariamente deben quedar fuera del alcance de un
curso como éste, ya que su estudio requerirı́a primero un tiempo del que no disponemos y
segundo el conocimiento de unas técnicas matemáticas bastante sofisticadas, que no forman
parte de la formación básica de un fı́sico (por ejemplo determinados temas avanzados de
Análisis Funcional, como son la teorı́a de los espacios de Hilbert y de Sobolev, o la teorı́a de
la medida).
Por falta de tiempo, tampoco abordaremos en este curso el estudio de los métodos
numéricos de resolución de edp, técnicas sumamente útiles en las aplicaciones concretas,
remitiendo al estudiante interesado a consultar textos más especializados (por ejemplo el libro ya clásico de Press, Flannery, Teukolsky y Vetterling que aparece citado en la bibliografı́a
recomendada).
Antes de comenzar con el desarrollo concreto de los capı́tulos en los que se ha organizado
el contenido del curso, parece pertinente hacer unos comentarios generales que conviene tener
presentes a lo largo del desarrollo de los temas que seguirán:
a) La teorı́a de las edp no se restringe, ni mucho menos, al caso de dos variables independientes (x, y) o (x, t), como pudiera deducirse tras el estudio de algunos libros de edp.
1
2
Capı́tulo 8. Introducción a las ecuaciones en derivadas parciales
Es cierto que haremos un énfasis especial en las ecuaciones con dos variables independientes (entre otras cosas porque su estudio es más sencillo y también por su interés
práctico), pero no serán las únicas que estudiemos, de manera que quien siga este curso
debe ser consciente de que los más modernos descubrimientos sobre las edp, sean éstas
lineales o no lineales, han permitido el análisis riguroso de edp con cualquier número
de variables independientes. En concreto, y como se verá más adelante en el caso de las
ecuaciones de segundo orden, es usual efectuar una clasificación de las edp en diveros
tipos estándar; esto se hace de manera bastante sencilla en el caso de dos dimensiones,
pero crea la falsa impresión en el estudiante de que existe algún tipo de esquema de
clasificación general válido en dimensión arbitraria, lo cual no es cierto.
b) Aunque en esta asignatura se insistirá sobre todo en el estudio de edp lineales, muchas
edp interesantes y de gran importancia práctica resultan ser no lineales. Hemos de decir
que actualmente se conocen muchos resultados sobre edp lineales y muy pocos sobre
edp no lineales (esto explica sin duda el énfasis que se pone habitualmente en el estudio
de las edp lineales).
c) Muchas de las edp que se estudiarán en el curso, en especial las edp no lineales de
primer orden, en general no poseen soluciones suficientemente suaves (es decir, soluciones que sean indefinidamente derivables). Resulta por tanto conveniente contemplar
la idea de que pueden existir otro tipo de soluciones menos regulares, que se suelen
denominar soluciones generalizadas o soluciones débiles de la edp. Este asunto resulta
ser extremadamente delicado, de manera que nosotros sólo lo comentaremos de manera
tangencial y de forma esporádica en el discurrir de la materia, centrándonos sobre todo
en la determinación de soluciones que sean suficientemente regulares, llamadas habitualmente soluciones clásicas de la edp, que serán definidas con mayor precisión en la
sección siguiente.
d) Finalmente, es conveniente saber que la manera de abordar la búsqueda de soluciones
de edp es radicalmente diferente de lo que el estudiante conoce para las ecuaciones
diferenciales ordinarias. Como ya se indicó, aquı́ no vamos a proceder a un análisis
de la teorı́a abstracta general de las edp, si no a mostrar una primera introducción al
tema para estudiantes cuyo interés primordial es el cálculo explı́cito de soluciones de
edp particulares con alguna relevancia en problemas fı́sicos.
En los comentarios anteriores se han ido incluyendo algunos conceptos que no han sido
aún definidos, pero que lo serán de forma inmediata o a lo largo del curso.
8.2
Conceptos básicos y notación
Tras los comentarios introductorios de la sección precedente, conviene indicar ahora (aunque
es probable que el estudiante ya sea consciente de ello) que nuestro interés por las edp se debe
a que este tipo de ecuaciones diferenciales aparecen en Fı́sica cuando se analizan modelos que
involucran la presencia de un número de variables independientes superior a uno, de manera
que entran en juego las derivadas parciales de una o varias funciones dependientes respecto
de las diversas variables independientes. Por ser precisos, hay que decir que las edp también
8.2. Conceptos básicos y notación
3
surgen al estudiar problemas puramente geométricos, como el estudiante probablemente recuerde del curso de geometrı́a diferencial, y al desarrollar el cálculo variacional , una rama
de las matemáticas con gran relevancia en Fı́sica, que se estudia en la asignatura de Fı́sica
Matemática.
Para evitar confusiones posteriores, conviene que seamos bastante sistemáticos y coherentes en el uso de la notación que vamos a usar en esta parte de la asignatura. Ası́ pues,
en lo sucesivo usualmente denotaremos a las variables independientes como {x1 , x2 , . . . , xn }
y a la función incógnita que se desea hallar como u(x1 , x2 , . . . , xn ). Obviamente no podemos
ser totalmente inflexibles en este convenio, de manera que, sea por comodidad, sea por el
significados fı́sico inherente a las variables del problema que estemos analizando, a veces
nos separaremos de esta convención y usaremos otras variables independientes, por ejemplo
las coordenadas cartesianas espaciales {x, y, z}, o la variable temporal t, o las coordenadas
esféricas {r, ϑ, ϕ}, etc.
Recordando brevemente algunas ideas básicas conocidas de cursos precedentes, sabemos
que dada una función de varias variables independientes u(x1 , . . . , xn ) que sea suficientemente
regular, se puede definir la derivada parcial de u como sigue.
Definición 1: la derivada parcial de u respecto de la variable xk , k = 1, . . . , n, es por
definición el siguiente lı́mite
u(x1 , . . . , xk + h, . . . , xn ) − u(x1 , . . . , xk , . . . , xn )
∂u(x1 , . . . , xn )
:= lim
.
h→0
∂xk
h
(8.2.1)
La notación ∂u/∂x fue introducida por primera vez por Legendre en 1786 (el sı́mbolo ∂
corresponde a la versión cursiva de nuestra letra d en el alfabeto cirı́lico). Una notación
también muy usada para las derivadas parciales es
∂u
:= uxj ,
∂xj
∂2u
:= uxj xk ,
∂xj ∂xk
∂3u
:= uxj xk x ,
∂xj ∂xk ∂x
etc.
(8.2.2)
A veces se utiliza también la notación llamada de los multiı́ndices, que se describe a continuación.
Definición 2: un vector α
= (α1 , . . . , αn ) tal que cada una de sus componentes αk es un
número entero no negativo (que en particular pudiera ser nulo), se denomina multiı́ndice de
orden [
α ] := α1 + · · · + αn .
Dado un multiı́ndice α
, se suele utilizar la siguiente notación para una derivada parcial
de orden [
α ]:
Dα u(x1 , . . . , xn ) :=
∂ [α ] u(x1 , . . . , xn )
:= ∂xα11 · · · ∂xαnn u(x1 , . . . , xn ).
∂xα1 1 · · · ∂xαnn
(8.2.3)
A continuación se ofrecen algunas definiciones que permitirán comenzar a fijar un poco
más algunas ideas que han ido apareciendo anteriormente de manera un tanto intuitiva e
imprecisa.
Definición 3: diremos que un conjunto U ⊂ Rn es una región si está formado por la unión
de un conjunto abierto y conexo de Rn junto con una parte de su frontera (la frontera de
4
Capı́tulo 8. Introducción a las ecuaciones en derivadas parciales
W se suele denotar como ∂W , sı́mbolo semejante al usado para la derivación parcial, pero
por el contexto no suele haber confusión posible). Si en U no está incluida en absoluto la
frontera del abierto, diremos que se trata de una región abierta; por contra, si U incluye
completamente la frontera del abierto, diremos que U es una región cerrada.
Aunque probablemente todos tenemos ya en mente qué entendemos por una edp, aún no
hemos dado una definición clara. En general entendemos por una edp una relación que involucra una función incógnita de varias variables, junto con algunas de sus derivadas parciales.
Vamos a dar una definición más técnica.
Definición 4: dada una región U ⊂ Rn , un intervalo I ⊂ R, otra región V ⊂ Rk y una
función F : U × I × V → R, llamaremos en lo sucesivo ecuación diferencial en derivadas
parciales con una función incógnita, a una relación de la forma
F (x1 , . . . , xn ; u; ux1 , . . . , uxn ; ux1 x1 , ux1 x2 , . . .) = 0,
(x1 , . . . , xn ) ∈ U,
(8.2.4)
que liga la función incógnita u de las n ≥ 2 variables independientes {x1 , . . . , xn }, con estas
variables y un número finito k de las derivadas parciales de u.
Esta definición se puede extender para considerar sistemas de varias ecuaciones diferenciales en derivadas parciales, digamos s. Para ello basta substituir el intervalo I ⊂ R
por un cierto subconjunto J ⊂ Rs y considerar una función vectorial con s componentes
F : U × J × V → Rs , junto con la relación vectorial
F (x1 , . . . , xn ; u; ux1 , . . . , uxn ; ux1 x1 , ux1 x2 , . . .) = 0,
(x1 , . . . , xn ) ∈ U,
(8.2.5)
donde u := (u1 , . . . , us ) son las s funciones desconocidas de las variables {x1 , . . . , xn } que se
desean determinar.
La definición que acabamos de dar es muy general y abarca desde los casos más sencillos
que podamos imaginar hasta otros extremadamente complicados y sin utilidad aparente.
Ejemplo 1: si u(x, y) es una función de dos variables, ejemplos de edp son
uyyy = 0,
ux = u y ,
(ux )uy = log(uxy ).
(8.2.6)
Nótese que debe especificarse, o sobreentenderse, el número de variables independientes de
la edp, que en los tres casos precedentes es siempre dos.
Definición 5: llamamos orden de la edp (8.2.4) al de la derivada parcial de mayor orden
que aparezca en la misma.
Ejercicio 1: hállese el orden de las tres edp mostradas en el Ejemplo 1.
Definición 6: diremos que la ecuación (8.2.4) es lineal si la función F es lineal respecto
de u y de todas las derivadas parciales de u que aparecen en ella. Usando la notación de
multiı́ndices, la forma general de una ecuación lineal de orden k es
k
Aα (x1 , . . . , xn ) Dα u(x1 , . . . , xn ) = f (x1 , . . . , xn ),
(8.2.7)
[
α ]=0
donde Aα y f son ciertas funciones conocidas que dependen exclusivamente de las variables
independientes, pero no de u ni de sus derivadas.
8.2. Conceptos básicos y notación
5
Definición 7: dada una edp lineal, diremos que es homogénea si en todos los términos de F
aparece u o alguna de sus derivadas, es decir, debe ocurrir que en (8.2.7) f = 0.
Definición 8: diremos que la ecuación (8.2.4) es cuasilineal si la función F es lineal respecto
de las derivadas parciales de mayor orden de u que aparecen en la ecuación. La forma más
general de una ecuación cuasilineal de orden k es
Bα (Dβ u) Dα u(x1 , . . . , xn ) + G(Dβ u) = 0,
] < [
[β
α ] = k,
(8.2.8)
[
α ]=k
donde la notación indica que las funciones Bα y G pueden depender tanto de las n variables
independientes, como de u y de las derivadas parciales de u hasta el orden k − 1.
Definición 9: diremos que la ecuación (8.2.4) es completamente no lineal si posee una
dependencia no lineal en las derivadas de mayor orden de u que aparecen en la ecuación.
Una vez establecido claramente el concepto de edp, debemos aclarar qué vamos a considerar como soluciones de tales ecuaciones. Parece obvio: diremos que somos capaces de resolver
la edp (8.2.4) si podemos encontrar todas las funciones u(x1 , . . . , xn ) que cumplen (8.2.4)
(normalmente escogidas entre aquellas funciones que satisfacen además ciertas condiciones
auxiliares en alguna parte Γ de la frontera ∂U de U ). Precisemos un poco más dando una
definición formal.
Definición 10: una función u de las variables {x1 , . . . , xn } diremos que es una solución
clásica de la edp (8.2.4) en la región U si se cumplen las siguientes condiciones:
• En U la función u(x1 , . . . , xn ) admite todas las derivadas que aparecen en F .
• La función u(x1 , . . . , xn ) y todas estas derivadas parciales son continuas en el interior
de la región U .
• Al sustituir en la edp u y sus derivadas, la ecuación (8.2.4) se convierte en una identidad
respecto de las variables independientes del problema.
• En ocasiones se exige también que la solución se continua hasta la frontera ∂U .
Ejemplo 2: he aquı́ otros casos sencillos de edp con dos variables independientes:
a) 3y 2 ux + uy = 2u + x3 y es una edp lineal, no homogénea y de primer orden.
b) u uxxx + cos(x + ey ) uyy = 0 es una edp cuasilineal de tercer orden.
c) uxx + uyy = 0 es una edp lineal, homogénea y de segundo orden. Es fácil ver que admite
como solución u(x, y) = x − y; la función u(x, y) = x2 − y 2 también es una solución de
la misma ecuación. Este es un indicio claro de que una misma edp puede poseer una
gran variedad de soluciones completamente diferentes unas de otras.
Para completar este apartado dedicado a definir ciertos conceptos básicos y a establecer la
notación que vamos a necesitar posteriormente, conviene comentar, al menos brevemente, el
uso de operadores diferenciales en la teorı́a de las edp. Al estudiar las ecuaciones diferenciales
6
Capı́tulo 8. Introducción a las ecuaciones en derivadas parciales
ordinarias, en concreto las lineales de orden n, se introdujo la notación de los operadores
diferenciales para representar la ecuación: recordemos que el operador diferencial
L := a0 (x)
dn
d
+ · · · + an−1 (x)
+ an (x)
n
dx
dx
(8.2.9)
permite escribir la ecuación diferencial en forma compacta como Ly(x) = 0. Al estudiar
las edp lineales usaremos también esta representación mediante operadores diferenciales. Un
ejemplo bien conocido y que volveremos a considerar pronto es precisamente el operador
laplaciano ∇2 en dimensión arbitraria. Otros operadores lineales, diferenciales o no, nos van
a servir para representar las condiciones iniciales y de contorno.
Para fijar ideas podemos considerar una función u(x, t) definida para x ∈ [0, 1], t ≥ 0. Es
fácil probar que operadores tales como
L1 (u) = u(x, 0),
L2 (u) =
∂u
(x, 0),
∂t
L3 (u) = u(1, t) +
∂u
(0, t),
∂x
etc,
(8.2.10)
son lineales. En lo sucesivo llamaremos problema lineal al formado por una edp lineal junto con unas condiciones auxiliares (iniciales y de contorno) también lineales. Este tipo de
problemas, que serán los que más detenidamente estudiaremos en los capı́tulos siguientes,
normalmente llevan asociados ciertos principios de superposición, que son una consecuencia
directa de la linealidad del problema.
8.3
Aparición de edp en problemas puramente matemáticos
Como ya se ha comentado, las edp aparecen aparecen en problemas puramente matemáticos,
por ejemplo al estudiar geometrı́a diferencial o cálculo variacional. A continuación presentaremos algunos ejemplos de la aparción de edp tomados de otro contexto también puramente
matemático: su aparición al eliminar constantes o funciones arbitrarias en expresiones conocidas.
• Eliminación de constantes arbitrarias
Lo más ilustrativo es mostrar cómo se procede en ejemplos sencillos:
i) Consideremos la función de dos variables independientes u(x, y) = ax2 + by 2 + ab,
que contiene además dos constantes arbitrarias. Deseamos eliminar estas constantes, hallando una ecuación satisfecha por u para cuales quiera valores de a y b.
Para ello calculamos las derivadas parciales de u respecto a x e y:
∂u
= 2ax,
∂x
∂u
= 2by
∂y
⇒
a=
1 ∂u
,
2x ∂x
b=
1 ∂u
.
2y ∂y
Sustituyendo estas derivadas en la expresion original obtenemos:
4xyu = 2x2 y
∂u ∂u ∂u
∂u
+ 2xy 2
+
,
∂x
∂y
∂x ∂y
que es una edp de primer orden no lineal.
8.3. Aparición de edp en problemas puramente matemáticos
7
ii) Otro caso: u(x, y) = ax3 + by 3 .
Las parciales de u respecto a x e y:
∂u
= 3ax2 ,
∂x
∂u
= 3by 2
∂y
Despejando a y b y sustituyendo obtenemos:
x
∂u
∂u
+y
= 3u,
∂x
∂y
que es una edp de primer orden lineal.
iii) Un tercer ejemplo u = ax + by + cxy, que tiene tres constantes arbitrarias.
Las derivadas son: ux = a + cy, uy = b + cx. Estas ecuaciones no son suficientes
para eliminar a, b, c. Seguimos derivando:
uxx = 0 que es una edp lineal de segundo orden.
uyy = 0 que es una edp lineal de segundo orden.
uxy = c que junto con las expresiones anteriores da:
u=x
∂u
∂u
∂2u
+y
− xy
,
∂x
∂y
∂y∂x
que es una edp lineal de 2 orden.
De lo hacho hasta ahora parece que si tenemos n variables independientes, la eliminación de n constantes arbitrarias da lugar a una edp de primer orden, mientras que
la eliminación de m > n constantes arbitrarias da lugar a una edp de orden más alto. Esta conclusión es un poco apresurada y no es del todo exacta, como veremos
inmediatamente.
• Eliminación de funciones arbitrarias
Analicemos un sencillo ejemplo: dada una función arbitraria φ(r, s), queremos eliminarla de la relación
u y
y
u
φ 3,
= 0,
r = 3, s = .
x x
x
x
Para ello calculamos las parciales respecto de las variables independientes x e y, que
serán cero:
1 ∂u
∂φ
∂φ ∂r
∂φ ∂s
∂φ
u
∂φ y =
+
=
−3 4 + 3
+
− 2 = 0.
∂x
∂r ∂x
∂s ∂x
∂r
x
x ∂x
∂s
x
1 ∂u
∂φ 1
∂φ ∂r
∂φ ∂s
∂φ
∂φ
+
= 0.
=
+
=
∂y
∂r ∂y
∂s ∂y
∂r x3 ∂y
∂s x
Para que el sistema tenga solucion no trivial, los coeficientes de las funciones
han de ser tales que
y −3 u + 1 ∂u
− 2 x4
x3 ∂x
x ∂u
∂u
+y
= 3u.
=0 ⇒ x
∂x
∂y
1
1
∂u
x3 ∂y
x ∂φ
∂r
y
∂φ
∂s
8
Capı́tulo 8. Introducción a las ecuaciones en derivadas parciales
Resulta una edp lineal de primer orden. Algunos comentarios a este ejemplo:
1.- La edp tiene soluciones que dependen de una función arbitaria, y por tanto la riqueza
de soluciones de una edp es mucho mayor que en las ecuaciones diferenciales ordinarias.
2.- Esta edp coincide con la obtenida al eliminar constantes de la relación u = ax3 +by 3 ,
que se puede escribir u/x3 − a − b(y/x)3 = 0, es decir, se trata de un caso particular en
el que φ(r, s) = r − a − bs3 .
3.- Si tomamos φ(r, s) = r − a − bs − cs2 − dv 3 siendo a, b, c y d constantes arbitrarias,
la relación escrita explı́citamente será u = ax3 + bx2 y + cxy 2 + dy 3 , y aún ası́ la edp
seguirá siendo x ∂u/∂x+y ∂u/∂y = 3u. En este caso tenemos 2 variables independientes
y 4 constantes, y al eliminarlas obtenemos simplemente una edp de primer orden. Las
soluciones de una edp de primer orden que contienen el mismo número de constantes
arbitrarias que de variables independientes son muy importantes y reciben un nombre
especial: soluciones completas.
8.4
Algunas ecuaciones en derivadas parciales de interés fı́sico
Conviene que seamos conscientes de que de que no existe en la actualidad ninguna teorı́a
que abarque la resolución de todas las edp. Una teorı́a como esa es muy poco probable que
pueda existir, dada la gran variedad de fenómenos fı́sicos, geométricos y probabilı́sticos que
se describen mediante las edp. En lugar de intentar descubrir una teorı́a tan extremadamente
general, las investigaciones se encaminan más bien hacia la comprensión de diversas edp muy
concretas, que son de gran importancia tanto teórica como aplicada, con la esperanza de
avanzar ası́ en el descubrimiento de nuevas e interesantes soluciones.
A continuación se ofrece una amplia lista, que dista mucho de ser exhaustiva, de diversas
edp que presentan gran interés incluso para los investigadores actuales de primera lı́nea, con el
fin de que nos familiaricemos con los nombres y las formas tan diversas que adoptan algunas
de las edp más famosas (para más información al respecto puede consultarse el libro de
Zwillinger mencionado en la bibliografı́a). En estas ecuaciones aparecen diversas constantes,
e incluso funciones de las coordenadas (r ), que no se especifican con todo detalle y que
tienen que ver con las propiedades fı́sicas del problema que se estudia en cada caso. En ellas
se utilizan con frecuencia los operadores gradiente, divergencia y laplaciano (en general en n
dimensiones), que en coordenadas cartesianas tienen la forma bien conocida:
∂u ∂u
∂u1 ∂u2
∂u
∂un
∂2u ∂2u
∂2u
∇u =
, ∇·u =
,
,...,
+
+. . .+
, ∇2 u =
+
+·
·
·+
.
∂x1 ∂x2
∂xn
∂x1 ∂x2
∂xn
∂x2n
∂x21 ∂x22
Como ya se ha indicado anteriormente, en cada ecuación se sobreentiende cuales son las
variables independientes, con frecuencia t y r (este último vector puede ser de dimensión
arbitraria).
8.4.1
Ecuaciones en derivadas parciales lineales
1. Ecuación de ondas: ∇2 u =
1
c2
utt .
2. Ecuación del calor, de la difusión o de Fick (versión simplificada): ∇2 u =
3. Ecuación de la difusión o del calor (versión general): ∇(κ(r, t) ∇u) = ut .
1
κ
ut .
8.4. Algunas ecuaciones en derivadas parciales de interés fı́sico
9
4. Ecuación de Laplace: ∇2 u = 0.
5. Ecuación de Poisson: ∇2 u = −4π (r ).
6. Ecuación de Helmholtz: ∇2 u + λu = 0.
∇2 u + V (r )u = i ut .
7. Ecuación de Schrödinger dependiente del tiempo: − 2m
2
8. Ecuación de Klein–Gordon: ∇2 u −
1
c2
utt = µ2 u.
9. Ecuación del telégrafo: uxx = a utt + b ut + c u.
10. Ecuación biharmónica: ∇2 (∇2 u) := ∇4 u = 0.
11. Ecuación biharmónica de ondas: ∇4 u = − p12 utt .
12. Ecuación de Fokker–Planck (en una dimensión espacial): ut = β (x u)x + d uxx .
13. Ecuación de Boussinesq: utt − α2 uxx = β 2 uxxtt .
14. Ecuación de Euler–Darboux: (x − y) uxy + α ux − β uy = 0.
15. Ecuación de Euler–Poisson–Darboux: (x + y) uxy + N ux + N uy = 0.
16. Ecuación de Onsager: (ex (ex uxx )xx )xx + b2 uyy = F (x, y).
17. Ecuación de los armónicos esféricos (en tres dimensiones):
1 ∂
sen ϑ ∂ϑ
∂
sen ϑ
∂ϑ
1
∂2
+
+ ( + 1) Ym = 0.
sen2 ϑ ∂ϕ2
18. Ecuación de los armónicos esféricos (en cuatro dimensiones):
1
uxx + 2(cot x) ux +
sen2 x
1
uyy + (cot y) uy +
uzz
sen2 y
+ (n2 − 1)u = 0.
19. Ecuación de Tricomi: uyy = y uxx .
20. Ecuación de transporte lineal o ecuación de continuidad: ut + (b · ∇u) = 0.
21. Ecuación de Liouville (lineal): ut − ∇ · (b u) = 0.
22. Ecuación de Airy: ut + uxxx = 0.
23. Ecuación de las vigas: ut + uxxxx = 0.
10
Capı́tulo 8. Introducción a las ecuaciones en derivadas parciales
8.4.2
Ecuaciones en derivadas parciales no lineales
1. Ecuación eikonal o de la óptica geométrica: (ux )2 + (uy )2 + (uz )2 = n2 (r ).
2. Ecuación de Burger: ut + u ux = ν uxx .
3. Ecuación de Korteweg–de Vries (KdV): ut + uxxx − 6u ux = 0.
4. Ecuación de KdV generalizada: ut − uxxxxx + u ux = 0.
5. Ecuación de KdV modificada (mKdV): ut + uxxx ± 6u2 ux = 0.
6. Ecuación de Kadomtsev–Petviashvili: (ut + uxxx − 6u ux )x ± uyy = 0.
7. Ecuación de Thomas: uxy + α ux + β uy + γ ux uy = 0.
8. Ecuación de Buckmaster: ut = (u4 )xx + (u3 )x .
9. Ecuación de Ginzburg–Landau: ut = (1 + ia)uxx + (1 + ic)u − (1 + id)|u|2 u.
10. Ecuación de Hamilton–Jacobi: St + H(q, Sq1 , . . . , Sqn , t) = 0.
11. Ecuación de Liouville (no lineal): ∇2 u + eλu = 0.
12. Ecuación de Liouville (otra versión): uxt = eηu .
13. Ecuación de Monge–Ampère: (uxy )2 − uy ux = f (x, y, ux , uy ).
14. Ecuación de Monge–Ampère (otra versión):

ux1 x1 ux1 x2 · · · ux1 xn
 ux x ux x · · · ux x
2 1
2 2
2 n

det  .
..
..
.
.
.
 .
.
.
.
uxn x1 uxn x2 · · · uxn xn



 = f (r, u, ∇u).

15. Ecuación φ-4: utt − uxx − u + u3 = 0.
16. Ecuación de Plateau: (1 + u2x )uxx − 2ux uy uxy + (1 + u2y )uyy = 0.
17. Ecuación de los medios porosos: ut = ∇ · (um ∇u).
18. Ecuación de ondas de Rayleigh: utt − uxx = (ut − u3t ).
19. Ecuación de Schrödinger no lineal: iut + uxx ± 2|u|2 u = 0.
20. Ecuación de Schrödinger no lineal en las derivadas: iut + uxx ± i(|u|2 u)x = 0.
21. Ecuación de “Sine–Gordon”: uxx − uyy ± sen u = 0.
22. Ecuación escalar de reacción–difusión: ut − ∇2 u = f (u).
23. Ley de conservación (escalar): ut + ∇ · F (u) = 0.
24. Ecuación de las superficies mı́nimas: ∇ · (∇u)/ 1 + (∇u)2 = 0.
8.4. Algunas ecuaciones en derivadas parciales de interés fı́sico
8.4.3
11
Sistemas de ecuaciones en derivadas parciales lineales
1. Ecuaciones de Cauchy–Riemann (variable compleja):
ux − vy = 0,
uy + vx = 0.
2. Ecuaciones de Maxwell (electromagnetismo):
= 4π ,
∇·D
= 0,
∇·B
= 4π J,
∇×H
c
+ 1 ∂ B = 0.
∇×E
c ∂t
3. Ecuaciones de Navier (elasticidad):
(λ + 2µ)∇(∇ · u ) − µ ∇ × ∇ × u =
8.4.4
∂ 2 u
.
∂t2
Sistemas de ecuaciones en derivadas parciales no lineales
1. Ecuaciones de Yang–Mills (teorı́a cuántica de campos):
(u∗ ut )t − (u∗ ux )x∗ = 0.
2. Ecuaciones del campo quiral (teorı́a cuántica de campos):
(u∗ ux )t + (u∗ ut )x = 0
3. Ecuaciones de Klein–Gordon–Maxwell:
∇2 s − (|a |2 + 1)s = 0,
∇2a − ∇(∇ · a) − s2 a = 0.
4. Ecuaciones de Euler (fluidos):
∂v
1
+ (v · ∇)v = − ∇P,
∂t
ρ
∇ · v = 0.
5. Ecuaciones de Heisenberg del ferromagnetismo: st = s × sxx .
6. Ecuaciones de von Kármán (dinámica de fluidos):
2
∇4 u = E(wxy
− wxx wyy ),
∇4 w = a + b(uyy wxx + uxx wyy − 2uxy wxy ).
7. Ecuaciones de Navier–Stokes (elasticidad):
ut + (u · ∇)u = −
1
∇P + ν∇2 u.
12
Capı́tulo 8. Introducción a las ecuaciones en derivadas parciales
Ejemplo 3: consideremos la ecuación de Laplace, el caso 4 de la sección 1.3.1. Las soluciones
de la ecuación de Laplace son llamadas funciones armónicas. Tomemos n = 2 y supongamos
2
2
que hemos encontrado una solución u(x, y) de la ecuación de Laplace ∂∂xu2 + ∂∂yu2 = 0. Sea
ahora v(x, y) una función tal que
∂u
∂v
=
,
∂x
∂y
Derivando estas expresiones, obtenemos
∂
∂2v
∂u
∂2u
=
−
=
−
,
∂x2
∂x
∂y
∂x ∂y
∂u
∂v
=− .
∂y
∂x
∂
∂2v
=
2
∂y
∂y
∂u
∂x
=
∂2u
.
∂y ∂x
Si suponemos que u y v son de clase C 2 (U ), donde U es una cierta región del plano real,
estas derivadas parciales están bien definidas en U . Además podemos aplicar el teorema
de Schwarz a las derivadas parciales con respecto a las dos variables. Recordemos que este
resultado nos dice que si u ∈ C 2 (U ), tenemos que
∂2u
∂2u
=
.
∂x ∂y
∂y ∂x
De todo lo anterior resulta entonces que v satisface también la ecuación de Laplace y es, por
lo tanto, una función armónica. Al verificar las condiciones de Cauchy–Riemann, u y v son
funciones armónicas conjugadas. Además la función u(x, y) + iv(x, y) es una función analı́tica
de variable compleja en U , considerándolo como una región del plano complejo C.
8.5
Comentarios finales
En los temas que siguen nuestro objetivo esencial será encontrar maneras de hallar soluciones
de diversos tipos de edp. Como puede apreciarse por la gran variedad de ejemplos mostrados en la sección anterior, esto no va a ser una tarea fácil. Nosotros nos vamos a centrar
esencialmente en el estudio de edp de primer y segundo oŕdenes.
A veces estaremos interesados en hallar la solución más general posible de una edp, pero
más frecuentemente habrá que hallar sólo la solución que verifique unas ciertas condiciones
auxiliares (llamadas normalmente condiciones iniciales, si afectan a una variable temporal, y
condiciones de contorno, o en la frontera, cuando tienen que ver con los valores de la solución
en ∂U ). Un problema de este tipo puede tener una solución, ninguna solución o incluso
infinitas soluciones (para las ecuaciones diferenciales ordinarias sucede algo parecido). Esto
nos lleva necesariamente a la consideración del adecuado planteamiento de los problemas de
edp.
Con mucha frecuencia las edp surgen al confeccionar modelos de un determinado fenómeno,
usando diferentes hipótesis. Evidentemente nos interesan aquellos esquemas que describen
adecuadamente la realidad y permiten además efectuar predicciones. Si nuestro modelo representa adecuadamente el fenómenos fı́sico que estamos estudiando, cabe esperar que posea una
solución única. A priori no es evidente si un problema de ecuaciones en derivadas parciales
está bien planteado: aunque fı́sicamente parezca razonable que la solución haya de ser única,
puede ocurrir que no tenga solución o que, de tener, no sea única. Aunque estemos seguros
de que la solución existe y es única, esto no basta para afirmar que el problema está bien
8.5. Comentarios finales
13
planteado. En efecto, en un problema realista los datos se obtienen a partir de experimentos,
ası́ que forzosamente no serán exactos, de manera que, para que el problema tenga sentido, ha
de ocurrir también que un pequeño cambio en esos datos no influya de manera notable en la
solución. Pero aún hay más: como en la mayor parte de la ocasiones estas ecuaciones tienen
que resolverse numéricamente, lo que siempre implica aproximaciones y errores de redondeo,
es preciso que estas aproximaciones no produzcan grandes desviaciones del resultado exacto,
ya que en caso contrario el modelo usado serı́a de muy poca utilidad.
El estudio de los problemas bien planteados es lo que se suele denominar “teorı́a clásica
de las ecuaciones en derivadas parciales”, y sólo de ellos nos ocuparemos en lo sucesivo (esto
no significa que los problemas mal planteados sean irrelevantes, ya que, por ejemplo, juegan
un papel destacado en mecánica de fluidos). Ya se comentó anteriormente que en ocasiones
no son suficientes las soluciones clásicas (definidas en la segunda sección de este tema) y
deberemos usar las soluciones débiles o generalizadas, que fueron introducidas por Sobolev
alrededor de 1930; se trata de soluciones que pueden no ser suficientemente regulares o incluso
tratarse de distribuciones (o funciones generalizadas).
Concretando un poco más, diremos que un problema para una cierta edp está bien planteado si se cumplen las tres condiciones siguientes:
1. El problema posee una solución.
2. La solución es única.
3. La solución es estable, es decir, depende de forma continua de los datos del problema
(de las condiciones iniciales y de las de contorno).
Las dos primeras exigencias son razonables, pero la tercera pudiera parecer caprichosa. Sin
embargo es especialmente importante para problemas que aparecen en aplicaciones fı́sicas,
ya que, como se ha comentado antes, es deseable que la solución que buscamos, además de
ser única, cambie muy poco cuando se modifican ligeramente las condiciones que especifican
el problema. Algunos tipos de ecuaciones, en particular las edp de segundo orden, han sido
estudiadas exhaustivamente y se conocen resultados para saber qué tipos de problemas están
bien planteados.
Ya comentamos anteriormente que nos preocuparemos principalmente por hallar las soluciones llamadas clásicas (véase la Definición 10). Algunas ecuaciones, por ejemplo la de
Laplace, admiten estas soluciones clásicas. Otras ecuaciones, sin embargo, no poseen en general este tipo de soluciones clásicas. Este es el caso la ley de conservación escalar (número
23 en los ejemplos de edp no lineales) ut + ∂x F (u) = 0, que rige diversos fenómenos unidimensionales en dinámica de fluidos, y que en particular sirve para elaborar modelos sobre
la formación y propagación de ondas de choque (una onda de choque es precisamente una
curva en la cual la solución u(x, t) presenta una discontinuidad). Si estamos interesados
en estudiar fenómenos regidos por este tipo de ecuación, deberemos aceptar también como
válidas soluciones que pueden no ser diferenciables o incluso pueden ser discontinuas (es lo
que llamaremos soluciones generalizadas o débiles). No insistiremos más en este punto, pero
ya veremos que en algunos de los ejercicios que se realicen a lo largo del curso aparecen estas
soluciones no clásicas.
Proseguiremos el estudio de las edp analizando en el próximo capı́tulo las de primer orden,
tanto lineales como no lineales. Este tipo de ecuaciones aparecen en problemas de geometrı́a
14
Capı́tulo 8. Introducción a las ecuaciones en derivadas parciales
y también en problemas de mecánica clásica, óptica geométrica, mecánica estadı́stica, superconductividad, teorı́a cuántica de campos, fı́sica de altas energı́as, y en teorı́a de la relatividad
especial y general. Después se estudiarán las edp lineales de segundo orden, que son sin duda las que más relevancia presentan en las aplicaciones fı́sicas, e incluyen las ecuaciones de
Laplace, del calor y de ondas. El estudio de las ecuaciones de primer y segundo orden se
realiza por separado porque las técnicas de resolución de unas y otras son muy diferentes.
8.6
Problemas
Se entregarán fotocopias.
8.7
Bibliografı́a
1. Castro Figueroa, A.R., Curso básico de ecuaciones en derivadas parciales, Addison
Wesley Iberoamericana, 1997. Libro reciente, claro y bien presentado, muy adecuado
para los temas de ecuaciones en parciales.
2. Kline, M., Mathematical Thought from Ancient to Modern Times, Oxford University
Press, 1972. Excelente recorrido por la historia de las Matemáticas.
3. Press, W.H., Flannery, B.P., Teukolsky, S.A., and Vetterling, W.T., Numerical Recipes.
The Art of Scientific Computing, Cambridge University Press, 1990. Muy buen manual
de cálculo numérico, recomendable a los estudiantes interesados en utilizar técnicas de
aproximación numérica. Hay versiones en FORTRAN, PASCAL y C.
4. Puig-Adam, P., Ecuaciones diferenciales, Nuevas Gráficas, 1962. Se trata de un libro
un poco anticuado, pero interesante en algunos detalles referentes a las ecuaciones en
derivadas parciales y a la interpretación geométrica de las ecuaciones diferenciales de
primer orden.
5. Sneddon, I. N., Elements of Partial Differental Equations, McGraw-Hill, 1957. Muy
adecuado para explicar los temas de ecuaciones en derivadas parciales.
6. Zwillinger, D., Handbook of Differential Equations, Academic Press, 1992. Es un interesante libro de referencia tanto para el profesor, como para el investigador, por su
clasificación sistemática de diferentes tipos de ecuaciones diferenciales y de métodos
variados de integración.