27/7/2020
Serie de Fourier - Wikipedia, la enciclopedia libre
Serie de Fourier
Una serie de Fourier es una serie infinita que converge puntualmente a una
función periódica y continua a trozos (o por partes). Las series de Fourier
constituyen la herramienta matemática básica del análisis de Fourier empleado para
analizar funciones periódicas a través de la descomposición de dicha función en una
suma infinita de funciones sinusoidales mucho más simples (como combinación de
senos y cosenos con frecuencias enteras). El nombre se debe al matemático francés
Jean-Baptiste Joseph Fourier, que desarrolló la teoría cuando estudiaba la ecuación
del calor. Fue el primero que estudió tales series sistemáticamente, y publicó sus
resultados iniciales en 1807 y 1811. Esta área de investigación se llama algunas
veces análisis armónico.
Es una aplicación usada en muchas ramas de la ingeniería, además de ser una
herramienta sumamente útil en la teoría matemática abstracta. Sus áreas de
aplicación incluyen análisis vibratorio, acústica, óptica, procesamiento de imágenes y
señales, y compresión de datos. En ingeniería, para el caso de los sistemas de
telecomunicaciones, y a través del uso de los componentes espectrales de frecuencia
de una señal dada, se puede optimizar el diseño de un sistema para la señal
portadora del mismo. Refiérase al uso de un analizador de espectros.
Las series de Fourier tienen la forma:
donde
y
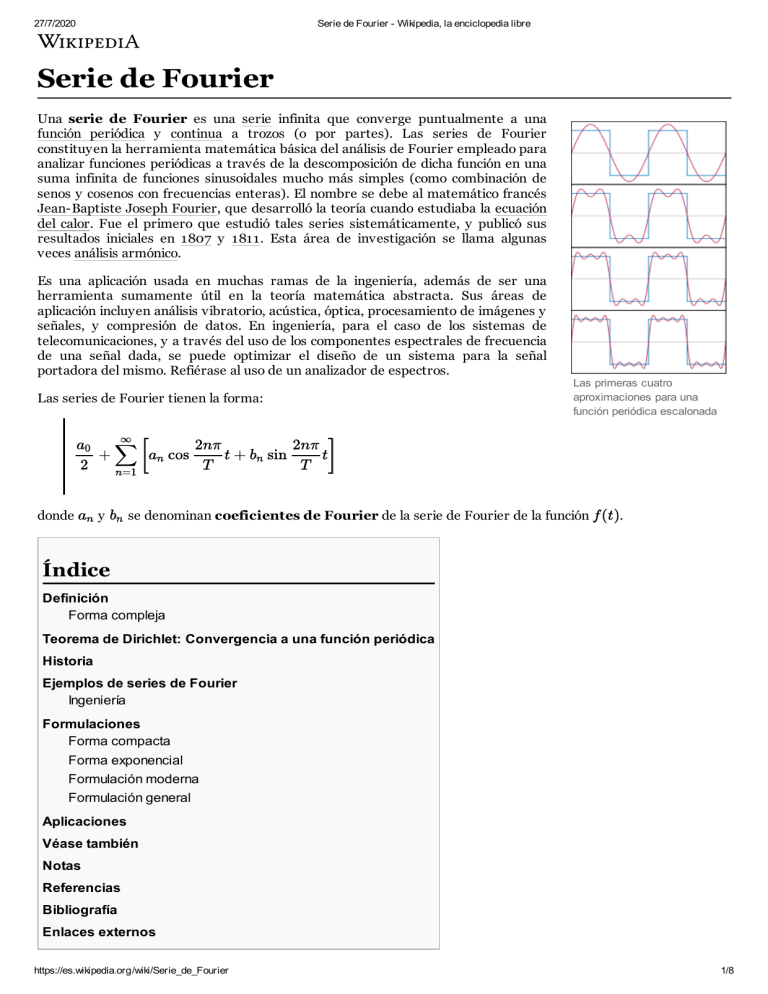
Las primeras cuatro
aproximaciones para una
función periódica escalonada
se denominan coeficientes de Fourier de la serie de Fourier de la función
.
Índice
Definición
Forma compleja
Teorema de Dirichlet: Convergencia a una función periódica
Historia
Ejemplos de series de Fourier
Ingeniería
Formulaciones
Forma compacta
Forma exponencial
Formulación moderna
Formulación general
Aplicaciones
Véase también
Notas
Referencias
Bibliografía
Enlaces externos
https://es.wikipedia.org/wiki/Serie_de_Fourier
1/8
27/7/2020
Serie de Fourier - Wikipedia, la enciclopedia libre
Definición
Si
es una función de variable real , que es integrable en el intervalo
entonces se puede obtener el desarrollo en serie de Fourier de
periódica, con período .
en ese intervalo. Fuera del intervalo la serie es
Si
es periódica en toda la recta real, la aproximación por series de Fourier también será válida en todos los
valores de .
Luego la serie de Fourier asociada a
Donde
,
y
es:
son los coeficientes de Fourier que toman los valores:
Otra forma de definir la serie de Fourier es:
donde
y
siendo:
a esta forma de la serie de Fourier se le conoce como la serie trigonométrica de Fourier.
Forma compleja
Por la identidad de Euler, las fórmulas de arriba pueden expresarse también en su forma compleja:
Los coeficientes ahora serían:
https://es.wikipedia.org/wiki/Serie_de_Fourier
2/8
27/7/2020
Serie de Fourier - Wikipedia, la enciclopedia libre
Teorema de Dirichlet: Convergencia a una función periódica
Supongamos que f(x) es una función periódica, continua a trozos y acotada, que en un periodo tiene un número
finito de máximos y mínimos locales y un número finito de discontinuidades, de período 2p. Sean
y
entonces la serie converge a
En donde
,y
Historia
Las series de Fourier reciben su nombre en honor a Jean-Baptiste Joseph Fourier (1768-1830), que hizo
importantes contribuciones al estudio de las series trigonométricas, que previamente habían sido consideradas por
Leonhard Euler, Jean le Rond d'Alembert y Daniel Bernoulli.a Fourier introdujo las series con el propósito de
resolver la ecuación de conducción del calor en una lámina de metal publicando sus resultados en 1807 Mémoire
sur la propagation de la chaleur dans les corps solides ('Memoria sobre la propagación del calor en los cuerpos
sólidos'), y publicando su Théorie analytique de la chaleur ('Teoría analítica del calor') en 1822. Ideas previas en
descomponer una función periódica en la suma de simples funciones de oscilación datan desde el siglo III a.C.,
cuando astrónomos antiguos propusieron un modelo empírico de movimiento planetario con base en epiciclo.
La ecuación del calor es una ecuación en derivadas parciales. Previamente al trabajo de Fourier, no se conocía
solución alguna para la ecuación de calor en forma general, aunque se conocían soluciones particulares si la fuente
de calor se comportaba de manera sencilla, en particular, si la fuente era una onda de seno o coseno. Estas
soluciones simples a veces son llamadas valores propios. La idea de Fourier era modelar una fuente de calor
compleja con una superposición (o combinación lineal) de simples ondas sinusoidales y para escribir la solución
como una superposición de los correspondientes valores propios. A la superposición o combinación lineal se le llama
Serie de Fourier.
Desde un punto de vista más actual, los resultados de Fourier son algo informales debido a la falta de precisión en la
noción de la función matemática y la integración a inicios del siglo XIX. Después, Peter Gustav Lejeune Dirichlet1 y
Bernhard Riemann2 3 4 expresaron los resultados de Fourier con mayor precisión y formalidad.
Aunque el motivo original era resolver la ecuación de calor, tiempo después fue obvio que se podía usar la misma
técnica a un gran conjunto de problemas físicos y matemáticos, especialmente aquellos que involucraban
ecuaciones diferenciales lineales con coeficientes constantes, para los cuales sus soluciones únicas eran sinusoidales.
Las series de Fourier tienen muchas aplicaciones en la ingeniería eléctrica, análisis de vibraciones, acústica, óptica,
procesamiento de señales, retoque fotográfico, mecánica cuántica, econometría,5 la teoría de estructuras con
cascarón delgado,6 etc.
Ejemplos de series de Fourier
Veamos un ejemplo:
https://es.wikipedia.org/wiki/Serie_de_Fourier
3/8
27/7/2020
Serie de Fourier - Wikipedia, la enciclopedia libre
En este caso, los coeficientes de Fourier nos dan esto:
Gráfico de una función periódica.
Animación de la suma de los 5 primeros armónicos.
Si la serie de Fourier converge hacia: ƒ(x) de cada punto x donde ƒ es diferenciable:
Ingeniería
En ingeniería, el análisis de señales en el dominio de la frecuencia se realiza a través de las series de Fourier, por
cuanto es muy común, reemplazar la variable x por ωt (el producto de la frecuencia angular por el tiempo),
resultando las componentes:
Por lo tanto:
Formulaciones
Forma compacta
En ocasiones es más útil conocer la amplitud y la fase en términos cosinusoidales en lugar de amplitudes
cosinusoidales y sinusoidal. Otra forma de expresar la compleja forma de la serie de Fourier es:
https://es.wikipedia.org/wiki/Serie_de_Fourier
4/8
27/7/2020
Serie de Fourier - Wikipedia, la enciclopedia libre
donde
Forma exponencial
Por la identidad de Euler para la exponencial compleja, operando adecuadamente, si
la serie de Fourier se puede expresar como la suma de dos series:
En forma más compacta:
estas ecuaciones solo son válidas cuando el periodo
de la serie de Fourier es:
con
. Otra forma de expresar la forma compleja
donde
https://es.wikipedia.org/wiki/Serie_de_Fourier
5/8
27/7/2020
Serie de Fourier - Wikipedia, la enciclopedia libre
Formulación moderna
Realmente el desarrollo en serie de Fourier se hace para funciones de cuadrado integrable, es decir, para funciones
que cumplan que:
El conjunto de todas las funciones integrables definidas en el intervalo
tiene definido un producto interno dado por:
se denota con
que lo dota de estructura de espacio de Hilbert. De este modo, todas las funciones de
desarrollarse en series de Fourier. Así,el conjunto
. El desarrollo de Fourier se puede expresar como:
Donde
. Este conjunto,
pueden
es una base ortonormal del espacio
son los coeficientes del desarrollo de Fourier.
Por último, la identidad de Parseval dice que dada una función
Fourier , se verifica que:
de cuadrado integrable y los coeficientes de
En lenguaje técnico, podríamos decir que hay una isometría entre el espacio de funciones de cuadrado integrable y
el espacio de sucesiones lineales indexadas en los enteros cuyos términos tienen cuadrados sumables.
Formulación general
Las propiedades útiles de las series de Fourier se deben principalmente a la ortogonalidad y a la propiedad de
homomorfismo de las funciones ei n x.
Otras sucesiones de funciones ortogonales tienen propiedades similares, aunque algunas identidades útiles,
concerniendo por ejemplo a las convoluciones, no seguirán cumpliéndose si se pierde la "propiedad de
homomorfismo".
Algunos ejemplos son las secuencias de funciones de Bessel y los polinomios ortogonales. Tales sucesiones se
obtienen normalmente como soluciones de una ecuación diferencial; una gran clase de tales sucesiones útiles son
soluciones de los llamados problemas de Sturm-Liouville.
Aplicaciones
Generación de formas de onda de corriente o tensión eléctrica por medio de la superposición de sinusoides
generados por osciladores eléctrónicos de amplitud variable cuyas frecuencias ya están determinadas.
https://es.wikipedia.org/wiki/Serie_de_Fourier
6/8
27/7/2020
Serie de Fourier - Wikipedia, la enciclopedia libre
Análisis en el comportamiento armónico de una señal.
Reforzamiento de señales.
Estudio de la respuesta en el tiempo de una variable circuital eléctrica donde la señal de entrada no es
sinusoidal o cosinusoidal, mediante el uso de transformadas de Laplace y/o solución en régimen permanente
sinusoidal en el dominio de la frecuencia.
La resolución de algunas ecuaciones diferenciales en derivadas parciales admiten soluciones particulares en
forma de series de Fourier fácilmente computables, y que obtener soluciones prácticas, en la teoría de la
transmisión del calor, la teoría de placas, etc.
Véase también
Transformada de Fourier
Análisis armónico
Fenómeno de Gibbs
Identidad de Parseval
Notas
a. Estos tres autores hicieron un trabajo importante en la ecuación de onda, especialmente D'Alembert. El trabajo
de Euler en esta área fue principalmenteen colaboración con Bernoulli, aunque el anterior hizo contribuciones
individuales a la teoría de ondas y vibraciones (Fetter y Walecka, 2003, pp. 209, 210)
Referencias
1. Lejeune-Dirichlet, P. "Sur la convergence des séries
trigonométriques qui servent à représenter une
fonction arbitraire entre des limites données". (In
French), transl. "On the convergence of trigonometric
series which serve to represent an arbitrary function
between two given limits". Journal f¨ur die reine und
angewandte Mathematik, Vol. 4 (1829) p. 157–169.
2. «Ueber die Darstellbarkeit einer Function durch eine
trigonometrische Reihe» [About the representability of
a function by a trigonometric series] (http://www.maths.
tcd.ie/pub/HistMath/People/Riemann/Trig/).
Habilitationschrift, Gotinga; 1854. Abhandlungen der
Königlichen Gesellschaft der Wissenschaften zu
Gotinga, vol. 13, 1867. Published posthumously for
Riemann by Richard Dedekind (en alemán).
Archivado (https://web.archive.org/web/20080520085
248/http://www.maths.tcd.ie/pub/HistMath/People/Rie
mann/Trig/) desde el original el 20 de mayo de
2008. Consultado el 19 de mayo 2008.
3. D. Mascre, Bernhard Riemann: Posthumous Thesis
on the Representation of Functions by Triginometric
Series (1867). Landmark Writings in Western
Mathematics 1640–1940 (http://books.google.co.uk/b
ooks?id=UdGBy8iLpocC&printsec=frontcover#v=one
page&q&f=false), Ivor Grattan-Guinness (ed.); pg.
492. Elsevier, 20 May 2005.Accessed 7 Dec 2012.</
4. Theory of Complex Functions: Readings in
Mathematics (http://books.google.co.uk/books?id=uP
8SF4jf7GEC&printsec=frontcover#v=onepage&q&f=f
alse), by Reinhold Remmert; pg 29. Springer, 1991.
Accessed 7 Dec 2012.
5. Nerlove, Marc; Grether, David M.; Carvalho, Jose L.
(1995). Analysis of Economic Time Series.
Economic Theory, Econometrics, and Mathematical
Economics (https://archive.org/details/analysisofecon
om0000nerl). Elsevier. ISBN 0-12-515751-7.
6. Flugge, Wilhelm (1957). Statik und Dynamik der
Schalen. Berlin: Springer-Verlag.
Bibliografía
M. R. Spiegel, J. Liu, L. Abellanas (2003): Fórmulas y tablas de matemática aplicada. Segunda edición. Serie
Schaum. Mc Graw-Hill.
Fetter, Alexander L.; Walecka, John Dirk (2003). Theoretical Mechanics of Particles and Continua (http://books.
google.co.uk/books?id=olMpStYOlnoC&pg=PA214&lpg=PA214&dq=bernoulli+solution+wave+equation&source
=bl&ots=h8eN69CWRm&sig=lRq2-8FZvcXIjToXQI4k6AVfRqA&hl=en&sa=X&ei=RqOhUIHOIOa00QWZuIHgCw&
ved=0CCEQ6AEwATg8#v=onepage&q=bernoulli%20solution%20wave%20equation&f=false).
Courier
Corporation. pp. 209, 210. ISBN 9780486432618.
Enlaces externos
https://es.wikipedia.org/wiki/Serie_de_Fourier
7/8
27/7/2020
Serie de Fourier - Wikipedia, la enciclopedia libre
Wikimedia Commons alberga una categoría multimedia sobre Serie de Fourier.
Weisstein, Eric W. «Fourier Series» (http://mathworld.wolfram.com/FourierSeries.html). En Weisstein, Eric W, ed.
MathWorld (en inglés). Wolfram Research.
The Feynman Lectures Capítulo 50 Harmonics (http://www.feynmanlectures.caltech.edu/I_50.html)
Obtenido de «https://es.wikipedia.org/w/index.php?title=Serie_de_Fourier&oldid=127767351»
Esta página se editó por última vez el 16 jul 2020 a las 08:28.
El texto está disponible bajo la Licencia Creative Commons Atribución Compartir Igual 3.0; pueden aplicarse cláusulas adicionales. Al usar
este sitio, usted acepta nuestros términos de uso y nuestra política de privacidad.
Wikipedia® es una marca registrada de la Fundación Wikimedia, Inc., una organización sin ánimo de lucro.
https://es.wikipedia.org/wiki/Serie_de_Fourier
8/8









