Pruebas estadísticas

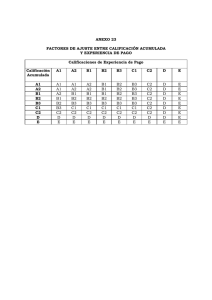
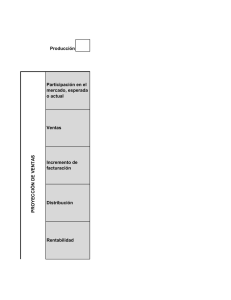
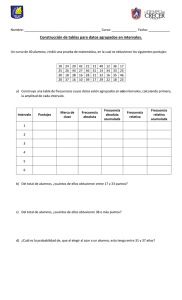
3.6
EQUIPO 4
Pruebas Estadísticas.
(Pruebas de bondad de
ajuste).
Pruebas de Bondad
de Ajuste
Las pruebas de bondad de ajuste
son aquellas que comparan los
resultados de una muestra con los
que se espera obtener cuando la
hipótesis nula es verdadera.
Esta metodología Resulta Útil para validar hipótesis sobre
la distribución teórica en la población que se realiza en la
estadística paramétrica, contrastes de hipótesis, intervalos
de confianza, regresión lineal, etc.
Es necesario colectar y procesar una cierta cantidad
determinada de datos, formular el modelo matemático
así como estimar parámetros.
Objetivo
Esta tienen por objetivo determinar si los
datos se ajustan a una determinada
distribución, la cual puede estar
completamente especificada (hipótesis
simple) o perteneciente a una clase paramétrica (hipótesis compuesta). se
destacan las siguientes:
Pasos Básicos
1. Definir nuestra variable a analizar. Para definir la
variable es importante revisar la problemática, y
analizar si los datos corresponden a datos discretos o
continuos.
2. Obtener media y varianza de los datos. Se hace uso de
estadística para obtener estos datos que nos sirven
para estimar los parámetros. Se pueden usar
herramientas tecnológicas.
3. Elaborar un histograma de Frecuencias. De preferencia
se buscan datos discretos se manejan de forma
puntual y datos continuos se manejan como rangos.
PRUEBA DE
CHICUADRADO
PRUEBAS
PRUEBA DE
KOLMOGÓRO
V-SMIRNOV
PRUEBA DE CHI-CUADRADO
n = es el numero de intervalos en
el histograma de frecuencias
Compara las frecuencias
observadas(Fo) por clase,
contra las frecuencias
esperadas, esta es una
prueba parametrica que
minimo requiere 5 clases asi
como 5 observaciones
minimas en cada clase.
Solución
Determinar el
número de
intervalos y
partiendo del límite
superior e inferior,
y el tamaño del
intervalo se calcula
cada uno para los
intervalos.
Determinar la
frecuencia
observada por
cada intervalo
Hallar la frecuencia
relativa esperada
acumulada
teniendo en cuenta
la función de
distribución a
utilizar, el límite
superior, la media
y desviación.
Hallar la frecuencia
relativa esperada
restando la
frecuencia relativa
esperada
acumulada con el
dato anterior de la
frecuencia dentro
de la columna.
Solución
Hallar la frecuencia
observada
esperada (FOE)
multiplicando la
frecuencia relativa
esperada con la
suma de los datos
de la frecuencia
observada.
Calcular el
estimador a partir
de la formula de
chi-cuadrado. Se
suman los datos
calculados en el
paso anterior
Se determinan los
grados de libertad
(V) restando el
número de
intervalos con 1 y
teniendo en cuenta
la suma anterior se
busca en la
siguiente tabla:
Si el estimador S2
es menor o igual al
valor
correspondiente en
la tabla entonces
se acepta Ho, en
caso contrario se
rechaza.
P.1
P.2
PRUEBA DE KOLMOGÓROVSMIRNOV
Es una prueba no para-métrica la cual se emplea solo para
distribuciones continuas. Esta tiene como objetivo
encontrar el tipo de distribución de una serie de datos, se
considera más eficiente que la prueba de chi-cuadrado
debido a que trabaja con la distribución de probabilidad
acumulada: la distribución acumulada de los datos
observados y la distribución acumulada teórica
correspondiente al modelo elegido.
Solución
Ordenar la muestra del
dato más pequeño al
más grande, es decir
obtener la secuencia
ordenada
x(0),x(1),…,x(n)
Calcular el valor de
la función de
distribución
empírica.
Calcular la
frecuencia
observada relativa
(frecuencia
observada de cada
intervalo/la
sumatoria total de
la frecuencia
observada).
Como la
distribución teórica
se encuentra
especificada en H0,
encontrar la
probabilidad
esperada F0(x)
para cada valor
ordenado de x.
P.3
Valor de la
tabla
0.409
H0 SE
ACEPTA