Sesion 5 Conversion de sistemas (Sexagesimal-Radian)

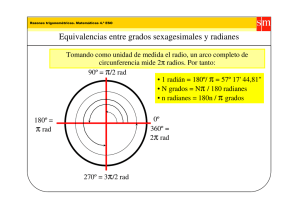
I.E.P “VIRGEN DE COCHARCAS”
Nivel: Primaria
Grado: 5° y 6°
Trimestre: I
Tema: Conversion de
unidades (Sexagesimal-rad)
Curso: Trigonometria
Alumno:
Profesor: Heider Mallma
Fecha:
Sesion 5
Resultado:
--------------------------Firma del padre
CONVERSIÓN DE SISTEMAS DE MEDICIÓN ANGULAR
(SEXAGESIMAL – RADIAN)
Sabemos
Simplificando :

360º  2 rad
:
180° = π rad
Para convertir grados sexagesimales a radianes o viceversa usaremos un
factor de conversión.
¿Qué es un factor de conversión?
Es una fracción que vale “1” (por que su numerador es igual a su
denominador) y sirve para convertir una unidad de medida en otra
equivalente.
 180º 


  rad 
  rad 


 180º 
I) Factor de conversión
II)
Convierte radianes a sexagesimales
Factor de conversión
Convierte sexagesimales a radianes
Ejemplos:
1.
Convertir 45º a radianes
Resolución:
Para convertir 45º grados radianes, tenemos que eliminar los
grados, para ello usamos el 2do factor de conversión, porque tiene
los grados en el denominador y se cancelarían.


π rad
45  
 180º
 20
 4
1
5


 
 4



45º 

rad
4
I.E.P “VIRGEN DE COCHARCAS”
2.
Sesion 5
Convertir a grupos sexagesimales
Resolución:
Ahora usaremos el 1er factor de conversión para eliminar los radianes:
 rad
5
1
 36º 
180º 

 36º
  rad 






rad= 36º
5
PROBLEMAS
Convertir:
1.
3
5 rad a grados sexagesimales
2.
2
5 rad a grados sexagesimales
3.
49º a radianes
4.
74º a radianes
5.
60º a radianes
6.

6 a grados sexagesimales
7.
120º a radianes
8.
96º a radianes.