DIAGNOSTICO DEL USO DE PROYECCIONES TRAN

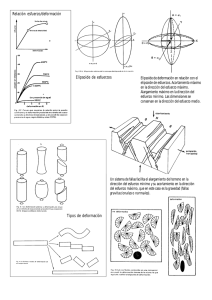
UNIVERSIDAD TECNOLÓGICA METROPOLITANA
FACULTAD DE HUMANIDADES Y TECNOLOGÍAS DE LA COMUNICACIÓN SOCIAL
ESCUELA DE CARTOGRAFÍA
DIAGNÓSTICO DEL USO DE PROYECCIONES
TRANSVERSALES DE MERCATOR EN ESCALAS
URBANAS
TESIS PARA OPTAR AL TÍTULO DE
CARTÓGRAFO Y AL GRADO DE LICENCIADO
EN CIENCIAS CARTOGRÁFICAS
PROFESOR GUÍA : Miguel Valladares Quiroz
AUTOR : Sebastián Alfredo Fuentes Santibáñez
SANTIAGO – CHILE
2006
Nota Obtenida : ___________________
_________________________________
(Firma y timbre de autoridad responsable)
2
A Claudia, Cristina, Flor, Mario, Juan Pablo y Alejandro
3
Agradecimientos:
A mi familia
A mi profesor Guía Miguel Valladares Quiroz
Al personal del sub departamento SIG del Servicio Agrícola Ganadero
A mis amigos Ana Tapia y David Castillo
Y a cuantos colaboraron de una u otra forma en el desarrollo de esta tesis
Gracias de Corazón
4
RESUMEN
La optima utilización de productos cartográficos como herramientas de análisis métrico
del terreno, está condicionada, por una parte por la deformación inherente a la escala de
representación, y por otra parte, por deformación propia de la proyección utilizada para
representar el terreno. En el contexto de la representación urbana, el desconocer el origen e
influencia de estas distorsiones puede derivar en la realización de mediciones erróneas y
desajustadas de la realidad.
La presente investigación busca definir el origen de las deformaciones métricas
producidas en diversas proyecciones transversales de Mercator, su significancia en relación a las
escalas de representación urbana y métodos para su corrección.
ABSTRACT
The optimal utilization of cartographic products as a tool of ground metric analysis, it’s
conditional, for first instance for the inherent deformation of representation scale, and on second
instance for the own deformation of the projection used to represent the ground. In the context of
the urban representation, to not known the origin and influences of this distortions may to
derivate in mistaken realizations of the measures and the may not fit the reality.
The followin investigation search to define the origin of metrical deformations producted
in several Transverse Mercator projections, his significance related to representation scale and
methods for his correction
5
ÍNDICE DE MATERIAS
1.
Aspectos generales
1.1. Introducción
1.2. Hipótesis de trabajo
1.3. Objetivos
1.3.1. Objetivo general
1.3.2. Objetivos específicos
2.
Errores y su cuantificación
2.1. Conceptos generales
2.1.1. Cifras significativas
2.1.2. Precisión
2.1.3. Exactitud
2.1.4. Equivocación
2.1.5. Errores sistemáticos
2.1.6. Errores aleatorios
2.2.
Conceptos básicos de probabilidades
2.2.1. Distribución de errores aleatorios
2.2.2. Probabilidad de ocurrencia de errores aleatorios
2.2.3. Cuantificación de errores aleatorios
2.2.4. Indicadores de precisión
3. Referenciales geodésicos
3.1. Elipsoide de Revolución
3.1.1. Coordenadas cartesianas en el espacio
3.1.2. Coordenadas geodésicas
3.1.3. Relación matemática entre coordenadas
3.1.4. Geometría del elipsoide
3.1.5. Arcos sobre el elipsoide
3.1.6. Línea geodésica
3.2. Referencia vertical
3.2.1. Geoide
3.2.2. Cuasi Geoide
3.2.3. Tipos de altura
3.2.4. Relación entre tipos de altura
3.2.5. Solución a las incompatibilidades entre tipos de altura
3.3. Sistemas geodésicos de referencia
3.3.1. Sistemas locales
3.3.2. Sistemas globales
4.
Proyecciones Cartográficas
12
12
15
16
16
16
17
18
18
18
18
19
20
20
21
22
25
26
28
29
31
33
34
37
38
42
45
46
47
48
48
51
52
53
54
59
62
6
4.1.
5.
Cálculo diferencial de elementos sobre el elipsoide
4.1.1. Elemento lineal
4.1.2. Elemento angular
4.1.3. Elemento superficial
4.2. Cálculo diferencial de elementos sobre el plano
4.2.1. Elemento lineal
4.2.2. Elemento angular
4.2.3. Elemento superficial
4.3. Módulos de deformación
4.3.1. Módulo de deformación lineal
4.3.2. Módulo de deformación angular
4.3.3. Módulo de deformación superficial
4.4. Elipse indicatriz de Tissot
4.4.1. Cálculo de semiejes según teorema de Apolonio
4.5. Clasificación de proyecciones
4.5.1. Según método de construcción
4.5.2. Según superficie de proyección utilizada
4.5.3. Según situación de la superficie de proyección
4.5.4. Según las propiedades que conserva
4.6. Proyecciones conformes
4.6.1. Uso de las proyecciones conformes
4.6.2. Condiciones de conformidad
Proyecciones transversales de Mercator
5.1. Generalidades
5.2. Transformación de coordenadas
5.2.1. Conversión de coordenadas geodésicas a rectangulares
5.2.2. Conversión de coordenadas rectangulares a geodésicas
5.3. Convergencia de meridianos
5.4. Diferencia arco-cuerda
5.5. Factor de magnificación de escala
5.5.1. En función de coordenadas geodésicas
5.5.2. En función de coordenadas rectangulares
5.6. El artificio de Tissot
5.7. Proyección Universal Transversal de Mercator
5.7.1. Generalidades
5.7.2. Falso Este
5.7.3. Falso Norte
5.7.4. Factor de escala en el meridiano central
5.8. Proyección Local Transversal de Mercator
5.8.1. Falso Este
62
63
63
63
64
65
66
69
70
70
71
71
72
73
76
76
78
79
81
83
83
84
88
88
90
90
93
98
99
101
101
102
102
104
104
105
105
106
108
109
7
6.
7.
5.8.2. Falso Norte
5.9. Proyecciones LTM y planos topográficos locales
5.10. Proyección Gauss Kruger
5.11. Proyección Modificada Transversa de Mercator
Metodología
6.1. Determinación de escalas de representación
6.2. Determinación de tolerancias
6.3. Determinación de proyecciones a utilizar
6.4. Determinación del área de estudio
6.5. Determinación de puntos muestrales
6.6. Proyección de la red de puntos muestrales
6.7. Determinación del factor de deformación de escala y
convergencia de meridianos
6.8. Determinación del coeficiente de correlación entre el factor de
deformación de escala y las coordenadas proyectadas
6.9. Determinación de magnitudes lineales de segmentos
proyectados y geodésicos
6.10. Determinación de escalas de representación según proyecciones
TM
6.10.1. Caso general
6.10.2. Caso particular
6.11. Relación entre proyecciones TM, elipsoide y superficie
topográfica
Resultados
7.1. Determinación de escalas de representación
7.1.1. Criterios de representación urbana
7.2. Determinación tolerancias
7.3. Determinación de proyecciones a utilizar
7.3.1. Universal Transversal de Mercator
7.3.2. Gauss Kruger
7.3.3. Local Transversal de Mercator
7.3.4. Modificada Transversa de Mercator
7.3.5. Plano Topográfico Local
7.4. Determinación Área de estudio
7.5. Determinación de puntos muestrales
7.6. proyección de la red y determinación de factores de
deformación de escala y convergencia de meridianos
7.7. Determinación del coeficiente de correlación entre el factor
de deformación de escala y las coordenadas proyectadas
7.8. Determinación de magnitudes lineales de segmentos
109
110
113
114
116
117
117
118
119
119
120
120
121
122
123
123
124
126
127
127
128
129
130
130
130
132
133
134
138
139
141
141
8
geodésicos y proyectado
Determinación de escalas de representación según proyecciones
TM
7.9.1. Caso general
7.9.2. Caso particular
7.10. Relación entre proyecciones TM, elipsoide y superficie
topográfica
7.10.1. Reducción plano TM – Elipsoide
7.10.2. Reducción Elipsoide – plano topográfico local
7.10.3. Reducción plano TM – plano topográfico local
7.10.4. Ejemplos de reducciones plano TM – Elipsoide
Análisis de resultados
8.1. Determinación del coeficiente de correlación entre el factor
de deformación de escala y las coordenadas proyectadas
8.2. Determinación de magnitudes lineales de segmentos
geodésicos y proyectados
8.3. Determinación de escalas de representación según tolerancias
8.3.1. Caso general
8.3.2. Caso particular
8.4. Relación entre proyecciones TM, elipsoide y superficie
topográfica
8.4.1. Reducción Plano TM – Elipsoide
8.4.2. Reducción Elipsoide – Plano Topográfico Local
Conclusiones y recomendaciones
Anexos
Anexo Nº1 “Mapa de ubicación”
Anexo Nº2 “Red de puntos muestrales”
Anexo Nº3 “Mapa de ubicación red de puntos muestrales”
Anexo Nº4 “proyección de puntos muestrales, factor de
deformación de escala y convergencia de meridianos”
Anexo Nº5 Determinación de arcos geodésicos y proyectados
Anexo Nº6 Diagrama de flujo metodología
Bibliografía
142
7.9.
8.
9.
10.
11.
144
144
145
147
148
149
151
151
155
155
156
158
158
159
162
162
163
166
169
170
172
175
177
192
197
199
9
ÍNDICE DE FIGURAS
Fig Nº1
Fig Nº2
Fig Nº3
Fig Nº4
Fig Nº5
Fig Nº6
Fig Nº7
Fig Nº8
Fig Nº9
Fig Nº10
Fig Nº11
Fig Nº12
Fig Nº13
Fig Nº14
Fig Nº15
Fig Nº16
Fig Nº17
Fig Nº18
Fig Nº19
Fig Nº20
Fig Nº21
Fig Nº22
Fig Nº23
Fig Nº24
Fig Nº25
Fig Nº26
Fig Nº27
Fig Nº28
Fig Nº29
Precisión y exactitud
Curva de distribución normal
Curva de distribución normal estandarizada
Coordenadas cartesianas en el espacio
Coordenadas geodésicas
Radio de curvatura de la elipse meridiana
Normal principal
Línea geodésica
Altura elipsoidal
Alturas normales
Altura geométrica
Cuadrilátero geodésico diferencial
Cuadrilátero diferencial proyectado
Deformación angular respecto al eje X
Deformación angular respecto al eje Y
Determinación semiejes según teorema de Apolonio
Clasificación de proyecciones perspectivas
Superficies de proyección
Clasificación de proyecciones según superficie de proyección
Sistema cilíndrico transverso conforme
Latitud isométrica
Convergencia de meridianos
Diferencia arco-cuerda
Variación longitudinal del factor de deformación de escala
Plano Topográfico Local
Codificación de puntos muestrales
Puntos muestrales
Relación plano TM – Elipsoide
Relación Plano Topográfico Local – Elipsoide – Plano TM
19
23
24
34
36
38
40
46
49
50
51
63
64
67
69
74
77
79
80
89
95
98
100
107
110
122
140
148
150
10
ÍNDICE DE TABLAS
Tabla Nº1
Tabla Nº2
Tabla Nº3
Tabla Nº4
Tabla Nº5
Tabla Nº6
Tabla Nº7
Tabla Nº8
Tabla Nº9
Tabla Nº10
Tolerancia según escala de representación
Disposición altimétrica Planos Topográficos Locales
Factor de deformación de escala Planos Topográficos Locales
Correlación Coordenadas TM – factor de deformación de escala
Arcos geodésicos y proyectados
Arcos de paralelo
Determinación de escalas de representación según tolerancia,
caso general
Determinación de escalas de representación según tolerancia,
caso particular “a”
Determinación de escalas de representación según tolerancia,
caso particular “b”
Determinación de escalas de representación según tolerancia,
caso particular “c”
129
136
137
142
143
144
145
146
146
147
11
CAPITULO 1
ASPECTOS GENERALES
1.1.
INTRODUCCIÓN
El vertiginoso crecimiento de las ciudades chilenas observado desde mediados del siglo
XX y el progresivo avance tecnológico vinculado a las actividades que en ella se realizan han
derivado, por una parte en la creciente necesidad de representar de forma precisa y exacta el
territorio y por otra parte, en un cambio de paradigma en cuanto a la concepción del espacio y la
conceptualización de su representación, observándose por ejemplo, una evolución en el concepto
de escala, ya que, mientras antiguamente se aceptaba este término como una “relación constante
entre la distancia medida sobre un mapa o plano y la distancia correspondiente medida sobre el
terreno representado”, hoy se acepta que este concepto involucra tanto la relación gráfica entre
elementos representados en una carta o mapa y sus correspondientes en el terreno, como la
cantidad de información que puede contener un elemento gráfico, la que evidentemente no se
relaciona con el tamaño relativo del elemento representado.
Con lo anteriormente señalado, se hace evidente que para satisfacer las necesidades
cartográficas acordes a este cambio de paradigma, se hace necesaria una conceptualización clara
12
de las variables que intervienen en la representación del terreno y en la influencia de las
distorsiones y errores inherentes al proceso proyectivo, para lograr con esto la optima utilización
de la cartografía como herramienta precisa de representación del terreno.
A pesar de la innegabilidad de esta necesidad, la realidad Chilena revela que el manejo de
cartografía en ambientes públicos y privados, no considera de manera correcta las limitantes
cartográficas impuestas por la escala de representación y la proyección a utilizar, resultando en la
mayoría de los casos, la acumulación grosera e inconsciente de errores métricos que pueden
interferir negativamente en la correcta toma de decisiones en el contexto del ordenamiento
territorial.
Como solución a esta problemática, la presente investigación analizará la relación
existente entre la exactitud que entregan diferentes proyecciones Transversales de Mercator (TM
en adelante) a distintas escalas de representación para el caso particular de la representación a
escalas urbanas o de detalle.
El primer capítulo expone las generalidades del tema a estudiar, la hipótesis de trabajo y
los objetivos generales y específicos de la investigación.
El capitulo Nº2 repasa los conceptos básicos de la teoría de errores y su cuantificación
destacando el aporte de la estadística al campo de la cartografía.
El capítulo Nº3 explica las características y alcances relativos a los referenciales
geodésicos. El elipsoide como figura de referencia geodésica mediante sus características y
13
propiedades geométricas. Conceptos de referencia altimétrica donde se hace referencia al
concepto de geoide, cuasi-geoide, tipos de altura, incompatibilidades entre tipos de altura y
soluciones a estas incompatibilidades y finalmente el concepto de Datum destacándose los de tipo
clásico y moderno.
El capítulo Nº4 “Proyecciones Cartográficas” expone los conceptos básicos de geometría
diferencial sobre el plano y el elipsoide, los módulos de deformación, la indicatriz de Tissot y con
especial atención, las propiedades y fundamento matemático de las proyecciones conformes.
El capítulo Nº5 explica los aspectos conceptuales de las proyecciones Transversales de
Mercator mediante el desarrollo analítico de las transformaciones entre coordenadas Geodésicas
y TM, aspectos geométricos de las proyecciones TM y ejemplos de proyecciones TM utilizadas
alrededor del mundo.
El capitulo Nº6 expone los pasos metodológicos utilizados en esta investigación para
analizar los aspectos métricos de las proyecciones y la influencia del error que ellos producen.
El capitulo Nº7 presenta los resultados de esta investigación según los pasos
metodológicos seguidos.
El capitulo Nº8 presenta el análisis de los resultados obtenidos.
El capitulo Nº9 expone las conclusiones alcanzadas tras el análisis de los resultados.
14
1.2.
HIPÓTESIS DE TRABAJO
Las proyecciones Transversales de Mercator ofrecen en su conjunto, diferentes grados de
exactitud, los cuales pueden resultar en ocasiones insuficientes para la representación del terreno
a escalas de detalle.
15
1.3. OBJETIVOS
1.3.1. Generales
•
Realizar un análisis comparativo entre las deformaciones producidas por distintas
proyecciones Transversales de Mercator en escalas de detalle.
1.3.2. Específicos
•
Establecer un criterio para la elección de una proyección Transversal de Mercator.
•
Establecer indicadores de comparación entre diferentes proyecciones Transversales de
Mercator en función de las deformaciones que producen y de la escala de representación.
•
Determinar la exactitud con que diferentes proyecciones Transversales de Mercator
representan los objetos a diferentes escalas de detalle.
•
Establecer indicadores que relacionen el plano de proyección y la superficie topográfica.
•
Determinar en la practica la influencia de los errores producidos por diferentes
proyecciones TM en mediciones indirectas realizadas en diferentes escalas de
representación.
16
CAPITULO 2
ERRORES Y SU CUANTIFICACIÓN
El enfoque geométrico de la cartografía es aquel que prioriza la utilización de productos
cartográficos para la representación precisa y exacta de los elementos facilitando con esto su
medición y análisis. Sin embargo, todo proceso de medición involucra una serie de errores
relativos al método, al dispositivo utilizado y a las limitaciones propias del ser humano que deben
ser cuantificadas y minimizadas para obtener así magnitudes probables o que se acerquen a la
realidad. En este ámbito, la estadística realiza un valioso aporte a la cartografía, ya que con la
identificación, cuantificación de errores y el cálculo de probabilidades de ocurrencia de estos, es
posible lograr un mejor desempeño de la disciplina cartográfica al permitir evaluar y estudiar las
características de un producto cartográfico y datos espaciales en general y así interpretar y
evaluar la exactitud que entrega un dato cualquiera como por ejemplo, el valor de una
coordenada. Si bien es cierto, la teoría de errores no producirá como resultado final, el que una
medición sea nominalmente igual a la realidad, si permitirá entre otras cosas conocer el la
magnitud del error probable asociado a un fenómeno o valor y con esto mejorar finalmente la
calidad de las representaciones cartográficas.
El presente capítulo interioriza al lector en los conceptos básicos asociados al estudio de
errores y en la cuantificación y métodos de manejo de los mismos.
17
2.1.
CONCEPTOS GENERALES
2.1.1. Cifras significativas
Constituidas por el numero de dígitos provenientes de una determinación cierta más un
digito incierto. Por ejemplo, en una medición hecha con cinta métrica graduada al centímetro el
ultimo digito cierto será la unidad de centímetro y el digito incierto estará dado por la estimación
de la fracción del centímetro (usualmente la mitad).
2.1.2. Precisión
En términos simples, la precisión es el grado de refinamiento en la ejecución de una
operación y que por ende está vinculada con la calidad del instrumental utilizado (y la capacidad
de este de leer pequeñas variaciones de la magnitud a medir), del operador, el procedimiento y
los métodos involucrados. Este concepto se asocia directamente con el número de cifras
significativas con que se representa el fenómeno.
En un aspecto mas amplio, la precisión se asocia con la varianza de un conjunto de
observaciones, de manera que la baja varianza de un conjunto de “N” valores es indicador de una
alta precisión y viceversa.
2.1.3. Exactitud
Se relaciona directamente con la distancia existente entre un valor representativo de un
conjunto de “N” observaciones, y un valor patrón considerado la medida real.
18
Ya que en rigor no es posible determinar la magnitud verdadera y exacta de una medición,
se recurre con frecuencia a patrones verdaderos derivados de observaciones como por ejemplo, la
suma de los tres ángulos de un triangulo o el promedio de “n” observaciones.
Y
Exactitud
X
Precisión
Figura Nº1 Precisión y Exactitud
Si para la figura Nº1, el eje Y representa el valor real de una magnitud, y un conjunto de
N mediciones se dispersa dentro de la zona coloreada, puede graficarse la exactitud como la
distancia que separa al conjunto de observaciones (representados por la zona coloreada) del valor
real “Y”, mientras que la precisión será inversamente proporcional a la magnitud de la dispersión
de las observaciones.
2.1.4. Equivocación
Son errores provocados generalmente por fallas en las lecturas, errores de digitación u
observaciones descuidadas. Usualmente son muy grandes y fáciles de determinar.
19
2.1.5. Errores sistemáticos
Siguen algún tipo de patrón y son generalmente constantes en magnitud y signo. En
mediciones cartográficas, estos errores son generados principalmente por instrumentos
desperfectos, errores en la determinación de escalas y cambios en las propiedades físicas de un
cuerpo a raíz de variaciones de temperatura o humedad o bien responden a hábitos o tendencias
del operador en los cuales reacciona de manera semejante ante condiciones similares. Los errores
sistemáticos pueden ser tratados eliminados cuando se conoce concretamente las causas de su
origen.
2.1.6. Errores aleatorios
Son los errores no considerados en los ítems anteriores y provienen de fuentes y causas
desconocidas y fuera del control del observador. Se caracterizan por:
•
Igual probabilidad de ocurrencia entre errores positivos y negativos.
•
Errores pequeños tienen mayor probabilidad de ocurrencia.
•
Errores grandes tienen una baja probabilidad de ocurrencia.
La probabilidad de que un error aleatorio no exceda cierta magnitud, puede ser inferida
mediante procesos estadísticos para un número finito de variables aleatorias.
20
2.2. CONCEPTOS BÁSICOS DE PROBABILIDADES
En términos sencillos, puede definirse probabilidad como la frecuencia de ocurrencia de
un evento en relación al número de posibles ocurrencias. La probabilidad de ocurrencia de
cualquier evento, estará entre cero y uno, si la probabilidad es 0 el evento nunca ocurrirá,
mientras que si la probabilidad es 1 el evento ocurrirá con seguridad. De esto pueden deducirse
cuatro reglas básicas de probabilidad .
Si se considera P(A) como la probabilidad del evento “A” y P(B) como la probabilidad del
evento “B”, se obtiene.
a.
la probabilidad de que un evento no ocurra o falle, es uno menos la probabilidad
de ocurrencia del evento
1 - P(A) = fallo del evento A
b.
La probabilidad de que alguno de los eventos “A” o “B” ocurra, es igual a la suma
de ambas probabilidades
P(A o B) = P(A) + P(B)
c.
La probabilidad de que ambos eventos “A” y “B” ocurran, es igual al producto de
sus respectivas probabilidades.
P(A y B) = P(A) · P(B)
21
2.2.1. Distribución de errores aleatorios
Existe una tendencia en la distribución de los valores de probabilidad de ocurrencia para
un fenómeno cualquiera, que puede ser representado según una curva denominada “curva de
distribución normal”, la que relaciona la magnitud del error (eje x) con la frecuencia de
ocurrencia de dicho error (eje y).
Cuando el numero de observaciones de un fenómeno estudiado tiende a infinito. La
probabilidad de ocurrencia de un fenómeno “x” queda representada según la función “modelo
probabilístico de distribución normal”.
P( x) =
1
σ 2π
−
( x−μ )2
2σ 2
e
Donde:
x = Magnitud de errores
μ = Parámetro que representa el promedio de x
σ = Desviación estándar de la variable
e = Base de logaritmo natural
siendo:
σ =
∑
n
i =1
( xi − μ ) 2
n
Donde:
n = número de medidas
22
Para “n” observaciones, la función expresada anteriormente que reducida a:
P( x) =
1
σ 2π
−
e
x2
2σ 2
ya que el promedio de los errores de las n observaciones será cero.
Así se puede llegar a la forma general de distribución normal de lo errores, representado
por la figura Nº2
f(x)
μ−σ
μ
μ+σ
x
Figura Nº2 Curva de Distribución Normal
El análisis de esta curva permite deducir las siguientes propiedades de la magnitud de
errores y de su distribución.
•
De la forma de campana de la curva, se puede deducir que los errores pequeños ocurren
mas frecuentemente que los errores grandes, por lo tanto, a mayor error, menos
probabilidad de ocurrencia.
•
La simetría de la curva indica que los errores de signo positivo y negativo, tienen la
misma probabilidad de ocurrencia.
23
•
La curva se extiende indefinidamente en forma asintótica respecto al eje X lo que indica
que errores de gran magnitud tendrán una muy baja probabilidad de ocurrencia.
Para el caso de mediciones finitas se emplea la curva de distribución normal estandarizada
(figura Nº3), que tiene por característica, el aproximarse a cualquier función de distribución de
error con una precisión tal que se hace innecesario definir una curva de errores por cada proyecto
involucrado. La utilización de esta curva estandarizada debe realizarse previa modificación de la
desviación estándar para pocas variables donde:
σ =
∑ (di
− d )2
n −1
Con
di = Valor de una observación cualquiera
d = Valor mas probable (promedio) del conjunto de observaciones
f(x)
0.4
−3
−2
−1
0
1
2
3
C=x/σ
Figura Nº3 Curva de Distribución Normal Estandarizada
24
La curva de distribución normal estandarizada cumple con poseer un promedio de errores
(μ) igual a cero y una desviación estándar igual a 1 lo que se interpreta como una precisión
unitaria.
El eje x esta tabulado según C = x/σ lo que permite representar un conjunto de
observaciones que posean una determinada desviación estándar y el eje Y representa frecuencias,
las que toman un valor máximo cercano a 0.4 obtenido reemplazando en la función, los valores
X=0 y σ=1
P ( x) =
1
= 0.3989 ≅ 0.4
2π
2.2.2. Probabilidad de ocurrencia de errores aleatorios
Considerando las propiedades de la distribución de errores, puede establecerse que la
probabilidad que ocurra un error determinado será siempre cero ya que para pocas observaciones
el promedio de errores es siempre cero y se utilizan rangos de error simétrico en torno al error
nulo. No obstante, puede determinarse el rango de error en el cual está inserta una observación
delimitando la curva de distribución normal según dos abscisas simétricas con respecto al eje x=0
y calculando el área encerrada bajo la curva. Es decir, el número de observaciones expresado en
porcentaje, que presentarán un error comprendido dentro del rango establecido en abscisas, será
igual a la probabilidad, área encerrada bajo la curva entre dichas abscisas, expresada en
porcentaje; el resto de las observaciones presentará errores fuera de los límites señalados.
Así por ejemplo:
25
Si se considera un mismo tramo medido 10 veces sobre una carta y los resultados arrojan
d = 1153.38m
σ = ±1.5m
y se quiere conocer la probabilidad de que una medición cualquiera (de las realizadas)
contenga un error de a lo mas 1.5m (un sigma), basta con hacer
C=
x
σ
=
1.5
= ±1
± 1.5
Buscando el valor C=1 en la tabla de áreas bajo la curva se obtiene el valor 68.27%, por lo
que puede decirse que “existe un 68.27% de probabilidades que una medición cualquiera posea
un error máximo de 1.5m” o de otra manera “una medición cualquiera de las realizadas, posee un
error máximo de 1.5m con un sigma”
Por otra parte, para conocer el rango de error que contiene una confianza del 90%, basta
con plantear:
x = C ·σ
considerando : C=1.6449 (área para un 90% de confianza)
se obtiene x = 1.5·1.6449 = 2.467 m
así, se podría decir que “para una confianza del 90%, el error máximo que se produce en
una de las 10 mediciones no debe ser superior a 2.467m”, es decir 9 de las 10 mediciones poseen
un error menor que 2.467 y solo una puede tener un error mayor que los 2.467m
26
2.2.3. Cuantificación de errores aleatorios
Como una forma de determinar la magnitud de los errores existentes en una medición o
conjunto de ellas. Se han determinado tres indicadores utilizados frecuentemente y expresados en
función de la desviación estándar (σ)
2.2.3.1. Error de una observación: determina la magnitud del error para una medición cualquiera,
de un conjunto de observaciones de igual precisión y corresponde a:
σ =
∑ (di
− d )2
n −1
2.2.3.2. Error del valor mas probable: Corresponde al promedio de errores asociados a las
mediciones y se representa por:
σn =
∑ (di
− d )2
n(n − 1)
o por su equivalente σ n = ±
σ
n
2.2.3.3. Error del resultado: Corresponde al error en el cual se involucra la combinación de
valores mas probables de varios elementos para dar como resultado una única magnitud.
El error de esa magnitud, será función del error de cada una de las partes involucradas, es
decir de cada uno de los valores mas probables con sus respectivos errores independientes. Por
ejemplo:
Sea R = f (a, b, c, . . .) una función cualquiera que involucra valores mas probables
de “a”, “b”, “c” etc. La desviación estándar corresponde a:
27
⎡⎛ δR ⎞ 2 ⎛ δR ⎞ 2 ⎛ δR ⎞ 2
⎤
σr = ⎢⎜ σa ⎟ + ⎜ σb ⎟ + ⎜ σc ⎟ + ....⎥
⎣⎢⎝ δa ⎠ ⎝ δb ⎠ ⎝ δc ⎠
⎦⎥
Si la función “f” corresponde a una suma, el resultado de estará dado por la suma
vectorial de los errores independientes, es decir:
σr = ± (σa 2 + σb 2 + σc 2 + ...σn 2 )2
1
Si la función “f” corresponde al promedio de los valores mas probables de cada
elemento o las medidas son ejecutadas con similar precisión, puede expresarse
según:
σ r = σm, i n
Si la función “f” corresponde a una multiplicación de los valores mas probables de
los elementos “a” y “b”, se obtiene:
σ r = σa·σb
28
2.2.4. Indicadores de Precisión
Comúnmente se utiliza una nomenclatura estandarizada para referirse a distintos tipos de
indicadores de precisión en función de la desviación estándar. Así, según el manual de carreteras
(MOP Vol Nº2 año 2001) se puede encontrar:
2.2.4.1. Error Estándar o Error medio cuadrático: equivale a una desviación estándar e implica
que la probabilidad de ocurrencia de un error de a lo más +/- 1σ sea de 68.27%.
E = +/- σ
2.2.4.2. Error Probable: o también llamado “error del 50%”, implica que existe igual probabilidad
de que el error cometido esté comprendido dentro de un rango o fuera de él.
E0 = +/- 0.6475 σ
2.2.4.3. Error del X%: Implica que el error cometido está comprendido dentro de un rango
determinado con una probabilidad o confianza del X%.
Ex%=+/- Cxσ
29
CAPITULO 3
REFERENCIALES GEODÉSICOS
La evolución de las necesidades del hombre y el consecuente avance de la tecnología, han
determinado la necesidad de entender las formas, dimensiones de la Tierra y procesos que en ella
se generan. Para esto, las herramientas y conocimientos cartográficos han constituido un pilar
fundamental para lograr su correcta representación. Sin embargo el vertiginoso avance del pensar
humano requiere también un veloz desarrollo en la disciplina cartográfica tendiente a lograr una
óptima representación del terreno y con ello alimentar una relación simbiótica con otras ciencias
y disciplinas.
Dadas las características elásticas de la Tierra, la representación de ella requiere que su
asimilación a una figura simplificada y susceptible de análisis matemático, la que constituirá el
llamado referencial geodésico. A lo largo de la historia, han sido diversos los intentos del hombre
por relacionar la Tierra a una figura regular que le permitiese estudiarla y representarla. Desde
Pitágoras quien en el siglo VI AC definió la esfericidad de la Tierra o Eratóstenes quien durante
el siglo III AC calculó las dimensiones de ella con gran exactitud, se tendió a considerar la Tierra
como una figura esférica perfecta. Sin embargo en 1687 el físico Isaac Newton por medio de su
“Ley de Gravedad Universal” señaló que la Tierra debería ser mas achatada en los polos que en
ecuador insinuándose con esto por primera vez al elipsoide de revolución como figura de
representación de la Tierra.
30
Posteriormente en 1740, Collin MacLaurin demostró científicamente la posibilidad de que
un elipsoide fuera una figura de equilibrio para una masa fluida en rotación. Tres años mas tarde
Clairaut definiría el achatamiento en función de la gravedad y de la velocidad de rotación. A
finales del siglo XVIII y principios del siglo XIX, científicos tales como Laplace, Bessel y Gauss
plantearían la necesidad de representar la Tierra mediante un modelo elipsoidal para satisfacer las
crecientes necesidades de precisión de posicionamiento.
Carl Friedrich Gauss en el año 1822 introdujo el concepto de “Geoide” y lo definió como
“una superficie en la que cualquiera de sus partes intersecta las direcciones de la gravedad en
ángulo recto y de la que es una parte la superficie oceánica en reposo en condiciones ideales”. A
finales del siglo XIX el geodesta Gabriel Stokes publicaría una solución al problema de
definición del Geoide mediante el establecimiento de la formula fundamental de Gravimetría, que
posteriormente seria desarrollada de manera mas rigurosa por Sergui Molodensky.
Con todos estos avances científicos, el hombre ya disponía de una idea bastante cercana
de la forma y dimensiones del planeta, sin embargo, el problema de la representación del mismo
estaba lejos de ser solucionado ya que por una parte, debe buscarse el relacionar los distintos
referenciales geodésicos y los métodos usados a lo largo de la historia y por otra parte se debe
relacionar la referencia planimétrica, la referencia vertical y los elementos a representar para dar
consistencia a una solución cartográfica acorde a las necesidades actuales.
31
3.1. ELIPSOIDE DE REVOLUCIÓN
Elipsoide de revolución, es una figura matemática resultante de la rotación de una elipse
cualquiera en torno a su semieje menor generando de esta forma un cuerpo tridimensional.
Analíticamente es de la forma:
x2 + y2 z2
+ 2 =1
2a 2
b
Si se considera a la Tierra como un cuerpo fluido homogéneo, se observará que debido al
movimiento de rotación del planeta, la masa de este tenderá a concentrarse en las bajas latitudes
en vez de en las cercanías de los polos formando así un elipsoide de revolución.
Matemáticamente se puede determinar utilizando un valor medio de gravedad y velocidad de
rotación, generándose con ellos, los valores semieje mayor “a” y acatamiento “f”. Un elipsoide de
referencia es por lo tanto el elipsoide que se usa como soporte analítico para las coordenadas de
puntos medidos en la superficie de la Tierra para su posterior representación y análisis. El
elipsoide de referencia puede ser de carácter local donde representará solo una parte del planeta o
de carácter global lo que implica que podrá representar con gran exactitud la forma global del
planeta.
Dentro los elipsoides de uso local utilizados en Chile , se pueden encontrar:
•
Internacional de 1909 (Internacional de 1924; Hayford)
o a = 6.378.388m
32
o f = 1/297
•
Elipsoide Sudamericano de 1969
o a = 6.378.160m
o f = 1/298.25
Dentro de los elipsoides de uso global, se puede encontrar:
•
GRS-80
o a = 6.378.137m
o f = 1/298.257222101
Elipsoide utilizado en el Sistema de Posicionamiento Global (GPS)
3.1.1. Coordenadas cartesianas en el espacio
Un sistema coordenado cartesiano en el espacio, está definido como se muestra en la
figura Nº4, por tres ejes mutuamente perpendiculares “x” “y” y “z”. Un punto en el espacio, se
podrá localizar considerando la distancia perpendicular que lo separa de cada recta, formando así
un trío coordenado (x,y,z).
De esta manera, un sistema cartesiano puede soportar a un sistema geodésico
considerando que:
•
El origen del sistema esta ubicado en el centro de masa de la Tierra
•
El eje “x” es coincidente con el plano ecuatorial
33
•
El eje “z” es coincidente con el eje de rotación terrestre
•
El eje “y” es coincidente con el plano ecuatorial y forma un ángulo recto respecto
al eje “x” definiendo el sistema como dextrógiro (giro hacia la derecha)
z
Polo
Meridiano
de
Greenwich
Y
Z
Y
x
X
Plano
Ecuatorial
y
Figura Nº4 Coordenadas Cartesianas en el Espacio
3.1.2. Coordenadas geodésicas
Al considerar la forma analítica de la Tierra como un elipsoide, es necesario determinar en
él ciertas líneas de referencia que permitan definir la posición de un punto sobre su superficie de
manera inequívoca.
Si el elipsoide de revolución rota en torno al semieje menor “b”, y en su punto medio se
levanta un plano normal a dicho semieje denominado plano ecuatorial, la intercepción de este
plano con el elipsoide, generará una línea de circulo máximo llamada ecuador, que dividirá al
elipsoide en dos mitades iguales denominadas hemisferio norte y hemisferio sur. La intercepción
34
de los infinitos planos paralelos al plano ecuatorial con el elipsoide, genera las líneas de circulo
menor llamadas paralelos.
Por otra parte, los infinitos plano que contengan al eje de rotación (planos meridianos)
definirán en su intersección con el elipsoide a las líneas llamadas meridianos. Convencionalmente
se ha establecido como origen de estos meridianos al que pasa por el observatorio de Greenwich
Inglaterra (figura Nº5)
3.1.2.1. Latitud Geodésica (φ)
Ángulo formado entre el plano ecuatorial y la normal a un punto cualquiera siguiendo la
dirección de un meridiano. Convencionalmente, se relaciona la línea de origen de las latitudes
con el eje Y=0 de un sistema cartesiano plano, para diferenciar las coordenadas de hemisferio
norte con las del hemisferio sur mediante los signos “+” y “-” respectivamente. De la misma
forma, se suele diferenciar las coordenadas mediante los prefijos “N” y “S” para los hemisferios
Norte y Sur respectivamente (Figura Nº5).
3.1.2.2. Longitud (λ)
Ángulo diedro formado por un plano meridiano de origen y el plano meridiano que
contiene al punto. Convencionalmente, se relaciona la línea de origen de las longitudes con el eje
X=0 de un sistema cartesiano plano, para diferenciar las coordenadas “Este” con las coordenadas
“Oeste” mediante los signos “+” y “-” respectivamente. De la misma forma, se suele diferenciar
35
las coordenadas mediante los prefijos “O” y “E” para los hemisferios según su si se localizan al
oeste o al este del meridiano de origen respectivamente. (Figura Nº5).
3.1.2.3. Altura geométrica o Elipsoidal (h)
Definida por la distancia normal entre el punto y la superficie del elipsoide (Figura Nº5).
De esta forma, las coordenadas geodésicas quedan definidas por latitud (φ) longitud (λ) y
altura geométrica (h).
Z
P
Merid
ia
de Gre no
enwic
h
λ
Ecu
ado
r
h
Q
O
φ
Y
λ
X
P1
Figura Nº5 Coordenadas Geodésicas
36
3.1.3. Relación Matemática entre Coordenadas
Diversos procesos de cálculo vinculados a la transformación de coordenadas y de sistemas
geodésicos, requieren expresar las coordenadas geodésicas φ, λ y h en términos de coordenadas
cartesianas tridimensionales y estas en coordenadas geodésicas. Las relaciones entre estas
coordenadas pueden escribirse:
X = (N + h ) cos φ cos λ
Y = (N + h ) cos φsenλ
( (
) )
Z = N 1 − e 2 + h senφ
la transformación inversa viene dada por:
⎛ Z + b·e' 2 ·sen 3ψ
2
3
⎝ d − a·e cos ψ
φ = arctg ⎜⎜
λ = arctg
h=
⎞
⎟⎟
⎠
y
x
d
−N
cos φ
Donde:
d=
x2 + y2
ψ = arctg
a· z
b·d
37
3.1.4. Geometría del Elipsoide
3.1.4.1. Normales Principales
a. Radio de curvatura de la elipse meridiana:
Si se considera un punto “P” sobre el elipsoide, y siguiendo por el meridiano otro
punto “Q” situado a una distancia infinitesimal del primero, se obtendrá un arco
diferencial de meridiano que corresponde con el de un circulo que contiene a “P” y “Q”,
luego, existe un único radio que define al círculo que contiene al segmento diferencial.
Este radio se denomina Radio de curvatura de la elipse meridiana “M”. Usando la figura
Nº6 se puede determinar el valor de M en función de la latitud de un punto.
Z
dz
ds
dx
dφ
M
Figura XX Radio de Curvatura
X
Figura Nº6 Determinación del Radio de Curvatura de la Elipse Meridiana
Tomando la distancia diferencial ds a lo largo de un arco de meridiano, se puede decir
que:
38
⎡ ⎛ dx ⎞ 2 ⎤
ds = Mdφ = (dx 2 + dz 2 ) = dz ⎢1 + ⎜ ⎟ ⎥
⎢⎣ ⎝ dz ⎠ ⎥⎦
= dz (1 + tan 2 φ )
=
dz
cos φ
dz
cos φ
= tan(90 + φ ) = − cot φ = −
dx
senφ
ya que :
Mdφ =
entonces :
dz
cos φ
⎛ 1 ⎞⎛ dz ⎞
⎟⎟⎜⎜ ⎟⎟
M = ⎜⎜
⎝ cos φ ⎠⎝ dφ ⎠
Ya que “z” puede escribirse en términos de la latitud como
z=
a(1 − e 2 ) senφ
(1 − e 2 sen 2φ )
Derivando respecto de la latitud se obtiene:
39
dz
a(1 − e 2 ) cos φ
=
dφ (1 − e 2 sen 2φ ) 3 / 2
y usando
M=
⎛ 1 ⎞⎛ dz ⎞
⎟⎟⎜⎜ ⎟⎟ resulta finalmente
M = ⎜⎜
⎝ cos φ ⎠⎝ dφ ⎠
a(1 − e 2 )
(1 − e 2 sen 2φ ) 3 / 2
dicho valor también conocido como ρ
b. Normal Principal:
La normal principal o gran normal “N” se determina según el largo del segmento
comprendido entre un punto cualquiera sobre el elipsoide y su intersección con el eje
menor siguiendo la normal al punto. Usando la figura Nº7 se puede deducir el valor de la
normal principal a partir de parámetros elipsoidales y la latitud geodésica de un punto.
z
φ
N
x
Figura Nº7 Determinación de la Normal Principal
40
Tomando la ecuación de la elipse:
x2 z2
+
=1
a2 b2
diferenciando se obtiene:
dz
b2 x
=− 2·
dx
a z
2 x 2 z dz
+
=0
a 2 b 2 dx
operando: tgφ = −
a2 z
·
b2 x
e2 =
como:
a2 − b2
b2
=
1
−
a2
a2
b2
entonces: 1 − e = 2
a
2
y despejando, se tiene que:
b = a (1 − e 2 )
sustituyendo en la ecuación anterior se tiene que :
tgφ =
1 z
a2
z
· =
·
2
2
a (1 − e ) x 1 − e 2 x
despejando se obtiene:
z = x(1 − e 2 )tgφ
luego, llevando la ecuación anterior y el valor de b a la ecuación principal de la elipse, se
x 2 x 2 (1 − e 2 ) 2 tg 2φ
=1
obtiene: 2 +
a
a 2 (1 − e 2 )
operando, se obtiene: x 2 + x 2 (1 − e 2 )tg 2φ = a 2
41
y:
a2
x2 =
1 + (1 − e 2 )
y finalmente x =
como
sen 2φ
cos 2 φ
=
a 2 cos 2 φ
cos 2 φ + (1 − e 2 ) sen 2φ
a·cos φ
(1 − e 2 sen 2φ )
x = N ·cos φ
Entonces:
x
=N
cos φ
Con lo que se obtiene finalmente:
N=
a
(1 − e 2 ·sen 2φ )
3.1.5. Arcos Sobre el Elipsoide
3.1.5.1. Longitud de un arco meridiano
Si una fracción diferencial de arco meridiano se puede representar por la expresión
ds = M dφ, luego integrando esta expresión entre φ1 y φ2 se obtiene:
φ2
S = ∫ Mdφ
φ1
= a(1 – e2)
φ2
∫φ
1
(1 − e 2 sen 2φ ) −3 / 2 dφ
El valor (1 – e2 sen2 φ)-3/2 se reduce mediante serie de McLaurin, cuya forma general es:
42
f ( x) = f (0) +
xf ' (0) x 2 f ' ' (0) x 3 f ' ' ' (0)
+
+
+ ...
1!
2!
3!
quedando:
3
15
35
(1 − e 2 sen 2φ ) −3 / 2 = 1 + e 2 sen 2φ + e 4 sen 4φ + e 6 sen 6 + ...
2
8
16
luego se reemplazan las potencias de senφ por ángulos múltiples para simplificar las integrales
siendo:
sen2φ = ½ - ½ cos2φ
sen4φ = 3/8 - ½ cos2φ + 1/8 cos4φ
sen6φ = 15/16 – 15/32 cos2φ + 3/16 cos4φ − 1/32 cos6φ
sen8φ = 35/128 – 7/16 cos2φ + 7/32 cos4φ − 1/16 cos6φ + 1/128 cos8φ
sen10φ = 63/256 – 105/256 cos2φ + 15/64 cos4φ − 45/512 cos6φ + 5/256 cos8φ - 1/512 cos10φ
Poniendo estas ecuaciones en la ecuación anterior y ordenando según los ángulos
múltiples se obtiene:
(1 – e2 sen2 φ)-3/2 = A – B cos2φ + C cos4φ − D cos6φ + E cos8φ - F cos10φ
Donde:
A = 1 + ¾ e2 + 45/64 e4 + 175/256 e6 + 11025/16384 e8 + 43659/65536 e10
B = ¾ e2 + 15/16 e4 + 525/512 e6 + 2205/2048 e8 + 72765/65536 e10
43
C = 15/64 e4 + 105/256 e6 + 2205/4096 e8 + 10395/16384 e10
D = 35/512 e6 + 315/2048 e8 + 31185/131072 e10
E = 315/16384 e8 + 3465/65536 e10
F = 693/131072 e10
Ahora se puede escribir la integral
φ2
a (1 − e 2 ) ∫ (1 − e 2 sen 2φ ) −3 / 2 dφ
como
φ1
φ2
s = a(1 − e 2 ) ∫ ( A − B cos 2φ + C cos 4φ − D cos 6φ + E cos 8φ − F cos10φ )dφ
φ1
Separando la integral en partes, se obtiene:
s = a(1 − e 2 ) ⎡⎢
⎣
φ2
∫φ
1
Adφ − B
φ2
∫φ
1
cos 2φdφ + C
φ2
∫φ
1
cos 4φdφ − D
φ2
∫φ
1
cos 6φdφ + E
φ2
∫φ
1
cos 8φdφ − ...⎤⎥
⎦
Resolviendo las integrales se obtiene:
B
C
D
E
F
⎡
⎤
s = a(1 − e 2 ) ⎢ Aφφφ12 − sen2φφφ12 + sen4φφφ12 − sen6φφφ12 + sen8φφφ12 − sen10φφφ12 ⎥
2
4
6
8
10
⎣
⎦
y finalmente se define la longitud de un arco de meridiano entre los puntos φ1 y φ2
B
C
⎡
⎤
⎢ A(φ2 − φ1 ) − 2 ( sen 2φ2 − sen 2φ1 ) + 4 ( sen 4φ2 − sen 4φ1 )⎥
⎢
⎥
E
2 ⎢ D
⎥
S = a (1 − e ) − ( sen6φ2 − sen6φ1 ) + ( sen8φ2 − sen8φ1 )
⎢ 6
⎥
8
⎢
⎥
⎢− F ( sen10φ2 − sen10φ1 ) + ...
⎥
⎢⎣ 10
⎥⎦
44
3.1.5.2. Longitud de un arco de paralelo (Sp)
Si se sitúa φ1 y φ2 sobre el mismo paralelo, su distancia sobre el elipsoide estará definida
en función de la separación angular entre ellos (Δλ) y el radio paralelo. Si se define el radio
paralelo “r” como r = N ·cos φ , entonces Sp = N ·cos φ ·Δλ
3.1.6. Línea Geodésica
Se entiende por “línea geodésica”, a aquella curva trazada sobre una superficie no plana,
que cumple con ser la distancia mas corta entre dos puntos cualquiera. En el elipsoide de
revolución posee una doble curvatura, y su aplicación en el campo de la Geodesia se remonta a
las investigaciones de Gauss, quien en 1827 definió las relaciones de esta curva con las secciones
normales 1 permitiendo con esto, una alternativa mas adecuada para la resolución de triángulos
elipsoidales (Figura Nº8).
Analíticamente, se caracteriza mediante el teorema de Clairaut, que señala que a lo largo
de la geodésica el producto del radio del paralelo por el seno del azimut es una cantidad
constante. Ello implica que mientras el recorrido de la línea geodésica aumenta en latitud, la línea
geodésica debe aumentar su acimut hasta que este alcance los 90º y el radio de paralelo alcance
su mínimo valor para descender nuevamente hacia el ecuador, donde el acimut irá disminuyendo
hasta ser cero en la latitud 0º.
1
La sección normal se define como “Cualquier sección plana que contenga la normal que pasa por el punto”
(Manual de carreteras Volumen 2 M.O.P sección 2.302.1
45
B
Geodésica
A
Secciones Normales
Figura Nº8 Línea Geodésica
3.2. REFERENCIA VERTICAL
Para definir el concepto de altura de un punto, primero es necesario establecer el tipo de
referencial que se usará como origen de ellas, el cual es adoptado arbitrariamente y se denomina
“Datum vertical”.
Clásicamente se ha adoptado como Datum vertical al nivel medio del mar, el cual es
determinado por una red de mareógrafos a partir de observaciones realizadas durante largos
periodos en distintos puntos del planeta. Sin embargo el gran dinamismo producido por las
mareas y los movimientos de la Tierra, así como las variaciones internas del agua en cuanto a
46
temperatura, corrientes oceánicas y salinidad hacen que esta determinación pueda variar en varios
metros entre distintos mareógrafos (SIRGAS, grupo de trabajo III).
Como una forma de superar los inconvenientes encontrados en la determinación del nivel
medio del mar se ha hecho necesario encontrar una figura de referencia de carácter global, que
manteniendo como condición que forme una superficie equipotencial, sea independiente del nivel
del mar observado.
3.2.1. Geoide
Se puede definir al Geoide como la figura formada por una superficie equipotencial del
campo de gravedad terrestre, que coincide con el nivel medio del mar en condiciones ideales. La
determinación exacta del geoide está en función de la cantidad de masa y distribución de ella al
interior de la Tierra. Produciéndose con esto, variaciones en el potencial de gravedad según
variaciones en la densidad de la tierra y por consiguiente una variación en la determinación del
Geoide. Luego, para determinar la forma y dimensiones de un geoide sería necesario conocer las
concentraciones de masa al interior de la Tierra y establecer en que medida influyen en el
potencial de gravedad. Como evidentemente esta es una tarea imposible, se recurre a formular
hipótesis geofísicas de concentración de masas lo que se traduce en variaciones del geoide a
partir de un cambio en la hipótesis de estimación de masas.
47
3.2.2. Cuasi-Geoide
Es una superficie no equipotencial que para su determinación no requiere de hipótesis
geofísicas de distribución de masa, sino que se basa en el modelamiento matemático del campo
de gravedad normal de un punto sobre la superficie física de la Tierra. Para su definición se
calcula la altura del lugar a medir, en función del potencial de gravedad existente en ese punto y
se asume como igual a lo largo del vector normal al punto. De esta forma se desprecian las
diferencias entre el vector generado por el modelo geofísico de distribución de masa y el vector
calculado para el punto.
3.2.3. Tipos de Altura
Se define altura de un punto, como la distancia vertical existente entre el punto y el Datum
vertical. En este sentido, la Geodesia clasifica distintos tipos de altura según su determinación o
consideración respecto al campo de gravedad terrestre, a su aplicación practica y al modelo
matemático o físico considerado en su definición.
A continuación, se exponen los tipos de altura relacionados con el presente estudio.
3.2.3.1. Alturas Elipsoidales (h)
Corresponde a la distancia que separa a la superficie física de la tierra y el elipsoide
medida sobre la normal a este último (figura Nº9). Corresponde al tipo de alturas entregado por
los sistemas de posicionamiento satelital.
48
Z
P
h
Q
O
Y
E
X
P1
Figura Nº9 Altura Elipsoidal (h)
3.2.3.2 Alturas Normales
La altura Normal, puede definirse como la distancia que separa un punto cualquiera con el
cuasigeoide siguiendo la dirección de la normal entre ellos. La determinación de esta altura no
requiere de la formulación de hipótesis acerca de la distribución de masas, y con esto, que la
exactitud de la altura se relacione únicamente con la exactitud del calculo del potencial de
gravedad en la superficie física terrestre (Figura Nº10).
49
P
W = WP
H(norm)
ζ
Superficie
topográfica
CuasiGeoide
Elipsoide
Figura Nº10 Alturas Normales
La determinación de las alturas Normales puede realizarse a partir de las alturas
elipsoidales (GPS) y de la cuantificación de la anomalía de altura (ζ) u ondulación cuasi-geoidal
mediante
H ( norm) = h − ζ
en donde la anomalía de altura puede obtenerse mediante cálculos gravimétricos o satelitales
3.2.3.3. Alturas Ortométricas
La altura Ortométrica corresponde a la distancia vertical entre la superficie Geoidal y la
superficie física de la tierra, siguiendo la dirección de la plomada (figura Nº11). Ya que como se
mencionó anteriormente, el potencial de gravedad no puede ser medido a lo largo de la línea de la
plomada, se estima su valor medio a partir de la gravedad observada en la superficie de la tierra y
propagándola mediante la utilización de alguna hipótesis de distribución de masa y densidad.
50
P
W = WP
H (ortom )
N
Su pe rficie
top ográfica
G eoide
W = W0
Elipsoide
Figura Nº11 Altura Ortométrica
Las alturas Ortométricas pueden obtenerse a partir de las elipsoidales mediante
H (ortom ) = h − N
Donde N corresponde a la ondulación geoidal o diferencia entre el geoide y el elipsoide
siguiendo la línea normal a las superficies equipotenciales.
3.2.4. Relación entre tipos de alturas
3.2.4.1. Alturas elipsoidales y Alturas físicas
El origen de las alturas elipsoidales es una figura analítica que corresponde a una
idealización de la forma de la Tierra, mientras que el origen de las alturas físicas se relaciona con
el comportamiento gravimétrico particular del lugar cuya altura se desee conocer. Por
consiguiente, las alturas de tipo físico solo se pueden relacionar con las elipsoidales modelando el
comportamiento de la gravedad local. Esto es conociendo la ondulación Geoidal o la Anomalía
de altura de lugar donde se encuentre el punto.
51
3.2.4.2. Alturas normales y Ortométricas
Martinec, 1993; 1998; Martinec et al., 1995; 1996; y Huang et al. 2001, han demostrado
en la actualidad, que es posible determinar la distribución de densidad con exactitudes suficientes
para arrojar errores subcentimétricos en la determinación de alturas para la mayoría de los
terrenos, por lo que las posibles limitantes acerca de la utilización de la determinación de alturas
Ortométricas, puede ser desestimada. Recomendándose incluso el uso combinado de estas alturas
para el ajuste de redes y establecimiento de puntos de nivelación.
3.2.5. Solución a las incompatibilidades entre tipos de altura
Como
se
observó
anteriormente,
las
distintas
alturas
expuestas
presentan
incompatibilidades o inconsistencias producto de la superficie a la cual están referidas que son
necesarias de corregir para su correcta utilización. Una forma de corregir estas discrepancias, es
calculando una red de puntos comunes donde sean conocidos los distintos tipos de altura antes
señalados y la situación geoidal/cuasigeoidal de los mismos. De esta forma podrán calcularse
parámetros o diferenciales de relación para diferentes alturas, logrando así una completa relación
entre observaciones de diversa índole (mas información al respecto en “Vinculación de las
alturas elipsoidales GPS al datum vertical clásico de Colombia”, L. Sánchez y W. Martinez;
“Algunos Aspectos Sobre Alturas Ortométricas y Normales”, P. Vanicek, M. Santos, R. Tenzer,
A. Hernández, año 2003)
52
En el contexto nacional, y considerando las características geomorfológicas del territorio
nacional, es urgente la determinación de un modelo Geoidal, que permita modelar con precisión,
el comportamiento gravitacional de nuestro territorio. Pese a que el Instituto Geográfico Militar,
en un esfuerzo por refinar el Datum vertical afín a los nuevos sistemas de referencia, se encuentra
realizando mediciones gravimétricas tendientes a generar un modelo Geoidal local, la solución
aun parece lejana.
Como solución para la determinación de un modelo Geoidal local, existen ciertos modelos
mundiales que permiten una precisión en la determinación de la ondulación Geoidal del orden de
los decímetros (R. Zepeda 2004) tales como el EGM96 (Earth Gravity Model 1996)
3.3.
SISTEMAS GEODÉSICOS DE REFERENCIA
La ubicación de puntos con coordenadas sobre la Tierra, requiere que estos estén referidos
a un mismo origen con el fin de evitar ambigüedades. Para determinar coordenadas precisas que
materialicen al sistema geodésico utilizado, se ha recurrido dos conceptualizaciones distintas. Por
una parte los sistemas geodésicos clásicos, que se materializan usando observaciones
astronómicas clásicas y mediciones gravimétricas locales. Y por otra parte, los sistemas
Geodésicos geocéntricos que incorporan variables tetradimensionales y modernos sistemas de
posicionamiento en su concepción.
53
3.3.1.
Sistemas locales
Como una forma de solucionar el problema del origen de las coordenadas para los
levantamientos. La geodesia clásica ha creado soluciones particulares para espacios reducidos
sobre la Tierra, en los que se determina con métodos astronómicos la posición precisa de un par
de estaciones geodésicas que constituirán la base de los levantamientos. Una de las estaciones
precisas determinadas será el denominado “punto Datum” o estación de coordenadas geodésicas
precisas conocidas, que servirá como origen para las coordenadas geodésicas del sistema. Un
punto Datum debe definirse utilizando un sólido de revolución (comúnmente un elipsoide) y debe
estar relacionado directamente al geoide de manera que ambas figuras constituyan en conjunto la
referencia horizontal y vertical para los futuros levantamientos ligados al Datum. No obstante,
esta solución se considerará aceptable hasta una determinada distancia del punto Datum que
considere el error implícito en el levantamiento de la red geodésica constituyente del sistema y la
tolerancia de los proyectos referidos al Datum.
Un punto Datum Clásico debe contar con:
•
Latitud astronómica conocida: Utilizando instrumentos ópticos adecuados, se observan las
diferencias de declinación de parejas de estrellas.
•
Longitud Conocida: Observando el paso de estrellas por el meridiano del lugar
•
Acimut inicial conocido: Mediante la observación de un ángulo acimutal entre una marca
terrestre y una estrella circumpolar a tiempo conocido.
54
•
Ondulación Geoidal conocida: Mediante observaciones gravimétricas en el área cercana al
punto Datum, se modela el comportamiento del geoide y se determina la separación entre el
elipsoide y el geoide para el punto Datum.
•
Meridiana y primer vertical conocidos: Las coordenadas obtenidas mediante observación
astronómica están referidas a la esfera celeste, por cuanto la latitud y longitud del punto
Datum es astronómica, para referir estas coordenadas al elipsoide es necesario establecer la
desviación de la vertical de la meridiana y del primer vertical.
Cumplidas estas condiciones, es posible asegurar una correcta adaptación entre el Geoide y el
Elipsoide.
Si bien un sistema clásico permite materializar redes clásicas de primer orden (del orden
de 1:100.000), su área de efectividad estará condicionada por la optima relación geométrica que
exista entre el elipsoide y el geoide. Debido a la falta de paralelismo entre ambas figura y a las
limitaciones propias de los métodos de posicionamiento clásico, la rigidez de la red que
materializa al sistema local irá empeorando hasta alcanzar en ocasiones, errores relativos de
varias decenas de metros para áreas lejanas al punto Datum.
3.3.1.1. Sistemas Locales Usados en Chile
En la actualidad, los productos cartográficos nacionales, son referidos principalmente a
dos sistemas locales, los cuales se materializan mediante redes clásicas de primer, segundo y
tercer Orden, constituyendo así, la referencia horizontal clásica nacional. La referencia vertical es
55
independiente de la horizontal y se determina según el nivel medio del mar calculado con una red
nacional de mareógrafos. Así, los sistemas locales usados en Chile corresponden a sistemas
bidimensionales en los cuales el posicionamiento horizontal y vertical no están necesariamente
relacionados en su concepción.
a. PSAD-56
Durante la década de los 40’s y parte de los 50`s, el ejercito de Estados Unidos en
cooperación con los países de América central y América del sur, construyó una red geodésica
desde México hasta el sur de Chile la que se constituyó en la vértebra del llamado Datum
Provisorio Sudamericano. El origen de este Datum se materializó en “La Canoa” Venezuela y su
determinación fue hecha mediante observaciones astrogeodésicas y observaciones gravimétricas
utilizadas para determinar la deflexión de la vertical. La figura de Referencia escogida fue el
Elipsoide Internacional de 1924 y la ondulación geoidal fue cero por definición.
La Heterogénea distribución de masas presentes en el continente sudamericano, ocasionan
un comportamiento Geoidal muy complejo e imposible de modelar con las escasas mediciones
gravimétricas realizadas en el marco del proyecto Psad-56. Debido a esto, la materialización de
dicho Datum cuenta con errores que lo imposibilitan para cubrir con aceptable precisión el
continente sudamericano y que generan por ejemplo, diferencias de hasta 300m entre el geoide y
el elipsoide para latitudes cercanas a los 40º S.
56
Por otra parte, la precisión del transporte de coordenadas no es mejor que 10PPM lo que
implica deformaciones para la representación del territorio nacional de hasta 50m en el valor de
la coordenada de un punto de primer orden respecto del origen del Datum.
Con estos antecedentes, el Instituto Panamericano de Geografía e Historia determinó que
el Datum Psad-56 no resultaba adecuado como marco geodésico para la cartografía regular de las
naciones sudamericanas por lo que se encargó el estudio de un Datum que se adecuara mas a las
necesidades de todos los países del subcontinente.
b. SAD-69
La comunidad científica americana presentó serias objeciones con respecto a la utilización
del Sistema PSAD-56 como referencia para el continente, ya que, por una parte, la posición del
punto Datum desfavorece la precisión que puede alcanzar los puntos mas alejados de él, y por
otra parte, se consideró que las observaciones gravimétricas tendientes a determinar la desviación
de la vertical eran insuficientes.
Debido a esto, el Instituto Panamericano de Geografía e Historia solicito la creación de un
grupo de trabajo que estudiara la creación de un Datum sudamericano que satisficiera las
necesidades de todos los países sudamericanos. Se propuso en la VIII reunión de consulta
celebrada en Cuba en 1958 que el punto Datum estuviera localizado entre los 15º y 27º sur y
entre los 45º y 63º Oeste y que el propósito de este proyecto fuera el “establecer un Datum
sudamericano unificado para las redes continentales de control de los levantamientos y para la
57
información de la Figura de la Tierra”. Durante la XI reunión de consulta de cartografía en la
ciudad de Guatemala en 1965 fue presentado un informe sobre el geoide a nivel continental que
sirvió como base para la creación de un nuevo sistema y como se establecería la conexión de las
redes nacionales a partir de los datos geoidales existentes, se evaluó el impacto de la utilización
de un nuevo Datum en términos de ondulación Geoidal y desvío de la vertical. De esta manera, se
buscó que el nuevo Datum respondiera a las necesidades de ondulación geoidal y desvío de la
vertical específicos logrando así que la ubicación escogida para el nuevo Datum estuviera en
función de valores deseados.
El elipsoide asociado a este Datum corresponde al Internacional de 1967 y sus valores son
a = 6.378.160m y f = 1/298.25. En primera instancia se consideraron dos posibles orígenes de
este sistema de referencia. Correspondientes a los orígenes de los Datum nacionales de Brasil
(Chua) y Argentina (Campo Inchauspe) a los que les fueron asignadas las alturas Geoidales 0m y
2m respectivamente. Finalmente se eligió el punto “Chua” como origen del sistema.
La utilización del Datum Sad-69 en Chile fue adoptada como oficial para la creación
mapas y planos a escala 1:25.000 y mayores y aquellas regiones ubicadas desde el paralelo 43º
30’ hacia el sur. Debido a la rigurosidad con la que fue establecido y al empleo de las emergentes
técnicas de posicionamiento moderno, el Datum Sad-69 es una solución mas consistente que el
Datum Psad-56 para la representación cartográfica a escalas medias y grandes. No obstante lo
anterior, se ha relegado a un segundo plano la utilización de este Sistema dentro de las
actividades cartográficas nacionales.
58
3.3.2. Sistemas globales
Son de origen geocéntrico lo que permite que el error del sistema no supeditado a la cercanía
del punto de origen. Su existencia se debe a la necesidad de un sistema geodésico acorde a las
precisiones entregadas por los modernos sistemas de posicionamiento (Interferometría de Base
Muy Larga, Medición Láser a Satélites, Sistemas de Posicionamiento Satelital, etc)
El sistema geocéntrico de mayor utilización es el ITRS (International Terrestrial Reference
System), el cual se define utilizando un eje cartesiano con origen en el centro de masas de la
Tierra, donde el eje Z es coincidente con el polo medio calculado originalmente por el BIH con
época 1984.0 y que es susceptible de vincular al polo instantáneo o verdadero para una
determinada época mediante una serie de parámetros calculados año a año por el International
Earth Rotation Service (IERS). Para una precisa y exacta determinación de los ejes cartesianos
que sustentan al sistema, las observaciones se vinculan a fuentes extragalacticas (Quasares,
Pulsares) lo que asegura la no inercialidad del sistema. Para la materialización del sistema ITRS
se recurre a múltiples estaciones alrededor del mundo, que por medio de técnicas combinadas
(Interferometria de base larga, observación a satélites artificiales, posicionamiento doppler, entre
otros) genera el llamado ITRF o (International Terrestrial Reference Frame) el cual representa la
materialización del sistema concebido.
59
3.3.2.1.WGS-84
Es un sistema de referencia creado por el Departamento de Defensa de Estados Unidos el
cual tiene por objetivo servir de base a las técnicas modernas de posicionamiento (en especial
GPS). Al estar orientado según los parámetros IERS es compatible con el ITRF y se vincula al
elipsoide WGS-84 (en la practica elipsoide GRS-80) el cual es utilizado por el sistema de
posicionamiento global (GPS).
3.3.2.2.SIRGAS
En un esfuerzo por crear un único referencial geodésico para América, que permita
terminar con las ambigüedades en la delimitación del territorio y como una forma de acercar el
trabajo mancomunado de las naciones americanas a las tecnologías de posicionamiento y
necesidades actuales, se creó con ayuda de organismos especializados de Estados Unidos y
Europa el Sistema de referencia Geocéntrico para las Américas, el cual es un sistema
tetradimensional compatible con las tecnologías de posicionamiento satelitario y que considera su
evolución a través del tiempo. Su materialización posee cerca de una veintena de estaciones
pertenecientes a la red ITRF lo que concluye en la compatibilidad del sistema con el marco ITRF
2000. La red geodésica nacional la constituyen alrededor de 400 vértices calculados en campañas
desarrolladas en 1995, en el año 2000 y en el 2003. Algunos de estos vértices son coincidentes
con las redes geodésicas clásicas, lo que posibilita la obtención de parámetros de transformación
entre sistemas de referencia clásicos y modernos.
60
Actualmente, el Instituto Geográfico Militar y diversas entidades públicas y privadas
usuarias de cartografía se encuentran en etapa de transición hacia la completa utilización de este
referencial Geodésico. Sin embargo, aun se observan ciertos impedimentos técnicos que
mantienen a nuestro país relegado a los últimos lugares de la implementación de este sistema
geodésico en el continente.
61
CAPITULO 4
PROYECCIONES CARTOGRÁFICAS
Una proyección cartográfica es la correspondencia matemática biunívoca entre los puntos
localizados en la superficie de una esfera, elipsoide u otro cuerpo geométrico de referencia y sus
transformados en un plano de proyección. Sin embargo, antes de asumir esta definición como
cierta, habrá que tener claro en una primera instancia, que una proyección cartográfica siempre
introducirá algún tipo de distorsión o deformación en cuanto a las longitudes, áreas, ángulos o
acimutes que se puedan determinar por medio de ella. Debido a esto, la elección de la proyección
mediante la cual se representará la superficie de la Tierra debe realizarse priorizando la o las
característica geométricas que se deseen mantener para el proyecto en cuestión evitando con esto
perjudicar la exactitud con que una proyección cartográfica puede representar el terreno.
4.1.
CÁLCULO DIFERENCIAL DE ELEMENTOS SOBRE EL ELIPSOIDE
Considérese un cuadrilátero ABCD formado por dos paralelos y dos meridianos
infinitesimalmente separados (Figura Nº12). El arco de meridiano AB y el arco de paralelo AD se
representan respectivamente por:
AB = M dφ ; AD = N cos φ dλ
62
C
B
dφ
A
θ
dλ
D
Figura Nº 12 Cuadrilátero geodésico diferencial
Sobre él se pueden definir los siguientes elementos
4.1.1. Elemento lineal (dl)
La diagonal AC se describe según
AC = dl =
(M
2
·∂φ 2 + r 2 ∂λ2
)
4.1.2. Elemento angular (θ)
El ángulo θ formado por AC y AD está implícito en
tgθ = Mdφ / rdλ
4.1.3. Elemento superficial (dS)
El área del cuadrilátero infinitesimal ABCD está representada por la función
DS = M ·r ·∂φ ·∂λ = M · N cos φ ·∂φ ·∂λ
63
4.2.
CÁLCULO DIFERENCIAL DE ELEMENTOS SOBRE EL PLANO
El estudio de las deformaciones producidas en la representación plana de la superficie
terrestre requiere de ciertas conceptualizaciones que permitan cuantificar las magnitudes
deformadas para conocer así los valores reales que los elementos proyectados tienen respecto de
su geometría.
Considérese primeramente un cuadrilátero A1, B1, C1 y D1 sobre un plano rectangular
cuyos ejes X e Y son coincidentes con un meridiano y paralelo cualquiera (Figura Nº13). Las
deformaciones producidas en la proyección, pueden ser estudiadas usando las funciones
X A1 = f (λ A , φ A )
Y A1 = g (λ A , φ A )
e
Siendo “f” y “g” las funciones de paso que dependerán de la proyección utilizada.
Y
C1
B1
dl1
dy
D1
θ1
X
A1
dx
Figura Nº13
64
4.2.1. Elemento lineal (dl1)
Las coordenadas del punto C1 con respecto a A1 serán
C1
XA1 + dx
YA1 + dy
Donde:
A1C1 = dl1 = dx 2 + dy 2
Para expresar los elementos “x” e “y” en relación con “φ” y “λ” se
diferencia la
expresión antes expuesta, resultando:
dx =
δx
δx
dλ +
dφ
δλ
δφ
dy =
δy
δy
dλ +
dφ
δλ
δφ
Luego, sustituyendo las expresiones anteriores para formar así el elemento lineal, se obtiene:
⎡⎛ δx ⎞ 2 ⎛ δy ⎞ 2 ⎤ 2 ⎡⎛ δx ⎞ 2 ⎛ δy ⎞ 2 ⎤ 2
⎡ δx δx δy δy ⎤
+
dl1 = ⎢⎜⎜ ⎟⎟ + ⎜⎜ ⎟⎟ ⎥ dφ + ⎢⎜ ⎟ + ⎜ ⎟ ⎥ dλ + 2 ⎢
⎥ dφ ·dλ
⎣ δφ δλ δφ δλ ⎦
⎣⎢⎝ δλ ⎠ ⎝ δλ ⎠ ⎦⎥
⎣⎢⎝ δφ ⎠ ⎝ δφ ⎠ ⎦⎥
Los elementos entre corchetes corresponden a las Cantidades Gaussianas Fundamentales “E”,
“G” y “F” respectivamente.
65
2
2
2
2
⎛ δx ⎞
⎛ δy ⎞
E = ⎜⎜ ⎟⎟ + ⎜⎜ ⎟⎟
⎝ δφ ⎠
⎝ δφ ⎠
⎛ δx ⎞
⎛ δy ⎞
G =⎜ ⎟ +⎜ ⎟
⎝ δλ ⎠
⎝ δλ ⎠
F=
δx δx δy δy
+
δφ δλ δφ δλ
y corresponden a expresiones diferenciales que expresan la razón de cambio de
coordenadas rectangulares respecto a las componentes de las coordenadas geodésicas (φ,λ) y que
permiten describir sus deformaciones. Siendo:
E = Elemento diferencial sobre el meridiano
G = Elemento diferencial sobre el paralelo
F = Elemento diferencial en función de la latitud y la longitud
Luego, la diagonal A1 C1 queda expresada como:
dl1 = Edφ 2 + Gdλ2 + 2 Fdφdλ
Sabiendo que para dos puntos sobre un mismo meridiano dλ = 0 y que para dos puntos
sobre un mismo paralelo dφ = 0, Luego
Distancia sobre el meridiano = Edφ 2
Distancia sobre el paralelo = Gdλ2
66
4.2.2. Elemento angular (θ1)
El acimut formado por A1C1 con el eje X corresponde a (Figura Nº13):
tgθ1 =
dy
dx
o también:
senθ1 =
dy
=
dl1
dy
dx 2 + dy 2
Debido a las deformaciones producidas, el lado A1D1 no forma un ángulo recto con el eje
Y, (Figura Nº14) luego es posible calcular el ángulo formado entre A1 D1 y A1 D’1 (donde D’1
es el homologo de D1 sobre el elipsoide) mediante:
tgθ AD1 =
1
D1 D'1
A1 D'1
Y
D1
dl1
θ
A1
D'1
X
Figura Nº14
67
Como A1 y D1 poseen la misma latitud y D1 es función de la variación de la longitud de A1,
entonces, D1D’1 es la variación en “y” al variar la longitud, por ende:
D1 D'1 =
δy
dλ
δλ
A1 D '1 =
δx
dλ
δy
tgθ AD11 =
δy δx
:
δλ δλ
Análogamente se obtiene:
Sustituyendo, se obtiene:
o
senθ AD11 =
D1 D'1
dl1p
=
δy
dλ : dl1p
δλ
siendo
dl1p = A1 D1
Operando, se obtiene
senθ AD11 =
δy 1
δλ G
De similar forma se obtiene el ángulo formado entre A1B1 con el eje X (Figura Nº15)
tgθ AB11 =
δy
δx
δy δx
dφ :
dφ =
δφ
δφ
δφ δφ
en función del seno:
senθ AB11 =
δy
δy 1
dφ : dl1M =
δφ
δφ E
68
Y
B1
B'1
dl1
θ
X
A1
Figura Nº15
4.2.3. Elemento superficial (dS1)
Considerando las características lineales y angulares recién mencionadas, puede
describirse la superficie formada por A1 B1 C1 D1 mediante
dS1 = A1 B1 * A1 D1 sen(θ AB11 − θ AD22 )
Desarrollando sen(a – b) y sustituyendo por las cantidades Gaussianas fundamentales, se obtiene:
⎡ δy 1 δx 1
δx 1 δy 1 ⎤
dS1 = ⎢
−
⎥ E * G * dφ * dλ
⎣ δφ E δλ G δφ E δλ G ⎦
Operando se obtiene:
⎡ δy δx δx δy ⎤
−
dS1 = ⎢
⎥ dφ * δλ
⎣ δφ δλ δφ δλ ⎦
Una vez definidas y explicadas las deformaciones existentes en un cuadrilátero
infinitesimal sobre el elipsoide, se está en condiciones de abordar las deformaciones que sufren
69
los elementos representados en cartografía y determinar así, las características fundamentales de
las proyecciones cartográficas.
4.3.
MÓDULOS DE DEFORMACIÓN
Relación existente entre los elementos diferenciales calculados en el elipsoide y sus
imágenes en el plano, mediante las cuales es posible determinar las condiciones que deben
cumplir cada proyección para mantener sus características en cuanto a la preservación de
ángulos, distancias y superficies.
4.3.1. Modulo de deformación lineal
Corresponde a la relación entre una unidad diferencial calculada en el plano y su
homólogo en el elipsoide. De esta manera se puede expresar
L=
dl1
dl
Si este valor “L” es igual a la unidad se tratará de una proyección automecoica o
equidistante en la que evidentemente no existirá diferencia en una distancia medida en el plano y
su correspondiente en el elipsoide.
70
4.3.2. Modulo de deformación angular
El ángulo que forman dos elementos lineales diferenciales en el elipsoide difiere del
ángulo que formaran sus imágenes en el plano debido a deformaciones que serán analizadas con
posterioridad. Esta diferencia de ángulos se conoce como “Modulo de deformación angular” y se
puede expresar como:
A = θ1 − θ
Aquellas proyecciones en que se verifica que A = 0 se denominan proyecciones
conformes.
4.3.3. Modulo de deformación superficial
La razón entre la superficie de un cuadrilátero diferencial calculado sobre el elipsoide y su
imagen en el plano se denomina “Modulo de deformación superficial” y se expresa según:
S=
dS1
dS
Cuando S = 1 se trata de una proyección Equivalente
71
4.4.
ELIPSE INDICATRIZ DE TISSOT
Para comprender las deformaciones que afectan, la representación plana de un área
urbana, habrá que considerar que en su extensión existirán infinitos valores de deformaciones
diferente entre si, los que habrán de ser racionalizados para determinar los valores máximos y
mínimos de estas deformaciones y la orientación de esta deformación para el área a estudiar.
Para solucionar esto, se recurre a la utilización de un concepto diferencial que representa
las características de la deformación asociada a un punto cualquiera, y que permite por repetición
a lo largo del área de estudio, la correcta caracterización de este.
Si tangente al centro de un circulo diferencial localizado sobre un elipsoide de revolución,
se sitúa un plano en el cual proyectar el circulo diferencial, la porción infinitesimal de meridiano
y de paralelo que antes fuesen rectas perpendiculares entre sí, ahora serán trazos que, habiendo
perdido su perpendicularidad, delata que un circulo trazado sobre un elipsoide se proyecta sobre
un plano como una elipse la que se denomina “Indicatriz de Tissot”.
El principio fundamental de esta indicatriz señala que para todo punto en la superficie de
un elipsoide, existen dos “direcciones principales” o perpendiculares entre sí, tales que en sus
imágenes también lo son. El estudio de las propiedades de esta elipse se basa en conocer la
orientación y la longitud de los trazos conformantes de las direcciones, para determinar así, las
deformaciones inherentes a un sistema proyectivo. Para esto se recurre a los teoremas de
72
Apolonio, que determinan los semiejes a y b de esta elipse indicatriz por medio de los trazos dsm
y dsp (proyecciones de dφ y dλ en el plano).
4.4.1. Cálculo de semiejes según teorema de Apolonio
Los semiejes “a” y “b” de la indicatriz corresponden a las direcciones principales
formadas en el elipsoide, es decir, corresponden a aquellos arcos diferenciales que habiendo
sufrido rotación durante la transformación, mantienen su perpendicularidad. Ahora, llamando “h”
al modulo de deformación lineal sobre el meridiano y “k” al modulo de deformación lineal sobre
el paralelo, se obtiene
2
h=
E ·dφ
⎛ ∂y ⎞
1 ⎛ ∂x ⎞
⎜⎜ ⎟⎟ + ⎜⎜ ⎟⎟
=
ρ ·dφ
ρ ⎝ ∂φ ⎠ ⎝ ∂φ ⎠
2
2
h=
G·dλ
1
⎛ ∂y ⎞
⎛ ∂x ⎞
=
⎜ ⎟ +⎜ ⎟
N ·cos φ ·dλ N ·cos φ ⎝ ∂λ ⎠
⎝ ∂λ ⎠
2
El teorema de Apolonio relaciona dos semidiámetros conjugados “m1” y “m2” con ángulo “A1”
formado entre ellos (Figura Nº16) con los semiejes a y b mediante
m12 + m22 = a 2 + b 2
y
m1 ·m 2 ·senA1 = a·b
73
A1
m1
a
m2
O
b
Figura Nº16 Determinación de Semiejes Según Teorema de Apolonio
Al aplicar el teorema de Apolonio a la elipse indicatriz se observará una diferencia en el
ángulo A1 con respecto a su proyección. Esta diferencia puede denotarse como “I” y
evidentemente será nula para las direcciones principales.
Considerando que los diferenciales de meridiano y paralelo sobre el elipsoide “dlm” y
“dlp” son unitarios y a su vez radios del circulo infinitesimal en dicho elipsoide, se puede
expresar:
h=dlm’
y
k=dlp’
donde dlm’ y dlp’ corresponden a la proyección en el plano de los diferenciales de
meridiano y paralelo “dlm” y “dlp” respectivamente.
Aplicando los teoremas de Apolonio a estas direcciones principales, se obtiene:
h2 + k 2 = a2 + b2
y
h·k ·cos I = a·b
74
de esta manera puede deducirse la deformación de escala en un punto dado que tendrá como
máximo y mínimo a las direcciones principales “a” y “b” de la indicatriz.
La indicatriz de Tissot permite también derivar un estudio de las deformaciones angulares
que sufre un determinado punto al ser proyectado en un plano. Tal como se vio anteriormente, el
modulo de deformación angular es (θ1 – θ) para el caso de las direcciones principales y de
particularmente las proyecciones conformes esta deformación es nula, sin embargo, se representa
en función de “a” y “b” como
tg (θ1 − θ ) =
(b − a)tgθ
(a + b·tg 2θ )
En tanto la alteración superficial en función de las direcciones principales de la elipse
indicatriz corresponde a
π ·a·b·dr 2
S=
= a·b
π ·dr 2
Así, teniendo las expresiones
a2 + b2 = h2 + k 2
y
2·a·b = 2S
se puede determinar los valores “a” y “b” del la elipse indicatriz a partir de las coordenadas
geodésicas de un punto y sus transformadas en el plano, de manera que ambos valores serán los
valores extremos de las deformaciones.
Sumando y restando las expresiones anteriores y formando productos notables se obtiene:
( a + b) 2 = h 2 + k 2 + 2 S
y
75
( a − b) 2 = h 2 + k 2 − 2 S
donde reemplazando convenientemente S por el modulo de deformación superficial se obtiene:
( a + b) 2 =
2
2
2
2
⎛ ∂y ⎞ ⎤ 1 ⎡⎛ ∂x ⎞
1 ⎡⎛ ∂x ⎞
2 ⎡ ∂y ∂x ∂x ∂y ⎤
⎛ ∂y ⎞ ⎤
⎢⎜⎜ ⎟⎟ + ⎜⎜ ⎟⎟ ⎥ +
−
+
⎢
⎥+
⎟
⎜
⎟
⎜
⎥
⎢
2
2
M ⎢⎣⎝ ∂φ ⎠
⎝ ∂λ ⎠ ⎦⎥ M ·r ⎣ ∂φ ∂λ ∂φ ∂λ ⎦
⎝ ∂φ ⎠ ⎥⎦ r ⎣⎢⎝ ∂λ ⎠
( a − b) 2 =
2
2
2
2
⎛ ∂y ⎞ ⎤ 1 ⎡⎛ ∂x ⎞
1 ⎡⎛ ∂x ⎞
2 ⎡ ∂y ∂x ∂x ∂y ⎤
⎛ ∂y ⎞ ⎤
⎢⎜⎜ ⎟⎟ + ⎜⎜ ⎟⎟ ⎥ +
−
+
⎢
⎜ ⎟ ⎥−
⎜ ⎟
2
2
M
·r ⎢⎣ ∂φ ∂λ ∂φ ∂λ ⎥⎦
φ
φ
λ
λ
∂
∂
∂
∂
M ⎢⎣⎝ ⎠
⎝ ⎠ ⎥⎦
⎝ ⎠ ⎥⎦ r ⎢⎣⎝ ⎠
luego ordenando y operando se obtienen las expresiones finales
2
⎡ 1 ∂y
⎡ 1 ∂x
∂x ⎤
∂y ⎤
1
1
+
−
( a + b) 2 = ⎢
⎥ +⎢
⎥
⎣ ρ ∂φ N ·cos φ dλ ⎦
⎣ ρ ∂φ N ·cos φ ∂λ ⎦
2
2
⎡ 1 ∂x
⎡ 1 ∂y
1
∂y ⎤
1
∂x ⎤
( a − b) = ⎢
+
+⎢
−
⎥
⎥
⎣ ρ ∂φ N ·cos φ dλ ⎦
⎣ ρ ∂φ N ·cos φ ∂λ ⎦
2
2
4.5.
CLASIFICACIÓN DE PROYECCIONES
4.5.1. Según método de construcción
4.5.1.1. Geométricas: se basan en los principios de la geometría plana y espacial que
determinan la posición de un punto en la superficie proyectada con respecto a un
punto de origen.
76
i. Perspectivas: Se originan a partir del trazado de rayos con origen en un “foco” que
proyectan la red de paralelos y meridianos sobre un plano tangente a la superficie
de referencia (Figura Nº17).
i.i. Ortográfica: Aquella en la cual los rayos yacen ortogonal al plano de
proyección. Por lo tanto se asume el foco a una distancia infinita del plano de
proyección.
i.ii. Estereográfica: El foco de esta proyección esta diametralmente opuesto al
punto de tangencia de la superficie de referencia con el plano de proyección.
i.iii. Gnomónica: Aquella en la cual el foco se localiza en el centro de la
superficie de referencia.
Foco
Foco
Foco
Figura 17 Clasificación de proyecciones perspectivas
ii.
Seudoperspectivas: En este tipo de proyecciones, se recurre a algún artificio
para obtener una característica especial de la proyección. Por ejemplo, aquellas
proyecciones perspectivas en que el foco se sitúa en el punto diametralmente
opuesto de cada elemento a proyectar
77
4.5.1.2. Analíticas: pierden el sentido geométrico en beneficio de la mantención de algunas
propiedades especiales.
4.5.1.3. Convencionales: a diferencia de las analíticas, estas se basan en convenciones
arbitrarias en función de las cuales determinan sus expresiones matemáticas
4.5.2. Según superficie de proyección utilizada
Se refiere a si la superficie en la cual se proyectan las coordenadas corresponde a un plano
o a una superficie desarrollable. Se pueden subdividir en:
4.5.2.1. Planas o azimutales: se considera el plano de proyección como tangente o secante al
Datum de referencia. Comúnmente son llamadas azimutales ya que mantienen el
azimut para los puntos coincidentes con el lugar de tangencia.
4.5.2.2. Desarrollables: parten de una superficie geométrica desarrollable que “envuelve” a la
figura de referencia, como es el caso de un cilindro, un cono (o muchos conos
sucesivos como el caso de la proyección policónica) o un poliedro para luego
extenderlo formando un plano final de proyección.
La Figura Nº18 representa las diversas situaciones de la superficie de proyección
utilizada.
78
PLANA
CONICA
CILINDRICA
POLIEDRICA
Figura Nº18 Superficies de proyección utilizadas
4.5.3. Según situación de la superficie de proyección
Esta clasificación se realiza en función de la posición espacial de la superficie de proyección
para el caso de las proyecciones planas o desarrollables. Las planas se clasifican en:
4.5.3.1. Polares: Centro de proyección en el polo y eje de rotación perpendicular al plano de
proyección.
4.5.3.2. Ecuatoriales: Centro de proyección coincidente con el ecuador y eje de rotación
paralelo al plano de proyección.
4.5.3.3. Oblicuas: Centro de proyección en un lugar distinto al polo y el ecuador, es decir el
eje de rotación permanece inclinado con relación al plano de proyección
Mientras que las proyecciones desarrollables se clasifican en:
4.5.3.4. Normal: Eje del cono coincidente con el eje de rotación
4.5.3.5. Ecuatorial: Eje del cilindro coincidente con el eje de rotación
79
4.5.3.6. Transversa: Eje del cono perpendicular al eje de rotación
4.5.3.7. Transversa o meridiana: Eje del cilindro perpendicular al eje de rotación
4.5.3.8. Oblicuas: Eje del cono o cilindro inclinado en relación al eje de rotación
La figura Nº19 representa las distintas proyecciones en función de la Situación de la superficie de
proyección
Figura Nº19 Clasificación de proyecciones según su superficie de proyección
80
4.5.4. Según las propiedades que conservan:
Las proyecciones cartográficas pueden clasificarse en función de alguna propiedad
especial que mantengan.
4.5.4.1. Equidistantes: Son aquellas que cumplen con manifestar nulas deformaciones lineales
manteniendo constante la relación entre una magnitud lineal medida en la proyección,
la magnitud lineal en la superficie de referencia. Posee un modulo de deformación
lineal “L” unitario y las elipses indicatrices de Tissot, poseen un semieje de magnitud
unitaria orientado sobre la línea de equidistancia .
La condición de equidistancia es válida para ciertas líneas en la proyección. Según el
sentido de ellas puede subclasificarse en:
i.
Equidistante meridiana: la equidistancia se mantiene en el sentido de los
meridianos.
ii.
Equidistante transversa: la equidistancia se mantiene en el sentido de los
paralelos.
iii.
Equidistante azimutal u ortodrómica: la equidistancia se mantiene en la
dirección de los círculos máximos que pasan por el centro de proyección.
4.5.4.2. Equivalentes: Se conserva una relación constante entre las áreas de los elementos
representados y la superficie de referencia. El módulo de deformación superficial “S”
es unitario y las elipses indicatrices de Tissot trazadas, conservaran las áreas en
desmedro de la excentricidad de ellas.
81
4.5.4.3. Proyecciones conformes: Son aquellas que mantienen como ángulos rectos las
intersecciones de meridianos y paralelos. De esta manera, son conservadas las formas
de un elemento en condiciones restringidas de extensión. De particular interés para la
geodesia y cartografía, debido a la posibilidad que ofrece, de realizar con relativa
sencillez, precisas transformaciones angulares que permitan relacionar el plano de
proyección con la superficie elipsoidal. En ellas, las elipses indicatrices de Tissot se
proyectan como circunferencias de radios variables
4.5.4.4. Proyecciones afilácticas: no mantienen ángulos, ni áreas, ni escalas lineales, sin
embargo, mantienen alguna otra propiedad importante de destacar y que justifica su
construcción, por ejemplo, la proyección gnomónica, que no mantiene ninguna de las
características anteriormente señaladas, pero que justifica su construcción en el hecho
que las loxodrómicas se proyectan como líneas rectas, facilitando así la navegación
apoyada en cartografía. En estas proyecciones, el comportamiento de las indicatrices
de Tissot dependerá de la característica principal de la proyección.
82
4.6.
PROYECCIONES CONFORMES
Una proyección conforme, es aquella en la cual se mantienen los ángulos entre el plano de
proyección y en el Elipsoide de Referencia. Para que una proyección sea conforme, se requiere
que sus paralelos y meridianos se intercepten en ángulo recto y que se mantenga la escala en
todas las direcciones alrededor del punto. Sabiendo que la deformación angular “A” será 0 en un
punto cualquiera ya que los ángulos en el plano y en el terreno serán iguales. Se obtiene entonces
A = ángulo en el plano – ángulo en el Datum horizontal = 0
Se asume esta condición para porciones pequeñas de terreno o mientras la exactitud
esperada lo permita.
4.6.1. Uso de proyecciones conformes
Para la representación de un área pequeña, el uso de un plano topográfico puede ser
suficiente ya que el error generado a partir de la no consideración de la esfericidad terrestre puede
diluirse en la precisión de los métodos de captura de la información. En el contexto del desarrollo
urbano, ante la falta de planificación en el crecimiento de las ciudades, la utilización de un plano
topográfico como referencial para la representación de una ciudad, puede provocar una gran
acumulación de errores y discrepancias internas, las que pueden perjudicar la representación de la
ciudad. En este sentido, la única alternativa satisfactoria para la correcta representación de un
área urbana es la utilización de una proyección cartográfica.
83
Como se señaló anteriormente las proyecciones cartográficas se pueden clasificar en
función de la propiedad que mantengan. En este sentido, debe destacarse que la representación de
áreas urbanas debe realizarse usando una proyección conforme ya que sus características
especiales permiten representar sin errores las formas de pequeños predios dentro de una carta,
hecho de gran importancia en la planificación territorial que involucra el loteo de terrenos de
pequeña extensión. Por otra parte, una proyección conforme satisface los requerimientos
generales de los trabajos geodésicos ya que corresponde a una función matemática repetible y
estudiable, representa correctamente los ángulos, hace posible la corrección en términos de
deformación lineal sin mayor problema y considera al elipsoide de revolución como superficie de
referencia. Así, una proyección conforme, se transforma al mismo tiempo en una herramienta de
representación cartográfica y en un instrumento matemático para cálculos geodésicos
4.6.2. Condiciones de Conformidad
Para que una proyección cartográfica sea conforme, se requiere que los incrementos
diferenciales de arcos de meridiano sean iguales a los de paralelos, es decir, que la indicatriz de
Tissot resultante posea valores a = b. Esto significa que para cada punto considerado, existirá
una única escala valida para todas las direcciones, pero distinta de un punto a otro, lo que
evidentemente señala la conformidad de la proyección.
84
Para cumplir con esto, se utilizan coordenadas intermedias llamadas “isométricas”, las que
permiten que Mδφ = rδλ. La longitud isométrica (λ) es correspondiente con la longitud geodésica
mientras que la latitud isométrica (q) se define según
∫
q
dq =
0
φ
∫
0
M
sec φ ·∂φ
N
como
M =
a(1 − e 2 )
(1 − e sen φ )
2
2
3/ 2
y
N=
a
(1 − e 2 sen 2φ )
se tiene que
φ
(1 − e 2 )(cos 2 φ + sen 2φ )
0
(1 − e 2 sen 2φ ) cos φ (cos 2 φ + sen 2φ )
∫
dφ
separando, se obtiene
φ
∫
0
φ
dφ
cos φdφ
− e2 ∫
0
cos φ
(1 − e 2 sen 2φ )
la primera integral se resuelve
φ
∫
0
⎡ ⎛ π φ ⎞⎤
dφ
= ln ⎢ tan⎜ + ⎟⎥
cos φ
⎣ ⎝ 4 2 ⎠⎦
resolviendo la segunda integral por sustitución y combinando ambos resultados se obtiene
finalmente
e⎤
⎡
⎢ ⎛ π φ ⎞⎛⎜ 1 − e·senφ ⎞⎟ 2 ⎥
q = ln ⎢ tan ⎜ + ⎟⎜
4 2 ⎠⎝ 1 + e·senφ ⎟⎠ ⎥
⎢⎣ ⎝
⎥⎦
85
Ya que como se indicó en un principio, en las proyecciones conformes las alteraciones
angulares son nulas, la indicatriz de Tissot es un circulo se puede decir que:
a=b=h=k =
E
G
=
M
r
Lo que señala que puede deducirse la condición de conformidad igualando las cantidades
Gaussianas E = G en función de la latitud isométrica, es decir:
δx δy
=
δλ δq
δx
δy
=−
δq
δλ
Sabiendo que:
2
⎛ δx ⎞
⎛ δy ⎞
E = ⎜⎜ ⎟⎟ + ⎜⎜ ⎟⎟
⎝ δφ ⎠
⎝ δφ ⎠
2
2
⎛ δx ⎞
⎛ δy ⎞
G =⎜ ⎟ +⎜ ⎟
⎝ δλ ⎠
⎝ δλ ⎠
;
2
y
F=
δx δx δy δy
+
δφ δλ δφ δλ
se hace
F=
δx δx δy δy
+
=0
δφ δλ δφ δλ
despejando se obtiene:
∂y
=
∂λ
−
∂x ∂x
∂q ∂λ
∂y
∂q
tomando esta expresión y sustituyéndola en
2
2
2
⎛ δy ⎞
⎛ δx ⎞
⎛ δx ⎞
⎛ δy ⎞
⎜⎜ ⎟⎟ + ⎜⎜ ⎟⎟ = ⎜ ⎟ + ⎜ ⎟
⎝ δλ ⎠
⎝ δλ ⎠
⎝ δq ⎠
⎝ δq ⎠
2
se obtiene luego de ordenar los miembros
86
⎛ δx ⎞
2
⎜ ⎟
⎛ δy ⎞
δλ
+ ⎜⎜ ⎟⎟ = ⎝ ⎠ 2
⎝ δq ⎠
⎛ δy ⎞
⎜⎜ ⎟⎟
⎝ δq ⎠
2
⎛ δx ⎞
⎜⎜ ⎟⎟
⎝ δq ⎠
2
⎡⎛ δx ⎞ 2 ⎛ δy ⎞ 2 ⎤
⎢⎜⎜ ⎟⎟ + ⎜⎜ ⎟⎟ ⎥
⎢⎣⎝ δq ⎠ ⎝ δq ⎠ ⎥⎦
como por definición
2
⎛ δx ⎞
⎜ ⎟
⎝ δλ ⎠ = 1
2
⎛ δy ⎞
⎜⎜ ⎟⎟
⎝ δq ⎠
se obtiene
δx
δy
=±
δλ
δq
tomando la raíz positiva y sustituyéndola en
2
⎛ δx ⎞
⎜⎜ ⎟⎟
⎝ δq ⎠
2
⎛ δx ⎞
⎜ ⎟ ⎡
2
2
⎛ δy ⎞
δλ ⎠ ⎛ δx ⎞ ⎛ δy ⎞ ⎤
⎝
⎢
⎜ ⎟⎟ + ⎜⎜ ⎟⎟ ⎥
+ ⎜⎜ ⎟⎟ =
2 ⎜
⎝ δq ⎠
⎝ δq ⎠ ⎥⎦
⎛ δy ⎞ ⎢⎣⎝ δq ⎠
⎜⎜ ⎟⎟
⎝ δq ⎠
2
se obtiene finalmente:
δx
δy
=−
δq
δλ
Finalmente, las “ecuaciones de Cauchy-Rieman” reveladoras de la condición de conformidad
son:
δx δy
=
δλ δq
δx
δy
=−
δq
δλ
87
CAPITULO 5
PROYECCIONES TRANSVERSALES DE MERCATOR
5.1.
GENERALIDADES
Esta proyección fue concebida inicialmente por el científico Alemán Johann Heinrich
Lambert en 1772, pero su desarrollo analítico se adjudica a Carl Friederich Gauss. Es
rigurosamente conforme, por lo que los meridianos y paralelos se interceptan en ángulo recto
manteniendo así las formas de los elementos representados.
Una forma didáctica de graficarlo es mediante la utilización de un cilindro transverso al
eje de rotación y que envuelve al elipsoide terrestre (Figura Nº20). Para cubrir todo el elipsoide
se utilizan numerosos cilindros transversos lo que deriva en que cada cilindro tiene un campo
especifico de acción llamado “huso”, el que está definido por un meridiano central al cual
pertenece y por un ancho de huso expresado en grados de desarrollo longitudinal, en estricto
rigor, se trata entonces de un sistema de proyecciones que cubre el elipsoide y que dada la
posición de cada cilindro, se hace recomendable para territorios donde predomine la extensión
Norte-Sur (como es el caso particular de Chile) ya que como se demostrará a continuación, las
distorsiones en sentido Este-Oeste son mayores que en sentido Norte-Sur. Como todos los husos
88
del sistema de proyección tienen igual ancho, analíticamente todos se definen de igual manera.
Así, las funciones matemáticas para efectuar todo tipo de cálculos son idénticas en cada huso.
Por definición este sistema proyectivo tiene un campo de escala definido por un error
máximo, esto significa que los límites del huso estarán dados mientras el error asociado no
exceda cierta norma.
El meridiano central de cada huso, posee la particularidad de ser el único representado por
una línea recta y poseer igual valor de escala en todo su largo y los valores X de la proyección
tienen como origen dicho meridiano.
Figura Nº20 2
Alrededor del mundo, son numerosos los ejemplos de la utilización de proyecciones TM
con diferentes parámetros que los países del mundo han adoptado para normar la representación
de su territorio siendo las mas utilizadas “Universal Transversal de Mercator”, “Gauss-Kruger”,
2
Fuente http://www.igm.cl/Proyeccion_utm.html
89
“Local Transversal de Mercator” “Modificada Transversa de Mercator” todas estas, desarrolladas
durante el presente capítulo.
5.2.
TRANSFORMACIÓN DE COORDENADAS
Si se considera que el mapeo conforme desde un plano complejo (λ, iq) en otro plano
complejo (x, iy) queda sujeto a la función
x + iy = f (λ +/- iq)
se observará que para deducir la función de traspaso desde ambos planos complejos, habrá que
determinar f(λ +/- iq) según las condiciones iniciales requeridas por la proyección deseada e
igualar posteriormente las partes real e imaginaria para obtener así las coordenadas reales de
mapeo x = x(λ, q) e y = y(λ, q).
5.2.1. Conversión de coordenadas geodésicas a rectangulares
La primera condición que debe satisfacer la función de mapeo conforme para el caso de la
proyección TM es la nula deformación en el meridiano central. Es decir, cuando λ = 0 debe
cumplirse x = 0, quedando la función analítica de la forma
iy = f (iq ) = iSφ
recordando que:
90
φ
∫
Sφ =
Mdφ
0
y que
q=
φ
∫
M
sec φ ·dφ =
N
0
φ
∫
0
M
dφ
N ·cos φ
donde
dq =
Mdφ
N ·cos φ
y
M ·dφ = N ·cos φ ·dq
se puede expresar entonces
Sφ =
φ
∫
N ·cos φ ·dq = f (q )
0
lo que permite calcular coordenadas que se encuentren únicamente sobre el meridiano central.
Ahora bien, para generalizar esta solución a puntos que se encuentren fuera del meridiano central,
donde el valor de la abscisa no será cero y el valor de la ordenada será diferente al del arco de
meridiano del punto considerado. Se expande la función x + iy = f (λ + iq) en torno al punto
z = iq según serie de Taylor quedando
x + iy = f (λ + iq) = f (iq) + λf ' (iq) +
λ2
2!
f ' ' (iq ) +
λ3
3!
f ' ' ' (iq ) + ...
considerando la expresión
f (iq ) = iSφ = if (q ) y diferenciando respecto a “z”, se obtiene
d
d
f (iq ) =
[if (q)]
dz
dz
o
f ' (iq ) =
d
[if (q)] dq
dq
dz
91
como
dz
d
1
d
f (iq ) y finalmente f ' (q ) ≡
= i , f ' (iq ) = if ' (q) ; = f ' (q) , donde f ' (iq ) ≡
f (q )
dq
dq
i
dz
las derivadas de orden superior continúan:
f ' ' (iq ) = −if ' ' (q )
f ' ' ' (iq ) = − f ' ' ' (q )
f iv (iq ) = if iv (q)
etc.
Reemplazando estos valores se obtiene:
x + iy = if (q ) + λf ' (q ) −
λ2
if ' ' (q) −
2!
λ3
3!
f ' ' ' (q) +
λ4
4!
if iv + ...
igualando las partes real e imaginaria, se obtiene
iy = if (q) −
y = f (q) −
λ2
2!
λ2
if ' ' (q) +
f ' ' (q) +
2!
λ4
4!
λ4
4!
if iv (q ) + ...
f iv (q ) + ...
también
x = λf ' ( q ) −
λ3
3!
f ' ' ' (q) +
λ5
5!
f v (q)
donde las derivadas son:
f ' (q) = N ·cos φ
⎡ dN
⎤ dφ
N
f ' ' (q) = ⎢
cos φ − N ·senφ ⎥
= − sen2φ
2
⎣ dφ
⎦ dq
(las derivadas de orden superior fueron calculadas por Thomas en 1952)
92
reemplazando las derivadas en las funciones anteriores y operando, se obtiene:
[
]
[
]
x
λ3 cos3 φ
λ5 cos5 φ
= λ cosφ +
1 − t 2 +η 2 +
5 −18t 2 + t 4 + 14η 2 − 58t 2η 2 + 13η 4 − 64t 2η 4 + 4η 6 − 24t 2η 6 + ...
6
120
N
[
y Sφ λ2 senφ ·cos φ λ4 senφ ·cos 3 φ
=
+
+
5 − t 2 + 9η 2 + 4η 4
2
24
N
N
con
]
t = tgφ ; η2 = e’2 cos2 φ y λ corresponde a la diferencia de longitud en radianes con
respecto al meridiano central.
las expresiones anteriormente desarrolladas pueden continuarse hasta sucesivos términos
logrando así una exactitud mayor en la transformación. No obstante el tercer término asegura una
exactitud suficiente para la mayoría de los trabajos geodésicos.
Los ejes de este sistema de coordenadas estarán dados por la transformada del meridiano
central del huso para las ordenadas y la transformada del ecuador para las abscisas. Es decir 0º de
latitud geodésica y λ0 de longitud geodésica. De lo anteriormente expuesto, se deduce que a
cualquier punto con un incremento de longitud geodésica negativa con respecto al meridiano
central le corresponderá un valor negativo de X y que cualquier punto al sur del ecuador poseerá
una coordenada Y también negativa.
5.2.2. Conversión de coordenadas rectangulares a geodésicas
Partiendo de la función general de mapeo conforme (x + iy) = f1(λ + iφ) se puede abordar
la transformación inversa desde la función (λ + iφ) = f2(x + iy). Expandiendo dicha función a
cualquier punto (z) sobre el plano con coordenadas X0, Y0 se tiene:
λ + iq = (λ0 + iq 0 ) + (Δλ + iΔq)
93
λ + iq = f 2 ( x0 + iy0 ) + f '2 ( x0 + iy0 )(Δx + iΔy ) + f ' '2
λ + iq = f 2 ( z ) + f ' 2 ( z 0 )(Δz ) + f ' ' 2
( x0 + iy0 )
(Δx + iΔy ) 2 + ...
2!
( z0 )
(Δz ) 2 + ...
2!
luego, seleccionando un punto sobre el meridiano central para ser evaluado con la serie
anteriormente expuesta se tiene
para
y para
x0 = 0
x = Δx; y = Δλ
y = y0
Δy = 0; Δq = 0
Considerando estos argumentos e incorporándolos en la expresión anterior se obtiene:
λ + iφ = f 2 (iy ) + f ' 2 (iy ) x + f ' ' 2
(iy ) 2
x + ...
2!
obsérvese que
x=0
y
iq = f 2 (iy )
El concepto asociado a la expresión anterior, puede describirse mediante la Figura Nº21
donde se recurre a una latitud φ1 denominada latitud base, que corresponde a la proyección recta
del paralelo en el meridiano central tal y como explica la figura. La latitud base isométrica
corresponderá a q1 y se puede escribir
iq1 = f 2 (iy )
94
Meridiano Central
Paralelo que pasa por y
φi
Paralelo del punto
φ
y
Sφ
Figura Nº21 Latitud Isométrica
ahora, evaluando f2(iy) y sus derivadas se obtiene:
f ' 2 (iy ) =
df 2 (iy ) d (iq )
dq dS q
=
=i
d (iy )
d (iy )
dS q d (iy )
donde iy = iSφ
y
iy = iSφ 1 = iS q1
entonces operando, la derivada será
f ' 2 (iy ) = q'
luego
f ' ' 2 (iy ) = −iq ' '
f ' ' ' 2 (iy ) = −q ' ' '
f 2iv (iy ) = iq iv
f 2v (iy ) = q v
ahora expresando la función de mapeo mediante la latitud base φ1 se obtiene:
95
λ + iq = iq1 + xq1i −
iq1ii 2 q1iii 3 iq1iv q1v 5
x −
x +
+
x + ...
2!
3!
4!
5!
luego, separando las partes reales e imaginarias:
x 3 iii x 5 v
q1 +
q1 + ...
3!
5!
x 2 ii x 4 iv
q = q1 −
q +
q + ...
2!
4!
λ = xq1i −
reemplazando las derivadas complejas por las reales se obtiene
qi =
q ii =
q iii =
1
N cos φ
1
N 2 cos φ
1
N cos φ
3
(1 + 2t 2 + η 2 )
(las derivadas de orden superior fueron calculadas por Thomas en 1952)
Finalmente, ordenando los términos se obtiene:
5
2
4
2
2 2
⎡ x 1 ⎛ x ⎞3
1 ⎛ x ⎞ ⎛⎜ 5 + 28t1 + 24t1 + 6η1 + 8t1 η1
2
2
⎢
⎜
⎟
⎜
⎟
− ⎜
+
+
+
1
2
t
λ = sec φ1
η
1
1
120 ⎜⎝ N 1 ⎟⎠ ⎜⎝ 3η14 − 4η16 + 4t12η14 + 24t12η16
⎢ N 1 6 ⎝ N1 ⎟⎠
⎣
(
φ = φ1 −
(
t1
1 + η12
2
)⎛⎜⎜ Nx ⎞⎟⎟
⎝
1
⎠
2
+
)
(
t1
1 + η12
24
)⎛⎜⎜ Nx ⎞⎟⎟ (5 + 3t
4
⎝
1
⎠
2
1
+ η12 − 4η14 − 9η12 t12
− ⎞⎟⎤
⎥
⎟⎥
⎠⎦
)
con las definiciones de “t” y “η” iguales que en la transformación anterior.
La latitud base φ1 se puede obtener mediante el método iterativo “Newton-Rapson” que
utiliza la razón entre la función que representa el arco de meridiano que subtiende la latitud base
96
y su primera derivada iterativamente partiendo de un valor inicial arbitrario hasta que las
iteraciones arrojen un error menor a la tolerancia aceptada. La forma general de este método es
φ1 = φn−1 −
f (φ )
f ' (φ )
como primer paso en la determinación de la latitud base debe escogerse un valor inicial
para el proceso iterativo (φτ). Ya que la latitud base es función del arco de meridiano central del
huso. Se considera la expresión
φτ =
y
a
como suficiente para una primera aproximación.
Como el valor φ1 es correspondiente con la magnitud del arco de meridiano entre el punto
φ1 y el ecuador entonces
f (φ ) = y
recordando el capitulo III se puede escribir
B
C
D
E
⎡
⎤
f (φτ ) = S ( 0−φτ ) = a (1 − e 2 ) ⎢ Aφτ − ( sen2φτ ) + ( sen4φτ ) − ( sen6φτ ) + ( sen8φτ ) − ...⎥
2
4
6
8
⎣
⎦
entonces la primera derivada se escribe
B
C
D
E
⎡
⎤
f ' (φτ ) = a (1 − e 2 ) ⎢ A − (cos 2φτ ) + (cos 4φτ ) − (cos 6φτ ) + (cos 8φτ ) − ...⎥
2
4
6
8
⎣
⎦
el procedimiento debe repetirse hasta que el valor de la coordenada φn-φn-1 < ε donde
ε = 10−12 . aproximadamente 2·10-7 segundos de arco. Esto asegura una precisión compatible con
cualquier proceso geodésico.
97
5.3.
CONVERGENCIA DE MERIDIANOS
Como sobre el elipsoide el azimut esta referido al norte geodésico, y en el plano
cartográfico las meridianos se presentan como línea cóncavas hacia el meridiano central, se
observarán diferencias angulares entre el meridiano que pasa por el punto y la línea recta del eje
“y”. A esta diferencia angular se le conoce como convergencia de los meridianos y será nula para
el meridiano central, ya que solamente este meridiano tiene la particularidad de proyectarse como
una línea recta, la que evidentemente será coincidente con el eje “y” del punto en cuestión.
Analíticamente, la convergencia de meridianos puede definirse como el ángulo formado
entre la tangente al meridiano en el punto y el eje Y que pasa por el mismo punto. O también
como el ángulo formado entre la tangente al paralelo en el punto y el eje X que pasa por el mismo
punto. como se observa en la Figura Nº22.
O
Ecuador
Sφ
y
φ
Paralelo
dx
x
γ
φ1
γ
M
er
id
ia
no
Meridiano Central
dy
Figura Nº22 Convergencia de Meridianos
98
Diferencialmente puede expresarse como:
∂y
∂y
∂
tgγ = λ =
∂x ∂x
∂λ
y su desarrollo puede expresarse en función de coordenadas geodésicas como:
γ = Δλsenφ +
(
)
(
)
Δλ3
Δλ5
senφ cos 2 φ 1 − 3η 2 + 2η 4 +
senφ cos 4 φ 2 − tg 2φ + ...
3
15
y en función de sus coordenadas planas
γ =
5.4.
(
)
(
)
x
x3
x5
2
2
4
tgφ '−
tg
φ
'
1
+
tg
φ
'
−
η
'
−
2
η
'
+
tgφ ' 2 + 5 yg 2φ '+3tg 4φ ' + ...
N'
3N '3
15 N '5
DIFERENCIA ARCO-CUERDA (ψ)
Se entiende como la diferencia entre el azimut geodésico proyectado “T” ( obtenido a
partir del azimut geodésico y la convergencia de meridianos) y el azimut plano “t” ( obtenido
directamente a partir de las coordenadas planas ). La diferencia de estos azimutes permite
relacionar las direcciones observadas o elipsoidales a direcciones de cuadricula o planas, y su
desarrollo puede observarse en la Figura Nº23.
99
NC
NG
A
2
t
γ
T
ψ
1
ψ = Reducción Arco - Cuerda ( T - t )
A = Azimut Geodésico
t = Azimut Plano
T = Azimut Geodésico proyectado
γ = Convergencia de Meridianos
NG = Norte Geodésico
NC = Norte Cartográfico
.
Figura Nº23 Diferencia Arco – Cuerda
(T − t ) BA =
( y B − y A )·(2· x A + x B )
·(1 + η m2 )
6· N m ·M m
(T − t ) BA =
( y B − y A )·(2·x B + x A )
·(1 + η m2 )
6·N m ·M m
Donde el subíndice “m” indica que la magnitud esta referida a la latitud media entre los
puntos “A” y “B”
100
5.5.
FACTOR DE MAGNIFICACIÓN DE ESCALA
5.5.1. En función de coordenadas geodésicas
Como se expuso en el capitulo Nº4, la expresión general de la deformación de escala en
una proyección conforme es:
2
k=
⎛ ∂x ⎞
⎛ ∂y ⎞
⎜ ⎟ +⎜ ⎟
⎝ ∂λ ⎠
⎝ ∂λ ⎠
N ·cos φ
2
ahora, usando la definición diferencial de la convergencia de meridianos:
2
⎛ ∂y ⎞
⎜ ⎟
∂λ
2
tan γ = ⎝ ⎠ 2
⎛ ∂x ⎞
⎜ ⎟
⎝ ∂λ ⎠
2
2
2
(
⎛ ∂x ⎞
⎛ ∂y ⎞
⎛ ∂x ⎞
2
⎜ ⎟ + ⎜ ⎟ = ⎜ ⎟ 1 + tan γ
⎝ ∂λ ⎠
⎝ ∂λ ⎠
⎝ ∂λ ⎠
)
sustituyendo en la expresión anterior, se obtiene:
∂x
1 + tan 2 γ
∂
λ
k=
N ·cos φ
ya que el termino tanγ es muy pequeño, se puede desarrollar la raíz cuadrada en términos
de una serie, y posteriormente evaluando la derivada parcial, se obtiene:
k = 1+
λ2
2
cos2 φ (1 + η 2 ) +
λ4
24
cos4 φ (5 − 4t 2 + 14η 2 + 13η 4 − 28t 2η 2 + 4η 6 − 48t 2η 4 − 24t 2η 6 )
101
5.5.2. En función de coordenadas rectangulares
Tomando el recíproco de la función anteriormente utilizada. Es decir:
1
=
k
N ·cos φ
∂λ
∂x
(1 + tan γ )
2
operando según la derivada parcial de la latitud isométrica, expresando la raíz cuadrada en
serie, y expandiendo N·cosφ en una serie de Taylor con punto de expansión en la latitud base φ
se obtiene:
2
1 + η12 ⎛ x ⎞ 5 + 6η12 − 3η14 − 4η16 + 24t12η14 + 24t12η16 ⎛ x ⎞
1
⎜ ⎟ +
⎜⎜ ⎟⎟
= 1+
k
2 ⎜⎝ N1 ⎟⎠
24
⎝ N1 ⎠
5.6.
4
EL ARTIFICIO DE TISSOT
Como una forma de graficar las características de las proyecciones transversales de
Mercator, se suele hacer referencia a un cilindro cuyo eje es perpendicular al eje de rotación de la
Tierra, y que conforma el plano de proyección. Las diferentes posiciones relativas que tome este
cilindro en cuanto a su secancia o tangencia con respecto al elipsoide condicionaran el valor de la
deformación de escala que tendrá el cilindro en sus diferentes posiciones. Así, la proyección
Gauss-Krugger por ejemplo, supone un cilindro tangente al elipsoide a lo largo de un meridiano,
en el cual se mantiene un factor de escala constante entre ambas figuras e igual a la unidad y que
aumenta de acuerdo a la distancia longitudinal que separe al punto en cuestión del meridiano de
102
tangencia hasta donde termine la faja o campo. Para otras proyecciones transversales (UTM,
LTM, etc) se considera a dicho cilindro secante, lo que geométricamente implica la generación de
dos líneas cóncavas hacia el meridiano central cuyo factor de escala es igual a 1, y que disminuye
hacia el meridiano central donde toma el valor nominal de la proyección (K0) y aumenta hacia el
borde del huso. Para conocer el comportamiento del factor de escala en esta condición de
secancia, se recurre al artificio de Tissot que implica lo siguiente.
El valor K0 correspondiente al valor nominal de escala, esto es, valido solamente para el
meridiano central de la proyección se deduce reduciendo a la mitad la deformación de los
extremos del huso. Por ejemplo:
En una proyección tangente, la deformación de escala en el borde del huso puede ser expresada
por:
(K’) = (1 + ε)
Entonces se puede hacer que
(K0) = (1 - ε/2)
lo que implica que en los extremos del huso, el factor de escala con el artificio de Tissot valdrá
(K) = K0 · (K’) = (1 - ε/2) · (1 + ε) = 1 + ε – ε/2 – ε2/2
ya que ε es un numero pequeño
(K) ≡ 1 + ε/2
por lo tanto, la deformación del borde de uso queda reducida a la mitad
103
5.7.
PROYECCIÓN UNIVERSAL TRANSVERSAL DE MERCATOR ( U T M )
5.7.1. Generalidades
La proyección UTM es obra del cuerpo de ingenieros del ejercito de Estados Unidos y fue
creada para homogenizar la representación cartográfica de países vinculados a los esfuerzos
militares de ese país.
Esta proyección, corresponde en rigor a una proyección TM a la que se le han impuesto
ciertos parámetros particulares. Es un sistema policilíndrico que abarca la totalidad del elipsoide
en sentido longitudinal y desde los 80ºS a los 84ºN en sentido latitudinal. Para controlar las
deformaciones producidas al alejarse del meridiano central, esta proyección está formada por 60
husos de 6º de ancho cada uno. El elipsoide asociado es el “Internacional de 1924”, y los Husos
se orientan desde los 180ºW aumentando hacia el Oeste, de tal manera que el meridiano de
Greenwich corresponde al borde o separación de los husos 30 y 31.
Como una forma de reducir las deformaciones producidas en los bordes de cada huso,
(lugar geométrico en que el plano de proyección está mas alejado del elipsoide) el meridiano
central no es equidistante (K0 = 0.9996), de manera que el cilindro que representa al plano
cartográfico es secante al elipsoide. Así, los factores de deformación de escala “K” tienen un
valor mínimo de k = 0.9996 en el meridiano central (1:2.500), nulo a lo largo de una línea
cóncava hacia el meridiano central que dista unos 180 Km de él (k = 1) y un valor máximo de k =
1.001 (1:1.000) en el borde del Huso.
104
El territorio nacional comprende los Husos 18 (MC = 75º W) y 19 (MC = 69º W) para
Chile Continental, el huso 17 para el archipiélago de Juan Fernández y el Huso 12 para la Isla de
Pascua.
5.7.2. Falso Este
Como una forma de evitar la existencia de coordenadas negativas dentro de un huso. Se
adoptó por convención el asignar un valor inicial al meridiano central que sea mayor que la
máxima diferencia en metros entre dicho meridiano y el borde de huso para la latitud 0º. Se optó
por el valor 500.000 metros, por lo que las coordenadas Este varían entre 166.000m y 834.000m
en el Ecuador y entre 443.000m y 557.000m aproximadamente para los límites latitudinales del
huso (80º)
5.7.3. Falso Norte
Dado que el origen latitudinal del sistema UTM se encuentra en el Ecuador. Se observa el
inconveniente de que todos los territorios del hemisferio sur tendrían coordenadas negativas,
como una forma de evitar la incomodidad inherente a trabajar con coordenadas negativas se
decidió asignar un valor de norte falso valido para el hemisferio, que sea superior a la máxima
distancia norte sur posible para la proyección. Así, se decidió asignar un valor de norte falso de
10.000.000m para el hemisferio sur y mantener el norte falso de 0m para el hemisferio norte.
105
5.7.4. Factor de Escala en el Meridiano Central
La proyección UTM confiere al meridiano central de cada huso un valor de escala menor
que la unidad y que se mantiene constante a través de este meridiano, esto con el fin de reducir
las deformaciones en los extremos del huso (como se vio en el apartado referente al artificio de
Tissot). El valor de este factor de escala se obtiene de reducir a la mitad la deformación asociada
a una proyección transversal de mercator en una latitud media de 40º en un huso de 6º, es decir
con un Δλ de 3º. Asi teniendo la función
(
)
⎡ Δλ 2
⎤
K = K 0 ⎢1 +
cos 2 φ 1 + η 2 ⎥
2
⎥⎦
⎣⎢
Evaluada para φ = 40º y Δλ = 3º
K = 1.0008
ε = 0.0008
Entonces, reduciendo la deformación de los bordes a la mitad, se obtiene
e/2 = 0.0004
Finalmente, como la deformación en los bordes es 1 + ε/2 y la deformación en el
meridiano central es 1 – ε/2 se llega a
K’ mc = K0 = 0.9996
K’ (φ = 40º; Δλ = 3º) = 1.0004
De la definición dada anteriormente, se desprende que los valores de la deformación de
escala de un punto variarán desde 0.9996 en el MC hasta 1.000981069 (Figura Nº 24). entre estos
valores existe un punto de equidistancia tal que aunque no corresponde a un meridiano. Permite
comprender las variaciones en las deformaciones de escala como sigue:
106
•
K = 0.9996, en el meridiano central
•
0.9996 < K < 1 entre las líneas de secancia
•
K > 1, fuera de las líneas de secancia
K0 = 0.9996
Cilindro de Proyección
K=1
K(max) = 1.00098
6º
Figura Nº24 Variación del factor de deformación de escala para el meridiano central en latitud 0º
Al corresponder esta proyección a una versión particular de la proyección TM, los
algoritmos de transformación y el análisis matemático se realiza de la misma manera y solo se
debe considerar el factor de escala K0 (como se observa en la función de factor de escala).
Siendo:
Coordenada Norte UTM = 10.000.000 + 0.9996 · y
Coordenada Este UTM = 500.000 + 0.9996 · x
Correspondiendo los valores “x” e “y” a los desarrollados en el presente capítulo
107
5.8.
PROYECCIÓN LOCAL TRANSVERSAL DE MERCATOR ( L T M )
La proyección LTM busca cubrir las necesidades cartográficas de proyección conforme de
alta precisión para proyectos de ingeniería. Al igual que la UTM corresponde a un sistema
cilíndrico transverso conforme secante, pero con parámetros particulares que la individualizan y
que permiten mediante la manipulación del ancho de huso y factor de escala, el incrementar la
exactitud en la representación de los elementos. Originalmente fue concebida como una
herramienta de apoyo a los proyectos de ingeniería donde debe representarse el terreno con gran
exactitud.
Para la definición de esta proyección se establece una precisión del meridiano central de
1/200.000, es decir K0 = 0.999995, y ya que las líneas de secancia se encuentran muy cerca del
meridiano central se determina un ancho de huso de 1º, en cuyos bordes existirá una exactitud
mínima de 1/30.000, no obstante, el ancho efectivo del huso puede estar dado por la precisión
esperada para la proyección. Así por ejemplo, para proyecto que requiera un control de orden
primario (1/100.000) basta con restringir el huso hasta unos 35 km o 18’52’’ donde se cuenta con
una precisión aproximada de 1/110.000.
Pese a que se recomienda que el meridiano central corresponda a grados enteros o
medio grados, en proyectos de ingeniería se debe considerar en una primera instancia, que el
meridiano central de la proyección sea coincidente con el área de estudio para lograr así un
108
cubrimiento total. Para áreas extensas o mayores precisiones, se recomienda usar múltiples fajas
que abarquen el total del área de estudio y/o que cumplan con la precisión señalada.
5.8.1. Falso Este
Como una forma de evitar la existencia de valores negativos en las coordenadas
proyectadas, se recurre a asignar un valor para el meridiano de origen, tal que sea mayor que la
máxima extensión posible en sentido Este-Oeste (1º de desarrollo longitudinal en el ecuador
corresponde a unos 111 km) de esta forma y para cubrir una posible extensión del huso mas allá
de 1º se opta por asignar un valor de 200.000m.
5.8.2. Falso Norte
Dada la cobertura latitudinal de la proyección LTM para el caso chileno (63º) se obtiene
una distancia máxima en sentido norte o sur de 6.988km con respecto al ecuador. Por esto, se
asigna un valor de 7.000.000 de metros como origen de las coordenadas Norte para el hemisferio
Sur y de 0 metros para el hemisferio Norte, lo que radica en la imposibilidad de existencia de
coordenadas negativas.
Al igual que todas las proyecciones Derivadas del desarrollo Transverso de Mercator, se
mantienen los algoritmos de transformación y de análisis planteados con anterioridad.
Coordenada Norte LTM = 7.000.000 + 0.999995 · y
Coordenada Este LTM = 200.000 + 0.999995 · x
109
5.9.
PROYECCIONES LTM Y PLANOS TOPOGRÁFICOS LOCALES
La forma de relacionar coordenadas sobre el elipsoide, el plano de proyección y
posteriormente el terreno, implica arduas labores de cálculo y con esto la posibilidad cierta de
cometer errores de distinto tipo haciendo aún mas complicada la racionalización del espacio por
medio de cartografía. Como una forma de solucionar la discrepancia existente entre mediciones
en terreno y cartografía sobre un plano de proyección, se suele utilizar una proyección LTM tal
que el plano de proyección sea coincidente con el terreno. Para esto, se debe considerar un
cilindro que pase por el terreno topográfico constituyendo así un plano topográfico local (PTL).
Considerando la Figura Nº25
Distancia PTL
Distancia NMM
Distancia Elipsoidal
H(ptl)
R
Figura Nº25 Plano topográfico local y superficie de referencia
Puede determinarse un valor K relacionado con la altura del terreno sobre el elipsoide
(cercana a la altura sobre el nivel del mar) de modo que implique tangencia con un punto del
110
terreno. De esta forma se obtiene para ese punto la directa relación terreno-plano de proyección
facilitando así el transporte de coordenadas y las labores de replanteo.
Por semejanza de triángulos, observando la figura Nº25 se obtiene:
K hptl =
R+h
R
Expresión que señala el factor de escala del meridiano central para el proyecto particular
que permite que el cilindro sea tangente al terreno (en desmedro de la relación de secancia o
tangencia entre el plano de proyección y elipsoide existentes para otras proyecciones TM).
Para efectos prácticos, los proyectos topográficos suelen utilizar Diversos planos
topográficos locales determinados según la inexactitud que provoca las diferencias de alturas
observadas en el terreno. La determinación del número y posición de los PTL se realiza
considerando la expresión
K hptl =
R+h
R
Que puede expresarse como el factor de escala de un desnivel haciendo
K Δhptl =
R + Δh
R
luego despejando Δh se obtiene la diferencia de altura que genera una imprecisión
determinada, por ejemplo:
Para un terreno cuyos valores altimétricos máximo y mínimo son 500 y 800 m
respectivamente, un radio arbitrario de 6378000m y que deben representarse con una precisión
mínima de 1:65.000 se obtiene
111
(K
hptl
·R ) − R = Δh
como 1:65.000 implica un error de 1.000015385, reemplazando se obtiene una diferencia de
altura de 98.126m que, con signo positivo y negativo, corresponderá a la altura que abarcará un
PTL para cumplir con la precisión esperada. Finalmente, debe considerarse que cada PTL debe
estar a un desnivel máximo de 196.252m uno del otro y procurar que cubran la totalidad del área
a representar.
Un sistema de coordenadas PTL corresponde a un sistema topocéntrico de carácter local
concebido para representar pequeñas extensiones de terreno. Al ser una versión de la proyección
TM corresponde a un sistema plano-rectangular cuyo origen corresponde a coordenadas
geodésicas, lo que se traduce en la georreferencia del sistema por medio de:
•
Posición: dada por las coordenadas geodésicas (φ,λ) del origen del sistema rectangular
(x,y).
•
Orientación: Dada por un azimut geodésico del eje “y” del sistema local
•
Altura del plano de referencia: Dada por la altura ho del plano de referencia
112
5.10. PROYECCIÓN GAUSS-KRUGER
La proyección Gauss-Kruger se considera la proyección base de las transversales de
Mercator. Corresponden en su concepción a la primera y única proyección cilíndrica transversa
conforme creada por Gauss durante el siglo XVIII y racionalizada posteriormente por Kruger.
Pese a su amplia utilización a nivel mundial, no existe (en conocimiento del autor) una normativa
o sugerencia acerca de su utilización a nivel mundial relacionada con las deformaciones que
provoca ni las escalas de representación que puede soportar.
El factor de escala en el meridiano central es 1, es decir corresponde a un cilindro
tangente al elipsoide. El ancho de huso se define generalmente en 3º aunque hay casos
documentados de países que utilizan una versión de esta proyección con un ancho de huso de 5º.
Los parámetros FN y FE son variables, y se definen según las necesidades particulares de
los países que las utilizan. Así por ejemplo, la republica Argentina utiliza el eje X para
representar el eje norte de la proyección al contrario del sistema cartesiano que vincula a la
dirección norte con el eje Y. El valor FN es igual en este caso, a la longitud del cuadrante
meridiano del elipsoide siendo así coincidente el origen del falso norte con el polo sur. Por otra
parte, las coordenadas Este (referidas al eje Y) se relacionan con el valor FE de 500.000m para
cada faja de cobertura anteponiendo un prefijo para señalar la faja. Así, es posible encontrar por
ejemplo
113
Norte (X) : 6.235.412
Este (Y) : 2.540.000
Donde la coordenada este señala en primera instancia que se refiere a la segunda faja del
sistema.
No obstante estas convenciones. La proyección Gauss-Kruger alrededor del mundo adopta
parámetros distintos según las necesidades o características de los usuarios siendo la nunca norma
el valor unitario del factor de escala en el meridiano central.
El principal inconveniente en la adopción de esta proyección como una solución mundial
para la cartografía sistemática, radica en la escasa cobertura del huso necesaria para mantener
aceptables precisiones. Teniendo por ejemplo, la necesidad de utilizar 120 husos de 3º para la
completa representación del planeta.
5.11. PROYECCIÓN MODIFICADA TRANSVERSA DE MERCATOR
Corresponde en rigor a cualquier proyección Transversa de Mercator desarrollada para
representar alguna región en particular con una situación geográfica singular y que difiera de
otras proyecciones transversales de Mercator institucionalizadas (UTM, Gauss-Kruger, etc).
Generalmente corresponde a una proyección cilíndrica secante por lo que el valor de
escala para el meridiano central tiende a ser menor que la unidad y se imponen parámetros
locales acerca del meridiano central, el ancho del huso y los valores de falso norte y falso este.
114
El caso de Canadá ejemplifica como ha de ajustarse una proyección TM para cumplir con
los requerimientos del país. Debido a las altas latitudes en las cuales se localiza ese país, el
sistema UTM y otros sistemas similares se tornan ineficaces. Para solucionar esto, se utiliza un
sistema TM con un ancho de huso de 3º y un factor de escala del meridiano central de 0.9999 lo
que mejora notablemente la precisión del meridiano central (1/10.000) y reduce la convergencia a
limites tolerables (1º30’’ a 82º de latitud).
115
CAPITULO 6
METODOLOGÍA
El estudio de las características particulares de una proyección cartográfica y de su
capacidad para representar de manera eficaz ciertos elementos requieren por una parte, la
definición de las exactitudes necesarias de alcanzar para los objetivos de cada proyecto y por otra
parte, el conocimiento claro de la extensión y localización del área a representar. En este sentido,
se deben establecer y considerar a la hora de ejecutar un proyecto cartográfico urbano, ciertos
parámetros y restricciones inherentes al sistema proyectivo y a la escala de representación, que
permitan representar de manera óptima el terreno.
A continuación se presenta una metodología de estudio de deformaciones para diferentes
proyecciones para el caso genérico de diversas proyecciones TM y de manera particular, en el
contexto de la representación urbana a través de un estudio de caso.
El anexo Nº6 presenta un diagrama de flujo de los pasos realizados en la presente
metodología.
116
6.1.
DETERMINACIÓN DE ESCALAS DE REPRESENTACIÓN
Antes de establecer las escalas de representación a estudiar, se hace necesario definir
concretamente el concepto de escala urbana. Para esto, se debe considerar los usos principales de
la cartografía como medio de representación del territorio para las actividades involucradas en el
desarrollo, catastro y planificación de una ciudad.
Con estos criterios y considerando diversos estudios sobre cartografía y documentos
técnicos de ingeniería vial y otras actividades usuarias de cartografía, se procede a determinar las
escalas urbanas de representación a utilizar.
6.2.
DETERMINACIÓN DE TOLERANCIAS
La determinación de la deformación asociada a un determinado producto cartográfico,
debe considerar la magnitud que involucra la resolución del ojo humano desnudo llevada a cada
escala de representación considerada en el presente estudio. De este modo, se obtiene un patrón
de comparación para cada escala de representación que permitirá verificar o refutar la idoneidad
de cada proyección cartográfica para diferentes escalas de representación.
117
6.3.
DETERMINACIÓN DE PROYECCIONES A UTILIZAR
Debido a la variedad de proyecciones TM utilizadas en el mundo, y a la falta de una
normativa sobre su utilización, se hace necesario definir un set de proyecciones TM para analizar
en la presente investigación, que cumplan con la condición de ser utilizadas comúnmente por
diferentes países o instituciones.
Para esto, se investigó las principales instituciones usuarias y generadores de cartografía
en Chile (IGM, DIFROL, MOP, entre otras) y a algunos organismo generadores de cartografía
alrededor del mundo. De este modo, se genera un listado de proyecciones definidas según las
siguientes características:
•
Elipsoide de Referencia
•
Falso Norte (si corresponde)
•
Falso Este (si corresponde)
•
Factor de Escala del meridiano central (K0)
•
Amplitud longitudinal del Huso
•
Identificación del Huso (si corresponde)
118
6.4.
DETERMINACIÓN DEL ÁREA DE ESTUDIO
Como una de forma contextualizar el presente estudio en la situación cartográfica
nacional y buscando una mejor ejemplificación del problema métrico de la representación
cartográfica, se recurre a estudiar la representación plana de una ciudad tipo de tamaño grande a
las distintas escalas de representación señaladas y usando las proyecciones TM definidas. Como
criterio secundario de selección del área de estudio, se desea la disponibilidad de cartografía
digital con el fin de mostrar de manera gráfica los diferentes aspectos del presente estudio.
6.5.
DETERMINACIÓN DE PUNTOS MUESTRALES
Buscando simplificar la racionalización de la presente investigación, se define una red de
puntos muestrales espacializados en el área de estudio con el objeto de determinar para cada uno
de ellos la distorsión que los afecta por medio del cálculo de las magnitudes que representan su
relación con el Datum de referencia y la superficie topográfica. La espacialización de ellos se
realiza usando coordenadas geodésicas referidas al elipsoide internacional de 1924 sobre los
meridianos y paralelos de manera obtener de forma sencilla patrones de comparación
distanciométrico.
119
Ya que la red de puntos muestrales corresponde a puntos teóricos no sometidos a la
influencia de los errores en su determinación, la distancia que los separe debe definirse de tal
manera que cubra la ciudad con una densidad tal que no constituya un impedimento técnico para
el cálculo de magnitudes en ellos.
6.6.
PROYECCIÓN DE LA RED DE PUNTOS MUESTRALES
Una vez definidos y espacializados los puntos conformantes de la red muestral se procede
a proyectarlos en los distintos sistemas referidos con anterioridad. Utilizando los algoritmos
desarrollados en el capitulo V y una planilla de cálculos, se obtiene una tabla de coordenadas
geodésicas con sus coordenadas homólogas para cada proyección.
6.7.
DETERMINACIÓN DEL FACTOR DE DEFORMACIÓN DE ESCALA Y
CONVERGENCIA DE MERIDIANOS
Utilizando los algoritmos desarrollados en el capitulo V, se adjunta en la matriz de
coordenadas el valor del factor de escala y de la convergencia de meridianos para cada punto.
120
6.8.
DETERMINACIÓN DEL COEFICIENTE DE CORRELACIÓN ENTRE EL
FACTOR DE DEFORMACIÓN DE ESCALA Y LAS COORDENADAS
PROYECTADAS
Para determinar el grado de dependencia del valor que representa el factor de escala
asociado a un punto con coordenadas proyectadas, se determina el coeficiente de correlación por
separado para cada una de las componentes Norte y Este. De esta manera, se puede determinar el
sentido de las distorsiones y la gradiente de ellas para el área de estudio en cada una las
proyecciones definidas.
La función “coeficiente de correlación”:
R=
∑ν ν
∑ν ·∑ν
E
2
E
N
2
N
Donde v es la desviación estándar de la muestra
Luego se determina el coeficiente de determinación múltiple usando el cuadrado de la
función anterior para obtener así un indicador del porcentaje de explicación del valor K respecto a
las coordenadas que lo definen.
121
6.9.
DETERMINACIÓN
DE
MAGNITUDES
LINEALES
DE
SEGMENTOS
PROYECTADOS Y GEODÉSICOS
Al representar la malla de puntos como una red de segmentos en el sentido de los
meridianos y de los paralelos, es posible calcular sin dificultad la longitud de cada segmento en el
caso geodésico y proyectado para su posterior comparación.
Para facilitar la localización de cada segmento se genera un código único que permita
localizarlo individualmente de manera sencilla y sin necesidad de recurrir a las coordenadas de
origen y término que lo definen. De esta forma se genera para los segmentos en sentido de los
meridianos un código único que empezando en la izquierda de la red y en sentido descendente de
la columna en cuestión se nombra a1, a2, a3, . . ., a9; para la columna siguiente, es decir a la
derecha de la recién codificada toma los nombres b1, b2, b3, . . .b9; etc
Para las filas creadas en la red, el código tiene sentido izquierda a derecha y comenzando
desde el de menor latitud se nombre 1a, 1b, 1c, . . . , 1i; para la fila siguiente los códigos son 2a,
2b, 2c, . . ., 2i; etc. Como se observa en la figura Nº26:
1a
1b
a1
2a
2b
d1
a2
3a
3b
d2
a3
4a
4b
d3
Figura Nº26 codificación de la red de puntos muestrales
122
Luego de establecer el código para cada segmento, se determinan sus longitudes usando
las formulas contenidas en el capítulo III para el caso de los segmentos geodésicos y como rectas
sobre el plano para el caso de los segmentos proyectados. Dichas longitudes se incorporan al
código creado para constituir una tabla en la cual se almacenaran y realizaran las comparaciones
de las magnitudes calculadas para su posterior análisis. Se procede también a agrupar los
segmentos según corresponda para líneas continuas en sentido de los meridianos o paralelos que
cubran la totalidad del área de estudio
6.10. DETERMINACIÓN
DE
ESCALAS
DE
REPRESENTACIÓN
SEGÚN
PROYECCIONES TM
6.10.1. Caso General
Como una forma de conocer los límites de una proyección TM en cuanto a la escala de
representación que toleran, se determina la escala de representación máxima para los casos
extremos y nominales dentro del territorio nacional.
En una primera instancia se determina el valor máximo del factor de deformación Kp
dentro del territorio nacional para cada proyección definida considerando una latitud extrema
norte para el caso nacional (17ºN) en el borde de huso de cada proyección definida. Para este
123
valor Kp calculado, se asocia un valor de factor de escala susceptible de soportar considerando la
tolerancia asociada a cada escala de representación y la exactitud que ofrece el valor Kp.
De la misma manera, se asocia el valor K0 de cada proyección con la máxima escala de
representación capaz de soportar obedeciendo al criterio recién expuesto.
6.10.2. Caso Particular
Como una forma de expresar cartográficamente las deformaciones producidas al
representar el área de estudio en cada una de las proyecciones TM analizadas, se definen las
escalas cartográficas de mayor detalle que toleran las proyecciones definidas. Para esto se
analizan tres aspectos vinculados a los valores K definidos según la red de puntos muestrales
espacializada en el área de estudio.
Como un primer análisis se consideran las diferencias existentes en los factores de escala
máximo y mínimo para una determinara proyección en el área de estudio. Dicha diferencia de
factores de escala se traduce en cantidad de deformación multiplicándola por un valor
considerado como máximo de representación urbana obteniendo con esto una cantidad métrica de
deformación susceptible de relacionarse con una determinada escala de representación por medio
de la tolerancia vinculada a ellas.
En este sentido, sabiendo que las ciudades de mayor tamaño en el territorio nacional
exceptuando a Santiago, poseen longitudes máximas, a saber:
•
Valparaíso / Viña del Mar = 18 Km
124
•
La Serena / Coquimbo = 14 Km
•
Antofagasta = 12 Km
•
Arica = 9 Km
Se define el valor máximo de representación urbana en 20 km considerando con esto, un
escenario crítico de deformación.
Un segundo aspecto a considerar, consiste en determinar las deformaciones existentes
entre el Datum horizontal y el plano de proyección para el área de estudio. Se determinan las
diferencias existentes entre los valores K obtenidos de la red de puntos muestrales y el valor de
escala unitario (K = 1). Se determina la máxima diferencia entre ellos y se expresa métricamente
usando el valor máximo de representación urbana (20 km), para con esto determinar la cantidad
de deformación para el peor caso posible. Una vez obtenido este valor, se determina la escala
cartográfica de máximo detalle que tolere la deformación.
Un tercer análisis derivado del estudio de los valores K para el área en cuestión, dice
relación con la deformación que genera una proyección TM respecto de la superficie topográfica.
Para expresar esta deformación en función de la escala cartográfica, se calculan las máximas
diferencias generadas entre los valores Kh y Kp para el área de estudio. Posteriormente se
expresan estas diferencias en términos de distancia multiplicándolas por el valor máximo de
representación urbana (20km). Con este valor, se determina la escala cartográfica de máximo
detalle que tolera esta deformación.
125
6.11. RELACIÓN ENTRE PROYECCIONES TM, ELIPSOIDE Y SUPERFICIE
TOPOGRÁFICA
Como una forma de determinar la exactitud con que un producto cartográfico representa
al elipsoide de revolución y al plano topográfico. Se estudia la relación geométrica entre el
elipsoide y dichas superficies analizando el origen y el sentido de las deformaciones ocurridas. Se
determinan las condiciones generales de reducción entre referenciales y se incorpora un ejemplo
de determinación de distancias geodésicas a partir de coordenadas proyectadas utilizando las
condiciones de relación antes mencionadas, en donde se establecen además, la inexactitud
asociada a cada reducción.
126
CAPITULO 7
RESULTADOS
7.1.
DETERMINACIÓN DE ESCALAS DE REPRESENTACIÓN
Para el presente trabajo se determinaron escalas cartográficas de representación acordes a
las necesidades de ejecución y planificación de proyectos de diversa índole en espacios urbanos y
criterios de representación de elementos de importancia para el catastro, el desarrollo de
proyectos y la planificación urbana. Para esto, se recurrió en una primera instancia a fuentes
bibliográficas, las que correspondieron a “Manual de Carreteras” MOP capitulo 2.300 y
“Cartografía y levantamientos urbanos” de Theodore Blachut.
La primera publicación clasifica las escalas de representación en “escalas grandes” a
1:500, 1:1.000 y 1:2.000, las que tienen por objeto el facilitar estudios definitivos de proyectos de
construcción vial así como su ejecución. Las escalas intermedias corresponden a 1:2.000, 1:5.000
y 1:10.000 y tienen por objeto el facilitar el estudio preliminar y alternativas de proyectos.
La segunda publicación señalada sostiene la conveniencia de la representación urbana a
una escala de máximo detalle de 1:500 y mantiene como alternativas viables de representación
urbana las escalas 1:000, 1:2.000, 1:5.000 y 1:10.000. Siendo las dos últimas aptas para la
planificación del crecimiento urbano y regularización de terrenos.
127
7.1.1. Criterios de representación urbana
El uso de la cartografía como herramienta de representación para el desarrollo de
distintas actividades vinculadas a la vida en la ciudad y al crecimiento de la misma,
implica una diversificación de los elementos representables en un producto cartográfico y
consecuentemente, el detalle con que estos deben ser plasmados en un modelo de
representación plano. Es por esto, que debe considerarse antes de representar un espacio
urbano, que la escala elegida, sea compatible con el desarrollo de la actividad para la cual
fue creado el producto cartográfico. Por ejemplo, la planificación del crecimiento de una
ciudad necesitará apoyarse en cartas a escala 1:5.000 y 1:10.000 3, el trazado de una
autopista urbana requerirá de una precisión compatible con escalas 1:1.000 4 y cercanas
mientras que la representación de una red de tuberías dentro de una ciudad necesitará una
alta precisión no alcanzable por las escalas antes señaladas. En vista de esto, se
determinaron finalmente que las escalas a estudiar en la presente investigación
correspondan a:
3
4
•
1:10.000
•
1:5.000
•
1:2.000
•
1:1.000
•
1:500
Blachut, T. Cartografía y levantamientos urbanos. Año 1979
M.O.P. Manual de Carreteras Vol2. Año 2001
128
•
1:250
La elección de la escala 1:250 se sostiene fundamentalmente en la tolerancia
necesaria para los levantamientos de plantas urbanas, y en las necesidades de precisión de
actividades relacionadas con obras sanitarias y tendido de redes en general.
7.2.
DETERMINACIÓN DE TOLERANCIAS
Considerando el criterio descrito en la metodología y tomando como resolución del ojo
humano desnudo los 0.2mm 5, las tolerancias para cada escala de representación se resumen en la
siguiente tabla.
Escala
Tolerancia (m)
1:250
1:500
1:1000
1:2000
1:5000
1:10000
0,05
0,1
0,2
0,4
1
2
Tabla Nº1 Tolerancia según escala de representación
5
Lousiana State University Health Sciences Center, en
http://www.medschool.lsuhsc.edu/pathology/pathist/HRLM_TEM/default.htm
129
7.3.
DETERMINACIÓN DE PROYECCIONES A UTILIZAR
La elección del set de proyecciones a estudiar en la presente investigación tomó como
criterio central la utilización de diferentes proyecciones Transversales de Mercator alrededor del
mundo. Se eligieron cinco clases de proyecciones TM subdivididas en casos particulares
determinados según su posición con respecto al área de estudio o a la tolerancia permitida:
7.3.1. Universal Transversal de Mercator (UTM) : Caso particular de las proyecciones
Transversales de Mercator utilizado alrededor del mundo. Debido a la rígida
normativa en cuanto a la definición de esta proyección, fue estudiada sin ningún tipo
de modificaciones. Para este caso:
ƒ
Huso : 19
•
Ancho Huso : 6º
•
K0 : 0.9996
•
EF : 500.000
•
NF : 10.000.000
•
Elipsoide : Internacional de 1924
7.3.2. Gauss Kruger (GK): Caso particular de la proyección Transversal de Mercator
utilizada en varios países del mundo. Esta proyección fue estudiada por separado para
130
dos situaciones de representación del área de estudio. La primera con el meridiano
central cercano al área de estudio (GK1) y la segunda con el meridiano central alejado
del área de estudio (GK2) para estudiar así, las características de esta proyección en
situaciones de borde o sobrepaso de huso.
7.3.2.1. GK1
•
Meridiano Central : 71º
•
Ancho Huso : 3º
•
K0 : 1
•
EF : 300.000
•
NF : 7.000.000
•
Elipsoide : Internacional 1924
7.3.2.2. GK2
• Meridiano Central : 70º
• Ancho Huso : 5º
• K0 : 1
• EF : 300.000
• NF : 7.000.000
• Elipsoide : Internacional 1924
131
7.3.3. Local Transversal de Mercator (LTM) : Versión de la proyección Transversal de
Mercator a la cual se le imponen parámetros que permitan minimizar la diferencia de
ángulos y distancias medidas en terreno y las cantidades obtenidas en un sistema
plano LTM para áreas reducidas. Utilizada en Chile en el marco de proyectos de
ingeniería, esta proyección fue estudiada por separado para dos situaciones de
representación del área de estudio. En primer lugar considerando el meridiano central
local mas cercano al área de estudio (LTM1) y en segundo lugar con el meridiano
central lejos del área de estudio para estudiar así una extensión de la proyección fuera
de los límites establecidos (LTM2)
7.3.3.1. LTM1
• Meridiano Central : 71º30’
• Ancho Huso : 1º
• K0 : 0.999995
• EF : 200.000
• NF : 7.000.000
• Elipsoide : Internacional 1924
7.3.3.2. LTM2
• Meridiano Central : 71º
• Ancho Huso : 2º
• K0 : 0.999995
132
• EF : 200.000
• NF : 7.000.000
• Elipsoide : Internacional 1924
7.3.4. Modificada Transversa de Mercator (MTM) : Modificación de la proyección
Transversal de Mercator utilizada en algunos países europeos o norteamericanos para
la representación de escalas medias. Esta proyección fue estudiada por separado para
dos situaciones de representación del área de estudio. El primer caso corresponde a
una proyección MTM con su meridiano central alejado del área de interés, donde se
hace necesario extender el huso para la representación completa del área de estudio
(MTM1) mientras que el segundo caso corresponde a una proyección MTM con el
meridiano central mas cercano al área de estudio (MTM2)
7.3.4.1. MTM1
• Meridiano Central : 71º
• Ancho Huso : 1º
• K0 : 0.9999
• EF : 300.000
• NF : 7.000.000
• Elipsoide : Internacional 1924
133
7.3.4.2. MTM2
• Meridiano Central : 71º30’
• Ancho Huso : 2º
• K0 : 0.9999
• EF : 300.000
• NF : 7.000.000
• Elipsoide : Internacional 1924
7.3.5. Plano Topográfico Local (PTL) : Caso particular de la proyección Transversa de
Mercator, que busca relacionar la superficie topográfica con el plano de proyección
por medio de la tolerancia inherente a cada escala de representación y la situación
altimétrica de la superficie topográfica.
7.3.5.1. Determinación de los PTL según situación altimétrica
Como se vio anteriormente, la tolerancia para una escala de representación es función
de la magnitud que representa la mínima diferencia discriminable en el producto
cartográfico. Entonces para vincular esta tolerancia con un PTL es necesario definir
que diferencia de altura genera una deformación a lo sumo igual a la deformación
definida según la escala.
Según lo estudiado en el capítulo V basta con plantear:
Δh = ( K ·R ) − R
134
para obtener una diferencia de cota definida según la tolerancia esperada y el radio
medio del lugar en estudio.
En la ecuación anterior. K corresponde a la deformación de escala que existe entre
un punto en la superficie topográfica. Su cálculo se realiza por medio de la razón entre
la tolerancia para la escala en estudio y un valor que represente la cantidad máxima de
terreno a representar (50km en este caso). Por otra parte, el valor R corresponde al
radio medio Gaussiano o media geométrica entre el radio de curvatura y la gran
normal para una coordenada media del área de estudio.
Por ejemplo, para el caso de la escala 1:250 se obtiene K = 0.05m / 20.000, es decir
K = 1.0000025. como las deformaciones ocurren con signo positivo y negativo
(deformaciones positivas y deformaciones negativas), se asignan los valores
1.0000025 y 0.9999975 como valores máximo y mínimo para la tolerancia estipulada.
Entonces:
Δh = (1.0000025·6369626.987) − 6369626.987
lo que equivale a 15.924 m.
Ahora considerando el valor K= 0.9999975 se obtiene
Δh = (0.9999975·6369626.987) − 6369626.987
se obtiene el valor –15.924 m.
La interpretación practica de los valores obtenidos dice que un plano
topográfico local colocado a una altura “h0” tiene un rango de +15.924 y –15.924
a partir de la cota de origen. Por lo tanto el rango total para esta escala será de
135
2·15.924 = 31.848 m. Para simplificar la solución, es conveniente truncar el
resultado convenientemente a 30m.
Una vez determinado el rango de cada plano topográfico local se definen los
“N” planos que den cobertura al área de estudio.
Para esto se define una altura h0 para cada PTL según el campo calculado
anteriormente (Tabla Nº2).
Escala
1:250
1:500
1:1000
1:2000
1:5000
1:10000
Δ h (Kh)
30m
60m
120m
250m
600m
1200m
PTL1 (m)
15
30
60
125
250
250
PTL2 (m)
45
90
180
375
PTL3 (m)
75
150
300
PTL4 (m)
105
210
420
PTL5 (m)
135
270
PTL6 (m)
165
330
PTL7 (m)
195
390
PTL8 (m)
225
450
PTL9 (m)
255
PTL10 (m)
285
PTL11 (m)
315
PTL12 (m)
345
PTL13 (m)
375
PTL14 (m)
405
PTL15 (m)
435
Tabla Nº 2 Disposición altimétrica de los Planos Topográficos Locales según tolerancia.
136
7.3.5.2.Determinación del factor de deformación de escala para cada PTL
Empleando las formulas desarrolladas en el capitulo V, y utilizando el valor Δh
coincidente con el definido anteriormente, se determinan los valores K para cada PTL
(Kptl) resultando (Tabla Nº3):
Escala
1:250
1:500
1:1000
1:2000
1:5000
1:10000
PTL1
1,0000023549
1,0000047099
1,0000094197
1,0000196244
1,0000392488
1,0000392488
PTL2
1,0000070648
1,0000141296
1,0000282591
1,0000588731
PTL3
1,0000117746
1,0000235493
1,0000470985
PTL4
1,0000164845
1,0000329690
1,0000659379
PTL5
1,0000211943
1,0000423887
PTL6
1,0000259042
1,0000518084
PTL7
1,0000306140
1,0000612281
PTL8
1,0000353239
1,0000706478
PTL9
1,0000400337
PTL10 1,0000447436
PTL11 1,0000494534
PTL12 1,0000541633
PTL13 1,0000588731
PTL14 1,0000635830
PTL15 1,0000682929
Tabla Nº3 Factor de deformación de escala según PTL
7.3.5.3.Determinación de los PTL según diferencias de longitud
Como caso particular de las proyecciones TM, un PTL es susceptible a dividirse en
husos de acuerdo a la diferencia longitudinal entre un punto y el meridiano central. Debe
estudiarse entonces las deformaciones producidas por el desarrollo longitudinal para un
PTL localizado a una altura Hptl y en un meridiano central determinado y procurar que
estas diferencias sean menores que la tolerancia requerida para la escala de
137
representación. Definiendo un punto de coordenadas medias φ = -32.91808994028 y λ =
71.5721722554º se le asigna un valor K0(Khptl) igual a cualquiera de los K0 de los PTL
por ejemplo para la escala 1:250 K0(Kptl1)=1.0000023549. con este valor K0 se calcula
el valor K para un punto extremo φ = -32.91808994028 y λ = 71.46º, donde
K=1.00000371181. La diferencia observada entre ambos factores de escala genera una
deformación de 0.027m para una magnitud de 20km, con lo que bastaría un único PTL
por segmento altimétrico para el área de estudio. Cabe señalar que al verificarse esta
situación para la escala de mayor exactitud se verifica automáticamente para el resto de
las escalas de representación.
7.4. DETERMINACIÓN DEL ÁREA DE ESTUDIO
Para concretar la presente investigación se decidió vincular un estudio de caso con una
ciudad tal que pueda considerarse como caso típico de un centro urbano de gran tamaño en el
contexto nacional. En vista de esto y de la existencia de cartografía a escala 1:5.000 que permite
una fácil representación del territorio, se decidió utilizar la ciudad de Valparaíso.
La ciudad de Valparaíso está localizada entre los 32º55’ y los 33º7’ de latitud Sur, y entre
los 71º28’ y los 71º39’ de longitud Oeste (véase en Anexo Nº1). Político-administrativamente, se
encuentra en la V Región del país, provincia de Valparaíso a unos 120 Km de la capital Santiago.
138
Económicamente, la actividad portuaria e industrial constituyen las principales fuentes de
ingreso de la ciudad y son el motor fundamental que regula el crecimiento de esta ciudad.
En términos cívicos y sociales, Valparaíso es la sede del poder legislativo de la nación y la
capital de la institucionalidad cultural del país. Así mismo, es la única ciudad Chilena declarada
por al UNESCO como Patrimonio de la Humanidad.
Topográficamente, Valparaíso está dominado por 44 cerros que albergan a mas del 95%
de sus habitantes, reflejando con esto, el acelerado crecimiento que ha tenido esta ciudad y la
necesidad de un ordenamiento territorial que permita a esta ciudad desarrollarse en armonía con
su entorno.
Para representar la ciudad, se utilizó una base cartográfica correspondiente al plan
regulador a escala 1:5.000 de las comunas de Valparaíso, y Viña del Mar en formato digital.
7.5. DETERMINACIÓN DE PUNTOS MUESTRALES
Como una forma de estudiar las deformaciones producidas en el área de estudio para las
proyecciones definidas anteriormente se creó una red de puntos muestrales espacializada en el
elipsoide internacional de 1924, con el objeto de medir en cada uno de ellos, los valores de
deformación K y determinar así la capacidad de cada proyección TM para representar el terreno a
escala urbana.
139
Se definió un espaciamiento entre puntos de 2.500m sobre el meridiano de manera que el
área de estudio fuera cubierta por unos 10 puntos para cada columna de la red asegurando con
esto una distribución homogénea y la representatividad de los puntos. En el caso de los paralelos,
se determinó también una distancia de 2.500m calculada sobre el paralelo de menor latitud. Así,
se obtuvo finalmente, una red de 100 puntos muestrales (véase en Anexo Nº2 y Nº3) definida
sobre el elipsoide y espacializada sobre los meridianos y paralelos lo que permite facilitar el
cálculo de magnitudes geodésicas.
Como una forma de facilitar la comprensión de los elementos geométricos derivados a
partir de esta red de puntos. Se creó una codificación en filas y columnas que permite referir cada
segmento formado por la union de dos puntos en sentido meridiano o paralelo a un único código.
(Figura Nº27)
Figura Nº 27 Puntos muestrales
140
7.6. PROYECCIÓN DE LA RED Y DETERMINACIÓN DE FACTORES DE
DEFORMACIÓN DE ESCALA Y CONVERGENCIA DE MERIDIANOS
La proyección de la red de puntos muestrales y el calculo de factor de deformación de
escala y convergencia de meridianos realizada para cada una de las proyecciones definidas, puede
apreciarse en el anexo Nº4
7.7. DETERMINACIÓN DEL COEFICIENTE DE
CORRELACIÓN ENTRE EL
FACTOR DE DEFORMACIÓN DE ESCALA Y LAS COORDENADAS
PROYECTADAS
Utilizando las formulas descritas en el capítulo II para los valores K y las coordenadas
Norte y Este se adjunta una tabla que muestra el coeficiente de correlación “R” y el coeficiente de
correlación múltiple “R2” (Tabla Nº4)
141
GK1
GK2
LTM1
LTM2
MTM1
MTM2
UTM
Este
Norte
Este
Norte
Este
Norte
Este
Norte
Este
Norte
Este
Norte
Este
Norte
2
R
R
-0,998723
0,001969
-0,999834
0,005307
-0,906571
0,000795
-0,998723
0,001969
-0,998723
0,001969
-0,906571
0,000795
-0,999938
0,008681
0,997447
0,000004
0,999669
0,000028
0,821870
0,000001
0,997447
0,000004
0,997447
0,000004
0,821870
0,000001
0,999877
0,000075
Tabla Nº4 Correlación Coordenadas TM y factor de deformación de escala
7.8. DETERMINACIÓN
DE
MAGNITUDES
LINEALES
DE
SEGMENTOS
GEODÉSICOS Y PROYECTADOS
Las magnitudes calculadas para cada segmento de meridiano se repiten para una misma
diferencia de latitud. Luego, cada arco de meridiano estará formado por “N” segmentos de
meridiano los que se repiten para distintas longitudes. Considerando esto, se determina la
magnitud total del arco de meridiano como la suma de sus partes siendo esta de 22393.320m
(Tabla Nº5).
142
Cada segmento de arco paralelo conforma el arco total es idéntico para una misma latitud.
Entonces, es posible determinar la magnitud total de cada arco paralelo multiplicando por el
número de segmentos la magnitud de un segmento cualquiera.
Segmento Meridiano
a1,b1. . .,j1
a2,b2. . .,j2
a3,b3. . .,j3
a4,b4. . .,j4
a5,b5. . .,j5
a6,b6. . .,j6
a7,b7. . .,j7
a8,b8. . .,j8
a9,b9. . .,j9
Segmento Paralelo
1a,1b. . .,1i
2a,2b. . .,2i
3a,3b. . .,3i
4a,4b. . .,4i
5a,5b. . .,5i
6a,6b. . .,6i
7a,7b. . .,7i
8a,8b. . .,8i
9a,9b. . .,9i
10a,10b. . .,10i
Magnitud (m)
2488,111
2488,120
2488,129
2488,138
2488,147
2488,156
2488,165
2488,174
2488,183
Magnitud (m)
2098,598
2098,068
2097,539
2097,008
2096,478
2095,947
2095,416
2094,884
2094,352
2093,820
Tabla Nº5 Arcos Geodésicos y proyectados
143
La tabla Nº6 muestra la magnitud total de arcos de paralelo utilizando los segmentos antes
descritos para cada latitud estudiada.
Fila
1
2
3
4
5
6
7
8
9
Latitud (º)
32,91808994
32,94052439
32,96295884
32,98539329
33,00782774
33,03026220
33,05269665
33,07513110
33,09756555
Arco paralelo (m)
18887,382
18882,616
18877,847
18873,075
18868,300
18863,522
18858,741
18853,957
18849,170
10
33,12000000
18844,381
Tabla Nº6 Arcos de paralelo
La determinación de distancias proyectadas y la diferencia entre estas y los valores geodésicos se
aprecian en el anexo Nº5
7.9. DETERMINACIÓN
DE
ESCALAS
DE
REPRESENTACIÓN
SEGÚN
PROYECCIÓN CARTOGRÁFICA
7.9.1. Caso general
Se calcularon los factores de deformación de escala para casos extremos de deformación
en el territorio nacional y para la situación nominal de cada proyección. Con esto se determinó la
escala cartográfica límite de representación para cada proyección (Tabla Nº7).
144
Valores típicos de distintas proyecciones TM para el territorio nacional
Lat min = 17º; Lat max = 57º
Nombre
K0
Precisión (K0)
K max
LTM 1 0,999995
LTM 2 0,999995
GK 1
1
GK 2
1
UTM
0,9996
MTM 1 0,9999
1/200.000
1/200.000
Optima
Optima
½.500
1/10.000
1,000030039
1,000135166
1,000315416
1,000876530
1,000862069
0,999935035
1/33.290
1/7.400
1/3.170
1/1.140
1/1.160
1/15.392
1.510
3.019
4.528
7.548
9.057
1.509
1:500
1:500
Máxima
Máxima
No urbana
1:10.000
1:5.000
No urbana
No urbana
No urbana
No urbana
1:10.000
MTM 2
1/10.000
1,000040152
1/24.905
3.019
1:10.000
1:5.000
0,9999
Precisión (K max) Conv Mer max ‘’ Escala carto K0 Esc carto K max
Tabla Nº7 Determinación de escalas de representación según tolerancia, caso general
7.9.2. Caso particular
Utilizando el valor K máximo obtenido desde la red de puntos muestrales proyectada, se
determinó el error máximo factible de ocurrir para una distancia de 20 km medidos en productos
cartográficos a diferentes escalas. La deformación obtenida se contrastó con la tolerancia
permitida para cada escala de representación pudiendo establecer con esto si dicha proyección
cumple o no con la tolerancia requerida para cada escala de representación.
La definición de escalas se llevó a cabo usando dos criterios centrales para el estudio de
los valores de deformación de escala calculados.
En primer lugar se determinó la máxima deformación generada a partir de la diferencia de
factores de escala existente entre los valores K calculados dentro del área de estudio. De esta
manera se determina la distorsión inherente al producto cartográfico sin considerar su relación
con el elipsoide ni la validez del factor de escala nominal de la proyección (Tabla Nº8).
145
Deformación
Escala Cartográfica
Proyección
Máxima (m)
Asociada
GK1
0.491
1:5.000
GK2
LTM1
1.381
0.056
1:10.000
1:500
LTM2
MTM1
0.491
0.491
1:5.000
1:5.000
MTM2
0.056
1:500
UTM
2.291
No urbana
Tabla Nº8 Determinación de escalas de representación según tolerancia, caso particular “a”
Un segundo criterio de estudio en las deformaciones lo constituye la capacidad de la
proyección de representar al elipsoide con exactitud, para esto se determinó la máxima
deformación producida por la diferencia entre el valor de escala unitario (K=1) y el máximo (o
mínimo) valor de escala calculado en el área de estudio.
Deformación
Escala Cartográfica
Proyección
Máxima (m)
Asociada
GK1
0.945
1:5.000
GK2
LTM1
5.958
0.100
No urbana
1:500
LTM2
MTM1
0.845
1.546
1:5.000
1:10.000
MTM2
2.000
1:10.000
UTM
7.283
No urbana
Tabla Nº9 Determinación de escalas de representación según tolerancia, caso particular “a”
En la tabla Nº9 se puede observar aquellas escalas de representación en las cuales se
puede considerar válida la relación directa entre el elipsoide y el plano de proyección. Es decir
donde se puede aceptar que:
146
Magnitud Elipsoidal = Magnitud Cartográfica · Escala de representación
Un tercer criterio a considerar, corresponde a la capacidad de un producto cartográfico de
representar la superficie topográfica. Siguiendo la metodología propuesta, se adjunta a
continuación una tabla que señala las deformaciones máximas existentes entre el plano de
proyección y la proyección cartográfica para una magnitud dada y la escala cartográfica que
tolera tal deformación (Tabla Nº10)
Deformación
Escala Cartográfica
Proyección
Máxima (m)
Asociada
GK1
0.912
1:5.000
GK2
LTM1
5.911
1.466
No urbana
1:10.000
LTM2
MTM1
1.012
2.912
1:10.000
No urbana
MTM2
3.366
No urbana
UTM
7.236
No urbana
Tabla Nº10
7.10. RELACIÓN ENTRE PROYECCIONES TM, ELIPSOIDE Y SUPERFICIE
TOPOGRÁFICA
Una proyección TM sitúa al producto cartográfico en un plano de proyección tal, que
posee una situación geométrica con respecto al Datum horizontal y al terreno, que no garantiza
una perfecta correlación en los elementos representados por medio de la cartografía, los definidos
en el elipsoide y los materializados en el terreno. Luego, para considerar válida la asociación
147
Carta / Elipsoide / Superficie Topográfica es necesario realizar una serie de reducciones o
correcciones así como determinar la tolerancia asociada a cada escala de representación.
7.10.1. Reducción Plano TM - Elipsoide
Observando la Figura Nº28:
K<1
K>1
K=1
Plano de
Proyección
Elipsoide
Figura Nº28 Relación Plano TM – Elipsoide
Se aprecia que dentro del área de secancia, un segmento considerado en el plano de
proyección, sufrirá deformaciones negativas, lo que indica que una magnitud considerada en el
elipsoide será representada por una magnitud menor en el plano de proyección. Por otra parte,
para las áreas fuera de la secancia se observará una deformación positiva lo que señala que una
magnitud obtenida en el producto cartográfico representará una magnitud menor en el elipsoide.
No obstante lo anterior en aquellas zonas con un factor de escala unitario, es decir donde el plano
de proyección intercepta al elipsoide existirá una correspondencia libre de deformaciones entre
ambas superficies.
148
Para eliminar estas deformaciones, debe considerarse el valor del factor de escala K de
cada punto a reducir, o en su defecto un valor KP que represente la totalidad del elemento a
representar dentro de los márgenes establecidos por la tolerancia asociada a la escala de
representación.
Una vez definido el factor K adecuado para la reducción, debe considerarse el inverso de
él con el fin que se cumpla el contrasentido de la deformación. Posteriormente debe multiplicarse
este factor corrector por la magnitud deseada.
Es decir:
−1
Dist ( geo) = K P ·Dist (TM )
Obteniéndose con esto, una función que reduce las magnitudes desde un plano de
proyección al elipsoide de revolución.
7.10.2. Reducción Elipsoide – Plano Topográfico
Aunque como es sabido, la cartografía utiliza el elipsoide como superficie de referencia,
los elementos representados están materializados sobre la superficie topográfica, lo cual puede
hacer presumir (incorrectamente) a un lector inexperto en cartografía que cualquier magnitud
considerada en la carta estará relacionada directamente con la realidad. Debido a esto, al
pretender determinar una magnitud topográfica mediante cartografía, debe realizarse un proceso
de reducción de magnitudes que permita homologar una distancia TM con una distancia
Topográfica.
149
Como se vio en el capitulo V la relación entre la superficie topográfica y el elipsoide está
determinada según la altura del plano topográfico, el radio medio del área a representar y la
tolerancia de la magnitud a determinar. Al observar la figura Nº29
Terreno
Kh
Ptl
Kp
Plano de Proyección
Elipsoide
Figura Nº29 Relación Plano Topográfico Local – Elipsoide – Plano TM
Se aprecia que la relación entre ambas superficies estará dada por el factor Kh estudiado
en el capítulo V. Bastará con incorporar el factor corrector Kh a la magnitud elipsoidal para que
esta sea transformada al Plano Topográfico Local. Recordando los tipos de alturas estudiados en
el capitulo III se comprenderá que dicho factor Kh debe vincularse a la altura geométrica de la
superficie topográfica en vez de la altura Ortométrica presente en productos cartográficos, lo que
condicionará la correcta ejecución de la reducción, a la existencia de puntos con altura
geométrica conocida o en su defecto, valores de ondulación Geoidal que permitan vincular las
alturas Ortométricas con alturas Geométricas.
150
En la presente investigación, se utiliza la altura Ortométrica en la determinación del factor
Kh asumiendo que el Elipsoide y el Geoide son cercanos en esta zona y que la diferencia entre
ambos tipos de altura es despreciable respecto al radio medio para el área de estudio.
7.10.3. Reducción Plano TM – Plano Topográfico Local
Considerando 7.10.1. y 7.10.2., puede introducirse de manera conjunta un nuevo
indicador que relacione directamente el plano de proyección y el plano topográfico local o “factor
de deformación de escala efectivo” (Ke). Siendo:
Ke = Kp −1 ·Kh =
Kh
Kp
7.10.4. Ejemplos de Reducciones Plano TM – Elipsoide
A continuación se construyen dos ejemplos para la determinación de distancias
geodésicas usando coordenadas proyectadas. Un primer ejemplo determina una magnitud lineal
geodésica usando coordenadas proyectadas y factor de escala para dos puntos sobre el mismo
meridiano y un segundo ejemplo determina una magnitud lineal geodésica usando coordenadas
proyectadas y factor de escala para dos puntos sobre el mismo paralelo. Para ambos casos, se
establece un patrón de comparación distanciométrico mediante las coordenadas geodésicas de los
puntos a estudiar. Sin embargo, debe recordarse que este patrón solo sirve para determinar la
151
deformación del método propuesto y con esto validar o rechazar la posibilidad del cálculo
geodésico mediante cartografía.
Debido a la diversidad de modelos de determinación de distancia geodésica por medio de
coordenadas geodésicas y de la variedad de resultados diferentes que estos modelos ofrecen. No
se considera en este estudio la determinación de distancias para dos puntos con coordenadas
diferentes en su aspecto latitudinal y longitudinal.
Para el presente estudio, se considera la máxima deformación entre el plano de proyección
y el elipsoide a partir de la proyección UTM en el área de estudio, la que se utiliza como caso
extremo considerando que una eventual validación del método será inmediatamente extrapolable
al resto de las proyecciones definidas. Posteriormente, con los mismos ejemplos se desarrolla la
reducción de magnitudes desde el plano de proyección hasta el plano topográfico.
A:
Para dos puntos “A” y “B” teóricos definidos sobre el elipsoide sobre el mismo
meridiano. llevados a la proyección UTM definida anteriormente, se determinará la distancia
geodésica que los separa, a partir de las coordenadas proyectadas de ambos puntos y el valor K
medio obtenido de cada uno de los puntos que perteneciendo a la red de puntos muestrales es
cercano a la coordenada media correspondiente con la magnitud a determinar (Pto medio 1 y Pto
medio 2). Esto con el fin de estimar la deformación producida por la no rigurosidad en la
determinación de la coordenada media.
152
Pto A
Pto B
Pto medio 1
Pto medio 2
Pto medio exacto
Este
270470.000
269945.770
270236.656
270178.408
270207.528
Norte
6332660.312
6355053.119
6342612.744
6345100.834
6343856.790
K
1.0002495767
1.0002525759
1.0002509108
1.0002512440
1.0002505560
φ
33.1200000000
32.9180899403
33.0302621957
33.0078277446
33.0190449701
λ
71.4600000000
71.4600000000
71.4600000000
71.4600000000
71.4600000000
La distancia geodésica calculada usando la longitud del arco de meridiano elíptico entre
los puntos A y B, corresponde al patrón de comparación distanciométrico del presente caso y su
magnitud es de: 22393.320m
La distancia proyectada entre los puntos A y B determinada según el teorema de Pitágoras
corresponde a: 22398.943m
Entonces, usando el valor K correspondiente al punto medio 1 se obtiene:
D ( geo) = 1.0002509108−1 ·22398.943m = 22393.324m
Por otra parte, usando el valor K correspondiente al punto medio 2 se obtiene:
D( geo) = 1.0002512440 −1 ·22398.943m = 22393.317m
La distancia reducida usando el punto medio exacto
D( geo) = 1.0002510774 −1 ·22398.943m = 22393.320m
Finalmente, la distancia reducida utilizando el promedio de los factores de deformación de
escala de los puntos muestrales ubicados sobre el meridiano 71.46ºW, resulta:
K Promedio = 1.0002510770
Distancia Reducida = K Promedio · Distancia Plana = 22393.320
153
B:
Para dos puntos “A” y “B” teóricos, definidos sobre el elipsoide en un mismo paralelo y
llevados a la proyección UTM definida anteriormente. Se obtiene un patrón distanciométrico de
18887.382m.
Pto A
Pto B
Pto medio 1
Pto medio 2
Pto medio exacto
Este
269945.770
251058.159
261551.427
259452.804
260502.118
Norte
6355053.119
6354594.027
6354853.556
6354802.546
6354828.107
K
1.0002525759
1.0003641421
1.0003010732
1.0003134695
1.0003066913
φ
32.9180899403
32.9180899403
32.9180899403
32.9180899403
32.9180899403
λ
71.4600000000
71.6619100597
71.5497378043
71.5721722554
71.5609550299
La distancia proyectada entre los puntos A y B determinada según el teorema de Pitágoras
corresponde a: 18893.190m
Entonces, usando el valor K correspondiente al punto medio 1 se obtiene:
D( geo) = 1.0003010732 −1 ·18893.190m = 18887.503m
Por otra parte, usando el valor K correspondiente al punto medio 2 se obtiene:
D( geo) = 1.0003134695−1 ·18893.190m = 18887.269m
La distancia geodésica usando el punto medio exacto
D( geo) = 1.0003066913−1 ·18893.190m = 18887.397m
Finalmente, usando el promedio de los valores “K” obtenidos de cada uno de los puntos
muestrales ubicados sobre el paralelo 32.9180899403º S, se obtiene:
K Promedio = 1.0003077064
Distancia Reducida = K Promedio · Distancia Plana = 18887.378
154
CAPÍTULO 8
ANÁLISIS DE RESULTADOS
8.1.
DETERMINACIÓN DEL COEFICIENTE DE
CORRELACIÓN ENTRE EL
FACTOR DE DEFORMACIÓN DE ESCALA Y LAS COORDENADAS
PROYECTADAS
Observando los resultados expuestos en la tabla Nº4 se aprecia que en todas las
proyecciones analizadas existe una alta correlación entre el valor del factor de deformación de
escala K y la diferencia de coordenadas Este y por consiguiente una baja correlación entre el
valor del factor de deformación de escala y la coordenada Norte.
Las proyecciones LTM1 y MTM2, ambas con meridiano central cercano al área de
estudio (71º30’ W) presentan un porcentaje de explicación del factor de deformación de escala
según el valor de la coordenada Este del 82.2%. Las proyecciones GK1, LTM2 y LTM1, con
meridiano central en 71º W presentan un porcentaje de explicación del factor de deformación de
escala según el valor de la coordenada Este del 99.7% Mientras que las proyecciones UTM y
GK2, con meridiano central en los 69º W y 70º W respectivamente presentan un porcentaje de
explicación del factor de deformación de escala según el valor de la coordenada Este del 100.0%
155
Según lo expuesto en el capitulo 5, el factor de deformación de escala para una proyección
conforme puede ser deducido a partir de la expresión:
2
k=
⎛ ∂y ⎞
⎛ ∂x ⎞
⎜ ⎟ +⎜ ⎟
λ
∂
⎝ ∂λ ⎠
⎝ ⎠
N ·cos φ
2
Ya que la latitud expresada en radianes, es pequeña en comparación a la gran normal N
que la acompaña en el denominador de la expresión, y que
∂x ∂y
, puede comprenderse sin
>
∂λ ∂λ
dificultad la alta relación entre el valor del factor de deformación de escala K y el valor de la
coordenada Este.
8.2.
DETERMINACIÓN
DE
MAGNITUDES
LINEALES
DE
SEGMENTOS
GEODÉSICOS Y PROYECTADOS
De los resultados expuestos en el anexo Nº4 se puede observar que:
Para los casos en que el área de estudio se sitúa dentro de la zona de secancia de la
proyección, las deformaciones de las magnitudes lineales consideradas en el sentido de los
meridianos tienden a crecer hacia el meridiano central. Ello se entiende por el comportamiento
del factor de deformación de escala “K” que se relaciona fuertemente a la variación de la
coordenada este y que como se observó en el capítulo V posee un mínimo en el meridiano central
donde la deformación es máxima.
156
Para los casos en que el área de estudio se ubica fuera de la zona de secancia de la
proyección (K>1), las deformaciones de las magnitudes lineales consideradas en el sentido de los
meridianos tienden a crecer a medida que crece la distancia al meridiano central. Ello se explica
por que el factor de escala tiende a crecer en dimensión mientras se aleja la coordenada del
meridiano central.
Las variaciones de las deformaciones de magnitudes lineales consideradas en el sentido
de los paralelos tienden a mantenerse constantes y con valores menores que para las
deformaciones observadas en el sentido de los meridianos. Este hecho puede confirmarse si se
considera que:
Al corresponder un segmento de meridiano geodésico a una magnitud invariable según la
latitud, y como se observa en el anexo Nº4, a menor latitud, mayor distorsión, se evidencia que
las magnitudes calculadas sobre el paralelo en un plano TM poseerán mayores deformaciones en
su comparación con la magnitud geodésica primitiva.
Por otra parte. Ya que los arcos geodésicos de paralelo para un mismo Δλ, son
magnitudes variables según la latitud, y poseen igual sentido de variación que su transformada,
estas magnitudes poseerán deformaciones en su comparación con la magnitud Geodésica
primitiva menores que en el sentido de los meridianos, hecho que se confirma mediante las
desviaciones estándar de estas diferencias
157
8.3.
DETERMINACIÓN
DE
ESCALAS
DE
REPRESENTACIÓN
SEGÚN
TOLERANCIAS
8.3.1. Caso general
Considerando la deformación nominal de cada proyección (K0) y la deformación máxima
considerable, es posible determinar que:
Las proyecciones GK1 y GK2 permiten nominalmente una óptima relación entre el
elipsoide y el plano de proyección al poseer un factor de escala en el meridiano central unitario
(K0=1). Pese a esto, las deformaciones máximas que hipotéticamente produce esta proyección
para el territorio nacional solo permiten la representación cartográfica para escalas 1:50.000 y
1:100.000 respectivamente ya que la situación tangencial de esta proyección aumenta las
deformaciones en las lejanías del meridiano central no haciendo recomendable su uso para la
representación urbana sin considerar la deformación para los casos particulares.
Las proyecciones LTM1 y LTM2 presentan una exactitud nominal compatible con escalas
1:500 lo que señala la idoneidad de estas proyecciones para la representación del espacio en
detalle en las cercanías del meridiano central. Sin embargo, estas proyecciones sometidas a una
situación crítica de borde de huso en bajas latitudes ofrecen exactitudes compatibles con escalas
1:5.000 y 1:20.000 respectivamente, lo que señala que la utilización de esta proyección debe estar
restringida a una cercanía al meridiano central que permita desarrollar exactitudes compatibles
con las necesidades cartográficas de cada proyecto en particular.
158
Las proyecciones MTM1 y MTM2 ofrecen para el meridiano central, exactitudes
compatibles con escalas de representación 1:10.000 lo que las hace adecuadas para ciertas
actividades relacionadas con la planificación urbana. Se observa que para estas proyecciones la
exactitud observada para el borde de huso en bajas latitudes no incrementa de sobre manera las
deformaciones, produciéndose para el caso de la MTM1 una mantención de la escala de
representación posible para el borde de huso (1:10.000) y para el caso de la MTM2 una mejora en
cuanto a la exactitud posible de alcanzar para esta proyección en el meridiano central (1:5.000)
La proyección UTM ofrece nominalmente exactitudes compatibles con la escala 1:50.000
y en el caso extremo exactitudes compatibles con la escala 1:100.000 lo que la hace totalmente
inadecuada para la representación urbana
8.3.2. Caso particular
En cuanto a la deformación ocurrida en el área de estudio debido a las diferencias de los
factores K es posible determinar que:
Aquellos casos en que el Huso de la proyección tiene su meridiano central dentro del
desarrollo longitudinal del área de estudio (en 71º30’W), se presentan deformaciones menores,
las que permiten representación cartográfica a una escala máxima 1:500. Para las demás
proyecciones se observa un incremento en las diferencias de factores de escala acorde a la
distancia que separa el área de estudio respecto al meridiano central. Así, las proyecciones con
meridiano central en 71ºW permiten representación cartográfica hasta escala 1:5.000 y las
159
proyecciones con meridiano central en 70ºW permiten una representación cartográfica de hasta
1:10.000. Por otra parte la proyección UTM no permite representación cartográfica a escala
urbana.
Atendiendo a esto, se observa que cada una de las proyecciones estudiadas, a excepción
de la UTM presenta algún grado de afinidad en cuanto a la representación a escala urbana y si
bien es cierto los resultados recién expuestos no son indicador de un óptima relación plano de
proyección – elipsoide – terreno, si indican las magnitudes de las deformaciones inherentes a
cada proyección las cuales habrá que considerar para casos en los cuales bastará una única
corrección al factor de deformación de escala para el área de estudio.
En cuanto a la deformación ocurrida entre el plano de proyección y el elipsoide dentro del
área de estudio, es posible determinar que:
La proyección LTM1 al corresponderse con un meridiano central cercano al área de
estudio (71º30’) y tener un factor de escala para el meridiano central cercano a uno, ve
aumentada su exactitud de representación del elipsoide entre el meridiano central y las zonas mas
alejadas de él. Así, puede considerarse que esta proyección para el caso local representa al
elipsoide con una exactitud compatible con la escala de representación 1:500
Las proyecciones GK1 y LTM2 presentan exactitudes en el área de estudio que las hacen
compatibles con escalas de representación 1:5.000 y menores. Esto se debe en el caso de la GK1
a su relativa cercanía con el meridiano central (45 km aproximadamente) que implica valores K
160
cercanos a la unidad. En el caso de la LTM2 la exactitud que entrega se explica por la cercanía
del área de estudio con la zona de secancia, lo que implica valores del factor de escala cercanos a
la unidad.
Las proyecciones MTM1 y MTM2 presentan exactitudes compatibles con escalas de
representación 1:10.000 debido fundamentalmente a su cercanía con el meridiano central y con la
línea de secancia, lo que permite que los valores calculados K se mantengan cercanos a la unidad.
En cuanto a la deformación ocurrida entre el plano de proyección y la superficie
topográfica, es posible determinar que:
La proyección GK1 posee los valores mas cercanos a la nula deformación entre el plano
de proyección y la superficie topográfica, por lo que presenta una exactitud compatible con la
escala de representación 1:5.000. Esta situación se explica básicamente por la escasa altitud que
alcanza el área de estudio (menor que 450 metros de altura ortométrica), lo que implica que los
valores Kh son cercanos en magnitud a los valores K presentes en esta situación.
Las proyecciones LTM1 y LTM2 poseen una exactitud que las hace compatibles con
escalas de representación 1:10.000 y menores. Esto, debido fundamentalmente por la relativa
cercanía en los valores K con los valores Kh máximos definidos para el área de estudio. Para este
caso particular, la proyección LTM1 provoca deformaciones negativas, Las que se manifiestan en
una representación subdimensionada de una porción de superficie topográfica, debido a la
condición de tangencia del cilindro TM para este caso. Por otra parte, la proyección LTM2
161
provoca deformaciones positivas, las que se manifiestan mediante una representación
sobredimensionada de una porción de superficie topográfica, debido a la condición de secancia
del cilindro TM para este caso.
Las proyecciones GK2, MTM1, MTM2 y UTM presentan deformaciones que sobrepasan
la tolerancia definida para las escalas urbanas de representación, debido a las notables diferencias
existentes entre los valores K observados en el área de estudio y los valores Kh definidos según la
situación altimétrica del terreno a representar.
8.4.
RELACIÓN ENTRE PROYECCIONES TM, ELIPSOIDE Y SUPERFICIE
TOPOGRÁFICA
8.4.1. Reducción Plano TM – Elipsoide
Para validar la reducción de una magnitud considerada sobre un plano de proyección, será
preciso el considerar el error inherente al método de producción cartográfica e interpretarlo como
la tolerancia propia de cada escala cartográfica de representación. De esta forma, una reducción
solo tendrá sentido si la diferencia entre la magnitud primitiva y la magnitud reducida es mayor
que la tolerancia cartográfica definida para la escala de representación.
La determinación del factor reductor de una determinada magnitud, debe hacerse de tal
modo que este, modele óptimamente la relación geométrica existente entre las superficies
162
consideradas. En este sentido, la determinación del factor K utilizado en la reducción deberá
realizarse poniendo especial atención en el error que puede introducirse a partir de la
determinación de dicho factor.
8.4.2. Reducción Elipsoide – Plano Topográfico Local
Pese a la sencillez del cálculo del factor reductor que transforma magnitudes elipsoidales
en Topográficas, la obtención de las alturas Geométricas es un factor crítico para validar el
método de reducción de magnitudes, ya que sin ello es imposible modelar la relación geométrica
entre el elipsoide y el plano topográfico local. Pese a lo anterior, en la presente investigación se
asume la coincidencia del elipsoide con el geoide para de esta forma utilizar la altura Ortométrica
en reemplazo de la altura Geométrica.
Al momento de realizar una reducción de este tipo, debe considerarse que esta será valida
únicamente para un rango de alturas en función de la tolerancia aceptada para la escala de
representación y que por lo tanto, para diferentes alturas del terreno, existirán diferentes niveles
de exactitud para la reducción y que habrá que considerar siempre, el error máximo del rango de
alturas a representar, para todo el Plano Topográfico Local.
Ejemplos de Reducciones
Para el ejemplo “a” expuesto en 7.10.4. se observa que la reducción de una magnitud
desde el plano TM hasta el elipsoide considerada sobre un único meridiano y utilizando el factor
163
de deformación de escala del punto medio exacto entre los puntos observados, es coincidente
hasta el milímetro con la medida patrón.
Para la reducción hecha a partir del promedio de los factores de deformación de escala
tomados de la red de puntos muestrales, la igualdad entre las magnitudes transformadas y patrón
se mantiene también hasta el orden de los milímetros.
Para las reducciones hechas utilizando un factor corrector proveniente del factor K de
puntos distantes unos 1250m de la coordenada media exacta, se obtiene un error de 3mm entre la
magnitud reducida y la magnitud patrón.
Obsérvese que la variación de coordenadas Este que separa ambos puntos corresponde a
524.23m mientras que la variación de sus coordenadas Norte corresponde a 22392.807m.
Para el ejemplo “b” expuesto en 7.10.4. se observa la reducción de una magnitud desde el plano
TM hasta el elipsoide considerada sobre un único paralelo y utilizando el factor de deformación
de escala del punto medio exacto entre los puntos observados, existe un error de 15 milímetros
respecto de la medida patrón.
Para la reducción hecha a partir del promedio de los factores de deformación de escala
tomados de la red de puntos muestrales, el error de la reducción se reduce hasta los 4 milímetros.
Para las reducciones hechas utilizando un factor corrector proveniente del factor K de un
punto distante unos 1050m de la coordenada media exacta en el sentido del paralelo, se obtiene
un error aproximado de 115mm entre la magnitud reducida y la magnitud patrón.
164
Obsérvese que la variación de coordenadas este que separa ambos puntos corresponde a
524.23m mientras que la variación de sus coordenadas norte corresponde a 22392.807m.
165
CAPITULO 9
CONCLUSIONES Y RECOMENDACIONES
A partir de los Objetivos planteados en la presente investigación y atendiendo a los
resultados obtenidos es posible concluir que:
Diferentes proyecciones TM presentan efectivamente diferentes niveles de exactitud, lo
que condiciona la utilización de ellas en determinados márgenes dados por la tolerancia impuesta
por la escala de representación y por la situación espacial del área a proyectar.
Para el presente estudio, las deformaciones fluctúan entre los 0.147m y los 7.236m al
considerar el plano de proyección y el plano topográfico. Entre los 0.845m y los 5.958m si se
considera el plano de proyección y el elipsoide, y entre los 0.491m y los 2.291m al considerar las
deformaciones producidas por la variación de los factores K al interior del área de estudio.
La elección de la utilización de una determinada proyección, debe realizarse previo
estudio de las deformaciones existentes para el área a representar en cuanto a:
•
La cantidad de deformación inherente a la proyección, definida según la máxima
diferencia de los valores K observados en el área a representar y su significancia
en la extensión a representar considerando la escala de representación.
166
•
La máxima y mínima deformación existente entre la proyección y el elipsoide de
referencia.
•
La máxima y mínima deformación existente entre la proyección y la superficie
topográfica.
La exactitud de representación de una proyección cartográfica debe definirse según la
escala de máximo detalle que permite representar una determinada proyección. Se recomienda
definir el tipo de relación optima que se espera del producto cartográfico en cuanto a la exactitud
referida al elipsoide de revolución, o superficie topográfica.
La óptima relación entre la superficie física de la Tierra y el plano de proyección debe
considerar, para aquellos productos cartográficos referidos un elipsoide, los máximos y mínimos
valores Kp y Kh presentes en el área a representar para con esto realizar las reducciones
necesarias mediante la formula referida en el capitulo Nº7. Para la generación de nuevos
productos cartográficos que deban referirse a la superficie física de la tierra, se debe optar por una
proyección TM con factor Kh referido a la exactitud esperada según la escala de representación
dependiendo de la situación altimétrica del área a representar y meridiano central variable.
Al utilizar una proyección cartográfica como instrumento de medición de los elementos
en él representado, debe considerarse la superficie de referencia del producto cartográfico y la
167
magnitud de deformación a la cual está sujeta la representación. debido a la alta correlación entre
el factor de deformación de escala y la variación de la coordenada Este, debe utilizarse el factor
de deformación promedio en la superficie a medir, para asegurar con esto, la exactitud de la
medición.
168
CAPITULO 10
ANEXOS
169
ANEXO Nº1
MAPA DE UBICACIÓN
170
171
ANEXO Nº 2
RED DE PUNTOS MUESTRALES
172
ID
Latitud
Longitud
ID
Latitud
Longitud
1
-33.12000000000
-71.46000000000
51
-33.00782774460
-71.46000000000
2
-33.12000000000
-71.48243445108
52
-33.00782774460
-71.48243445108
3
-33.12000000000
-71.50486890216
53
-33.00782774460
-71.50486890216
4
-33.12000000000
-71.52730335324
54
-33.00782774460
-71.52730335324
5
-33.12000000000
-71.54973780432
55
-33.00782774460
-71.54973780432
6
-33.12000000000
-71.57217225540
56
-33.00782774460
-71.57217225540
7
-33.12000000000
-71.59460670648
57
-33.00782774460
-71.59460670648
8
-33.12000000000
-71.61704115756
58
-33.00782774460
-71.61704115756
9
-33.12000000000
-71.63947560864
59
-33.00782774460
-71.63947560864
10
-33.12000000000
-71.66191005972
60
-33.00782774460
-71.66191005972
11
-33.09756554892
-71.46000000000
61
-32.98539329352
-71.46000000000
12
-33.09756554892
-71.48243445108
62
-32.98539329352
-71.48243445108
13
-33.09756554892
-71.50486890216
63
-32.98539329352
-71.50486890216
14
-33.09756554892
-71.52730335324
64
-32.98539329352
-71.52730335324
15
-33.09756554892
-71.54973780432
65
-32.98539329352
-71.54973780432
16
-33.09756554892
-71.57217225540
66
-32.98539329352
-71.57217225540
17
-33.09756554892
-71.59460670648
67
-32.98539329352
-71.59460670648
18
-33.09756554892
-71.61704115756
68
-32.98539329352
-71.61704115756
19
-33.09756554892
-71.63947560864
69
-32.98539329352
-71.63947560864
20
-33.09756554892
-71.66191005972
70
-32.98539329352
-71.66191005972
21
-33.07513109784
-71.46000000000
71
-32.96295884244
-71.46000000000
22
-33.07513109784
-71.48243445108
72
-32.96295884244
-71.48243445108
23
-33.07513109784
-71.50486890216
73
-32.96295884244
-71.50486890216
24
-33.07513109784
-71.52730335324
74
-32.96295884244
-71.52730335324
25
-33.07513109784
-71.54973780432
75
-32.96295884244
-71.54973780432
26
-33.07513109784
-71.57217225540
76
-32.96295884244
-71.57217225540
27
-33.07513109784
-71.59460670648
77
-32.96295884244
-71.59460670648
28
-33.07513109784
-71.61704115756
78
-32.96295884244
-71.61704115756
29
-33.07513109784
-71.63947560864
79
-32.96295884244
-71.63947560864
30
-33.07513109784
-71.66191005972
80
-32.96295884244
-71.66191005972
31
-33.05269664676
-71.46000000000
81
-32.94052439136
-71.46000000000
32
-33.05269664676
-71.48243445108
82
-32.94052439136
-71.48243445108
33
-33.05269664676
-71.50486890216
83
-32.94052439136
-71.50486890216
34
-33.05269664676
-71.52730335324
84
-32.94052439136
-71.52730335324
35
-33.05269664676
-71.54973780432
85
-32.94052439136
-71.54973780432
36
-33.05269664676
-71.57217225540
86
-32.94052439136
-71.57217225540
37
-33.05269664676
-71.59460670648
87
-32.94052439136
-71.59460670648
38
-33.05269664676
-71.61704115756
88
-32.94052439136
-71.61704115756
39
-33.05269664676
-71.63947560864
89
-32.94052439136
-71.63947560864
40
-33.05269664676
-71.66191005972
90
-32.94052439136
-71.66191005972
Continúa en página siguiente
173
ID
Latitud
Longitud
ID
Latitud
Longitud
41
-33.03026219568
-71.46000000000
91
-32.91808994028
-71.46000000000
42
-33.03026219568
-71.48243445108
92
-32.91808994028
-71.48243445108
43
-33.03026219568
-71.50486890216
93
-32.91808994028
-71.50486890216
44
-33.03026219568
-71.52730335324
94
-32.91808994028
-71.52730335324
45
-33.03026219568
-71.54973780432
95
-32.91808994028
-71.54973780432
46
-33.03026219568
-71.57217225540
96
-32.91808994028
-71.57217225540
47
-33.03026219568
-71.59460670648
97
-32.91808994028
-71.59460670648
48
-33.03026219568
-71.61704115756
98
-32.91808994028
-71.61704115756
49
-33.03026219568
-71.63947560864
99
-32.91808994028
-71.63947560864
50
-33.03026219568
-71.66191005972
100
-32.91808994028
-71.66191005972
174
ANEXO Nº 3
MAPA DE UBICACIÓN RED DE PUNTOS MUESTRALES
175
176
ANEXO Nº4
PROYECCIÓN DE PUNTOS MUESTRALES, FACTOR DE DEFORMACIÓN DE
ESCALA Y CONVERGENCIA DE MERIDIANOS
177
GK1
ID
Este
Norte
Def escala
ID
Este
Norte
Def Escala
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
238082.019
238097.645
238113.281
238128.927
238144.582
238160.246
238175.920
238191.604
238207.296
238222.999
240180.673
240195.770
240210.876
240225.991
240241.115
240256.248
240271.391
240286.543
240301.704
240316.874
242279.323
242293.890
242308.466
242323.051
242337.644
242352.247
242366.858
242381.478
242396.107
242410.745
244377.970
244392.007
244406.053
244420.107
244434.170
244448.242
244462.322
244476.410
244490.507
3356086.152
3353597.972
3351109.784
3348621.587
3346133.382
3343645.167
3341156.943
3338668.711
3336180.470
3333692.220
3356099.104
3353610.930
3351122.746
3348634.554
3346146.353
3343658.143
3341169.924
3338681.696
3336193.459
3333705.213
3356111.611
3353623.440
3351135.261
3348647.073
3346158.876
3343670.671
3341182.456
3338694.232
3336206.000
3333717.759
3356123.670
3353635.504
3351147.329
3348659.146
3346170.953
3343682.751
3341194.541
3338706.322
3336218.093
1.0000472485
1.0000472245
1.0000472004
1.0000471763
1.0000471522
1.0000471281
1.0000471040
1.0000470798
1.0000470557
1.0000470316
1.0000440999
1.0000440774
1.0000440549
1.0000440325
1.0000440100
1.0000439875
1.0000439650
1.0000439424
1.0000439199
1.0000438974
1.0000410598
1.0000410389
1.0000410180
1.0000409970
1.0000409761
1.0000409552
1.0000409342
1.0000409132
1.0000408923
1.0000408713
1.0000381283
1.0000381089
1.0000380895
1.0000380700
1.0000380506
1.0000380311
1.0000380117
1.0000379922
1.0000379727
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
248575.252
248588.230
248601.216
248614.210
248627.211
248640.221
248653.238
248666.264
248679.297
248692.338
250673.888
250686.337
250698.793
250711.256
250723.727
250736.206
250748.692
250761.185
250773.687
250786.195
252772.522
252784.440
252796.366
252808.299
252820.240
252832.187
252844.142
252856.104
252868.073
252880.050
254871.152
254882.541
254893.937
254905.339
254916.749
254928.166
254939.589
254951.020
254962.457
3356146.449
3353658.291
3351170.125
3348681.949
3346193.764
3343705.571
3341217.368
3338729.157
3336240.936
3333752.707
3356157.169
3353669.015
3351180.852
3348692.680
3346204.499
3343716.309
3341228.110
3338739.903
3336251.686
3333763.460
3356167.442
3353679.291
3351191.132
3348702.964
3346214.786
3343726.600
3341238.405
3338750.201
3336261.988
3333773.766
3356177.268
3353689.121
3351200.965
3348712.800
3346224.627
3343736.444
3341248.252
3338760.051
3336271.842
1.0000325910
1.0000325744
1.0000325578
1.0000325412
1.0000325246
1.0000325079
1.0000324913
1.0000324747
1.0000324580
1.0000324414
1.0000299852
1.0000299699
1.0000299547
1.0000299394
1.0000299241
1.0000299088
1.0000298935
1.0000298782
1.0000298629
1.0000298475
1.0000274880
1.0000274740
1.0000274600
1.0000274460
1.0000274319
1.0000274179
1.0000274039
1.0000273898
1.0000273758
1.0000273618
1.0000250993
1.0000250865
1.0000250737
1.0000250609
1.0000250481
1.0000250353
1.0000250225
1.0000250097
1.0000249969
40 244504.613 3333729.856 1.0000379533
90
254973.902 3333783.623 1.0000249841
Continúa en página siguiente
178
ID
Este
Norte
Def escala
ID
Este
Norte
Def Escala
41
42
43
44
45
46
47
48
49
246476.612
246490.120
246503.636
246517.160
246530.692
246544.233
246557.782
246571.338
246584.904
3356135.283
3353647.121
3351158.950
3348670.771
3346182.582
3343694.385
3341206.178
3338717.963
3336229.739
1.0000353054
1.0000352874
1.0000352694
1.0000352514
1.0000352334
1.0000352154
1.0000351974
1.0000351793
1.0000351613
91
92
93
94
95
96
97
98
99
256969.779
256980.638
256991.504
257002.377
257013.256
257024.142
257035.034
257045.933
257056.838
3356186.648
3353698.505
3351210.352
3348722.190
3346234.020
3343745.840
3341257.652
3338769.454
3336281.248
1.0000228192
1.0000228076
1.0000227959
1.0000227843
1.0000227727
1.0000227610
1.0000227494
1.0000227377
1.0000227261
50 246598.477 3333741.506 1.0000351433 100 257067.751 3333793.033 1.0000227144
179
GK2
ID
Este
Norte
Def Escala
ID
Este
Norte
Def escala
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
144530.048
144569.298
144608.571
144647.869
144687.190
144726.535
144765.904
144805.296
144844.713
144884.153
146629.006
146667.725
146706.468
146745.234
146784.024
146822.837
146861.674
146900.535
146939.419
146978.326
148727.953
148766.142
148804.354
148842.590
148880.849
148919.130
148957.435
148995.764
149034.115
149072.490
150826.891
150864.550
150902.232
150939.936
150977.664
151015.414
151053.187
151090.983
151128.802
3355054.983
3352566.440
3350077.890
3347589.331
3345100.764
3342612.189
3340123.606
3337635.014
3335146.414
3332657.806
3355087.854
3352599.323
3350110.785
3347622.237
3345133.682
3342645.118
3340156.546
3337667.966
3335179.378
3332690.781
3355120.278
3352631.759
3350143.232
3347654.696
3345166.152
3342677.599
3340189.039
3337700.470
3335211.893
3332723.307
3355152.256
3352663.748
3350175.231
3347686.707
3345198.174
3342709.633
3340221.083
3337732.526
3335243.959
1.0002978963
1.0002977444
1.0002975925
1.0002974406
1.0002972886
1.0002971366
1.0002969845
1.0002968323
1.0002966801
1.0002965279
1.0002899066
1.0002897588
1.0002896110
1.0002894631
1.0002893152
1.0002891673
1.0002890192
1.0002888712
1.0002887231
1.0002885749
1.0002820255
1.0002818818
1.0002817380
1.0002815941
1.0002814502
1.0002813063
1.0002811623
1.0002810183
1.0002808742
1.0002807301
1.0002742531
1.0002741133
1.0002739735
1.0002738336
1.0002736937
1.0002735537
1.0002734137
1.0002732737
1.0002731335
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
155024.740
155061.338
155097.958
155134.601
155171.266
155207.953
155244.663
155281.394
155318.148
155354.924
157123.650
157159.718
157195.808
157231.920
157268.053
157304.209
157340.387
157376.586
157412.808
157449.051
159222.551
159258.089
159293.648
159329.229
159364.832
159400.456
159436.102
159471.769
159507.458
159543.169
161321.443
161356.451
161391.480
161426.530
161461.602
161496.694
161531.808
161566.944
161602.100
3355214.869
3352726.383
3350237.889
3347749.386
3345260.875
3342772.356
3340283.828
3337795.292
3335306.748
3332818.195
3355245.505
3352757.030
3350268.546
3347780.054
3345291.554
3342803.045
3340314.528
3337826.003
3335337.469
3332848.927
3355275.694
3352787.229
3350298.756
3347810.275
3345321.785
3342833.287
3340344.781
3337856.266
3335367.743
3332879.211
3355305.436
3352816.981
3350328.519
3347840.048
3345351.569
3342863.081
3340374.585
3337886.081
3335397.568
1.0002590343
1.0002589022
1.0002587702
1.0002586381
1.0002585059
1.0002583737
1.0002582415
1.0002581092
1.0002579768
1.0002578445
1.0002515878
1.0002514596
1.0002513313
1.0002512030
1.0002510747
1.0002509463
1.0002508178
1.0002506893
1.0002505608
1.0002504322
1.0002442500
1.0002441255
1.0002440010
1.0002438764
1.0002437518
1.0002436272
1.0002435025
1.0002433777
1.0002432530
1.0002431281
1.0002370208
1.0002369000
1.0002367792
1.0002366583
1.0002365374
1.0002364164
1.0002362954
1.0002361744
1.0002360533
40 151166.644 3332755.385 1.0002729934
90
161637.278 3332909.047 1.0002359322
Continúa en página siguiente
180
ID
Este
Norte
Def Escala
ID
Este
Norte
Def escala
41
42
43
44
45
46
47
48
49
152925.820
152962.949
153000.100
153037.273
153074.469
153111.688
153148.929
153186.193
153223.480
3355183.786
3352695.289
3350206.784
3347718.270
3345229.748
3342741.218
3340252.680
3337764.133
3335275.578
1.0002665894
1.0002664535
1.0002663176
1.0002661816
1.0002660456
1.0002659095
1.0002657734
1.0002656373
1.0002655011
91
92
93
94
95
96
97
98
99
163420.327
163454.804
163489.303
163523.822
163558.363
163592.924
163627.506
163662.109
163696.733
3355334.730
3352846.287
3350357.834
3347869.374
3345380.905
3342892.427
3340403.942
3337915.447
3335426.945
1.0002299003
1.0002297831
1.0002296659
1.0002295487
1.0002294314
1.0002293141
1.0002291967
1.0002290793
1.0002289618
50 153260.789 3332787.014 1.0002653648 100 163731.378 3332938.434 1.0002288444
181
LTM1
ID
Este
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
184854.427
184858.249
184862.073
184865.900
184869.729
184873.560
184877.394
184881.230
184885.069
184888.909
186953.017
186956.310
186959.604
186962.901
186966.199
186969.500
186972.802
186976.107
186979.413
186982.722
189051.607
189054.370
189057.134
189059.901
189062.669
189065.438
189068.210
189070.983
189073.757
189076.534
191150.196
191152.429
191154.664
191156.900
191159.137
191161.376
191163.616
191165.858
191168.101
Norte
3356287.109
3353799.007
3351310.896
3348822.775
3346334.646
3343846.508
3341358.360
3338870.204
3336382.039
3333893.864
3356290.109
3353802.008
3351313.897
3348825.778
3346337.650
3343849.512
3341361.366
3338873.211
3336385.047
3333896.873
3356292.662
3353804.561
3351316.452
3348828.334
3346340.206
3343852.070
3341363.925
3338875.770
3336387.607
3333899.434
3356294.768
3353806.669
3351318.560
3348830.442
3346342.316
3343854.180
3341366.035
3338877.882
3336389.719
Def Escala
0.9999978270
0.9999978256
0.9999978241
0.9999978227
0.9999978212
0.9999978198
0.9999978183
0.9999978169
0.9999978155
0.9999978140
0.9999970978
0.9999970968
0.9999970957
0.9999970946
0.9999970936
0.9999970925
0.9999970914
0.9999970904
0.9999970893
0.9999970882
0.9999964773
0.9999964765
0.9999964757
0.9999964750
0.9999964742
0.9999964735
0.9999964727
0.9999964720
0.9999964712
0.9999964705
0.9999959652
0.9999959647
0.9999959642
0.9999959637
0.9999959632
0.9999959627
0.9999959623
0.9999959618
0.9999959613
40 191170.345 3333901.547 0.9999959608
ID
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
Este
195347.373
195348.547
195349.722
195350.897
195352.073
195353.250
195354.428
195355.606
195356.786
195357.965
203741.723
203740.779
203739.834
203738.889
203737.943
203736.996
203736.049
203735.101
203734.153
203733.204
197445.960
197446.605
197447.250
197447.895
197448.541
197449.187
197449.833
197450.480
197451.128
197451.775
201643.135
201642.721
201642.306
201641.891
201641.475
201641.060
201640.644
201640.228
201639.811
Norte
3356297.641
3353809.543
3351321.435
3348833.318
3346345.193
3343857.058
3341368.915
3338880.762
3336392.600
3333904.430
3356298.029
3353809.931
3351321.823
3348833.706
3346345.581
3343857.446
3341369.303
3338881.151
3336392.989
3333904.819
3356298.408
3353810.310
3351322.202
3348834.086
3346345.961
3343857.826
3341369.683
3338881.531
3336393.369
3333905.199
3356298.602
3353810.504
3351322.396
3348834.280
3346346.155
3343858.020
3341369.877
3338881.725
3336393.564
Def Escala
0.9999952668
0.9999952666
0.9999952665
0.9999952664
0.9999952662
0.9999952661
0.9999952660
0.9999952658
0.9999952657
0.9999952656
0.9999951725
0.9999951725
0.9999951724
0.9999951723
0.9999951722
0.9999951721
0.9999951720
0.9999951719
0.9999951718
0.9999951718
0.9999950804
0.9999950804
0.9999950803
0.9999950803
0.9999950802
0.9999950802
0.9999950801
0.9999950801
0.9999950801
0.9999950800
0.9999950333
0.9999950333
0.9999950332
0.9999950332
0.9999950332
0.9999950332
0.9999950332
0.9999950332
0.9999950331
90 201639.395 3333905.393 0.9999950331
Continúa en página siguiente
182
ID
Este
41
42
43
44
45
46
47
48
49
193248.784
193250.488
193252.193
193253.899
193255.606
193257.313
193259.022
193260.732
193262.443
Norte
3356296.428
3353808.329
3351320.221
3348832.104
3346343.978
3343855.843
3341367.699
3338879.546
3336391.384
Def Escala
0.9999955617
0.9999955614
0.9999955611
0.9999955609
0.9999955606
0.9999955603
0.9999955600
0.9999955597
0.9999955594
ID
91
92
93
94
95
96
97
98
99
Este
199544.548
199544.663
199544.778
199544.893
199545.008
199545.123
199545.239
199545.354
199545.469
Norte
3356298.728
3353810.630
3351322.523
3348834.406
3346346.281
3343858.147
3341370.004
3338881.852
3336393.690
Def Escala
0.9999950026
0.9999950026
0.9999950026
0.9999950026
0.9999950026
0.9999950025
0.9999950025
0.9999950025
0.9999950025
50 193264.155 3333903.213 0.9999955591 100 199545.585 3333905.520 0.9999950025
183
LTM2
ID
Este
Norte
Def Escala
ID
Este
Norte
Def Escala
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
138082.329
138097.955
138113.591
138129.236
138144.891
138160.555
138176.229
138191.913
138207.605
138223.308
140180.972
140196.069
140211.175
140226.290
140241.414
140256.547
140271.690
140286.841
140302.002
140317.172
142279.612
142294.179
142308.754
142323.339
142337.933
142352.535
142367.146
142381.766
142396.395
142411.033
144378.248
144392.285
144406.331
144420.385
144434.448
144448.519
144462.599
144476.688
144490.785
3356104.371
3353616.204
3351128.029
3348639.844
3346151.651
3343663.449
3341175.238
3338687.018
3336198.789
3333710.551
3356117.324
3353629.162
3351140.991
3348652.811
3346164.622
3343676.424
3341188.218
3338700.002
3336211.778
3333723.545
3356129.830
3353641.672
3351153.506
3348665.330
3346177.146
3343688.952
3341200.750
3338712.539
3336224.319
3333736.090
3356141.890
3353653.736
3351165.574
3348677.402
3346189.222
3343701.033
3341212.835
3338724.628
3336236.412
1.0000422483
1.0000422242
1.0000422001
1.0000421760
1.0000421519
1.0000421278
1.0000421037
1.0000420796
1.0000420555
1.0000420313
1.0000390997
1.0000390772
1.0000390547
1.0000390322
1.0000390098
1.0000389873
1.0000389647
1.0000389422
1.0000389197
1.0000388972
1.0000360596
1.0000360387
1.0000360178
1.0000359968
1.0000359759
1.0000359550
1.0000359340
1.0000359130
1.0000358921
1.0000358711
1.0000331281
1.0000331087
1.0000330893
1.0000330698
1.0000330504
1.0000330309
1.0000330115
1.0000329920
1.0000329725
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
148575.509
148588.487
148601.473
148614.467
148627.468
148640.478
148653.495
148666.520
148679.553
148692.594
150674.135
150686.583
150699.039
150711.502
150723.973
150736.452
150748.938
150761.432
150773.933
150786.441
152772.758
152784.676
152796.602
152808.535
152820.475
152832.423
152844.378
152856.340
152868.309
152880.286
154871.377
154882.766
154894.162
154905.565
154916.975
154928.391
154939.815
154951.245
154962.683
3356164.669
3353676.523
3351188.369
3348700.205
3346212.033
3343723.852
3341235.662
3338747.463
3336259.255
3333771.038
3356175.388
3353687.246
3351199.096
3348710.936
3346222.768
3343734.590
3341246.404
3338758.209
3336270.005
3333781.792
3356185.661
3353697.523
3351209.376
3348721.220
3346233.055
3343744.881
3341256.699
3338768.507
3336280.306
3333792.097
3356195.488
3353707.353
3351219.209
3348731.057
3346242.895
3343754.725
3341266.546
3338778.358
3336290.160
1.0000275909
1.0000275743
1.0000275576
1.0000275410
1.0000275244
1.0000275078
1.0000274911
1.0000274745
1.0000274579
1.0000274412
1.0000249851
1.0000249698
1.0000249545
1.0000249392
1.0000249239
1.0000249086
1.0000248933
1.0000248780
1.0000248627
1.0000248474
1.0000224878
1.0000224738
1.0000224598
1.0000224458
1.0000224318
1.0000224178
1.0000224037
1.0000223897
1.0000223757
1.0000223616
1.0000200992
1.0000200864
1.0000200736
1.0000200608
1.0000200480
1.0000200352
1.0000200224
1.0000200096
1.0000199968
40 144504.890 3333748.188 1.0000329531
90
154974.127 3333801.954 1.0000199839
Continúa en página siguiente
184
ID
Este
Norte
Def Escala
ID
Este
Norte
Def Escala
41
42
43
44
45
46
47
48
49
146476.880
146490.388
146503.903
146517.427
146530.960
146544.500
146558.049
146571.606
146585.171
3356153.502
3353665.353
3351177.195
3348689.027
3346200.851
3343712.666
3341224.472
3338736.269
3336248.058
1.0000303052
1.0000302872
1.0000302692
1.0000302512
1.0000302332
1.0000302152
1.0000301972
1.0000301792
1.0000301611
91
92
93
94
95
96
97
98
99
156969.994
156980.854
156991.719
157002.592
157013.471
157024.357
157035.249
157046.148
157057.053
3356204.867
3353716.736
3351228.596
3348740.447
3346252.288
3343764.121
3341275.945
3338787.760
3336299.566
1.0000178191
1.0000178074
1.0000177958
1.0000177842
1.0000177725
1.0000177609
1.0000177493
1.0000177376
1.0000177260
50 146598.744 3333759.837 1.0000301431 100 157067.965 3333811.364 1.0000177143
185
MTM1
ID
Este
Norte
Def Escala
ID
Este
Norte
Def Escala
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
238088.211
238103.836
238119.470
238135.114
238150.767
238166.430
238182.103
238197.784
238213.476
238229.177
240186.655
240201.750
240216.854
240231.968
240247.091
240262.223
240277.364
240292.514
240307.674
240322.842
242285.095
242299.661
242314.235
242328.818
242343.411
242358.012
242372.621
242387.240
242401.868
242416.504
244383.532
244397.568
244411.612
244425.665
244439.727
244453.797
244467.875
244481.962
244496.058
3356450.543
3353962.613
3351474.673
3348986.725
3346498.768
3344010.802
3341522.828
3339034.844
3336546.852
3334058.850
3356463.495
3353975.569
3351487.634
3348999.690
3346511.738
3344023.777
3341535.807
3339047.827
3336559.839
3334071.843
3356475.999
3353988.078
3351500.148
3349012.209
3346524.261
3344036.304
3341548.338
3339060.363
3336572.379
3334084.387
3356488.058
3354000.141
3351512.215
3349024.280
3346536.336
3344048.383
3341560.421
3339072.451
3336584.472
0.9999472438
0.9999472197
0.9999471957
0.9999471716
0.9999471475
0.9999471234
0.9999470993
0.9999470751
0.9999470510
0.9999470269
0.9999440955
0.9999440730
0.9999440505
0.9999440281
0.9999440056
0.9999439831
0.9999439606
0.9999439381
0.9999439155
0.9999438930
0.9999410557
0.9999410348
0.9999410139
0.9999409929
0.9999409720
0.9999409511
0.9999409301
0.9999409091
0.9999408882
0.9999408672
0.9999381245
0.9999381051
0.9999380857
0.9999380662
0.9999380468
0.9999380273
0.9999380079
0.9999379884
0.9999379689
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
248580.395
248593.371
248606.356
248619.348
248632.349
248645.357
248658.373
248671.397
248684.429
248697.469
250678.821
250691.268
250703.723
250716.185
250728.655
250741.132
250753.617
250766.109
250778.609
250791.117
252777.244
252789.162
252801.086
252813.018
252824.958
252836.904
252848.858
252860.819
252872.787
252884.762
254875.665
254887.052
254898.447
254909.849
254921.258
254932.673
254944.095
254955.525
254966.961
3356510.835
3354022.926
3351535.008
3349047.081
3346559.145
3344071.200
3341583.246
3339095.284
3336607.312
3334119.332
3356521.553
3354033.648
3351545.734
3349057.810
3346569.878
3344081.937
3341593.987
3339106.029
3336618.061
3334130.084
3356531.825
3354043.924
3351556.013
3349068.093
3346580.165
3344092.227
3341604.281
3339116.326
3336628.362
3334140.388
3356541.651
3354053.752
3351565.845
3349077.929
3346590.004
3344102.070
3341614.127
3339126.175
3336638.215
0.9999325878
0.9999325712
0.9999325546
0.9999325379
0.9999325213
0.9999325047
0.9999324881
0.9999324714
0.9999324548
0.9999324381
0.9999299822
0.9999299669
0.9999299517
0.9999299364
0.9999299211
0.9999299058
0.9999298905
0.9999298752
0.9999298599
0.9999298446
0.9999274852
0.9999274712
0.9999274572
0.9999274432
0.9999274292
0.9999274152
0.9999274011
0.9999273871
0.9999273731
0.9999273590
0.9999250968
0.9999250840
0.9999250712
0.9999250584
0.9999250456
0.9999250328
0.9999250200
0.9999250072
0.9999249944
40 244510.162 3334096.483 0.9999379495
90
254978.404 3334150.245 0.9999249816
Continúa en página siguiente
186
ID
Este
Norte
Def Escala
ID
Este
Norte
Def Escala
41
42
43
44
45
46
47
48
49
246481.965
246495.471
246508.986
246522.508
246536.039
246549.578
246563.126
246576.681
246590.245
3356499.670
3354011.756
3351523.835
3349035.904
3346547.964
3344060.015
3341572.058
3339084.091
3336596.116
0.9999353019
0.9999352839
0.9999352659
0.9999352479
0.9999352299
0.9999352119
0.9999351939
0.9999351758
0.9999351578
91
92
93
94
95
96
97
98
99
256974.082
256984.940
256995.805
257006.677
257017.555
257028.439
257039.331
257050.228
257061.133
3356551.030
3354063.135
3351575.231
3349087.318
3346599.396
3344111.465
3341623.526
3339135.577
3336647.620
0.9999228169
0.9999228053
0.9999227937
0.9999227820
0.9999227704
0.9999227587
0.9999227471
0.9999227354
0.9999227238
50 246603.817 3334108.131 0.9999351398 100 257072.044 3334159.653 0.9999227121
187
MTM2
ID
Este
Norte
Def Escala
ID
Este
Norte
Def Escala
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
284855.865
284859.687
284863.511
284867.338
284871.166
284874.997
284878.831
284882.667
284886.505
284890.345
286954.257
286957.549
286960.843
286964.139
286967.437
286970.738
286974.040
286977.344
286980.650
286983.958
289052.647
289055.410
289058.174
289060.940
289063.708
289066.477
289069.248
289072.021
289074.795
289077.571
291151.037
291153.270
291155.504
291157.740
291159.977
291162.216
291164.456
291166.697
291168.940
3356633.264
3354145.398
3351657.523
3349169.639
3346681.746
3344193.844
3341705.933
3339218.013
3336730.084
3334242.146
3356636.263
3354148.398
3351660.524
3349172.641
3346684.749
3344196.848
3341708.939
3339221.020
3336733.092
3334245.155
3356638.816
3354150.952
3351663.079
3349175.197
3346687.306
3344199.406
3341711.497
3339223.579
3336735.652
3334247.716
3356640.922
3354153.059
3351665.186
3349177.305
3346689.415
3344201.516
3341713.607
3339225.690
3336737.764
0.9999028267
0.9999028253
0.9999028238
0.9999028224
0.9999028210
0.9999028195
0.9999028181
0.9999028166
0.9999028152
0.9999028137
0.9999020976
0.9999020966
0.9999020955
0.9999020944
0.9999020934
0.9999020923
0.9999020912
0.9999020902
0.9999020891
0.9999020880
0.9999014771
0.9999014764
0.9999014756
0.9999014749
0.9999014741
0.9999014733
0.9999014726
0.9999014718
0.9999014711
0.9999014703
0.9999009651
0.9999009646
0.9999009641
0.9999009636
0.9999009631
0.9999009627
0.9999009622
0.9999009617
0.9999009612
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
295347.815
295348.989
295350.163
295351.339
295352.515
295353.692
295354.869
295356.048
295357.227
295358.406
303741.368
303740.424
303739.479
303738.533
303737.588
303736.641
303735.694
303734.747
303733.798
303732.850
297446.203
297446.847
297447.492
297448.138
297448.783
297449.429
297450.076
297450.722
297451.370
297452.017
301642.979
301642.565
301642.150
301641.735
301641.319
301640.904
301640.488
301640.072
301639.655
3356643.795
3354155.933
3351668.061
3349180.181
3346692.292
3344204.393
3341716.486
3339228.570
3336740.645
3334252.710
3356644.182
3354156.320
3351668.449
3349180.569
3346692.680
3344204.782
3341716.875
3339228.959
3336741.033
3334253.099
3356644.562
3354156.699
3351668.828
3349180.948
3346693.059
3344205.161
3341717.254
3339229.339
3336741.414
3334253.480
3356644.755
3354156.893
3351669.022
3349181.142
3346693.254
3344205.356
3341717.449
3339229.533
3336741.608
0.9999002668
0.9999002666
0.9999002665
0.9999002663
0.9999002662
0.9999002661
0.9999002659
0.9999002658
0.9999002657
0.9999002655
0.9999001725
0.9999001724
0.9999001724
0.9999001723
0.9999001722
0.9999001721
0.9999001720
0.9999001719
0.9999001718
0.9999001717
0.9999000804
0.9999000803
0.9999000803
0.9999000803
0.9999000802
0.9999000802
0.9999000801
0.9999000801
0.9999000801
0.9999000800
0.9999000333
0.9999000333
0.9999000332
0.9999000332
0.9999000332
0.9999000332
0.9999000332
0.9999000332
0.9999000331
40 291171.184 3334249.829 0.9999009607
90
301639.239 3334253.674 0.9999000331
Continúa en página siguiente
188
ID
Este
Norte
Def Escala
ID
Este
Norte
Def Escala
41
42
43
44
45
46
47
48
49
293249.426
293251.129
293252.834
293254.540
293256.246
293257.954
293259.663
293261.373
293263.083
3356642.582
3354154.719
3351666.847
3349178.967
3346691.077
3344203.178
3341715.270
3339227.354
3336739.428
0.9999005617
0.9999005614
0.9999005611
0.9999005608
0.9999005605
0.9999005602
0.9999005599
0.9999005597
0.9999005594
91
92
93
94
95
96
97
98
99
299544.591
299544.706
299544.821
299544.936
299545.051
299545.167
299545.282
299545.397
299545.513
3356644.882
3354157.020
3351669.149
3349181.269
3346693.380
3344205.482
3341717.575
3339229.659
3336741.735
0.9999000026
0.9999000026
0.9999000026
0.9999000026
0.9999000026
0.9999000025
0.9999000025
0.9999000025
0.9999000025
50 293264.795 3334251.493 0.9999005591 100 299545.628 3334253.801 0.9999000025
189
UTM
ID
Este
Norte
Def Escala
ID
Este
Norte
Def Escala
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
251058.159
251121.046
251183.970
251246.933
251309.934
251372.974
251436.051
251499.167
251562.321
251625.513
253156.844
253219.199
253281.592
253344.023
253406.492
253468.999
253531.544
253594.126
253656.746
253719.404
255255.513
255317.337
255379.198
255441.098
255503.035
255565.009
255627.021
255689.070
255751.157
255813.281
257354.166
257415.459
257476.789
257538.157
257599.561
257661.003
257722.482
257783.999
257845.552
6354594.027
6352105.805
6349617.576
6347129.340
6344641.097
6342152.847
6339664.590
6337176.326
6334688.055
6332199.777
6354646.828
6352158.625
6349670.415
6347182.198
6344693.973
6342205.742
6339717.503
6337229.257
6334741.005
6332252.745
6354699.182
6352210.997
6349722.806
6347234.607
6344746.400
6342258.187
6339769.967
6337281.739
6334793.505
6332305.263
6354751.088
6352262.922
6349774.748
6347286.567
6344798.379
6342310.184
6339821.982
6337333.772
6334845.556
1.0003641421
1.0003637523
1.0003633624
1.0003629724
1.0003625823
1.0003621920
1.0003618016
1.0003614111
1.0003610204
1.0003606296
1.0003513107
1.0003509276
1.0003505442
1.0003501608
1.0003497772
1.0003493935
1.0003490096
1.0003486257
1.0003482416
1.0003478573
1.0003385882
1.0003382115
1.0003378347
1.0003374577
1.0003370807
1.0003367034
1.0003363261
1.0003359486
1.0003355710
1.0003351933
1.0003259744
1.0003256042
1.0003252338
1.0003248633
1.0003244927
1.0003241219
1.0003237510
1.0003233800
1.0003230089
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
261551.427
261611.658
261671.926
261732.229
261792.570
261852.947
261913.361
261973.811
262034.297
262094.820
263650.035
263709.735
263769.471
263829.243
263889.052
263948.896
264008.777
264068.694
264128.648
264188.637
265748.628
265807.797
265867.002
265926.242
265985.518
266044.831
266104.179
266163.563
266222.983
266282.439
267847.207
267905.844
267964.517
268023.226
268081.971
268140.751
268199.566
268258.418
268317.304
6354853.556
6352365.426
6349877.288
6347389.143
6344900.991
6342412.832
6339924.665
6337436.491
6334948.310
6332460.122
6354904.119
6352416.006
6349927.886
6347439.759
6344951.625
6342463.483
6339975.334
6337487.178
6334999.014
6332510.843
6354954.233
6352466.138
6349978.036
6347489.926
6345001.809
6342513.685
6340025.554
6337537.415
6335049.269
6332561.115
6355003.900
6352515.823
6350027.738
6347539.645
6345051.546
6342563.439
6340075.325
6337587.203
6335099.075
1.0003010732
1.0003007157
1.0003003580
1.0003000002
1.0002996423
1.0002992843
1.0002989261
1.0002985679
1.0002982095
1.0002978509
1.0002887858
1.0002884345
1.0002880831
1.0002877316
1.0002873800
1.0002870282
1.0002866763
1.0002863243
1.0002859722
1.0002856200
1.0002766070
1.0002762620
1.0002759168
1.0002755715
1.0002752261
1.0002748806
1.0002745350
1.0002741892
1.0002738433
1.0002734973
1.0002645371
1.0002641982
1.0002638592
1.0002635201
1.0002631808
1.0002628415
1.0002625020
1.0002621624
1.0002618227
40 257907.143 6332357.332 1.0003226376
90
268376.227 6332610.938 1.0002614829
Continúa en página siguiente
190
ID
Este
Norte
Def Escala
ID
Este
Norte
Def Escala
41
42
43
44
45
46
47
48
49
259452.804
259513.566
259574.365
259635.201
259696.073
259756.983
259817.929
259878.912
259939.932
6354802.546
6352314.398
6349826.242
6347338.079
6344849.909
6342361.732
6339873.548
6337385.356
6334897.158
1.0003134695
1.0003131056
1.0003127416
1.0003123775
1.0003120132
1.0003116489
1.0003112844
1.0003109197
1.0003105550
91
92
93
94
95
96
97
98
99
269945.770
270003.877
270062.019
270120.196
270178.408
270236.656
270294.939
270353.257
270411.611
6355053.119
6352565.059
6350076.991
6347588.916
6345100.834
6342612.744
6340124.647
6337636.543
6335148.431
1.0002525759
1.0002522431
1.0002519102
1.0002515772
1.0002512440
1.0002509108
1.0002505774
1.0002502440
1.0002499104
50 260000.989 6332408.952 1.0003101901 100 270470.000 6332660.312 1.0002495767
191
ANEXO Nº5
DETERMINACIÓN DE ARCOS GEODÉSICOS Y PROYECTADOS
192
Proyección GK1
Arco Meridiano Arco Meridiano
Arco Paralelo
Arco Paralelo
Proyección Columna Proyectado (m) Geodésico (m) Diferencia (m) Fila Proyectado (m) Geodésico (m) Diferencia (m)
GK1
a
22394.376
22393.320
-1.056
1
18888.029
18887.382
-0.647
b
22394.304
22393.320
-0.984
2
18883.264
18882.616
-0.648
c
22394.239
22393.320
-0.919
3
18878.494
18877.847
-0.647
d
22394.171
22393.320
-0.851
4
18873.719
18873.075
-0.644
e
22394.107
22393.320
-0.787
5
18868.947
18868.300
-0.647
f
22394.050
22393.320
-0.730
6
18864.168
18863.522
-0.646
g
22393.989
22393.320
-0.669
7
18859.387
18858.741
-0.646
h
22393.935
22393.320
-0.615
8
18854.601
18853.957
-0.644
i
22393.881
22393.320
-0.561
9
18849.815
18849.170
-0.645
j
22393.827
22393.320
-0.507
10
18845.025
18844.381
-0.644
Arco Paralelo
Arco Paralelo
Proyección GK2
Arco Meridiano Arco Meridiano
Proyección Columna Proyectado (m) Geodésico (m) Diferencia (m) Fila Proyectado (m) Geodésico (m) Diferencia (m)
GK2
a
22399.976
22393.320
-6.656
1
18892.354
18887.382
-4.972
b
22399.797
22393.320
-6.477
2
18887.584
18882.616
-4.968
c
22399.621
22393.320
-6.301
3
18882.809
18877.847
-4.962
d
22399.447
22393.320
-6.127
4
18878.034
18873.075
-4.959
e
22399.276
22393.320
-5.956
5
18873.255
18868.300
-4.955
f
22399.107
22393.320
-5.787
6
18868.473
18863.522
-4.951
g
22398.942
22393.320
-5.622
7
18863.690
18858.741
-4.949
h
22398.777
22393.320
-5.457
8
18858.902
18853.957
-4.945
i
22398.615
22393.320
-5.295
9
18854.109
18849.170
-4.939
j
22398.457
22393.320
-5.137
10
18849.319
18844.381
-4.938
193
Proyección LTM1
Arco Meridiano Arco Meridiano
Arco Paralelo
Arco Paralelo
Proyección Columna Proyectado (m) Geodésico (m) Diferencia (m) Fila Proyectado (m) Geodésico (m) Diferencia (m)
LTM1
a
22393.269
22393.320
0.051
1
18887.303
18887.382
0.079
b
22393.252
22393.320
0.068
2
18882.537
18882.616
0.079
c
22393.242
22393.320
0.078
3
18877.767
18877.847
0.080
d
22393.233
22393.320
0.087
4
18872.995
18873.075
0.080
e
22393.224
22393.320
0.096
5
18868.219
18868.300
0.081
f
22393.215
22393.320
0.105
6
18863.441
18863.522
0.081
g
22393.206
22393.320
0.114
7
18858.661
18858.741
0.080
h
22393.206
22393.320
0.114
8
18853.877
18853.957
0.080
i
22393.206
22393.320
0.114
9
18849.091
18849.170
0.079
j
22393.215
22393.320
0.105
10
18844.301
18844.381
0.080
Arco Paralelo
Arco Paralelo
Proyección LTM2
Arco Meridiano Arco Meridiano
Proyección Columna Proyectado (m) Geodésico (m) Diferencia (m) Fila Proyectado (m) Geodésico (m) Diferencia (m)
LTM2
a
22394.264
22393.320
-0.944
1
18887.937
18887.382
-0.555
b
22394.196
22393.320
-0.876
2
18883.169
18882.616
-0.553
c
22394.124
22393.320
-0.804
3
18878.399
18877.847
-0.552
d
22394.061
22393.320
-0.741
4
18873.627
18873.075
-0.552
e
22393.998
22393.320
-0.678
5
18868.850
18868.300
-0.550
f
22393.935
22393.320
-0.615
6
18864.071
18863.522
-0.549
g
22393.881
22393.320
-0.561
7
18859.292
18858.741
-0.551
h
22393.822
22393.320
-0.502
8
18854.508
18853.957
-0.551
i
22393.770
22393.320
-0.450
9
18849.721
18849.170
-0.551
j
22393.719
22393.320
-0.399
10
18844.930
18844.381
-0.549
194
Proyección MTM1
Arco Meridiano Arco Meridiano
Arco Paralelo
Arco Paralelo
Proyección Columna Proyectado (m) Geodésico (m) Diferencia (m) Fila Proyectado (m) Geodésico (m) Diferencia (m)
MTM1
a
22392.135
22393.320
1.185
1
18886.140
18887.382
1.242
b
22392.065
22393.320
1.255
2
18881.376
18882.616
1.240
c
22392.000
22393.320
1.320
3
18876.606
18877.847
1.241
d
22391.933
22393.320
1.387
4
18871.834
18873.075
1.241
e
22391.870
22393.320
1.450
5
18867.059
18868.300
1.241
f
22391.811
22393.320
1.509
6
18862.280
18863.522
1.242
g
22391.748
22393.320
1.572
7
18857.499
18858.741
1.242
h
22391.694
22393.320
1.626
8
18852.715
18853.957
1.242
i
22391.640
22393.320
1.680
9
18847.930
18849.170
1.240
j
22391.591
22393.320
1.729
10
18843.139
18844.381
1.242
Arco Paralelo
Arco Paralelo
Proyección MTM2
Arco Meridiano Arco Meridiano
Proyección Columna Proyectado (m) Geodésico (m) Diferencia (m) Fila Proyectado (m) Geodésico (m) Diferencia (m)
MTM2
a
22391.145
22393.320
2.175
1
18885.508
18887.382
1.874
b
22391.127
22393.320
2.193
2
18880.742
18882.616
1.874
c
22391.118
22393.320
2.202
3
18875.974
18877.847
1.873
d
22391.100
22393.320
2.220
4
18871.202
18873.075
1.873
e
22391.091
22393.320
2.229
5
18866.427
18868.300
1.873
f
22391.091
22393.320
2.229
6
18861.649
18863.522
1.873
g
22391.082
22393.320
2.238
7
18856.869
18858.741
1.872
h
22391.082
22393.320
2.238
8
18852.086
18853.957
1.871
i
22391.082
22393.320
2.238
9
18847.300
18849.170
1.870
j
22391.082
22393.320
2.238
10
18842.511
18844.381
1.870
195
Proyección UTM
Arco Meridiano Arco Meridiano
Arco Paralelo
Arco Paralelo
Proyección Columna Proyectado (m) Geodésico (m) Diferencia (m) Fila Proyectado (m) Geodésico (m) Diferencia (m)
UTM
a
22401.432
22393.320
-8.112
1
18893.193
18887.382
-5.811
b
22401.149
22393.320
-7.829
2
18888.416
18882.616
-5.800
c
22400.865
22393.320
-7.545
3
18883.641
18877.847
-5.794
d
22400.583
22393.320
-7.263
4
18878.860
18873.075
-5.785
e
22400.303
22393.320
-6.983
5
18874.076
18868.300
-5.776
f
22400.026
22393.320
-6.706
6
18869.290
18863.522
-5.768
g
22399.752
22393.320
-6.432
7
18864.501
18858.741
-5.760
h
22399.480
22393.320
-6.160
8
18859.710
18853.957
-5.753
i
22399.211
22393.320
-5.891
9
18854.914
18849.170
-5.744
j
22398.943
22393.320
-5.623
10
18850.117
18844.381
-5.736
196
ANEXO Nº6
DIAGRAMA DE FLUJO METODOLOGÍA
197
Determinación área de
estudio
Determinación de
puntos muestrales
Definición de
proyecciones
Proyección de puntos
muestrales
Segmentos lineales y
geodésicos
Determinación de
factores “K”
Coeficiente de
correlación
Determinación de
tolerancias
Escala de
representación según
proyecciones TM
Caso general
Deformación según
diferencia ElipsoidePlano TM
Caso particular
Deformación según
diferencia de factores
“K”
Deformación según
diferencia PTL-plano
TM
198
CAPITULO 11
BIBLIOGRAFÍA
IPGH, Revista Cartográfica Nº70, Proyecciones Cartográficas Conformes, Enero-Junio
2000.
Hosmer G, Geodesy, Segunda edición 1930, ed John Wiley & Sons, Inc, EE.UU, 461pp.
Ministerio de Obras Públicas (MOP), Manual de Carreteras, Volumen II, Ingeniería
básica aspectos geodésicos y topográficos, Santiago, Chile, 2001.
Romero L, Maulén V, Sistema de proyección local transversal de Mercator y uso de
planos topográficos locales aplicados a la ingeniería, Universidad de Santiago, Facultad
de ingeniería, Departamento de ingeniería geográfica, Santiago, Chile, 2001.
Borre, K, Elipsoidal geometry and conformal mapping, Edición revisada, Abril 2003.
Martín Asin F, Geodesia y cartografía matemática, 1990, ed Parainfo, Tercera edición,
Madrid, España.
Blanchut, T, Chrzamowsky, A, Saastamoinen, J, Cartografía y Levantamientos
Urbanos, 1979, ed. Springer-Verlag New York. Inc., New York, EE.UU.
Izaurieta, R, Alcances relativos a la representación conforme del territorio nacional,
racionalización de las operaciones cartográficas, Instituto Profesional de Santiago,
Carrera de Cartografía, Santiago, Chile, 1982.
Rapp, R, Geodesia Geométrica, Volumen I, Servicio Geodésico Interamericano DMAIAGS, departamento de Ciencias Geodésicas, Universidad Estatal de Ohio, EE UU, 1981.
Vanicek, P, Santos, M, Tenzer, R, Hernández-Navarro, A, Algunos aspectos sobre
alturas ortométricas y normales, Revista Cartográfica Nº76-77, Enero-Diciembre 2003.
Spiegel, M, Estadística, 1988, ed Mc Graw-Hill, segunda edición, Madrid, España.
199
Gripp, J, Estudio comparativo de deformaciones en diferentes regiones del sistema
UTM y LTM, Paper profesional, Universidad federal de Vicosa, Departamento de
ingeniería civil, Sector de ingeniería en agrimensura.
Sabber, G, Satellyte Geodesy, Fundations, methods and applications, 2003, Nueva
York, EE.UU.
Zepeda, R, Geodesia Geométrica, Apuntes de clases, 2004, Santiago, Chile.
http://www.posc.org/Epicentre.2_2/DataModel/ExamplesofUsage/eu_cs34h.html
http://www.gpsglobal.com.br/Artigos/sisref.pdf
200