MATEMÁTICAS
Tema 1.- Matemáticas (Sesión 1)
Objetivo: En esta sesión se introducen el conjunto de los números reales y sus
propiedades.
1.1.
Definición de matemáticas
Cuando uno piensa en la palabra matemáticas, piensa que es necesario ser “listo”
para poder entenderlas, sin embargo, no es así. Todos necesitamos entender las
matemáticas, sin ellas la vida es inconcebible. Las matemáticas son necesarias para
construir una casa, para comprar, llevar las cuentas de la casa, comprobar facturas,
dirigir un negocio, asegurar un auto, pedir hipotecas, para viajar, etc. En realidad
convivimos con ellas a diario, las matemáticas son el motor de una civilización
industrializada.
Desde niños aprendemos los números, a contar, a calcular y a medir. Desde ese
momento vemos estas bases como algo elemental, y de esta manera deberían
considerarse todas las matemáticas, desde las básicas hasta las avanzadas. Que
algunas personas tengan más conocimiento de estas que otras, depende de qué tanto
lo requieran en la vida profesional.
Así, la nomenclatura de los números se vuelve más difícil a medida que éstos crecen.
¿Cómo podemos nombrar a los números de modo que al mencionar uno sepamos
cuál es el siguiente? Pero si sabemos que los números continúan indefinidamente, no
podemos inventarnos nuevos nombres eternamente a medida que van aumentado.
1.2. Sistemas numéricos
Para contar es necesario tener un patrón, es decir, un sistema de números. A lo largo
de la historia, la humanidad ha desarrollado diferentes sistemas numéricos, tales como
el sistema binario, el cual es un lenguaje que se utiliza en la informática y tiene base
2 ya que consta de dos elementos (0,1). El sistema hexadecimal, el cual está en
base 16, cuyos elementos que forman esta base son (A, B, C, D, E , F, 0, 1, 2, 3, 4, 5,
6, 7, 8, 9). Otro sistema numérico y quizá el más conocido por nosotros es el sistema
decimal que está en base 10: (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). De este último podemos ver
que sus elementos tienen un orden, la combinación y operaciones entre ellos nos
permiten expresar cantidades pequeñas y grandes.
Entonces, podemos definir un sistema numérico como un conjunto de elementos
que satisfacen dos ecuaciones básicas que son la suma y multiplicación entre sus
elementos. El sistema decimal es la punta del iceberg, ya que sus elementos en
realidad forman parte de otro sistema, conocido como números naturales y estos a
su vez pertenecen a otro conjunto de números llamados números reales. Este último
conjunto en particular contiene todos los números que conocemos y por eso nos
ocupará estudiarlo durante el resto del curso. Así, el conjunto de los números reales
está compuesto por otros conjuntos que se mencionan a continuación.
Sistema de los números naturales
Es el conjunto representado por ℕ = {0,1,2,3,…} que con las operaciones de adición y
multiplicación. Además cumple con las propiedades de asociatividad, conmutación,
distributiva.
Sistema de los números enteros
Es el conjunto denotado por ℤ = {…. -2, -1, 0, 1, 2, 3, …. } que con las operaciones de
adición y multiplicación cumple las mismas propiedades que el sistema de los
números naturales, además la existencia de inversos aditivos.
Sistema de los números racionales
Es el conjunto de los números que tienen la forma a/b y se denotan por ℚ = {a/b, | a, b
∈ ℤ; b ≠ 0} que con las operaciones de adición y multiplicación cumple las mismas
propiedades que el sistema de los números enteros, además la existencia de inversos
multiplicativos. Cualquier número racional se puede representar en forma decimal y
esta representación tiene cifras finitas o infinitas periódicas.
Sistema de los números irracionales
Por otro lado existen números con infinitas cifras decimales no periódicas y además no
se pueden expresar como el cociente de dos enteros, estos números pertenecen a
otro conjunto numérico llamado sistema de los números irracionales.
Sistema de los números reales
Todos estos conjuntos de números forman a un conjunto mayor denominado conjunto
de los números reales y se denotan como ℝ. Así, los reales es el conjunto de
números que puede representarse por expresiones decimales finitas o infinitas
periódicas (racionales) o infinitas no periódicas (irracionales) que junto con las
operaciones de suma y multiplicación ( + , · ), la relación de orden menor que (<), se
denomina el sistema de los números reales. Se denota como (R, +, ·, <) y se simplifica
como ℝ.1
Propiedades algebraicas
Las propiedades algebraicas se basan en las operaciones fundamentales de suma y
multiplicación mostrando las leyes de la aritmética entre los elementos 𝑥 y 𝑦, de ℝ.
A continuación se enuncian:
Sean 𝑎 e 𝑏 dos elementos del conjunto ℝ que se relacionan mediante:
Propiedad 1.- Ley asociativa para la suma
𝑎 + (𝑏 + 𝑐) = ( 𝑎 + 𝑏) + 𝑐,
Propiedad 2.- Existencia de una identidad para la suma
𝑎 + 0 = 0 + 𝑎 = 𝑎.
Propiedad 3.- Existencia de inversos para la suma
𝑎 + (−𝑎) = (−𝑎) + 𝑎 = 0.
Propiedad 4.- Ley conmutativa para la suma
𝑎 + 𝑏 = 𝑏 + 𝑎
Propiedad 5.- Ley asociativa para la multiplicación
𝑎 ∙ (𝑏 ∙ 𝑐) = (𝑎 ∙ 𝑏) ∙ 𝑐
Propiedad 6.- Existencia de una identidad para la multiplicación
𝑎 ∙ 1 = 1 ∙ 𝑎 = 𝑎;
1 ≠ 0.
Propiedad 7.- Existencia de inversos para la multiplicación
1
SOLER FRANCISCO, Fundamentos de Cálculo, Ecoe Ediciones, Bogotá, 2005.
𝑎 ∙ 𝑎−1 = 𝑎−1 ⋅ 𝑎 = 1
para 𝑎 ≠ 0.
Propiedad 8.- Ley conmutativa para la multiplicación
𝑎 ⋅ 𝑏 = 𝑏 ⋅ 𝑎.
Propiedad 9.- Ley distributiva
𝑎 ∙ ( 𝑏 + 𝑐) = 𝑎 ∙ 𝑏 + 𝑎 ∙ 𝑐
Propiedad 16.- Ley de Tricotomía2. Para todo número 𝑎 se cumple una y solo una de
las siguientes igualdades:
a) 𝑎 = 0.
b) 𝑎 pertenece al conjunto ℝ
c) – 𝑎 pertenece al conjunto ℝ
Propiedad 11.- La suma es cerrada. Si 𝑎 y 𝑏 pertenecen a ℝ , entonces 𝑎 + 𝑏
pertenece a ℝ.
Propiedad 12.- La multiplicación es cerrada. Si 𝑎 y 𝑏 pertenecen a ℝ, entonces 𝑎 ∙ 𝑏
pertenece a ℝ.
Orden de los números reales: propiedades:
Las propiedades que se enuncian a continuación hacen referencia al orden de los
números reales. Aquí, mencionamos que es importante considerar las dos nociones
de desigualdad, 𝑎 < 𝑏 (𝑎 es menor que 𝑏) y 𝑎 > 𝑏 (𝑎 es mayor que 𝑏). Los números 𝑎
que satisfacen 𝑎 > 0 se llaman positivos, mientras que los números 𝑥 que satisfacen
𝑎 < 0 se llaman negativos. A continuación se enuncian.
Propiedad 10.- 𝑎 < 𝑏 ⇒ 𝑎 + 𝑐 < 𝑏 + 𝑐
Propiedad 11.- 𝑎 < 𝑏 ⇒ 𝑎 − 𝑐 < 𝑏 − 𝑐
Propiedad 12.- 𝑎 < 𝑏 y 𝑐 > 0 ⇒ 𝑎𝑐 < 𝑏𝑐
2
SPIVAK MICHAEL, Cálculo Infinitesimal, Editorial Reverté, México, 1996.
Propiedad 13.- 𝑎 < 𝑏 y 𝑐 < 0 ⇒ 𝑏𝑐 < 𝑎, un caso especial ocurre cuando 𝑎 < 𝑏 ⇒ −𝑏 <
−𝑎
Propiedad 14.- 𝑎 > 0 ⇒
1
𝑎
>0
Propiedad 15.- Si tanto 𝑎 como 𝑏 son ambos positivos o ambos negativos, entonces
𝑎<𝑏 ⇒
1 1
<
𝑏 𝑎
Donde el símbolo ⇒ significa “implica que”.
Estas propiedades deben complementarse con las definiciones:
𝑎 > 𝑦 si 𝑎 − 𝑏 pertenece a ℝ
𝑎 < 𝑏 si 𝑏 > 𝑎
𝑎 ≥ 𝑦 si 𝑎 > 𝑏 o 𝑎 = 𝑏
𝑎 ≤ 𝑏 si 𝑎 < 𝑏 o 𝑎 = 𝑏
Al momento de realizar operaciones con desigualdades tengamos en cuenta las
operaciones de multiplicar y dividir por un número positivo o negativo, ya que el
sentido de la desigualdad puede cambiar. Esto es:
1.- Si se multiplica la desigualdad por un número positivo, el sentido de la desigualdad
de conserva.
2.- Si se multiplica por un número negativo, el sentido de la desigualdad se invierte.
3.- La operación de tomar recíprocos invierte el sentido de la desigualdad cuando los
números son del mismo signo.
De todas las propiedades mencionadas anteriormente se deben deducirse las reglas
usuales que rigen las operaciones con desigualdades.
En cuanto a la propiedad de completez de los números reales, afirma que el conjunto
de los números reales ℝ contiene elementos suficientes para completar la recta real ,
en el sentido de que no hay huecos en ella. Esta propiedad puede sonar trivial pero es
fundamental en el concepto de límite.
Representación geométrica de los números reales
Geométricamente, la representación de los números reales se hace usualmente por
medio de los puntos de una recta; se elige un punto para representar el cero y otro,
que e coloca a la derecha del cero, será el número 1. Este orden determina la escala y
a cada número real corresponde uno y sólo un punto de la recta, y recíprocamente, a
cada punto de la recta le corresponde un número real y sólo uno. Por esta razón, la
recta se denomina recta real. Esta recta da una idea del orden que deberán tomar los
números reales. Así, el cero es localizado al centro de la recta, mientras que los
números positivos (> 0) son a la derecha del cero y los negativos (< 0) a la izquierda
del cero.
Figura 1 Imagen que muestra la representación gráfica de los números reales en la
recta real.
En la Figura 1 se muestra el orden que siguen los números reales. Si 1 > 2, el número
1 se encuentra localizado a la izquierda del 2. Ahora, si 𝑎 < 𝑏, un punto 𝑥 satisface las
desigualdades 𝑎 < 𝑥 < 𝑏 si, y sólo si, 𝑥 está entre 𝑎 y 𝑏. El conjunto de todos los
puntos comprendidos entre 𝑎 y 𝑏 se denominan. Los intervalos pueden ser abiertos,
cerrados, semi-abiertos o semi-cerrados.
Definición3: Supongamos 𝑎 < 𝑏. El intervalo abierto (𝑎, 𝑏) se define por
(𝑎, 𝑏) = {𝑥: 𝑎 < 𝑥 < 𝑏}.
El intervalo cerrado [𝑎, 𝑏] es el conjunto {𝑥: 𝑎 ≤ 𝑥 ≤ 𝑏}.
Sin embargo hay intervalos que pueden solo incluir uno de los extremos, Estos
intervalos se separan según sea el extremo izquierdo o el extremo derecho:
Intervalo semiabierto por la derecha: Este intervalo no contiene el extremo de la
derecha y se representa por [𝑎, 𝑏) y se definen utilizando las desigualdades 𝑎 ≤ 𝑥 < 𝑏.
Intervalo semiabierto por la izquierda: este intervalo no contiene el extremo de la
izquierda y se representa por (𝑎, 𝑏] y se definen mediante la desigualdad 𝑎 < 𝑥 ≤ 𝑏.
Los intervalos mencionados arriba, corresponden a segmentos de la recta real. Sin
embargo pueden considerarse intervalos en los que uno de sus extremos es el ±∞.
Estos intervalos se conocen como intervalos infinitos o semirectas y se definen como:
3
APOSTOL T.M, Análisis Matemático, Editorial Reverté, Barcelona 1976.
(𝑎, +∞) = {𝑥: 𝑥 > 𝑎},
[𝑎, + ∞) = {𝑥: 𝑥 ≥ 𝑎}
(−∞, 𝑎) = {𝑥: 𝑥 < 𝑎}
(∞, 𝑎] = {𝑥: 𝑥 ≤ 𝑎}
donde la notación ( : ) significa “tal que”. Siguiendo esta notación, el intervalo de los
reales ℝ se denota como (−∞, +∞).
Se pueden realizar operaciones con los intervalos, estos pueden unirse o
intersectarse. La unión de dos intervalos (𝑎, 𝑏) y (𝑐, 𝑑) es el conjunto formado por los
elementos que pertenecen a uno o a otro intervalo. Esta operación se representa
como
(𝑎, 𝑏) ∪ (𝑐, 𝑑)
Ejemplo : (1, 9) ∪ (6, 10) = (1, 10)
Figura 2.- En la figura se muestran dos intervalos abiertos.
La intersección de dos intervalos (𝑎, 𝑏) y (𝑐, 𝑑) es el conjunto formado por los
elementos que pertenecen a la vez a uno y otro intervalo. Esta operación se
representa como (𝑎, 𝑏) ∩ (𝑐, 𝑑).
Ejemplo: (1, 9) ∩ (6, 10) = (6, 9)
Cuando los intervalos no tienen elementos comunes su intersección es el conjunto
vacío (∅).
1.2.1
Desigualdades lineales y sus propiedades
Al proceso de encontrar el intervalo o intervalos de números que satisfacen una
desigualdad en 𝑥 se llama resolver la desigualdad. Existen diferentes tipos de
desigualdades, dependiendo del exponente de la variable para la que se buscan los
valores. Las hay lineales, cuadráticas, cúbicas etc. Pero aquí solo mencionaremos
lineales y cuadráticas. A continuación mostramos cómo resolver para los intervalos de
dichas desigualdades.
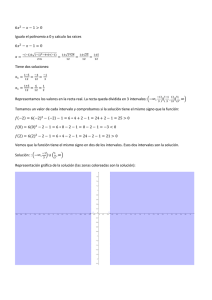
Resolver la desigualdad:
1.-
6
𝑥−1
≥5
a) El objetivo es despejar a la variable 𝑥.
b) Analizamos ambos términos de la desigualdad y vemos que, en el término
derecho tenemos el número real 5 positivo, mientras que en el término
6
izquierdo tenemos el cociente 𝑥−1 , el cual debe 𝑥 ≠ 1 para que la desigualdad
no esté indefinida. Además de que esta desigualdad sólo puede satisfacerse si
(𝑥 − 1) > 1, esto es, para 𝑥 > 1, (valores positivos de x) y el intervalo (1, ∞).
1
c) Para resolver, multiplicamos ambos términos por 𝑥−1, y se obtiene
6 ≥ 5(𝑥 − 1)
y el sentido de la desigualdad no se invierte por que hemos multiplicado por un
número positivo (𝑥 − 1) > 1.
d) Despejamos a la variable 𝑥, y se obtiene
6 + 5 ≥ 5𝑥 ⇒
11
≥𝑥
5
e) Ahora, encontremos el intervalo para 𝑥
que se expresa como la intersección entre los intervalos de: la condición
inicial de 𝑥 > 1 y
11
5
≥ 𝑥. Así 𝑥 ∈ (1, ∞) ∩ (−∞,
11
]
5
= (1,
11
]
5
que es la zona azul
de la figura anterior.
1.1 Valor absoluto y sus propiedades
Si x es un número real, el valor absoluto |x| de 𝑥 se define como sigue:
𝑥,
|𝑥| = {
−𝑥,
si 𝑥 ≥ 0,
si 𝑥 < 0.
Notemos que |𝑥| es siempre positivo excepto para 𝑥 = 0. Además
|𝑥| = √𝑥 2
donde el símbolo √𝑥 denota siempre la raíz cuadrada positiva de 𝑥.
El valor absoluto tiene las propiedades siguientes.
1.-Un número real 𝑎 y su inverso aditivo o negativo – 𝑎 tienen el mismo valor absoluto.
|−𝑎| = |𝑎|
2.- El valor absoluto de un producto es el producto de sus valores absolutos.
|𝑎𝑏| = |𝑎||𝑏|
3.- El valor absoluto de un cociente es el cociente de los valores absolutos.
|𝑎|
𝑎
| |=
|𝑏|
𝑏
4.- La desigualdad del triángulo. El valor absoluto de la suma de dos números es
menor o igual que la suma de sus valores absolutos.
|𝑎 + 𝑏| ≤ |𝑎| + |𝑏|
A continuación mencionamos un teorema importante sobre valor absoluto.
Cuando se realizan operaciones con valor absoluto, en particular desigualdades, es
importante considerar los intervalos de la recta real. Por eso, a continuación
mencionamos:
Es interesante mencionar sobre valores absolutos y los intervalos. Para esto
consideremos las siguientes propiedades para un número real4,
1.- |𝑥| = 𝑎 si y sólo si 𝑥 ≠ ±𝑎
2.- |𝑥| < 𝑎 si y sólo si − 𝑎 < 𝑥 < 𝑎
3.- |𝑥| > 𝑎 si y sólo si 𝑥 > 𝑎 o 𝑥 < −𝑎
4.- |𝑥| ≤ 𝑎 si y sólo si − 𝑎 ≤ 𝑥 ≤ 𝑎
5.- |𝑥| ≥ 𝑎 si y sólo si 𝑥 ≥ 𝑎 o 𝑥 ≤ −𝑎
Resolvamos ahora una desigualdad con valor absoluto.
1.- |2𝑥 − 3| ≥ 1
Debido a que es una desigualdad de valor absoluto, este puede tomar dos valores
2𝑥 − 3 ≥ 1
o
2𝑥 − 3 ≥ −1
a) Resolvemos el primer caso (positivo)
4
THOMAS BRINTON, Cálculo: una variable. Editorial Pearson Addison Wesley
𝑥≥2
donde 𝑥 está en el intervalo de la recta real 𝑥 ∈ [2, +∞).
b) Resolvemos el segundo caso (negativo)
𝑥≤1
donde x está en el intervalo de la recta real 𝑥 ∈ (−∞, 1].
c) El resultado es la unión de los intervalos de los dos casos.
Esto es 𝑥 ∈ (−∞, 1] ∪ [2, +∞).
Hasta aquí hemos mencionado las propiedades fundamentales que rigen a los
números reales.
Actividades complementarias:
Descomponer el siguiente número en base 10
100005089
NOTA: La siguiente actividad es de carácter voluntario para reforzar lo aprendido en
esta lección; por lo que no tiene ningún porcentaje en la evaluación.
BIBLIOGRAFÍA
SOLER FRANCISCO, Fundamentos de Cálculo, Ecoe Ediciones, Bogotá, 2005.
SPIVAK MICHAEL, Cálculo Infinitesimal, Editorial Reverté, México, 1996.
APOSTOL T.M, Análisis Matemático, Editorial Reverté, Barcelona 1976
THOMAS BRINTON, Cálculo: una variable. Editorial Pearson Addison Wesley