EJERCICIO 5 JOAQUIN ALFORJA RUIZ

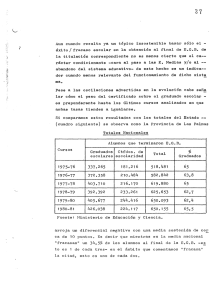
JOAQUÍN ALFORJA RUIZ
ADE Y DERECHO
TEMA 9: EJERCICIO NÚMERO 5
En una región, se pretende determinar la intencionalidad de continuar los estudios entre los
graduados universitarios que han finalizados sus estudios entre los años 2017-2019. Según
una prueba piloto a 30 de estos graduados, el 40% tenían intención de proseguir sus estudios.
En este momento se pretende realizar un estudio concluyente con una fiabilidad del 95% y un
nivel de error del 5%. Se pide:
a. Calcular el tamaño de la muestra necesario para realizar un muestreo probabilístico si
la población la forman 5000 graduados.
Población finita = 5.000 graduados
E= 5%
Nivel de confianza: 95% (z=1,96)
Dispersión poblacional: P = 40% ; 1-P = 60%
n = Z2*N*P*(1-P) / e2*(N-1) + Z2*P*(1-P) = 1,962 * 5.000*40*60 / 52*4.999 + 1.962*40*60 =
46.099.200 / 134.194,84 = 343,524  344 personas
b. b. También es importante considerar la influencia del año de finalización de los
estudios de grado en los resultados del estudio. Por ello, se decide utilizar un muestreo
estratificados según este criterio. Si el 50% de los graduados que conforman la
población lo hicieron en 2017, el 30% lo hicieron en 2018 y el 20% en 2019, ¿cuántas
encuestas habría que realizar en cada uno de los estratos poblacionales si
consideramos el número total de encuestas calculado en el punto a?
Grupo 2017: 0.5 * 344 = 172 encuestas
Grupo 2018: 0.3 * 344 = 103 encuestas
Grupo 2019: 0.2 * 344 = 69 encuestas
Por otro lado, se desea conocer:
c. Si se redujera el tamaño de la muestra resultante en el punto “a” en un 25%, ¿cuál
sería el nivel de error de muestreo que se cometería en el diseño del Plan de
muestreo? (los otros condicionantes del cálculo del tamaño de la muestra
permanecerían igual que en el contexto inicial)
Para calcular esto deberíamos realizar la siguiente operación:
n – 0.25*n = Z2*N*P*(1-P) / e2*(N-1) + Z2*P*(1-P)
344 – 86 = Z2*5000*40*60/ e2*(4999) + Z2*40*60
258 = Z2*12.000.000 / e2*4999 + 2.400*Z2
No he sabido como despejar la ecuación, pero he ido probando valores y el error debería ser
alrededor de un 10%
JOAQUÍN ALFORJA RUIZ
ADE Y DERECHO
d. Si se aumentase el nivel de confianza hasta el 99%, ¿cuál sería ahora el tamaño de la
muestra?
Población finita = 5.000 graduados
E= 5%
Nivel de confianza: 99% (z=2,575)
Dispersión poblacional: P = 40% ; 1-P = 60%
n = Z2*N*P*(1-P) / e2*(N-1) + Z2*P*(1-P) = 2,5752 * 5.000*40*60 / 12*4.999 + 2,5752*40*60 =
79.567.500 / 20912.5 = 3804.782  3805 personas
e. Y si la población fuera infinita, ¿cuál sería ahora el tamaño de la muestra?
n = Z2 * P * (1-P) / e2 = 1,962 * 60 * 40 / 52 = 9.219,84 / 25 = 368,7936  369 personas
n = Z2 * P * (1-P) / e2 = 2,5752 * 60 *40 / 12 = 15.913,5  15914 personas