clase2

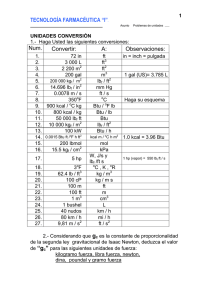
UNIVERSIDAD NACIONAL DE INGENIERIA
FACULTAD DE INGIENIERIA QUIMICA Y TEXTIL
BALANCE DE MATERIA Y ENERGIA
PI-111B
CLASE 2
ING. MBA MARIO R. DE LA CRUZ AZABACHE
Marzo 2018
DIMENSIONES Y CANTIDADES FÍSICAS
DIMENSIÓNEs una descripción puramente
cualitativa de una percepción sensorial; que
proviene de una entidad física o una apariencia
natural.
Por ejemplo, la longitud puede experimentarse como
altura, ancho o profundidad, la masa se presenta así
misma como un cuerpo liviano o pesado. El tiempo
como un momento corto o un periodo largo.
La dimensión de la longitud es Longitud (L), de
una masa es Masa (M) y así sucesivamente.
Cada concepto físico; puede asociarse con una
cantidad y a ésta a su vez se le puede asignar
una dimensión.
Puede suceder que diferentes conceptos físicos
tengan la misma dimensión. Por ejemplo; la
difusividad (D; m2/seg), la difusividad térmica (a;
m2/seg) y la viscosidad cinemática (u; m2/seg)
tienen la misma dimensión [L2T-1]
CANTIDAD FÍSICA- Representa una descripción
cuantitativa de una cualidad física. cualidad
física(dimensión). A través de un valor numérico y
una unidad de medida se describe una dimensión
Cantidad Física = Valor numérico x unidad de medida
Por ejemplo:
-Una masa de 5 kilos
masa = 5 kg
m = 5 kg
m [M] = 5 kg
-Una masa de 20 libras
masa = 20 lb
m = 20 lb
m [M] = 20 lb
- Una longitud de 20 metros
longitud = 20 m
l = 20 m
l [L] = 20 m
- Una longitud de 20 pies
longitud = 20 ft
l = 20 ft
l [L] = 20 ft
- Una cantidad de energía de 2000 kg.m 2.s-2
energía = 2 000 kg.m2.s-2
[ML2T-2] = 2 000 joules = 2 000 J
UNIDAD DE
MEDIDA
Temperatura de reacción = 200 ºC
DIMENSIÓN O
CANTIDAD FÍSICA
VALOR NUMÉRICO
UNIDAD DE MEDIDA- Medio como expresar las dimensiones
o cantidades físicas.
VALOR NUMÉRICO.- Cantidad con la que se expresa una
dimensión o cantidad física.
-Los valores numéricos pueden sumarse o restarse
siempre y cuando tengan la misma unidad:
masa:
5 kg + 10 kg = 15 kg
-Los valores numéricos y
sus unidades pueden
combinarse al multiplicar o dividir:
Fuerza = masa x aceleración
= (200 gr ) x (10 cm/s2)
= 2 000 gr.cm/s2
= 2000 dinas
CANTIDADES FÍSICAS
BÁSICAS Y DERIVADAS
CANTIDAD FÍSICA BÁSICA O PRIMARIA- Se basan en
valores estándar y se cuantifican en comparación con éstos.
CANTIDAD DERIVADA O SECUNDARIA- Se derivan de
las cantidades primarias, a través de leyes físicas.
Por ejemplo:
velocidad = longitud/tiempo
[v] = [L/T]
Unidades de medida coherentes: m/s
Relacionados a cantidades básicas
CONVERSIÓN DE UNIDADES
FACTOR DE CONVERSION.- relación adimensional, entre
dos expresiones que expresan la misma cantidad. En
términos absolutos es igual a 1.
100 cm = 1
1m
1000 mg
=1
1g
10 hr
=1
600min
ECUACION DIMENSIONAL
Relación que transforma una cantidad con
unidades compuestas a su equivalente en
otro conjunto de unidades utilizando
factores de conversión.
Problema .Empleando ecuaciones dimensionales transformar:
a)
b)
c)
d)
Tres semanas a milisegundos
38.1 ft/s a milla/hora
554 m4/(día.kg) a cm4/(min.g)
5.37 x 103 kJ/min a hp
Problema.- Utilice una sola ecuación dimensional para
calcular el número de pelotas de golf que necesitaría para
llenar su salón de clases. Asuma que el diámetro de la pelota
de golf es 2¨ y que el aula tiene las dimensiones 40 ft x 20ft x
15 ft.
SISTEMA DE UNIDADES
Conjuntos de unidades homogéneas, que tienen los
siguientes componentes:
UNIDADES FUNDAMENTALES.- (masa, longitud, tiempo,
temperatura, etc): ejemplo metro para longitud.
UNIDADES MÚLTIPLOS.- múltiplos o fracciones de
unidades fundamentales. Ej. Centímetro como fracción del
metro; m.
UNIDADES DERIVADAS.- generadas al multiplicar o dividir
unidades; cm2, ft/min, kg.m/s2
O como valores equivalentes definidos de unidades
compuestas: ergio = erg = 1g.cm2/s2
SISTEMA COMUNES DE UNIDADES
longitud
tiempo
masa
1. Cgs
centímetro segundo
gramo
2. Fps
pie
segundo
libra
3. SI
metro
segundo
kilogramo
pie
segundo
slug
pie
segundo
libra masa
4. Británico
de Ingeniería
5. Americano de
Ingeniería
hora
SISTEMA COMUNES DE UNIDADES
temperat.
fuerza
energía
1. Cgs
K , ºC
dina
erg, joule
2. Fps
ºR, ºF
poundal
caloría
3. SI
K, ºC
newton
joule
4. Británico Ingeniería
ºR, ºF
libra peso
Btu
5. Americano Ingeniería
ºR, ºF
libra fuerza
Btu
PROBLEMA 2.2.- Convertir 20 gal/h a m3/s
PROBLEMA 2.3 .- Una corriente de acetona
líquida fluye en una razón de 236 gal/min.
Expresar el flujo en kmol/h
PM acetona: 58.08
P.E. acetona: 0.791
PRINCIPIO FUNDAMENTAL DEL
ANALISIS DIMENSIONAL
El análisis dimensional se fundamenta;
en el reconocimiento de que la fórmula
matemática de un problema tecnológico de
naturaleza química o física, puede ser
generalmente
valida
sólo
si
es
dimensionalmente homogénea. Esto es; si
es válida en cualquier sistema de
dimensiones.
FERMENTACION UVA QUEBRANTA
EN FUNCION A TIEMPO DE COSECHA
FUNDO LA CARAVEDO-ICA PERU 2007-2008
1.11
1.09
DENSIDAD, gr/cc
1.07
1.05
1.03
1.01
0.99
0.97
0.95
0.0
2.0
4.0
6.0
8.0
10.0
12.0
TIEMPO, Días
02-Mar
11-Mar
23-Mar
02-Abr
03-Abr-08
GRADO ALCOHOLICO DE CORTE, ºGL
DESTILACION DE MOSTO
FERMENTADO
GRADO ALCOHOLICO VS CORTE
90
80
70
60
50
40
30
20
10
0
0
20
40
60
80
CORTE, %
M1
M2
M3
M4
100
HOMOGENEIDAD DIMENSIONAL Y
CANTIDADES ADIMENSIONALES
HOMOGENEIDAD DIMENSIONAL: Todos los términos
que se suman en ambos lados de una ecuación TIENEN
LAS MISMAS dimensiones. Ej.
U (m/s) = U0 (m/s) + g (m/s2) t (s)
CANTIDAD ADIMENSIONAL: Que carece de dimensiones.
Ej.
C= M(g)/M0(g)
HOMOGENEIDAD DIMENSIONAL Y
CANTIDADES ADIMENSIONALES
Son también cantidades adimensionales
- Los exponentes, como 3 en X3.
- Las funciones trascendentes como log, ln y exp
- Los argumentos de éstas funciones como Y en cos Y
GRUPO ADIMENSIONAL Conjunto de unidades que
derivan en una cantidad adimensional. Ej.
Número de Reynolds Nre = D u r / u
PROBLEMA.- Cierta concentración C(mol/L) varía con
el tiempo (min) según la ecuación:
C= 3.0 exp (-2.00t)
¿Cuáles son las unidades de 3.00 y 2.00?
PROBLEMA 4 (Sección 1.1 Himmelblau).- Un medidor
de orificio se usa para medir el régimen de flujo en
tubos. El régimen de flujo se relaciona con la caída de
presión mediante una ecuación de forma:
u=C
P
r
u : velocidad del fluido
P : caída de presión
r : densidad del fluido
C :constante de proporcionalidad.
¿Cuáles son las unidades de C en el sistema SI?
¡ADIMENSIONAL!
PROBLEMA 2.26.- La densidad de un fluido se obtiene mediante la siguiente
ecuación empírica :
r = 70.5 exp (8.27 x 10
donde
r
–7
P)
es la densidad ( en lbm/f t3) y P es la presión ( en lbf/in2)
a) ¿Cuáles son las unidades de 70.5 y 8.27 x 10 –7 ?
b) Calcule la densidad en g/cm3 para una presión de 9.0 x 106 N/m2
c) Derive una fórmula para r ( en g/cm3) en función de P( en N/m2)
MASA, FUERZA, PESO, g y gc
Segunda ley del movimiento de Newton: La fuerza es
proporcional al producto de la masa por la aceleración
F= C ma
Constante de proporcionalidad
En el sistema Cgs, la fuerza se expresa en dina que es la
fuerza que causa que una masa de 1 gramo acelere a 1
cm/s2
1 dina = C x 1gr x 1cm/s2
C = dina/(gr.cm/s2)
En el sistema SI, el Newton (N) es la fuerza que causa que
una masa de 1 kilogramo acelere 1 m/s2
1 N = C x 1kg x 1m/s2
C = N/ kg x 1m/s2
En el Sistema Americano de Ingeniería, la libra fuerza, lbf
es la fuerza (de la gravedad) que causa que una masa de 1
libra masa acelere a 32.174 ft/s2; al nivel del mar y 45º de
latitud (valor estándar).
1 lbf = C x 1 lbm x 32.174 ft/s2
Donde:
C = ( lbf / lbm )/ 32.174 ft/s2
Por convención:
gc= 1/C
Por tanto:
gc = 32.174(1 lbm/ lbf )(1ft/s2)
PESO
Es la fuerza que ejerce la gravedad sobre una determinada
masa, dándole una aceleración que varía según el lugar y
que se denominada aceleración de la gravedad.
El valor estándar de la aceleración de la gravedad; g;
en la tierra es:
- Sistema Cgs
- Sistema SI
- Sistema Americano
de Ingeniería
: 980.66 cm/s2
: 9.8066 m/s2
: 32.174 ft/s2
PROBLEMA.- ¿Cuál es el peso o la fuerza de gravedad
en lbf sobre un objeto que tiene una masa de 1 lbm en un
lugar donde la aceleración de la gravedad es 32 ft/s2.
F= (1/gc) ma = (1/gc) m.
F=
1
32.174 (lbm/lbf) x ft/s2
F= 1,194 lbf
1,0 lbm x 32 ft/s2
PROBLEMA.- ¿Cuál es el peso o la fuerza de gravedad
en lbf sobre un objeto que tiene una masa de 1 lbm en un
lugar donde la aceleración de la gravedad es 32,174 ft/s2.
F= (1/gc) ma = (1/gc) m.
F=
1
32,174 (lbm/lbf) x ft/s2
F= 1,0 lbf
1,0 lbm x 32,174 ft/s2
ESTEQUIOMETRÍA Y RELACIONES DE COMPOSICIÓN
La
estequiometría
considera
las
relaciones de masas y volumétricas de
gas en las reacciones químicas .
RELACIONES DE MASA

En las reacciones químicas es
fundamental conocer las relaciones
de masa que existen entre los
reactivos y productos.
Reglas a tener en cuenta:
1.- La ecuación debe estar bien escrita
Ca(OH)2 + Cl2
Ca(OCl)2 + CaCl2 +H20
¿Está correctamente escrita?
Forma correcta
2 Ca(OH)2 + 2 Cl2
Ca(OCl)2 +CaCl2 + 2 H20
2. Cerciorarse de los pesos atómicos de cada
elemento que interviene en la reacción y determinar los
pesos moleculares. ¿Exactitud?
Pesos atómicos
Calcio, Ca
: 40.08
40.0
Oxígeno, O
: 15.9994
16.0
Hidrógeno, H
:1.0079
1.0
Cloro, Cl
: 35.453
35.5
2 Ca(OH)2 + 2 Cl2
Ca(OCl)2 +CaCl2 + 2 H20
Pesos Moleculares
Hidróxido de calcio; Ca(OH)2
: 74.0946
74.0
Cloro; Cl2
: 70.906
71.0
Cloruro de calcio; CaCl2
: 110.986
111.0
Agua; H20
: 18.0152
18.0
Hipoclorito de calcio;Ca(OCl)2
: 142.9848
143.0
3. Calcular los pesos relativos de los reactivos y productos
multiplicando los pesos moleculares o atómicos por los
coeficientes de la reacción.
2 Ca(OH)2 +
(2 x 74.0946)
(18.0152)
148.1892
2 Cl2
(2 x 70.906)
141.812
Reactantes: 290.0012
Ca(OCl)2 + CaCl2 +
(1 x142.9848)
142.9848
(1 x 110.986)
110.986
2 H20
2x
36.0304
Productos: 290.0012
¿ Cuantos kilos de hidróxido de
calcio y de cloro gaseoso se
requiere para producir 2,000 libras
de hipoclorito de calcio?
¿Cuántos kilos de un material que
contiene 74 % en peso de hidróxido
de calcio; se requerirá para
producir 2 TM de cloruro de calcio?
RELACIONES DE VOLUMEN
Una ecuación de reacción correctamente escrita, deberá
indicar también los volúmenes relativos de los reactivos y
productos que se encuentran en estado gaseoso. Por
ejemplo.
3 Fe + 4 H2O(v)
Fe3O4 + 4H2 (g)
A una misma presión y temperatura, 4 volúmenes de
vapor de agua producirán 4 volúmenes de hidrógeno.
Por otro lado, en una mezcla
comportamiento ideal se cumple:
H2O
H2
O2
N2
%
Volumen
%
molar
21.0
15.0
52.0
12.0
100.0
21.0
15.0
52.0
12.0
100.0
gaseosa;
con