Resumen tema 1. La ciencia y su método. Medida de magnitudes.

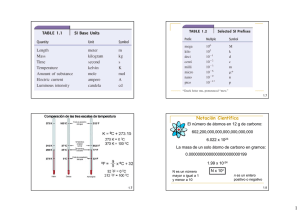
Resumen tema 1. La ciencia y su método.
Medida de magnitudes.
1. Las magnitudes físicas y sus unidades
En 1789 en parís se estableció el metro comunidad de longitud. Se longitud quedó
fijada en la diezmillonésima parte del cuadrante del meridiano terrestre que pasa
por parís. También estableció el gramo, la masa de un centímetro cúbico de agua,
como unidad de masa.
En 1889 se adoptó el sistema métrico decimal, que establecía el metro como
unidad de longitud, el kilogramo como unidad de masa y el segundo como unidad
de tiempo.



El metro es la diezmillonésima parte de un cuadrante del meridiano terrestre.
El kilogramo es la masa de un cilindro patrón de platino-iridio conservado en
Francia.
El segundo es la 1/86400 parte del día solar medio
En 1960 se acordó el sistema internacional de medidas (S. I) este sistema mantuvo la
definición de kg comunidad de más pero estableció nuevas definiciones más precisas
para el metro y el segundo:


El metro es la longitud recorrida por la luz en el vacío en 1/299.792.458
segundos.
El segundo se define a partir del periodo de una determinada radiación emitida
por el átomo de cesio.
(Poner tablas múltiplos y submúltiplos y tabla del sistema internacional y unidas.)
2. Instrumentos de medida. Sensibilidad y precisión.
Pedir una magnitud física es comparar un Valor de esa magnitud con otra
cantidad de la misma que es elegido como unidad patrón.
 La precisión de un instrumento de medida es el Valor mínimo de la
magnitud que se puede apreciar.
 La sensibilidad y un instrumento es la capacidad para detectar
variaciones de la magnitud a medir.
La incertidumbre de una medida es el máximo error con que viene afectada como
consecuencia de la precisión del instrumento.
En General, suele tomarse como incertidumbre de una medida la precisión del
instrumento. 120 +/- 10 ml.
La notación científica.
En notación científica se escribe la parte entera con una sola cifra, seguida de la parte
decimal y de una potencia de diez, positiva o negativa.
3. Cifras significativas y errores.
Las siguientes reglas permiten determinar cuántas cifras son significativas:




Todas las cifras distintas de cero son significativas.
Los ceros que aparecen a la derecha de la, son significativos.
Los ceros del principio de un número no se consideran cifras significativas.
Los cerros del final de un número sin coma decimal no son significativos
excepto si se indica expresamente con un punto.
Redondeo.
En este caso es importante redondear el resultado siguiendo unas normas sencillas:



Si el primer dígito despreciado es cinco o mayor que cinco la cifra anterior se
aumenta en una unidad.
Si la primera cifra despreciaba es menor que cinco la cifra anterior permanecer
inalterada.
En las operaciones matemáticas:
-Sumas o restas: el resultado no debe tener más cifras decimales que el dato
que menos cifras decimales tenga.
-multiplicaciones o divisiones: el resultado no debe superar en cifras
significativas al dato con menor número de ellas.
Ejemplo:
24,31 x 3,6= 87,516 se redondea a 88 (ya que 3,6 tiene 2 cifras significativas).
Errores experimentales.
Todas las medidas experimentales están afectadas por algún error según su origen los
errores pueden ser:

Errores sistemáticos. Tienen que ver con la forma de realizar la medida. El más
frecuente es el error de calibrado o error de puesta cero. También puede
producirse un error de paralaje cuando un observador mira oblicuamente una
escala analógica.

Errores accidentales o aleatorios. Son aquellos que se producen al azar debido
causas imposibles de controlar. Afortunadamente se distribuyen
estadísticamente en torno a la medida correcta. Para minimizar su efecto se
realiza cada medida varias veces y se toma como Valor más probable la media
aritmética.
Calculo de errores.
El error absoluto Ea, es la diferencia entre el Valor de la medida y el Valor
exacto. Como el Valor exacto se desconoce se toma la media aritmética.
Ejemplo:
Ea =xi-x
El error relativo, Er, es el cociente entre el error absoluto y el Valor exacto.
Er= Ea/x
Si se multiplica por 100 el error relativo, se tiene porcentaje de error.