campo-elc389ctrico

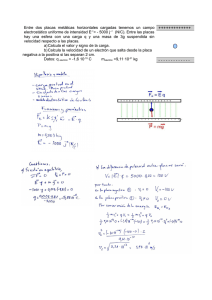
CAMPO ELÉCTRICO.
JUNIO 1997:
1.- Se sitúan tres cargas eléctricas q1, q2 y q3, en los puntos A (0,0,0); B (0,4,0) y C
(0,4,3), respectivamente, donde las coordenadas vienen dadas en metros. Se pide:
a.- Si q1 = 0.1 C, calcular q2 y q3 para que sea nulo el campo eléctrico en el punto P
(0,0,3). q2 = - 0.463 C; q3 = 0.237 C
b.- Si q1 = 0.1 C, q2 = 0.4 C y q3 = 0.2 C, calcular el trabajo necesario para llevar una
carga unitaria desde el infinito hasta el punto P (0,0,3). W = -3*107 J
Dato: 1/4o = 9x109 S.I.
2.- El ciclotrón: fundamentos y aplicaciones.
SEPTIEMBRE 1997:
3.- ¿Es lo mismo el potencial eléctrico que la energía potencial eléctrica? Justifica la
respuesta.
JUNIO 1999:


4.- Sea un campo eléctrico uniforme dado por E  500i N/C. Se pide:
a.- ¿Cómo serán las superficies equipotenciales de dicho campo?
Planos paralelos entre sí, y perpendiculares al eje X.
b.- Calcular el trabajo necesario para trasladar una carga de 2 C desde el punto P
(2,3,0) m hasta el punto Q (6,5,0) m. W =-4.47*10-3 J
c.- Calcular la distancia entre las superficies equipotenciales V1 = 10 V y V2 = 20 V.
0.02 m
SEPTIEMBRE 1999:
5.- Dadas dos cargas puntuales q1=2C y q2=3C, separadas una distancia d=40 cm,
calcular el campo eléctrico en el punto medio del segmento que les une.
Dato: o=8,85x1012 C2N1m2. 1.13*1012 i N/C
JUNIO 2000:
6.- Un dipolo eléctrico está formado por dos cargas puntuales de 2 C y 2 C,
distantes entre sí 6 cm. Calcular el campo y el potencial eléctrico:
a.- En un punto de la mediatriz del segmento que las une, distante 5 cm de cada carga.
E = 8.64*106 i N/C; V = 0 V
b.- En un punto situado en la prolongación del segmento que las une y a 2 cm de la
carga positiva. E = -4.22*107 i N/C; V = 6.75*105 V
Datos: K = 9x109 SI.
SEPTIEMBRE 2001:
7.- Una carga de 3 C está localizada en el origen de coordenadas; una segunda carga
de 4 C está localizada a 20 cm de la primera, sobre el eje OX positivo, y una tercera
carga Q está situada a 32 cm de la primera sobre el eje OX positivo. La fuerza total que
actúa sobre la carga de 4 C es de 120 N en la dirección positiva del eje OX. Determina
el valor de la carga Q. -49.1 μC
Dato: K = 9x109 S.I.
JUNIO 2003:
8.- En el rectángulo mostrado en la figura los lados tienen una longitud de 5 cm y 15
cm, y las cargas son q1 = 5’0C y q2 = +2’0C.
a.- Calcula el módulo, la dirección y el sentido del campo eléctrico en A y B.
EA = (-2, 7.2)*106 N/C EA = 7.47*106 N/C α = 105º31’
EB = (-0.08, 1.8)*107 N/C EB = 1.8*107 N/C α = 92º33’
b.- Calcula el potencial eléctrico en A y B. VA = 6*104 V; VB = -7.8*105 V
c.- Determina el trabajo que realiza la fuerza del campo eléctrico para trasladar a una
tercera carga de + 3C desde A hasta B. W = 2.52 J
Dato: K = 9x109 SI
SEPTIEMBRE 2003:
9.- Dos cargas puntuales de 3C y 5C se hallan situadas, respectivamente, en los
puntos A (1,0) m y B (0,3) m. Se pide:
a.- El modulo, la dirección y el sentido del campo eléctrico en P (4,0) m.
(1.56, 1.08) *103 N/C
b.- Trabajo realizado por la fuerza eléctrica para trasladar una carga de 2 C, desde P a
R (5,3) m. 7.2*10-3 J
10.- Se colocan cuatro cargas puntuales en los vértices de un cuadrado de 1 m de lado.
Calcula el módulo, la dirección y el sentido del campo eléctrico en el centro del
cuadrado, en los siguientes casos:
a.- Las cuatro cargas son iguales y valen 3μC. E = 0
b.- Las cargas situadas en A y B son iguales a 2 μC, y las situadas en C y D son iguales
a - 2 μC. E = (0, -1.02*105) N/C
c.- Las cargas situadas en A, B y C son iguales a 1 μC y la situada en D vale -1μC.
E = (2.54, -2.54)*104 N/C
Dato: K = 9x109 Nm2/C2.
JUNIO 2004:
11.- En un relámpago típico, la diferencia de potencial entre la nube y la tierra es 10 9 V
y la cantidad de carga transferida vale 30 C. ¿Cuánta energía se libera? 3*1010 J
Suponiendo que el campo eléctrico entre la nube y la tierra es uniforme y perpendicular
a la tierra, y que la nube se encuentra a 500 m sobre el suelo, calcula la intensidad del
campo eléctrico. 2*106 N/C
SEPTIEMBRE 2004:
12.- El potencial y el campo eléctrico a cierta distancia de una carga puntual valen 600
V y 200 N/C, respectivamente. ¿Cuál es la distancia a la carga puntual? 3 m
¿Cuál es el valor de la carga? 0.2 μC
JUNIO 2005:
13.- Una partícula con carga q1=106 C se fija en el origen de coordenadas.
a.- ¿Qué trabajo será necesario realizar para colocar una segunda partícula, con carga
108 C, que está inicialmente en el infinito, en un punto P situado en la parte positiva del
eje Y a una distancia de 30 cm del origen de coordenadas? -3*10-4 J
b.- La partícula de carga q2 tiene 2 mg de masa. Esta partícula se deja libre en el punto
P, ¿qué velocidad tendrá cuando se encuentre a 1’5 m de distancia de q1? (suponer
despreciables los efectos gravitatorios). 15.5 m/s
Dato: Ke = 9x109 Nm2/C2.
SEPTIEMBRE 2005:


14.- Disponemos de un campo eléctrico uniforme E  100kN / C .
a.- Indica cómo son las superficies equipotenciales de este campo.
Planos paralelos entre sí y perpendiculares al eje Z.
b.- Calcula el trabajo que realiza el campo eléctrico para llevar una carga q = 5 C
desde el punto P1(1,3,2) m hasta el punto P2 (2,0,4) m. 10-3 J
c.- Si liberamos la carga q en el punto P2 y la única fuerza que actúa es la del campo
eléctrico, ¿en qué dirección y sentido se moverá? Sentido contrario a E.
JUNIO 2006:
15.- ¿Qué relación hay entre el potencial y el campo eléctricos? ¿Cómo se expresa
matemáticamente esa relación en el caso de un campo eléctrico uniforme?
SEPTIEMBRE 2006:
16.- Un modelo eléctrico simple para la molécula de cloruro de sodio consiste en
considerar a los átomos de sodio y cloro como sendas cargas eléctricas puntuales de
valor 1’6x1019 C y 1’6x1019 C respectivamente. Ambas cargas se encuentran
separadas una distancia d=1’2x1010 m. Calcula:
a.- El potencial eléctrico originado por la molécula en un punto O localizado a lo largo
de la recta que une a ambas cargas y a una distancia 50d de su punto medio. Considera
el caso en que el punto O se encuentra más próximo a la carga positiva. 4.8 mV
b.- El potencial eléctrico originado por la molécula en un punto P localizado a lo largo
de la recta mediatriz del segmento que une las cargas y a una distancia 50d de su punto
medio. 0 V
c.- El trabajo necesario para desplazar a un electrón desde el punto O hasta el punto P.
-7.68*10-22 J
Datos: Ke = 9x109 Nm2/C2 y e=1’6x1019 C.
JUNIO 2007:

17.- Una carga q > 0 se encuentra bajo la acción de un campo eléctrico uniforme E . Si
la carga se desplaza en la misma dirección y sentido que el campo eléctrico, ¿qué ocurre
con su energía potencial eléctrica? Disminuye
¿Y si movemos la carga en dirección perpendicular al campo? Justifica ambas
respuestas. Se mantiene constante.
SEPTIEMBRE 2007:


18.- Se tiene un campo eléctrico uniforme Eo  3000i V/m que se extiende por todo el
espacio. Seguidamente se introduce una carga Q = 4C, que se sitúa en el punto (2,0)
m.
a.- Calcula el vector campo eléctrico resultante en el punto P (2,3) m y su módulo.
E = (3000, 4000) N/C
b.- A continuación se añade una segunda carga Q’ en el punto (0,3) m. ¿Qué valor ha de
tener Q’ para que el campo eléctrico resultante en el punto P no tenga componente X?
Q’ = -1.33 μC
Dato: Ke = 9x109 Nm2/C2
JUNIO 2008:
19.- Colocamos tres cargas iguales de valor 2 C en los puntos (1,0), (1,0) y (0,1) m.
a.- Calcula el vector campo eléctrico en el punto (0,0). E = (0, -1.8*104) N/C
b.- ¿Cuál es el trabajo necesario para trasladar una carga eléctrica puntual de valor 1 C
desde el punto (0,0) al punto (0,1) m? 1.96*10-2 J
Dato: Ke = 9x109 Nm2/C2
SEPTIEMBRE 2008:
20.- Se tiene una carga q = 40 nC en el punto A (1,0) cm y otra carga q’ = 10 nC en el
punto A’ (0,2) cm. Calcula la diferencia de potencial eléctrico entre el origen de
coordenadas y el punto B (1,2) cm. -2.25*104 V
Dato: Ke = 9x109 Nm2/C2
JUNIO 2010:


21.- Un electrón se mueve dentro de un campo eléctrico uniforme E  E ( j ) . El
electrón parte del reposo desde el punto A, de coordenadas (1,0) m y llega al punto B
con una velocidad de 107 m/s después de recorrer 50 cm.
a.- Indica la trayectoria del electrón y las coordenadas de B. (1,0.5) m

b.- Calcula el módulo de E . 1137.5 N/C
Datos: e=1’6.10-19C; melectrón=9’1.10-31Kg.
22.- ¿Qué energía libera una tormenta eléctrica en la que se transfieren 50 rayos entre
las nubes y el suelo? Supón que la diferencia de potencial media entre las nubes y el
suelo es de 109 V y que la cantidad de carga media transferida en cada rayo es de 25 C.
5*1011 J
JUNIO 2011:
23.- Dos cargas puntuales de valores q1=–16 C y q2=2 C y vectores de posición

 



r1  4i y r2  1i (en m) ejercen una fuerza total F  2'7.109 i (en N) sobre una carga
positiva situada en el origen de coordenadas. Calcula el valor de esta carga. 0.3 C
Dato: k=9.109 SI.
SEPTIEMBRE 2011:
24.- Una carga puntual q que se encuentra en un punto A es trasladada a un punto B,
siendo el potencial electrostático en A mayor que en B. Discute como varía la energía
potencial de dicha carga dependiendo de su signo.
Carga + aumenta; carga - disminuye
JUNIO 2012:
25.- Una carga puntual de valor q1 = 3 mC se encuentra situada en el origen de
coordenadas mientras que una segunda carga, q2, de valor desconocido, se encuentra
situada en el punto (4, 0) m. Estas cargas crean conjuntamente un potencial de 18·106 V
en el punto P (0, 3) m. Calcula la expresión teórica y el valor numérico de:
a.- La carga q2. 5*10-3 C
b.- El campo eléctrico total creado por ambas cargas en el punto P. Representa
gráficamente los vectores campo de cada carga y el vector campo total.
(4.44, 1.08)*106 N/C
Dato: Constante de Coulomb, k = 9·109 N·m2/ C2
SEPTIEMBRE 2012:
26.- Una carga puntual de valor q1 = -2 μC se encuentra en el punto (0,0) m y una
segunda carga de valor desconocido, q2 se encuentra en el punto (3,0) m. Calcula el
valor que debe tener la carga q2 para que el campo eléctrico generado por ambas cargas
en el punto (5,0) m sea nulo. Representa los vectores campo eléctrico generados por
cada una de las cargas en ese punto. 3.2*10-7 C
JUNIO 2013:
27.- Una carga eléctrica q1 = 2 mC se encuentra fija en el punto (-1,0) cm y otra q2 = -2
mC se encuentra fija en el punto (1,0) cm. Representa en el plano XY las posiciones de
las cargas, el campo eléctrico de cada carga y el campo eléctrico total en el punto (0,1)
cm. Calcula el vector campo eléctrico total en dicho punto. (1.27*1011, 0) N/C
Dato: constante de Coulomb, k = 9·109 N·m2/C2
JULIO 2013:
28.- Dos cargas eléctricas q1 = 5 μC y q2 = -3 μC se encuentran en las posiciones (0,0)
m y (4,0) m respectivamente, como muestra la figura. Calcula:
a.- El vector campo eléctrico en el punto B (4,-3) m. (1440, 1920) N/C
b.- El potencial eléctrico en el punto A (2,0) m. Determina también el trabajo para
trasladar una carga de -10–12 C desde el infinito hasta el punto A. (Considera nulo el
potencial eléctrico en el infinito). VA = 9000 V; W = 9*10-9 J
Dato: constante de Coulomb, k = 9·109 N·m2/C2
JUNIO 2014:
29.- Dos cargas puntuales iguales de 9 μC están situadas sobre el eje X. Una se
encuentra en el punto de coordenadas (-a, 0); la otra está en el punto (a, 0), siendo a = 5
m. Una tercera carga de 5 μC se sitúa sobre el eje Y en y = 5 m. Calcula la fuerza
ejercida sobre esta última carga. F = (0, 0.115) N
Dato: K = 9 109 Nm2/C2.
JULIO 2014:
30.- Un electrón se mueve dentro de un campo eléctrico uniforme E = E i con E > 0. El
electrón parte del reposo desde el punto A de coordenadas (0, 0) cm, y llega al punto B
con una velocidad de 106 m/s después de recorrer 20 cm. Considerando que sobre el
electrón no actúan otras fuerzas y sin tener en cuenta los fenómenos relativistas:
a.- Discute cómo será la trayectoria del electrón y calcula las coordenadas del punto B
(en cm) Trayectoria rectilínea. (0.2,0) m
b.- Calcula razonadamente el módulo del campo eléctrico. 14.21 N/C
Datos: e = 1.6 10-19 C; me = 9.1 10-31 kg.
JUNIO 2015:
31.- Dada la distribución de cargas representada en la figura, calcula:
a.- El campo eléctrico (módulo, dirección y sentido) en el punto A. (625, 2519.5) N/C
b.- El trabajo mínimo necesario para trasladar una carga q3 = 1 nC desde el infinito
hasta el punto A. Considera que el potencial eléctrico en el infinito es nulo. 3.3*10-6 J
Dato: K = 9 109 Nm2/C2.
JULIO 2015:
32.- Una carga puntual de valor q1 = - 3 μC se encuentra en el punto (0, 0) m y una
segunda carga de valor desconocido, q2 se encuentra en el punto (2, 0) m.
a.- Calcula el valor que debe tener la carga q2 para que el campo eléctrico generado por
ambas en el punto (5, 0) m sea nulo. Representa los vectores campo eléctrico generados
por cada una de ambas cargas en ese punto. 1.08*10-6 C
b.- Calcula el trabajo necesario para mover una carga q3 = 0.1 μC desde el punto (5, 0)
m hasta el punto (10, 0) m. – 6.75*10-5 J
JUNIO 2016:
33.- Tres cargas eléctricas iguales de valor 3 μC se sitúan en los puntos (1,0) m, (-1,0)
m y (0.-1) m.
a.- Dibuja en el punto (0,0) los vectores campo eléctrico generados por cada una de las
cargas. Calcula el vector campo eléctrico resultante en dicho punto. (0,27000) N/C
b.- Calcula el trabajo realizado en el desplazamiento de una carga puntual de 1 μC entre
(0,0) m y (0,1) m. Razona si la carga se puede mover espontáneamente a dicho punto
(0,1) m. 0.029 J. Proceso espontáneo.
JULIO 2016:
34.- Se colocan tres cargas puntuales en tres de los cuatro vértices de un cuadrado de 3
m de lado. Sobre el vértice A(3, 0) m hay una carga Q1 = -2 nC, sobre el vértice B(3, 3)
m hay una carga Q2 = -4 nC y sobre el vértice C(0, 3) m hay una carga Q2 = -2 nC.
Calcula:
a.- El vector campo eléctrico resultante generado por las tres cargas en el cuarto vértice,
D, del cuadrado. (1.414, 1.414) N/C
b.- El potencial eléctrico generado por las tres cargas en dicho punto D. ¿Qué valor
debería tener una cuarta carga, Q4, situada a una distancia de 9 m del punto D, para que
el potencial en dicho punto fuese nulo? -20.5 V; 2.05*10-8 C
Dato: K = 9 109 Nm2/C2.
JUNIO 2017:
35.- Una partícula de carga 3 μC que se mueve con velocidad 2 103 i m/s entra en una
región del espacio en la que hay un campo eléctrico uniforme E = -3 j N/C y también un
campo magnético uniforme B = 4 k mT. Calcula el vector fuerza total que actúa sobre
esa partícula y representa todos los vectores involucrados (haz coincidir el plano XY
con el plano del papel). -3.3*10-5 j N
36.- Un electrón se mueve dentro de un campo eléctrico uniforme E = - E i. El electrón
parte del reposo desde el punto A, de coordenadas (0, 1) , y llega al punto B con una
velocidad de 106 m/s después de recorrer 1 m.
a.- Indica la trayectoria que seguirá el electrón y las coordenadas del punto B.
Trayectoria rectilínea B = (1, 1)
b.- Calcula razonadamente el trabajo realizado por el campo eléctrico sobre la carga
desde A a B y el valor del campo eléctrico. W = 4.55*10-19 J; E = 2.84 N/C
Datos: carga elemental, q = 1,6 10-19 C; masa del electrón, m = 9,1 10-31 kg
JULIO 2017:
37.- Se sitúan sobre el eje 8 dos cargas positivas q, puntuales e idénticas, separadas una
distancia 2a, tal y como se muestra en la figura. Calcula la expresión del vector campo
eléctrico total en el punto P situado en el eje Y, a una distancia a del origen. Dibuja los
vectores campo generados por cada carga y el total en el punto P.
ET = (0, Kq√2/2a2
JUNIO 2018:
38.- Atendiendo a la distribución de cargas representada en la figura, calcula:
a.- El vector campo eléctrico debido a cada una de las cargas y el total en el punto P.
Dibuja todos los vectores. E = (-243.57, -2109.38) N/C
b.- El trabajo mínimo necesario para trasladar una carga q3 = 1 nC desde el infinito
hasta el punto P. Considera que el potencial eléctrico en el infinito es nulo. 6.75*10-6 J
Dato: constante de Coulomb, Ke = 9*109 Nm2/C2
JULIO 2018:
39.- En los puntos A (0,0) m; B (0,2) m y C (2,2) m se sitúan tres cargas eléctricas
iguales, de valor – 3 μC.
a.- Dibuja, en el punto D (1,1) m, los vectores campo eléctrico generados por cada una
de las cargas y calcula el vector campo eléctrico resultante. E = (- 9546, 9546) N/C
b.- Calcula el trabajo realizado en el desplazamiento de una carga eléctrica puntual de 1
μC, entre los puntos D (1,1) m y E (2,0) m, razonando si la carga puede realizar
espontáneamente dicho desplazamiento. W = - 2.073*10-5 J. Espontáneo.
Dato: constante de Coulomb, Ke = 9*109 Nm2/C2
JUNIO 2019:
40.- Sabiendo que el potencial eléctrico en el punto P es nulo, determina el valor de la
carga q2. Razona si será nulo el campo eléctrico en el punto P. q2 = - 3*10-3. El campo
eléctrico no será nulo.
41.- Una carga puntual de valor q1 = - 4μC se encuentra en el punto (0, 0) m y una
segunda carga de valor desconocido, q2, se encuentra en el punto (2, 0) m. Calcula el
valor que debe tener la carga q2 para que el campo eléctrico generado por ambas cargas
en el punto (4, 0) m sea nulo. Representa los vectores campo eléctrico generados por
cada una de las cargas en ese punto. q2 = 10-6 C
JULIO 2019:
42.- Las posiciones, respecto al origen de coordenadas, de dos cargas q1 = - 4 μC y q1 =
- 6 μC son, respectivamente, ̅ 1 = 3 ̅ m y ̅ 2 = - 3 ̅ m. Calcula el valor de una carga q,
situada en el origen de coordenadas, si la fuerza eléctrica total que actúa sobre ella es ̅
= 2*10-3 ̅ N.
Dato: constante de Coulomb, k = 9*10-9 Nm2/C2.
q = - 1 μC
43.- Explica brevemente qué es un campo de fuerzas conservativo. Una carga positiva
se encuentra en el seno de un campo electrostático. El trabajo realizado por el campo
para desplazarla entre los puntos A y B de la figura es de 0,01 J si se sigue el camino (1)
¿Cuál es el trabajo si se sigue el camino (2)? ¿En qué punto, A o B, es mayor el
potencial eléctrico? Razona las respuestas.
W (2) = 0.01 J. VA > VB