Análisis Geostadístico
de datos funcionales
Proyecto Fin de Máster - Máster en Técnicas Estadísticas
Alumna: María José Ginzo Villamayor
Tutor: Manuel Febrero Bande
Resumen
El análisis de datos funcional se ocupa de la modelización estadística de variables aleatorias que
toman valores en un espacio de funciones (variables funcionales). Varias técnicas estadísticas
estándares tales como la regresión, ANOVA o componentes principales, entre otros, han sido
considerados desde el punto de vista funcional. En general, estas metodologías se centran en
variables funcionales independientes e idénticamente distribuidas. Sin embargo, en varias disciplinas de las ciencias aplicadas, existe un gran interés en la modelización de datos funcionales
espacialmente correlados. En particular, la mayoría de ellos están interesados en el modelado
de datos funcionales espacialmente correlacionados. Este es el tema aquí tratado. En concreto,
este proyecto trata la predicción de curvas, cuando se dispone de una muestra de las curvas de
una región con continuidad espacial.
Se revisan tres métodos para la predicción espacial de los datos funcionales. Inicialmente,
se propone un predictor que tiene la misma forma que el predictor kriging clásico, pero teniendo
en cuenta las curvas en lugar de datos de una sola dimensión. Los otros predictores surgen
de adaptaciones de modelos lineales funcionales con respuesta funcional en el caso de datos
funcionales espacialmente correlacionados. Por un lado, se define un predictor que es una combinación de kriging y del modelo funcional lineal point-wise (concurrente). Por otra parte, se
utiliza el modelo funcional lineal total para extender dos métodos clásicos geoestadísticos multivariantes para el contexto funcional. El primer predictor se define en términos de parámetros
escalares. En el resto de los casos, los predictores implican parámetros funcionales. Se adapta
un criterio de optimización, criterio utilizado en predicción espacial multivariante para estimar
los parámetros escalares y funcionales que intervienen en los predictores propuestos. En todos
los casos se da un enfoque no paramétrico basado en la expansión en términos de bases de funciones que se usa para obtener las curvas a partir de datos discretos.
Las metodologías propuestas se ilustran mediante el análisis de un conjunto de datos real
correspondiente a la curva de temperatura que es función del tiempo.
Palabras clave: base de funciones; Cokriging; validación cruzada; modelo lineal funcional;
Kriging; predicción espacial multivariante.
iii
Contenidos
Introducción
1
2
1
Geostadística Univariante
1.1 Tipos de datos espaciales . . . . . . . . . . . . . . . . . . . . . .
1.2 Análisis estructural . . . . . . . . . . . . . . . . . . . . . . . . .
1.2.1 Variable regionalizada . . . . . . . . . . . . . . . . . . .
1.2.2 Hipótesis de estacionariedad . . . . . . . . . . . . . . . .
1.3 Estudio del semivariograma . . . . . . . . . . . . . . . . . . . . .
1.4 Anisotropía . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.4.1 Anisotropía geométrica . . . . . . . . . . . . . . . . . . .
1.4.2 Anisotropía zonal . . . . . . . . . . . . . . . . . . . . . .
1.5 Condición de positividad . . . . . . . . . . . . . . . . . . . . . .
1.6 Versiones muestrales de algunas medidas de variabilidad espacial .
1.7 Factores a tener en cuenta para la modelización . . . . . . . . . .
1.8 Métodos de estimación de los parámetros del variograma . . . . .
1.8.1 Estimación por mínimos cuadrados (MC) . . . . . . . . .
1.8.2 Estimación máximo verosímil (MV) . . . . . . . . . . . .
1.9 Kriging: predicción e interpolación . . . . . . . . . . . . . . . . .
1.9.1 Kriging Simple (SK) . . . . . . . . . . . . . . . . . . . .
1.9.2 Kriging Ordinario (OK) . . . . . . . . . . . . . . . . . .
1.9.3 Kriging universal(UK) . . . . . . . . . . . . . . . . . . .
1.9.4 Cokriging . . . . . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
5
6
7
7
7
10
12
13
13
13
14
15
16
16
17
18
20
21
25
27
Geostadística Multivariante
2.1 Análisis estructural . . . . .
2.2 Cokriging . . . . . . . . . .
2.2.1 Cokriging simple . .
2.2.2 Cokriging ordinario .
2.3 Cokriging universal . . . . .
2.4 Condición de insesgadez . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
29
29
31
32
34
35
36
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
v
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
CONTENIDOS
vi
3
4
Análisis de datos funcionales
3.1 Preliminares . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2 Técnicas exploratorias para Datos Funcionales . . . . . . . . . . . . . . . . . .
3.2.1 Media, Varianza, covarianza, correlación, covarianza cruzada y correlación
cruzada . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2.2 Componentes principales . . . . . . . . . . . . . . . . . . . . . . . . .
3.3 Bases para datos funcionales . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.3.1 Bases de Fourier . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.3.2 Bases B-Splines . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.3.3 Bases de Wavelets . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.4 Suavización de datos funcionales . . . . . . . . . . . . . . . . . . . . . . . . .
3.5 Elección de la suavización . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.5.1 Regresión - representación en base . . . . . . . . . . . . . . . . . . . .
3.5.2 Regresión Lineal Funcional . . . . . . . . . . . . . . . . . . . . . . .
37
39
40
Ejemplo real de Kriging con datos reales funcionales
4.1 Conceptos básicos de meteorología . . . . . . . . . . . . . . . . . . . . . . . .
4.2 Kriging ordinario para funciones-valores de datos espaciales . . . . . . . . . .
4.2.1 Predicción y estimación de los parámetros . . . . . . . . . . . . . . . .
4.2.2 Estimación la traza del variograma . . . . . . . . . . . . . . . . . . . .
4.2.3 Enfoque no paramétrico . . . . . . . . . . . . . . . . . . . . . . . . .
4.2.4 Resultados de la aplicación . . . . . . . . . . . . . . . . . . . . . . . .
4.3 Kriging variación de tiempo continua para la predicción espacial de datos funcionales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.3.1 Predictor y problema de minimización . . . . . . . . . . . . . . . . . .
4.3.2 Una solución basada en bases de funciones . . . . . . . . . . . . . . .
4.3.3 Resultados: predicción espacial de las curvas de temperatura en Galicia
4.4 De multivariante a geostadística funcional . . . . . . . . . . . . . . . . . . . .
4.4.1 Cokriging basado en datos funcionales . . . . . . . . . . . . . . . . . .
4.4.2 Kriging funcional: modelo total . . . . . . . . . . . . . . . . . . . . .
4.4.3 Resultados: Predicción espacial de la temperatura en las curvas Galicia
4.5 Comparación de las tres técnicas . . . . . . . . . . . . . . . . . . . . . . . . .
49
49
53
54
58
58
60
A Histogramas y boxplots de la Temperatura de Galicia año 2009
41
41
42
42
43
43
44
44
45
45
68
68
69
72
75
76
80
83
85
99
Bibliografía
105
Glosario
107
Index
108
Introducción
La mayoría de los fenómenos naturales que se estudian son variables medidas tanto en el espacio
como en el tiempo. Considerando una superficie de un suelo, por ejemplo, en ocasiones se puede
observar una alta variabilidad en distancias pequeñas. Esta variabilidad es el resultado de los
procesos naturales. Si se tienen datos de una de esas variables en n sitios de una región con
continuidad espacial, implícitamente en cada uno de ellos hay una observación funcional y así
usando técnicas de suavizado los valores encontrados pueden convertirse en un dato funcional.
Por ello, en este proyecto se mostrará cómo las técnicas de permiten identificar tendencia en
media y varianza y explorar la estructura de autocorrelación inherente a un conjunto de datos
medidos en una región con continuidad espacial mediante el uso de varios ejemplos. Muchos de
los datos recogidos en problemas de las ciencias aplicadas son curvas. Para modelizar este tipo
de información está el Análisis de Datos Funcionales (FDA), (se puede ver en [26]) se utiliza
desde finales de los años noventa. En ciencias como la agronomía, meteorología, ecología y
otras el análisis geostadístico, (véase [6]) se utiliza, a menudo, para describir la distribución
espacial.
La palabra geoestadística se compone de dos partes, geo y estadística de manera similar a
términos como geofísica o geoquímica. Se usa con dos acepciones diferentes:
1. como una colección de todos los métodos estadísticos y probabilísticos aplicados a las
geo-ciencias,
2. y como nombre para la teoría de variables regionalizadas.
La geoestadística fue usada primero por la industria minera, debido a los altos costes altos
que suponían las perforaciones que se hacían, de ahí que el análisis de los datos fuera de suma
importancia. De hecho muchos libros y publicaciones sobre geoestadística están en su mayoría
orientados a problemas de minería.
La motivación de este trabajo es ofrecer una solución al problema de predecir curvas en
aquellas zonas no muestreadas de una región, basándonos en estas dos ramas estadísticas, el
análisis de datos funcionales y la estadística espacial. Los capítulos 1-3 recogen el fundamento
teórico más importante, necesario para este proyecto, para ambas ramas.
La modelización de variables medidas en diferentes sitios de una región con continuidad
espacial,(véase en [6]) ha tenido desde los años sesenta junto con el desarrollo del análisis
geostadístico un gran uso en varias ciencias medioambientales, en minería, geología, ecología.
1
2
CONTENIDOS
Por convención, el análisis geostadístico es un procedimiento de dos pasos. El primero, la estructura espacial de la variable es examinada con el análisis del varioagrama. Una vez se tiene una
estructura espacial y precisado un modelo adecuado (esférico, exponencial o gasussiano, según
sea el caso), se utiliza algún procedimiento kriging para interpolar la variable no muestreada.
En el contexto geostadístico multivariante consideramos simultáneamente p procesos aleatorios espaciales, (véase en [6]). Es necesario encontrar un modelo para la covarianza espacial en
el que todas las variables estén incluidas en el análisis. Se va a utilizar la información multivariante para predecir cada uno de los puntos no muestreados. Un caso particular de geostadística
multivariante es el método cokriging bivariante, (en [6]).
Otra rama importante de la geostadística es el análisis de datos espacio-temporales. Los
modelos geostadísticos espacio-temporales proporcionan una herramienta probabilísstica para
el análisis de datos y predicciones basadas en la dependencia temporal entre las observaciones.
En contraposición a la geostadística multivariante, donde a menudo hay unas cuantas variables
en cada ubicación, los conjuntos espacio-temporales de datos pueden ser muy grandes.
La comunidad estadística ha estado interesada en desarrollar modelos para datos funcionales,
ya desde trabajos publicados a finales de los años setenta a otros más actuales como el trabajo de
Ramsay, ([24]). Nuevas metodologías que combinan los modelos no paramétricos con los datos
funcionales se puenden consultar en [8].
De la misma manera que los métodos estadísticos estándares han sido generalizados para ser
utilizados en FDA, es posible pensar que los métodos geostadísticos pueden ser adaptados a este
tipo de datos.
El proyecto ha sido estructurado del siguiente modo, en el Capítulo 1 se hace una breve descripción de la geostadística univariante, en el Capítulo 2 se generalizan los conceptos anteriores
en un contexto multivariante. En dicho contexto, m procesos aleatorios espaciales se consideran
simultáneamente. Es necesario encontrar un modelo de covarianza espacial para todas las variables incluidas en el modelo. Por tanto, se usa la información multivariante para predecir en
cada uno de los puntos no muestreados. El Capítulo 3 revisa la teoría fundamental del análisis
de datos funcionales. Las técnicas habituales para la modelización de datos funcionales se centran en funciones independientes. Sin embargo, en varias áreas de las ciencias aplicadas, existe
un gran interés por la modelización de datos funcionales correlados. De ahí que métodos estadísticos para la modelización de variables correladas, como por ejemplo el análisis geostadístico,
hayan sido adaptadas al contexto funcional. Una vez que el lector está entrenado con todos estos conceptos, en el Capítulo 4, se le ofrece una aplicación de los mismos combinando ambas
técnicas a unos conjuntos de datos.
En resumen, lo que contiene este proyecto fin de máster es una revisión crítica de los métodos
que se han considerado previamente, en estadística espacial con datos funcionales y aplicados a
un conjunto de datos real como es el de la temperatura en Galicia.
Este conjunto de datos tiene tanto componente espacial y funcional.
Datos metereológicos de Galicia
La predicción espacial en datos meteorológicos es un factor importante para muchos tipos de
modelos como los hidrológicos, los de crecimiento y mortalidad de los ecosistemas forestales.
Como caso particular se tiene el modelado de datos de temperatura. A lo largo de la historia
geostadística se han desarrollado y utilizado muchos métodos para hacer predicción espacial
CONTENIDOS
3
de temperatura, aunque, en la mayoría de las ocasiones, no se ha tenido en cuenta su carácter
funcional. En este proyecto se usa un conjunto de datos meteorológicos, se dispone de datos
de temperatura media del ambiente para Galicia en 66 estaciones distribuidas por Galicia del
siguiente modo:
• 13 (en 13 municipios distintos) en la provincia de A Coruña (94 municipios)
• 20 (en 19 municipios distintos) en la provincia de Lugo (67 municipios)
• 15 (en 15 municipios distintos) en la provincia de Orense (92 municipios)
• 18 (en 16 municipios distintos) en la provincia de Pontevedra (62 municipios)
15
10
5
−5
0
Temperatura (grados C)
20
25
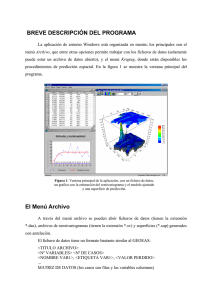
En particular se analiza la información de la temperatura promedio diaria durante el año
2009 (Figura 1).
0
100
200
300
Día
Figura 1: Valores medios de las curvas diarias de la temperatura media observado en 66 estaciones meteorológicas de Galicia.
Los datos de cada estación se obtuvieron la página web de Meteogalicia - Xunta de Galicia
(http://www.meteogalicia.es/web/index.action). Las coordenadas geográficas de estaciones meteorológicas (Figura 2) también se han obtenido de esa página. Estos datos son analizados en el
Capítulo 4.
Figura 2: Estaciones metereológicas. El punto marcado en rojo corresponde a la Facultad de
Matemáticas, punto no muestreado.
Capítulo 1
Geostadística Univariante
La Geostadística es la ciencia que estudia los fenómenos que fluctúan en el espacio y/o tiempo,
oferciendo una colección de herramientas estadísticas para la descripción y modelización de la
variabilidad espacial (y temporal).
El término Estadística Espacial se usa para describir una amplia variedad de modelos y
métodos adecuados para el análisis de datos referenciados espacialmente. En el libro [6] se
puede encontrar una descripción general de éstos.
El análisis espacial comprende el conjunto de conceptos y procedimientos utilizados para
abordar el estudio de la estructura y las relaciones territoriales a partir del conocimiento de la
posición de las entidades geográficas y las características de las variables seleccionadas para su
investigación.
Cuando la distribución espacial de los datos es importante para su estudio e interpretación,
la aplicación de técnicas específicas para datos espaciales cobra importancia puesto que puede
proporcionar mayor información que las técnicas tradicionales.
Las bases de datos espaciales deben contener observaciones de una (o varias) variables estadísticas de interés y una referencia cartográfica. Estas variables van a ser continuas, la única
condición que se le impone es que exista alguna dependencia entre dos variables con distinta referencia cartográfica, es decir, dos observaciones son más similares cuanto más cercanas son sus
realizaciones muestrales y a su vez, a medida que la distancia de las localizaciones muestrales
aumenta, la correlación entre las variables tiende a anularse. La característica de dependencia es
una diferencia importante respecto al análisis estadístico efectuado con datos independientes lo
que va a suponer ventajas, ya que las predicciones serán más precisas, como inconvenientes, las
estimaciones menos precisas.
No existe ninguna restricción en las referencias cartográficas, que pueden ser una referencia
territorial explícita como latitud y longitud (datos geográficos) o una referencia implícita como
domicilio o código postal (datos socio-económicos).
En estadística espacial se distinguen tres tipos de datos (véase [6]): datos geoestadísticos o
georreferenciados (geostatistical data), datos en rejilla o datos en un área (lattice data), y datos
de procesos puntuales (point processes data).
5
6
C APÍTULO 1. G EOSTADÍSTICA U NIVARIANTE
1.1 Tipos de datos espaciales
1. Datos geoestadísticos o georreferenciados (geostatistical data)
Los datos espacialmente continuos son mediciones tomadas en puntos fijos con localizaciones continuas en el espacio. Las mediciones clásicas en salud ambiental, tales como
contaminación de suelos y de aire o la radiación natural, suelen pertenecer a esta categoría.
La variable medida, sin embargo, puede ser tanto continua como discreta. El objetivo es
el de, dados los valores tomados en puntos de muestreo fijos, extender la distribución espacial de los valores de un atributo sobre la región total de estudio. Por lo tanto el análisis
de los datos geoestadísticos puede contemplar tanto la modelización del patrón de variabilidad, la determinación de los factores con los que pueda estar relacionado, como la de
obtener una buena predicción de la variable en puntos donde no se ha muestreado. Estos
métodos son muy utilizados en estudios del área de geociencias (suelo, clima, hidrología,
geología minera, etc) por lo que también suelen ser denominados datos geoestadísticos.
2. Datos en rejilla o datos en un área (lattice data)
Los datos en rejilla son observaciones procedentes de un proceso aleatorio, observadas
sobre una colección contable de regiones espaciales, que pueden estar regular o irregularmente distribuidas, complementados con lo que se denomina estructura de vecindad, es
decir, información sobre las regiones vecinas. Matemáticamente una rejilla queda definida
como un conjunto de lados y de vértices, es decir, un conjunto de índices de localizaciones
con un conjunto asociado de vecinos. Ya que los datos en rejilla están definidos en regiones espaciales, las localizaciones concretas especificadas por el vector suelen referirse
al centroide de la región.
3. Datos de procesos puntuales (point processes data)
Se denominan datos patrones de puntos o procesos puntuales, cuando las localizaciones
(y no las mediciones) son las variables de interés. Consisten en un número finito de localizaciones observadas en una región determinada. El objetivo de los procesos puntuales es
el de conocer la variación de la intensidad de los eventos sobre la región de estudio y el de
buscar modelos que ayuden a explicar o comprender el fenómeno. Tan importante como
la variable estudiada suele ser el patrón de variación espacial.
Independientemente del tipo de datos, los objetivos principales del estudio de la Estadística
Espacial son, como en casi todos los campos de la Estadística, dos:
1. Descripción de los datos. Esto puede incluir no sólo el estudio descriptivo del proceso
Z(u), tal como se entiende dentro de la estadística clásica, sino también la modelización
del tipo de dependencia espacial.
2. Predicción. Sin duda en muchas ocasiones la predicción es el objetivo que motiva el
estudio de datos espaciales.
1.2 A NÁLISIS ESTRUCTURAL
7
1.2 Análisis estructural
En geoestadística los datos se observan en u localizaciones de un conjunto D ∈ Rd donde
d indica la dimensión del espacio. Las localizaciones se expresan en dos o tres coordenadas
espaciales, como por ejemplo, longitud, latitud, y/o altitud. Las observaciones se toman en cada
localización y se consideran como una realización de un proceso estocástico espacial denotado
generalmente por Z(u).
La función de distribucíón acumulada de una variable aleatoria continua dependiente de la
localización espacial u, Z(u) viene definida por:
F (u; z) = P {Z(u) ≤ z}
siendo P la función de probabilidad asociada. En la práctica se suele trabajar con información
de n datos, por lo que la variable aleatoria se suele denotar por Z(ui ) = z(ui ), i = 1, . . . , n y
en ese caso se trabaja con la función de distribución acumulada condicional dada por:
F (u; k|n) = P {Z(u) ≤ z|n}
En geostadística es importante modelizar el grado de correlación o dependencia espacial entre
una cierta variable Z(ui ), i = 1, . . . , n.
1.2.1
Variable regionalizada
Una variable medida en el espacio de forma que presente una estructura de correlación, se dice
que es una variable regionalizada. De manera más formal se puede definir como un proceso
estocástico con dominio contenido en un espacio D ∈ Rd . En términos prácticos Z(u) puede
verse como una medición de una variable aleatoria (por ejemplo concentración de un contaminante) en un punto u de una región de estudio. Un proceso estocástico es una colección de
variables aleatorias indexadas, esto es, para cada u en el conjunto de índices D, Z(u) es una
variable aleatoria. En el caso de que las mediciones sean hechas en una superficie, entonces
Z(u) puede interpretarse como la variable aleatoria asociada a ese punto del plano (u representa
las coordenadas, planas o geográficas, y Z la variable en cada una de ellas). Estas variables
aleatorias pueden representar la magnitud de una variable ambiental medida en un conjunto de
coordenadas de la región de estudio.
1.2.2
Hipótesis de estacionariedad
Una variable aleatoria Z(u), u ∈ A se dice que es estacionaria en la región A si la función de
distribución acumulada es invariante bajo cualquier traslación C efectuada sobre sus localizaciones:
F (u1 , . . . , uk ; Z1 , . . . , Zk ) = F (u1 + C, . . . , uk + C; Z1 + C, . . . , Zk + C)
para cualquier vector de traslación C. Es decir, esta hipótesis establece el grado de homogeneidad espacial del fenómeno.
8
C APÍTULO 1. G EOSTADÍSTICA U NIVARIANTE
Como sólo se dispone de una realización discreta de la variable Z(u), es inevitable que haya
que asumir ciertas hipótesis para poder llevar a cabo algún tipo de estudio estadístico. El tipo de
estacionariedad asumido indica qué tipo de inferencia estadística puede realizarse con el modelo
probabilístico.
Se considera un proceso estocástico {Z(u), u ∈ D}, donde D es un subconjunto de Rd
(espacio Euclídeo d-dimensional). El proceso Z se dice que es Gaussiano si, para cualquier
natural k ≥ 1 y las localizaciones u1 , . . . , uk , el vector (Z(u1 ), Z(u2 ), . . . , Z(uk )) tiene una
distribución normal multivariante.
Estrictamente Estacionario
Si la correspondiente distribución de (Z(u1 ), Z(u2 ), . . . , Z(uk )) es la misma que la del vector
(Z(u1 + h), Z(u2 + h), . . . , Z(uk + h)) para cualesquiera u1 , u2 , . . . , uk puntos espaciales y
cualquier h ∈ Rd , el proceso se dice que es estrictamente estacionario.
Estacionario de segundo orden
El proceso Z se dice que es estacionario de segundo orden, o estacionariamente débil si µ(u) ≡
µ, es decir, la media es la misma para todas las u y Cov {Z(u1 ), Z(u2 )} = C (u1 − u2 ), para
todos u1 ∈ D, u2 ∈ D, donde C(u) es la función de covarianza entre una observación u y
de otra en el 0. C(u) recibe el nombre de covariograma. Como consecuencia de la definición
tenemos:
• σZ2 = C(0), ∀x ∈ D.
• C es una función simétrica: C(h) = C(−h).
• Aplicando la desigualdad de Cauchy-Schwarz puede demostrarse que
|C(h)| ≤ C(0).
• C(h) es una función definida positiva.
• Una función relacionada es el correlograma, ρ(h) = C(h)/C(0), verificando que
|ρ(h)| ≤ ρ(0) = 1
Se puede ver que si todas las varianzas son finitas entonces un proceso estrictamente estacionario es también estacionario de segundo orden. La afirmación inversa es falsa, en general,
pero un proceso Gaussiano que es a la vez estacionario de segundo orden será también estrictamente estacionario, ([6]).
Hipótesis intrínseca
Si se asume que µ(u) es una constante, la cual podemos suponer cero sin pérdida de generalidad,
se puede definir:
2γ(u1 − u2 ) = Var {Z(u1 ) − Z(u2 )}
1.2 A NÁLISIS ESTRUCTURAL
9
La ecuación anterior sólo tiene sentido si la parte izquierda depende de u1 y u2 sólo a través
de su diferencia u1 − u2 . Un proceso que satisface esta propiedad se llama intrínsicamente
estacionario. La función 2γ(·) se llama variograma y γ(·) semivariograma.
1. γ es una función simétrica γ(h) = γ(−h).
2. |γ(h)| ≥ γ(0) = 0.
3. Variograma estandarizado: γs (h) = γ(h)/σZ2 , γs (0) = 0.
La propiedad intrínsecamente estacionario es más débil que la estacionariedad de segundo
orden.
Si se supone que el proceso es estacionario de segundo orden se verifica que:
Var {Z(u1 ) − Z(u2 )} = Var {Z(u1 )} + Var {Z(u2 )} − 2Cov {Z(u1 ), Z(u2 )}
= 2C(0) − 2C(u1 − u2 )
y también si se verifica la condición de estacionario de segundo orden, entonces:
γ(h) = C(0) − C(h)
Como consecuencia,ambas funciones son equivalentes para caracterizar la dependencia espacial
de la variable regionalizada Z(h).
Además el variograma debe cumplir:
1. γ(h) es una función condicionalmente definida negativa.
2. lim|h|→+∞
γ(h)
|h|2
= 0.
Desde este punto de vista, las distintas formas (más fuertes) de estacionariedad no son necesarias. La estacionariedad tanto intrínseca como la de segundo orden son suposiciones más
naturales. Por ello, hay que ser cauto cuando un análisis preliminar de los datos indica que el
proceso es intrínsecamente estacionario y no estacionario.
Isotropía
Un concepto diferente es el de isotropía. Si se supone que el proceso es intrínsecamente estacionario con semivariograma γ(h), h ∈ Rd . Si γ(h) = γ0 (khk), es decir, si el semivariograma
depende del vector h sólo a través de su longitud khk, entonces el proceso es isotrópico.
Un proceso que es a la vez intrínsecamente estacionario e isotrópico se dice que es homogéneo.
10
C APÍTULO 1. G EOSTADÍSTICA U NIVARIANTE
1.3 Estudio del semivariograma
El estudio del semivariograma, o variograma, es más habitual que el estudio del covariograma.
Las razones son dos:
• La hipótesis de intrínsecamente estacionaria incluye la condición de estacionaria de segundo orden.
• Para el cálculo del semivariograma no es necesario conocer la media de la variable.
Por otra parte, si la variable es estacionaria de segundo orden, siempre puede obtenerse la función de covariograma a partir de la función de semivariograma: γ(h) = σZ2 − C(h).
De ahora en adelante, por facilidad de notación, se denotará el variograma isotrópico por
γ(h), donde h representa la longitud del vector, en lugar del propio vector. El semivariograma
representa un índice de cambio que muestra una variable con la distancia. Su forma describe el
patrón de variación espacial en términos de su magnitud y forma general.
La pediente del semivariograma indica la intensidad de cambio del atributo (variable) analizado con la distancia al mismo tiempo que el porcentaje de disminución en la dependencia
espacial. El máximo valor que alcanza un semivariograma se llama meseta (sill) o varianza a
priori, e indica la escala bajo la cual los datos definen un proceso estacionario de segundo orden.
La meseta puede ser o no finita. Los semivariogramas que tienen meseta finita cumplen con la
hipótesis de estacionariedad fuerte; mientras que cuando ocurre lo contrario, el semivariograma
define un fenómeno natural que cumple sólo con la hipótesis intrínseca.
El lag o distancia para la que el sill es alcanzado se llama rango o alcance y define el
límite de la dependencia espacial. El rango se interpreta como la zona de influencia. Existen
algunos modelos de semivariograma en los que no existe una distancia finita para la cual dos
observaciones sean independientes; por ello se llama rango efectivo a la distancia para la cual el
semivariograma alcanza el 95% de la meseta. Cuanto más pequeño sea el rango, más cerca se
está del modelo de independencia espacial. El rango no siempre aparece de manera explícita en
la fórmula del semivariograma.
Finalmente un semivariograma con término independiente define la varianza llamada Efecto
Pepita (nugget), la cual define la variabilidad intrínseca en los datos y que no ha sido captada
por el rango de distancia analizadas así como cualquier variación puramente aleatoria. Representa una discontinuidad puntual del semivariograma en el origen. Puede ser debido a errores
de medición en la variable o a la escala de la misma. En algunas ocasiones puede ser indicativo
de que parte de la estructura espacial se concentra a distancias inferiores a las observadas.
Denotando por |h| = khk, algunos ejemplos de semivariogramas isotrópicos son:
1. Modelo Nugget effect.
1.3 E STUDIO DEL SEMIVARIOGRAMA
11
Es la estructura más básica del semivariograma indicando falta de estructura espacial.
Viene dado por:
0 si |h| = 0,
γ (|h|) =
1 en otro caso.
2. Modelo lineal.
Define un modelo no acotado en función de dos constantes positivas. La función tiende
a infinito para distancias grandes lo que hace que este modelo no se corresponda con un
proceso estacionario,
0
si |h| = 0
γ (|h|) =
c0 + c1 h si |h| > 0.
3. Modelo esférico.
Definido por un rango actual a, una varianza a priori (sill) c1 y un efecto nugget c0 ,
3
|h|
c0 + c1 · 1.5 a − 0.5 |h|
si |h| ≤ a
a
γ (|h|) =
c0 + c1
si |h| ≥ a.
4. Modelo Exponencial.
Definido por un rango efectivo a (rango integral a/3), una varianza a priori (sill) c1 y un
efecto nugget c0 ,
3 |h|
γ (|h|) = c0 + c1 · 1 − exp −
.
a
5. Modelo Gaussiano.
Definido por un rango efectivo a, una varianza a priori c1 y un efecto nugget c0 ,
"
!#
(3 |h|)2
γ (|h|) = c0 + c1 · 1 − exp −
.
a2
6. Modelo potencial (Power).
Definido por un factor 0 < ω < 2, una pendiente positiva c1 y un efecto nugget c0 ,
γ (|h|) = c0 + c1 · |h|ω .
7. Modelo del efecto Hole o sinusuidal.
Se utiliza para definir componentes cíclicas subyacentes. Con una varianza a priori de c1
y un efecto nugget de c0 , se define como
|h|
γ (|h|) = c0 + c1 · 1.0 − cos
·π .
a
Para ser un modelo de variograma correctamente definido, este modelo de efecto hole
debe ser sólo aplicado en una dirección.
12
C APÍTULO 1. G EOSTADÍSTICA U NIVARIANTE
8. Familia Matérn.
Esta clase se define mejor en términos de la función de covarianza definida por
1
C0 (|h|) = θ2 −1
2
Γ (θ2 )
√
θ
√
2 θ2 |h| 2
2 θ2 |h|
kθ2
.
θ1
θ1
En este caso, θ1 > 0 define un parámetro de dependencia espcial y θ2 > 0 es un parámetro
de forma. La función Γ (·) representa la función gamma mientras que kθ2 es la función
modificada de Bessel de tercera clase de orden θ2 . Como casos especiales se tiene que
θ2 → 21 tiende a la forma exponencial y el límite de θ2 → ∞ daría lugar a la forma
Gaussiana.
Todos los modelos anteriores (excepto el lineal y el potencial) son acotados, lo que significa
que el sill (umbral) se alcanza realmente en el límite a una cierta distancia marcada por el rango.
Además se tienen las siguientes observaciones:
• Para el modelo de efecto nugget, el sill es alcanzado tan pronto la distancia se hace positiva.
• El modelo esférico alcanza realmente el sill a una distancia equivalente a su rango.
• Los modelos exponencial y Gaussiano alcanzan asintóticamente el sill, definiéndose un
rango práctico como aquella distancia para la que el modelo se encuentra al 95% del sill.
Los modelos acotados también se suelen llamar modelos de transición. Por otra parte, los modelos potencial y lineal no tienen sill, y por tanto, carece de su correspondiente función de covarianza.
Alrededor del origen podemos ditinguir tres tipos de comportamiento:
1. Comportamiento parabólico: (modelo Gaussiano) tal comportamiento es característico de
fenómenos altamente regulares.
2. Comportamiento lineal: (modelos esférico o exponencial) tal comportamiento es característico de aquellos fenómenos que muestran dependencias espaciales a cortas distancias
aumentándolas linealmente con las mismas.
3. Comportamiento discontínuo: (modelo de efecto nugget) evidencia de gran variabilidad
intrínseca a los datos que enmascara cualquier posible dependencia espacial.
El comportamiento cerca del origen del modelo potencial depende de los valores del parámetro
ω, siendo lineal para ω = 1 y parabólico para valores de ω cercanos a 2.
1.4 Anisotropía
Hay varias formas de trabajar con procesos anisótropicos considerando éstos como generalizaciones más o menos directas de procesos isotrópicos.
1.5 C ONDICIÓN DE POSITIVIDAD
1.4.1
13
Anisotropía geométrica
La forma más simple es considerar la anisotropía geométrica. Esta se refiere a un semivariograma de la forma
γ(h) = γ0 (kAhk)
donde γ0 (kAhk) es un variograma isotrópico y A una matriz de dimensión d x d representando una transformación lineal de Rd . Lógicamente si A es la identidad, esto se reduce al caso
isotrópico. La idea subyacente es esta situación es que el proceso no es isotrópico en el espacio
original, pero sí en algún espacio transformado linealmente, el cual puede, por ejemplo, corresponder a una transformación de las coordenadas. En el caso más lógico y usual en el que A
es una matriz definida positiva, los contornos de igual covarianza se corresponden con elipses
inscritas en círculos.
1.4.2
Anisotropía zonal
Una posible generalización de anisotropía surge de la simple observación de que si Z1 , . . . , Zp
son procesos independientes intrínsecamente estacionarios, entonces Z = Z1 + . . . + Zp , es
también intrínsecamente estacionario, con semivariograma dado por γ(h) = γ1 (h)+. . .+γp (h),
denotando γ1 , . . . , γp los semivariogramas de Z1 , . . . , Zp respectivamente. Así,
γ(h) =
p
X
γ0 (Ai h) ,
i=1
siendo γ0 un semivariograma isotrópico y A1 , . . . , Ap matrices, es un semivariograma válido
que generaliza la anisotropía geométrica. Esta anisotropía se llama anisotropía zonal.
Una idea más complicada es asumir que, para alguna función no lineal g(u), el proceso
Z(g(u)), en lugar del original Z(u), es un proceso isótropico estacionario. Esta idea puede, de
hecho analizar, tanto la no estacionariedad como la no isotropía.
1.5
Condición de positividad
Una restricción importante en geostadística es que no se puede definir una covarianza espacial
o una función de semivariograma de forma arbitraria. Necesariamente la primera de ellas debe
cumplir con la condición de positividad. En el caso más general en el que Cov {Z (u1 ) , Z (u2 )} =
C (u1 , u2 ), el cual no supone ninguna condición de estacionariedad, la condición de positividad
significa que la relación
XX
ai aj C (ui , uj ) ≥ 0
i
j
se cumple para cualquier conjunto finito de puntos u1 , . . . , un y coeficientes reales
P arbitrarios
a1 , . . . , an . Es necesario que la parte izquierda de la ecuación es la varianza de i ai Z (ui ).
También se tienen estas mismas condiciones en la versión de variogramas. Supongamos que
14
C APÍTULO 1. G EOSTADÍSTICA U NIVARIANTE
γ (·) es el semivariograma
de un proceso estacionario de segundo orden, entonces si a1 , . . . , an
P
son constantes con ai = 0, tenemos
XX
i
j
ai aj γ (ui − uj ) ≤ 0
Esta es la condición de no positividad condicional,(explicada en [6]). La anterior condición es
una condición necesaria para que γ (·) sea un semivariograma válido en el caso general.
1.6 Versiones muestrales de algunas medidas de variabilidad espacial
Se considera ahora el problema de la estimación del variograma y de otras medidas de variabilidad espacial. En general disponemos de un proceso {Z (u) , u ∈ D} observado en un número
finito de localizaciones u1 , . . . , uN .
El estimador más simple viene dado por el método de los momentos, el cual, suponiendo que
los puntos de muestreo u1 , . . . , uN estén definidos en un retículo regular, viene definido por
2γ̂(h) =
1
#N (h)
X
(ui ,uj )∈N (h)
{Z(ui ) − Z(uj )}2 .
N (h) denota todos aquellos pares (ui , uj ) para los que ui − uj = h y #N (h) denota el cardinal
de N (h). En el caso, por otra parte más común, de que los puntos de muestreo no estén en un
retículo regular, se aplica la fórmula anterior pero con la nueva definición de N (h),
N (h) = {(ui , uj ) : ui − uj ∈ T (h)} ,
siendo T (h) alguna vecindad o región de tolerancia sobre h.
Si disponemos de dos atributos medidos sobre las mismas localizaciones espaciales, puede
ser de interés evaluar la variabilidad espacial (cruzada) entre ambos atributos Z, Y . La medida
adecuada viene de la mano del estimador del variograma cruzado dado por:
2γ̂ZY (h) =
1
#N (h)
X
(ui ,uj )∈N (h)
(Z(ui ) − Z(uj )) (Y (ui ) − Y (uj )).
Una posible objeción al método de los momentos es que no es robusto frente a valores extremos
de Z.
Otra objeción surge del hecho del sesgo de la distribución: si suponemos que el proceso es
Gaussiano, para valores concretos de u y h, la distribución de {Z (u + h) − Z(u)}2 es de la
forma 2γ(h)χ21 , y la distribución de χ21 está sesgada. Sin embargo, si X ∽ χ21 entonces X 1/4
tiene una distribución casi simétrica y por tanto las medias muestrales de |Z(u1 ) − Z(u2 )|1/2 se
comportarán mejor que las de {Z(u1 ) − Z(u2 )}2 .
1.7 FACTORES A TENER EN CUENTA PARA LA MODELIZACIÓN
15
La función de covarianza muestral puede ser también obtenida mediante el método de los
momentos se la siguiente forma:
X
1
Ĉ(h) =
Z(ui )Z(uj ) − m2
#N (h)
(ui ,uj )∈N (h)
P
donde m = #N1(h) i Z(ui ). Si además definimos σ 2 =
estandarizar la covarianza para definir el correlograma
ρ(h) =
1
#N (h)
P
i Z(ui )
2
− m2 , podemos
C(h)
σ2
Por otra parte, el madograma es una medida similar al variograma del método de los momentos en el que el cuadrado de las diferencias entre Z(ui ) y Z(uj ) es sustituido por la diferencia
absoluta, dando lugar a la siguiente expresión
X
1
2γ̂M (h) =
|Z(ui ) − Z(uj )|
#N (h)
(ui ,uj )∈N (h)
Algunas de las anteriores medidas de variación espacial pueden ser usadas cualitativamente
para conseguir estructuras de continuidad espacial. Más de un tipo de medidas puede ser
obtenida al mismo tiempo. En general, las características observadas a través del eje de las
abcisas (distancias) son comunes para todas las medidas de variabilidad / continuidad. Sin embargo los valores del eje de ordenadas que definen el variograma son específicos del tipo de
variograma elegido.
Se tienen dos reglas prácticas que deberían ser tenidas en cuenta al estimar un variograma:
1. el variograma empírico sólo debe ser considerado para distancias para las que el número
de pares es superior a 30, (ver [? ]);
2. la distancia de fiabilidad para un variograma experimental es h < D/2 siendo D la distancia máxima que presentan las localizaciones muestreadas.
1.7
Factores a tener en cuenta para la modelización
En la práctica de la modelización tres son los puntos claves del problema:
1. Determinación del variograma o covarianza experimental.
2. Análisis de los posibles variogramas permisibles.
3. Utilización de información auxiliar, como el conocimiento físico del área y fenómeno bajo
estudio o medidas robustas tales como el madrograma.
La modelización consiste en la conjunción de estas diferentes fuentes de información para
construir un modelo adecuado que retenga la mayoría de las características de los atributos bajo
estudio.
Algunas decisiones importantes en una modelización se centran en:
16
C APÍTULO 1. G EOSTADÍSTICA U NIVARIANTE
1. Cómo obtener un modelo isotrópico o anisotrópico;
2. Cuál es el número y tipo de estructuras básicas que constituyan el variograma;
3. Elección adecuada de los parámetros asociados a los variogramas (sill, rango y nugget).
Respecto a la decisión sobre modelo isotrópico o anisotrópico, en la práctica se suele comparar diferentes variogramas experimentales calculados en distintas direcciones (para decidir si
existe anisotropía geométrica, por lo menos, tres direcciones deben ser consideradas). Una opción que nos puede ayudar para la detección de anisotropía direccional, es un scartterplot del
mapa del variograma en el sistema de coordenadas usual. El centro del mapa corresponde con el
origen del variograma γ(0) = 0. Cuando la variación es isotrópica, el incremento es similar en
cada dirección y por contra, la anisotropía geométrica aparece como líneas de contorno elípticas
indicando la dirección de máxima variabilidad espacial. Por esto, la evaluación de un mapa de
semivariogramas requiere considerar algunas direcciones e intervalos de distancias (lags).
El último peldaño en el proceso de la modelización consiste en la determinación de los
parámetros asociados a los modelos seleccionados.
1.8 Métodos de estimación de los parámetros del variograma
Asumamos que muestreamos a partir de un proceso espacial homogéneo para el que el variograma ha sido estimado por alguno de los métodos anteriores.
Los semivariogramas γ̂(h) y γ̄(h) carecen de la propiedad de no positividad condicional.
Como consecuencia, es posible que algunas predicciones espaciales derivadas a partir de tales
estimadores presenten varianzas negativas. La forma más clara y común de evitar esta dificultad
es reemplazando el semivariograma empírico γ̂(h) por algún modelo paramétrico, que se sabe
que cumple con la condición de semidefinido negativo. En general, no es necesario restringirse
a modelos isotrópicos, aunque suelen ser los primeros a ser considerados. Se consideran tres
métodos:
1. Estimación por mínimos cuadrados (least squares estimation).
2. Estimación por máxima verosimilitud (maximum likelihood).
1.8.1
Estimación por mínimos cuadrados (MC)
Supongamos que tenemos estimado el semivariograma γ(h) en un conjunto finito de valores de
h, y queremos ajustar un modelo especificado por una función paramétrica γ(h; θ) en términos
de un vector finito de parámetros θ. Este vector suele contener tres parámetros, efecto nugget,
sill y rango. Supóngase que se ha utilizado el estimador de los momentos γ̂ y sea γ̂ el vector
que contiene los valores estimados y γ(θ) el vector de los valores derivados por el modelo sobre
los mismos valores de h.
Se tienen tres posibilidades para los métodos de estimación mínimo cuadrática no lineal:
• Mínimos cuadrados ordinarios (MCO), en los que se toma θ como aquel valor que minimiza {γ̂ − γ(θ)}′ {γ̂ − γ(θ)} . (donde ′ indica la transposición de matrices).
1.8 M ÉTODOS DE ESTIMACIÓN DE LOS PARÁMETROS DEL VARIOGRAMA
17
• Mínimos cuadrados ponderados (MCP), en los que se toma θ como aquel valor que minimiza {γ̂ − γ(θ)}′ W (θ)−1 {γ̂ − γ(θ)}. En este caso W (θ) es una matriz diagonal cuyos
elementos de la diagonal son las varianzas de γ̂, aunque no covarianzas como si lo hace
el MCG. Por tanto MCP admite varianzas de γ̂, aunque no covarianzas aunque si lo hace
el MCG.
• Mínimos cuadrados generalizadoss (MCG), en los que se toma θ como aquel valor que
minimiza {γ̂ − γ(θ)}′ V (θ)−1 {γ̂ − γ(θ)} . Aquí V (θ) denota la matriz de covarianzas
de γ̂, la cual depende de θ.
En general, los tres estimadores MCO, MCP y MCG, aparecen en orden creciente de eficiencia pero decreciente en simplicidad. Notar que MCO es fácilmente implementable por algún procedimiento de mínimos cuadrados no lineales, mientras que MCP y MCG requieren la
especificación de las matrices W (θ) y V (θ).
1.8.2
Estimación máximo verosímil (MV)
Si se asume que se muestrea a partir de un proceso Gaussiano, entonces es bastante sencillo
obtener la forma exacta de la verosimilitud y maximizarla numéricamente. Consíderese el proceso espacial Z ∽ N (Xβ, Σ), con Z un vector de observaciones n-dimensional, X una matriz
n x q de covariables (q < n; X de rango completo), β un vector de dimensión q de parámetros
desconocidos y Σ la matriz de covarianzas de las observaciones. En la práctica se puede asumir
que Σ = αV (θ) siendo α un parámetro de escala conocido y V (θ) es una matriz de covarianzas estandarizadas determinadas por el parámetro desconocido θ. Con Z, Z ∽ N (Xβ, Σ), su
función de densidad es de la forma
1
−1/2
′ −1
−n/2
(2π)
det (Σ)
exp − (Z − Xβ) Σ (Z − Xβ) .
2
Y por tanto, la log-verosimilitud negativa será:
l(β, α, θ) =
n
n
1
1
log(2π) + log(α) + logdet(V (θ)) +
(Z − Xβ)′ V (θ)−1 (Z − Xβ) .
2
2
2
2α
Aunque este método es computacionalmente factible, su mayor dificultad frente a por ejemplo el método de MCP lo hace menos usado.
Supóngase {Y1 , . . . , Yn } son variables aleatorias independientes y normales N (µ, σ 2 ) con
parámetros desconocidos µ y σ 2 . Los estimadores máximo verosímiles de µ y σ 2 son µ̂ = Ȳ =
2
1 P
1 P
2
. Pero este estimador resulta sesgado y se suele usar el estii Yi y σ = n
i Yi − Ȳ
n
2
1 P
2
mador insesgado de σ , n−1 i Yi − Ȳ . Supóngase ahora que en lugar de trabajar con el
vector Y1 , . . . , Yn lo hacemos con la densidad conjunta de Y1 − Ȳ , . . . , Yn − Ȳ , cuya distribu2
1 P
.
ción no depende de µ. Ahora el estimador verosímil de σ 2 es directamente n−1
i Yi − Ȳ
′
Esta idea puede ser extendida al modelo general, Z ∽ N (Xβ, Σ). Si se define W = A Z
un vector de n − q contrastes linealmente independientes, es decir, las n − q columnas de A
18
C APÍTULO 1. G EOSTADÍSTICA U NIVARIANTE
son linealmente independientes y A′ X = 0, tenemos que W ∽ N (0, A′ σA), y el logaritmo
negativo de la función de verosimilitud en W será de la forma,
lW (α, θ) =
n−q
n−q
1
1
log(2π) +
log(α) + log A′ V (θ)A +
W ′ A′ V (θ)A W.
2
2
2
2α
Es posible elegir A que satisfaga A′ A = I − X (X ′ X)−1 X ′ , A′ A = I. En este caso la
expresión anterior se simplifica a:
lW (α, θ) =
+
n−q
n−q
1
log(2π) +
log(α) + log X ′ X +
2
2
2
1
1
1 2
′
−1
log X V (θ) X + logdet (V (θ)) +
G (θ),
2
2
2α
donde G2 (θ) denota la suma de cuadrados generalizados de los residuos
′
G2 = Z − X β̂ V −1 Z − X β̂
y β̂ = Z − X β̂ X ′ V −1 Z es el estimador MCG de β basado en la matriz de covarianzas V .
La estimación MVR proporciona mejores estimaciones que el MV pues, en general, da lugar
a estimadores con menores desviaciones para muestras con pocos datos. La estimación MVR
es ampliamente utilizada en modelización geostadística. Sin embargo, es más sensible que el
estimador MV de máxima verosimilitud bajo incorrecta especificación del vector de medias β.
En general, como los variogramas estimados por los métodos de verosimilitud (MV, MVR)
no están basados en los variogramas empíricos, hay claras diferencias entre éstos y los estimadores MCO o MCP.
1.9 Kriging: predicción e interpolación
Una vez conocida la varianza específica el objetivo es predecir e interpolar procesos espaciales.
El problema tiene los siguientes fundamentos dado un conjunto de observaciones de un
atributo espacial Z(u1 ), Z(u2 ), . . . , Z(un ), el objetivo es predecir el valor de Z(u0 ), para algún
u0 ∈
/ {u1 , . . . , un }.
Kriging es un nombre genérico adoptado en geostadística para dar nombre a una metodología
de interpolación basada en una familia de algoritmos de regresión generalizados por mínimos
cuadrados.
Todas las clases de estimaciones de krigings, no son más que variantes de las estimaciones
de regresión lineal básicas, las cuales para predecir el valor del atributo Z en la localización u0 ,
denotado por Z ∗ (u0 ), vienen definidas por
n(u0 )
∗
Z (u0 ) − m(u0 ) =
X
α=1
λα (u0 ) [Z(uα ) − m(uα )]
donde λα define la ponderación, peso asignado a los datos que intervienen en el sumatorio,
m(u0 ) y m(uα ) son los correspondientes valores esperados de Z(u0 ) y Z(uα ) respectivamente
1.9 K RIGING :
19
PREDICCIÓN E INTERPOLACIÓN
y n(u0 ) + 1 elementos: n(u0 ) atributos. A partir de ahora y sin pérdida de generalidad para que
la notación resulte más sencilla se usará n en lugar de n(u0 ).Obsérvese que sólo actúan aquellas
localizaciones uα vecinas a la localización de predicción de u0 .
Cualquier base de kriging tiene como objetivo la minimización de la varianza del error
σE2 (u), la cual en su formato general viene dado por
σE2 (u) = Var [Z ∗ (u) − Z(u)]
donde el superíndice * indica el valor estimado para esa localización.
Además σE2 (u) = Var [Z ∗ (u) − Z(u)] se minimiza bajo la restricción de insesgadez, es decir, E [Z ∗ (u) − Z(u)] = 0. Normalmente, la variable aleatoria que define el atributo en estudio
se descompone en una componente residual R(u) y otra determinista que define la tendencia
m(u),
Z(u) = R(u) + m(u)
La componente residual se modeliza como una variable aleatoria estacionaria de media cero y
covarianza Cr (h), siendo
E {R(u)} = 0
Cov {R(u), R(u + h)} = E {R(u) · R(u + h)} = CR (h)
De esta forma, el valor esperado de la variable aleatoria Z en una cierta localización u viene
dado por el valor de la componente tendencia en esa localización E {Z(u)} = m(u).
De acuerdo con el modelo considerado para la tendencia, podemos considerar las siguientes
variantes kriging lineales: simple (SK), ordinario (OK), con modelo de tendencia o universal
(UT), en bloques y factorial. En cuanto a los no lineales se pueden mencionar: lognormal,
multi-Gaussiano, de rango, indicatriz y disyuntivo.
En la Tabla 1.1 se resumen los principales tipos de kriging lineal que detallaremos a continuación.
Kriging
para Z(u)
Simple
Ordinario
Universal
Media
m(u)
Constante conocida
Constante desconocida
No constante y desconocida
Análisis estructural
Y (u)
Covariograma
Semivariograma
Semivariograma
Propiedades
Son óptimos si hay normalidad
multivariada.
Independiente de la distribución
son los mejores predictores
linealmente insesgados.
Tabla 1.1: Principales tipos de kriging lineal y propiedades
Antes de comenzar el estudio de cada uno de ellos, se presentan dos particularidades importantes:
1. La condición de estacionariedad, necesaria para el análisis estructural, no es ahora imprescindible para la predicción kriging. Por esta razón, en muchas de las expresiones que
se utilizarán se podemos encontrar γ(uα − uβ ) o C(uα − uβ ) en vez de γ(h) o C(h)
utilizadas anteriormente.
20
C APÍTULO 1. G EOSTADÍSTICA U NIVARIANTE
2. En la estapa de predicción la dependencia espacial se supone totalmente modelizada por
las funciones γ(h) y/o C(h) obtenidas en la etapa de análisis estructural.
1.9.1
Kriging Simple (SK)
Supóngase que hay una variable regionalizada estacionaria con media m y covarianza conocidas.
De manera análoga a como se define en modelos lineales el modelo establecido en este caso es
igual a la media más un error aleatorio con media cero. La diferencia es que en este caso los
errores no son independientes. Sea Z(u) la variable de interés medida en el sitio u.
E[Z(u)] = m
Z(u) = m + ǫ(u), con E[ǫ(u)] = 0.
El predictor de la variable de interés en un sitio u0 donde no se tiene información se define
como:
Z ∗ (u0 ) = m + ǫ∗ (u0 ),
con ǫ∗ (u0 ) que corresponde a la predicción del error aleatorio en el sitio u0 . Despejando de la
ecuación anterior ǫ∗ (u0 ) = Z ∗ (u0 ) − m. El predictor del error aleatorio se define por:
ǫ∗ (u0 ) =
n
X
λα ǫ(uα ) =
α=1
n
X
α=1
λα (Z(uα ) − m)
de donde el predictor de la variable de estudio es:
" n
#
n
X
X
∗
Z (u0 ) = m +
λα (Z(uα ) − m) = m +
λα ǫ(uα )
α=1
El predictor es insesgado si:
cuando E (ǫ∗ (u0 )) = 0.
E∗ (Z(u
∗
E (ǫ (u0 )) =
0 ))
n
X
α=1
α=1
= E(Z(u0 ) = m. Luego el predictor será insesgado
λα ǫ(uα ) =
n
X
λα (0) = 0.
α=1
Por tanto en este caso no existen restricciones para las ponderaciones tendientes al cumplimiento
de la condición de insesgadez. La estimación de los pesos del método kriging simple se obtiene
de tal forma que se minimice V (ǫ∗ (u0 ) − ǫ(u0 )).
V (ǫ∗ (u0 ) − ǫ(u0 )) = E (ǫ∗ (u0 ) − ǫ(u0 ))2
!
!2
n
X
= E
λα ǫ(uα ) − ǫ(u0 )
=
α=1
n
n
XX
α=1 β=1
usando:
λα λβ E (ǫ(uα )ǫ(uβ )) − 2
n
X
α=1
λα E (ǫ(uλ )ǫ(u0 )) + E (ǫ(u0 ))2
1.9 K RIGING :
21
PREDICCIÓN E INTERPOLACIÓN
1. E [ǫ(u0 )] = 0
2. E (ǫ (uλ ) ǫ (uβ )) = Cov (ǫ (uλ ) , ǫ (uβ )) = Cλβ
3. E (ǫ (u0 ))2 = σ 2
n X
n
X
V (ǫ∗ (u0 ) − ǫ(u0 )) =
α=1 β=1
λα λβ E (ǫ(uλ )ǫ(uβ )) − 2
n
X
λα λβ Cλβ + σ 2
α=1
derivando respecto a λ1 se tiene:
∂V (ǫ∗ (u0 ) − ǫ (u0 ))
∂λ1
igualando a cero
Pn
α=1 λα C1λ
= 2
n
X
α=1
λα C1λ − 2C10
= C10 . En general para cualquier λ, λ = 1, 2, . . . , n, se obtiene:
n
X
∂
λβ Cαβ = Cα0
=
∂λα
β=1
Con las n ecuaciones resultantes se construye el siguiente sistema de ecuaciones:
C11 C12 . . . C1n
λ1
C10
C21 C22 . . . C2n λ2 C20
..
.. = ..
..
..
.
.
.
. .
. .
.
Cn1 Cn2 . . . Cnn
λn
Cn0
La varianza de predicción Kriging Simple será,
2
σSK
= σ2 −
n
X
λα Cα0 .
α=1
Finalmente, el peso asignado a la media m vendrá dado por,
λ(u0 ) = 1 −
1.9.2
n
X
λα (u0 ).
α=1
Kriging Ordinario (OK)
Supóngase que se hacen mediciones de la variable de interés Z en los puntos uα , α = 1, . . . , n,
de la región de estudio, es decir, se tienen realizaciones de las variables Z(u1 ), ..., Z(un ), y se
desea predecir Z(u0 ), en el punto u0 donde no hubo medición. El Kriging Ordinario (OK) tiene
en cuenta las posibles fluctuaciones locales de la tendencia o media, limitando el dominio de
estacionariedad de la media a la vecindad local W (u) : m(u∗ ) es una constante (desconocida)
para todo u∗ ∈ W (u).
22
C APÍTULO 1. G EOSTADÍSTICA U NIVARIANTE
El estimador Kriging Ordinario puede predecirse como una combinación lineal de las n
variables aleatorias así:
Z ∗ (u0 ) = λ1 Z(u1 ) + λ2 Z(u2 ) + . . . + λn Z(un )
n
X
=
λα Z(uα )
α=1
en donde los λα representan los pesos o ponderaciones de los valores originales. Dichos pesos
se calculan en función de la distancia entre los puntos muestreados y el punto donde se va a hacer
la correspondiente predicción. La suma de los pesos debe ser igual a uno para que la esperanza
del predictor sea igual a la esperanza de la variable. Esto último se conoce como el requisito de
insesgadez.
Estadísticamente la propiedad de insesgadez se expresa a través de E (Z ∗ (u0 )) = E (Z(u0 )).
Asumiendo que el proceso es estacionario de media m (desconocida) y utilizando las propiedades
del
que la suma de las ponderaciones debe ser igual a uno, es decir,
Pnvalor esperado, se demuestra
∗ (u ) es el mejor predictor, lineal en este caso, porque los pesos
λ
=
1.
Se
dice
que
Z
0
α=1 α
se obtienen de tal manera que minimicen la varianza del error de predicción, es decir que minimicen la expresion V (Z ∗ (u0 ) − Z(u0 )).
Esta última es la característica distintiva de los métodos kriging, ya que existen otros métodos de
interpolación como el de distancias inversas o el poligonal, que no garantizan varianza mínima
deP
predicción. La estimación de los pesos se obtiene minimizando V (Z ∗ (u0 ) − Z(u0 )) sujeto
a nα=1 λα = 1.
Se tiene que V (Z ∗ (u0 ) − Z(u0 )) = V (Z ∗ (u0 )) − 2Cov [Z ∗ (u0 ), Z(u0 )] + V [Z(u0 )].
Desagregando las componentes de la ecuacion anterior se obtiene lo siguiente:
" n
#
X
∗
V [Z (u0 )] = V
λα Z(u0 )
α=1
=
n X
n
X
λα λβ Cov [Z(uα ), Z(uβ )]
α=1 β=1
En adelante se usará la siguiente notación: Cov [Z(uα ), Z(uβ )] = Cαβ y V [Z(u0 )] = σ 2 . De
lo anterior
" n
#
X
Cov [Z ∗ (uα ), Z(uβ )] = Cov
λα Z(uα , Z(u0 ))
α=1
n
X
=
α=1
n
X
=
Cov [λα Z(uα , Z(u0 ))]
λα Cα0
α=1
Entonces reemplazando, se tiene que:
V (Z ∗ (u0 ) − Z(u0 )) =
n
n X
X
α
β
λα λβ Cαβ − 2
n
X
α
λα Cα0 + σ 2 (0)
1.9 K RIGING :
23
PREDICCIÓN E INTERPOLACIÓN
P
Luego se debe minimizar la función anterior sujeta a la restricción nα=1 λα = 1. Este problema
de minimización con restricciones se resuelve mediante el método de los Multiplicadores de
Lagrange.
!
n X
n
n
n
X
X
X
σk2 =
λα λβ Cαβ − 2
λα Cα0 + 2µ
λα − 1
α
α
β
α=1
Siendo µ los Multiplicadores de Lagrange. Siguiendo el procedimiento acostumbrado para
obtener valores extremos de una función, se deriva e iguala a cero, en este caso con respecto
a λα y a µ.
n
X
∂ σk2
λβ C1β − 2C10 + 2µ
= 2
∂λ1
β=1
Por tanto
n
X
λβ C1β + µ = C10
β=1
De manera análoga se determinan las derivadas con respecto a λ2 , ..., λn :
n
X
λβ C2β + µ = C20
n
X
λβ Cnβ + µ = Cn0
β=1
..
.
β=1
por último derivamos con respecto a µ:
∂ σk2
∂µ
Por tanto
n
X
= 2
n
X
β=1
λα − 2
λα = 1
α=1
De las ecuaciones anteriores resulta un sistema de (n + 1) ecuaciones con (n + 1) incógnitas,
que matricialmente puede ser escrito como:
C11 C12 . . . C1n 1
λ1
C10
C21 C22 . . . C2n 1 λ2 C20
..
..
.. .. = ..
. . ..
.
. .
.
. . .
Cn1 Cn2 . . . Cnn 1 λn Cn0
1
1
... 1
0
µ
1
El sistema anterior se puede plantear:
Cαβ λ = Cα0
24
C APÍTULO 1. G EOSTADÍSTICA U NIVARIANTE
por lo cual los pesos que minimizan el error de predicción se determinan mediante la función de
covariograma a través de
λ = (Cαβ )−1 Cα0 .
Encontrando los pesos se calcula la prediccion en el punto u0 . De forma análoga se procede para
cada punto donde se quiera hacer predicción. La varianza de predicción del Kriging Ordinario
será por tanto:
2
σOK
= σ2 −
n
X
α=1
λα Cα0 − µ
Validación del kriging
Una modelización estadística general exige una validación a posteriori de sus resultados, y de
forma particular la modelización geostadística requiere de dicha validación y la basa en una
reestimación de los valores conocidos bajo las condiciones de implementación de los modelos
construidos. Estas implementaciones incluyen los modelos de variogramas, el tipo de kriging y
la elección de la estrategia general de modelización.
Existen diferentes métodos para evaluar la bondad de ajuste del modelo de semivariograma
elegido con respecto a los datos muestrales y por ende de las predicciones hechas con kriging.
La técnica más empleada es la de Validación Cruzada (cross-validation, CV) sirve para comparar valores estimados por los modelos con los reales. La idea consiste en un proceso iterativo
en el que cada vez se excluye un dato de la muestra y se estima con el resto de los datos el
modelo de semivariograma escogido, predecir vía kriging el valor de la variable en estudio en la
ubicación del punto que se excluyó. Cada uno de estos valores se compara, por ejemplo mediante regresión lineal, con el valor real. Buenos coeficientes de correlación / determinación serán
indicativos de una correcta modelización. Si el modelo de semivarianza elegido describe bien la
estructura de autocorrelación espacial, entonces la diferencia entre el valor observado y el valor
predicho debe ser pequeño. Este procedimiento se realiza de forma secuencial con cada uno
de los puntos muestrales y así se obtiene un conjunto de n errores de predicción. Lo usual es
calcular medidas que involucren a estos errores de predicción para diferentes modelos de semivarianza y seleccionar aquél que optimice algún criterio como por ejemplo el del mínimo error
cuadrático medio (MECM). Una forma descriptiva de hacer la validación cruzada es mediante
un gráfico de dispersión de los valores observados contra los valores predichos. En la medida
en que la nube de puntos se ajuste más a una línea recta que pase por el origen, mejor sera el
modelo de semivariograma utilizado para realizar el kriging.
Sin embargo, la utilización de la validación cruzada para seleccionar modelos de semivariogramas, tiene algunas restricciones:
1. Un remuestreo del modelo de semivariograma no influye en los pesos y krigings. Así, los
valores de sill total no pueden ser obtenidos por validación cruzada de valores restimados.
2. El sill relativo y el comportamiento del semivariograma en el origen nugget, no pueden
ser usados simultáneamente con la validación cruzada.
1.9 K RIGING :
PREDICCIÓN E INTERPOLACIÓN
25
3. Si el modelo es inadecuado, entonces no está claro qué parámetros deben ser cambiados.
Representación de las predicciones
Una vez se ha hecho la predicción en un conjunto de puntos diferentes de los muestrales vía
kriging, se debe elaborar un mapa que de una representación global del comportamiento de
la variable de interés en la zona estudiada. Los más empleados son los mapas de contornos,
los mapas de residuos y los gráficos tridimensionales. En el caso de los mapas de contornos,
en primer lugar se divide el área de estudio en un enmallado y se hace la predicción en cada
uno de los nodos de este mismo. Posteriormente se unen los valores predichos con igual valor,
generando asi las líneas de contorno (isolíneas de distribución). Este gráfico permite identificar
la magnitud de la variable en toda el área de estudio. Es conveniente acompañar el mapa de
interpolaciones de la variable con los correspondientes mapas de isolíneas de los errores y de
las varianzas de predicción (posiblemente estimados a través de métodos matemáticos), con el
propósito de identificar zonas de mayor incertidumbre respecto a las predicciones.
Intervalos de Confianza
Asumiendo que los errores de predicción siguen una distribución normal estándar y que son
del 100(1 − α)%, 0 < α < 1, para Z(u) es:
hindependientes, un intervalo de confianza
i
∗
∗
∗
α
α
z (u) − z1− 2 σk , z (u) + z1− 2 σk , con z el valor calculado de la predicción y z1− α2 el percentil de una normal estándar.
1.9.3
Kriging universal(UK)
Este tipo de kriging (UK) considera que la media local no es conocida y varía suavemente en
cada vecindad local W (u). La componente de tendencia se modeliza como una combinación lineal de funciones fl (u) de las coordenadas. Para tratar este tipo de variables es frecuente descomponer la variable Z(u) como la suma de la tendencia, tratada como una función determinística,
más una componente estocástica estacionaria de media cero. Asúmase que Z(u) = m(u)+ǫ(u),
con E (ǫ(u)) = 0, V (ǫ(u)) = P
σ 2 y por consiguiente E(Z(u)) = m(u). La tendencia puede
p
expresarse mediante m(u) =
l=1 al fl (u) donde las funciones fl (u) son conocidas y p es
el número de términos empleados para ajustar m(u). El predictor Kriging Universal se define
como:
Z ∗ (u0 ) =
n
X
α=1
λα Z(uα )
26
C APÍTULO 1. G EOSTADÍSTICA U NIVARIANTE
este será insesgado si:
n
X
E
n
X
α=1
p
X
α=1
n
X
E (Z ∗ (u0 )) = m (u0 )
!
λα Z(uα )
λα m(uα )
α=1
p
X
λα
al fl (uα )
l=1
n
X
al
λα fl (uα )
α=1
n
X
l=1
= m (u0 )
!
!
!
= m (u0 )
=
=
λα fl (uα ) =
α=1
p
X
l=1
p
X
l=1
p
X
al fl (u0 )
al fl (u0 )
fl (u0 )
l=1
La obtención de los pesos en el Kriging Universal, análogo a los otros métodos kriging, se hace
de tal forma que la varianza del error de predicción sea mínima.
V (Z ∗ (u0 ) − Z(u0 )) = E (Z ∗ (u0 ) − Z(u0 ))2
n
X
= E
=
α=1
n X
n
X
α
β
λα (m(uα ) − ǫ(uα ))
!
− (m(u0 ) − ǫ(u0 ))
λα λβ=1 E (ǫ(uα=1 )ǫ(uβ )) − 2
n
X
!2
λα E (ǫ(uα )ǫ(u0 )) + E (ǫ(u0 ))2
α=1
usando:
1. Cαβ = Cov(ǫ(uα ), ǫ(uβ ))
2. σ 2 = E (ǫ(u0 ))2
se tiene
V (Z ∗ (u0 ) − Z(u0 )) =
n X
n
X
α=1 β=1
λα λβ Cαβ − 2
n
X
λα λβ Cλ0 + σ 2
α=1
Luego incluyendo la restricción dada por la condición de insesgadez, se debe minimizar:
2
σ =
n X
n
X
α=1 β=1
λα λβ Cαβ + 2
n
X
α=1
2
λα Cα0 + σ +
p
X
l=1
µl
"
n
X
α=1
λα fl (uα ) − fl (u0 )
#
1.9 K RIGING :
27
PREDICCIÓN E INTERPOLACIÓN
o en términos de la funcion de semivarianza
" n
#
p
n X
n
n
X
X
X
X
σ2 = −
λα λβ + 2
λα + σ 2 +
µl
λα fl (uα ) − fl (u0 )
α=1 β=1
α=1
α=1
l=1
derivando la expresion anterior respecto a λ1 , λ2 , . . . , λn , µ1 , µ2 , . . . , µp e igualando a cero las
correspondientes derivadas se obtienen las siguientes ecuaciones:
n
X
p
X
λβ γαβ +
β=1
l=1
n
X
µl fl (uα ) = γα0 , α = 1, 2, . . . , n
λβ fl (uβ ) = fl (u0 ), β = 1, 2, . . . , p
β=1
en términos matriciales
γ11
γ21
..
.
γn1
f11
..
.
fp1
γ12
γ22
..
.
...
...
..
.
γ1n
γ2n
..
.
f11
f21
..
.
...
...
..
.
f1n
f2n
..
.
γn2 . . .
f12 . . .
..
..
.
.
fp2 . . .
γnn
f1n
..
.
f1n . . .
0
...
..
..
.
.
0
...
fpn
0
..
.
fpn
0
λ1
λ2
...
λn
µ1
...
µn
=
γ10
γ20
...
γn0
f10
...
fp0
donde flβ = fl (uβ ) es la l-ésima función en el punto j-ésimo. La varianza de predicción del
Kriging Universal esta dada por:
σU2 K
=
n
X
α=1
λα γα0 +
p
X
µl fl (u0 )
l=1
Nótese que si p = 1 y fl (u) = 1, el sistema de ecuaciones del Kriging Universal y la varianza
de predicción coinciden con las del Kriging Ordinario. En este orden de ideas puede decirse que
el Kriging Ordinario es un caso particular del Kriging Universal.
1.9.4
Cokriging
El término cokriging se utiliza para los métodos de regresión en los que intervienen varios atributos. Supongamos, pues, que disponemos de dos variables regionalizadas Z, Y definidas en las
mismas localizaciones. La ecuación para la estimación del valor de la variable principal Z en la
localización u0 viene dada por
Z ∗ (u0 ) =
n1
X
α1 =1
λα1 (u0 )Z(uα1 ) +
n2
X
λ∗α2 (u0 )Y (u∗α2 )
α2 =1
Este tipo de kriging requiere un modelo para la matriz de funciones de covarianza, incluida la
covarianza de Z, CZ (h), la covarianza de Y , CY (h), la covarianza cruzada de Z −Y , CZY (h) =
Cov {Z(u), Y (u + h)}, y la covarianza cruzada de Y − Z, CY Z (h).
Capítulo 2
Geostadística Multivariante
Hasta ahora se ha estudiado como estimar una propiedad utilizando los valores conocidos de
dicha propiedad obtenidos en puntos vecinos o cercanos o bien como hacer uso de una función
de tendencia para guiar la estimación de la propiedad.
multivariantes:
Se consideran entonces procesos espaciales
Z(U ) = (Z1 (u), Z2 (u), . . . , Zp (u))′ /u ∈ D , D ⊂ Rd De forma que:
• Estos p procesos espaciales univariantes se suponen intercorrelacionados.
• Cada Zi (u) se observa en un conjunto Si = {ui,1 , ui,2 , . . . , ui,ni } de ni > 0 localizaciones. Dos conjuntos Si y Sj son, en general, diferentes para i 6= j.
• Zi (u) = mi (u) + Yi (u), i = 1, 2, ·, p donde mi (u) es la componente determinista y representa los cambios o evolución a gran escala e Yi (u) es la componente aleatoria (errática)
y representa el comportamiento local o evolucióon a pequeña escala.
Sin pérdida de generalidad, suele suponerse que la variable de interés (variable a predecir) es Z1
mientras que las restantes se denominan variables secundarias.
2.1
Análisis estructural
Al igual que en el caso univariante, sólo se dispone de una realización del proceso multivariante
y por eso es necesario asumir ciertas hipótesis de estacionariedad sobre Z(u).
Proceso multivariante de segundo orden
• Existe E [Zi(u)] = mi , ∀i = 1, 2, . . . , p, ∀u ∈ D.
• Existe Cov (Zi (u), Zj (u + h)) = Ci,j (h); ∀i, j = 1, 2, . . . , p, ∀u ∈ D y ∀h ∈ Rd .
Las funciones Ci,j (h) reciben el nombre de covariogramas cruzados.
29
30
C APÍTULO 2. G EOSTADÍSTICA M ULTIVARIANTE
1. En general los covariogramas cruzados, al contrario que en el caso unidimensional, no son
simétricos:
Ci,j (h) = Cov (Zi (u), Zj (u + h)) 6= Cov (Zj (u), Zi (u + h)) = Ci,j (−h).
2. Se verifica que Ci,j (h) = Cj,i (−h)
3. Por la desigualdad de Cauchy-Schwarz
|Ci,j (h)|2 ≤ |Ci,j (h)| |Cj,j (h)| ≤ |Ci,i (0)| |Cj,j (0)|,
por lo que los covariogramas cruzados están siempre acotados superiormente.
Proceso multivariante intrínsecamente estacionario
• Existe E [Zi(u) − Zi(u + h)] = mi (h), ∀i = 1, 2, . . . , p, ∀u ∈ D.
• Existe
1
2 Cov ((Zi (u) − Zi (u + h)) , (Zj (u) − Zj (u + h))) = γi,j (h);
∀i, j = 1, 2, . . . , p, ∀u ∈ D y ∀h ∈ Rd .
Las funciones γi,j (h) reciben el nombre de semivariogramas cruzados.
1. Los semivariogramas cruzados son simétricos: γi,j (h) = γi,j (−h).
2. Los semivariogramas cruzados son nulos en el origen: γi,j (0) = 0.
3. En el caso de variables estacionarias de segundo orden, existe una relación entre semivariograma y covariograma cruzados:
γi,j (h) = Ci,j (0) −
1
[Ci,j (h) + Ci,j (−h)]
2
4. El semivariograma cruzado es estimable sólo si Si = Sj .
Es importante señalar que ésta no es la única definición de semivarigrama cruzado que puede
encontrarse en la bibliografía ya que existen diversas formas de generalizar los semivariogramas unidimensionales al caso multidimensional. Así, por ejemplo, una segunda definición muy
extendida es:
1
Var (Zi (u) − Zj (u + h)) = γi,j (h); ∀i, j = 1, 2, . . . , p; ∀u ∈ D y ∀h ∈ Rd .
2
A esta segunda expresión se le suele denominar pseudosemivariograma cruzado.
1. Por lo general, los pseudosemivariograma cruzados no son simétricos:
γi,j (h) = γj,i (−h) 6= γi,j (−h)
2. Los pseudosemivariograma cruzados pueden ser no nulos en el origen: γi,j (0) ≥ 0.
3. En el caso de variables estacionarias de segundo orden, no existe una relación entre pseudosemivariograma y covariograma cruzados.
2.2 C OKRIGING
31
4. El pseudosemivariograma cruzado siempre es estimable, aún cuando Si 6= Sj .
En todo caso, si los covariogramas, o los semivariogramas, o los pseudosemivariograma cruzados son sólo función de la distancia khk y no de la dirección del vector, se denominan isotrópicos. En caso contrario se habla de anisotropía.
A continuación estudiaremos algunas técnicas geoestadísticas propuestas para obtener estimaciones de la propiedad de interés cuando se dispone de observaciones de otras variables
secunadarias relacionadas con la variable en estudio.
Entre este tipo de técnicas se encuentran:
• Cokriging Simple y Ordinario
• Cokriging colocado (collocated cokriging)
Al igual que en el caso de geoestadística univariada, lo fundamental es contar con una herramienta que mida la correlación espacial de las variables involucradas y su interrelación.
La correlación espacial de cada una de las variables involucradas se obtiene como antes a
través de la función de covarianza o del variograma.
La correlación espacial conjunta o la interrelación se obtiene a través de la función de covarianza cruzada que se estudiará a continuación
2.2
Cokriging
Planteamiento básico de la estimación por Cokriging:
Considerar la estimación de Z1 (u) como una combinación lineal de las observaciones disponibles
de Z1 más combinaciones lineales de las observaciones de las variables relacionadas.
Ejemplo:
• Z, propiedad o variable principal, por ejemplo porosidad.
• Y , información o variable secundaria, por ejemplo impedancia acústica.
∗
Zcok
(u) =
N
X
α=1
λα (u)Z(uα ) +
M
X
βα (u)Y (xα )
α=1
El primer sumando es una combinación lineal de la variable principal y el segundo de la variable
secundaria.
En el caso general lo único que se complica es la notación:
• Z, propiedad o variable principal, por ejemplo porosidad.
• Yi , variables secundarias, por ejemplo atributos sísmicos.
32
C APÍTULO 2. G EOSTADÍSTICA M ULTIVARIANTE
∗
Zcok
(u)
=
N
X
λα (u)Z(uα ) +
α=1
N1
X
βα1 (u)Y1 (xα1 ) + . . . +
α1 =1
Nk
X
βαk (u)Yk (xαk )
αk =1
El primer sumando es una combinación lineal de la variable principal y los siguientes de las
variables secundarias.
∗
Zcok
(u)
=
N
X
λα (u)Z(uα ) +
α=1
2.2.1
Nj
K X
X
βαj (u)Yj (xαj )
j=1 αj =1
Cokriging simple
El caso más simple se denomina cokriging simple y la hipótesis básica es la estacionaridad de
todas las variables junto con el hecho de que se asume que las medias de todas las variables son
conocidas. Esto es,
E(Z(u)) = m conocida
E(Yj (u)) = mj conocida ∀j.
A continuación se obtienen las ecuaciones de cokriging simple en el caso en que se considera
sólo una variable secundaria. En este caso el estimador propuesto es,
∗
Zcok
(u) = m +
N
X
α=1
λα (u)(Z(uα ) − m) +
N1
X
αj =1
βα1 (u)(Y1 (xα1 ) − m1 )
Al igual que en el caso anterior, las condiciones de optimalidad son:
∗ (u)) = E (Z(u)).
1. Estimador insesgado, E (Zcok
∗ (u)] mínima.
2. Var [Z(u) − Zcok
La primera condición se obtiene automáticamente al utilizar que:
E(Z(uα ) − m) = 0
E(Y1 (xα )) − m1 = 0
Con lo cual,
∗
E(Zcok
(u)) = m = E(Z(u))
La condición de varianza mínima se obtiene derivando respecto a los parámetros α y β e
igualando a cero cada una de las derivadas obtenidas.
∗ (u)]
∂Var [Z(u) − Zcok
∂λj
∗ (u)]
∂Var [Z(u) − Zcok
∂βj
= 0, j = 1, 2, . . ., N
= 0, j = 1, 2, . . . , N1
2.2 C OKRIGING
33
Para calcular explícitamente la expresión de la varianza hay que proceder con cautela debido
a que aparecen nuevos términos a considerar.
∗
∗
∗
Var [Z(u) − Zcok
(u)] = Var [Z(u)] + Var [Zcok
(u)] − 2Cov (Z(u), Zcok
(u))
T1 = Var [Z(u)] = σ 2
∗
T2 = Var [Zcok
(u)]
X
X
= Var
λi (Z(ui − m)) + Var
βj (Y (xj − mj ))
X
X
+ 2Cov
λi (Z(ui − m)),
βj (Y (xj − mj ))
XX
XX
=
λi λj CZ (ui − uj ) +
βi βj CY (xi − xj )
XX
+ 2
λi βj CZY (ui − xj )
∗
T3 = 2Cov (Z(u), Zcok
(u))
X
X
= 2
λi CZ (u − ui ) + 2
βj CZY (u − xj )
Al calcular las derivadas respectivas se obtiene que
∗ (u)]
∂Var [Z(u) − Zcok
∂λi
∗ (u)]
∂Var [Z(u) − Zcok
∂βi
= 2
N
X
j=1
λj CZ (ui − uj ) + 2
N
X
βj CZY (ui − xj )
N
X
λj CZY (ui − xj )
j=1
− 2CZ (u − ui ), i = 1, 2, . . ., N
= 2
N
X
j=1
βj CY (xi − xj ) + 2
j=1
− 2CZY (u − xi ), i = 1, 2, . . . , N1
Ahora la expresión detallada del sistema de ecuaciones es
CZ
CZY
λ
CZU
=
CY Z CY
β
CY U
Siendo cada una de las submatrices las siguientes:
CZ (0)
CZ (u1 − u2 )
CZ (u2 − u1 )
C
Z (0)
..
..
.
.
CZ
CZ (uN − u1 )
CZ (uN − u2 )
=
CY Z (x1 − u1 ) CY Z (x2 − u1 )
CY Z
CY Z (x2 − u1 ) CY Z (x2 − u2 )
..
..
.
.
. . . CZ (u1 − uN )
. . . CZ (u2 − uN )
.
. . . ..
...
...
...
...
CY Z (x1 − uN ) CY Z (xN − u2 ) . . .
CZ (0)
CY Z (x1 − uN )
CY Z (x2 − uN )
..
.
CY Z (xN − uN )
34
C APÍTULO 2. G EOSTADÍSTICA M ULTIVARIANTE
2.2.2
CZY
CY
=
CY Z (u1 − x1 )
CY Z (u2 − x1 )
..
.
CY Z (u1 − x2 )
CY Z (u2 − x2 )
..
.
. . . CY Z (u1 − xN )
. . . CY Z (u2 − xN )
.
. . . ..
CY Z (uN − x1 ) CY Z (uN − x2 ) . . . CY Z (uN − xN )
CY (0)
CY (x1 − x2 )
. . . CY (x1 − xN )
CZ (x2 − x1 )
CY (0)
. . . CY (x2 − xN )
..
..
..
.
.
... .
CY (xN − x1 ) CY (xN − x2 ) . . . CY (0)
λ1
CZ (u − u1 )
λ2
CZ (u − u2 )
..
..
.
.
λN C Y U
CZ (u − uN )
λ
=
CY U = CY (u − x1 )
β
β
1
β2
CY (u − x2 )
..
..
.
.
βN
CY (u − xN )
Cokriging ordinario
Al igual que en el caso de kriging ordinario, se asume que las medias de las variables son
desconocidas y se imponen condiciones para filtrarlas.
El estimador propuesto es:
∗
Zcok
(u)
=
N
X
λα (u)Z(uα ) +
α=1
Nj
K X
X
βαj (u)Yj (xαj )
j=1 αj =1
Con lo cual,
∗
E (Zcok
(u))
= m
X
λα +
K
X
j=1
mj
Nj
X
β αj
αj =1
P
PN
Y se obtienen las condiciones λα = 1, αjj=1 βαj = 0, j = 1, 2, . . . , K.
Ahora se procede nuevamente como en el kriging ordinario pero con K + 1 parámetros
de Lagrange. Cuando se tiene tan solo una variable secundaria, el sistema de ecuaciones del
cokriging ordinario es,
CZ
CZY 1 0
λ
CZU
CY Z CY
0 1
β = CY U
1
0
0 0 µ1 1
0
1
0 0
µ2
0
Obsevaciones:
2.3 C OKRIGING UNIVERSAL
35
1. Con sólo 2 variables se requieren 4 funciones de covarianza. En general, con N variables
secundarias se requieren 2N +1 funciones de covarianza.
2. Debe existir una correlación lineal entre las variable principal y las variables secundarias.
3. Las variables secundarias deben poseer un número mucho mayor de observaciones que la
variable principal.
4. Imposible estimar las covarianzas cruzadas con datos NO coincidentes.
5. Resultados satisfactorios se obtienen con datos parcialmente coincidentes.
6. Con datos totalmente coincidentes. Conveniente para estimar de manera consistente el
tope y la base de un yacimiento. No se obtiene una mejora sustancial sobre los métodos
de kriging cuando la variable secundaria es la información sísmica.
Cuando las variables están intrínsicamente relacionadas, es decir, cuando ocurre que los
modelos de variograma o covarianza de todas las variables son proporcionales a un mismo
modelo de variograma o covarianza, entonces el kriging y el cokriging con datos totalmente
coincidentes son iguales.
2.3
Cokriging universal
Representamos por {Zi (ui,j ), i = 1, . . . , p; j = 1, . . . , n1 } la muestra a partir de la cual pretendemos predecir Z1 (u0 ), u0 ∈ D. Al igual que en el caso univariante, dependiendo de
las suposiciones sobre las funciones de tendencia m1 (u), ..., mp (u) se distinguen tres tipos de
predicción lineal óptima multivariante:
1. Cokriging simple. Si las funciones de tendencia son conocidas.
2. Cokriging ordinario. Si las funciones de tendencia son desconocidas pero constantes.
3. Cokriging universal. Si las funciones de tendencia son desconocidas.
Evidentemente, el último caso es el más general y, por ello, el más utilizado. En el caso de
cokriging universal se asume que cada tendencia mi (u) puede expresarse como combinación
lineal de funciones regresoras conocidas:
mi (u) =
Li
X
ai,l fil (u); i = 1, 2, . . . , p.
l=0
El predictor cokriging se define como el mejor predictor lineal insesgado (BLUP) calculado con
todas las variables observadas:
Z1∗ (u0 ) =
p X
ni
X
i=1
j
λi,j Zi (ui,j ).
36
C APÍTULO 2. G EOSTADÍSTICA M ULTIVARIANTE
2.4 Condición de insesgadez
Para que el predictor sea insesgado son condiciones necesarias:
n1
X
λ1,j f1l (u1,j ) = f1l (u0 ); l = 0, 1, . . . , L1 ; u1,j ∈ S1 .
j
ni
X
j
λi,j fil (ui,j ) = 0; l = 0, 1, . . . , Li ; ui,j ∈ Si , i = 2, . . . , p.
Si ambas se verifican, entonces:
E [Z1∗ (u0 )]
=
L1
X
a1,l f1l (u) = E [Z1 (u0 )] .
l=0
Condición de varianza mínima
Al igual que en el caso unidimensional, se trata de un problema de minimización de varianza
de predicción sujeto a las restricciones necesarias para asegurar la insesgadez del predictor. La
función a minimizar se plantea utilizando L1 + . . . + Lp + p Multiplicadores de Lagange:
L1
n1
X
X
Var (Z1∗ (u0 ) − Z1 (u0 )) + 2
µ1,l
λ1,j f1l (u1,j ) − f1l (u0 )
l=0
+ 2
p X
Li
X
i=2 l=0
j=1
µi,l
ni
X
j=1
λi,j fil (ui,j )
Mediante derivadas parciales de la expresión anterior se obtiene la expresión matricial de la cual
se deduce el vector de pesos óptimo y la varianza de predicción. A continuación se muestra el
aspecto del sistema matricial a resolver en el caso de p = 2 variables estacionarias de segundo
orden y con tendencióas m1 y m2 desconocidas pero constantes (Cokriging Ordinario).
Capítulo 3
Análisis de datos funcionales
En muchas áreas se ha empezado a trabajar con grandes bases de datos, que cada vez con más
frecuencia, corresponden a observaciones de una variable aleatoria tomadas a lo largo de un
intervalo continuo (o en discretizaciones cada vez más extensas de este intervalo continuo).
En campos como la espectrometría, el resultado de la medición es una curva que representa
a la muestra concreta que al menos se ha evaluado en una centena de puntos. Este tipo de datos,
que llamaremos datos funcionales, surgen de manera natural en muchas disciplinas, y como este
ejemplo podríamos citar muchos otros en diversos campos como la economía, ingeniería, medio
ambiente, . . .. Ante estos nuevos retos surge como respuesta la estadística de datos funcionales
que originalmente identificaba dato funcional con función en un intervalo continuo. Básicamente, los problemas a los que se debe enfrentar la estadística con datos funcionales responde
a las mismas necesidades que la estadística clásica. Estos se podrian categorizar de la siguiente
manera:
1. Explorar y describir el conjunto de datos funcionales resaltando sus características más
importantes.
2. Explicar y modelar la relación entre una variable dependiente y una independiente (modelos de regresión).
3. Métodos de Clasificación Supervisada o no Supervisada de un conjunto de datos respecto
a alguna característica.
4. Contraste, validacion y predicción.
En ambos casos todas las técnicas incluídas están restringidas al espacio de funciones L2 ,
es un espacio con características específicas que lo hacen especialmente tratable. Una variable
aleatoria X se dice que es una variable funcional si toma valores en un espacio funcional E
(Espacio normado o seminormado completo), como se puede ver en [8].
Un conjunto de datos funcionales {Xn . . . , Xn } es la observación de n variables funcionales
X1 . . . , Xn idénticamente distribuidas.
La primera dificultad que siempre tendremos al analizar datos funcionales, es encontrar una
representación adecuada para los datos.
37
38
C APÍTULO 3. A NÁLISIS DE DATOS FUNCIONALES
Estas defniciones se pueden aplicar a muchos tipos de espacios. En particular, Rp con las
métricas usuales es un espacio funcional y por tanto puede deducirse que toda técnica que se
desarrolle para datos funcionales puede ser aplicada con ciertas garantías en el entorno multivariante. El espacio más comunmente usado cuando se habla de datos funcionales es el espacio L2 [S], esto es, las funciones de cuadrado integrable en el intervalo S = [a, b] ⊂ R.
p
Desde
un punto de vista
R másp general podemos tener datos funcionales en la familia: L [S, µ] =
f : S → R tal que |f (t)| dµ , donde (S, µ) es un espacio de medida y 1 < p < ∞. Estos
espacios son semi-normados salvo el caso p = 2 que es el único de esta familia que es un espacio
de Hilbert separable. Cuando se desarrolla una nueva técnica para datos funcionales la primera
preocupación es siempre determinar en que espacio funcional vamos a trabajar. Esto determinará decisivamente el conjunto de herramientas que podremos usar. Una preocupación similar
la tendremos al aplicar una técnica de datos funcionales a un conjunto de datos. La métrica del
espacio funcional que se elija para encuadrar estos datos debe ser coherente con la interpretación
física del fenómeno que describan.
En general, la representación de un dato funcional en una base ortonormal proporcionará
ventajas tanto desde el punto de vista teórico como práctico sirviendo de puente entre la inevitable discretización del dato funcional y su verdadera forma funcional.
Una base es un conjunto de funciones conocidas e independientes {φk }k∈N tales que cualquier
función puede ser aproximada, tan bien como se quiera, mediante una combinación lineal de K
de ellas con K suficientemente
grande. De esta forma, la observación funcional puede aproxiP
marse como x(t) ≈ K
c
φ
(t).
k=1 k k
Si los elementos de la base son fácilmente diferenciables hasta orden q tenemos x(q) (t) ≈
PK
(q)
k=1 ck φk (t).
Básicamente, la idea clave cuando se pueden usar bases ortonormales es representar cada
dato funcional en la base usando aquellas coordenadas que son más significativas. Debido a la
alta dimensión de los datos funcionales, se elige en general un número K para representar los
datos en el subespacio, convirtiendo el problema de dimensión infinita en un problema multidimensional. La elección del parámetro K y de la base más adecuada para los datos observados
se antoja crucial y, en principio, no hay ninguna regla que permita hacer una selección óptima
de forma universal. El parámetro K es, en cierto modo, un parámetro de suavización de los
datos funcionales. Si K es bajo tendremos un modelo muy manejable pero posiblemente habremos perdido información relevante. Si K es alto representaremos muy bien los datos pero el
problema de la dimensión cobra importancia. Si atendemos a la elección de la base, para datos
periódicos se suele emplear la base de Fourier y para datos no periódicos la base B-spline o la
Wavelet. Una base muy popular está basada en la expansión de Karhunen-Loève que no es más
que la extensión del análisis de componentes principales multivariante a procesos estocásticos
y por añadidura a datos funcionales. Calculando a partir del operador momento de segundo
orden muestral las correspondientes autofunciones y autovalores es posible construir específicamente una base ortonormal adaptada para cada conjunto de datos. Esta técnica se denomina
Componentes Principales Funcionales (FPCA) y ha dado lugar a muchas técnicas interesantes
para datos funcionales. Sin embargo, esta técnica puede ser muy sensible a la aparición de datos
atípicos y la representación del dato funcional puede no ser relevante para el objetivo del estudio como podría ser la relación con otra variable funcional o no. La decisión sobre qué base
3.1 P RELIMINARES
39
elegir debe tomarse en función del objetivo del estudio y los datos y aprovechando las ventajas
e inconvenientes que presenta cada tipo de base. Si se trunca cualquiera de estas bases en un
número determinado de elementos obtendremos una semimétrica que también podremos usar
para manejar los datos funcionales. En este caso, cualquier métrica o semi-métrica en el espacio no es más que una forma de determinar qué elementos del espacio están cercanos y cuáles
lejanos.
La estadística con datos funcionales tiene frontera con otros campos relevantes de la estadística como el análisis multivariante, el análisis de datos longitudinales o las series temporales.
Como se comentó anteriormente, una técnica de datos funcionales puede aplicarse con ciertas
garantías a datos multivariantes. Al revés, en general, no es cierto. Para la mayoría de las técnicas multivariantes que basan mucho de su trabajo en propiedades del álgebra matricial puede ser
un problema casi insalvable tratar datos funcionales de alta frecuencia con seguramente, muy
fuerte colinealidad. Según aumenta el grado de resolución con el que somos capaces de ver una
curva, más difícil resulta para las técnicas multivariantes obtener un resultado convirtiendo el
aumento de resolución en una dificultad más que en una oportunidad de obtener mejor información. Algo similar podría decirse del análisis de datos longitudinales. En este campo se obtienen
medidas repetidas a lo largo del tiempo para el mismo sujeto, pero en general, éste es un número
pequeño y las técnicas multivariantes pueden adaptarse para trabajar con ellas. La principal dificultad para tratar datos longitudinales como datos funcionales suele ser precisamente la baja
calidad de representación de las curvas. La relación con el campo de las series temporales es
totalmente diferente. Así, ejemplos clásicos de datos funcionales se han construido a base de
cortar una serie temporal en ciclos homogéneos. Por ejemplo, en [25] se usan los datos de un
índice bursátil estadounidense troceados por años (como unidad funcional) para deducir a partir
de la forma de cada curva anual la tipología de los distintos años (de expansión, de crisis, ...).
Considerados los datos como una serie temporal, el objetivo es predecir alguno de los periodos
del próximo año. Como conjunto de datos funcionales, el objetivo es resumir la información
y el resultado será siempre un dato funcional, esto es, un ciclo anual completo. Por tanto, la
relación entre estos dos campos es peculiar. Muchas veces trabajan sobre la misma información
pero desde ópticas completamente diferentes.
3.1
Preliminares
Se presentan unas definiciones preliminares sobre medidas clásicas y distancias entre vectores
en Rp en contexto funcional. Se asume que X(t), Y (t), Z(t), t ∈ T son funciones definidas en
algún espacio de funciones.
• Producto interior
hX(t), Y (t)i =
Z
Propiedades:
1. Simetría: hX(t), Y (t)i = hY (t), X(t)i.
2. Positividad: hX(t), X(t)i ≥ 0.
X(t)Y (t)dt.
T
40
C APÍTULO 3. A NÁLISIS DE DATOS FUNCIONALES
3. Bilinealidad: haX(t) + bY (t), Z(t)i = a hX(t), Z(t)i + b hY (t), Z(t)i, para cualesquiera números reales a y b.
• Norma
kX(t)k2
q
kX(t)k2 , donde
Z
= hX(t), X(t)i =
X(t)X(t)dt.
kX(t)k =
T
Propiedades:
1. kX(t)k ≥ 0.
2. kaX(t)k = |a| kX(t)k, para cualquier número real a.
3. kX(t) + Y (t)k ≤ kX(t)k + kY (t)k.
p
4. |hX(t), Y (t)i| ≤ kX(t)k kY (t)k = |hX(t), X(t)i| |hY (t), Y (t)i|.
5. −1 ≤
|hX(t),Y (t)i|
(kX(t)k(Y (t)))
≤1
Un dato funcional χi (t)t ∈ T , se representa generalmente como un conjunto finito de pares
(tj , yij ), tj ∈ T , j = 1, · · · , M e yij = χj (tj ) (si no hay ruido blanco) o yij = χj (tj ) + ǫj
(si hay ruido blanco), ǫj tiene media cero. El conjunto de puntos {tj }M
j=1 ⊂ T puede ser considerado el mismo para todas las funciones en un conjunto de datos funcionales. Métodos de
interpolación (si no hay ruido blanco) o métodos no paramétricos de suavización (en caso contrario) son comunmente usados para representar los conjuntos discretos (tj , yij ), j = 1, · · · , M ,
como una función real χi . En este sentido se puede decir que el hereda la metodología de la
estimación no paramétrica funcional.
3.2 Técnicas exploratorias para Datos Funcionales
En [25] se recogen como herramientas para resumir los datos: la media funcional, la varianza
funcional y la función de covarianza. En un capítulo posterior se emplean las componentes principales funcionales como herramientas del análisis descriptivo. Básicamente esto era todo el
análisis descriptivo de un conjunto de datos funcionales. Sin embargo, el análisis descriptivo se
revela decisivo para el tratamiento de datos funcionales. La cuestión se complica si pensamos
que nuestros datos pueden estar sujetos a métricas no usuales y por tanto, las representaciones
usuales engañarían nuestra mirada. En este campo se echan en falta herramientas descriptivas
que en otros ámbitos como el multivariante se han desarrollado expresamente. Manejando diferentes conceptos sobre profundidad estadística también se han definido extensiones de medidas
robustas para datos funcionales, incluyendo incluso el bootstrap para datos funcionales como
herramienta para analizar la variabilidad de los distintos estimadores. Durante todo este trabajo
estamos en L2 (T ).
3.2 T ÉCNICAS EXPLORATORIAS PARA DATOS F UNCIONALES
3.2.1
41
Media, Varianza, covarianza, correlación, covarianza cruzada y correlación
cruzada
• Media: X t =
1
n
Pn
i=1 Xi (t).
′
Xi (t) − X(t) Xi (t) − X(t) .
1 Pn
• Covarianza: Cov(X(t1 ), X(t1 )) = n−1
i=1 (Xi (t1 ) − x(t1 )) (Xi (t2 ) − x(t2 )).
• Varianza: Var(X) =
1
n−1
Pn
i=1
• Correlación: Corr(X(t1 ), X(t1 )) = √
Cov(X(t1 ),X(t1 ))
.
Var(X(t1 ))Var(X(t2 ))
• Covarianza cruzada: Cov(X(t1 ), Y (t2 )) =
1
n−1
• Correlación cruzada: Corr(X(t1 ), Y (t2 )) = √
3.2.2
Pn
i=1
Xi (t1 ) − X(t1 )
Cov(X(t1 ),Y (t2 ))
.
Var(X(t1 ))Var(Y (t2 ))
Yi (t2 ) − Y (t2 ) .
Componentes principales
Componentes principales Multivariante
Las componentes principales son una herramienta básica en el entorno multivariante diseñada
para explicar un conjunto de datos X = (Xij )nxp mediante una combinación de variables
ortonormales que cumplen la propiedad de maximizar la varianza. Es la solución del siguiente
algoritmo:
• P
Encontrar el vector ξ1 de norma 1 tal que la combinación lineal f~1 = ξ ′ X maximice
p
2
i=1 fi1 .
• Repetir el proceso anterior, exigiendo además en el paso m que ξm ⊥ξk , k < m.
Componentes principales para FDA (FPCA)
Algoritmo adaptado para datos funcionales:
• Encontrar
P la función ξ1 (s) de norma 1
imice pi=1 fi1 2 .
R
R
ξ1 (s)2 ds = 1 tal que f1 = ξ1 (s)Xi (s) max-
• Repetir el proceso anterior, exigiendo además en el paso m que ξm (s)⊥ξk (s), k < m.
La descomposición en esta base ortonormal permite escribir cada dato como:
X̂i (t) =
K
X
fik ξk (t)
k=1
R
donde fik es el valor de la componente principal Xi ξk .
Las características más notables de las componentes principales son las siguientes:
42
C APÍTULO 3. A NÁLISIS DE DATOS FUNCIONALES
• Resumen rápidamente la información de la muestra.
• Permiten obtener una base ortonormal empírica adaptada a los datos.
• Pueden servir para detectar datos atípicos (aunque también pueden esconderlos).
• La rotación de las componentes pueden ayudar a encontrar mejores explicaciones de las
componentes.
• Posibilidad de modificar el algoritmo para conseguir suavidad en las componentes.
3.3 Bases para datos funcionales
Una base es un conjunto de funciones conocidas e independientes {φk }k∈N tales que cualquier
función puede ser aproximada, tan bien como se quiera, mediante una combinación
Plineal de K
de ellas. De esta forma, la observación funcional puede aproximarse como χ(t) = k∈N ck φk (t) ≈
PK
k=1 ck φk (t).
Si los elementos de la base son fácilmente diferenciables hasta orden q tenemos χ(q) (t) =
P
PK
(q)
(q)
k∈N ck φk ≈
k=1 ck φk (t).
Las bases que se suelen usar para datos funcionales son las bases de Fourier si los datos son
períodicos, bases B-spline para cálculos rápidos y flexibles, bases de Wavelets apropiada para
modelizar discontinuidades, exponencial, potencial, polonomial, · · · .
Bibliografía adecuada, con respecto a esto se encuentra en los libros de [30] y [26].
Una vez que se ha decidido usar la representación en bases de las funciones surgen las tres
preguntas siguientes:
1. ¿Qué tipo de base de funcionaes son las más adecuadas?.
2. ¿Cuántas bases se deben seleccionar describir nuestros datos?.
3. ¿Cómo se determinan los coeficientes c basados en las funciones parcialmente observada?.
En el libro [26] se encuentran detalladamente resueltas estas preguntas. A continuación se
describen las bases más habituales y a lo largo del capítulo 4 se definen criterios útiles para la
elección del número de bases de funciones. El método de mínimos cuadrados estándar se usa
para estimar el vector de coeficientes c, aunque, una matriz de penalización también puede ser
incluida en el problema de minimización.
3.3.1
Bases de Fourier
Una base de Fourier es una base periódica de período 2π
ω que cuando se seleccionan datos {tj }
equiespaciados en T = [0, T ] y ω = 2π
está
formada
por
las siguientes funciones ortonormales:
T
3.3 BASES PARA DATOS FUNCIONALES
43
1
φ0 (t) = √ ,
T
sin(rωt)
φ2r−1 (t) = q
,y
T
2
φ2r (t) =
cos(rωt)
q
.
T
2
3.3.2 Bases B-Splines
Un spline es un conjunto de polinomios (de orden m) definidos en subintervalos construidos de
tal modo que al final del polinomio en un subintervalo coincida con el inicio del polinomio del
siguiente subintervalo (hasta derivada m − 2). Los puntos de corte de subintervalos se llaman
nodos. τ = {τl }L
l=0 . Los B-splines (Bases de splines) se calculan fácilmente con el algoritmo
de Boor. Entre ellos los más utilizados son los cúbicos. El número de parámetros para definir
una función spline es el número de nodos interiores (L − 1) + el orden del polinomio (m).
S(t) =
m+L−1
X
ck Bk (t, τ )
k=1
3.3.3
Bases de Wavelets
La
El wavelet padre φ que verifica que
R base de Wavelets se construye a partir de dos funciones.
R
φ(t)dt = 1 y el wavelet madre ψ que verifica que ψ(t)dt = 0. Los elementos de la base se
obtienen a partir de estas dos funciones ortogonales por traslación y cambio de escala.
Z
Z
Z
j
φj,k (t) = 2− 2 φ 2−j t − k ,
j
ψj,k (t) = 2− 2 ψ 2−j t − k ,
φj,k (t)φj,k′ (t)dt = δk,k′ ,
ψj,k (t)φj ′ ,k′ (t)dt = 0,
ψj,k (t)ψj ′ ,k′ (t)dt = δj,j ′ δk,k′ .
Elegida la base la aproximación ortogonal wavelet de una función f (t) viene dada por:
44
C APÍTULO 3. A NÁLISIS DE DATOS FUNCIONALES
f (t) ≈
+
X
SJ,k φJ,k (t) +
k
X
k
X
dJ,k ψJ,k (t)
k
dJ−1,k ψJ−1,k (t) + · · · +
X
d1,k ψ1,k (t)
k
Llamando:
SJ (t) =
X
SJ,k φJ,k (t)
k
DJ (t) =
X
dJ,k ψJ,k (t)
k
DJ−1 (t) =
X
dJ−1,k ψJ−1,k (t)
k
D1 (t) =
X
d1,k ψ1,k (t)
k
A la función Sj (t) se la conoce como señal suave y a las funciones Dj (t) como las funciones
detalle. A esta descomposición se la llama descomposicón multiresolución.
3.4 Suavización de datos funcionales
Supongamos que obseervamos y(tj ) = x(tj ) + ǫ(tj ) donde el término ǫ(tj ) representa el ruido
originado al medir los datos. Para recuperar la señal original podemos usar un suavizador lineal,
es decir,
x̂(tj ) =
N
X
i=1
sj (ti )y(ti ) ⇒ X̂ = SY
• Suavización tipo Kernel (h): sj (ti ) = h1 K
ti −tj
h
.
• Representación truncada (K) en una base: S = Φ (Φ′ W Φ)−1 Φ′ W .
• Suavización penalizada (λ): S = Φ (Φ′ W Φ + λR)−1 Φ′ W .
Grados de libertad del ajuste: df = traza(SS′ ).
3.5 Elección de la suavización
En general, se pretende minimizar el error cuadrático medio:
3.5 E LECCIÓN DE LA SUAVIZACIÓN
45
h
i
M SE [x̂(t)] = E {x̂(t) − x(t)}2
= Sesgo2 (x̂(t)) + Var (x̂(t)) .
Minimizar (por ejemplo), tenemos el criterio del GCV:
GCV(θ) =
n
(y − x̂θ ) W (y − x̂θ )
.
n − df (θ)
n − df (θ)
La varianza de la predicción viene dada por:
ŷ = Sy → Var(ŷ) = SΣe S′ .
3.5.1
Regresión - representación en base
Observados los pares (X1 , y1 ), · · · , (Xn , yn ), podemos escribir:
Xi (t) =
Kx
X
cik ψk (t) → X = CΨ (t),
X
bk θk (t) ⇒ β = θ′ b
k
Kβ
β(t) =
k
donde resulta
−1 ′
−1 ′
b = Z′ Z
Z y, ŷ = CJψθ by = Zby = Z Z′ Z
Z y = Sy
R
con Jψθ = ψ(t)θ′ (t)dt.
Versión penalizada
b = Z′ Z + λR0
3.5.2
−1
Z′ y, ŷ = CJψθ by = Zby = Z Z′ Z + λR0
Regresión Lineal Funcional
−1
Z′ y = Sy
Asúmase que (X, Y ) es un par de variables aletorias con (X, Y ) ∈ L2 (T )×L2 (T ). Suponiendo
que ambas variables está centradas, es decir, E [X(t)] = 0 para t ∈ T y E(Y (t)) = 0 establecemos la siguiente relación entre X e Y .
Yi (t) =
Z
X(s)β(s, t)ds + ǫi (t),
T
46
C APÍTULO 3. A NÁLISIS DE DATOS FUNCIONALES
donde ahora el parámetro β es de cuadrado integrabñe en S × T y ǫi (t) es una variable
funcional con media cero.
Escribiendo β como una doble expansión en términos de dos bases ηk y θl se tiene:
β(s, t) =
k X
L
X
bkl ηk (s)θl (t) = η(s)′ Bθ(t).
k=1 l=1
Observados los pares (X1 , Y1 ), · · · , (Xn , Yn ) para estimar el modelo previo, se sugiere estimar β minimizando:
2
Z X
Z
n ′
LM SSE(β) =
Yi (t) − Xi (s)η(s) Bθ(t)ds dt,
i=1
Como antes debe restringirse el tamaño de las bases para que la estimación sea razonable.
Y (t) =
Z
X(s)η ′ (s)Bθ(t)ds + ǫ(t) = XBθ(t) + ǫ(t)
R
donde X es una matriz n × K de la forma X = X(s)η ′ (s)ds.
Por tanto, de la ecuación anterior, usando la representación de θ(t)
′
X XB
Z
′
′
θ(t)θ (t)dt = X
Z
Y (t)θ ′ (t)dt,
que se puede reescribir:
donde Jθθ =
R
Z
′
′
Y (t)θ (t)dt ,
Jθθ ⊗ (X X) vec(B) = vec X
′
θ(t)θ′ (t)dt. Si además Y = Cφ entonces:
−1
vec(B̂) = Jθθ ⊗ (X′ X)
Jφθ ⊗ X′ vec(C)
R
donde Jφθ = φ(t)θ′ (t)dt.
La penalización de estos estimadores puede hacerse tanto en s como en t. Sea
R =
S =
Z
Z
[Ls ηs ] L′η (s) ds,
[Lt θt ] L′θ (t) dt.
3.5 E LECCIÓN DE LA SUAVIZACIÓN
47
Con términos de penalización pueden escribirse las anteriores ecuaciones como:
′
′
X XBJθθ + λs RBJθθ + λt Jηη BS = X
donde Jηη =
R
Z
Y (t)θ′ (t)dt
η(t)η ′ (t)dt. Si como antes Y = Cφ entonces:
−1
vec(B̂) = Jθθ ⊗ (X′ X) + λs Jθθ ⊗ R + λt S ⊗ Jηη
Jφθ ⊗ X′ vec(C)
R
donde Jφθ = φ(t)θ′ (t)dt.
Capítulo 4
Ejemplo real de Kriging con datos
reales funcionales
En los tres capítulos anteriores se ha presentado el marco teórico necesario para poder llevar
a cabo la aplicación a datos reales combinando ambas técnicas. Se usará para cada técnica el
conjunto de datos de la temperatura descrito en la intoducción.
Antes de describir las técnicas kriging usadas se presenta una estadística descriptiva básica
y funcional de los datos junto con unos conceptos básicos de meteorología que ayudarán a
interpretar los resultados.
En la parte superior de la Figura (4.1) se tiene la temperatura de Galicia a lo largo del año
2009 y en la inferior lo mismo salvo que destacando la temperatura en la Facultad de Matemáticas (Santiago de Compostela) punto no muestreado.
La Figura (4.2) presenta la temperatura en Galicia a lo largo del año 2009 distribuida a lo
largo de las cuatro estaciones del año (primavera, verano, otoño e invierno) destacando siempre
la temperatura en el punto no muestreado.
En el Capítulo 3 se ha tratado con detalle la metodología del Análisis de Datos Funcionales,
pero como en cualquier análisis estadístico es básico conocer la media, la varianza, el mínimo,
máximo, · · · de los datos, que es lo que se presenta en la Figura (4.3). El cálculo de estos
estadísticos queda desarrollado en dicho capítulo.
4.1
Conceptos básicos de meteorología
Se define el tiempo atmosférico como el estado de la atmósfera en un determinado momento.
Para determinarlo se analizan algunas características como son la temperatura, humidad, presión atmosférica y el viento. El clima es el conjunto de valores medios de estas condiciones
atmosféricas durante muchos anos. Depende fundamentalmente de 3 factores que son:
• Latitud. Los rayos solares calientan más a latitudes próximas al Ecuador (los rayos caen
más perpendicularmente) que aquellas que se encuentran en los polos.
• Relieve o altitud. La temperatura de la troposfera disminuye con la altitud (las capas altas
de la atmósfera son menos densas y non retienen el calor). Cuando una corriente de aire
49
50
C APÍTULO 4. E JEMPLO REAL DE K RIGING CON DATOS REALES FUNCIONALES
10
−10
ºC
Temperaturas de Galicia año 2009
0
100
200
300
días
10
Tª Santiago
−10
ºC
Temperaturas de Galicia año 2009
0
100
200
300
días
Figura 4.1: En la parte superior Temperatura de Galicia año 2009. En la inferior la de Santiago.
circula por la superficie y se encuentra una cadena montañosa, asciende por ella y la enfría.
El vapor de agua que contiene el aire, se condensa y cae en forma de precipitaciones. En
las montañas hay temperaturas baijas y llueve más.
• Distancia al mar. El agua tiene una elevada capacidad calorífica (tarda mucho en calentarse y luego tarda mucho también en enfriar). En el verano la Tierra se calienta con más
intensidad (no transmite el calor, lo acumula en la superficie) con el mar. Por eso si el auga
del mar está más fría, refresca el ambiente de las zonas costeras. En el invierno la Tierra
enfría más que el mar, y el mar así modera el frío en las zonas costeras. (Por ejemplo: las
brisas costeras: terrestres y marinas, nocturnas y diurnas)
Otros conceptos que cabe citar son:
• Isotérmicas. Son líneas que unen puntos de igual temperatura.
• Isobaras. Son líneas que unen puntos de igual presión atmosférica.
• Vegetación. La vegetación también influye en el clima, cuanta más vegetación, mayor
cantidad de lluvia. (Hay que tener en cuenta que el movimiento del aire, viento, se produce
de las zonas frías, alta presión atmosférica, a las calientes, poca presión atmosférica, a ras
del suelo y al revés de las capas altas de la atmósfera.
• Predición meteorológica. La predición meteorológica se hace en base a los datos suministrados por: las estaciones meteorológicas (instalaciones que cuentan con instrumentos
de medición, como barómetros, termómetros, pluviómetros y anemómetros), radares meteorológicos (instrumentos que permiten conocer en tiempo real donde llueve y con que
4.1 C ONCEPTOS BÁSICOS DE METEOROLOGÍA
51
Tª verano de Galicia año 2009
(21 junio a 20 septiembre)
ºC
0
10
15
10
5
ºC
15
20
20
25
25
Tª primavera de Galicia año 2009
(21 marzo a 20 junio)
100
120
140
160
180
200
220
240
260
días
Tª otoño Galicia año 2009
(21 septiembre a 20 diciembre)
Tª invierno de Galicia año 2009
(21 diciembre a 20 marzo)
5
ºC
10
15
20
10 15 20 25
días
−10 −5
−5
0
0
5
ºC
80
Tª Santiago
5
Tª Santiago
Tª Santiago
280
300
320
340
Tª Santiago
360
días
380
400
420
440
días
Figura 4.2: Temperatura de Galicia año 2009.
intensidad lo hace) y satélites meteorológicos (satélites artificiales que se situan en órbita
alrededor de la Tierra y permiten el análisis de imágenes e información de la atmósfera
desde gran altura).
Todos estos factores determinan que en Galicia predomine el clima oceánico templado.
Este clima se caracteriza por unas temperaturas suaves en el verano y moderadamente frías en
el invierno, así como por unas precipitacions muy abundantes, sobre todo en el invierno. En
la Tabla (4.1) se recogen la temperaturas mínimas, medias y máximas en las 66 estaciones de
estudio.
Mínima
Media
Máxima
Primavera
-3.2
26.0
11.7
Verano
3.7
16.9
28.2
Otoño
-8.2
11.7
24.2
Invierno
-9.0
7.2
19.8
Tabla 4.1: Temperatura mínima, media y máxima en las 66 estaciones. Año 2009.
Sin embargo, al estudiar con detalle las características climatológicas de nuestra Comunidad,
podemos distinguir las siguintes variedades de clima: oceánico costero, oceánico continental,
oceánico mediterráneo y oceánico de montaña.
• En el oceánico costero predomina en las zonas costeras de Pontevedra, A Coruña y Lugo,
es decir, abarca toda la zona costera desde A Garda hasta Ribadeo. Se caracteriza por
C APÍTULO 4. E JEMPLO REAL DE K RIGING CON DATOS REALES FUNCIONALES
Varianza de la Tª
ºC
4
6
10
0
2
5
ºC
8
15
10
20
12
Media de la Tª
100
200
300
0
200
día
Tª mínima
Tª máxima
25
300
ºC
20
10
−5
10
0
15
5
ºC
100
día
15
0
−10
52
0
100
200
día
300
0
100
200
300
día
Figura 4.3: Estadísticos descriptivos para la temperatura de Galicia año 2009.
tener temperaturas suaves en el verano y en el invierno y precipitaciones abundandantes,
que pueden alzanzar los 1.000 o 1.500mm anuales.
• El oceánico continental se localiza en las zonas del interior. Se caracteriza por tener veranos cálidos e inviernos fríos con posibilidades de heladas. Las precipitacións alrededor
de los 1.000mm anuales, podiendo ser de nieve en el invierno.
• El oceánico mediterráneo es propio de los valles del Miño y del Sil. Se caracteriza por
tener temperaturas elevadas en el verano e suaves en el invierno. Pluviosidad más escasa,
sobre todo en el verano, oscilando entre los 600 y 1.000mm anuales.
• El oceánico de montaña propio de las zonas montañosas como las sierras de los Ancares,
El Caurel, Queixa, · · · . Se caracteriza por tener veranos frescos e inviernos menos fríos
que en otras zonas montañosas más alejadas del mar. Precipitaciones abundantes, de hasta
1.500mm anuales, que en el invierno pueden ser de nieve.
4.2 K RIGING ORDINARIO PARA FUNCIONES - VALORES DE DATOS ESPACIALES
4.2
53
Kriging ordinario para funciones-valores de datos espaciales
En esta sección se considera un primer enfoque con respecto al problema de predicción espacial
de datos funcionales. Se propone un procedimiento de kriging funcional donde la curva a predecir es una combinación lineal de las curvas observadas y donde los coeficientes son números
reales.
Este problema ha sido estudiado inicialmente por Goulard y Voltz (1993), (véase [11]). En
su caso, las funciones eran conocidas solamente por un conjunto finito de puntos y el modelo paramétrico los ajustaba para reconstruir la curva entera. En este contexto, el modelo
paramétrico se suponía conocido y tanto el número de puntos conocidos para cada función como
el número de los parámetros en el modelo paramétrico, se asumía que eran pequeños.
En el caso que nos ocupa se propone aplicar un ajuste no paramétrico al pre-proceso de
las funciones observadas par ello se usarán bases de Fourier para la suavización. Por ello se
reconstruyen los datos a datos a continuo, es decir, representándolos en una base. Los valores
medios de temperatura, por la naturaleza de los sistemas atmosféricos, son una función continua
x(t) a lo largo período de tiempo t ∈ [1, 365]. En el seguimiento de la temperatura, el proceso
continuo es observado y registrado como discreto en intervalos de tj , j = 1, 2, ..., J. Para cada
día se tiene registrado 66 observaciones, una en cada estación. Es decir, para una observación de
cualquiera en un día i se tienen 66 registros discretos, XM,I,1 , ..., Xm,I,66 . Estos puntos discretos
se pueden utilizar para reconstruir una observación continua mediante técnicas de interpolación,
de suavizado o el uso de bases, ([23]). Una base es un conjunto de funciones conocidas e
independientes φk , k ∈ N tales que cualquier función puede ser aproximada, tan bien como se
quiera mediante una combinación K de ellas. Mediante esta difinición podemos expresar la
temperatura en una base para un día i del modo que sigue:
xm,i (t) =
K
X
cm,i,k φk (t)
k=1
Las bases más usadas son las B-splines y las de Fourier. Las primeras se usan para cálculos rápidos y flexibles y las segundas para datos periódicos tales como los ciclos diarios de la temperatura como es el caso que nos ocupa. Una vez se tiene un dato expresado en la forma de la base de
Fourier se pueden expresar todos los datos como elementos de esa base. Si XM,I,1 , ..., Xm,I,66
son todas las observaciones de una de las variables, se puede obtener una representación de la
base minimizando:
Q =
66
X
j=1
[Xm,i,j − xm,i (tj )]2
con respecto a los cm,i,k , (con K ≤ 66, ya que cada día se tienen 66 observaciones). El número
de bases K determina la suavidad resultante del ajuste, esto es, valores pequeños o grandes de
K proporccionan más o menos suavidad en el ajuste. Hay que tener cuidado que no suceda se
que se esté interpolando, ([23]).
54
C APÍTULO 4. E JEMPLO REAL DE K RIGING CON DATOS REALES FUNCIONALES
Para cada estación y tanto para la temperatura se ha representado el 1 de enero del 2009
como elemento de una base de Fourier de 21, 33 y 65 elementos. Se ha determinado que en
ambos casos la base de Fourier de 65 proporcciona un nivel de ajuste aceptable para los datos
diarios. Después de esta conversión el objeto de estudio es recontruir no sólo el 1 de enero del
2009 sino los 365 días del año. En la Figura 4.4 puede observarse el proceso seguido.
20
Nº bases: 21
Nº bases: 33
5
10
ºC
15
Nº bases: 65
0
100
200
300
01/01/2009
Figura 4.4: Representación en bases.
Este enfoque está totalmente de acuerdo con las tendencias actuales del FDA, y, en particular, con la metodología funcional de estimación no paramétrica. La propuesta de Giraldo et
al. es hacer Kriging basado en predicción espacial de curvas aleatorias formalmente coincide
con el Kriging funcional introducido por Goulard y Voltz, ([11]), pero la versión no paramétrica
desarrolla notables diferencias (por ejemplo, la representación de los datos) y un problema adicional cómo es el de la elección de los parámetros de suavización (la clave de los métodos no
paramétricos). El predictor está basado en la filosofía básica de los datos funcionales, esto es, las
curvas son entidades singulares, más que una secuencia de observaciones individuales (Ramsay
y Silverman, 2005). El desarrollo de las fórmulas en las tres técnicas pueden consultarse con
detalle en los artículos de Giraldo et al.
4.2.1
Predicción y estimación de los parámetros
Se considera un proceso aleatorio funcional χs : s ∈ D ⊆ Rd , generalmente d = 2, tal que
χs es una variable funcional para cualquier s ∈ D. Sean s1 , . . . , sn puntos arbitrarios en D, y
considerese que se puede observar una realización funcional del proceso aleatorio χs en los n
lugares, χs1 , . . . , χsn . Se asume que se tiene un proceso aleatorio estacionario de segundo orden
4.2 K RIGING ORDINARIO PARA FUNCIONES - VALORES DE DATOS ESPACIALES
55
e isotrópico, es decir, la media y la varianza son funciones constantes y la covarianza depende
sólo de la distancia entre los puntos muestreados. Formalmente se asume que:
• E (χs (t)) = m(t), ∀t ∈ T, s ∈ D.
• V (χs (t)) = σ 2 (t), ∀t ∈ T, s ∈ D.
• Cov χsi (t), χsj (t) = C(h, t) = Csi sj (t), ∀si , sj ∈ D, t ∈ T, donde h = ksi − sj k.
• 12 V χsi (t) − χsj (t) = γ(h; t) = γsi sj (t), ∀si , sj ∈ D, t ∈ T, donde h = ksi − sj k.
La función γ(h; t), es una función de h, llamada semivariograma de χ(t). Además, se considera la familia de predictores lineales para χ(t)s0 :
χ̂s0 (t) =
n
X
i=1
λi χsi (t), λ1 , . . . , λn ∈ R
El predictor, χ̂s0 (t), tiene la misma expresión que un kriging ordinario, pero considerando
curvas en vez de variables, es decir, la curva de predicción es una combinación lineal de las
curvas observadas. Se asume por tanto que cada curva medida es un dato completo. Este enfoque
trata la curva completa como una entidad singular. Los λ′ s en la ecuación χ̂s0 (t) muestran la
influencia de las curvas que están alrededor de la localización no muestreada donde se llevará a
cabo la predicción. Las curvas de las ubicaciones más cercanas al punto de predicción tendrán
mayor influencia que las más alejadas. Este es un primer paso y natural en el modelado de datos
espaciales funcionales.
Se considera la condición insesgadez para encontrar el mejorPpredictor lineal insesgado
(BLU P ). De la condición anterior, media constante, se exige que ni=1 λi = 1. En geostadísticaclásica univariante se asume que las observaciones son
de una muestra aleatoPrealizaciones
n
d
ria Z(s) : s ∈ D, D ∈ R . El Kriging se define como i=1 λi Z(si ) y el mejor predictor linP
eal insesgado (BLU P ) se obtiene minimizando σs20 = V (Ẑ(si ) − Z(si )) sujeto a ni=1 λi = 1.
Por otro lado en geostadística multivariante,
([28]), los datos, {Z(s1 ), . . . , Z(sn )} se tienen de
observaciones de un proceso espacial Z(s) : s ∈ D, Z(s) ∈ Rm , D ∈ Rd . En este contexto
V (Ẑ(s0 ) − Z(s0 )) es una matriz y el BLU PPde m variables en una localización no muestreada
m
s0 se puede obtener minimizando σs20 =
i=1 V (Ẑ(si ) − Z(si )) sujeto a las restricciones
que garanticen la condición de insesgadez, esto es, minimizar la traza de la matriz del error
cuadrático medio sujeto a alguna restricción dada por la condición de insesgadez ([16]). Extendiendo el criterio al contexto funcional, es decir, remplazando el sumatorio por una integral,
los n parámetros en el Kriging de χs0 considerados se obtienen como solución del siguiente
problema de optimización:
Z
min
V (χ̂(s0 )(t) − χ(s0 )(t))dt,
λ1 ,...,λn
T
s.t.
n
X
i=1
λi = 1
56
C APÍTULO 4. E JEMPLO REAL DE K RIGING CON DATOS REALES FUNCIONALES
P
Donde ni=1 λi = 1 son las restricciones de insesgadez. De las condiciones de insesgadez y del
teorema de Fubini se obtiene:
Z
T
V (χ̂s0 (t) − χs0 (t)) = E
Z
(χ̂s0 (t) − χs0 (t)) dt
2
T
Con lo que se necesita minimizar:
!
Z
n
X
V (χ̂s0 (t) − χs0 (t)) + 2µ
λi − 1 ,
T
i=1
Pn
donde el predictor χ̂s0 (t) = i=1 λi χ(t)si (t) y µ es el multiplicador de Lagrange usado para
tener en cuenta la restricción de insesgadez. La integral en la ecuación anterior se puede escribir
como:
σs20
=
n X
n
X
λi λj
i=1 j=1
Z
Cij (t)dt +
T
Z
2
T
σ (t) − 2
n
X
i=1
λi
Z
Ci0 (t)dt.
T
Así, la función objetivo se puede escribir:
!
Z
Z
Z
n
n
n X
n
X
X
X
2
Ci0 (t)dt + 2µ
λi − 1 .
σ (t) − 2
λi
Cij (t)dt +
λi λj
i=1 j=1
T
T
T
i=1
i=1
Minimizando la ecuación anterior con respecto a λ1 , . . . , λn y µ se obtienen el siguiente conjunto de (n + 1) ecuaciones:
Z
Z
n
X
C10 (t)dt
C1j (t)dt + µ =
λj
j=1
n
X
λj
j=1
n
X
j=1
T
T
λj
Z
Z
C2j (t)dt + µ =
T
..
.
Cnj (t)dt + µ =
T
n
X
Z
Z
C20 (t)dt
T
Cn0 (t)dt
T
λi = 1
i=j
Las cuales podemos expresar en notación matricial como sigue:
R
R
R
λ1
T Cs1 s1 (t)dt . . .
T Cs1 sn (t)dt 1
T Cs1 s0 (t)dt
.
..
.
.
..
.
.. ..
..
..
.
.
R
= R
R
C
(t)dt
.
.
.
C
(t)dt
1
λ
C
s
s
s
s
n
s
n 1
n n
n s0 (t)dt
T
T
T
1
...
1
0
µ
1
4.2 K RIGING ORDINARIO PARA FUNCIONES - VALORES DE DATOS ESPACIALES
57
También se pueden obtener las estimaciones basadas en la traza del variograma. Asumiendo
estacionariedad, se tiene que
γsi sj (t) = σ 2 (t) − Cij (t)
Entonces
Z
Cij (t)dt =
T
Z
T
σ 2 (t)dt −
Z
T
γsi sj (t)dt
Reemplazando la ecuación anterior en el sistema de ecuaciones, se obtiene el sistema:
R
R
γs1 s1 (t)dt . . . T γs1 sn (t)dt 1
λ1
..
.
.
.
..
..
.. ...
.
R
R
λn
T γsn s1 (t)dt . . .
T γsn sn (t)dt 1
1
...
1
0
−µ
T
R
γs1 s0 (t)dt
..
.
= R
γ
(t)dt
T sn s0
1
T
De las primeras n ecuaciones del primer sistema, se tiene la relación
n X
n
X
λi λj
i=1 j=1
Z
Cij (t)dt =
T
n Z
X
i=1
T
Ci0 (t)dt −
n
X
λi µ.
i=1
Reemplazando la ecuación anterior en la ecuación σs20 , se obtiene:
σ
2
=
Z
2
T
σ (t)dt −
n
X
i=1
λi
Z
T
Ci0 (t)dt − µ.
R
R
R
Si además se considera la relación T Cij (t)dt = T σ 2 (t)dt − T γsi sj (t)dt, la traza de la
varianza, de la predicción del kriging ordinario funcional basado en la traza del variograma
vendrá dado por
σs20 =
n
X
i=1
λi γ(h) − µ
El parámetro definido en la ecuación anterior debería ser considerado como una medida global
de incerteza, en el sentido que es un versión integrada de la predicción clásica point-wise de
la predicción de la varianza del Kriging Ordinario. Bajo alguna especificación en la traza del
modelo del variograma, se podrán usar estimaciones de este parámetro para identificar esas
zonas que presentan gran incerteza en las predicciones. Si se fija t ∈ T y se reemplaza la traza
del variograma en la ecuación anterior por el variograma de una variable aleatoria χ(t), t ∈ T
se obtendría la varianza de predicción del Kriging Ordinario (modelo clásico), (véase en [14]).
Este resultado se puede usar para calcular intervalos de confianza point-wise.
58
4.2.2
C APÍTULO 4. E JEMPLO REAL DE K RIGING CON DATOS REALES FUNCIONALES
Estimación la traza del variograma
Para resolver el (4.2.1), es necesario un estimador de la traza del variograma. Ya que se asume
que χs (t) tiene una función de media constante m sobre D,
h
2 i
V χsi (t) − χsj (t) = E χsi (t) − χsj (t)
.
Notar que, usando el teorema de Fubini,
Z
2
1
χsi (t) − χsj (t) dt , para si , sj ∈ D con h = ksi − sj k
γ(h) = E
2
T
Entonces una adaptación del modelo clásico de los momentos (M oM ) para esta cantidad da el
siguiente estimador
X Z
2
1
γ̂(h) =
χsi (t) − χsj (t) dt
2 |N (h)|
T
i,j∈N (h)
donde N (h) = {(si , sj ) : ksi − sj k = h}, y |N (h)| es el número de elementos distintos en
N (h). Debido a la irregularidad de los datos espaciales, generalmente, no hay observaciones
sufiencientes separadas exactamente a una distancia h. Entonces N (h) se modifica por N (h) =
{(si , sj ) : ksi − sj k ∈ (h − ǫ, h + ǫ)}, con ǫ > 0 un valor pequeño. Una vez que se ha estimado
la traza del variograma para una secuencia de K valores hk , se propone un ajuste paramétrico
del modelo γα (h) (como el esférico, el Gaussiano, el exponencial o el Matérn podrían ser utilizados) en los puntos (hk , γ̂(hk )), k = 1, . . . , K como si se obtuvieran bajo los argumentos
de la geostadística clásica. Generalmente, este tipo de ajuste, se hace por mínimos cuadrado
ordinarios o mínimos cuadrados ponderados (ver, [6]). Notar que el ajuste paramétrico de la
traza del variograma es siempre un variograma válido porque sus propiedades son las de un variograma paramétrico ajustado por un conjunto geostadístico univariante.
Un procedimiento diferente, como alternativa al ajuste paramétrico, consiste en aplicar técnicas de suavización (splines o regresión local lineal, ver Wasserman, 2006) al conjunto de datos
(hk , γ̂(hk )), k = 1, . . . , K para ser capaz de evaluar aproximadamente γ̂(h) mediante cualquier
valor de h ∈ R+ . Sin embargo, en este caso, si γ
e(h) denota la versión suavizada de γ̂(h), la
condición de semifinida negativa de γ
e(h) merece más atención. Si γα̂(h) denota la traza del variograma estimado paramétricamente, esta forma funcional se usa para obtener los coeficientes
λi del Kriging en el sistema (4.2.1), y para estimar la traza de la varianza de predicción a través
de la ecuación σs20 .
4.2.3
Enfoque no paramétrico
En el artículo [11] tratan el mismo problema de geostadística de interpolación de curvas y específicamente consideran el predictor χ̂s0 (t). Consideran que las curvas son sólo conocidas
por un conjunto finito de sus puntos: χsi (tj ) : j = 1, . . . , M , i = 1, . . . , n y muestran tres
argumentos para la predicción de curvas en zonas no visitadas:
4.2 K RIGING ORDINARIO PARA FUNCIONES - VALORES DE DATOS ESPACIALES
59
• Enfoque Multivariante 1: Cokrige First, Fit later (CFP). El vector de valores observados
χsi (t1 ) , . . . , χsi (tM ) se considera como la observación de una variable aleatoria M dimensional en el sitio si . El Cokriging se aplica, entonces, para predecir
los valores de
este vector aleatorio en el sitio no muestreado s0 : χ̂si (t1 ) , . . . , χ̂si (tM ) . Por tanto,
un
modelo paramétrico χ(·; θ), θ ∈ Rp se ajusta a los valores χ̂si (t1 ) , · · · , χ̂si (tM ) para
reconstruir la función entera en s0 : χ(·; θ̂s0 ).
• Enfoque Multivariante 2: Fit first, Cokrige later (FCP). Primero, el modelo paramétrico
se ajusta a la curva observada: χ(·; θ̂si ), i = 1, . . . , n. Los valores de los parámetros pdimensionales se consideran como observaciones de la variable aleatoria. El Cokriging se
aplica para predecir el valor del parámetro θ en la posición s0 , decimos que θ̂s∗0 , y χ(·; θ̂s∗0 )
es el resultado de predecir la función en s0 .
• Enfoque de una curva kriging (CKP). Dado que las funciones χsi son sólo conocidas para
M valores, Goulard y Voltz (1993) proponen un modelo paramétrico χ(·; θ), θ ∈ Rp para
estos datos para obtener χ(·; θ̂si ) como una aproximación de la función entera χsi . Por
tanto, el predictor χ̂s0 (t) se puede reescribir como
χ̂s0 =
n
X
i=1
λi χ ·; θ̂si
y las integrales en T para la estimación de los coeficientes λi se calculan usando χ(·; θ̂si )
en vez de χsi .
Considérese ahora el caso común donde un gran número de valores M son observados para
cada función muestreada y no hay un modelo paramétrico que los ajuste adecuadamente. En
este contexto el segundo propósito, CF P (Cokrige first, Fit later) que puede llegar a ser extremadamente caro en términos de recursos computacionales. La razón es que CF P desarrolla
un primer paso del Cokriging donde la dimensión de la observación multivariante es igual a M .
El coste computacional de este paso es razonable si M está en decenas, pero es inaceptable si
M es del orden de varios cientos o miles. Cuando un modelo paramétrico es adecuado para
representar las funciones observadas, la alternativa F CP (Fit first, Cokrige later) es factible,
porque en este caso el paso Cokriging tiene en cuenta p vectores dimensionales, donde p es el
número de parámetros en el modelos paramétrico. Aquí el problema aparece cuando el modelo
no paramétrico se considera para ajustar los valores observados. Entonces se podría hacer un
ajuste no paramétrico, pero este proceso es esencialmente equivalente al ajuste paramétrico con
número de parámetros pM creciente con el número de valores observados M . Sin embargo,
la flexibilidad extra proporcionada por un modelo no paramétrico es generalmente obtenida a
expensas de permitir grandes valores pM (incluso pM ≤ M ). Por tanto se concluye que el
coste computacional del argumento F CP podría también ser prohibitivo. Así que nos limitamos a utilizar la curva de kriging predictor (CKP ). Del sistema (4.2.1) y la sección anterior,
es evidente que, el paso crucial para la estimación de la traza del variograma γ(h) y para calcular los coeficientes Kriging λi en el predictor χ̂s0 (t), está el cálculo de integrales a través de
2
R
T con la forma genérica T χsi (t) − χsj (t) . Cuándo se ajusta bien un modelo paramétrico
60
C APÍTULO 4. E JEMPLO REAL DE K RIGING CON DATOS REALES FUNCIONALES
los valores de las funciones observadas están disponibles. Se trata de sustituir esta integral
2
R por T χ(t; θ̂si ) − χ(t; θ̂sj ) , que por lo general tiene una expresión analítica cerrada. Cabe
plantearse qué es lo que se puede hacer si no existe un modelo paramétrico aceptable que ajuste
las funciones observadas. La propuesta que se plantea es la de sustituir el paso paramétrico del
ajuste por uno no paramétrico.
4.2.4
Resultados de la aplicación
No es fácil proponer un modelo para estas curvas y que hay un cierto grado de ruido observacional. Suavizamos las funciones observadas usando bases de funciones de Fourier.
En las Figuras 4.5 y 4.6 podemos ver una comparación entre los datos sin suavizar y suavizados con 85 y 35 bases de Fourier.
Tª suavizada con 85 bases.
Año 2009 − Galicia
10
5
Temperatura (ºC)
10
−5
0
0
−10
Temperatura (ºC)
15
20
20
25
Tª real.
Año 2009 − Galicia
0
100
200
Días
300
0
100
200
300
Días
Figura 4.5: Estadísticos descriptivos para la temperatura de Galicia año 2009.
4.2 K RIGING ORDINARIO PARA FUNCIONES - VALORES DE DATOS ESPACIALES
Tª suavizada con 35 bases.
Año 2009 − Galicia
10
5
Temperatura (ºC)
10
−10
−5
0
0
Temperatura (ºC)
15
20
20
25
Tª real.
Año 2009 − Galicia
61
0
100
200
Días
300
0
100
200
300
Días
Figura 4.6: Estadísticos descriptivos para la temperatura de Galicia año 2009.
Visualmente los datos se representan bien con 35 bases de Fourier. Si tenemos muchas
bases se produce un sobrestimamiento y además el coste computacional es mayor. Para decicir
el número de bases más indicado se usó la libreria f da.usc de Febrero-Bande, M. y Oviedo de
la Fuente, M.. Se ha usado el método min.np. Este método realiza una suavización funcional de
los datos usando una estimación no paramétrica del kernel con métodos de validación cruzada
(CV) o mediante métodos de validación cruzada generalizada (GCV). En la sección siguiente se
explicará más en detalle la elección del número de bases por tratarse de una técnica que expresa
la solución basada en bases de funciones. El parámetro h de la ventana es 4.56. Cuando se han
obtenido que 85 era un buen número para considerar de bases en el método de suavización se ha
usado un método de validación cruzada y la matriz de estimación calculada mediante Regresión
Local Lineal (LLR), y la traza de la matriz vale 87.49. En el caso de 35 bases el método
de validación usado es de validación cruzada generalizada y la matriz se calcula mediante la
62
C APÍTULO 4. E JEMPLO REAL DE K RIGING CON DATOS REALES FUNCIONALES
estimación del kernel de Nadaraya-Watson. En este caso la traza obtenida es 32.37.
Criterio de evaluación del Kriging
En cualquier problema de predicción, el modelo ideal de evaluación consiste en dividir el conjunto de datos en dos partes: una muestra de entrenamiento (estimación) para el modelo de
ajuste y otra muestra de test (validación). Este planteaminto, sin embargo, no es eficiente, salvo
que el tamaño de la muestra sea grande. La idea que está detrás es el de validación cruzada,
donde se conmutan los papeles de muestra test y entrenamiento. En el contexto de datos funcionales espacialmente correlacionados, donde la meta es predecir la curva entera de la función
χs0 (t) en el punto s0 no muestreado, la técnica de validación cruzada de dejar uno fuera trabaja
del siguiente modo: cada dato de la localización se saca del conjunto de datos y mediante una
función de suavización se predice en esa localización usando Kriging funcional como predictor.
Llamamos a este procedimiento validación cruzada funcional (F CV ). Calculamos el SSE de
F CV por:
SSEF CV =
n
X
SSEF CV (i) =
i=1
n
X
i=1
(i)
χsi (tj ) − χ̂si (tj ) | ,
donde χ̂isi (tj ) es la predicción en si evaluada en tj , j = 1, . . . , M , sacando el sitio si temporalmente fuera de la muestra.
Para decidir que modelo de semivariograma usar se han probado mediante validación cruzada
cuatro ejemplos de semivariogramas isotrópicos, el Matérn, Exponencial, Esférico y Circular descritos en el Capítulo 1. En la Figura 4.7 se muestran los resultados de predicción en la Facultad
de Matemáticas obtenidos al calcular el Kriging Ordinario mediante validación cruzada para
elegir el modelo más apropiado.
En la Tabla 4.2 se concluye que todos los modelos tienen un comportamiento similar. Por
tanto se trabajárá con el esférico de aquí en adelante. Suponemos que no se aprecian estas diferencias debido a que las distancias entre las estaciones no es muy grande, la máxima distancia
de una estación a otra son 225.32Km y la máxima distancia de cualquier estación al punto no
muestreado es 155.82Km.
Estadístico
Mínimo
1st Qu.
Mediana
Media
3rd Qu.
Máximo
Matérn
687.7
1544.0
2394.0
2872.0
3132.0
16290.0
Exponencial
687.7
1544.0
2394.0
2872.0
3132.0
16290.0
Esférico
687.6
1545.0
2394.0
2872.0
3132.0
16290.0
Circular
687.3
1552.0
2394.0
2876.0
3127.0
16290.0
Tabla 4.2: Principales tipos de kriging lineal y propiedades.
En la Figura 4.8 se muestra el variograma obtenido al calcular la predicción en el punto
no muestreado con el método esférico, como se explicó con los otros modelos el resultado es
4.2 K RIGING ORDINARIO PARA FUNCIONES - VALORES DE DATOS ESPACIALES
25
Pred. F. Matemáticas(Exponential)
25
Pred. F. Matemáticas(Matern)
20
KO
5
10
15
original
−5
−5
0
5
10
15
Temperatura (ºC)
original
0
100
200
300
0
100
200
300
Pred. F. Matemáticas(Spherical)
Pred. F. Matemáticas(Circular)
25
día
25
día
20
KO
15
original
0
−5
−5
0
5
10
15
Temperatura (ºC)
original
10
20
KO
5
Temperatura (ºC)
20
KO
0
Temperatura (ºC)
63
0
100
200
300
0
día
100
200
300
día
Figura 4.7: Predicción en función del tipo de modelo.
análogo.
Una vez que se tiene determinado que modelo se va a usar se procede a hacer la predicción. La Figura 4.9 muestra el variograma obtenido al calcular la predicción en la Facultad de
Matemáticas.
En la Figura 4.10 se muestran los resultados de predicción comparados con el dato real, pues
aunque consideramos como no muestreado la Facultad de Matemáticas, se tienen los resultados
para el mismo año de la estación Santiago-EOAS situada a excasos metros de nuestro punto de
interés. Se verifica que el λ mayor correponde a la estación más cercana geográficamente al
punto no muestreado. En la Figura 4.11 se prensentan todos los λ’s.
Sergude, (está en el ayuntamiento de Boqueixón), es la estación con el mayor λ y la que
tiene el menor λ está en Malpica. En la Tabla 4.3 se presenta un resumen de los resultados
obtenidos.
λ
Distancia en Km
Sergude
0.61
9.78
Río do Sol
0.17
26.89
Punta Candieira
0.144
101.08
Malpica
-0.02
56.13
Tabla 4.3: λ’s y distancias más representativos.
En la Figura 4.12 se ven las temperaturas de aquellas estaciones más representativas, por un
lado se tiene la temperatura de Santiago, luego la de Sergude, Río do Sol y Punta Candieira, por
ser las estaciones con mayores λ’s y por último Malpica la de menor λ. La temperatura media
anual de estas estaciones se ve en la Tabla 4.4
Del análisis de validación cruzada se concluye que la estación óptima para la predicción en
C APÍTULO 4. E JEMPLO REAL DE K RIGING CON DATOS REALES FUNCIONALES
20000
0
5000 10000
semivariance
30000
64
0
50
100
150
200
distance
Figura 4.8: Predicción en función del tipo de modelo.
Santiago
13.28
Sergude
13.28
Río do Sol
11.02
Punta Candieira
13.20
Malpica
13.18
Tabla 4.4: Temperaturas medias en el año 2009.
la Facultad de Matemáticas (s0 ) es la de Sergude, estación más cercana a s0 . Los coeficientes λi
del kriging se obtuvieron resolviendo el sistema de ecuaciones 4.2.1 con γh estimado mediante
el variograma esférico γ̂h , como ha quedado justificado anteriormente. El método de validación
cruzada funcional (FCV) usado para para elegir el número de parámetros de suavización, también puede ser considerado una herramienta útil para comparar curvas observadas y predichas,
esto es, define una medida de distancia entre estas dos curvas. De hecho el SSS(i) puede
considerarse como una aproximación al error cuadrático medio integrado (MISE). Cuando se
usa validación cruzada la idea es que los valores predichos deberían estan cerca de los observados (utilizando la técnica de dejar uno fuera en cada iteración). En la Figura 4.13 la parte
de la izquierda muestra una comparación gráfica entre las curva observadas (las reales) y la
predicha(utilizando FCV).
La Tabla 4.5 muestra el resumen de los residuos de validación cruzada para el Kriging Ordinario y los datos suavizados mediante bases de Fourier.
Por último antes de cambiar a la técnica 2, debido a que no se aprecian cambios en el variograma ni en las estimaciones dependiendo del modelo considerado se ha intentando hacer lo
mismo pero con Kriging Universal. Hemos creído que la altitud influye en la estimación de la
temperatura e incluso la latitud. Por tanto se han creado 8 modelos diferentes con estas variables.
65
20000
0
5000
10000
semivariance
30000
4.2 K RIGING ORDINARIO PARA FUNCIONES - VALORES DE DATOS ESPACIALES
0
50
100
150
200
distance
Figura 4.9: Variograma.
Los modelos serán combinaciones T emp0 (t) = α0 (t) + β1 (t) × Altitud0 + ǫ̂0 (t) (modelo1)
y T emp0 (t) = α0 (t) + β1 (t) × Altitud0 + β2 (t) × Latitud0 + ǫ̂0 (t) (modelo2). Es decir el
modelo1 considerando la temperatura centrada o no y modelo con constante o sin ella y de modo
análogo el modelo2. En la Tabla 4.6 se presenta un resumen del coeficiente de determinación
para esos modelos.
A continuación se ha hecho la estimación del Kriging Universal primero con los modelos que
usan com variable a la altitud. Los resultados obtenidos eran muy similares a los que se tenían
en el Kriging Ordinario, por ello, se han omitido para no hacer muy extenso este trabajo. De
la Tabla 4.6 los modelos que tienen mayor coeficiente determinación (R-Squared) corresponden
Estadístico
Mínimo
1st Qu.
Mediana
Media
3rd Qu.
Máximo
Desviación típica
Suma
Kriging Ordinario
1326.0
2931.0
3861.0
4306.0
4847.0
12880.0
2279.5
284222.1
Tabla 4.5: Resumen de los residuos de validación cruzada para el Kriging Ordinario.
66
C APÍTULO 4. E JEMPLO REAL DE K RIGING CON DATOS REALES FUNCIONALES
Predicción Santiago
10
0
5
Temperatura (ºC)
15
20
KO
Original
Suavizada
0
100
200
300
día
Figura 4.10: Predicción en función del tipo de modelo.
a aquellos que usan además la variable latitud. En la Tabla 4.7 se consideran los tres modelos
anteriores mejores y se muestra el número de veces que las variables han resultado significativas.
Si nos fijamos en la Tabla 4.7 los modelos de la dos primeras filas arrojan los mismos resultados. En el último modelo la variable latitud ha sido siempre significativa y debido a que
el R-Squared es el mayor hemos optado por este modelo. Se va a trabajar en vez de con la
temperatura con los residuos respecto a la media del modelo que tienen a su vez estructura de
dato funcional. Luego a estos residuos se les aplicarán las técnicas del Kriging. La Figura 4.14
muestra los residuos del modelo con altitud y latitud junto con los residuos suavizados con una
base de Fourier de 35 elementos.
modelo1 - no centrado sin constante
modelo1 - centrado sin constante
modelo1 - no centrado con constante
modelo1 - centrado con constante
modelo2 - no centrado con constante
modelo2 - centrado con constante
modelo2 - no centrado sin constante
modelo2 - centrado sin constante
Tabla 4.6: R-Squared.
R-Squared
0.48
0.17
0.56
0.56
0.73
0.73
0.97
0.56
4.2 K RIGING ORDINARIO PARA FUNCIONES - VALORES DE DATOS ESPACIALES
67
0.3
0.0
0.1
0.2
lambdas
0.4
0.5
0.6
Lambdas por KO
50
100
150
día
Figura 4.11: Lambdas obtenidos por Kriging Ordinario.
modelo2 - no centrado con constante
modelo2 - centrado con constante
modelo2 - no centrado sin constante
R-Squared
0.73
0.73
0.97
Constante
305
275
-
Altitud
342
342
318
Latitud
270
270
365
Tabla 4.7: R-Squared y número de veces que las variables han sido significativas.
En la Figura 4.15 se tiene el variograma con los distintos modelos, y como en el caso del
Kriging Ordinario se obtiene la misma estimación, con lo cuál se optará por el esférico nuevamente. Lo que si que se observa es que la varianza ha disminuido.
Se tiene la predicción para los residuos en la Figura 4.16. Hay que decir que las estaciones
que tiene los λ’s representativos son las mismas que en el Kriging Ordinario, por tanto no se
incidirá más en eso. El siguiente paso es deshacer el cambio en el modelo para ver la predicción
auténtica en la la Facultad de Matemáticas. Ya no se presentan estos resultados porque lo que se
pretendía era ver si la el efecto de la altitud y/o la latitud ayudaban a definir que modelo usar.
También se ha aplicado Kriging Universal a los datos eliminándole a los residuos el efecto de
la latitud y longitud. Los resultados obtenidos se pueden consultar en la tabla (4.14) y servirán
para decidir al final con qué metodología nos quedamos.
68
C APÍTULO 4. E JEMPLO REAL DE K RIGING CON DATOS REALES FUNCIONALES
Temperatura en las estaciones con
lambdas más representativos
15
10
5
Temperatura (ºC)
20
Santiago
Sergude
Río do Sol
Punta Candieira
Malpica
0
100
200
300
día
Figura 4.12: Estaciones con λ’s representativos.
4.3 Kriging variación de tiempo continua para la predicción espacial de datos funcionales
En esta técnica se considera el problema de predicción espacial de datos funcionales con ponderación de cada curva observada por un parámetro funcional. Esta técnica es una combinación
del Kriging Ordinario y el modelo funcional lineal concurrente (punto-wise) tal y como se muestra en [26]. Se propone una solución basada en bases de funciones. Tanto las curvas como los
parámetros funcionales se expanden en términos de un conjunto de bases de funciones. Entonces, el problema pasa a ser el de estimación de los coeficientes de estas bases de funciones
para cada parámetro funcional. Para proporcionar una solución, se usa el modelo lineal de corregionalización para estimar la covarianza a través de los coeficientes de cada curva.
4.3.1
Predictor y problema de minimización
Con esta técnica se propone usar la familia lineal para predictores point-wise χs0 (t), t ∈ T ,
dada por
n
X
χ̂s0 (t) =
λi (t)χsi (t), λ1 (t), · · · , λn (t) : T → R.
i=1
Este predictor fue mencionado en [11]. Se asumen las mismas afirmaciones dadas en la técnica anterior. Para cada t ∈ T , el predictor, χ̂s0 (t), tiene la misma expresión que el predictor
del Kriging Ordinario. En el resto del proyecto a este predictor se le llamará Kriging Continuo
4.3 K RIGING VARIACIÓN DE TIEMPO CONTINUA PARA LA PREDICCIÓN ESPACIAL DE DATOS FUNCIONALES69
variable en el tiempo para datos funcionales (CTKFD). Este procedimiento del modelo es coherente con el modelo linal funcional concurrente ([12], [26]) tal como se ve en la ecuación
Y (t) = X(t)β(t) + ǫ(t), en la cuál la influencia de cada covariable en la respuesta es simultánea
o point-wise. En este modelo, la respuesta Yi (t) y cada covariable Xij (t), j = 1, · · · , q son
funciones con los mismos argumentos y Xj (t) sólo influye en Y (t) a través de su valor en el
tiempo t. La estimación de parámetros funcionales α(t), βj (t), j = 1, · · · , q, se lleva a cabo
resolviendo (Ramsay and Silverman, 2005)
min
α(·),β1 (·),··· ,βq (·)
E Ŷ (t) − Y (t)
2
.
En este contexto, las covariables son las curvas observadas en n sitios de una región y la respuesta funcional es un función no observada en una zona no muestreada. Consecuentemente,
el problema de optimización es
min
λ1 (·),··· ,λn (·)
E kχ̂s0 (t) − χs0 (t)k2 ,
o equivalentemente usando el teorema de Fubini
Z
min
E (χ̂s0 (t) − χs0 (t))2 dt.
λ1 (·),··· ,λn (·) T
Si se consideran las afirmaciones estacionarias, el problema pasa a ser
Z
V (χ̂s0 (t) − χs0 (t))2 dt.
min
λ1 (·),··· ,λn (·) T
(4.1)
Como en la sección anterior, el problema de minimización (4.1) es una extensión del cripor
terio de minimización dado por en [16] al contexto funcional,
h reemplazando el sumatorio
i
la integral y los vectores aleatorios [Z1 (s0 ), · · · , Zm (s0 )] y Ẑ1 (s0 ), · · · , Ẑm (s0 ) por las variables funcionales χ(t) y χ̂(t) respectivamente,
Pn con t ∈ T . El predictor, χ̂s0 (t) es insesgado
si E (χ̂s0 (t)) = m(t), ∀t ∈ T , esto es, si i=1 λi (t) = 1, ∀t ∈ T . Consecuentemente, para
encontrar el BLUP, los n parámetros funcionales en el predictor propuesto vendrán dados por la
solución del siguiente problema de optimización
min
Z
2
λ1 (·),··· ,λn (·) T
4.3.2
V (χ̂s0 (t) − χs0 (t)) dt, sujeto a :
n
X
i=1
λi (t) = 1, ∀t ∈ T.
(4.2)
Una solución basada en bases de funciones
Se asume que cada función observada puede ser expresada en términos de K bases de funciones
por
χsi (t) =
K
X
l=1
ail Bl (t) = aTi B(t), i = 1, · · · , n.
70
C APÍTULO 4. E JEMPLO REAL DE K RIGING CON DATOS REALES FUNCIONALES
Teniendo en cuenta que χsi (t), i = 1, · · · , n son funciones aleatorias con dependencia espacial,
se asume que la matriz
A=
a11
a21
..
.
a12
a22
..
.
...
...
..
.
a1K
a2K
..
.
an1 an2 . . . anK
= (α1 , · · · , αK )(n×K)
constituye un vector aleatorio K multivariante con E(αi ) = vi(nx1) y matriz de covarianzas
Σ=
Σ11
Σ21
..
.
Σ12 . . .
Σ22 . . .
..
..
.
.
Σk2 . . .
ΣK1
Σ1K
Σ2K
..
.
ΣKK
(K×n)x(n×K)
donde Σij = C(αi , αj )n×n . Los coeficientes aij se asumen como una realización del vector
aleatorio espacial αj , j = 1, · · · , K. Se propone usar geostadística multivariante y específicamente un modelo lineal de corregionalización (LMC) para la estimación de la matriz de
covarianzas Σ. Para establecer la condición de insesgadez y para llevar a cabo la estimación de
los parámetros en χ̂s0 (t), se expande cada parámetro funcional λi (t) por
λi (t) =
K
X
bil Bl (t) = bTi B(t).
l=1
Por tanto, con las expresiones de χsi (t) y λi (t), se obtienen para la ecuación del predictor χ̂s0 (t):
χ̂s0 (t) =
n
X
bTi B(t)B(t)T ai .
i=1
Mediante λi (t) y la expansión de la función constante 1,
restricción de insesgadez se puede expresar como
n
X
bTi B(t)
i=1
T
= c B(t), ∀t, ⇔
n
X
PK
l=1 cl Bl (t)
= cT B(t) = 1, la
bi = c,
i=1
o más específicamente por:
n
X
i=1
bi1 = c1 , · · · ,
n
X
biK = cK .
i=1
Desarrollando la varianza en la función objetivo en el problema de minimización (4.2) se
tiene:
4.3 K RIGING VARIACIÓN DE TIEMPO CONTINUA PARA LA PREDICCIÓN ESPACIAL DE DATOS FUNCIONALES71
V (χ̂s0 (t) − χs0 (t)) = V (χ̂s0 (t)) + V (χs0 (t)) − 2C (χ̂s0 (t), χs0 (t))
!
n
X
= V
bTi B(t)B T (t)ai + B T (t)V (a0 )B(t)
−
=
i=1
n
X
2
bTi B(t)B T (t)C(ai , a0 )B(t)
i=1
n
X
bTi B(t)B T (t)V (ai )B(t)B T (t)bi
i=1
+ 2
X
bTi B(t)B T (t)C(ai , aj )B(t)B T (t)bj
i<j
+ B T (t)V (a0 )B(t) − 2
n
X
bTi B(t)B T (t)C(a0 , ai )B(t).
i=1
En la ecuación anterior, V (χ̂s0 (t) − χs0 (t)), para i < j, i, j = 0, 1, · · · , n se tiene:
Var(ai1 )
Cov(ai1 , ai2 ) . . . Cov(aiK , aiK )
Cov(ai2 , ai1 )
Var(ai2 )
. . . Cov(ai2 , aiK )
V (ai ) =
..
..
..
..
.
.
.
.
Cov(aiK , ai1 ) Cov(aiK , ai2 ) . . .
y
C(ai , aj ) =
Cov(ai1 , aj1 )
Cov(ai2 , aj1 )
..
.
Cov(ai1 , aj2 )
Cov(ai2 , aj2 )
..
.
...
...
..
.
Var(aiK )
Cov(ai1 , ajK )
Cov(ai2 , ajK )
..
.
Cov(aiK , aj1 ) Cov(aiK , aj2 ) . . . Cov(aiK , ajK )
Si se definen:
Qi =
Qij
=
D =
Ji =
Z
ZT
ZT
ZT
T
(K×K)
(K×K)
B(t)B T (t)V (ai )B(t)B T (t) dt
B(t)B T (t)C(ai , aj )B(t)B T (t) dt
B(t)V (a0 )B(t)dt
B(t)B T (t)C(a0 , ai )B(t) dt
y considerando K multiplicadores de Lagrange mT = (m1 , · · · , mK ) la función objetivo en el
problema de minimización (4.2) puede expresarse como:
!
n
n
n
X
X
X
X
T
T
T
T
bi Q i bi + 2
bi Qij bj + D − 2
bi Ji + 2m
bi − c
min
b1 ,··· ,bn ,m
i=1
i<j
i=1
i=1
72
C APÍTULO 4. E JEMPLO REAL DE K RIGING CON DATOS REALES FUNCIONALES
Teniendo en cuenta β = bT1 , · · · , bTn , mT
resumir a:
T
(K(n+1)x1)
, la expresión anterior aún se puede
minβ T Qβ + D − 2β T J
(4.3)
β
donde
Q11
Q21
..
.
Q12
Q22
..
.
...
...
..
.
Q1n
Q2n
..
.
I
I
..
.
Q=
Qn1 Qn2 . . . Qnn I
I
I
... I
0
J1
J2
..
.
,J =
Jn
c
La matriz identidad en la ecuación anterior es de orden K. Minimizando la ecuación del problema de minimización (4.3) con respecto a β se obtiene:
minβ̂ = Q−1 J.
β
En la práctica, se empieza estimando ambos mediante un LMC para la variable aleatoria multivariante A = (α1 , · · · , αK ) y la matriz de covarianzas Σ. Consecuentemente, se pueden
calcular las matrices Q y J. Reemplazando estas matrices en β̂ = Q−1 J, se pueden estimar bi ,
i = 1, · · · , n y los parámetros funcionales dadosR de λi (t). Por otro lado, una estimación plug-in
de la varianza de la predicción integrada σs20 = T V (χ̂s0 (t) − χs0 (t)) dt vendrá dada por
σs20 = β̂ T Qβ̂ + D − 2β̂ T J,
donde la matriz D se calcula usando, V̂ (a0 ) el cuál se obtiene por el ajuste LMC.
La predicción integrada de la varianza σs20 es una medida de incerteza en la predicción
de toda la curva. Basados en los parámetros estimados y usando el desarrollo de la varianza,
V (χ̂s0 (t) − χs0 (t)), se puede estimar la varianza de predicción point-wise.
4.3.3
Resultados: predicción espacial de las curvas de temperatura en Galicia
En este apartado se muestra esta técnica aplicada al conjunto de los datos de temperatura de
Galicia. Inicialmente se seleccoina un número apropiado de bases funcionales. En un segundo
paso se realiza la predicción en un punto no visitado usando el predictor propuesto y se describen
los resultados desde un punto de vista práctico. Para evitar un gran trabajo computacional se han
elegido el número de bases usando la metodología explicada en la técnica anterior y posteriormente se hace validación cruzada funcional con el K elegido, es decir K = 35.
Como ha quedado explicado con la otra técnica los datos de Galicia quedan bien representados en una base de 35. No se considera penalización robusta en este caso, es decir, se supone
η = 0 en:
min
k
c∈R
M
X
j=1
2
(yj − χ(tj )) + η
Z
χ′′′ (t) + ω 2 χ′ (t)
T
2
dt.
4.3 K RIGING VARIACIÓN DE TIEMPO CONTINUA PARA LA PREDICCIÓN ESPACIAL DE DATOS FUNCIONALES73
Cuando los datos son periódicos, las bases de Fourier con un número impar de bases funcionales
son la opción más apropiada ([26]). Por tanto una base de Fourier con 35 bases de funciones será
una buena elección para los datos de Galicia. Aunque que se pueden expresar en función de una
base de Fourier con número infinito de sinusoides, tomamos 365 como el límite porque este es el
número de datos discretos de cada sitio en nuestro conjunto de datos. Frecuencias superiores a
365 en este caso distorsionarán la señal. Esto se conoce como el problema de aliasing (Lfeachor
y Jervis, 1993).
Se trata de predecir la curva de la temperatura en un sitio no visitado con coordenadas
536.07 (Este) y 4747.02 (Norte), que corresponde a la Facultad de Matemáticas. La Facultad de Matemáticas está situada casi en el centro geográfico de Galicia. El clima de Santiago se
aproxima al oceánico costero, que se caracteriza por tener temperaturas suaves en el verano y
en el invierno y precipitacións abundandantes.
En esta sección se sigue la misma metodología de la sección anterior, es decir, se hace la
predicción en el lugar no visitado y después un análisis de validación cruzada. Teniendo en
cuenta que en los datos de Galicia para ajustar la media de la función no es constante, los
datos suavizados están inicialmente sin tendencia usando un modelo de regresión funcional con
respuesta funcional (suavizando las curvas de temperatura) y dos covariables escalares (las coordenadas: longitud y la latitud), es decir, se considera que el modelo de regresión funcional
es
χsi (t) = α̂(t) + β̂1 (t)Longitud + β̂2 (t)Latitud + ǫsi (t).
(4.4)
Posteriormente, el residuo, ǫsi (t), en un sitio no visitado se predice por CT KF D y por último,
la predicción de la temperatura en s0 se obtiene mediante la adición a la predicción del kriging
a la tendencia del modelo dado (4.4).
Los parámetros estimados para el modelo ajustado se muestran en la Figura 4.17.
La variables latitud y longitud en el modelo (4.4) fueron estandarizados anteriormente. La
Figura 4.18 muesta la influencia de la constante, de la longitud y de la latitud en el modelo. Los
parámetros estimados muestran claramente que la temperatura está mucho más influenciada por
las coordenadas en invierno que en verano para la longitud y al revés para la latitud.
Las Figuras 4.19, 4.20 y 4.21 muestan respectivamente los efectos de la variable longitud,
latitud y residuos del modelo (4.4), al que se le aplicará el Kriging
En la Figura 4.22 se muestran las curvas de temperatura suavizadas. La Tabla (4.8 se presenta
un resumen estadístico de las variables longitud y latitud después de centrarlas.
Estadístico
Mínimo
1st Qu.
Mediana
Media
3rd Qu.
Máximo
Longitud
-88.74
-51.57
2.19
0.00
45.88
91.10
Latitud
-88.67
-41.98
-12.93
0.00
45.80
111.20
Tabla 4.8: Resumen estadístico de las variables longitud y latitud.
74
C APÍTULO 4. E JEMPLO REAL DE K RIGING CON DATOS REALES FUNCIONALES
En la Figura 4.24 se muestran los correspondientes residuos de este modelo, es decir los
residuos obtenidos al aplicar el Kriging a los residuos del modelo de regresión funcional de la
temperatura frente a las coordenadas, (longitud y latitud).
Deshaciendo el cambio, se obtiene la curva de predicción para la Facultad de Matemáticas
(Figura 4.17). De las Figuras 4.17 y 4.24 se puede concluir que el modelo de regresión ajustado
tiene un buen rendimiento.
Altos residuos en la Figura 4.24 se deben a malas estimaciones en las estaciones se trata de
Cabeza de Manzaneda (ayuntamiento de Manzaneda (Ourense)) y Pedro Murias (ayuntamiento
de Ribadeo (Lugo), 7124.53 y 6509.01, respectivamente. Cabeza de Manzaneda está al sur este
de Galicia, la diferencia entre la temperatura máxima y la mínima es de 28.5◦ C. El clima se
encuadra dentro de lo que se ha definido por oceánico de montaña que se caracteriza por tener
veranos frescos e inviernos menos fríos. Por el contrario en la estación de Pedro Murias en
Ribadeo, noreste de Galicia, posee clima oceánico costero, que se caracteriza por tener temperaturas suaves en el verano y en el invierno y precipitacións abundandantes. La diferencia de
temperaturas máxima y mínima es esta estación es 25.5◦ C.
Por el contrario las estaciones de las Vigo-Campus (ayuntamiento de Vigo (Pontevedra)) y
Melide (A Coruña), son las estaciones con menores residuos por validación cruzada, 254.13 y
397.53, respectivamente. La diferencias entre el máximo y el mínimo son de 21.5◦ C y 23.4,
para cada una. En Vigo-Campus el clima es oceánico costero y en Melide oceánico continental,
se caracteriza por tener veranos cálidos e inviernos fríos con posibilidades de heladas.
La Figura 4.23 muestra un gráfico de los parámetros funcionales estimados. El mayor
parámetro funcional estimado corresponde a la estación de Sergude (ayuntamiento de Boqueixón
(A Coruña)) que es la estación más cercana al punto a estimar.
Otras estaciones cercanas a la Facultad de Matemáticas, y por tanto con influencia en la
predicción, son Muralla (ayuntamiento de Lousame (A Coruña)) (valores en torno a 0.16), Río
do Sol (ayuntamiento de Coristanto (A Coruña)) (alrededor de 0.13 pesos), Fontecada (ayuntamiento de Santa Comba (A Coruña)) valores en torno a 0.009, en la Figura 4.23. La suma de
los parámetros funcionales estimados es igual a 1 para todo t (Figura 4.23)), lo que indica que la
restricción de insesgadez se cumple. La estación que proporcciona menos información es la de
Malpica, igual que sucede con la técnica 1. La predicción en la Facultad de Matemáticas 4.17,
es consistente con los valores reales registrados.
Una comparación entre la predicción en validación cruzada y las curvas suavizadas (Figuras
4.17 y 4.24) muestran que las predicciones tienen el mismo comportamiento en el tiempo que
las curvas suavizadas.
Se puede observar que hay algunas estaciones con grandes curvas residuales positivas o
negativa. Se aprecia que la desviación estándar residual es menor en la primavera y en el verano
donde las curvas suavizadas y pronosticadas tienen menor variación y se comprueba con los
datos de los promedios de la desviación típica en la Tabla 4.9.
Promedio de la desviación típica
Primavera
2.77
Verano
2.42
Otoño
2.91
Tabla 4.9: Promedios de la desviación típica.
Invierno
2.91
4.4 D E MULTIVARIANTE A GEOSTADÍSTICA FUNCIONAL
75
La media residual varía alrededor de cero, lo que indica que las predicciones son insesgadas.
En la Tabla 4.10 se obtienen los promedios por estación del año.
Promedios
Primavera
5.6
Verano
9.06
Otoño
1.25
Invierno
1.62
Tabla 4.10: Promedios de la media.
En la Tabla (4.11) se muestran los estadísicos de la suma de los errores al cuadrado por
validación cruzada para las 66 estaciones.
Estadístico
Mínimo
1st Qu.
Mediana
Media
3rd Qu.
Máximo
Desviación típica
Suma
CTKFD
865.3
2373.8
2768.0
3212.3
3793.2
10061.0
1474.8
212009.0
Tabla 4.11: Resumen estadístico de la suma de los cuadrados de los errores de validación
cruzada.
4.4
De multivariante a geostadística funcional
En esta técnica, se propone un predictor Cokriging para hacer la predicción univariante (como
en el sentido del Cokriging multivariante), pero considerando como información auxiliar curvas
en vez de observaciones de vectores aleatorios. Del mismo modo, se amplía el Kriging multivariante de vectores aleatorios al contexto funcional definiendo un Kriging predictor funcional,
que permite hacer predicciones de la curva entera en la estación no visitada.
Esto mismo ha sido también estudiado por Nerini y Monestiez (2008), [17]. Ellos proponen
una solución basada en bases de funciones ortonormales, condición no requerida en este trabajo.
En estadística espacial y específicamente en geoestadística, tanto en el análisis Cokriging
([? ], [4]) como en el Kriging multivariante ([13]) se utilizan para modelar observaciones del
vector aleatorias. En este trabajo se adaptan estas metodologías al contexto funcional. Se propone un predictor Cokriging haciendo una predicción univariante (como en el sentido del Cokriging multivariante), pero considerando como información auxiliar funciones en lugar de observaciones de vectores aleatorios. Del mismo modo, se extiende el Kriging multivariante de
vectores aleatorios al contexto funcional mediante la definición de un predictor Kriging funcional que permite hacer una predicción de la curva completa de la zona no muestreada mediante el uso de la información de las curvas muestreadas a sitios cercanos al sitio de predicción. En ambos casos (Cokriging basado en funciones y Kriging funcional) da una solución noparamétrica basada en bases de funciones, y se prueba que ambos propósitos coinciden cuando
76
C APÍTULO 4. E JEMPLO REAL DE K RIGING CON DATOS REALES FUNCIONALES
se utiliza este enfoque. Las metodologías propuestas con esta técnica son del mismo modo a
las soluciones dadas en la técnica anterior, es decir, cada curva observada es ponderada por
un parámetro funcional. Sin embargo aquí la flexibilidad aumenta porque se estima el doble
índice de los parámetros funcionales. Ahora, cada curva se pondera por un parámetro funcional
para llevar a cabo la realización de la predicción en cada momento. Esta metodología sigue la
filosofía básica del
R modelo lineal funcional de respuesta funcional (modelo total) de la ecuación
Yi (t) = β0 (t) + T Xi (v)β (v, t) dv + ǫi (t), donde se debe estimar el coeficiente de regresión
bivariante (Malfait y Ramsay, 2003).
4.4.1
Cokriging basado en datos funcionales
Sean χs (t), t ∈ T, s ∈ D ⊂ Rd una función aleatoria definida en algún conjunto compacto T
de R. Supongamos una muestra de curvas χs1 (t), · · · , χsn (t) definidas ∀t ∈ T, si ∈ D, i =
1, · · · , n. Se asume que estas curvas pertenecen a un espacio separable Hilbert H de funciones integrables definidas en T . Considérese que para cada t ∈ T se tiene un segundo
proceso aleatorio isótropo y estacionario, es decir, la media y la varianza son funciones constantes y la covarianza sólo depende de la distancia entre los puntos de muestreo. Se quiere
predecir una única variable en un único lugar de una muestra de datos funcionales espacialmente correlados χs1 (t), · · · , χsn (t). Sea χs0 (v) la variable aleatoria a predecir en una localización no observada P
s0 en P
v ∈ T . Para llevar a cabo esta tarea se extiende el Cokrign
m
k
ing predictor Ẑk (s0 ) =
i=1
j=1 λij Zj (si ), reemplazando los n × m parámetros λij por
v
n parámetros funcionales λi (t) y las n × m variables aleatorias Zj (si ) por n variables funcionales χsi (t), i = 1, · · · , n, j = 1, · · · , m. En el esquema siguiente se ven claramente estas
transformaciones:
• Parámetros
Cokriging multivariante
λ11 · · · λ1m
λ21 · · · λ2m
..
.
⇒
⇒
..
.
Cokriging BC
λv1 (t), t ∈ T
λv2 (t), t ∈ T
..
.
λn1 · · · λnm
⇒
λvn (t), t ∈ T
Cokriging multivariante
Z1 (s1 ) · · · Zm (s1 )
Z1 (s2 ) · · · Zm (s2 )
..
.
⇒
⇒
..
.
Cokriging BC
χs1 (t), t ∈ T
χs2 (t), t ∈ T
..
.
Z1 (s1 ) · · · Zm (sn )
⇒
χsn (t), t ∈ T
• Variables
4.4 D E MULTIVARIANTE A GEOSTADÍSTICA FUNCIONAL
77
Por lo tanto, el predictor Cokriging de χs0 (v) basado en datos funcionales (CBFD) viene
dado por
n Z
X
χ̂s0 (v) =
λvi (t)χsi (t)dt
i=1
T
Para cada v ∈ T específico, los parámetros funcionales λvi (t), i = 1, · · · , n se estiman teniendo
en cuenta las restricciones clásicas de geoestadística, es decir, insesgadez y mínima varianza
de predicción. Este problema se resuelve utilizando un enfoque basado bases de funciones.
Ampliamos las variables funcionales mediante la expresión
χsi (t) = aTi B(t), i = 1, · · · , n
y los parámetros funcionales por
λvi (t) = bTiv B(t)
Por lo tanto el predictor se expresa como
χ̂si (v) =
n
X
bTiv W ai
i=1
donde
W =
Z
B(t)B T (t)dt
T
Para cualquier base ortonormal como la base de Fourier, la matriz W de Gram es la matriz
identidad. Para otras bases de funciones tales como las bases B-Splines, W debe ser calculada usando integración numérica. Asumiendo la hipótesis de estacionariedad de las funciones
aleatorias la matriz:
a11 a12 . . . a1K
a21 a22 . . . a2K
A= .
= (α1 , · · · , αK )(n×K)
..
..
.
.
.
.
. .
.
an1 an2 . . . anK
constituyen un vector aleatorio multivariante K con
E(a1j )
ϑj
E(a2j ) ϑj
E(αj ) = .
= ..
..
.
E(anj )
y matriz de covarianzas
Σ=
Σ11
Σ21
..
.
ΣK1
ϑj
Σ12 . . .
Σ22 . . .
..
..
.
.
Σk2 . . .
, j = 1, · · · , k,
Σ1K
Σ2K
..
.
ΣKK
78
C APÍTULO 4. E JEMPLO REAL DE K RIGING CON DATOS REALES FUNCIONALES
donde Σij = C(αi , αj )n×n , obteniéndose así:
E(ai1 )
E(ai2 )
E(ai ) = .
..
E(aik )
Entonces, la media del predictor está dada por:
E (χ̂s0 (v)) =
=
n
X
ϑ1
ϑ2
..
.
ϑK
=ϑ
bTiv W ϑ
i=1
Por otro lado, la media de la función en el sitio s0 no observado en el instante v es
E (χs0 (v)) = B T (v)E(a0 ) = B T (v)ϑ
Consecuentemente el predictor propuesto es insesgado si
n
X
bTiv = B T (v)W −1
i=1
R
La matriz Gram es en general semidefinida positiva, la matriz W Gram, W = T B(t)B T (t)dt,
es definida positiva porque las funciones Bl (t), l = 1, · · · , K, son linealmente independientes.
Consecuentemente el predictor propuesto está bien definido. Para encontrar el mejor predictor
lineal insesgado (BLUP), los n parámetros funcionales propuestos en el predictor se dan como
solución al siguiente problema de optimización:
min
λv1 (·),··· ,λvn (·)
V (χ̂s0 (v) − χs0 (v)) sujeto a : E (χ̂s0 (v)) = E (χs0 (v))
(4.5)
Desarrollando la varianza en la función objetivo se tiene la siguiente expresión:
V (χ̂s0 (v) − χs0 (v)) =
n
X
bTiv W V (ai )W T biv + 2
i=1
+ B T (v)V (a0 )B(v) − 2
X
bTiv W C(ai , aj )W T bjv
i<j
n
X
bTiv W C(a0 , ai )B(v)
i=1
V (ai ), C(ai , aj ) y C(a0 , ai ) se pueden calcular si Σ, la matriz de covarianzas, ha sido previamente estimada. Podemos usar geostadística multivariante ([28]) y específicamente un modelo
lineal de corregionalización (LMC) para estimar estas matrices. Si se definen:
Mi = W V (ai )W T (K×K)
Mij = W C(ai , aj )W T (K×K)
Ni (v) = (W C(a0 , ai )B(v))(K×1)
D(v) = B T (v)V (a0 )B(v)
4.4 D E MULTIVARIANTE A GEOSTADÍSTICA FUNCIONAL
79
la función objetivo está dada por
V (χ̂s0 (v) − χs0 (v)) =
n
X
bTiv Mi biv + 2
i=1
X
i<j
bTiv Mij bjv + D(v) − 2
n
X
bTiv Ni (v) (4.6)
i=1
De (4.6) y considerando los K multiplicadores de Lagrange mTv = (m1v , · · · , mKv ) el problema de optimización (4.5) puede ser expresado como:
min
b1v ,··· ,bnv ,mv
n
X
bTiv Mi biv + 2
i=1
X
i<j
bTiv Mij bjv + D(v) − 2
Tomando βv = bT1v , · · · , bTnv , mTv
forma:
T
(K(n+1)x1)
n
X
bTiv Ni (v) + 2mTv
i=1
βv
y
M11
M21
..
.
M12
M22
..
.
...
...
..
.
M1n
M2n
..
.
I
I
..
.
M =
Mn1 Mn2 . . . Mnn I
I
I
... I
0
i=1
biv − W −1 B(v)
, se puede reescribir la ecuación anterior de la
minβvT M βv + D(V ) − 2βvT N (V )
donde
n
X
N1 (v)
N2 (v)
..
.
N (v) =
Nn (v)
W −1 B(v)
(4.7)
[K(n+1)]×[K(n+1)]
[K(n+1)]×1
Finalmente, si se minimiza la ecuación reducida respecto a βv , se obtiene:
β̂v = M −1 N (v)
Una estimación plug-in de la varianza de predicción σs20 (v) = V (χ̂s0 (v) − χs0 (v)) está dada
por
σ̂s20 (v) = β̂vT M β̂v + D(v) − 2β̂vT N (v)
donde la matriz D(v) se calcula usando una estimación de V̂ (a0 ) obtenida mediante el ajuste de
medias del modelo linal de corregionalización (LMC).
!
80
C APÍTULO 4. E JEMPLO REAL DE K RIGING CON DATOS REALES FUNCIONALES
4.4.2
Kriging funcional: modelo total
Para definir el Kriging funcional (modelo total) predictor (FKTM), se asumen los mismos supuestos
de estacionariedad e isotropía que
el Cokriging basado en datos funcionales. El Cokriging
Pen
n R
predictor definido allí, χ̂s0 (v) = i=1 T λvi (t)χsi (t)dt, está definido para un v ∈ T específico.
Si se quiere predecir la curva completa en s0 , el parámetro funcional λvi (t) se reemplaza por un
parámetro que depende de dos índices λi (t, v). Así, el predictor para toda la curva está dada por
χ̂s0 (v) =
n Z
X
i=1
T
λi (t, v)χsi (t)dt, v ∈ T,
tal que λ1 (t, v), · · · , λn (t, v) : T xT → R. Notar que de acuerdo a los reemplazamientos
dados en los esquemas tanto para parámetros
P como para variables en el caso del Cokriging
basado en datos funcionales, el predictor ni=1 bTiv = B T (v)W −1 se extiende al contexto
T
funcional mediante la sustitución del vector Ẑ1 (s0 ), · · · , Ẑm (s0 )
por χ̂s0 (v), v ∈ T , y
1
1
m
m
1
1
m
el vector de parámetros
λ11 · · · λ1m · · ·
λ11 · · · λ1m , · · · , λn1 · · · λnm · · · λm
n1 · · · λnm por
1
m
λ11 (t) · · · λm
1 (t) , · · · , λn (t) · · · λn (t) , t ∈ T , respectivamente.
Además, teniendo en cuenta que v varía
de forma continua en T , el conjunto discreto de
parámetros funcionales λ1i (t) · · · λm
(t)
,
i
=
1, · · · , n se sustituye por el doble índice del
i
parámetro funcional λi (t, v), t, v ∈ T . Es evidente que para un fijo v ∈ T la expresión del
predictor FKTM es igual a la del Cokriging basado en datos funcionales (CBFD). El parámetro
funcional λi (t, v) determina el impacto de la i-ésima función observada en el tiempo t en la
función no observada al tiempo v. Este modelo es coherente con el modelo funcional lineal con
respuesta funcional (modelo total):
Z
Yi (t) = β0 (t) +
Xi (v)β(v, t)dv + ǫi (t).
T
La estimación funcional de los parámetros se lleva a cabo mediante la resolución (Ramsay y
Silverman, 2005) de:
min
α(·),β1 (·,·),··· ,βq (·,·)
E Ŷ (v) − Y (v)
2
.
En nuestro contexto las covariables son las curvas observadas en n lugares de una región y la
respuesta funcional es una función no observada en un lugar no visitado. Por lo tanto la función
objetivoR es E kχ̂s0 (v) − χs0 (v)k2 , dependiendo de λ1 (·, ·), · · · , λn (·, ·) o usando el Teorema de
Fubini T E (χ̂s0 (v) − χs0 (v))2 dv. Teniendo en cuenta la estacionalidad de la función objetivo
R
se tiene, T V (χ̂s0 (v) − χs0 (v))2 dv.
Una vez más, los parámetros funcionales λi (t, v) de χ̂s0 (v) se calculan teniendo en cuenta
las restricciones de insesgadez y la predicción con mínima varianza. Por lo tanto el problema de
optimización es
Z
min
V (χ̂s0 (v) − χs0 (v)) sujeto a : E (χ̂s0 (v)) = E (χs0 (v)) , ∀v ∈ T. (4.8)
λ1 (·,·),··· ,λn (·,·) T
4.4 D E MULTIVARIANTE A GEOSTADÍSTICA FUNCIONAL
81
Resolvemos el problema utilizando un enfoque basado en bases de funciones. Se extienden las
variables funcionales de la ecuación:
χsi (t) = aTi B(t), i = 1, · · · , n
y los parámetros funcionales bivariantes:
λi (t, v) = B T (t)Ci B(v)
donde
ci11
ci21
..
.
Ci =
ci12
ci22
..
.
···
···
..
.
ci1K
ci2K
..
.
ciK1 ciK2 · · · ciKK
(K×K)
Con estas consideraciones el predictor χ̂s0 (v) se expresa:
χ̂s0 (v) = B T (v)â0 ,
R
donde la matriz de producto interior W , definida, W = T B(t)B T (t)dt. El predictor χ̂s0 (v)
también ha sido considerado por Nerini y Monestiez (2008). En su trabajo de Nerini y Monestiez
(2008) se supone que W es una matriz de identidad ya que consideran una solución basada en
expansiones de bases ortonormales, en este caso no es una condición necesaria. Se consideran
las propiedades de insesgadez y mínima varianza del predictor propuesto, se supone que los
coeficientes ai en la ecuación anterior son un vector aleatorio multivariante estacionario. En
consecuencia, el valor esperado de la la curva en el sitio no visitado s0 viene dado por
E (χs0 (v)) = B T (v)ϑ∀v ∈ T.
Por otro lado, teniendo en cuenta el valor esperado para el estimado se tiene:
E (χ̂s0 (v)) = B T (v)
n
X
i=1
CiT W ϑ ∀v ∈ T.
Consecuentemente de las ecuaciones E (χs0 (v)) y E (χ̂s0 (v)), se observa que el predictor χ̂s0 (v)
es insesgado si y sólo si
B T (v)
n
X
i=1
CiT W ϑ = B T (v)ϑ∀v ∈ T,
esto es, si y sólo si,
n
X
CiT W ϑ = ϑ.
i=1
Esta condición es equivalente a
Pn
i=1 Ci
= W −1 .
82
C APÍTULO 4. E JEMPLO REAL DE K RIGING CON DATOS REALES FUNCIONALES
Los n parámetros funcionales en el predictor, χ̂s0 (v), vienen dados por la solución del siguiente problema de optimización
min
C1 ,··· ,Cn
Z
T
n
X
V B T (v)â0 − B T (v)a0 dv sujeto a :
Ci = W −1 .
(4.9)
i=1
Desarrollando la integral en la función objetivo se obtiene que
Z
B T (v)V (â0 − a0 ) B(v)dv = T rV (â0 − a0 ) W.
T
La varianza en la expresión anterior es
V (â0 − a0 ) =
n
X
n
X
CiT W V (ai )W Ci + 2
i=1
i<j
CiT W V (ai , aj )W Cj + V (a0 ) − 2
n
X
CiT W C(ai , a0 ).
i=1
Definiendo las siguientes matrices Qii = (W V (ai )W ), Qij = (W C(ai , aj )W ), Ni =
W C(ai , a0 ). El problema de optimización (4.3) puede ser expresado como
min
C1 ,··· ,Cn ,m
n
X
T r CiT Qii Ci W
i=1
+ 2
n
X
T r CiT Qij Cj W
i<j
+ T r (V (a0 )W ) − 2
+ 2m
n
X
i=1
Ci − W
n
X
(4.10)
T r CiT Ni W
i=1
−1
!
(4.11)
(4.12)
Derivando con respecto a Ci , i = 1, · · · , n y m:
∂
∂Ci
= 2
∂
∂m
=
n
X
j=1
n
X
i=1
Qij Cj W − 2Ni W + 2m
Ci − W −1 .
La solución del problema se obtiene igualando a cero estas derivadas. Esta solución en notación
matricial queda:
Q11
Q21
..
.
Q12
Q22
..
.
...
...
..
.
Q1n
Q2n
..
.
I
I
..
.
Qn1 Qn2 . . . Qnn I
I
I
... I
0
C1
C2
..
.
Cn
m∗
N1
N2
..
.
=
Nn
W −1
4.4 D E MULTIVARIANTE A GEOSTADÍSTICA FUNCIONAL
83
donde m∗ = mW −1 . De V (â0 − a0 ) y de las matrices Qii , Qij y Ni , una estimación de la
predicción de la varianza integrada
Z
2
σint =
V (χ̂s0 (v) − χs0 (v)) dv
T
viene dada por
2
σ̂int
=
n
X
i=1
Tr
ĈiT Q• Ĉi W
+ T r (V (a0 )W ) − 2
n
X
+2
n
X
i<j
T r ĈiT Qij Ĉj W
T r ĈiT Ni W
i=1
donde las matrices Ĉ1 , · · · , Ĉn se obtienen resolviendo el sistema matricial anterior.
En el resto de esta sección, se discute sobre la conexión entre los dos métodos introducidos en el proyecto. La relación entre CBFD y FKTM es análoga al análisis del Cokriging y la
predicción espacial multivariante, en el sentido de que la predicción obtenida por CBFD es a la
vez idéntica a la predicción obtenida por FKTM al mismo tiempo. Las expresiones de estos predictores, las restricciones de insesgadez y la respectiva función objetivo, son equivalentes para
cada v fijo. De hecho, la siguiente proposición establece la equivalencia entre ambas alternativas
cuando, se usa la expansión bases.
Proposición 1:
Supongamos que la representación χsi (t) = aTi B(t) es correcta para χsi (t). Permitamos
T
χC
s0 (t), v ∈ T sea el conjunto de predictores para χs0 (v) derivados de las χsi (t) = ai B(t)
v
T
y λi (t) = biv B(t), donde los coeficientes biv , i = 0, 1, · · · , n son una solución al problema
F
(4.7)
R cada v ∈ T . Sea χ̂s0 (v), v T∈ T el predictor dado por las ecuaciones χ̂s0 (v) =
Pn para
i=1 T λi (t, v)χsi (t)dt y λi (t, v) = B (t)Ci B(v), donde los coeficientes de las matrices Ci ,
i = 0, 1, · · · , n son la solución al problema (4.12). Entonces
F
χ̂C
s0 (v) = χ̂s0 (v)
para todo v ∈ T y para todo s0 ∈ D.
La diferencia entre resolver un número infinito predicciones punto a punto (point-wise) mediante CBFD y hacerlo sólo mediante una predicción de una curva completa por FKTM se debe
a la utilización de un doble expansión en términos de bases de funciones para los parámetros
funcionales de FKTM. Una característica distintiva entre estas metodologías se da en términos
de la varianza de predicción. La predicción de la varianza estimada por FKTM en la expresión
2 , se puede utilizar como una medida global de la incertidumbre en la predicción de una
de σ̂int
curva completa, mientras que la varianza de predicción estimada de CBFD σ̂s20 (v) se puede utilizar en un sentido clásico, es decir, podemos, por ejemplo, calcular intervalos de confianza para
la predicción.
4.4.3
Resultados: Predicción espacial de la temperatura en las curvas Galicia
En la sección anterior se concluyó que una base con 35 funciones era adecuada para suavizar
este conjuntos de datos, por tanto ahora usamos ese mismo número de bases de funciones. De
84
C APÍTULO 4. E JEMPLO REAL DE K RIGING CON DATOS REALES FUNCIONALES
la Proposición 1 sabemos que las predicciones obtenidas por CBFD coinciden con aquellas
dadas por FKTM. Así que sólo muestran los resultados obtenidos por FKTM por no hacer muy
extensivo este trabajo. Para cada caso, se estimó una LMC y se utiliza para el cálculo de las
matrices Qij , Ni , i, j = 1, · · · , 66 en la ecuación matricial
Q I
C
N
=
I 0
m∗
W −1
y consecuentemente para la estimación de los parámetros indicados en dicho sistema. Para ajustar el LMC todos los variogramas simples (directos)y variogramas cruzados fueron modelados
como una combinación lineal de modelos con efecto pepita (nugget) y modelo exponencial. Se
ha usado para ello la librería gstat, (Pebesma, 2004), del lenguaje R.
La Figura 4.25 muestra la predicción en Facultad de Matemáticas (punto no muestreado),
junto con una comparación gráfica entre curvas suavizadas y predichas, lo que muestra un buen
resultado de las predicciones.
La Figura 4.26 presenta los residuos obtenidos por validación cruzada, la media y la desviación
típica. Se puede ver en esta Figura que hay buenas predicciones en una alta proporción de los
sitios (teniendo residuos cercanos a cero). Residuos grandes, negativos o positivos se obtienen
en tan sólo un número pequeño de estaciones. No se observa, dependiendo de la estación del
año en la que estemos que los residuos sean más grandes o pequeños que en otras estaciones.
A final del año se aprecian residuos superiores a 6◦ C, se podría decir que se tiene una mayor
incertidumbre en la predicción durante este período, pero como no se nota al principio y es un
dato periódico más bien se trate de un atípico. Si se recuerda en la Figura 1 parece que se entrevé
una curva que sobresal al final del año, lo que se sugiere que pueda tratarse de un atípico.
Se aprecia que la desviación estándar residual es menor en el otoño y en el invierno donde
las curvas suavizadas y pronosticadas tienen menor variación y se comprueba con los datos de
los promedios de la desviación típica en la Tabla 4.12.
Promedio de la desviación típica
Primavera
2.07
Verano
2.03
Otoño
1.91
Invierno
1.92
Tabla 4.12: Promedios de la desviación típica.
La media residual varía alrededor de cero, lo que indica que las predicciones son insesgadas.
En la Tabla 4.13 se obtienen los promedios por estación del año.
Promedios
Primavera
0.00
Verano
-0.11
Otoño
0.05
Invierno
0.12
Tabla 4.13: Promedios de la media.
Las estaciones Lardeira (ayuntamiento de Carballeda de Valdeorras (Ourense)) y Alto do
Rodicio (ayuntamiento de Maceda (Ourense)) están al sur este de Galicia son las estaciones
con mayores residuos por validación cruzada, 10474.70 y 10227.14, respectivamente. Aunque
la temperatura media diaria en estas estaciones tiene un comportamiento muy similar todo el
tiempo, en Lardeira la diferencia entre el máximo y el mínimo es de 28.1◦ C y en Alto do
4.5 C OMPARACIÓN DE LAS TRES TÉCNICAS
85
Rodicio es de 27.7◦ C. Esto genera residuos altos en ambos casos. En estas dos estaciones el
clima que tienen se encuadra dentro de lo que se ha definido por oceánico de montaña que se
caracteriza por tener veranos frescos e inviernos menos fríos que en otras zonas montañosas más
alejadas del mar.
Por el contrario las estaciones de las Islas Cíes (ayuntamiento de Vigo (Pontevedra)) e Isla
de Ons (ayuntamiento de Bueu (Pontevedra)) están al sur oeste de Galicia son las estaciones con
menores residuos por validación cruzada, 1040.85 y 1053.69, respectivamente. La diferencias
entre el máximo y el mínimo son de 9.3◦ C y 18.7, para cada una.
Con respecto a la predicción en la Facultad de Matemáticas, observamos en la Figura 4.26
que la curva predicha muestra un comportamiento estacional similar a las curvas suavizadas y
es consistente con los valores reales registrados en la estación de Santiago.
Tres de los parámetros estimados para hacer esta predicción se muestran en las Figuras 4.27
y 4.28, corresponden a las estaciones de A Pontenova (Lugo),Monte Aloia (ayuntamiento de Tui
(Pontevedra)), Malpica (A Coruña) y Sergude (ayuntamiento de Boqueixón (A Coruña)).
De la Figura 4.28 se puede destacar que los parámetros de Malpica son casi nulos, son
los más pequeños y por el contrario en Sergude son los más grandes. Otra vez se pone de
manifiesto la cercanía al punto no muestreado. Por tanto esto quiere decir que Sergude tiene una
mayor influencia sobre la predicción que Malpica (cuyos parámetros funcionales son casi nulos).
Además la estimación funcional de los parámetros revela que hay un efecto a corto temporal en la
predicción. Ambos resultados eran de esperar. Por un lado, el primer resultado es coherente con
la filosofía de geoestadística, es decir, los sitios más cerca de la ubicación de predicción tienen
una mayor influencia que otros más alejados. Al igual que en el caso de Malpica, otras estaciones
muy separadas de la Facultad de Matemáticas tienen una baja influencia en la predicción.
Finalemente se ha aplicado esta técnica a los datos de la temperatura de Galicia (2009),
eliminándole a los residuos el efecto de la latitud y longitud. Los resultados obtenidos se pueden
consultar en la tabla (4.14) y servirán para concluir en la comparación con qué metodología nos
quedamos.
4.5 Comparación de las tres técnicas
Para llevar a cabo la comparación se usa el resumen estadístico de SSEF CV (i):
SSEF CV =
n
X
i=1
n X
M 2
X
(i)
SSEF CV (i) =
χsi (tj ) − χ̂si (tj )
i=1 j=1
para comparar las metodologías propuestas en el proyecto. Evaluamos en j = 1, · · · , 365 las
predicciones obtenidas por validación cruzada para OKFD,
R v y FKTM. Para incluir el
Pn CTKFD
predictor CBFD en este análisis calculamos χ̂s0 (v) = i=1 T λi (t)χsi (t)dt. Los valores del
estadístico resumen SSEF CV obtenidos por CBFD y FKTM coinciden porque las predicciones
por CBFD se calculan con los mismos argumentos donde se evalúan las curvas predichas por
FKTM. Para el conjunto de datos, que inicialmente se elimina la tendencia de los datos mediante
un modelo de regresión funcional. Aplicamos los métodos de predicción espacial propuestos
86
C APÍTULO 4. E JEMPLO REAL DE K RIGING CON DATOS REALES FUNCIONALES
para los residuos de la regresión. Las predicciones de temperatura para estos conjunto de datos
se obtienen agregando las predicciones residual a la tendencia.
Estadístico
Mínimo
1st Qu.
Mediana
Media
3rd Qu.
Máximo
Desviación típica
Suma
OKFD
1326.0
2931.0
3861.0
4306.0
4847.0
12880.0
2279.5
284222.1
OKFD*
812.6
2017.0
2626.0
2990.0
3403.0
11090.0
1551.3
197345.3
CTKFD
865.3
2373.8
2768.0
3212.3
3793.2
10061.0
1474.8
212009.0
FKTM
1041.0
1971.0
2554.0
3030.0
3261.0
10470.0
1852.1
199959.1
FKTM*
805.3
1951.0
2499.0
3009.0
3468.0
10180.0
1780.6
198569.1
Tabla 4.14: Resumen estadístico de la suma de los cuadrados de los errores de validación
cruzada. (Nota: ∗, método de la columna anterior sin los efectos de la longitud y la latitud.)
Se observa en la Tabla (4.14) que donde existen las mayores diferencias entre los métodos
son en términos de los valores mínimos o máximos y también influenciadas por el efecto de la
longitud y la latitud.
Los predictores tienen un comportamiento similar cuando las curvas son relativamente homogéneas y las diferencias entre los mismos con los datos de temperatura para Galicia son
fundamentalmente debidas a su desempeño en las estaciones con temperaturas extremas como
se explicó anteriormente.
Los resultados mostrados en la Tabla (4.14) indican que la inclusión de un doble índice
funcional en los parámetros (efecto temporal en el conjuntos de datos) no reflejan cambios sustanciales en las predicciones del análisis. Es decir, el trabajo de estimar tantos parámetros no
revierte mejores resultados, aunque, si a los datos se les elimina el efecto de la latitud y la longtud
se obtienen mejores
En principio si las curvas son homogéneos podríamos usar cualquiera de los tres enfoques.
Sin embargo, si lo observado en los datos tiene una variabilidad alta CTKFD podría ser la mejor
opción.
En resumen, podemos concluir que OKFD sin los efectos de la longitud y la latitud es la
mejor opción para llevar a cabo la predicción espacial de datos funcionales en Galicia. Por
lo tanto todos ellos son buenas alternativas para hacer la predicción espacial de los datos funcionales. Teniendo en cuenta que es más simple OKFD sin los efectos de la longitud y la latitud
que otros desde un punto de vista práctico y computacional en aplicaciones con grandes conjuntos de datos este método puede ser preferible.
10
Residuos
Media
−10
−10
0
−5
0
Residuos
10
Temperatura (ºC)
5
20
Desviación típica
0
100
200
Día
300
0
100
200
300
Día
Figura 4.13: Izquierda: muestra una comparación gráfica entre las curva observadas (las reales)
y la predicha(utilizando FCV). Derecha: la de la derecha lo residuos de validación cruzada
funcional, media residual y desviación típica residual.
Residuos suavizados
−5
−5
0
0
X(t)
residuos
5
5
10
10
Residuos
0
100
200
300
0
100
200
t
Figura 4.14: Residuos del modelo con altitud y latitud.
300
6000
4000
0
2000
semivariance
8000
Mat
Exp
Sph
Cir
0
50
100
150
200
distance
Figura 4.15: Variograma para los residuos.
6
Predicción de los residuos
enSantiago
0
−2
−4
−6
Temperatura (ºC)
2
4
KO
Original
Suavizada
0
100
200
300
día
Figura 4.16: Predicción para los residuos.
20
10
0
Temperature (degrees C)
0
100
200
time
100
Smoothed
Prediction
Real data
300
Influencia de la longitud
0
100
200
Day
200
time
300
Influencia de la latitud
300
0
100
200
time
300
Figura 4.18: Influencia de la constante, de la longitud y latitud en el modelo.
Influencia de la constante
Figura 4.17: Datos suavizados, predicción en Santiago y datos reales en Santiago.
−10
0
0.02
0.01
0.00
−0.01
−0.02
−0.03
0.00
−0.01
−0.02
−0.03
−0.04
20
15
10
5
−0.02
−0.04
−0.03
longitud
−0.01
0.00
Efecto de la longitud
g
p
e
c5
u
a
o
s0
xW
w
vn
zg
m
rQ
e
u
a
o
m
ttP
3
6
8
9
0
7
1
2
4
d
b
h
iJyq
3
k2
lT
JIq
ffB
U
A
D
E
G
H
2
1
4
K
L
3
M
N
O
6
R
S
T
8
9
V
7
X
1
4
d
b
Q
h
3
A
B
E
G
2
1
4
K
L
M
O
P
S
X
Y
g
p
q
p
jF
e
c5
u
a
o
s0
xp
w
vn
zg
m
n
rQ
5
jF
tb
3
6
8
9
0
e
7
cjF
u
a
1
2
4
sY
xW
w
vZ
zrV
d
b
m
n
h
iyq
3
k2
lC
fB
U
A
C
D
E
G
H
2
1
4
K
L
M
N
O
P
R
S
V
W
X
Y
Z
5
tP
3
6
8
9
7
1
4
d
Q
h
iyIIq
3
ko
lK
JV
fB
U
A
C
D
E
G
H
I1
2
4
L
M
N
O
R
S
T
X
Y
Z
p
q
p
jF
e
cg
u
a
sM
w
vxW
zrQ
m
n
jF
5
e
u
cg
a
tP
3
6
sM
8
9
0
w
vxW
zrQ
7
m
n
2
1
4
d
b
h
iyO
ko
lR
JV
fB
U
A
C
D
E
G
H
I5
K
L
N
S
T
X
Y
Z
tP
3
6
8
9
0
7
1
2
4
d
b
3
h
iyO
JV
ko
lK
fB
U
A
C
D
E
G
H
I1
2
4
L
N
R
S
T
X
Y
Z
g
y
p
q
g
y
p
q
j
e
u
c
a
o
s
x
w
v
z
m
n
r
j
e
c
u
a
o
s
x
w
v
z
m
n
r
5
tP
3
6
8
9
0
7
1
4
d
b
Q
5
h
iO
3
kC
lK
JV
tP
3
fB
6
U
8
9
A
0
7
D
E
F
G
H
I1
2
4
L
M
N
1
2
R
S
4
T
W
X
Y
d
b
Z
Q
h
iO
3
kC
lR
JV
fB
U
A
D
E
F
G
H
I1
2
42
K
L
M
N
S
T
W
X
Y
Z
g
y
p
q
jF
e
u
ch
a
sM
w
vxW
zrQ
m
n
5
tP
3
6
8
9
0
7
1
4
d
b
iO
3
ko
lK
JV
fB
U
A
C
D
E
G
H
I1
2
4
L
N
R
S
T
X
Y
Z
p
q
jF
e
cg
u
a
sM
w
vxW
zrQ
m
n
5
tP
3
6
8
9
0
7
1
2
4
d
b
3
h
iyO
JV
ko
lR
fB
U
A
C
D
E
G
H
I1
2
42
K
L
N
S
T
X
Y
Z
p
q
jF
e
u
cg
a
sM
w
vxW
zrQ
m
n
5
tP
3
6
8
9
0
7
1
2
4
d
b
h
iyO
3
ko
lK
JV
fB
U
A
C
D
E
G
H
I1
2
4
L
N
R
S
T
X
Y
Z
g
y
p
q
j
e
c
u
a
o
s
x
w
v
z
m
n
r
5
t
3
6
8
9
0
7
1
2
4
d
b
Q
3
h
i
J
k
l
f
U
A
B
C
D
E
F
G
H
I
2
1
4
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
g
p
g
p
jF
e
cjF
u
a
sY
xW
w
vZ
zg
m
r1
p
q
jF
e
c5
u
a
sM
xW
w
vn
tP
zV
3
6
m
n
8
9
0
7
rQ
1
2
4
d
b
Q
h
iJyIcO
3
ko
l2
JIq
fB
U
A
D
E
G
H
Ijzr1
2
4
K
L
M
N
R
jF
S
T
V
X
Y
Z
e
cg
u
a
sM
w
vxW
zrQ
m
n
5
tb
3
6
8
9
0
7
1
2
4
d
b
h
iJyq
3
ko
lC
fB
U
A
C
D
E
G
H
2
1
4
K
L
N
O
P
R
S
T
V
X
Y
Z
5
tP
3
6
8
9
0
7
1
2
4
d
b
3
h
iyO
JV
ko
lK
fB
U
A
C
D
E
G
H
I1
2
4
L
N
R
S
T
g
X
Y
Z
yq
p
q
e
u
c
a
o
s
x
w
v
z
m
n
r
5
t
3
6
8
9
0
7
1
2
4
d
b
Q
h
i
3
y
k
l
f
U
A
B
C
D
E
G
H
p
4
K
L
M
N
O
P
R
S
T
W
X
e
u
a
o
s
x
w
v
m
n
5
t
3
6
8
9
0
7
1
2
4
d
Q
h
3
i
J
k
l
f
U
A
B
C
D
E
F
G
H
I
2
1
4
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
g
y
p
q
jF
e
u
ch
a
sM
w
vxW
zrQ
m
n
5
tP
3
6
8
9
0
7
1
2
4
d
b
3
iO
JV
ko
lR
fB
U
A
C
D
E
G
H
I1
2
4
K
L
N
S
T
X
Y
Z
p
q
yO
p
q
jF
yO
e
cg
u
a
p
q
sM
w
vxW
zrQ
m
n
5
tP
jF
3
6
8
p
9
0
7
e
cg
u
a
1
2
4
o
sM
d
b
w
vxW
zrQ
jF
m
n
e
cg
u
a
h
iyO
3
ko
l
J
o
f
s
U
x
w
v
z
A
B
C
D
E
m
G
H
n
I1
2
42
K
L
r
N
R
S
T
V
X
Y
Z
g
g
5
y
t
3
6
8
p
9
q
0
7
jF
5
1
2
4
e
cO
a
u
t
d
b
3
6
8
9
sY
0
7
xW
w
vn
zg
h
i
m
3
k
l
J
1
2
4
rV
f
U
d
b
A
B
C
D
E
G
H
Q
I
2
1
4
K
L
N
P
R
S
T
h
i
3
k
V
l
J
X
Y
Z
f
U
A
B
C
D
E
G
H
I
2
1
4
K
L
M
N
P
R
S
T
V
W
X
Y
Z
p
tP
3
j
6
8
9
7
e
c5
a
e
u
u
c
a
1
o
4
o
s0
s
d
b
xW
w
vn
zg
x
w
v
z
m
m
Q
n
rQ
r
3
h
iJyIq
ko
lK
fB
U
A
C
D
E
G
H
IjzrV
2
1
4
L
M
N
R
S
T
X
Y
jF
e
cjF
a
u
5
sY
xp
w
vn
zrV
t
m
tP
3
3
6
6
8
9
8
0
9
0
7
7
1
2
1
2
4
4
d
b
d
b
Q
h
3
h
iJyq
i
3
J
k2
k
lK
l
f
fB
U
U
A
A
B
C
C
D
D
E
E
F
G
G
H
H
I
2
1
2
1
4
K
L
L
M
M
N
N
O
O
P
R
R
S
S
T
T
V
W
X
X
Y
Z
Z
5
tP
3
6
8
9
7
1
4
g
d
Q
3
h
iJyIq
ko
lK
p
q
fB
U
A
C
D
E
G
H
2
1
4
L
M
N
O
R
S
T
W
X
Y
Z
jF
e
c5
a
u
o
s0
xp
w
vn
zg
m
rV
tb
3
6
8
9
0
7
1
4
d
b
Q
h
iJyq
3
k2
lK
p
fB
U
A
C
D
E
G
H
2
1
4
L
M
N
P
R
S
T
V
W
X
Z
p
q
jF
e
u
a
o
sY
xW
w
vd
zg
m
n
rQ
e
cO
a
u
s4
xW
w
vZ
m
p
q
g
5
jF
tP
3
6
p
p
q
q
8
9
7
e
cg
u
a
1
4
sM
w
vxW
zrQ
b
m
n
h
iyIcO
3
k2
l2
Jq
fB
U
A
C
D
E
G
H
IO
2
1
4
K
L
M
N
R
S
T
V
X
tP
Y
Z
3
6
8
9
0
7
p
1
2
4
d
b
Q
h
iJyO
3
ko
lK
JIV
fB
U
A
C
D
E
F
G
H
I1
2
4
L
M
N
R
S
T
jF
5
X
Y
Z
e
u
cg
a
tP
3
6
8
9
0
7
sM
jF
jF
w
vxW
zrQ
m
n
1
2
4
e
c5
a
u
e
cg
u
a
d
b
sM
sM
xW
w
vn
zrQ
w
vxW
zrQ
m
h
n
iyq
m
3
ko
n
lK
JyjzV
fB
U
A
C
D
E
G
H
I1
2
4
L
N
O
R
S
T
X
Y
Z
jF
e
u
cg
a
o
s0
xW
w
vd
zg
m
n
5
rQ
tP
3
6
8
9
0
7
5
5
1
2
4
tP
tP
3
3
d
b
6
6
8
8
9
9
0
0
7
7
3
h
iyO
1
2
JV
4
ko
lR
1
4
d
b
fB
d
U
b
A
C
D
E
G
H
I1
2
42
K
L
h
N
iJyO
h
3
ko
iyO
S
lK
T
JV
ko
lR
X
Y
fB
Z
fB
U
U
A
C
A
D
E
C
D
G
E
H
I5
G
H
I1
2
4
L
K
N
L
N
R
S
T
S
T
5
X
Y
Z
X
Y
Z
tP
3
6
8
9
0
7
1
2
4
d
b
y
h
iJycO
3
k2
lT
JIq
fB
U
p
A
C
D
E
G
H
1
4
K
L
M
N
R
S
T
V
X
Z
j6
e
u
a
o
s
x
w
v
z
m
n
r
g
y
p
q
5
g
t
3
yq
6
8
9
0
7
p
1
q
4
b
Q
h
i5
3
k
l7
J
f3
U
A
B
C
D
E
F
G
H
I
2
1
4
K
L
M
N
P
R
S
T
V
W
X
Y
Z
j
e
c
a
u
o
s
x
w
v
z
m
n
g
r
p
j
e
u
c
a
o
s
x
w
v
z
m
n
r
5
t
3
6
8
9
0
7
1
2
4
d
b
g
Q
yO
3
5
h
i
k
l
f
p
U
q
t
A
3
B
C
D
6
E
F
G
H
8
I
2
1
9
4
0
K
L
M
7
N
O
P
R
S
T
g
e
c
u
a
V
W
X
Y
y
Z
1
2
g
4
o
y
d
b
s
x
w
v
Q
p
m
q
n
p
r
q
h
i
k
l
f
U
A
B
C
D
E
F
G
H
2
1
4
K
L
M
N
O
P
R
S
V
W
X
Y
Z
5
j
t
3
6
8
9
0
e
c
7
a
u
o
1
2
4
s
x
w
v
z
d
b
m
n
Q
r
j
h
i
k
j
l
J
e
u
c
a
f
U
A
e
u
c
o
B
a
C
D
E
F
G
H
I
s
o
x
K
w
v
L
z
M
N
O
P
R
s
S
m
T
n
x
w
v
z
V
W
X
r
Y
m
Z
n
r
g
g
y
y
p
q
p
q
5
tP
3
6
8
9
0
7
1
2
4
d
5
b
Q
t
3
3
h
6
i
k
JV
8
l
t
9
0
7
8
f
9
U
0
A
B
C
D
E
F
G
1
2
H
I1
4
2
4
K
L
M
N
d
b
R
S
T
Q
W
X
d
b
Y
Z
Q
3
h
i
J
k
l
3
h
i
J
f
k
l
U
A
B
C
f
D
U
E
F
G
H
I
2
1
A
4
B
C
D
K
E
L
F
M
G
N
H
O
I
P
R
S
2
1
T
4
K
L
M
V
N
W
O
X
P
R
Y
S
Z
T
V
W
X
Y
Z
j
j
e
c
u
a
e
c
a
u
o
o
s
s
x
w
v
z
x
w
v
z
m
n
m
n
r
r
g
y
p
q
5
5
t
3
t
6
3
8
6
9
0
8
9
7
0
7
1
2
4
1
2
4
d
b
d
b
Q
Q
3
h
i
J
k
3
h
l
i
J
k
l
f
U
g
f
U
A
B
C
D
y
E
A
F
B
G
C
H
D
I
E
2
1
F
4
G
H
I
2
K
1
L
4
M
N
O
K
P
L
R
M
S
N
T
O
P
R
S
T
V
W
X
p
Y
Z
V
q
W
X
Y
Z
g
y
y
j
p
q
p
q
e
c
u
a
o
s
x
w
v
z
m
n
r
g
y
g
j
y
p
q
e
c
u
a
p
q
g
o
s
y
5
x
w
v
z
m
n
t
r
3
p
6
q
8
9
0
7
j
jh
1
2
e
c
4
u
a
d
b
e
u
cg
a
o
s
Q
x
w
v
o
z
s
m
n
x
h
w
v
i
z
3
k
l
r
J
m
n
f
rkC
U
A
B
C
D
E
F
G
H
I
2
1
4
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
5
t
3
6
8
9
0
7
j
1
2
4
j
d
e
b
u
c
a
Q
5
e
u
c
o
a
s
5
x
w
h
v
z
i
o
3
k
l
J
m
t
n
s
j
3
x
6
w
v
f
z
r
8
tG
9
U
m
3
0
7
n
A
B
6
C
D
E
8
e
F
c
u
a
r
G
9
H
0
I
2
1
7
4
K
L
M
1
2
N
4
O
P
o
R
S
T
s
V
d
1
2
b
W
X
4
x
w
v
Y
z
Z
g
m
Q
d
n
b
y
r
5
Q
h
i
3
k
l
J
i
3
f
l
J
p
q
U
A
B
C
f
D
E
F
U
G
H
I
2
1
A
4
B
D
K
E
L
F
M
N
H
O
I
P
R
2
S
1
T
4
K
L
M
N
V
O
W
P
X
R
Y
S
Z
T
V
W
X
Y
Z
g
y
g
y
p
q
5
p
q
5
t
3
6
8
9
0
t
7
3
6
8
9
0
7
1
2
4
d
b
1
2
4
t
Q
3
d
b
6
8
9
0
Q
7
h
i
3
k
l
J
h
f
i
3
1
2
k
4
l
J
U
A
B
C
D
E
d
b
F
f
G
H
I
U
2
1
4
A
K
B
Q
L
C
M
D
N
E
O
F
P
G
R
H
S
I
T
2
1
4
K
V
L
W
M
X
N
h
Y
O
i
Z
P
3
R
k
S
l
T
J
V
W
X
Y
Z
f
U
A
B
C
j
D
E
F
G
H
I
2
1
4
K
L
M
N
O
P
R
e
S
u
c
T
a
V
W
X
Y
Z
o
s
x
w
v
z
m
n
r
j
j
e
u
c
a
e
c
u
a
o
s
x
o
w
v
z
s
m
n
x
w
v
z
r
m
n
r
5
t
3
6
8
9
0
7
1
2
4
d
b
Q
h
i
3
5
k
l
J
g
f
5
y
U
A
t
B
C
D
3
E
F
G
6
H
I
2
1
8
4
9
K
0
t
L
M
3
N
7
O
P
6
R
S
p
T
8
q
9
0
V
W
7
X
Y
Z
1
2
4
1
2
d
b
4
Q
d
b
Q
3
h
i
J
k
l
h
i
3
f
k
l
J
U
A
B
C
f
D
E
F
G
U
H
I
2
1
A
4
B
C
D
K
E
L
F
M
G
N
H
O
I
P
R
S
T
K
L
M
V
N
W
O
X
P
R
Y
S
Z
T
V
W
X
Y
Z
g
y
p
q
j
e
u
c
a
o
s
x
w
v
z
g
m
n
y
r
p
q
j
e
c
u
a
o
s
x
w
v
z
m
n
r
5
t
6
8
9
0
7
1
2
4
d
b
Q
h
i
3
k
l
J
f
U
A
j
B
C
D
E
F
G
H
I
2
1
4
K
L
M
N
O
e
u
P
c
R
a
S
T
V
W
X
Y
Z
o
s
x
5
w
v
z
m
n
r
t
3
g
6
8
9
0
y
7
1
2
4
p
q
d
b
Q
h
i
3
k
l
JIV
g
fB
U
A
D
E
F
G
H
I2
K
L
M
N
P
R
S
T
p
q
W
X
Y
Z
5
tP
3
6
8
9
0
7
1
4
d
b
Q
h
iq
3
kd
lC
JyO
p
fB
q
U
A
C
D
E
F
G
H
IV
2
1
4
K
L
M
N
O
R
S
T
jF
V
W
X
Y
Z
p
e
ch
a
u
sM
p
w
q
vxW
zrQ
m
n
jF
e
u
c5
a
sM
xp
w
vn
zg
m
n
rQ
jF
5
e
u
tP
cg
a
3
6
8
9
0
7
sM
w
vxW
zrQ
jF
m
n
1
2
4
e
cg
u
d
a
b
jF
5
sM
xW
w
vU
zrQ
iO
e
u
cg
3
a
ko
m
lK
tP
JV
n
3
6
8
fB
9
0
U
sM
A
7
C
D
xW
w
E
vU
zrQ
G
H
I1
2
4
m
n
L
N
1
4
R
S
T
d
X
b
Y
Z
3
h
iyq
Jyq
ko
lC
fB
U
A
C
D
E
G
H
IjzV
2
1
4
K
L
N
O
R
S
T
V
W
X
Y
Z
5
tP
3
6
8
9
0
7
5
1
2
4
tP
d
b
3
6
5
8
9
0
7
3
h
iyO
JV
ko
lR
tP
3
1
2
4
6
fB
8
U
9
0
7
d
b
A
C
D
E
G
H
I1
2
42
K
1
2
L
4
N
S
T
h
iJyO
3
d
ko
b
lC
JIO
X
Y
Z
g
fB
U
g
A
C
D
E
G
h
H
iJyO
3
2
ko
1
lT
4
JIV
K
L
N
R
fB
S
T
U
V
p
A
X
Y
C
Z
D
E
G
H
I1
2
42
K
L
N
R
S
T
X
Y
Z
g
yO
g
yq
p
q
p
q
jF
jF
e
u
c5
a
e
u
c5
a
o
o
sM
xW
sM
w
vn
zrQ
xW
w
vn
zg
m
n
m
rQ
5
j
tP
3
t
6
3
8
j
6
9
0
e
8
c
u
7
a
9
0
7
o
e
c
u
a
1
2
4
s
1
2
4
x
w
v
o
z
b
m
d
s
b
n
x
w
v
z
g
r
m
y
n
h
r
i
3
k
l
J
h
i
3
k
l
J
f
p
U
f
q
A
B
U
D
E
A
B
G
H
D
I
E
2
1
G
4
H
I
K
L
2
1
4
N
K
R
L
S
T
N
O
P
R
S
T
X
Y
Z
X
Y
Z
5
5
t
3
y
6
8
9
t
0
3
7
6
8
9
0
p
7
1
4
d
b
1
2
4
Q
d
b
Q
3
h
i
J
k
l
3
h
f
i
U
k
l
A
B
C
D
E
f
F
G
H
I
2
1
4
A
j
B
K
C
L
D
M
E
N
F
G
P
R
H
S
g
T
2
1
4
K
V
L
y
W
M
X
N
Y
O
e
u
Z
c
P
a
R
S
T
V
W
X
o
Y
Z
s
p
x
w
q
v
z
m
n
r
g
y
e
u
c
a
g
o
p
q
s
y
x
w
5
v
m
r
t
p
q
6
8
9
0
7
d
b
Q
j
3
h
i
e
k
c
u
l
a
f
o
A
B
s
C
D
E
F
x
w
G
v
z
H
2
1
4
m
K
L
n
M
N
O
P
R
S
r
V
W
X
Y
Z
t
3
6
8
9
0
7
1
2
4
d
b
j
Q
e
c
u
a
g
h
i
3
k
l
J
j
o
y
f
s
y
x
w
U
v
z
A
B
C
e
m
c
u
D
a
E
F
G
H
5
I
2
1
4
r
p
q
K
L
M
o
N
O
P
R
S
p
T
s
q
x
V
w
t
v
W
z
X
3
Y
Z
6
m
n
8
9
0
r
7
1
2
4
d
b
Q
3
h
i
J
k
l
f
U
A
B
C
D
E
F
G
H
I
2
1
4
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
t
3
6
8
9
5
0
7
t
1
2
4
6
8
9
d
b
0
7
Q
h
i
j
3
k
l
J
d
b
j
f
Q
U
e
u
c
a
A
B
C
D
E
F
G
H
e
u
c
I
a
h
i
2
1
3
4
o
k
l
K
J
L
M
N
s
O
P
o
R
S
x
T
w
v
z
f
V
U
s
W
m
X
Y
n
A
Z
B
x
w
v
C
z
D
E
F
G
r
H
m
I
2
1
n
4
K
L
M
N
r
O
P
R
S
T
g
V
W
X
y
Y
Z
p
q
g
y
g
y
p
q
p
q
g
y
5
p
q
5
tP
3
6
tb
8
3
9
6
7
8
9
0
7
1
4
1
4
Q
d
b
Q
iIO
3
kZ
l2
JV
3
h
iO
fB
kd
lC
U
A
C
fB
D
E
U
F
G
H
I1
2
A
4 gp
C
D
K
E
L
F
M
G
N
H
R
2
1
S
4
T
K
L
M
N
W
X
P
R
Y
S
Z
jF
V
W
X
Y
e
u
ch
a
o
s0
xW
w
vd
zh
m
n
jF
rQ
jF
e
u
ch
a
e
u
ch
a
s4
xW
w
vU
zV
sM
w
vxW
zrQ
rQ
m
n
jF
e
u
c5
a
sM
xW
w
vn
z6
m
n
rQ
5
tP
3
6
8
9
0
7
1
2
4
p
5
b
5
tP
3
6
8
tP
3
9
iJO
3
0
JIV
k2
7
lT
6
8
9
0
fB
U
7
1
A
4
D
E
G
p
H
1
d
4
5
1
2
K
4
L
M
N
R
S
T
d
b
X
Y
Z
tb
3
iJO
3
6
ko
lT
JIV
8
9
0
3
iO
fB
7
JV
ko
lR
U
A
D
E
fB
G
U
H
I1
2
1
42
4
A
K
L
C
M
D
N
E
G
R
H
S
d
I1
T
b
2
42
K
L
X
N
Y
Z
S
T
X
Y
Z
3
h
iq
ko
lC
fB
U
A
C
D
E
G
H
2
1
K
L
N
O
P
R
S
T
V
X
Y
Z
jF
e
u
a
s4
xW
w
vn
zrQ
m
n
jF
e
u
cg
a
o
s0
xW
w
v2
zg
m
rQ
5
tP
3
8
9
7
1
4
d
tb
3
6
3
h
iyIO
8
9
ko
lC
0
7
fB
A
C
1
2
D
4
E
G
H
2
1
4
d
K
b
L
M
N
R
S
X
Y
Z
yO
h
iJycO
3
k2
lm
JIq
fB
U
p
A
q
D
E
G
H
2
1
K
L
M
N
P
R
S
T
V
X
Y
Z
jF
e
cg
a
u
o
sM
w
vxW
zrQ
m
n
y
q
5
t
3
6
8
9
0
7
1
2
4
d
b
h
i
3
k
l
J
f
U
A
B
C
D
E
G
H
I1
2
4
K
L
N
P
R
S
T
V
X
Y
Z
j
e
c
u
a
o
s
x
w
v
z
m
n
r
5
t
3
6
8
9
0
7
1
2
4
d
b
Q
h
i
3
k
l
J
f
U
A
B
C
D
E
F
G
H
I
2
1
4
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
g
y
p
q
jF
e
u
ch
a
sM
w
vxW
p
zrQ
q
m
n
5
tP
3
6
8
9
0
7
1
2
4
d
b
jF
3
iO
JV
e
ko
cg
u
lR
a
fB
U
A
sM
C
D
E
w
G
vxW
zrQ
H
I1
2
4
K
m
L
n
N
S
T
X
Y
Z
5
tP
3
6
8
9
0
7
1
2
4
d
b
h
iyO
3
ko
lK
JV
fB
U
A
C
D
E
G
H
I1
2
4
L
N
R
S
T
X
Y
Z
p
q
p
q
jF
e
cg
a
u
o
s0
xW
w
vd
zg
m
rQ
jF
e
cg
u
a
sM
w
vxW
zrQ
m
n
tP
3
6
8
9
0
7
1
2
4
d
b
h
iJycO
3
k2
5
lK
JIq
fB
U
A
tP
C
D
E
3
G
H
6
2
1
4
8
9
L
0
M
7
N
R
S
T
V
X
Y
1
2
4
d
b
h
iyO
3
ko
lK
JV
fB
U
A
C
D
E
G
H
I1
2
4m
L
N
R
S
T
X
Y
Z
p
jF
e
a
u
s4
yO
xW
w
vZ
zrQ
m
n
p
q
g
y
p
q
5
tP
3
8
9
7
1
4
3
h
iyIq
ko
JV
lK
jF
fB
U
A
C
D
E
G
H
g
I1
e
u
2
cg
a
4
L
M
N
O
R
o
S
T
sM
X
Y
Z
j
w
vxW
zrQ
m
n
p
q
e
c
a
u
o
s
x
w
v
z
m
n
r
5
t
3
6
8
9
0
7
5
1
2
4
t
3
d
b
6
8
9
0
7
jF
3
h
i
J
k
1
2
l
4
e
c5
a
u
f
U
d
b
A
B
Q
C
D
E
G
H
I
2
sM
1
4
K
xW
L
w
vn
z6
N
P
3
h
R
i
S
T
k
m
J
l
n
V
X
Y
Z
rQ
f
U
A
B
C
D
E
F
G
H
I1
2
4 2
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
g
y
p
q
5
tb
3
6
8
9
0
7
1
4
d
b
h
iyO
3
ko
lK
fB
U
A
C
D
E
G
H
2
1
L
N
P
R
S
T
V
X
Y
Z
j
e
c
u
a
o
s
x
w
v
z
n
r
5
tP
3
6
8
9
0
7
1
2
4
d
b
Q
h
iO
3
kC
lK
JV
fB
U
A
D
E
F
G
H
I1
2
4
L
M
N
R
S
T
W
X
Y
Z
p
q
p
jF
e
jF
cg
u
a
e
cg
a
u
sM
w
vxW
zrQ
m
n
sM
p
w
vxW
zrQ
m
n
yc5
p
q
5
5
tP
3
6
8
9
0
7
tP
3
6
8
9
0
1
2
7
4
d
b
1
2
4
d
b
jF
h
iyq
3
ko
lK
JyV
fB
u
h
a
iyO
U
3
ko
lK
A
JV
C
D
E
G
H
o
I5
2
fB
1
4
s4
L
U
N
A
O
xW
w
C
vn
R
zg
D
S
E
T
G
H
m
I1
2
n
4
X
Y
Z
L
rQ
N
jzg
R
S
T
X
Y
Z
u
e
cjzg
a
o
s0
xe
w
vk2
m
n
r7
1
2
4
d
b
Q
h
iIq
3
Jyq
lC
f
U
A
B
C
D
E
F
G
H
I
2
1
4
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
g
5
y
t
3
6
p
8
9
7
1
2
4
5
g
d
b
y
t
3
6
8
9
h
i
3
0
k
J
l
7
p
q
f
U
A
B
D
E
G
H
I
2
1
4
K
L
M
N
O
P
R
S
T
V
X
Y
Z
g
y
p
q
g
j
y
u
e
c
a
o
p
q
s
x
w
v
z
m
r
j
u
e
c
a
o
s
x
w
v
z
m
n
r
j
e
c
a
u
o
s
x
w
v
z
m
n
r
t
3
6
8
9
0
1
4
d
j
b
5
Q
e
u
c
a
t
3
h
i
3
6
k
J
l
8
9
o
0
7
f
s
U
x
w
v
z
A
B
C
m
D
E
n
F
G
H
I
1
2
2
1
4
4
r
K
L
M
N
O
P
R
S
d
b
T
V
W
X
Q
Y
Z
3
h
i
J
k
l
f
U
A
B
C
D
E
F
G
H
2
1
5
K
L
M
N
O
P
R
S
T
V
W
X
t
Y
Z
3
6
8
9
0
7
1
2
4
g
y
d
b
Q
h
3
i
p
k
q
l
J
f
U
5
A
B
C
D
E
F
G
H
I
2
1
4
K
L
M
t
N
O
P
R
S
T
3
6
V
W
g
X
8
Y
9
Z
0
7
y
1
2
4
y
d
b
p
q
Q
p
q
h
i
3
k
J
l
f
U
A
B
C
D
E
F
G
H
I
2
1
4
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
j
e
c
u
a
o
s
x
w
v
z
m
n
r
u
e
c
a
j
o
s
u
e
c
a
x
w
v
m
o
n
r
s
x
w
v
z
m
n
r
g
p
t
3
6
8
9
0
7
1
2
4
d
b
Q
5
3
h
i
J
k
l
t
f
5
U
3
6
A
B
8
C
9
D
E
0
F
G
H
I
7
2
1
4
t
K
L
M
N
O
6
P
R
S
T
8
9
0
V
1
2
W
4
X
Y
7
Z
d
b
Q
1
2
4
d
b
3
h
i
J
k
l
Q
f
U
3
h
i
A
J
B
C
k
D
l
E
F
G
H
I
f
K
U
L
M
N
O
P
R
S
A
T
B
C
D
E
F
V
G
W
H
X
I
Y
Z
2
1
4
K
L
M
N
O
P
R
S
T
V
W
X
j
Y
Z
e
c
u
a
o
s
x
w
v
z
m
n
r
5
t
3
6
8
9
0
7
g
y
1
2
4
d
b
Q
p
q
3
h
i
J
k
l
f
U
A
B
C
D
E
F
G
H
I
2
1
4
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
g
y
p
q
j
e
u
c
a
o
s
x
w
v
z
m
n
r
g
y
p
q
j
5
u
e
c
g
a
t
3
y
6
8
9
o
0
7
s
x
w
v
z
m
n
p
q
1
2
4
r
d
b
Q
3
h
i
J
k
l
f
U
A
B
C
D
E
F
G
H
I
2
1
4
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
g
y
j
p
q
e
c
a
u
o
s
x
w
v
z
g
m
n
y
r
5
p
q
t
3
6
8
9
0
7
1
2
4
d
b
Q
j
h
i
3
k
J
l
f
e
c
u
a
U
A
B
C
D
E
o
F
G
H
I
2
1
4
s
K
L
M
x
w
N
v
z
O
P
R
S
T
m
n
V
W
X
Y
Z
r
5
t
3
6
8
9
0
7
j
1
2
4
d
e
b
c
a
u
Q
o
s
x
w
v
3
z
h
i
k
J
l
m
n
f
r
U
j
A
B
C
D
E
F
G
H
I1
2
4
g
K
L
e
M
c
u
y
N
a
O
P
R
S
T
V
W
X
Y
o
Z
s
5
x
w
v
z
p
q
m
n
r
t
3
6
8
9
0
7
1
2
4
d
b
Q
g
y
3
h
i
J
k
l
f
U
p
q
A
B
C
D
E
F
G
H
I
2
1
4
K
L
M
N
5
O
P
R
S
T
V
W
X
Y
Z
t
3
6
8
9
0
7
1
2
4
d
b
5
Q
t
3
3
h
i
6
k
J
l
8
9
0
7
f
U
A
B
C
D
E
1
2
F
G
4
H
I
2
1
4
K
L
M
d
b
N
O
P
R
S
T
Q
V
W
X
Y
Z
j
h
i
3
k
l
J
e
u
c
a
f
U
o
A
B
C
D
E
F
s
G
H
I
2
1
x
4
w
v
z
K
L
M
m
N
O
n
P
R
S
T
r
V
W
X
Y
Z
j
e
u
c
a
o
s
x
w
v
z
m
n
r
5
t
3
6
8
9
0
7
g
y
1
2
4
d
b
Q
p
q
3
h
g
i
J
k
l
y
5
f
U
A
B
C
D
E
F
G
H
I
2
1
t
4
K
3
p
L
M
q
N
6
O
P
R
S
8
T
9
0
7
V
W
X
Y
Z
1
2
4
d
b
Q
h
i
3
k
J
l
f
U
A
B
C
D
E
F
G
H
I
2
1
4
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
j
u
e
c
a
o
s
x
w
v
z
j
m
n
r
e
c
a
u
o
s
x
w
v
z
m
n
r
g
y
p
q
5
t
3
6
8
9
0
7
5
1
2
4
d
b
t
3
6
Q
8
9
0
7
h
i
3
k
J
l
1
2
4
f
U
d
b
A
B
C
D
E
F
G
H
I
Q
2
1
4
K
L
M
N
O
P
R
S
T
h
i
3
V
k
W
l
X
Y
J
Z
f
U
A
B
C
D
E
F
G
H
I
2
1
4
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
j
e
u
c
a
o
s
x
w
v
z
m
n
g
r
y
p
tP
3
6
8
9
0
7
1
2
4
d
b
Q
p
h
iJO
3
JIV
lT
fB
U
A
D
E
F
G
H
jF
I1
2
42
K
L
M
N
R
S
T
e
u
a
W
X
Y
Z
s4
xW
w
vn
z6
m
n
rQ
p
jF
5
e
u
cg
a
tb
3
6
8
9
s4
xW
w
vd
7
zg
rQ
g
1
4
d
b
p
q
3
h
iIq
ko
lC
fB
U
A
C
D
E
G
H
2
1
4
K
L
M
N
O
P
R
S
V
X
Y
Z
yq
jF
e
u
cg
a
p
q
o
s0
xW
w
v2
z6
m
5
n
rQ
tP
3
8
9
0
7
1
4
d
h
iJycO
3
ko
JIq
lT
fB
U
A
D
E
G
H
2
1
4
K
L
M
N
jF
R
S
T
V
X
Y
Z
e
u
c5
a
sM
xW
w
vkU
zV
m
n
5
rQ
tb
3
6
8
9
0
7
1
2
4
jF
d
b
e
u
cg
a
o
h
iJycO
3
k2
JIq
lm
sM
xp
w
vn
zrQ
fB
m
U
n
A
C
D
E
G
H
2
1
K
L
M
N
P
R
S
T
V
g
X
Y
Z
yO
p
5
q
yIcO
tP
3
6
8
9
0
p
7
g
yq
1
2
4
d
b
p
q
3
h
iJIyO
ko
lC
fB
U
A
5
C
D
E
G
H
2
1
4
K
L
N
R
S
t
3
V
6
X
Y
8
Z
9
0
7
1
4
d
b
h
i
3
k
J
l
f
U
A
B
C
D
E
g
G
H
I
2
1
4
K
y
L
N
O
P
R
S
T
V
W
X
Y
Z
j
p
q
u
e
c
a
o
s
j
x
w
v
z
m
n
r
e
u
a
o
s
j
x
w
v
z
m
n
r
e
u
c
a
o
s
x
w
v
z
m
n
r
5
t
3
6
8
9
j
0
7
5
e
u
c
a
1
2
4
t
d
o
b
8
9
s
0
Q
x
w
v
7
z
5
m
n
h
i
r
3
k
J
l
t
3
f
6
U
8
A
9
B
Q
C
0
D
E
F
G
7
H
I
2
1
4
K
L
M
N
3
P
h
R
i
S
J
T
k
l
1
2
4
V
W
X
Y
Z
f
U
d
b
A
B
C
D
E
Q
F
G
H
I
2
1
4
K
L
M
N
g
3
P
R
h
S
i
T
k
l
V
W
y
X
Y
Z
f
U
A
B
C
D
E
F
G
H
2
1
p
q
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
5
t
6
8
9
0
7
d
b
Q
h
i
3
k
l
g
f
y
A
B
C
D
E
F
G
H
I
2
1
4
K
L
M
N
O
P
R
S
T
p
q
W
X
Y
Z
j
e
c
a
u
o
s
x
w
v
z
m
n
r
3
g
y
1
2
4
p
q
g
y
j
e
u
a
o
s
x
5
w
v
g
z
m
y
n
r
t
3
6
8
9
0
7
p
q
1
2
4
d
b
Q
h
i
3
k
l
J
f
U
A
B
C
D
E
F
G
H
I1
2
4
K
L
M
N
O
P
R
S
T
V
W
X
Z
j
e
u
c
a
o
s
j
x
w
v
z
J
m
k
l
5
n
r
f
e
u
U
c
a
A
B
C
t
D
o
E
F
3
G
H
6
2
1
4
8
s
K
9
L
M
0
N
x
w
v
O
z
P
R
7
S
T
m
V
W
X
Y
Z
r
1
2
4
d
b
Q
3
h
i
J
k
l
f
U
j
A
B
C
D
E
F
G
H
I
2
1
4
K
L
M
N
O
u
e
P
c
R
a
S
T
V
W
X
o
Y
Z
s
x
w
v
z
m
n
r
5
t
3
6
8
9
0
7
5
1
2
4
t
3
d
b
6
8
9
0
Q
7
h
i
3
1
2
4b
d
Q
3
h
iq
kd
lC
fB
U
A
C
D
E
F
G
H
IV
2
1
4
K
L
M
N
O
P
S
T
V
W
tP
X
Y
Z
3
6
8
9
0
7
1
2
4
d
b
Q
3
h
iO
JV
lR
fB
U
A
D
E
G
H
I1
2
4
K
L
M
N
S
T
W
X
Y
Z
p
q
p
q
jF
u
e
cg
a
sM
w
vxW
zrQ
m
jF
p
e
q
cg
a
u
sM
w
vxW
zrQ
m
n
5
g
tP
3
6
8
9
0
7
p
1
2
4
d
b
h
iJyO
3
ko
JIV
lT
fB
U
A
D
E
G
H
I1
2
4
K
L
N
R
S
T
X
Y
Z
5
tP
3
6
8
9
0
7
jF
1
4
d
b
e
cg
a
u
sM
h
iyO
w
vxW
3
zrQ
ko
lK
JV
m
n
fB
U
A
C
D
E
G
H
I1
2
4Y
L
N
R
S
T
X
Y
Z
jF
g
e
u
c5
a
sR
xp
w
vn
zg
m
p
n
q
rQ
g
5
tP
3
6
8
9
0
7
1
2
4
p
d
b
3
h
iyO
ko
JV
lK
5
fB
U
A
tP
C
D
E
G
3
H
I1
2
6
42
8
L
9
N
0
7
R
S
T
X
Y
Z
1
2
4
b
jF
h
iJyq
ko
lC
u
e
c5
a
fB
U
A
D
E
G
H
sM
K
w
L
vkxW
zrQ
M
N
O
R
m
S
T
n
W
X
Y
Z
jF
u
e
cO
a
o
sY
xW
w
vZ
zg
m
n
rQ
5
tP
3
6
8
9
0
7
g
1
2
4
d
b
p
h
iyO
3
ko
JF
lC
fB
U
A
C
D
E
G
H
I1
2
4
K
L
N
R
S
T
V
X
Y
Z
5
tP
3
6
8
9
7
jF
1
4
u
e
b
ch
a
o
s0
3
h
xp
w
vd
iyIcO
Jq
zg
k2
lK
m
g
n
fB
U
rV
A
C
D
E
G
H
2
1
4
L
M
N
R
S
T
V
X
Y
Z
jF
u
e
cO
a
s4
xW
w
vn
zrQ
m
n
tP
3
6
8
9
0
7
1
2
4
d
b
Q
iJq
3
k2
JyIq
lK
fB
U
A
C
D
E
jF
G
H
2
1
4
L
M
N
R
S
T
e
u
c5
a
V
5
W
X
o
s0
tP
xW
w
vn
zh
3
6
m
8
9
0
7
rQ
1
2
4
d
b
h
iyIO
3
ko
lC
fB
U
A
C
D
E
G
g
H
2
1
4
yO
K
L
M
N
R
S
V
X
Y
Z
p
q
tP
3
6
8
9
0
7
1
2
4
d
b
3
h
iJyq
JyIO
k2
lC
fB
U
A
D
E
G
H
Iq
2
g
1
4
K
L
M
N
O
yIq
R
S
T
V
X
Y
Z
p
yIq
jK
p
p
u
e
c5
a
o
s
x
w
v
z
m
n
rO
5
tR
3
6
8
9
0
7
j
j
1
2
4
e
u
c
a
u
e
a
d
b
o
Q
o
s
s
x
w
v
z
x
w
v
z
h
iW
m
m
k
lN
n
r
r
fM
U
A
B
C
D
E
F
G
H
K
L
M
N
P
R
S
T
W
X
Y
Z
g
y
p
q
5
j
t
t
3
6
3
e
u
c
a
8
6
9
0
8
9
0
7
7
o
s
x
w
v
z
1
2
4
1
m
4
n
d
b
r
d
b
Q
Q
3
h
i
J
h
i
k
3
l
k
J
l
f
U
f
U
A
B
A
B
D
C
E
D
F
E
G
F
H
G
H
2
I
1
2
1
K
4
L
K
M
L
N
M
N
P
R
O
S
P
R
T
S
T
V
W
V
X
W
Y
X
Z
Y
Z
j
u
e
c
a
g
o
s
y
x
w
v
z
5
m
n
r
p
q
t
3
6
8
9
7
1
4
d
b
Q
3
i
J
k
l
f
U
A
B
C
D
E
F
G
H
2
1
4
K
L
M
N
P
R
S
T
V
W
X
Y
Z
g
y
p
q
5
t
3
6
8
9
0
7
1
2
4
d
b
Q
3
h
i
J
k
l
j
f
U
A
e
B
c
a
C
u
D
E
F
G
H
I
2
1
4
K
L
M
o
N
O
P
R
S
s
T
x
w
v
z
V
W
X
Y
Z
m
n
r
g
y
p
j
e
u
c
a
o
s
x
w
v
z
m
n
r
5
t
3
6
8
9
0
7
1
2
4
d
b
Q
h
i
3
k
l
J
f
U
A
B
C
D
E
F
G
H
I1
2
4
K
L
M
N
O
P
R
S
T
V
W
X
Y
5
j
t
3
6
8
9
0
7
u
e
c
a
o
1
2
4
s
x
w
v
z
d
b
m
n
Q
r
3
h
J
i
k
l
f
U
A
B
C
D
E
F
G
H
I
2
1
4
L
P
S
T
V
X
Y
Z2
5
tP
3
6
8
9
0
7
1
4
d
b
Q
h
iq
3
kd
lK
fB
U
A
C
D
E
F
G
H
2
1
4
L
M
N
O
R
S
T
V
W
X
Y
Z
p
q
jF
e
cg
a
u
sM
w
vxW
zrQ
m
n
p
q
p
5
tP
3
6
8
9
0
7
p
q
1
4
d
b
h
iyO
3
ko
lK
JV
fB
U
A
C
D
E
G
H
I1
2
4 Z
jF
L
N
R
S
T
X
Y
u
Z
e
cg
a
sM
w
vxW
zrQ
m
n
jF
u
e
cg
a
sM
xW
w
vo
zrQ
m
n
jF
u
e
cg
a
sM
w
vxW
zrQ
m
n
5
tP
3
6
8
9
0
7
1
2
4
d
b
h
iyO
3
JV
ko
lK
fB
5
U
A
C
D
E
G
H
I1
2
4
tP
L
3
N
6
R
S
T
8
9
0
X
7
Y
Z
1
2
4
b
5
3
h
iJyq
JyIjzrV
ko
lK
tP
3
6
fB
8
9
0
7
A
C
D
E
G
H
I1
2
4
L
1
2
N
4
O
S
T
d
b
X
Y
Z
h
iyO
3
p
ko
JV
q
lR
fB
U
A
C
D
E
G
H
I1
2
4
K
L
N
S
T
X
Y
Z
jF
e
cg
a
u
sM
w
vxW
zrQ
m
n
5
tP
3
6
8
9
0
7
1
2
4
d
b
h
iyO
3
ko
lK
JV
fB
U
A
C
D
E
G
H
I1
2
42
L
N
R
S
T
X
Y
Z
p
p
jF
e
cg
a
u
sR
xW
w
vU
zrV
m
yO
p
q
g
u
e
cg
a
p
q
sR
tP
xp
3
w
vU
6
m
8
n
9
0
7
1
2
4
d
b
Q
3
h
iJycO
JIq
ko
lK
fB
U
A
C
D
E
G
H
2
Ijzr1
4
L
M
N
R
S
T
V
X
Y
jF
u
e
cg
a
o
sM
w
vxW
zrQ
m
n
5
t
3
6
8
9
0
7
1
2
4
jF
d
b
Q
e
c5
a
u
3
h
i5
J
k
l6
sM
xW
w
vn
z6
f3
U
m
A
B
C
D
E
F
G
H
rQ
I
2
1
4
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
5
t
3
6
8
9
0
7
1
2
4
d
b
3
h
J
i
k
l
f
U
A
B
C
D
E
G
H
I
2
1
4
K
L
N
P
R
S
T
tb
V
3
X
Y
6
Z
8
9
0
7
1
2
4
d
b
h
iJyq
3
ko
lK
fB
A
C
D
E
G
H
2
1
L
N
O
P
S
T
g
X
Y
Z
y
p
q
g
y
p
q
j
u
e
c
a
o
s
x
w
v
z
m
n
r
j
5
e
c
a
u
t
3
o
6
8
s
9
0
7
x
w
v
z
m
n
r
1
2
4
d
b
Q
h
i
3
k
J
l
f
U
A
B
C
D
E
F
G
g
H
I
p
2
1
4
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
q
g
p
q
5
tP
3
6
8
9
0
7
1
2
4
d
b
Q
3
h
iO
kC
JV
lK
fB
U
A
D
E
F
G
H
I1
2
42
L
M
N
R
S
T
W
X
Y
Z
e
a
u
jF
s4
xW
w
vZ
m
u
e
n
ch
a
sM
jF
w
vxW
zrQ
m
n
e
c5
a
u
sM
xW
w
vn
zrQ
m
n
5
tP
3
8
9
0
7
1
2
4
tP
d
8
9
0
7
Q
5
1
2
4
h
iyO
3
ko
lK
tP
JV
3
d
b
6
fB
8
9
0
U
7
A
C
D
E
F
G
H
2
I1
4
iyq
3
ko
JyjzrV
L
lK
M
1
N
4
R
S
T
fB
p
d
b
q
U
X
Y
Z
A
C
D
E
G
H
I1
2
4
L
N
O
R
3
h
S
iyO
T
ko
lK
X
Y
Z
fB
U
A
C
D
E
G
H
Ig
2
1
4
yO
L
N
R
S
T
V
X
Y
Z
p
q
jF
u
e
cg
a
sM
w
vxW
zrQ
m
n
jF
e
cg
a
u
o
sM
w
vxW
zrQ
m
n
5
tP
3
6
8
9
0
7
1
2
4
d
b
5
h
iyO
3
JV
ko
lK
fp
U
t
3
A
B
6
C
D
E
8
G
9
H
I
0
2
7
1
4
L
N
R
S
T
1
2
4
X
Y
Z
d
b
h
i
3
k
l
J
f
U
A
B
C
D
E
G
H
I
2
1
4
K
L
N
P
R
S
T
V
X
Y
Z
g
p
g
u
e
c
y
a
o
s
x
w
v
p
m
q
n
g
y
5
p
t
q
3
6
8
9
0
7
1
2
4
d
b
Q
j
3
h
J
i
k
l
u
e
c
a
f
p
U
q
o
A
B
C
D
E
g
F
G
H
s
I
2
1
4
x
w
v
z
K
L
M
y
N
m
O
P
R
n
S
T
r
V
W
X
Y
Z
p
q
j
e
c
a
u
5
o
s
x
w
v
z
t
m
3
n
6
8
r
9
0
7
1
2
4
jF
d
b
e
cg
Q
a
u
o
3
h
i
J
k
sM
l
w
vxW
zrQ
f
j
U
m
n
A
B
C
D
E
F
G
H
I
e
c
2
a
1
u
4
K
L
M
N
O
P
R
S
T
o
V
W
X
s
Y
Z
x
w
v
z
m
n
r
5
t
3
6
8
9
0
7
1
2
4
d
b
Q
5
h
i
3
k
l
J
f
g
tP
U
A
y
B
C
D
E
8
F
G
9
H
0
I
2
1
4
7
K
L
M
N
O
P
R
S
T
5
V
q
W
X
Y
Z6
d
b
tP
3
6
8
9
0
7
3
h
iyO
JV
k
lK
1
2
4
f
U
d
b
A
B
C
D
E
G
H
2
I1
Q
4
L
N
R
S
T
h
iO
3
kC
lK
X
JV
Y
Z
fB
U
A
D
E
F
G
H
I
2
1
4
L
M
N
R
S
T
W
X
Y
Z
jF
u
e
ch
a
o
sM
w
vxW
zrQ
g
m
n
y
p
q
5
tP
3
6
8
9
0
7
1
2
4
d
b
3
J
i
k
l
f
U
A
B
C
D
E
j
G
H
I
2
1
4
K
L
N
O
R
S
T
u
e
c
a
V
X
Y
Z
o
s
x
w
v
z
m
n
r
5
t
3
6
8
9
0
7
1
2
4
d
b
Q
h
i
3
k
J
l
f
U
A
B
C
D
E
F
G
H
I
2
1
4
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
g
y
p
q
j
e
c
a
u
o
s
x
w
v
z
m
n
r
g
y
p
q
g
y
p
q
5
t
3
6
8
9
0
7
1
2
4
d
b
Q
h
i
3
k
l
J
f
U
A
B
C
D
g
E
F
G
H
I
2
1
4
y
K
L
g
M
N
O
P
R
S
T
y
V
W
X
Y
Z
p
q
p
q
j
u
e
c
a
o
s
j
x
w
v
z
m
n
r
u
e
c
a
o
s
x
w
v
z
m
n
r
y
p
q
5
j
t
3
6
j
8
9
e
c
a
0
u
7
5
e
c
a
u
o
s
1
2
4
x
w
v
z
t
o
3
d
s
b
m
6
n
8
x
w
v
z
9
0
Q
r
7
m
n
r
h
i
3
k
J
l
1
2
4
f
U
d
b
A
B
C
Q
D
E
F
G
H
I
2
1
4
K
L
M
N
O
3
P
R
h
S
i
J
T
k
l
V
W
X
Y
Z
f
U
A
B
C
D
E
F
G
H
I
2
1
4
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
g
y
p
q
jG
u
e
cg
a
5
o
s
5
x
w
v
t
z
3
m
n
6
8
t
9
rM
0
7
3
6
8
9
0
7
1
2
4
d
b
1
2
4
Q
d
b
Q
h
i
3
k
l
J
h
i
f
3
k
l
J
U
A
B
C
D
E
f
F
G
H
I
2
1
4
U
A
B
K
C
L
D
M
E
N
F
O
G
P
H
R
I
S
2
1
T
4
K
L
V
M
W
N
X
O
Y
P
Z
R
S
T
V
W
X
Y
Z
5
t
3
6
j
8
9
0
7
e
c
a
u
1
2
4
o
d
b
s
x
w
v
z
Q
m
n
r
h
i
3
J
k
l
f
U
A
B
C
D
E
F
H
I1
2
4 2
K
L
N
O
P
R
S
T
V
W
X
Y
Z
g
p
q
5
tP
3
6
8
9
0
7
1
2
4
d
b
Q
3
h
iO
JV
kC
lK
fB
U
A
D
E
F
G
H
2
I1
4
L
M
N
R
S
T
W
X
Y
Z
jF
u
e
c5
a
sM
xW
w
vn
zg
m
n
rQ
5
tP
3
6
8
9
0
7
1
4
d
b
h
iyq
3
ko
Jyq
lC
fB
U
A
C
D
E
G
H
Iyjz1
2
4
K
L
N
O
R
S
T
V
X
Y
Z
yO
p
q
g
p
jF
e
cg
a
u
o
sM
w
vxW
zrQ
m
n
j
u
e
c
a
o
s
x
w
v
z
m
5
r
t
3
6
8
9
0
7
1
2
4
d
b
3
h
i
k
J
l
g
g
f
U
y
y
A
B
C
D
E
G
H
I
2
1
4
K
L
N
P
R
S
T
p
p
q
q
V
X
Y
Z
t
3
6
8
9
0
7
1
2
4
d
b
Q
3
h
J
i
k
l
f
U
A
B
D
E
F
G
H
I
2
1
4
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
p
j
j
u
e
u
c
e
a
c
a
o
o
s
s
x
w
x
v
w
z
v
z
m
m
n
n
r
r
5
5
t
3
t
3
6
6
8
9
8
u
0
e
c
9
a
0
7
7
g
o
y
s
1
2
1
2
4
4
x
w
v
m
n
d
b
d
b
r
p
q
Q
Q
3
h
h
J
i
i
3
k
k
J
l
l
f
f
U
U
A
A
B
B
C
C
D
D
E
E
F
F
G
G
H
H
I
I
2
1
2
1
4
4
K
K
L
L
M
M
N
N
O
O
P
P
R
R
S
S
T
T
V
V
W
W
X
X
Y
Y
Z
Z
5
t
3
6
8
9
0
7
1
2
4
d
b
Q
3
h
J
i
j
k
l
f
g
U
e
c
a
u
A
B
y
C
D
E
F
G
H
I
2
1
o
4
K
L
M
s
N
O
P
R
x
S
w
v
T
z
p
V
q
W
X
m
Y
Z
n
r
g
y
g
p
q
y
g
y
p
q
p
5
q
t
3
6
8
9
0
7
1
2
4
g
d
b
y
Q
j
g
h
i
y
3
k
l
p
J
q
e
u
c
a
f
U
o
A
B
C
D
p
E
q
F
s
G
H
I
2
1
x
4
w
v
z
K
L
M
m
N
O
n
P
R
S
T
g
r
V
W
X
Y
Z
g
y
j
p
q
u
e
c
a
jF
o
s0
xW
w
vd
zh
e
m
u
a
n
rQ
s4
xW
w
vd
zg
m
n
5
rV
p
tb
3
6
8
9
7
jF
1
4
e
d
ch
b
a
u
jF
Q
sM
e
ch
a
u
w
vxW
zrQ
h
iIO
3
kd
lK
m
n
fB
sM
U
w
vxW
zrQ
A
C
D
E
F
m
G
H
n
2
1
jjF
L
M
N
P
p
R
S
T
e
c5
W
u
a
X
Y
Z
5
o
s0
xW
w
vn
zg
tP
m
3
6
5
8
rQ
9
0
7
jF
tP
3
1
u
e
4
a
8
9
0
d
b
7
o
sY
xW
w
vd
zg
1
m
4
n
h
icO
3
k2
J5
rQ
lR
Q
fB
U
A
C
D
E
F
G
H
3
JIq
iJcO
1
4
ko
lK
K
L
M
N
S
5
T
fB
U
V
X
A
Z
e
cO
C
u
a
D
E
G
H
IO
tP
2
1
4
3
5
6
L
M
N
8
R
9
S
sY
0
T
7
xW
w
vn
zrV
V
tP
X
Y
p
Z
3
q
m
6
8
1
2
9
4
0
7
d
b
1
4
d
b
iO
3
ko
lK
ttP
JV
3
6
fB
8
9
U
0
7
A
iO
3
C
ko
D
lK
E
jF
JV
G
H
I1
2
4 2
fB
L
N
1
2
4
U
R
S
A
T
C
e
u
D
a
E
G
d
b
H
X
I1
2
Y
5
Z
4 2
L
o
N
R
S
T
sY
xW
w
v2
zg
tP
X
Y
Z
3
m
h
iiJyq
6
3
n
k2
llK
8
JyIq
9
rQ
7
ffB
U
A
C
D
E
G
1
H
4
2
4
L
M
N
O
b
R
S
g
T
X
p
q
iIcO
3
k2
Jq
l2
fB
p
q
U
A
C
D
3
E
G
6
H
2
8
1
4
9
K
7
L
M
N
jF
R
S
T
V
X
Z
1
4
e
u
ch
a
d
b
o
Q
s0
jF
xW
w
v2
z6
m
n
h
3
ko
e
cg
a
u
rV
U
A
B
C
sM
D
E
F
G
w
vxW
H
zrQ
2
4
K
L
m
M
N
n
O
P
R
S
T
tb
X
Y
3
Z
6
8
9
0
7
yIq
1
4
b
p
h
iyIcO
3
k2
Jq
lm
fB
U
A
C
D
E
G
H
2
1
4
K
L
M
N
P
R
S
T
jF
V
X
Z
5
u
e
cg
a
jF
tb
e
sM
c5
u
3
a
6
w
vxW
zrQ
8
9
m
0
7
n
o
s0
5
xp
w
vn
zg
1
2
4
m
tP
3
d
b
rQ
6
8
9
0
Q
7
iJO
3
1
4
k2
JIch
lK
yq
g
yO
fB
d
b
U
A
C
D
E
G
H
p
2
1
L
M
N
h
iyO
P
p
R
3
S
ko
q
T
lK
JV
V
X
Y
fB
Z
U
A
C
D
E
G
H
2
I1
4 3
L
N
R
S
T
X
Y
Z
jF
p
e
u
a
o
5
sY
xW
w
vn
zg
m
tP
n
3
6
rQ
8
9
0
7
tb
3
6
8
1
2
9
4
0
7
d
b
1
2
4
d
b
h
iyO
3
JV
ko
lK
fB
U
h
A
iJyq
3
C
k2
D
lK
E
G
H
I1
2
4 2
fB
L
N
U
R
S
A
T
C
D
E
G
H
X
2
Y
1
g
Z
4
L
M
N
P
R
yO
S
T
V
W
X
Z
jF
g
p
j
q
y
e
u
a
e
u
c
a
o
5
s4
o
xp
w
vn
p
zg
m
s
n
x
w
v
z
t
3
rQ
m
6
n
8
9
0
r
7
jF
g
1
4
e
yO
u
a
d
b
sY
xp
w
p
vZ
z1
q
3
h
i
J
m
k
l
rV
f
U
A
B
C
D
E
G
H
I
2
1
4
K
L
M
N
O
P
R
S
T
V
X
Y
Z
5
5
t
6
t
8
3
9
0
7
6
8
9
0
j
7
e
c
a
u
1
2
4
o
d
j
b
5
s
x
w
v
z
Q
h
i
m
3
n
J
k
e
u
c
l
a
tP
3
3
r
h
i
J
f
6
k
l
U
8
o
9
A
B
7
f
s
C
D
U
E
x
G
w
v
H
z
I
2
1
4
A
B
C
K
D
L
E
M
F
N
G
H
P
1
I
R
4
S
2
1
r
T
4
K
L
M
V
N
W
X
P
d
Y
R
Z
S
T
V
Q
W
X
Y
Z
j
3
h
iJIIyq
Jjzr1
ko
e
lK
u
c
a
fB
o
A
C
s
D
E
G
x
w
H
v
2
z
I1
4
m
L
M
n
N
O
R
S
T
r
V
W
X
Y
Z
5
t
3
6
8
9
0
5
7
1
2
4
t
3
6
d
8
b
9
0
7
g
Q
y
1
4
h
i
3
k
l
J
d
f
Q
U
A
B
5
C
D
E
F
G
H
I
2
1
4
h
i
K
3
L
M
k
J
N
l
P
R
S
t
T
3
f
V
6
W
X
U
Y
8
Z
9
0
A
B
C
D
7
E
F
G
H
I
2
1
4
K
L
M
N
O
P
R
S
1
2
T
4
y
V
W
X
Y
Z
d
b
Q
p
q
3
h
i
k
l
f
U
A
B
C
D
E
F
G
H
2
1
4
K
L
M
N
P
R
S
T
g
W
X
Y
Z
p
q
g
y
p
q
j
e
u
c
a
o
s
g
x
w
v
z
m
y
r
p
q
j
e
u
c
a
o
s
x
w
v
z
m
n
r
jF
e
c5
u
a
sM
xW
w
vn
zrQ
m
n
5
t
j
3
6
8
9
0
7
e
c
a
u
g
y
o
1
2
4
s
x
w
v
z
d
b
m
n
Q
p
q
r
h
i
3
5
J
k
l
f
U
j
A
t
B
C
3
D
E
F
6
G
H
I
2
1
8
4
9
0
K
L
7
e
u
c
M
a
N
O
P
R
S
T
V
W
o
X
Y
Z
1
2
4
s
x
w
v
z
d
b
m
n
Q
r
5
h
i
3
k
J
l
f
U
tP
A
B
6
C
D
E
8
F
G
9
H
I
0
7
2
1
4
K
L
M
N
O
P
R
S
T
1
2
V
W
4
X
Y
Z
d
b
5
h
iyO
3
ko
lK
t
3
6
f
8
9
U
0
A
B
7
C
D
E
G
H
2
Ic5
1
4
L
N
1
2
4
R
S
T
V
d
X
b
Y
Z
Q
j
5
3
h
i
k
J
l
g
f
e
c
a
u
U
y
t
3
A
B
C
6
D
E
F
o
8
G
H
9
I
2
1
0
4
7
s
K
g
L
M
N
x
w
O
v
z
P
R
S
y
T
p
m
q
V
n
W
X
1
2
Y
4
Z
r
y
d
b
p
q
Q
p
q
h
i
3
J
k
l
f
U
A
B
C
D
E
F
G
H
I
2
1
4
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
5
t
3
6
8
9
g
0
7
y
1
2
4
d
b
p
q
Q
j
h
3
i
k
l
J
e
u
c
a
f
j
U
o
A
B
C
D
e
E
cg
u
F
a
G
H
j
s
I
2
1
4
x
e
w
u
v
c
z
K
a
L
M
N
O
m
P
R
n
S
T
sM
o
e
u
c
V
a
r
W
xW
w
X
vU
Y
Z
s
x
w
v
m
z
o
n
m
n
s
x
w
v
z
r
m
n
r
5
j
t
3
6
5
8
9
0
7
e
u
c
a
tP
5
3
t
6
3
8
6
o
9
0
7
8
1
2
4
9
s
0
t
7
x
w
v
3
z
d
6
b
m
8
n
1
2
9
4
0
7
Q
r
1
2
4
g
d
b
g
3
d
h
b
i
J
y
1
2
Q
4
k
y
l
Q
d
f
b
U
h
iyO
3
ko
A
lK
B
Q
JV
C
3
D
h
p
E
J
i
F
q
G
p
k
H
l
q
I
fB
2
1
4
K
L
U
M
f
h
N
U
i
O
3
A
P
R
J
k
C
S
l
D
T
E
F
G
A
H
B
2
I1
V
C
W
4
D
X
f
E
Y
F
Z
G
H
L
U
I
2
1
N
4
R
A
K
S
B
L
T
C
M
D
N
E
O
F
P
G
R
H
S
I
T
X
2
1
Y
4
Z
K
V
L
W
M
X
N
Y
O
Z
P
R
S
T
V
W
X
Y
Z
g
y
p
q
5
t
3
6
8
9
0
7
1
2
4
d
b
Q
h
i
3
k
J
l
f
g
U
A
y
B
C
D
E
F
G
H
I
2
1
4
K
L
M
N
O
j
P
R
S
T
g
j
V
W
y
X
p
Y
Z
q
e
c
a
u
e
c
a
u
o
o
p
s
q
x
w
v
z
s
x
w
v
z
m
n
m
n
r
r
j
e
u
c
a
o
s
x
w
v
z
m
n
r
5
5
t
3
t
3
6
6
8
9
8
0
9
7
0
7
j
g
1
2
4
1
2
4
e
u
y
c
d
a
b
d
b
j
o
Q
Q
s
x
w
p
v
z
q
e
h
u
c
i
a
3
m
k
h
l
3
n
i
J
k
J
l
o
r
f
f
U
s
A
U
B
C
x
w
v
D
z
E
A
F
B
G
C
H
D
I
2
E
1
m
F
4
G
n
H
I
K
2
1
L
4
M
N
O
K
r
P
L
R
M
S
N
5
T
O
P
R
S
T
V
W
X
Y
Z
V
W
X
Y
Z
t
3
6
8
9
0
7
1
2
4
d
b
Q
3
h
J
i
k
l
g
f
U
y
A
B
C
D
E
F
G
H
I
2
1
4
K
L
M
N
O
P
R
S
T
p
q
V
W
X
5
Y
Z
t
3
6
5
8
9
0
7
t
3
6
g
1
2
4
8
9
0
y
7
d
b
Q
1
2
4
p
3
q
h
i
J
d
b
k
l
Q
f
U
A
B
C
D
E
F
h
G
J
i1
H
I
kd
2
1
l3
4
K
L
M
N
O
P
fB
R
U
S
T
V
W
A
X
Y
C
Z
D
E
F
G
H
I9
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
y
j
p
q
e
c
u
a
o
s
x
w
v
z
m
n
r
j
yO
e
c
u
a
o
s
x
p
w
v
z
q
g
m
j
n
y
r
e
c
a
u
p
q
o
s
x
w
v
z
m
n
r
g
y
5
g
t
3
y
p
6
q
8
9
0
7
j5
p
1
2
q
4
e
u
j
cg
a
d
b
o
Q
s
x
w
v
z
m
n
h
i
3
k
l
J
r6
5
f
U
A
B
C
D
E
F
t
G
H
3
2
I
1
4
6
K
8
L
M
9
N
O
0
P
7
R
S
T
V
W
X
Y
Z
1
2
5
4
d
b
t
3
jF
Q
6
8
9
0
7
h
i
3
e
u
cg
a
k
l
J
f
1
2
4
o
U
j
sM
A
B
C
d
D
b
E
w
vxW
F
zrQ
G
H
2
I
1
4
m
Q
n
K
L
M
N
e
u
O
c
a
P
R
S
T
V
W
3
h
X
i
Y
Z
o
k
J
l
s
x
w
v
z
f
U
m
n
A
B
C
D
E
F
r
G
H
I
2
1
4
K
5
L
M
N
O
P
R
S
T
V
W
X
Y
t8
Z
g
j
3
6
y
8
9
0
7
t
e
u
c
a
j
o
1
2
4
p
q
s
e
c
a
u
x
w
v
b
z
m
n
Q
o
r
s
x
w
v
z
h
i4
3
J
k2
l7
m
n
f
r
U
i
A
l
B
C
D
E
F
G
H
I
f
2
1
4
K
L
M
N
O
P
R
S
T
5
I
V
W
X
Y
Z
M
N
O
P
R
S
T
t
3
V
W
X
6
g
Y
Z
8
9
0
7
yO
5
g
y
1
2
4
t
3
p
q
6
d
b
8
9
0
7
p
q
h
1
2
i
3
4
J
k
l
d
b
f
U
Q
A
B
C
D
E
G
H
I
2
5
1
4
K
h
L
i
3
N
k
J
P
l
R
S
T
V
f
X
t
Y
Z
3
U
6
A
5
B
8
C
D
9
E
F
0
G
H
I
7
2
1
4
K
L
M
N
t
O
P
R
S
3
T
6
V
1
2
W
8
X
4
Y
9
Z
0
7
d
b
Q
1
2
4
e
u
c
a
d
b
3
h
i
J
k
l
o
Q
f
U
s
x
w
v
z
A
B
h
C
i
D
3
m
E
k
F
l
n
G
H
J
I
2
1
4
r
K
L
f
M
N
O
P
R
S
U
T
A
B
C
D
V
E
W
F
X
G
Y
H
Z
I
2
1
4
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
jF
jj
e
c
u
a
e
u
c
a
o
s
w
vxW
zrQ
o
m
s
n
x
w
v
z
m
n
r
g
y
5
p
q
3
6
8
9
0
7
1
2
4
d
b
Q
3
h
J
k
U
A
B
C
D
E
F
G
H
2
1
4
K
L
5
tP
3
6
8
9
tt
0
7
0
1
2
4
d
b
d
b
Q
h
i
3
k
l
JV
h
f
ii
3
J
k
ll
U
A
B
C
ff
D
E
G
U
H
2
I1
4
A
B
K
C
L
D
M
E
N
F
G
H
R
II
S
T
2
1
4
K
L
j
M
N
X
O
Y
P
Z
R
S
T
V
W
X
Y
Z
e
u
c
a
o
s
x
w
v
z
m
n
r
g
y
p
q
5
g
t
3
y
6
8
9
0
7
p
q
1
2
4
d
b
Q
h
i
3
k
J
l
f
U
A
B
C
D
E
F
G
H
I
2
1
4
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
j
e
u
c
a
o
s
x
w
v
z
g
m
n
y
r
p
q
j
e
c
a
u
o
s
x
w
v
z
m
n
r
5
t
6
8
9
0
7
d
b
Q
h
i
3
k
J
l
f
U
5
A
B
C
j
D
E
F
G
H
I
2
1
4
K
L
M
N
t
O
P
3
R
e
u
S
c
T
a
6
8
V
9
W
X
0
Y
7
Z
o
g
s
y
x
w
v
z
1
2
4
m
n
d
b
r
p
q
Q
h
i
3
k
l
J
f
U
A
B
C
D
E
F
G
H
I
2
1
4
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
g
g
y
y
g
y
p
q
p
q
p
q
5
t
3
6
8
9
0
7
1
2
4
d
b
Q
3
h
i
J
k
l
j
f
U
A
B
C
D
E
F
e
G
u
c
H
a
I
2
1
4
K
L
M
N
O
o
P
R
S
T
s
V
W
X
Y
x
w
Z
v
z
m
n
r
j
j
e
c
a
u
e
c
u
a
jV
o
s
o
x
w
s
v
z
x
w
v
z
m
n
m
n
r
r
5
tP
3
6
8
9
0
7
g
yO
1
2
4
d
b
Q
p
q
3
h
JV
iO
kC
lK
fB
U
A
D
E
F
G
H
I1
2
4
5
L
M
N
5
R
S
T
W
X
Y
t
Z
3
6
t
8
3
9
0
6
8
7
9
0
7
tZ
1
2
4
1
2
4
d
b
d
b
Q
Q
3
h
i
k
J
l
h
i
3
k
l
J
f
U
f
A
B
C
U
D
E
i
F
A
G
B
H
C
l
I
2
D
1
E
4
F
G
H
K
2
I
1
L
4
M
N
f
O
P
K
R
L
S
M
T
N
O
P
R
S
V
T
W
X
Y
Z
V
W
I
X
Y
Z
e
jj
u
c
a
o
e
u
c
a
s
x
w
v
z
m
o
n
s
r
x
w
v
z
m
n
r
5
g
5
3
6
y
8
9
0
7
tt
3
6
8
9
p
0
q
7
1
2
4
d
b
Q
1
2
4
d
b
3
h
J
Q
k
U
h
ii
3
k
A
J
ll
B
C
D
E
F
G
H
ff
2
1
4
U
K
L
M
N
O
A
P
B
R
C
S
D
T
E
F
G
H
II
W
2
1
X
4
Y
K
L
M
N
P
R
S
T
V
W
X
Y
Z
g
y
p
q
g
j
y
e
c
a
u
p
q
o
s
x
w
v
z
m
n
r
g
y
p
q
j
e
c
a
u
o
s
x
w
v
z
m
n
5
r
t
3
6
8
9
0
7
1
2
4
j
d
b
Q
e
c
a
u
o
h
i
3
k
l
J
s
x
w
v
z
f
U
m
n
A
B
C
D
E
F
G
r
H
g
I
2
1
4
K
L
M
y
N
O
P
R
S
T
V
W
X
Y
Z
p
q
jF
5
e
ch
u
a
tP
3
6
8
9
0
7
sM
w
vxW
zrQ
m
1
2
n
4
d
b
Q
3
h
iO
JV
kC
lK
fB
U
A
D
E
F
G
H
2
I1
4
L
M
N
R
S
T
tP
3
6
W
X
Y
8
Z
9
0
7
1
2
4
d
b
Q
3
h
iJO
JI1
lK
fB
U
A
C
D
E
F
G
H
I1
2
4 2
5
L
jF
M
N
R
S
T
V
W
X
tP
Y
Z
3
e
c5
a
u
6
8
9
0
7
sM
w
vkxW
zrQ
1
4
m
n
d
b
iO
3
ko
lK
JV
fB
U
A
C
D
E
G
H
2
I1
42
L
N
R
S
T
X
Y
Z
p
5
q
tP
3
6
8
9
0
7
1
2
4
d
b
3
h
iO
ko
lK
fB
U
A
C
D
E
G
H
2
4
L
N
R
S
T
V
X
Y
Z
jF
e
u
cg
a
sM
w
vxW
zrQ
m
n
5
g
tP
3
6
8
9
0
7
p
1
2
4
d
b
h
iyO
3
ko
JV
lK
fB
U
A
C
D
E
G
H
I1
2
4
L
N
R
S
T
X
Y
Z
yO
p
g
yO
p
q
jjF
g
u
e
c5
a
yq
sY
xW
w
vn
zV
m
p
q
rQ
u
e
cjF
a
o
j
sY
xW
w
vZ
zg
m
e
c
u
a
rQ
o
s
x
w
v
z
m
n
ttP
r
3
6
8
9
0
7
1
2
4
d
b
h
3
iiJyIq
J
ko
llC
u
e
c5
a
ffB
U
A
C
o
D
E
G
H
s0
II
2
1
4
xW
w
vn
zg
K
L
M
N
O
R
m
S
T
n
V
rQ
X
Y
Z
3
6
8
9
7
5
1
2
4
t
3
6
d
b
8
9
0
7
1
3
4
h
J
k
d
b
U
Q
A
B
D
E
F
G
H
2
1
4
h
i
K
3
L
M
k
N
l
J
P
R
S
T
f
V
X
Y
U
Z
A
B
C
D
E
F
G
H
2
I
1
4
5
K
L
M
N
P
R
S
T
V
W
X
t
Y
Z
3
6
8
9
0
7
1
2
4
d
b
h
3
i
k
l
f
U
A
B
C
D
E
G
H
I
2
1
4
K
L
M
N
O
P
R
S
T
X
j
g
y
p
q
t
j
i
l
u
e
c
a
f
o
s
I
x
w
v
z
m
n
r
g
y
p
q
5
t
3
6
8
9
0
7
1
2
4
d
b
Q
h
3
i
J
k
l
f
U
A
B
C
D
E
F
G
H
2
1
4
K
L
M
N
O
P
R
S
T
V
W
X
Z
yO
jF
e
ch
a
u
p
q
sM
w
p
vxW
zrQ
q
m
n
5
tP
3
6
8
9
0
7
1
2
4
jF
d
b
u
e
ch
a
jF
3
iO
JV
ko
sM
e
lK
u
cg
a
xp
w
vn
zrQ
fB
m
U
n
A
C
sM
D
E
G
w
H
vxW
2
zrQ
I1
4
m
L
n
N
R
S
T
X
Y
Z
p
q
tP
5
6
8
9
0
7
tP
yO
3
6
8
9
0
7
d
b
p
1
2
4
d
b
3
p
JyO
iq
q
ko
lC
fB
U
3
h
JV
iyO
A
ko
C
lK
D
E
G
H
IV
2
1
4
fB
U
K
L
N
R
A
S
T
C
D
E
G
V
H
W
I1
X
2
Y
4
Z
L
N
R
S
T
X
Y
Z
jF
u
e
cg
a
sM
w
vxW
zrQ
m
n
jF
u
a
jF
sM
xp
w
e
vn
cg
zg
u
a
m
n
rV
sM
w
vxW
zrQ
m
n
g
yc5
p
q
5
tP
3
tP
3
6
6
8
9
8
0
9
7
0
7
1
2
4
1
2
4
d
b
d
b
Q
5
3
h
iq
3
h
JV
iJyO
lK
ko
lR
fB
U
tP
fB
U
3
A
6
5
C
D
A
E
8
F
C
9
G
D
H
E
7
2
1
G
4
H
I1
2
45
L
M
N
K
O
L
R
N
S
tP
T
3
S
T
6
1
2
4
W
X
8
Y
Z
9
X
0
Y
7
Z
d
b
Q
1
2
4
d
b
h
iJq
3
g
JyIq
ko
lK
fB
U
A
C
h
D
iyO
E
3
G
ko
H
lK
IjzrV
2
JV
1
4
L
fB
N
R
S
T
U
A
V
C
W
D
X
E
Y
Z
G
H
2
I1
42
L
N
R
S
T
X
Y
Z
jzg
e
u
c5
a
o
s0
xe
w
vk2
m
n
g
r7
y
g
p
q
j3
e
u
c
a
o
s
x
w
v
z
m
r
j
e
c
u
a
j
o
s
x
w
v
z
u
e
m
c
a
n
r
o
s
x
w
v
z
m
r
t
3
6
8
9
0
1
4
d
b
Q
h
i1
3
J
k
l4
f2
U
A
B
C
D
E
F
G
H
I
2
1
4
K
L
M
N
O
P
R
S
T
5
W
X
Y
Z
t
3
6
8
9
0
5
7
1
t
4
3
6
8
d
b
9
0
7
Q
1
2
4
h
i
3
k
l
J
d
b
f
Q
U
A
B
C
D
E
F
G
H
2
I
1
4
h
i
3
K
k
J
L
l
M
N
O
P
R
S
T
f
V
U
W
X
Y
Z
A
B
D
E
F
G
H
I
2
1
g
4
K
L
M
y
N
P
R
S
T
W
X
Y
Z
p
q
p
q
y
j
p
u
e
c
a
jF
o
s
x
e
w
v
cg
z
a
u
m
n
r
o
sM
w
vxW
zQ
m
g
n
rN
y
p
q
p
5
t
3
6
8
9
0
7
tP
3
1
2
4
6
8
9
e
u
c
7
0
a
d
b
Q
o
1
2
4
s
x
w
v
3
d
b
h
i
m
k
n
l
f
U
A
B
C
D
h
E
iyO
F
G
3
H
I
2
lR
1
4
JV
K
L
M
fB
N
O
P
R
S
T
U
A
V
W
C
X
D
Y
E
Z
G
j
H
2
I1
4
K
L
S
T
e
u
c
a
X
Y
Z
o
s
x
w
v
z
g
m
n
e
r
cjF
a
u
o
sY
xW
w
vd
zg
m
rV
5
p
q
tP
6
8
9
0
7
d
b
Q
3
h
JyO
iq
kd
lC
fB
5
A
C
D
E
F
G
H
I1
2
tP
4
K
3
L
M
N
6
O
R
yO
S
8
T
9
0
7
W
X
Y
Z
1
2
4
p
q
tP
d
b
3
6
8
Q
9
7
h
iO
3
kC
JV
1
lK
4
fB
d
b
U
jF
A
D
Q
E
F
G
H
I1
2
4
L
M
e
c5
N
a
u
R
h
S
iJyIO
T
3
k2
lK
JIq
W
X
Y
Z
fB
sM
U
xW
w
vn
z6
A
C
D
E
G
H
2
m
1
4
jF
L
M
N
rQ
R
S
T
V
X
Y
Z
e
cg
a
u
sM
w
vxW
zrQ
m
n
jF
u
e
cg
a
sM
tb
w
vxp
zrQ
3
6
m
n
8
9
0
7
1
2
4
5
d
b
tP
3
6
8
9
h
iJyq
0
3
7
ko
lK
fB
U
1
2
4
A
C
D
E
G
H
2
1
d
b
L
N
O
P
R
S
T
X
Y
Z
h
iyO
3
ko
lK
JV
fB
U
A
C
D
E
G
H
2
I1
42
L
N
R
S
T
X
Y
Z
5
tP
3
6
8
9
0
7
1
2
4
d
b
3
h
iq
JyjzrV
g
ko
lu
yO
fB
U
A
C
D
E
G
H
I1
2
4m
K
p
L
N
yIO
R
S
T
W
X
Y
Z
g
p
p
q
p
yO
p
q
g
yO
p
q
e
c5
a
u
jF
o
s0
xp
w
vn
zg
e
cjF
u
a
m
rQ
jF
s4
xp
w
vn
zrQ
e
c5
m
a
u
n
sM
w
vkxW
zQ
m
n
rN
jF
e
u
cg
a
g
o
jF
sM
yO
xp
w
vU
zV
m
n
e
u
cg
a
rQ
p
o
q
s
x
w
v
z
m
n
tP
j
3
6
r
5
8
9
0
7
e
c
u
a
tP
1
3
o
4
8
s
9
5
d
7
0
b
x
w
v
z
m
n
1
4
r
tP
3
6
h
8
iJq
3
9
k2
0
lK
7
fB
U
A
1
2
C
4
D
E
G
h
H
iq
2
1
3
4
ko
lK
d
JyO
b
L
M
N
fB
R
S
T
V
W
A
X
C
Z
D
E
G
H
2
1
IV
4
3
h
iyO
L
ko
JV
M
lR
N
R
S
T
fB
V
W
U
X
5
Y
Z
A
C
D
E
G
H
2
I1
4
K
tcw
L
3
S
6
T
8
9
0
X
5
Y
7
Z
t
1
2
4
3
6
8
9
b
0
7
1
2
5
4
3
h
J
ia
k
j
le
d
b
fm
U
t
3
Q
e
A
6
c
u
a
B
D
8
E
9
G
0
H
I
2
1
4
7
3
h
J
i
K
L
o
k
N
l
P
R
s
S
T
x
f
w
v
z
U
V
1
2
W
X
4
Y
Z
m
A
n
B
C
D
d
E
b
G
H
r
I
2
1
4
Q
K
L
M
N
P
R
S
T
V
W
X
Y
3
h
Z
i
J
k
l
f
U
A
B
C
D
E
F
G
H
2
I
1
4
K
L
M
N
P
R
S
T
V
W
X
Y
Z
5
t
3
6
8
9
0
7
g
g
1
2
y
4
d
b
Q
p
q
h
i
3
k
l
J
f
U
A
B
C
D
E
F
G
H
2
I
1
4
K
L
M
N
P
R
S
T
V
W
X
Y
Z
g
yq
p
q
j
e
u
c
a
e
c
a
o
o
s
x
w
v
z
s
x
w
v
n
m
r
n
jF
e
c5
a
u
o
5
sM
xW
5
w
vn
zrQ
m
n
t
3
t
6
3
8
6
9
0
7
8
9
0
7
1
2
4
1
2
4
d
b
d
b
Q
Q
h
i
3
k
J
l
3
h
i
J
k
l
f
U
f
A
U
B
C
D
E
F
G
H
A
I
B
2
1
C
4
D
E
F
K
G
L
H
M
I
2
N
1
O
4
P
R
S
K
T
L
M
N
O
P
V
R
W
S
X
T
Y
Z
V
W
X
Y
Z
jF
e
cg
u
a
o
sM
xW
w
vU
zrQ
5
m
t
3
6
8
9
0
7
g
1
2
y
4
d
b
q
h
i
3
k
l
f
U
A
B
C
D
E
G
H
2
1
I
4
K
L
N
O
P
R
S
T
V
X
Y
Z
5
t
6
8
9
0
7
d
b
h
i
3
g
k
l
J
y
f
g
U
A
B
y
C
D
E
G
H
2
1
I
4
K
p
L
q
N
P
R
S
T
p
q
X
Y
Z
g
jgp
y
u
p
q
o
s
x
v
z
n
rq
j
5
j
u
e
tco
c
a
3
6
e
c
a
8
u
9
o
7
0
s
x
w
v
o
z
s
m
1
2
x
4
w
n
v
z
j
r
d
m
b
n
r
Q
e
c
a
u
h
ia
3
o
J
k
le
s
x
fm
w
v
z
U
m
A
n
B
C
D
E
F
G
H
r
I
2
1
4
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
5
5
t
3
6
8
9
0
t
7
3
6
8
9
0
7
1
2
4
5
1
2
4
d
b
d
b
Q
t
3
Q
6
3
8
h
J
9
i
0
7
k
l
h
f
i
3
U
k
l
J
1
2
4
A
f
B
C
D
E
F
G
H
U
I
2
d
1
b
4
A
B
C
D
K
E
L
F
M
G
N
H
O
2
1
I
P
4
R
Q
S
T
K
L
M
V
N
W
O
X
P
R
Y
S
Z
T
h
i
V
3
W
k
X
l
Y
J
Z
f
g
U
A
B
C
D
y
E
F
G
H
2
I
1
4
K
L
M
N
O
P
R
S
T
V
p
W
X
q
Y
Z
g
y
g
g
y
y
p
q
p
q
p
q
j
e
u
c
a
g
o
s
y
x
w
v
z
j
m
n
r
j
e
c
j
p
u
a
q
o
e
c
u
a
e
c
a
u
s
x
w
v
z
o
o
m
n
s
s
x
w
v
z
x
w
v
r
z
m
n
m
n
r
r
5
t
3
6
8
9
0
7
g
1
4b
5
d
tP
3
6
p
q
8
Q
9
0
7
tP
3
tP
3
6
6
8
h
9
iq
3
8
0
9
kd
JjzrV
lu
0
jF
7
1
2
7
4
fB
U
d
b
A
1
2
e
u
ch
C
4
a
1
2
D
E
4
Q
F
G
H
I1
2
432
d
b
K
d
b
L
M
o
N
O
P
R
S
sM
T
3
Q
h
iO
Q
JV
w
vxW
zrQ
lK
W
X
Y
Z
m
n
fB
h
U
iq
3
h
JjzrV
iO
ke
lK
JV
A
lK
C
D
E
F
fB
G
H
2
fB
I1
4 gp
U
U
L
A
M
N
C
A
D
E
R
C
F
S
D
G
T
E
H
F
Ic5
G
H
2
I1
41
W
X
L
Y
M
Z
N
L
O
M
N
R
S
T
R
S
T
W
X
Y
W
Z
X
Y
Z
yO
jF
tP
3
e
ch
u
a
6
8
9
0
7
sM
w
vxW
zrQ
1
4
m
n
d
b
iO
3
JV
lK
fB
U
A
C
D
E
G
H
I1
2
4
L
N
R
S
T
X
Y
Z
5
tP
3
6
8
jF
9
0
7
u
4
d
b
sM
w
vxp
zrQ
n
iyO
3
ko
lK
JV
fB
p
q
U
A
C
D
E
G
H
2
I1
42
L
N
R
S
T
X
Y
Z
5
tP
3
6
8
9
7
0
1
2
4
d
b
h
iq
3
JjzrV
ke
lu
fB
jF
U
A
C
D
E
G
H
I1
2
42
u
e
cg
a
K
L
N
R
S
T
o
W
X
Y
Z
sM
w
vxW
zrQ
m
n
p
p
q
tP
3
6
8
9
0
7
1
4
g
d
b
q
3
h
p
JV
iyO
q
lR
fB
U
A
C
D
E
G
H
I1
2
42
K
L
N
S
T
g
X
Y
Z
p
e
cg
a
sM
xW
w
vn
m
n
jF
q
e
cg
a
u
sM
w
vxW
zQ
m
n
rN
g
jF
jF
e
u
a
p
e
c5
q
a
u
sY
xW
w
vkZ
o
zrQ
sM
m
w
vkxW
zrQ
5
m
n
tP
3
6
8
9
0
7
c5
u
a
1
4
o
b
s0
xp
w
vn
Q
m
n
h
iyq
ko
5
lC
fB
U
A
C
tP
D
3
E
F
G
6
H
I1
2
4
8
9
jF
K
7
0
L
N
O
R
S
T
X
e
ch
Y
a
u
1
Z
4
d
b
sM
w
vxW
zrQ
m
n
5
h
iyO
3
ko
lR
JV
fB
tP
3
U
6
A
C
8
D
E
9
tP
3
G
7
H
2
I1
4
6
8
K
9
L
0
7
S
T
1
4
X
Y
Z
jF
d
b
1
2
4
d
b
e
u
c5
a
h
5
iJyIIO
3
ko
lK
JV
sM
3
fB
h
iyO
w
JV
vkxW
zrQ
lK
U
tP
3
A
m
C
fB
D
6
E
G
8
U
H
2
I1
9
4 2
0
7
A
C
L
D
M
E
N
G
R
H
2
S
I1
T
42
L
1
2
X
N
4
Y
Z
R
S
T
d
b
X
Y
Z
Q
h
iyq
3
k2
lK
5
fB
U
A
C
D
tP
E
F
G
H
3
2
1
4
6
8
L
M
9
N
0
7
R
S
T
V
W
X
Z
1
4
d
b
iyq
3
ko
lK
JyV
fB
U
A
5
C
D
E
G
H
2
I1
42
L
N
O
R
tP
S
T
3
6
X
Y
8
Z
9
0
7
1
2
4
d
b
3
h
iJyO
JIV
ko
lK
g
fB
U
A
C
D
E
G
H
I1
2
4
L
N
R
S
T
p
X
Y
Z
g
p
q
cg
a
sM
xW
w
vn
m
n
g
g
p
p
e
cO
u
a
sY
xp
w
vn
zrV
jjF
m
e
c5
u
a
o
s0
xW
w
vn
zg
m
5
rQ
jF
tP
3
6
8
9
7
0
e
cg
u
a
1
2
4
sM
w
vxW
zrQ
d
b
m
n
Q
h
iyq
3
ko
lC
fB
U
A
C
D
E
F
G
H
2
1
4
K
L
N
jF
O
R
S
T
jF
X
Y
Z
u
e
c5
a
e
u
c5
a
3
6
sM
8
9
w
vkxW
zrQ
7
sM
m
n
xW
w
vn
zrV
m
1
4
d
ttP
b
3
6
8
9
Q
0
7
h
3
ko
1
2
4
d
b
U
A
B
C
D
5
E
F
G
H
2
1
4
K
L
M
N
P
R
S
3
T
h
iiJyq
tP
JyIO
3
k2
llK
V
W
X
6
Y
Z
8
9
ffB
7
0
U
A
g
C
D
E
G
H
2
1
1
4
4
L
M
N
O
R
d
S
b
T
X
q
h
iyO
g
3
ko
lK
JV
fB
U
A
5
C
D
E
G
H
2
I1
5
42
p
L
q
N
R
tP
S
T
3
6
tP
X
8
Y
3
Z
9
7
0
6
8
9
0
7
1
2
4
1
2
d
b
4
d
b
Q
h
iJyO
3
JI1
ko
lT
h
fB
iJyq
ko
lK
U
A
fB
C
U
D
E
G
H
I1
2
4 2
A
D
K
E
L
G
N
H
R
S
T
L
V
N
O
X
R
Y
S
Z
T
X
Y
Z
jF
e
u
a
sM
xW
w
vn
zrQ
jF
m
e
c5
a
u
sM
w
vkxW
zrQ
m
n
tP
3
6
8
9
0
7
p
5
1
2
4
d
b
tP
3
6
8
9
0
7
3
h
iyIO
ko
lK
1
4
fB
U
d
b
A
C
D
E
G
H
2
1
4
L
N
R
S
T
h
iJyO
V
3
ko
X
lK
Y
p
Z
JIV
g
fB
U
yO
A
C
D
E
G
H
2
I1
42
L
N
R
S
T
p
X
Y
Z
yO
jF
e
u
cg
a
p
q
o
s0
xW
w
vd
zg
m
rV
jF
e
cg
a
u
o
sM
xW
w
vn
jF
zrQ
m
n
e
u
c5
a
g
yq
sM
xp
w
vn
zV
m
p
rQ
q
tP
3
6
8
9
0
7
jF
1
2
4
d
b
e
cg
a
u
Q
o
sM
h
jzrV
iJyO
3
w
vxW
k2
zQ
JIq
lK
5
fB
m
n
U
e
u
c5
a
rN
A
C
D
E
tP
G
H
IcO
2
3
1
o
6
L
8
M
s4
N
9
0
R
7
xp
S
w
vn
T
V
5
m
X
n
Y
Z
1
2
4
tP
d
b
3
6
8
9
0
7
y
h
i
3
k
l
1
2
J
4
f
p
d
b
U
A
B
C
D
E
G
H
2
1
I
4
K
L
N
O
R
3
j
S
h
JyIq
T
iJq
ko
lC
V
X
Y
Z
fB
U
u
e
c
a
A
D
E
G
H
I5
2
1
4
o
K
L
s
N
R
x
S
w
v
T
z
V
W
m
X
Y
n
Z
5
r
t
3
6
8
9
0
7
1
4
d
b
h
i
3
k
l
JV
f
U
A
B
C
D
g
E
G
H
2
I1
4
y
K
L
P
R
S
T
X
Y
Z
p
q
5
t
6
8
9
7
0
d
b
Q
h
i
3
k
l
f
U
A
B
C
D
E
F
G
H
2
4
K
L
M
N
O
P
R
S
V
W
X
Y
Z
j
5
e
c
a
u
t
3
6
o
8
9
s
7
x
w
v
z
m
n
g
1
4
r
y
b
Q
p
q
3
h
i
J
k
l
g
f
U
A
B
C
D
E
F
G
H
2
1
4
K
L
M
N
P
R
S
T
W
X
Y
Z
5
t
3
6
8
9
0
7
1
2
4
d
b
Q
3
h
i
k
l
g
f
y
U
g
A
B
C
D
E
F
y
j
G
H
2
1
4
K
L
M
N
O
P
p
R
S
q
T
e
c
u
a
V
W
X
p
Y
Z
q
o
s
x
w
v
z
j3
m
n
r
e
u
c
a
o
s
x
w
v
z
m
r
5
t
3
6
8
9
7
0
j
1
2
4
j
e
c
a
u
d
b
t
3
Q
6
u
e
c
o
a
8
s
9
7
0
x
w
v
z
o
h
i
3
k
m
l
s
J
x
w
1
2
v
z
4
f
r
m
U
n
d
A
b
B
C
D
E
r
F
G
H
2
1
I
4
Q
K
L
M
N
O
P
R
S
T
h
V
i1
3
W
X
J
k
Y
l4
Z
f2
g
U
A
y
B
D
E
F
G
H
I
2
1
4
K
L
M
N
O
P
R
S
T
p
V
q
W
X
Y
Z
5
t
3
g
6
8
y
9
t
0
7
3
6
8
9
0
7
1
2
4
p
d
b
1
2
4
Q
d
b
Q
h
i
3
k
l
J
f
3
h
J
i
k
U
l
A
B
C
D
f
E
F
G
U
H
2
1
I
4
K
A
L
B
M
N
D
E
P
R
F
S
G
T
H
I1
2
4
V
W
K
X
L
M
Z
N
P
R
S
T
W
X
Y
Z
p
g
p
q
e
u
ch
a
o
s0
xW
w
vd
zg
m
n
rQ
tZ
jF
e
u
cjF
a
sY
xW
w
vZ
zrQ
iJIIj1
m
l2
n
fY
I m
5
jjF
tP
e
c5
a
u
6
8
9
0
7
sM
xW
w
vn
zrQ
m
n
d
b
3
Jq
iO
k2
lR
fB
U
A
C
D
E
G
H
2
1
4
K
L
M
N
5
S
T
V
e
cO
a
u
X
tP
3
6
8
sY
9
7
xW
w
vU
zrV
m
g
1
4
y
b
p
q
h
iyIO
3
JO
ko
lC
fB
U
A
5
C
D
E
G
H
IV
2
1
4
K
L
M
N
ttP
R
S
T
3
6
V
X
8
Y
9
Z
0
7
1
2
4
d
b
h
iiyO
3
ko
llK
JO
ffB
A
C
D
E
G
H
4
L
N
R
S
T
X
Z
3
6
8
9
0
7
1
2
4
d
b
Q
h
3
ko
U
A
B
C
D
E
F
G
H
2
1
j
4
K
L
M
N
P
R
S
T
e
c
a
u
V
X
Y
o
s
x
w
v
z
m
n
r
5
t
3
6
8
9
7
0
1
2
4
d
b
Q
h
i
3
k
l
J
f
U
A
B
C
D
E
F
G
H
2
1
I
4
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
p
q
jF
e
cg
u
a
sM
w
vxW
zrQ
n
5
tP
3
6
8
9
0
7
1
2
4
d
b
3
h
iyO
JV
ko
lK
fB
U
A
C
D
E
G
H
2
I1
42
L
N
R
S
T
X
Y
Z
p
q
jF
e
cg
a
u
sM
w
vxW
zrQ
m
n
5
tP
3
6
8
9
0
7
1
4
d
b
3
h
iyO
JV
ko
lK
fB
U
A
C
D
E
G
H
2
I1
4
L
N
R
S
T
X
Y
Z
p
q
jF
e
cg
u
a
sM
w
vxW
zrQ
m
n
5
tP
3
6
8
9
7
0
1
2
4
d
b
h
iyq
3
ko
lK
JyV
fB
U
A
C
D
E
G
H
2
I1
42
L
N
O
R
S
T
X
Y
Z
p
q
jF
e
cg
a
u
sM
w
vxW
zrQ
m
n
5
tP
3
6
8
9
0
7
1
4
p
d
b
h
iyO
3
ko
lK
JV
fB
U
A
C
D
E
G
H
2
I1
4
L
N
R
S
T
X
Y
Z
jm
e
cg
u
a
o
s
x
w
v
z
m
n
ra
5
tP
3
6
8
9
7
0
1
2
4
d
b
Q
h
i1
3
k
l3
JyO
f2
U
A
B
C
D
E
F
G
H
2
1
I5
4
K
L
M
N
O
R
S
T
V
W
X
Y
Z
g
yO
p
q
j
e
c
a
u
o
s
x
w
v
z
m
n
r
g
p
q
t
3
6
8
9
0
7
1
2
4
d
b
Q
h
i
3
k
l
J
f
U
A
B
C
D
E
F
G
H
2
1
I
4
K
L
M
N
P
R
S
T
V
W
X
Y
Z
j3
e
c
u
o
s
x
w
v
z
n
r
5
t
6
8
9
0
7
4
d
b
Q
3
h
i1
J
k
l4
f2
U
A
B
C
D
E
F
G
H
2
1
I
4
K
L
M
N
P
R
S
T
V
W
X
Y
Z
g
y
p
q
g
y
p
q
j
e
c
a
u
o
s
x
w
v
z
m
n
r
j
e
c
a
u
o
s
5
x
w
v
z
m
n
r
t
3
6
8
9
0
7
1
4
d
b
Q
h
iIO
3
kU
lK
JV
fB
U
A
C
D
E
F
G
H
2
I1
4
L
M
N
P
R
S
T
W
X
Y
Z
5
tP
6
8
9
0
7
d
b
Q
3
h
iO
JV
k2
lK
fB
A
C
D
E
F
G
H
2
1
4
L
M
N
R
S
T
W
X
Y
Z
0
100
200
300
Figura 4.19: Efecto de la variable longitud en el modelo (4.4), al que se le aplicará el Kriging.
−0.03
−0.02
−0.01
latitud
0.00
0.01
0.02
Efecto de la latitud
yjJg
g
q
p
yjIO
u
p
a
cq
e
sa
vP
w
o
xiU
zh
tw
5
m
rlm
n
9
6
8
7
yjS
q
p
u
b
4
cW
d
1
2
e
Q
sX
vo
w
o
xiZ
zrlC
JIg
h
kH
n
U
f0
A
B
C
D
E
F
G
H
4
1
K
L
M
N
O
R
S
V
Y
u
e
yjIO
g
sa
vP
w
xiU
z7
o
tE
p
m
rlm
n
9
8
b
4
d
1
2
Q
3
JO
kP
yj6
g
A
fT
B
C
D
F
G
H
4
IV
2
1
K
L
M
N
R
T
p
V
W
X
Y
Z
yj6
g
p
5
tw
9
3
6
8
7
b
4
1
2
Q
JIg
u
kE
U
A
fT
B
cW
C
e
D
E
F
G
H
4
1
K
sX
o
L
vo
M
xiZ
zrlC
N
R
S
V
Y
n
u
a
cq
e
o
sM
v3
w
xi5
z7
m
rlm
n
u
a
cq
e
sM
vP
w
xiU
z7
o
m
rlm
n
5
tw
0
9
3
8
yjS
b
4
d
1
Q
JO
3
q
p
h
kP
A
B
fT
C
D
F
G
H
4
2
1
K
t2
5
L
M
N
R
T
V
W
Y
Z
0
9
3
8
7
yjS
b
4
d
1
2
Q
5
t2
3
p
h
kv3
0
9
3
6
8
7
f0
A
B
D
F
G
4
2
1
K
L
N
O
b
4
d
1
2
R
Q
S
T
V
W
X
Y
Z
J6
3
h
kE
A
fB
D
F
G
H
4
2
1
K
L
N
R
T
V
W
X
Y
Z
u
a
cq
e
s3
vP
xiU
zrlQ
n
u
a
cq
e
s3
vP
w
xiU
zrlC
n
yjg
g
tvP
5
p
0
9
3
6
8
7
b
4
d
1
3
h
kE
A
f2
B
D
F
G
H
4
I1
2
K
L
5
M
N
tE
R
T
W
X
Y
Z
0
9
3
8
b
4
d
1
Q
JIO
3
h
kE
A
B
f2
D
F
G
H
4
2
1
K
L
M
N
R
T
V
W
X
Y
Z
u
a
cq
e
sa
o
vd
w
xicq
zh
m
rlC
n
yjS
g
5
t2
yjO
g
0
q
9
3
p
6
8
7
p
b
4
d
1
2
Q
JIO
h
kE
A
B
f0
C
D
F
G
H
IO
K
L
M
N
O
R
S
V
W
X
Y
Z
u
a
cq
e
sX
vP
xiU
zrlC
u
o
a
c6
e
m
n
sM
w
o
xiW
zrlC
m
n
tE
5
0
9
3
6
8
tE
5
yS
7
g
0
9
3
6
8
b
4
d
1
2
7
Q
q
p
JIO
3
h
b
4
d
1
2
kE
Q
U
A
fB
D
F
G
3
H
J
IV
4
2
1
K
L
h
M
N
k
P
R
S
U
T
f
A
V
B
W
C
X
D
Y
E
Z
F
G
H
4
I
2
1
K
L
N
P
R
S
T
V
X
Y
Z
yjO
g
jJO
u
a
c
e
p
sM
w
xiU
zrlQ
m
n
tP
5
y
g
0
9
6
8
7
q
p
b
d
u
a
c
e
3
JV
h
s
o
v
w
x
ko
z
U
A
fB
C
D
E
F
G
H
m
4
I1
r
n
2
K
L
N
R
T
W
X
Y
Z
y
g
q
p
5
t
j
u
0
9
3
6
8
7
a
c
e
s
v
w
x
z
o
b
4
d
2
1
Q
m
r
n
J
3
h
i
k
l
U
A
B
f
C
D
F
G
H
4
2
1
K
L
M
N
P
R
S
T
V
W
X
Y
Z
j
t
5
u
a
c
e
0
9
3
6
8
s
v
o
w
x
7
z
m
r
n
b
4
d
1
2
Q
J
3
h
i
k
l
U
A
B
f
D
F
G
H
I
4
2
1
K
L
M
N
P
R
S
T
W
X
Y
Z
y
g
q
p
y
g
5
t
q
p
0
9
3
6
8
7
b
4
d
1
2
Q
3
J
h
i
k
l
U
A
f
B
C
D
E
F
G
H
I
4
2
1
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
j
u
a
c
e
s
v
w
y
x
z
o
g
y
g
m
r
n
q
p
q
p
m
y
g
q
p
5
t
0
9
3
6
8
7
b
4
d
1
2
Q
J
3
h
i
k
l
j
U
A
f
j
B
u
C
D
E
j
F
u
G
H
I
u
4
2
1
a
K
c
e
L
M
N
a
c
O
e
P
a
c
R
e
S
s
T
v
o
w
x
z
V
W
s
v
X
w
o
x
Y
z
Z
s
v
w
x
z
o
m
r
n
m
r
n
r
n
M
y
g
y
yS
g
g
q
p
q
p
q
p
j3
u
a
c
e
s
o
v
w
x
z
yjO
m
r
n
q
p
5
t
t
5
5
t
0
9
3
6
8
0
9
3
6
8
7
0
7
9
3
6
8
7
b
4
d
1
2
b
4
Q
d
1
2
b
4
d
1
2
Q
Q
3
J
3
h
J
i
k
J
l
3
h
i
h
k
i
l
U
A
k
f
B
l
C
D
U
f
E
A
F
B
U
G
C
A
H
f
D
B
I
E
C
4
F
2
1
D
K
G
E
L
H
F
M
4
I
G
2
1
N
H
O
K
I
P
L
4
2
1
M
K
R
N
L
S
O
T
P
N
O
V
R
P
W
S
X
T
R
Y
S
Z
V
T
W
X
V
Y
W
Z
X
Y
Z
5
t
j
u
0
9
3
6
8
j
a
jO
c
e
u
7
u
s
v
o
a
w
c
x
e
z
a
c
e
s
o
v
b
4
w
d
1
2
x
z
o
s
vxiW
Q
w
zrlQ
m
r
n
J
m
3
r
n
j
m
n
h
i1
u
k
l4
U
A
B
f2
a
C
c
e
D
E
F
G
H
I
4
2
1
K
s
o
L
v
w
M
x
z
N
O
u
P
R
S
T
V
a
cg
W
e
X
Y
Z
m
r
n
sM
o
vxiW
w
zrlQ
m
n
5
t
5
t
tP
5
0
9
3
6
8
7
0
9
3
6
8
0
9
3
6
8
7
7
b
4
d
1
2
Q
5
b
4
d
1
2
t
b
4
Q
d
1
2
3
J
h
i
k
l
J
3
3
0
JV
9
3
U
6
8
A
f
B
h
C
5
i
D
k
E
tP
7
h
l
F
G
H
k
U
I
4
2
1
K
A
U
f
L
B
M
C
N
D
A
f
O
E
B
P
F
C
G
D
H
R
E
I
S
F
0
4
T
G
9
3
2
1
6
y
8
K
H
g
L
4
V
I1
b
4
2
d
1
2
Q
M
W
N
X
K
O
Y
L
7
P
Z
M
N
R
S
T
R
V
S
W
T
X
Y
Z
J
X
Y
Z
h
b
4
q
i
p
d
1
2
k
l
U
A
f
B
C
D
E
F
G
J
3
H
I
K
L
h
M
N
k
O
P
R
U
S
T
A
B
f
V
C
W
D
X
E
Y
F
Z
G
H
I
4
2
1
K
L
N
R
S
T
V
X
Y
Z
y
g
y
g
q
p
q
p
j
u
a
c
e
j
s
o
v
w
x
z
u
a
c
e
m
r
n
s
v
w
x
z
o
3
m
r
n
4
2
1
y
g
q
p
y
g
q
p
5
t
0
9
3
6
8
5
t
7
0
9
6
8
b
4
d
1
2
Q
7
J
3
b
d
h
i
Q
k
l
U
A
f
B
C
D
E
F
G
J
H
3
I
4
2
1
h
K
i
L
M
k
N
l
O
P
R
U
S
A
T
B
f
C
V
D
W
E
X
F
Y
G
Z
H
I
4
2
1
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
j
u
a
c
e
s
v
w
x
z
o
m
r
n
j
u
a
c
e
s
v
o
w
x
z
m
r
n
y
g
q
p
5
t
0
9
3
6
8
7
b
4
d
1
2
Q
t
5
J
3
h
i
0
k
9
3
6
8
l
7
U
A
f
B
C
D
E
F
G
H
I
4
2
1
K
L
M
N
O
P
b
4
d
1
2
R
S
T
Q
V
W
X
Y
Z
3
J
h
i
k
l
U
A
f
B
y
C
g
D
E
F
G
H
I
4
2
1
K
L
M
N
O
P
R
S
y
T
g
V
W
X
q
p
Y
Z
j
u
q
p
a
c
e
s
v
o
w
x
z
m
r
n
y
g
y
g
q
p
y
q
p
g
y
g
q
p
q
p
5
t
jg
u
0
9
6
8
7
a
c6
e
j
u
sM
vo
w
xiq
zrlC
o
b
a
d
c
e
Q
m
n
s
v
w
x
z
o
3
J
h
i
k
l
m
r
n
U
A
f
B
C
D
E
F
G
H
I
4
2
1
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
j
u
a
c
e
j
u
o
s
v
w
x
z
a
c
e
s
v
w
jO
x
m
z
o
r
n
u
a
ch
e
m
r
n
j
u
sM
vxiW
w
zrlQ
a
c
e
5
ta
m
s
n
v
w
x
o
z
5
t
0
9
3
6
8
7
m
r
n
0
9
3
6
8
b
7
4
d
1
Q
J
3
b
4
d
1
2
h
Q
kd
U
A
B
fm
C
D
E
F
J
3
G
H
Ie
h
4
i
2
1
K
k
L
l
N
O
P
U
A
R
f
B
S
C
T
D
E
V
F
W
G
X
H
Y
I
Z
4
2
1
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
t
5
5
0
9
3
6
8
t
7
y
g
0
9
3
6
8
5
7
tP
b
4
d
1
2
Q
q
p
3
0
b
9
4
3
6
J
tP
d
8
1
2
5
Q
7
h
i
k
l
U
f
A
B
J
C
0
9
3
3
6
D
8
E
h
F
i
G
7
H
k
b
4
I
d
1
2
4
l
2
1
K
L
M
U
N
A
O
f
B
P
C
D
R
E
S
F
T
G
H
V
I
JV
W
4
3
2
1
X
b
4
K
d
1
2
Y
L
Z
M
N
Q
O
P
ko
R
S
T
U
V
A
W
fB
X
C
Y
D
Z
3
E
JV
F
G
H
I1
h
42
i
2
K
k
L
l
N
U
A
f
R
B
S
C
T
D
E
F
G
X
H
Y
4
I1
2
Z
K
L
M
N
O
R
S
T
W
X
Y
Z
y
g
p
j
u
a
c
e
s
v
w
x
z
o
m
r
n
j
u
a
c
e
5
t
s
v
w
x
z
m
0
r
n
9
3
6
8
7
b
4
d
1
2
Q
J
3
h
i
k
l
U
A
f
B
C
D
E
F
G
H
I
4
2
1
y
K
g
L
M
N
O
P
R
S
T
V
W
X
Y
Z
q
p
5
t
0
9
3
8
7
b
4
1
2
Q
J
3
h
i
k
l
U
A
B
f
D
E
F
G
H
I
4
2
1
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
y
q
p
y
g
q
p
j
u
c
s
v
w
x
z
o
r
n
y
g
q
p
y
g
q
p
y
g
j
j
u
u
a
a
c
c
e
e
5
q
p
t
s
s
v
v
w
w
x
x
z
z
o
o
0
9
3
6
8
7
m
m
r
r
n
n
b
4
d
1
2
Q
J
h
i
k
l
U
A
B
f
C
D
E
F
G
H
I
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
j
u
a
c
e
s
v
o
w
x
z
m
r
n
j
u
a
c
e
5
5
t
t
s
v
o
w
x
z
0
0
m
9
3
9
6
3
8
6
r
8
n
7
7
y
g
j
u
b
b
4
4
d
d
1
2
1
2
Q
Q
a
c
e
q
p
J
s
J
y
v
3
3
w
x
g
z
o
h
h
i
i
k
k
l
l
U
U
A
A
f
B
f
B
C
C
D
D
m
E
r
E
n
F
F
G
G
H
H
I
I
4
4
2
2
1
1
K
K
q
p
L
L
M
M
N
N
O
O
P
P
R
R
S
S
T
T
V
V
W
W
X
X
Y
Y
Z
Z
y
g
5
t
q
p
0
9
3
6
8
7
b
4
d
1
2
Q
t
5
3
J
h
i
k
l
0
9
3
6
8
U
A
f
B
7
C
D
E
F
G
H
I
4
2
1
K
L
M
N
O
P
R
S
b
4
d
1
2
T
V
Q
W
X
Y
Z
5
t
3
J
h
i
k
l
U
A
f
B
C
0
D
9
3
6
8
E
F
G
7
H
I
4
2
1
K
L
M
N
O
P
R
S
T
V
W
j
X
b
4
d
1
2
Y
Z
Q
u
a
c
e
J
3
h
s
v
i
w
x
z
k
o
l
j
U
A
u
B
f
C
D
E
5
F
G
t
H
m
r
a
I
n
c
e
4
2
1
K
L
M
N
O
P
s
R
v
w
S
x
o
z
T
V
W
0
9
3
6
X
8
Y
Z
7
m
r
n
j
u
b
4
d
1
2
Q
a
c
e
s
v
w
x
z
o
J
3
h
i
k
l
U
A
m
f
B
r
n
C
D
E
F
G
H
I
4
2
1
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
yjO
q
p
tP
5
0
9
3
6
8
7
b
4
d
1
5
tP
3
JV
0
h
9
3
6
8
iW
kC
lQ
7
U
A
fB
D
E
F
G
H
4
I1
2
K
L
b
4
d
1
2
M
N
O
R
S
T
X
Y
Z
JV
3
h
iW
kC
lQ
U
A
fB
D
E
F
G
H
I1
4
2
K
L
M
N
O
R
S
T
X
Y
Z
u
a
cg
e
sM
vxiW
w
zrlQ
m
n
tP
5
0
9
3
6
8
7
b
4
d
1
2
3
JV
h
ko
U
fB
A
C
D
E
F
G
H
I1
42
2
K
L
N
R
S
T
X
Y
Z
yjO
g
q
p
u
a
c
e
y
s
o
v
w
x
z
g
m
r
n
q
p
5
t
0
9
3
6
8
7
y
g
b
4
d
1
2
Q
y
g
J
3
q
p
h
i
k
l
j
U
A
f
B
u
C
q
D
p
E
F
G
H
I
4
a
2
1
c
K
e
L
M
N
P
R
o
S
s
v
T
w
x
z
y
V
g
W
X
Y
Z
m
r
n
q
p
5
t
j
0
u
9
3
6
8
7
a
c
j
e
u
s
v
o
w
x
z
a
c
e
b
4
d
1
2
Q
s
v
w
x
o
z
m
r
n
J
3
h
i
k
l
m
r
n
U
j
A
B
f
C
D
u
E
F
G
H
I
yjO
4
2
1
K
L
a
c
M
e
N
O
P
R
S
T
s
v
V
w
x
o
W
z
X
Y
Z
q
p
m
r
n
t
5
tP
5
0
9
3
6
8
7
0
9
3
6
8
7
b
4
d
1
2
Q
b
4
d
1
2
5
3
t
Q
J
h
i
k
l
U
A
f
3
JV
B
C
D
0
E
h
9
3
6
8
F
i
G
k
H
l
7
I
4
2
1
K
L
U
M
N
A
f
O
B
P
C
D
E
R
F
S
G
T
H
42
I1
V
2
W
K
X
L
Y
b
4
M
Z
d
1
2
N
O
Q
R
T
W
X
Y
Z
J
u
3
h
i
k
l
a
cg
e
U
A
B
f
C
D
E
sM
F
vxiW
w
G
zrlQ
H
I
4
2
1
K
L
M
N
O
P
R
S
T
m
n
V
W
X
Y
Z
yjIg
g
yS
p
p
jS
u
cq
e
sX
w
o
xU
zh
rC
n
5
tN
0
9
3
6
8
7
b
4
d
1
2
J
3
h
ko
U
A
fB
C
D
E
F
G
H
IR
4
2
1
K
L
P
S
yjO
T
V
X
Y
Z
u
a
cW
e
q
p
sX
vo
o
xiZ
zrlC
n
yjO
g
q
p
yjO
q
p
yjS
g
5
tw
5
tw
q
p
0
9
3
8
9
3
6
8
7
yS
g
b
4
d
1
u
4
Q
d
1
2
Q
a
cg
e
p
3
JI6
sM
vxiW
w
h
zrlQ
kvP
iU
kE
lm
A
fT
B
D
A
fT
B
F
m
C
G
n
D
H
E
4
2
1
F
G
K
H
L
4
M
1
N
K
O
L
M
N
R
O
u
R
V
W
Y
V
Z
Y
a
cq
e
sM
vxiW
w
zrlQ
m
n
u
a
cg
e
sM
vxiW
w
zrlQ
m
n
5
tP
u
a
cq
e
0
9
3
6
8
sa
vP
w
o
xiU
z7
7
m
rlm
n
jJO
b
4
d
1
2
u
5
a
t2
cq
e
3
JV
s3
vP
w
xiU
h
zrlC
ko
0
9
3
U
8
A
fB
C
7
D
E
F
G
n
H
I1
4m
2
K
L
N
R
S
T
b
4
d
1
2
X
Y
Z
J6
3
h
kvo
U
A
fB
D
E
F
G
H
4
2
1
K
L
N
P
R
tP
5
S
T
V
X
Y
Z
yjO
0
9
3
6
8
7
q
p
b
4
d
1
2
t2
5
3
JV
0
9
3
6
8
h
ko
7
U
fB
A
C
D
E
F
G
H
I1
42
2
4
K
d
1
L
5
tE
N
Q
R
S
T
X
Y
Z
3
JI6
0
9
3
8
kH
7
A
fB
C
D
F
G
H
4
2
1
K
b
4
d
1
L
M
N
O
Q
P
R
T
V
W
Y
Z
3
JIO
kE
A
yS
f2
B
D
F
G
H
4
IV
2
1
K
L
M
N
R
T
V
q
W
p
X
Y
Z
yjJg
g
p
u
yjO
a
cIg
e
sM
vxiW
w
zrlQ
q
p
m
n
jO
u
yjS
a
cg
e
sM
vp
w
xiq
o
zrlQ
p
m
n
tP
5
0
9
3
8
7
u
a
cq
e
b
4
d
1
sb
vP
w
o
xiU
zh
JV
3
u
h
m
rlm
n
ko
a
cg
e
U
A
fB
C
D
E
F
G
H
sM
vxiW
I1
w
zrlQ
4
2
K
L
N
R
S
T
m
n
X
Y
Z
tvP
5
0
9
3
6
8
7
b
4
d
1
3
JzrV
u
h
k
t2
5
a
U
cq
A
e
f
B
C
D
E
F
G
H
o
42
I1
sX
2
vP
xiU
K
zrlQ
L
N
0
9
3
6
8
R
7
T
W
X
m
Y
n
Z
5
tP
b
4
d
1
2
Q
yjO
0
9
3
6
8
g
7
3
JI6
h
kE
A
f0
B
b
4
D
d
1
2
p
F
G
4
2
1
K
L
M
N
O
R
JV
3
V
h
W
X
yjO
Y
ko
Z
g
U
A
fB
C
D
E
F
G
H
I1
4
2
K
L
N
R
q
p
S
T
X
Y
Z
5
tE
0
9
8
7
b
d
yjO
3
h
kE
A
fT
B
D
q
p
F
G
4
2
1
K
L
M
N
R
T
W
X
Y
Z
u
yjO
g
a
c6
e
sM
w
xiW
o
zrlC
p
m
n
u
a
c
e
o
s
v
w
x
z
r
n
u
t
5
a
cg
e
sM
vxiW
w
zrlQ
0
9
3
6
8
7
m
n
b
4
d
1
2
Q
5
t
u
J
3
h
0
9
3
6
8
k
a
cq
e
7
U
A
B
f
C
D
o
E
sb
vP
F
w
xiU
G
zh
H
I
4
2
1
K
L
N
P
b
4
d
1
2
R
S
T
m
Q
rlC
n
V
X
Y
Z
3
J
h
i
k
l
U
A
f
B
C
D
E
F
G
H
I
4
2
1
K
L
M
N
P
R
S
T
V
W
X
Y
Z
5
tP
0
9
3
6
8
7
b
4
d
1
2
3
JV
tE
5
h
ko
U
A
fB
C
D
E
F
G
0
9
3
H
6
8
I1
yS
4
2
g
K
L
N
7
R
S
T
yjS
g
X
Y
Z
b
4
q
d
1
p
Q
3
h
kE
A
fB
C
D
F
G
H
4
2
1
K
L
M
N
R
S
T
V
W
X
Y
Z
jJO
u
a
cq
e
u
sM
vP
w
o
xiU
zrlQ
a
c
e
o
s
w
x
m
n
m
n
y
g
p
y
g
q
p
tvP
5
t
5
0
9
3
6
8
7
0
9
3
6
8
7
b
4
d
1
2
b
4
d
1
2
Q
3
JIO
h
kH
3
J
A
fB
C
D
h
F
i
G
H
k
4
l
2
1
K
U
L
N
A
f
B
C
D
R
E
F
T
G
H
4
V
I
2
1
W
X
K
Y
L
Z
M
N
j
O
P
R
u
S
T
V
W
X
Y
a
Z
c
e
s
v
w
x
o
z
m
r
n
j
u
a
c
e
y
g
s
v
w
o
x
z
m
r
q
p
n
t
5
0
9
6
8
7
b
d
Q
3
J
h
i
k
l
A
f
B
C
D
y
F
G
g
H
4
I
2
1
K
L
M
N
O
t
R
S
5
T
V
W
X
Y
Z
q
p
0
9
3
6
8
7
b
4
d
1
2
Q
3
J
j
h
i
k
u
l
U
f
A
B
C
a
c
D
e
E
F
G
H
I
4
2
1
K
L
s
M
v
w
o
N
x
z
O
P
R
S
T
V
W
X
Y
Z
m
r
n
y
g
q
p
y
g
q
p
j
u
a
c
e
s
v
w
x
o
z
5
t
m
r
n
0
9
3
6
8
7
b
4
d
1
2
Q
J
3
h
i
k
l
U
A
B
f
C
D
E
F
G
H
I
4
2
1
K
L
M
N
O
j
P
R
S
u
T
yjS
V
g
W
X
Y
Z
a
c
e
s
v
w
x
o
z
j
q
p
u
a
c
m
e
r
n
o
s
v
w
x
z
m
r
n
5
t
0
9
3
6
8
7
b
4
d
1
2
Q
J
3
h
i
k
l
U
A
B
f
C
D
E
F
G
H
I
4
2
1
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
t
5
yjO
0
9
3
6
8
7
yjO
b
4
d
1
2
q
p
y
Q
g
q
p
u
3
J
h
a
c
i
e
k
l
q
p
U
A
f
s
B
w
o
C
xiU
zrlQ
D
E
F
G
H
4
I
2
1
K
L
M
N
O
P
m
n
R
S
T
V
W
y
X
Y
Z
g
y
g
q
p
q
p
tvP
5
y
g
0
u
9
3
6
8
7
u
a
cg
e
q
p
a
cg
e
sM
vxiW
w
zrlQ
j
b
4
d
1
2
sM
vxiW
w
zrlQ
u
m
n
a
c
e
3
JIzrV
m
n
o
h
s
v
w
x
z
k
U
A
f
B
C
D
E
F
G
H
m
r
432
I1
n
2
K
L
M
N
R
S
j
T
j
W
u
X
Y
u
Z
a
c
e
a
c
e
o
s
v
w
x
z
s
v
o
w
x
z
m
r
n
m
r
n
5
tP
tP
5
0
9
3
6
8
7
0
9
3
6
8
t
5
7
j
t
u
b
4
d
1
2
5
0
9
3
6
8
b
4
d
1
a
c
7
e
JV
3
0
s
9
3
6
v
8
w
x
o
z
h
7
3
ko
JV
b
4
h
U
d
1
2
A
ko
fB
Q
C
D
E
m
F
r
n
U
G
t
A
5
fB
H
I1
t
C
4
D
2
b
4
5
K
d
1
2
E
3
L
F
J
G
N
H
Q
I1
4
2
K
h
R
L
i
S
T
N
k
l
0
9
3
6
8
X
U
R
Y
S
Z
0
T
A
f
9
3
3
6
8
J
B
C
D
7
X
E
h
Y
F
7
i
Z
G
k
H
l
I
4
2
1
K
L
M
U
N
A
f
O
B
P
C
D
E
R
F
S
G
T
b
4
H
d
1
2
4
I
V
2
1
Q
b
4
W
d
1
2
K
X
L
Y
M
Z
Q
N
O
P
R
S
T
3
V
J
W
X
3
Y
Z
J
h
i
h
k
i
l
k
l
U
A
f
U
B
A
C
f
B
D
C
E
D
F
E
G
F
H
G
4
I
2
1
H
I
K
4
2
1
L
K
M
L
N
M
O
N
P
O
P
R
S
R
T
S
T
V
W
V
X
W
Y
X
Z
Y
Z
t
5
0
9
3
6
8
7
b
4
d
1
2
Q
3
J
h
i
k
l
U
A
f
B
C
D
E
F
G
H
4
I
2
1
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
y
g
q
p
y
g
yjO
q
p
q
p
j
u
a
c
e
o
s
v
w
x
z
m
r
n
j
u
a
c
e
u
o
s
w
x
a
cg
e
o
sM
vxiW
w
zrlQ
m
n
m
n
t
5
0
9
3
6
8
7
b
4
d
1
2
Q
3
J
5
t
h
i
k
l
U
5
t
f
A
B
C
D
0
9
3
E
6
8
F
G
H
I
4
2
1
K
7
L
M
N
O
P
0
9
3
6
8
R
S
T
7
V
W
X
Y
Z
b
4
d
1
2
Q
b
4
d
1
2
J
h
i
k
l
J
3
U
A
f
B
h
C
D
k
E
F
G
H
U
I
4
2
1
K
A
L
B
f
M
C
N
D
O
E
P
F
G
H
R
I
S
4
T
2
1
K
L
V
W
N
X
Y
P
Z
R
S
T
V
X
Y
Z
y
g
q
p
y
g
q
p
j
u
a
c
e
s
v
w
o
x
z
m
r
n
j
u
a
c
e
s
v
o
w
x
z
m
r
n
5
tP
yjO
0
9
3
6
8
7
q
p
b
4
d
1
2
3
JV
h
iW
kvxyjzrC
lQ
U
A
fB
D
E
F
G
H
I1
4
2
K
L
tvP
M
N
5
O
R
S
T
X
Y
Z
0
9
3
6
8
7
b
4
d
1
2
yjO
3
h
iq
ke
lQ
A
fB
q
p
C
D
E
F
G
H
I7
4
2
1
K
L
M
N
O
R
T
V
W
X
Y
Z
u
a
cg
e
sM
vxiW
w
zrlQ
m
n
u
a
cg
e
sM
vo
o
w
xiq
zrlQ
m
yjO
n
q
p
5
tP
0
9
3
6
8
7
b
4
d
1
JV
3
h
ko
U
A
fB
C
D
E
F
G
H
I1
4
2
K
L
N
R
S
T
yjO
X
Y
Z
q
p
5
tE
0
9
3
6
8
7
b
4
d
1
2
3
h
kd
A
fB
C
D
F
G
H
4
2
1
K
L
N
u
R
T
V
W
X
a
cIg
Y
e
Z
sM
vxiW
w
o
zrlQ
m
n
yjO
q
p
u
a
cg
e
sM
vxiW
w
zrlQ
m
n
tP
5
0
9
3
b
4
d
1
3
JIV
h
kE
U
A
fB
D
G
H
I1
4
2
K
L
N
R
S
T
X
Y
Z
g
tP
5
yS
g
0
9
3
q
6
p
8
u
7
p
a
cg
e
sM
vxiW
w
zrlQ
b
4
d
1
2
m
n
JV
3
h
ko
U
A
fB
C
D
E
F
G
H
I1
42
2
K
L
N
R
S
T
X
Y
Z
5
tP
0
9
3
6
8
7
jJ6
u
u
a
cq
e
b
4
d
a
1
2
c6
o
sM
w
yS
sa
o
w
xiU
z7
g
JV
3
h
m
n
ko
m
rl8
n
U
A
fB
C
p
D
E
F
G
H
I1
4
2
K
L
N
R
S
T
X
Y
Z
5
tP
t2
5
0
9
6
8
0
9
3
6
8
7
7
b
d
b
4
d
1
Q
3
JIV
3
h
iU
J6
kH
lQ
h
U
kd
A
jJg
fB
D
A
fB
u
F
G
C
H
D
I1
4
2
F
K
G
L
H
a
4
N
c6
2
1
e
K
L
M
R
N
S
O
T
R
sM
W
vP
w
X
xiU
T
zrlC
Y
Z
V
W
Y
Z
m
n
5
tE
0
9
3
6
8
7
b
4
1
2
Q
3
JIg
h
kE
A
rlC
fB
C
D
F
G
yjS
4
2
1
K
L
N
O
R
T
V
W
Y
Z
p
yjO
q
p
tE
5
9
3
yS
g
4
d
1
2
Q
q
p
3
JF
iZ
kvP
U
A
fT
B
D
F
G
H
4
2
1
K
L
M
N
P
R
S
T
V
W
X
Y
u
Z
a
cg
e
yS
o
sb
vP
w
xiU
zh
m
rl8
n
p
u
a
cg
e
sM
vxiW
w
zrlQ
yjO
g
m
n
q
p
yjS
g
p
jJzC
u
cq
e
o
sX
tn
5
w
xU
m
0
9
3
8
7
b
4
1
2
tP
5
Q
3
0
9
3
6
8
h
kE
7
jJO
A
f0
u
B
C
D
E
F
G
H
IO
a
cyS
4
e
2
1
K
L
M
b
4
N
d
1
2
O
o
R
s3
vP
w
xiU
zrlC
V
W
X
Y
3
JV
h
n
ko
U
A
fB
C
D
E
F
G
H
I1
42
2
K
L
u
N
R
S
T
a
cq
e
X
Y
Z
sM
vxiW
w
zrlQ
m
n
u
a
c6
e
sa
vP
w
o
xiU
z7
m
rl8
n
5
tE
0
9
3
8
b
4
d
1
Q
5
3
JIO
tP
kE
A
f2
B
0
D
9
3
6
8
F
G
7
4
2
1
K
L
M
N
P
R
S
T
V
5
W
t2
X
b
4
Y
d
1
2
Z
0
9
3
8
JV
3
h
7
kvo
U
A
fB
C
D
E
F
G
H
b
4
I1
d
1
2
4 gp
2
K
L
Q
N
R
S
T
X
3
Y
Z
h
kH
A
fB
D
F
G
4
2
1
K
L
M
N
O
R
T
V
W
Y
Z
yS
p
q
p
jJI6
u
a
cq
e
sX
vP
w
o
xiU
z7
m
rlm
n
5
tE
0
9
3
6
5
tkvP
jJIg
u
cq
e
0
9
3
b
8
4
d
1
2
Q
o
7
sX
w
xU
zh
3
h
b
4
m
iZ
d
1
2
rC
n
lC
Q
A
fT
B
D
F
G
H
4
2
1
K
L
h
M
N
O
kH
R
T
A
V
f
B
W
C
X
D
Y
E
Z
F
G
H
I
4
1
K
L
M
N
O
R
V
W
X
Y
y
g
p
y
j
u
q
a
c
e
s
w
x
o
z
m
r
n
5
t
0
9
3
6
8
7
j
u
a
c
e
b
4
d
1
2
Q
o
s
v
w
x
z
J
3
h
i
k
m
l
r
n
U
A
B
f
C
y
D
g
E
F
G
H
I
4
2
1
K
L
M
N
O
P
R
S
T
V
W
X
Y
q
p
Z
5
t
0
9
3
6
8
7
b
4
d
1
2
Q
J
3
h
i
k
l
U
A
f
B
C
D
E
F
G
H
I
4
2
1
K
L
M
N
O
P
R
S
T
j
V
W
X
u
Y
Z
a
c
e
s
v
w
x
o
z
m
r
n
5
t
0
9
3
6
8
7
b
4
d
1
2
JV
3
h
iW
kC
lQ
U
A
fB
D
E
F
G
H
I1
4
2
K
L
M
N
O
P
R
S
T
X
Y
Z
yjO
g
q
p
u
a
cq
e
sM
vxiW
w
zrlQ
m
n
5
tP
0
9
3
6
8
7
b
4
d
1
2
JIV
3
h
kH
U
A
fB
D
G
H
I1
4
2
K
L
N
R
S
T
X
Y
Z
yjO
g
p
yjO
q
p
u
a
cq
e
sM
vo
w
xiW
zrlC
m
n
u
a
cg
e
sM
vxiW
w
zrlQ
m
n
5
tE
0
9
3
6
8
7
b
4
d
1
2
Q
JIF
3
h
kE
U
A
fB
D
G
4
2
1
K
L
N
tP
5
P
R
S
T
V
X
Y
Z
0
9
3
6
8
7
b
4
d
1
2
3
JV
h
ko
U
A
fB
C
D
E
F
G
H
I1
4
2
K
L
N
R
S
T
X
Y
Z
yjO
g
p
u
a
cq
e
sM
vo
w
xiW
o
zrlC
m
n
5
tE
0
9
3
6
8
7
b
4
d
1
2
Q
JIF
3
h
kE
U
A
fB
C
D
F
G
H
4
2
1
K
L
N
P
R
S
T
V
X
Y
Z
yjO
q
p
yS
g
u
a
cg
e
q
p
sM
vxiW
w
zrlQ
yjjg
m
n
g
p
y
g
p
5
tP
0
9
3
6
8
7
b
4
d
1
2
u
yjO
a
cq
e
g
JV
3
o
h
sM
vP
w
ko
xU
zrC
U
A
fB
C
D
E
F
q
p
G
H
I1
m
4 2
n
2
K
L
N
u
R
S
T
a
cq
X
e
Y
Z
o
sa
vd
w
xiiU
zh
m
rllC
n
yjO
q
p
j
u
a
c
e
s
v
w
x
o
z
m
r
n
5
y
g
0
9
3
6
8
7
q
p
5
ttw
b
4
d
1
2
Q
3
JIIO
0
9
3
6
8
u
h
7
kE
U
a
cq
e
A
B
D
E
F
G
H
sM
vP
4
w
2
1
o
xiU
K
zrlQ
L
b
4
d
1
2
Q
N
P
R
T
V
W
m
X
n
3
Y
JIO
Z
h
kE
A
ff0
B
C
D
F
G
H
4
2
1
K
L
M
N
O
R
5
T
t
V
W
X
Y
u
Z
a
cg
e
0
9
3
6
8
7
sM
vxiW
w
zrlQ
m
b
4
d
1
2
n
Q
J
3
h
i
k
l
U
A
f
B
C
D
F
G
H
4
2
1
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
j
u
a
5
c
e
tP
s
o
v
w
x
z
0
9
3
8
7
m
r
n
b
4
d
1
2
JIV
3
h
kE
U
A
fB
C
D
E
F
G
H
5
I1
tP
4
2
K
L
N
R
S
T
W
X
0
Y
9
3
6
8
Z
7
y
g
b
4
d
1
2
yjS
JV
3
h
q
p
ko
U
A
fB
C
D
E
F
G
H
q
I1
p
4 2
2
K
L
N
R
S
T
X
5
Y
t
Z
0
9
3
6
8
7
b
4
d
1
Q
J
3
h
i
k
l
U
A
f
B
C
D
E
F
G
H
I
4
2
1
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
yj6
g
j
p
u
a
c
e
u
s
o
v
w
x
z
c
e
o
m
s
r
n
v
x
z
y
g
m
r
n
p
tP
5
t
0
9
u
9
3
8
a
c
e
yjO
7
b
4
g
d
1
2
Q
s
v
o
w
x
z
J
3
b
4
1
2
Q
h
ip
q
p
m
kZ
r
n
lq
U
A
fg
B
3
C
J
D
E
F
G
H
Iy1
i
4
2
K
k
L
l
M
N
U
O
f
A
R
B
j2
S
T
D
E
V
F
u
W
G
X
H
Y
I
4
Z
2
1
K
L
M
N
a
c6
e
P
R
S
T
V
W
sM
X
v
w
o
Y
x
z
Z
m
r1
n
5
t
0
9
3
6
8
7
b
4
d
1
2
Q
3
J
h
i
u
k
5
l
t
A
f
a
B
c
e
C
D
F
G
H
4
2
1
s
K
v
w
L
x
o
0
z
9
3
M
6
8
N
O
P
7
R
S
T
V
W
X
Y
m
Z
r
n
b
4
d
1
Q
J
3
h
i
k
l
A
f
B
C
D
F
G
H
4
2
1
K
L
N
O
R
yj6
S
T
V
W
X
Y
Z
y
g
q
p
q
p
5
t
0
9
3
6
8
7
b
4
d
1
2
Q
J
3
h
i
k
l
U
A
f
B
C
D
E
F
G
H
I
4
2
1
K
L
M
N
P
R
S
T
V
W
X
Y
Z
y
g
q
p
u
a
cg
e
j
sM
u
v3
w
xi5
z7
a
c
e
m
rl8
n
o
s
v
w
x
z
m
r
n
5
t2
j
0
5
9
3
t
6
8
u
7
a
c
e
0
9
3
6
8
s
v
w
o
x
b
4
z
7
d
1
2
Q
m
r
n
J
3
b
4
d
1
2
Q
h
ko
U
A
fB
C
D
3
J
E
F
G
H
I1
4
h
2
1
K
i
L
k
l
N
O
P
U
R
A
f
S
B
T
C
D
V
E
W
F
X
G
Y
H
I
4
2
1
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
tP
5
yjO
0
9
3
8
7
q
p
b
4
d
3
JV
h
iW
kC
lQ
U
A
fB
D
E
F
G
H
I1
4
2
K
L
M
N
O
R
yj6
S
T
g
X
Y
Z
yjO
q
p
q
p
yjO
q
p
u
a
cg
e
sM
vxiW
w
zrlQ
m
n
u
a
cq
e
u
sM
a
v3
cS
w
e
xi5
z7
s3
vxiW
w
zrlQ
m
rlm
n
u
yjO
n
a
cg
e
sM
vxiW
w
zrlQ
q
p
m
n
jO
u
a
ch
e
tP
5
sM
vxiW
w
zrlQ
m
0
9
3
6
n
8
7
b
4
d
1
2
3
JV
h
ko
U
A
fB
C
D
E
F
G
H
I1
4
2
K
L
N
tP
5
R
S
T
X
Y
Z
tP
0
9
3
8
7
0
9
8
5
tP
b
4
d
1
2
Q
b
4
d
1
2
0
9
3
8
Jg
7
h
kvo
3
JV
U
A
fB
h
D
ko
E
F
G
H
5
b
4
IC
d
1
2
U
4
tP
1
A
f2
K
B
L
D
N
E
O
F
G
H
R
I1
4
2
T
K
3
V
JV
M
W
N
u
X
Y
0
Z
9
3
6
8
R
h
T
ko
a
cg
e
U
X
Y
Z
A
fB
C
D
E
sM
vxiW
F
w
G
zrlQ
H
I1
4 5
2
b
4
K
d
L
N
R
S
T
m
n
X
Y
Z
JV
3
ko
U
A
fB
C
D
E
F
G
H
I1
4 2
2
K
L
N
R
S
T
X
Y
Z
yjO
yjO
q
p
q
p
5
tP
0
9
3
6
8
7
b
4
d
1
JV
3
h
ko
U
A
fB
C
D
E
F
G
H
I1
4
2
K
L
N
R
S
T
X
Y
Z
u
a
cg
e
u
sM
vxiW
w
zrlQ
a
cg
e
sM
vxiW
w
m
zrlQ
n
m
n
5
tP
5
tP
0
9
3
6
8
7
yjO
0
9
3
6
8
7
b
4
d
1
2
q
p
b
4
d
1
2
3
JV
h
ko
U
A
fB
J6
C
3
D
E
h
F
G
H
ko
I6
4
2
1
K
L
N
U
A
fB
C
D
R
E
S
F
T
G
H
I6
4
X
2
1
K
Y
L
Z
N
R
S
T
V
X
Y
Z
yjO
q
p
u
a
cg
e
sM
vxiW
w
yjO
zrlQ
g
m
n
p
u
a
cg
e
sM
vxiW
w
zrlQ
yjS
m
n
5
tP
q
p
0
9
3
6
8
7
b
4
d
1
2
JV
3
h
ko
U
A
fB
u
C
D
E
F
G
H
I1
4 2
a
2
c6
K
e
L
N
R
S
sM
T
w
xiW
zrlC
X
Y
Z
m
n
5
tP
0
9
3
6
8
7
b
4
d
1
JV
3
h
ko
U
A
fB
C
D
E
F
G
H
I7
4
2
1
K
L
u
N
yjO
R
S
a
T
cg
e
X
Y
Z
sM
vxiL
w
zrlQ
q
p
tP
m
n
0
9
3
6
8
7
b
4
d
1
2
Q
JV
h
ko
U
A
fB
C
D
E
F
G
H
I7
K
L
N
R
S
T
X
Y
Z
5
tP
0
9
3
6
8
yjO
b
4
d
1
2
u
q
p
3
JV
h
ko
a
cg
e
U
A
fB
C
D
E
sM
vxiW
F
w
G
zrlQ
H
I1
4
2
K
L
N
O
R
S
T
m
n
W
X
Y
Z
5
tP
0
9
3
8
yjO
7
u
a
cg
b
4
e
d
1
2
q
p
sM
vxiW
w
zrlQ
3
JV
h
ko
m
n
U
A
fB
C
D
E
F
G
H
I1
4
2
K
L
N
R
S
T
X
Y
Z
5
tP
0
9
3
6
8
7
u
b
4
d
1
2
a
cg
e
JV
3
sM
vxiW
w
zrlQ
h
ko
U
A
fB
C
D
E
m
F
n
G
H
I1
4 2
2
K
L
N
R
S
T
X
Y
Z
yjO
tP
5
q
p
0
9
3
6
8
7
b
4
d
1
2
3
JV
h
ko
U
fB
A
C
D
E
F
G
H
I1
4 2
2
K
L
N
R
S
T
X
Y
Z
yjO
g
q
p
u
a
cg
e
sM
vxiW
w
zrlQ
o
m
n
5
tP
u
0
a
9
3
c
6
8
e
7
o
s
v
w
x
z
b
4
d
1
2
m
r
n
J
3
h
k
U
A
f
B
C
D
E
F
G
H
I
4
2
1
K
L
N
R
S
T
V
X
Y
Z
y
g
q
p
5
t
0
9
3
6
8
7
b
4
d
1
Q
J
3
h
i
k
l
U
A
B
f
C
D
E
F
G
H
I
4
2
1
K
L
M
N
P
R
S
T
V
W
X
Y
Z
j
u
a
c
e
y
g
s
v
w
x
o
z
m
r
q
n
p
y
g
q
p
5
t
0
9
3
6
8
7
b
4
d
1
Q
3
J
y
j
g
h
i
k
u
l
U
f
A
B
C
a
D
c
e
E
F
G
H
I
4
2
1
K
q
p
L
s
M
v
w
N
x
o
z
O
j
P
R
S
u
T
V
W
X
Y
Z
m
a
r
n
c
e
s
v
o
w
x
z
m
r
n
y
g
y
g
q
p
q
p
5
t
0
9
3
6
8
7
5
t
b
4
d
1
2
j
Q
0
9
3
6
8
u
7
a
c
e
J
3
h
i
k
s
l
v
w
x
o
z
b
4
d
1
2
U
A
Q
B
f
C
D
E
F
G
H
I
4
2
1
K
m
L
r
n
M
3
N
J
O
P
h
R
i
S
T
k
l
V
W
X
Y
U
Z
A
f
B
C
D
E
F
G
H
I
4
2
1
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
j
y
g
u
j
u
a
c
e
a
c
e
s
v
w
x
z
o
q
p
s
v
o
w
x
z
m
r
n
m
r
n
t
5
0
9
3
6
8
7
b
4
d
1
2
Q
3
J
h
i
k
l
U
f
A
B
C
D
E
F
G
H
I
4
2
1
K
L
M
N
O
P
R
S
T
V
t
5
W
X
Y
Z
t
5
0
9
3
6
8
0
7
9
3
6
8
7
b
4
d
1
2
Q
j
b
4
d
1
2
Q
u
J
a
3
c
e
h
i
3
J
k
l
h
iW
sM
vxiW
w
kC
U
A
zrlQ
lK
fB
D
E
U
F
A
fB
G
H
I1
D
4
E
2
K
F
L
G
M
H
N
m
I1
O
n
4
2
P
L
R
M
S
N
T
O
P
V
W
R
X
S
Y
T
Z
V
X
Y
Z
5
tP
0
9
3
6
8
7
b
4
d
1
2
JV
3
h
ko
U
A
fB
C
D
E
F
G
H
I1
4
2
K
L
N
O
R
S
T
X
Y
Z
yjO
q
p
yjO
q
p
yjO
q
p
u
a
cg
e
sM
vxiW
w
zrlQ
u
m
a
n
cg
e
sM
vxiW
w
zrlQ
u
m
n
a
cg
e
sM
vxiW
w
zrlQ
m
n
5
tP
0
9
3
6
8
7
5
tP
b
4
d
1
2
0
9
3
6
8
7
5
tP
3
JV
h
ko
b
4
d
1
2
U
fB
A
C
0
D
9
3
6
8
E
F
G
H
7
I1
42
2
K
L
N
3
JV
h
R
S
ko
T
X
Y
U
A
b
4
Z
fB
d
1
2
C
D
E
F
G
H
I1
4
2
K
L
N
JV
3
R
S
T
h
ko
X
Y
Z
U
A
fB
C
D
E
F
G
H
I1
4 C
2
K
L
N
R
S
T
X
Y
Z
yjO
q
p
u
a
cg
e
yS
sM
vxiW
w
zrlQ
m
n
q
p
tP
5
0
9
3
6
8
7
b
4
d
1
3
JV
h
ko
jJg
u
U
A
fB
C
yjO
D
E
F
G
a
H
cyg
e
I1
42
2
K
L
N
o
sa
vP
w
R
xiU
zh
S
T
X
Y
Z
q
p
m
rlQ
n
5
tw
0
9
3
6
8
yj6
g
7
4
1
2
p
yjIO
JIg
u
kE
a
cg
U
e
A
f0
B
C
D
E
F
sM
p
G
vxiW
w
H
zrlQ
4
2
1
K
L
M
N
O
R
S
m
V
n
Y
5
tP
u
0
9
3
6
8
7
a
cq
e
sM
vP
w
xiU
o
z7
b
4
d
1
u
m
rlm
n
cW
e
JV
3
h
ko
sX
vo
o
xiZ
zrlC
U
A
fB
C
D
E
F
G
H
I1
4 2
2
K
L
n
N
R
S
T
X
Y
Z
yjO
yjO
q
p
q
p
t2
5
0
9
3
6
8
7
tE
5
b
4
d
1
2
Q
9
3
8
3
h
kE
A
fB
b
4
d
1
2
D
F
Q
G
H
4
2
1
K
L
N
O
R
3
JO
T
V
W
X
kP
Y
Z
A
fT
B
C
D
E
F
G
H
IV
4
2
1
K
L
M
N
R
T
V
W
X
Y
Z
u
u
yjO
a
cg
e
a
cg
e
sM
vxiW
w
zrlQ
sM
vxiW
w
zrlQ
q
p
m
n
m
n
5
tP
5
tP
0
9
3
6
8
0
9
7
3
6
8
7
b
4
d
1
b
4
d
1
3
JV
JV
u
3
h
ko
h
U
ko
a
cg
e
g
fB
A
yjO
U
C
D
E
A
F
fB
G
C
H
D
sM
vxiW
I1
4
E
w
2
F
zrlQ
K
G
L
H
I1
N
4 m
2
K
L
R
N
S
T
p
R
S
m
q
p
X
T
n
Y
Z
X
Y
Z
yjS
q
p
yjO
5
tP
q
p
0
9
3
6
8
7
b
4
d
1
2
jO
JV
3
u
h
u
ko
U
a
cq
e
A
fB
a
C
cg
e
D
E
F
G
H
sb
I1
vd
w
42
xiq
o
2
zh
K
L
sM
vxiW
w
o
N
zrlQ
R
S
T
m
X
rlC
yjO
n
Y
Z
g
m
n
u
q
p
a
cq
e
s3
vP
w
xiU
zrlQ
m
n
u
a
cg
e
o
sM
vxiW
w
zrlQ
5
t
tP
5
m
n
0
9
3
6
8
0
9
3
6
8
7
7
b
4
d
1
2
b
4
Q
d
1
2
5
t
J
JV
3
h
k
h
k
y
A
f
B
U
C
A
0
D
9
3
6
B
f
8
g
C
F
D
G
E
7
H
F
I
G
H
K
I
L
4
M
2
1
K
N
L
N
u
R
S
T
R
S
V
T
q
p
W
X
b
a
4
Y
d
c
1
e
Z
X
Y
Z
s
v
o
w
x
z
3
J
h
k
m
r
n
U
A
f
B
D
F
G
H
I
4
2
1
K
L
M
N
P
R
S
T
W
X
Y
5
Z
t
0
9
3
6
8
7
b
4
d
1
2
3
J
h
k
U
A
f
B
C
D
E
F
G
H
I
4
2
1
K
L
N
P
R
S
T
V
X
Y
Z
t
5
0
9
3
6
8
7
j
u
b
4
d
1
2
Q
a
c
e
o
s
v
w
3
x
z
J
h
i
k
l
U
A
f
B
m
C
r
n
D
E
F
G
H
I
4
2
1
K
L
M
N
P
R
S
T
V
W
X
Y
Z
y
g
y
g
q
p
q
p
5
t
0
9
3
6
8
7
b
4
d
1
2
Q
3
J
h
i
k
l
U
f
A
B
C
D
E
F
G
H
I
4
2
1
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
y
g
q
p
j
j
u
u
a
c
e
a
c
e
o
s
v
w
x
z
s
v
w
x
o
z
m
r
n
r
n
y
g
p
y
g
5
t
5
t
j
u
q
p
0
9
3
6
8
a
c
e
0
7
9
3
6
8
7
y
s
g
v
o
w
x
z
b
4
d
1
2
Q
b
4
m
d
1
2
r
n
Q
q
p
3
J
J
3
h
i
k
h
l
i
k
U
l
f
A
B
U
C
A
D
B
f
E
C
F
D
G
E
H
F
I
G
4
2
1
H
K
I
L
4
M
2
1
K
N
L
O
M
P
N
O
R
P
S
T
R
S
V
T
W
X
V
Y
W
Z
X
Y
Z
j
u
a
c
e
y
g
o
s
v
w
x
z
m
r
n
q
p
5
t
0
9
3
6
8
7
j
u
a
c
e
b
4
d
1
2
Q
o
s
v
w
x
z
3
J
h
m
i
r
n
k
j
l
u
U
A
f
B
C
D
E
F
G
a
H
c
e
I
4
2
1
K
L
M
N
O
P
s
v
w
o
R
x
z
S
T
V
W
X
Y
Z
m
r
n
5
tP
0
9
3
6
8
7
b
4
d
1
2
3
JV
h
jO
iW
kyjC
lQ
u
U
A
fB
D
E
a
ch
F
e
5
tP
G
H
I1
42
2
K
L
M
N
sM
vxiW
O
w
zrlQ
R
S
T
0
9
3
6
8
X
Y
Z
7
m
n
b
4
5
d
1
tP
3
JV
0
9
3
6
8
h
iq
7
kg
lQ
U
A
fB
C
D
E
F
G
H
I1
4
2
K
b
4
L
d
1
2
M
N
O
R
T
W
X
Y
Z
3
JV
h
iW
kC
lQ
U
A
fB
D
E
F
G
H
I1
4 2
2
K
L
M
N
O
R
S
T
X
Y
Z
5
tP
yjO
0
9
3
6
8
7
q
p
b
4
d
1
2
JV
3
ko
U
A
fB
C
D
E
F
G
H
I1
4a
2
K
L
N
R
S
T
X
Y
Z
yj6
q
p
u
a
cS
e
s3
vxiW
w
zrlQ
n
tP
u
0
9
8
a
cg
e
sM
v3
w
xi5
z7
b
4
d
1
2
m
rlm
n
3
JV
h
ko
U
A
f2
B
D
E
F
G
H
I1
4
2
K
L
M
N
R
S
T
X
Y
Z
yjO
q
p
5
tP
0
9
3
6
8
7
b
4
d
1
Q
Jg
h
ko
U
A
fB
C
D
E
F
G
H
IC
4
1
K
L
N
O
R
T
V
W
X
Y
Z
u
a
cg
e
sM
vxiW
w
zrlQ
q
p
m
n
yjS
p
yjO
5
tP
q
p
yjO
0
9
3
6
8
7
q
p
b
4
d
1
u
JV
3
h
ko
a
cg
e
yjO
U
A
fB
C
D
E
sM
vxiW
F
w
G
zrlQ
H
I1
4
2
K
L
N
R
S
T
m
q
n
p
X
Y
Z
u
a
ch
e
sM
vxiW
w
zrlQ
m
n
u
a
cg
e
5
tP
sM
vxiW
w
zrlQ
u
0
9
3
6
8
m
n
a
cg
e
7
sM
vxiW
w
zrlQ
b
4
d
1
2
m
n
3
JV
h
ko
u
U
A
fB
C
D
E
cg
e
F
G
H
I1
42
2
K
L
5
N
tP
sM
vxiW
O
w
zrlQ
R
S
T
X
Y
Z
m
0
9
3
n
6
8
7
b
4
d
1
yjO
3
JV
ko
U
A
fB
C
D
E
F
q
p
G
H
I1
42
tP
2
K
5
L
yjO
N
O
R
T
X
Y
Z
0
9
3
6
8
7
q
p
5
tP
b
4
d
1
0
9
3
6
8
7
3
JV
h
ko
b
4
U
d
1
fB
A
C
D
E
F
G
H
I1
4
2
5
K
tP
L
N
JV
3
R
h
S
T
ko
X
Y
U
Z
A
0
9
3
fB
6
8
C
D
E
F
7
G
H
I1
4 2
2
K
L
N
R
S
T
b
4
d
1
2
X
Y
Z
yjO
JV
3
h
ko
U
A
fB
C
q
p
D
E
F
G
H
I1
42
2
K
L
N
R
S
T
X
Y
Z
u
a
cg
e
sM
vxiW
w
zrlQ
u
m
n
a
cg
e
sM
vxiW
w
zrlQ
m
n
u
a
cg
e
sM
vxiW
w
zrlQ
tP
5
m
n
0
9
3
6
8
7
tP
5
b
4
d
1
0
9
3
6
8
7
3
JV
h
ko
U
b
4
A
d
1
2
fB
C
D
E
F
G
H
I1
4
2
K
L
N
3
JV
R
S
T
h
ko
X
Y
Z
U
fB
A
C
D
E
F
G
H
I1
42
2
K
L
N
R
S
T
X
Y
yjO
Z
q
p
tP
5
0
9
3
6
8
7
b
4
d
1
3
JV
h
ko
U
fB
A
C
D
E
F
G
H
I1
42
2
K
L
N
R
S
T
yjO
X
Y
Z
q
p
u
a
cg
e
sM
vxiW
w
zrlQ
yjO
m
n
q
p
u
a
cg
e
sM
vxiW
w
zrlQ
m
n
5
tP
0
9
3
6
8
b
4
d
1
2
yjO
3
JV
h
ko
q
U
p
A
fB
C
D
E
F
G
u
H
I1
4 2
2
K
L
N
a
cg
e
R
S
T
X
sM
vxiW
Y
w
yS
Z
zrlQ
m
n
q
p
5
tP
0
9
3
6
8
7
b
4
d
1
2
JV
h
ko
U
A
fB
C
D
E
F
G
H
I7
K
L
N
R
S
T
X
Y
Z
5
tP
0
9
3
6
8
7
u
yjO
a
cg
e
b
4
sM
d
1
2
vxiW
w
zrlQ
q
p
m
JV
3
n
h
ko
jO
U
A
fB
u
C
D
E
F
G
H
I1
42
2
K
a
cg
L
e
N
R
S
T
sM
vxiW
w
o
zrlQ
X
Y
Z
m
n
5
tP
0
9
3
6
8
7
b
4
d
1
2
5
tP
3
JV
h
u
ko
0
U
9
3
6
8
A
fB
a
7
cg
C
e
D
E
F
G
H
I1
42
o
2
K
sM
vxiW
L
w
zrlQ
N
R
S
b
4
d
1
T
X
Y
Z
m
n
3
JV
h
k
U
A
f
B
C
D
E
F
G
H
I1
45
2
K
L
N
R
T
X
Y
Z
5
t
0
9
3
6
8
yjO
7
b
4
d
1
q
p
3
J
h
k
U
f
A
B
C
D
E
F
G
H
I
4
2
1
K
L
N
P
R
S
T
V
X
Y
Z
y
g
u
q
p
a
cg
e
sM
vxiW
w
zrlQ
m
n
5
tP
0
9
3
6
8
7
j
u
b
4
d
1
2
a
c
e
o
s
v
w
x
JV
z
3
h
ko
U
m
A
r
fB
n
C
D
E
F
G
H
I1
42
2
K
L
N
R
S
T
X
Y
Z
yjO
q
p
5
t
0
9
3
6
8
7
b
4
d
1
Q
3
J
h
i
k
l
U
A
f
B
C
D
E
F
G
H
I
4
2
1
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
y
g
q
p
yS
u
g
a
cg
e
y
g
o
s
v
w
x
z
q
p
m
r
n
q
p
y
y
g
g
q
p
q
p
yjO
jO
g
u
t
a
ch
e
sM
vxiW
q
p
w
o
zrlQ
0
9
6
8
7
m
n
b
d
Q
j
u
3
J
j
h
a
i
c
e
k
u
l
U
A
o
f
B
s
v
C
w
x
a
D
z
c
e
E
F
G
H
I
4
2
1
K
L
o
M
s
v
N
w
x
z
P
m
r
n
R
S
T
V
W
X
yjO
Y
Z
m
r
n
j
j
u
u
q
p
a
c
e
a
c
e
o
s
v
w
x
s
z
v
w
o
x
z
m
r
n
m
r
n
t
5
0
9
3
6
8
7
b
4
d
1
2
u
a
c
e
J
3
5
t
k
s
v
w
x
o
z
U
A
f
B
C
5
t
D
E
F
G
H
0
9
3
I
6
8
4
2
1
K
m
L
r
n
N
7
P
R
S
0
9
3
6
T
8
V
X
Y
7
Z
b
4
d
1
2
Q
b
4
d
1
2
3
J
Q
5
t
t
5
h
i
k
l
3
J
U
A
f
B
C
h
0
D
9
3
6
i
8
E
F
k
G
0
l
9
3
6
H
8
I
U
7
4
2
1
K
7
L
f
A
M
B
N
C
O
D
P
E
F
R
G
S
H
T
I
4
2
1
V
K
W
L
X
M
Y
N
u
Z
O
b
4
P
d
1
2
Q
b
4
d
1
2
R
S
T
Q
a
cg
V
e
W
X
Y
Z
y
3
J
sM
vxiW
w
zrlQ
3
J
g
h
i
h
k
i
l
k
l
U
A
f
U
B
f
C
A
m
D
B
n
E
C
F
D
G
E
H
F
I
G
4
H
2
1
q
K
I
p
4
L
2
1
M
K
N
L
O
M
P
N
O
P
R
S
T
R
S
V
T
W
X
V
Y
W
Z
X
Y
Z
5
t
0
9
3
6
8
7
b
4
d
1
2
Q
J
3
h
i
k
l
U
A
B
f
C
D
E
F
G
H
I
4
2
1
K
L
M
N
P
R
S
T
V
W
X
Y
Z
5
tP
0
9
3
6
8
7
b
4
d
1
y
g
JV
3
h
ko
j
U
A
u
fB
C
D
q
E
p
F
G
H
I1
42
2
a
c
K
e
L
y
N
g
R
o
S
s
v
T
w
x
z
X
Y
Z
m
r
n
q
p
5
t
0
9
3
6
8
7
j
u
a
c
b
4
e
d
1
2
Q
o
s
v
w
x
z
3
J
j
h
i
k
l
u
m
U
r
n
A
f
B
C
D
a
c
E
e
F
G
H
I
4
2
1
K
L
o
M
s
N
v
w
O
x
z
P
R
S
T
V
W
X
Y
Z
m
r
n
5
t
0
9
3
6
8
7
5
t
4b
d
1
2
0
9
3
6
8
7
3
JV
h
iW
kC
lQ
U
fB
A
D
b
4
d
1
2
E
F
G
H
I1
4
2
K
L
M
N
O
P
3
JV
yjO
R
S
T
g
h
X
iW
Y
kC
Z
lQ
U
A
fB
D
E
F
G
H
I1
p
4
2
K
L
M
N
O
P
R
S
T
X
Y
Z
yjO
g
q
p
yjO
q
p
u
a
c6
e
o
sM
vo
w
xiq
zrlm
m
n
yjO
g
q
p
u
a
cq
e
s3
vP
w
xiU
zrlQ
u
a
n
cg
e
sM
vxiW
w
zrlQ
5
t2
m
n
0
9
3
6
8
7
b
4
d
1
Q
3
h
kd
A
fB
C
D
F
G
H
4
2
1
K
L
N
R
T
V
W
X
Y
Z
u
a
cq
e
sM
vxiW
tP
5
w
zrlQ
m
0
n
9
3
8
tP
5
b
4
d
1
0
9
3
6
8
7
3
JIV
kE
b
4
d
1
U
A
f2
B
D
G
H
I1
4
2
K
L
M
N
JV
3
h
R
S
ko
T
W
X
Y
U
A
Z
fB
C
D
E
F
G
H
I1
4
2
K
L
N
R
S
T
X
Y
Z
5
tP
0
9
3
6
8
7
b
4
d
1
2
3
JV
h
kvo
U
A
fB
D
E
F
G
H
I1
42
2
K
L
N
R
S
T
X
Y
Z
yS
g
yjO
p
q
p
yjIO
g
yjO
p
yjO
q
p
q
p
jJ6
u
a
cq
e
u
sa
vP
w
xiU
z7
a
cg
e
sM
vxiW
m
w
rlm
n
zrlQ
m
n
yjO
u
q
p
cW
e
u
o
sX
vo
xiZ
zrlC
a
cg
e
u
sM
vxiW
5
tw
w
a
cg
zrlQ
e
n
sM
vxiW
w
zrlQ
5
tP
m
0
n
9
3
8
7
m
n
0
9
3
6
8
7
b
4
1
Q
yjS
JIh
b
4
d
1
h
kE
U
A
q
p
3
f0
JV
B
C
D
E
F
G
h
H
ko
4
1
K
L
U
M
N
O
fB
A
C
R
D
S
E
F
G
V
H
I1
4
2
Y
K
L
N
R
S
T
X
Y
Z
5
tE
tP
5
9
3
6
8
7
tP
5
u
0
9
3
6
8
7
a
cg
e
b
4
d
1
2
0
9
3
6
Q
8
7
sM
vxiW
w
zrlQ
b
4
d
1
2
3
JF
h
kP
m
b
4
n
d
1
2
A
3
fT
JV
B
C
D
h
F
G
H
ko
4
2
1
K
L
JV
3
U
M
N
fB
A
h
C
D
R
E
ko
S
F
T
G
H
V
I1
42
W
2
U
X
K
A
fB
Y
L
Z
C
N
D
E
F
G
R
H
S
I1
42
T
2
K
L
X
N
Y
Z
R
S
T
X
yjO
Y
g
Z
u
a
cyg
e
p
o
sa
vP
w
xiU
zh
m
rlm
n
j6
5
tP
u
a
cq
e
0
9
3
6
8
sM
v3
w
o
xi5
7
z7
m
rlm
n
b
4
d
1
2
JV
3
h
ko
U
A
fB
C
D
E
F
G
H
I1
42
2
K
L
N
R
S
T
X
Y
Z
tw
0
9
u
b
4
1
2
Q
a
cq
e
JIg
sM
w
xiW
zrlC
h
kE
U
A
f0
B
C
D
m
E
n
F
G
H
4
1
K
L
M
5
t2
N
O
R
S
V
Y
0
9
3
6
g
8
7
4
p
d
1
2
Q
3
J6
h
kd
A
fB
C
D
F
G
H
4
2
1
K
L
N
yjO
O
R
T
V
W
X
Y
Z
yjO
q
p
yjIg
g
q
p
5
tP
p
0
9
3
8
7
b
4
d
1
2
Q
3
JIV
h
kE
yjO
U
A
fB
D
F
G
H
I1
4 2
2
K
L
N
R
S
T
q
p
X
Y
Z
u
a
cg
e
u
sM
vxiW
w
zrlQ
a
cg
e
sM
vxiW
w
zrlQ
u
m
n
cW
e
m
n
sX
vo
xiZ
o
zrlC
n
yjO
yjO
q
p
u
q
p
a
cg
e
sM
vxiW
w
zrlQ
m
n
5
tP
tP
5
0
9
3
6
8
7
0
9
3
6
8
tw
7
b
4
d
1
9
8
b
4
d
1
3
JV
h
ko
U
A
fB
JV
3
C
D
E
h
b
4
d
1
2
F
G
ko
H
Q
I1
42
2
K
L
U
A
N
fB
C
D
E
R
F
S
G
T
H
3
JO
I1
4
2
K
X
L
Y
Z
N
kP
R
S
T
A
fT
B
C
D
X
Y
F
Z
G
H
4
2
1
K
L
M
N
O
5
tP
R
T
V
W
X
Y
Z
0
u
9
3
6
8
yjS
7
a
cg
e
u
sM
vxiW
w
zrlQ
b
4
d
1
a
cg
e
q
p
m
sM
vxiW
n
w
zrlQ
3
JV
h
ko
U
m
n
A
fB
C
D
E
F
G
H
I1
42
2
K
L
N
R
S
T
X
Y
Z
yjO
g
p
yjO
g
5
tP
yj6
g
q
p
0
5
9
3
6
8
tP
7
q
p
0
9
3
6
8
7
b
4
d
1
2
3
JV
u
b
4
d
1
2
h
a
ko
cq
e
U
fB
A
JV
C
3
s3
D
vP
w
E
xiU
zrlC
F
G
h
H
I1
4 2
2
ko
K
L
U
N
A
fB
R
C
S
D
n
T
E
F
G
H
X
I1
Y
4
2
Z
K
L
N
R
S
T
X
Y
Z
u
a
cy6
e
yjO
g
sM
vo
w
xiW
o
zrlC
m
n
q
p
u
a
cq
e
u
5
t2
sM
vxiW
w
o
zrlQ
a
cq
e
0
sb
9
3
v3
8
w
o
xi5
z7
m
n
7
m
rl8
n
b
4
d
1
Q
3
JI6
h
kE
U
A
f2
B
D
E
F
G
H
Ig
4
2
1
K
L
M
N
P
R
S
tE
T
5
V
W
X
Y
Z
0
9
y
6
8
7
b
d
q
p
Q
y
3
J
g
h
k
u
U
A
f
B
C
a
D
c
e
F
G
5
H
t
q
p
4
2
1
K
L
s
v
N
w
o
x
z
y
P
t
R
5
S
g
T
V
0
9
3
X
6
8
Y
Z
7
m
r
n
0
9
3
6
8
q
p
7
b
4
d
1
2
b
4
d
1
2
Q
3
J
h
k
U
J
f
A
B
C
h
D
E
k
F
G
H
I
4
2
1
K
U
L
A
f
B
N
C
D
P
E
F
G
R
H
S
I
T
K
V
L
M
X
N
Y
O
Z
P
R
S
T
V
W
X
Y
Z
t
5
j
u
a
c
e
0
9
3
6
8
7
s
v
x
o
z
j
m
b
4
r
d
1
n
u
Q
a
c
e
J
h
s
v
o
i
w
x
z
k
l
U
j
f
A
B
C
D
E
u
F
G
m
H
r
n
I
K
L
M
a
c
N
e
P
R
S
T
o
V
s
v
W
w
x
X
z
Y
Z
m
r
n
y
g
y
g
q
p
q
p
5
t
0
9
3
6
8
7
5
t
b
4
d
1
2
Q
0
9
3
6
8
3
J
7
h
i
k
l
5
t
U
A
j
f
B
D
E
F
G
H
b
4
d
1
I
4
2
1
Q
K
L
M
N
0
O
9
3
6
8
P
R
S
T
7
V
W
3
J
X
Y
Z
h
i
k
l
U
A
f
B
C
b
4
d
1
2
D
Q
E
F
G
H
I
4
2
1
K
L
M
N
O
P
3
J
R
S
T
V
h
W
i
X
Y
k
Z
l
U
A
f
B
C
D
E
F
G
H
I
4
2
1
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
j
u
a
j
c
e
u
o
s
v
w
x
z
a
c
e
s
v
w
q
p
x
o
z
m
r
n
y
m
r
n
g
t
q
p
y
g
q
p
i
l
f
I
y
g
5
t
q
p
5
t
0
9
3
6
8
7
0
9
3
6
8
7
b
4
d
1
2
Q
y
g
b
4
d
1
2
3
J
Q
u
h
i
k
l
U
p
a
c
A
e
f
3
J
B
C
D
E
h
F
i
G
k
H
l
I
s
4
v
2
1
w
x
o
K
z
L
U
M
N
A
f
O
B
P
C
D
E
R
F
S
G
T
H
I
4
V
2
1
W
K
X
m
L
Y
r
jj
n
M
Z
N
O
P
u
R
S
T
V
W
X
a
c
Y
e
Z
y
s
v
g
w
x
o
z
m
r
n
p
j
u
a
c
e
s
v
w
x
o
z
m
r
n
j
u
a
c
e
s
v
w
x
o
z
5
y
g
m
r
n
0
9
3
8
7
q
p
j
u
5
b
4
tt
d
1
a
Q
c
e
s
v
w
o
x
z
0
3
J
9
3
6
8
h
7
k
U
m
A
r
n
B
C
D
E
F
G
H
4
b
4
2
1
d
1
2
K
L
M
Q
N
O
P
R
S
5
T
t
V
W
X
Y
3
Z
J
h
ii
k
j
ll
u
0
9
3
U
6
8
A
ff
B
C
7
D
E
F
G
a
H
c
e
II
4
2
1
K
L
M
N
O
P
s
v
w
o
R
x
z
S
T
b
4
d
1
2
V
W
Q
X
Y
Z
m
r
n
J
3
h
iW
kC
lK
tP
5
U
A
fB
D
E
F
G
H
I1
4
2
L
M
N
O
0
P
9
3
6
8
R
yjO
S
7
T
V
X
Y
Z
b
4
d
1
2
q
p
JV
3
tP
5
h
iW
kC
lQ
U
A
fB
D
E
F
G
j6
H
0
9
3
6
I1
8
42
2
K
u
L
7
M
N
O
yjO
R
S
a
c6
T
e
X
Y
Z
o
sa
v3
b
4
w
d
1
2
xi5
z7
q
p
m
rl8
3
n
JV
h
iW
kyC
lQ
U
A
fB
D
tP
E
F
G
H
I1
4
2
K
L
M
N
O
R
S
T
9
X
Y
Z
4
d
1
2
3
JV
iU
lQ
U
fT
A
B
D
E
F
G
H
I1
4
2
K
L
M
N
R
S
T
W
X
Y
Z
u
5
tw
a
cIg
e
sM
vp
w
xiq
zrlQ
0
9
3
6
8
yjO
7
m
n
b
4
d
1
2
q
p
Q
3
u
h
k3
a
cg
e
f0
A
B
C
D
F
sM
vxiW
G
w
H
zrlQ
4
2
1
K
L
M
N
O
R
T
m
V
n
W
Y
Z
yS
g
q
p
5
tvP
yS
g
yjO
0
9
3
8
7
p
q
p
b
4
d
1
3
JzrV
h
ko
t2
5
fB
A
C
D
E
F
G
H
I1
4 2
2
u
K
L
0
9
3
6
8
N
7
a
cg
R
e
T
W
X
Y
Z
sM
vxiW
w
zrlQ
b
4
d
1
2
m
n
3
J6
h
ko
U
A
fB
C
D
E
F
G
H
4
2
1
K
L
N
P
R
S
T
V
X
Y
Z
u
cq
e
sX
vP
o
xU
zrC
m
n
jjJO
u
u
a
c6
e
a
cg
e
5
o
sb
vP
tP
w
xiiU
zh
sM
vxiW
w
zrlQ
m
rllC
0
n
9
3
6
8
m
7
n
b
4
d
1
yjO
JV
3
h
ko
U
A
fB
C
D
E
F
G
H
I1
4 2
q
2
p
K
L
N
R
S
T
X
Y
Z
5
9
8
7
b
4
d
1
2
Q
5
ttkE
5
tP
3
JIIO
h
kE
0
9
3
8
A
0
7
B
9
3
6
8
D
F
7
G
H
4
2
1
K
L
M
N
P
R
S
b
4
d
1
2
T
V
Q
W
b
4
d
1
X
Y
Z
3
JIO
JV
h
3
kE
h
ko
ff0
A
B
C
U
D
A
F
fB
G
C
H
D
E
4
2
1
F
K
G
L
H
M
I1
4m
N
2
K
L
R
N
V
R
W
S
X
T
Y
Z
X
Y
Z
u
a
cg
e
sM
vxiW
w
zrlQ
m
n
5
tP
q
p
0
9
3
6
8
7
b
4
d
1
yjO
3
JV
h
ko
U
A
fB
C
D
E
q
F
p
G
H
I1
4
2
K
L
N
R
S
T
X
Y
Z
yjO
q
p
yjS
jO
u
a
cg
e
sM
vxiW
w
zrlQ
m
n
u
a
cg
e
sM
vxiW
w
zrlQ
m
n
u
a
cg
e
sM
vxiW
w
zrlQ
yjO
m
n
5
tP
u
q
p
a
cg
e
0
9
3
6
8
7
sM
w
xiU
b
4
m
d
n
3
JV
h
ko
U
A
fB
5
tP
C
D
E
F
G
H
I1
4
2
K
L
N
R
0
9
3
6
S
8
T
7
X
Y
Z
b
4
d
1
2
JV
3
h
ko
U
tP
5
A
fB
C
D
E
F
G
H
I1
42
2
K
L
N
0
9
3
6
R
8
S
T
7
X
Y
Z
b
4
d
1
5
tP
3
JV
h
ko
0
9
6
8
7
U
yjO
A
fB
C
D
E
F
G
H
I1
u
42
2
K
L
N
b
d
a
R
cg
e
S
T
X
q
p
Y
Z
sM
vxiW
w
zrlQ
3
JV
h
ko
lQ
m
n
U
A
fB
C
D
E
F
G
H
I1
4 1
2
K
L
N
O
R
T
yjO
W
X
Y
Z
q
p
tP
5
0
9
3
6
8
7
b
4
d
1
2
u
a
cg
e
3
JV
h
sM
vxiW
w
ko
zrlQ
U
A
fB
C
D
E
F
G
H
m
I1
4
n
2
K
L
N
R
S
T
X
Y
Z
u
a
cg
e
sM
vxiW
w
zrlQ
n
5
tP
0
9
3
6
8
7
b
4
d
1
2
JV
3
h
ko
5
U
tP
A
fB
C
D
E
F
G
H
I6
4
2
1
K
L
N
0
9
3
6
8
R
7
S
T
X
Y
Z
yjO
g
b
4
d
1
2
q
p
JV
3
h
ko
U
A
fB
C
D
E
F
G
H
I1
4
2
K
L
N
R
S
T
X
Y
Z
u
a
cq
e
sM
vxiW
w
zrlQ
m
n
5
tP
0
9
3
8
7
b
4
d
1
2
JV
3
h
kvo
U
A
fB
C
D
E
F
G
H
I1
4
2
K
L
N
R
S
T
X
Y
Z
yjO
g
yjO
g
q
p
q
p
yjS
g
q
p
y
g
q
p
u
a
c
e
o
s
v
w
u
x
z
y
g
a
c
e
m
r
n
o
s
v
w
x
z
q
p
m
r
n
u
a
c
e
o
s
v
w
x
z
m
r
n
5
t
j
y
u
g
a
c
e
0
9
3
6
8
5
t
7
o
s
v
w
x
z
q
p
0
9
3
6
8
m
b
4
d
1
2
r
n
7
Q
3
J
b
4
d
1
2
h
i
Q
k
l
U
j
A
f
B
C
u
D
3
J
E
F
G
H
I
4
2
1
h
K
a
i
c
L
e
M
k
N
l
U
P
R
S
A
f
T
B
s
v
C
w
x
o
V
D
z
W
E
X
F
5
Y
G
t
Z
H
I
4
2
1
K
L
M
N
P
m
R
r
n
S
T
V
0
9
3
W
6
8
X
Y
Z
7
b
4
d
1
2
Q
3
J
h
i
k
l
U
A
f
B
C
D
E
y
F
G
H
g
I
4
2
1
K
L
M
N
O
P
5
R
t
S
T
V
W
X
Y
Z
q
p
y
g
0
9
3
6
8
7
q
p
b
4
d
1
2
Q
j3
u
3
J
a
c
e
h
i
k
l
U
5
t
s
o
v
w
x
A
z
f
B
C
D
E
F
G
H
I
4
2
1
K
L
M
N
m
0
O
r
9
3
n
6
8
P
R
7
S
T
V
W
X
Y
Z
b
4
d
1
2
Q
3
J
h
i
k
l
y
g
U
A
f
B
C
D
E
F
G
H
I
4
2
1
K
L
M
N
O
P
R
S
T
p
V
W
X
Y
Z
j
u
a
c
e
5
t
s
v
w
o
x
j
z
u
0
9
3
6
8
a
c
m
e
7
r
n
s
v
o
w
x
z
b
4
d
1
2
Q
m
r
n
J
3
h
i1
k
l4
U
A
f2
B
C
D
E
F
G
H
I
4
2
1
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
y
g
j
q
p
u
a
c
e
s
w
x
o
z
5
t
m
r
n
0
9
3
6
8
7
5
t
b
4
d
1
2
0
9
3
6
8
Q
7
3
J
h
i
k
l
b
4
d
1
2
Q
U
A
f
B
C
D
E
F
G
H
I
4
2
1
K
3
L
J
M
N
O
h
P
i
R
k
S
l
T
V
W
U
X
A
f
Y
B
Z
C
D
E
F
G
H
I
4
2
1
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
5
t
0
9
3
6
8
j
7
u
a
c
e
b
4
d
1
2
Q
o
s
v
w
x
z
J
3
m
r
n
h
i
k
l
U
A
f
B
C
D
E
F
G
H
I
4
2
1
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
y
g
p
5
tP
0
9
3
6
8
7
yS
g
b
4
d
1
2
p
JV
3
h
iW
kC
lQ
U
A
fB
D
E
F
G
H
I1
42
2
K
L
M
N
O
R
S
T
X
Y
Z
yjO
q
p
jjO
u
a
c6
e
sM
o
vo
w
xiiq
zrllC
m
n
u
a
cq
e
sM
vP
w
xU
zrQ
m
n
5
ttE
u
a
cg
e
0
9
6
8
sM
vxiW
w
zrlQ
7
m
n
b
d
Q
JO
3
h
kd
A
ffB
C
D
F
G
H
4
2
1
K
L
N
R
T
V
W
X
Y
Z
5
0
9
3
8
7
b
4
1
2
JIIV
3
h
kE
U
A
5
B
tP
D
F
G
H
4 2
2
1
K
L
N
P
R
0
9
3
S
6
8
T
W
X
7
Y
Z
b
4
d
1
3
JV
h
ko
yjO
U
A
fB
C
D
E
F
G
H
I1
4gp
2
K
L
N
R
q
p
S
T
X
Y
Z
yjO
yjO
q
p
q
p
yjO
u
a
cg
e
q
p
sM
vxiW
w
zrlQ
m
n
u
u
a
cg
e
a
cg
e
sM
vxiW
w
zrlQ
sM
vxiW
w
zrlQ
m
n
m
n
5
tP
0
9
3
6
8
7
b
4
u
d
1
a
cg
e
3
JV
sM
vxiW
w
zrlQ
h
ko
5
tP
U
tP
5
A
fB
C
D
E
m
F
n
G
H
I1
4
2
K
L
0
9
3
6
8
N
0
9
3
6
8
7
R
S
T
7
X
Y
Z
b
4
d
1
b
4
d
1
JV
3
3
h
JV
ko
h
ko
U
A
fB
C
U
D
A
fB
E
F
C
G
D
H
E
I1
42
F
2
G
K
H
L
I1
42
2
N
K
L
N
R
S
T
R
S
T
X
Y
Z
X
Y
Z
tP
5
0
9
3
6
8
7
b
4
d
1
JV
3
h
ko
U
A
fB
C
D
E
F
G
H
I1
4 2
2
K
L
N
R
S
T
X
Y
Z
yjO
q
p
yjO
q
p
u
a
cg
e
sM
vxiW
w
zrlQ
m
n
yjO
q
u
5
tP
a
cg
e
sM
vxiW
w
zrlQ
0
9
3
6
8
7
m
n
b
4
d
1
JV
3
h
ko
U
A
fB
C
D
E
F
G
H
I1
4
2
K
L
N
R
S
T
u
X
Y
Z
a
ch
e
sM
vxiW
w
zrlQ
m
n
5
tP
0
9
3
6
8
7
b
4
d
1
2
3
JV
h
ko
U
A
fB
C
D
E
F
G
H
I1
42
2
K
L
N
R
S
T
X
5
Y
Z
tP
0
9
3
8
7
b
4
d
1
2
3
JV
ko
U
A
fB
C
D
E
F
G
H
I1
4a
2
K
L
N
R
S
T
X
Y
Z
yjO
q
p
yjO
q
p
yjO
q
p
u
a
cg
e
sM
vxiW
w
zrlQ
m
n
yjO
g
u
q
p
a
cg
e
sM
vxiW
w
o
zrlQ
m
n
u
a
cg
e
o
sM
vxiW
w
zrlQ
m
n
t2
5
0
9
3
6
8
7
b
4
d
1
2
t
3
J6
5
h
ko
U
A
fB
C
D
E
F
0
9
3
G
6
8
H
I6
4
7
2
1
K
L
N
P
R
u
S
T
V
X
Y
Z
a
c
b
4
e
d
1
2
s
v
w
x
o
z
3
J
h
k
m
r
n
U
A
f
B
C
5
D
t
E
F
G
H
I1
4
2
K
L
N
P
R
S
T
0
9
3
6
8
V
X
Y
Z
7
yjO
g
b
4
d
1
2
q
p
3
J
h
k
U
A
f
B
C
D
E
F
G
H
I
4
2
1
K
L
N
P
R
S
T
V
X
Y
Z
5
t
0
9
3
6
8
7
b
4
d
1
2
Q
J
3
yjO
h
i
k
l
U
A
f
B
C
D
E
F
G
H
I
4
2
1
K
q
p
L
M
N
P
R
S
T
V
W
X
Y
Z
u
c
e
s
v
o
w
x
z
m
r
n
u
a
cg
e
y
t
5
g
o
sM
vxiW
w
zrlQ
0
9
3
6
8
m
n
7
q
p
b
4
d
1
2
Q
3
J
h
i
k
l
U
A
f
B
C
D
E
F
G
H
I
4
2
1
K
L
M
N
P
R
S
T
V
W
X
Y
Z
5
tP
0
9
3
6
8
7
b
4
d
1
2
J
3
h
j
k
u
U
A
B
f
C
D
E
F
G
a
c
H
e
I
4
2
1
K
L
N
o
s
v
w
x
R
z
S
T
V
X
Y
Z
m
r
n
5
t
0
9
3
8
y
g
7
q
p
b
4
d
1
Q
3
J
h
i
k
l
U
A
f
B
C
D
E
F
G
H
I
4
2
1
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
y
g
y
q
p
g
q
p
y
g
j
u
a
c
e
q
p
s
v
o
w
x
z
m
r
n
j
u
a
c
e
s
v
w
x
o
z
j
u
5
t
m
a
r
n
c
e
o
s
v
w
x
z
0
9
3
6
8
7
m
r
n
j
b
4
d
1
2
u
Q
a
c
e
3
J
h
s
i
v
w
o
x
k
z
l
U
A
f
B
C
D
E
F
G
H
m
I
r
n
4
2
1
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
y
g
t
5
q
p
0
9
3
6
8
7
5
t
b
4
d
1
2
0
9
3
6
8
Q
7
J
3
h
i
k
l
b
4
d
1
2
Q
U
A
B
f
C
D
5
E
F
t
G
H
I
4
2
1
K
y
3
L
J
M
g
N
O
P
h
y
i
R
S
k
T
l
0
g
9
3
V
6
8
W
U
X
Y
A
7
f
Z
B
C
D
E
F
G
H
I
q
p
4
2
1
K
L
M
N
O
P
q
p
R
b
4
d
1
2
S
T
Q
V
W
X
Y
Z
3
J
h
i
k
l
U
A
f
B
C
D
E
F
G
H
I
4
2
1
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
j
u
a
c
e
o
s
v
w
x
z
m
r
n
y
j
g
u
j
a
u
c
e
q
p
a
s
c
v
e
w
o
x
z
o
s
v
w
x
z
m
r
n
m
r
n
y
g
q
p
5
t
0
9
3
6
8
7
b
4
d
1
2
Q
3
J
h
i
k
l
U
A
f
B
C
D
E
F
G
H
I
4
2
1
K
L
M
N
O
t
P
5
R
S
T
V
5
W
X
t
Y
Z
0
9
3
6
8
7
0
9
3
6
8
7
b
4
d
1
2
j
Q
u
b
4
d
1
2
Q
a
c
e
3
J
h
i
k
3
J
s
l
v
o
w
x
z
U
h
A
f
i
B
C
k
D
l
E
F
U
G
H
I
A
f
4
2
1
B
m
K
C
r
n
L
D
M
E
N
F
O
G
P
H
I
R
4
2
1
S
K
T
L
M
V
N
W
O
X
P
Y
j
Z
R
S
T
u
V
W
X
Y
Z
a
c
y
e
g
s
v
o
w
x
z
m
q
p
r
n
5
tP
0
9
3
6
8
7
b
4
d
1
2
5
tP
3
JV
h
iW
kC
lQ
U
A
fB
0
9
3
6
8
D
E
F
G
7
H
I1
4
2
K
L
M
N
O
R
S
T
X
b
4
d
1
2
Y
Z
JV
3
jO
h
iW
u
kC
lQ
U
A
fB
a
ch
e
D
E
F
G
H
I1
42
2
K
L
sM
vxiW
M
w
N
zrlQ
O
R
S
T
X
Y
Z
m
n
5
tP
0
9
3
6
8
7
b
4
d
1
JV
3
ko
U
A
fB
C
D
E
F
G
H
I1
4
2
K
L
N
R
S
T
X
Y
Z
yjO
q
p
yjO
q
p
u
a
cg
e
sM
vxiW
w
zrlQ
yjO
m
n
q
p
yjO
q
p
u
a
cg
e
5
t2
sM
vxiW
w
zrlQ
0
9
3
6
8
m
n
7
b
4
d
1
2
J7
3
h
ko
U
A
fB
C
D
E
F
u
G
H
4
2
1
K
L
N
a
cg
e
P
R
S
T
V
sM
X
vxiW
w
Y
zrlQ
Z
yjO
m
n
q
p
5
tP
u
0
9
3
6
8
a
7
cg
e
sM
vxiW
w
zrlQ
b
4
d
1
2
m
n
3
JV
h
ko
U
A
fB
C
D
E
F
G
H
I1
4
2
K
L
N
R
S
T
tP
5
X
Y
Z
0
9
3
6
8
7
b
4
d
1
3
JV
h
ko
U
A
fB
C
D
E
F
G
H
u
I1
4m
2
K
N
a
cIg
e
R
T
X
Y
sM
vxiW
Z
w
zrlQ
5
tP
m
n
yjO
0
9
3
6
8
7
q
p
b
4
d
1
2
JV
3
h
ko
U
A
fB
C
D
E
F
G
H
I1
42
2
K
L
N
R
S
T
X
Y
Z
tP
0
9
b
4
d
1
JV
3
h
ko
U
A
fB
C
D
E
F
G
H
I1
4
2
K
L
N
R
S
T
u
X
Y
Z
a
cg
e
sM
vxiW
w
zrlQ
m
n
5
tP
0
9
3
6
8
7
b
4
d
1
3
JV
h
ko
U
A
fB
C
D
E
F
G
H
I1
42
2
K
L
N
R
S
T
X
Y
Z
yjO
q
p
yjO
g
q
p
yjS
g
q
p
u
a
cg
e
yj6
g
sM
vxiW
w
zrlQ
m
n
q
p
u
a
cq
e
sM
vxiW
w
o
zrlQ
n
u
a
c6
e
o
sM
vo
w
xiL
zrlQ
m
n
5
tP
0
9
3
6
8
7
tP
b
4
d
1
2
5
3
JV
0
9
3
8
h
ko
7
u
U
A
fB
C
D
a
c6
E
e
F
G
H
yjS
I1
45
2
K
g
L
b
4
d
1
2
sa
v3
N
w
xi5
o
zrl8
R
S
T
X
Y
Z
m
3
JV
n
h
q
p
kE
U
A
fB
C
D
E
F
G
H
I1
4
2
K
L
5
t2
N
R
S
T
X
Y
Z
0
9
3
6
8
7
b
4
d
1
2
J6
h
kd
U
A
fB
C
D
E
F
G
H
I6
K
L
N
O
P
R
S
T
V
W
X
Y
Z
5
tw
0
9
3
6
8
7
b
4
d
1
2
Q
JO
3
h
kd
u
A
fB
C
D
F
G
cW
e
H
4
2
1
K
L
M
N
O
o
sX
P
xU
R
S
T
V
Y
Z
m
n
yjO
q
p
yjO
q
p
y
g
p
y
g
q
p
u
a
cg
e
sM
vxiW
w
zrlQ
m
n
u
a
cg
e
yjO
sM
vxiW
w
zrlQ
q
p
m
n
j
u
a
c
e
s
v
w
x
o
z
5
tP
m
r
n
0
9
3
6
8
j
5
tvP
7
u
a
c
e
0
9
3
8
b
4
d
1
s
v
w
7
x
z
JV
3
m
r
n
h
b
4
1
2
ko
U
A
fB
C
D
E
F
G
JIzrV
H
3
I1
4
2
K
L
h
iU
N
kE
lQ
R
S
T
A
fB
C
X
5
D
Y
E
tP
Z
F
G
H
I1
4
2
K
L
M
N
R
T
0
9
3
6
8
W
X
7
Y
Z
b
4
d
1
2
t
5
JV
3
h
u
ko
U
A
0
fB
a
9
3
cg
8
e
C
D
E
7
F
G
H
I1
42
2
sM
K
vxiW
w
L
zrlQ
N
R
S
T
b
4
d
1
X
Y
Q
Z
m
n
3
5
J
t
h
i
k
l
U
A
f
B
C
D
0
9
3
F
8
G
H
4
2
K
7
L
M
N
O
P
R
S
T
V
W
X
Y
Z
b
4
1
2
Q
3
J
h
i
k
l
U
A
f
B
C
D
E
F
G
H
I
4
2
1
K
L
M
N
O
y
P
g
R
S
T
V
W
X
Y
Z
q
p
tP
0
9
3
6
8
7
b
4
d
1
2
3
JV
h
ko
U
A
fB
C
D
E
F
G
H
I1
4
2
K
L
N
R
S
T
X
Y
Z
j
u
a
ch
e
yjO
sM
vxiW
w
zrlQ
m
n
q
p
5
tP
0
9
3
6
8
yjO
7
b
4
d
1
q
p
3
JV
ko
u
U
A
fB
C
D
E
a
F
cg
e
G
H
I1
4I1
2
K
L
N
O
sM
vxiW
w
zrlQ
R
S
T
X
Y
Z
m
n
5
tP
u
a
cg
e
0
9
3
6
8
7
sM
vxiW
w
zrlQ
m
b
4
d
1
n
3
JV
h
ko
U
A
fB
C
D
E
F
G
H
I1
4 2
2
K
L
N
R
S
T
X
Y
Z
tP
5
0
9
3
6
8
7
b
4
d
1
2
JV
3
h
ko
U
A
fB
C
D
E
F
G
H
I1
42
2
K
L
N
R
S
T
X
Y
Z
yjO
q
p
u
a
cg
e
sM
vxiW
w
zrlQ
yjO
m
n
q
p
5
tP
yjO
0
9
6
8
7
q
p
b
d
JV
3
h
ko
U
A
fB
C
D
E
F
G
H
I1
4
2
K
L
u
N
R
S
yjO
T
a
cg
e
X
Y
Z
sM
vxiW
w
zrlQ
q
p
m
n
u
a
cg
e
sM
vxiW
w
zrlQ
5
tP
m
n
0
9
3
6
8
7
b
4
d
1
2
JV
3
u
h
ko
U
a
cg
e
A
fB
C
D
E
F
G
H
I1
sM
vxiW
4
w
2
K
zrlQ
L
N
R
S
T
X
m
Y
n
Z
5
tP
0
9
3
6
8
7
b
4
d
1
3
JV
h
ko
U
A
fB
C
D
E
F
G
H
I1
4
2
K
tP
L
5
yjO
N
R
S
T
X
Y
Z
0
9
3
6
8
7
q
p
b
4
d
1
2
3
JV
h
ko
U
A
fB
C
D
E
F
G
H
I1
4m
2
K
L
N
R
S
T
X
Y
Z
u
a
cg
e
sM
vxiW
w
zrlQ
m
n
5
tP
0
9
3
6
8
7
b
4
d
1
2
3
JV
h
ko
U
A
fB
C
D
E
F
G
H
I1
42
2
K
L
N
R
S
T
X
Y
Z
yjO
q
p
u
a
cg
e
sM
vxiW
w
zrlQ
n
yjO
q
p
5
tP
0
9
3
6
8
7
b
4
d
1
2
3
JV
h
ko
U
A
fB
C
D
E
F
G
H
I1
4
2
K
L
N
R
S
T
X
Y
Z
yjO
q
p
u
a
cIg
e
sM
vxiW
w
zrlQ
o
m
n
yjO
q
p
u
a
cg
e
t
sM
5
vxiW
w
zrlQ
m
n
0
9
3
6
8
7
b
4
d
1
2
JV
3
h
k
U
A
f
B
C
D
E
F
G
H
I1
4
2
K
L
N
P
R
S
T
u
X
Y
Z
a
cg
e
s
v
o
w
x
z
m
rgp
n
5
tP
0
9
3
6
8
7
b
4
d
1
2
3
JV
h
ko
U
A
fB
C
D
E
F
G
H
I1
4
2
K
L
N
R
S
T
X
Y
Z
5
tq
0
9
3
6
8
7
yjO
g
b
4
d
1
2
Q
q
p
J
3
h
ia
k
le
U
A
fm
B
C
D
E
F
G
H
4
2
1
K
L
M
N
P
R
S
T
V
W
X
Y
Z
u
a
c
e
o
s
v
w
x
z
m
r
n
5
t
0
9
3
6
8
7
b
4
d
1
2
Q
3
J
h
i
k
l
U
A
f
B
C
D
E
F
G
H
I
4
2
1
K
L
M
N
P
R
S
T
V
W
X
Y
Z
y
g
q
p
y
y
g
q
p
j
u
a
c
e
s
o
v
w
x
z
m
r
n
j
u
c
j
5
t
u
s
v
w
x
z
o
a
c
e
0
9
3
6
8
o
s
v
w
x
r
n
z
7
m
r
n
b
4
d
1
2
Q
J
3
h
i
k
l
U
A
f
B
C
D
E
F
G
H
I
4
2
1
K
L
M
N
O
P
R
S
T
V
W
X
Y
Z
y
t
5
y
tP
g
0
9
3
6
8
7
0
9
p
b
4
d
1
2
Q
4
d
1
2
JF
3
h
iW
kcC
lC
A
3
fB
JIV
D
F
G
H
iU
4
2
lQ
K
L
M
U
N
O
A
f2
B
R
yjO
D
E
T
F
G
V
H
I1
X
4
2
Y
K
Z
L
M
N
R
S
T
W
X
Y
q
p
Z
jS
sM
vP
w
xiU
zrlN
j6
u
m
a
c6
e
o
sM
v3
w
xi5
z7
m
rl8
n
u
a
cg
e
sM
vxiW
w
zrlQ
m
n
5
tkvP
0
9
3
6
8
7
JI1
kE
b
4
U
d
1
2
Q
D
H
3
R
T
h
kd
W
Z
A
fB
C
D
E
F
5
G
H
tP
IO
4
1
K
L
N
O
R
V
0
W
9
3
6
8
X
Y
7
b
4
d
1
2
3
JV
h
ko
U
A
fB
C
D
E
F
G
H
I1
4m
2
K
L
N
R
S
T
X
Y
Z
yS
g
q
p
jJzh
u
a
cq
e
o
sb
w
xU
m
rC
n
Q
3
JO
h
iZ
lC
A
fT
B
D
F
G
H
4
2
1
K
L
M
N
P
R
S
T
V
W
X
Y
Z
5
tkE
0
9
3
8
7
b
4
1
2
yjO
q
p
u
a
cg
e
sM
vxiW
w
zrlQ
n
5
tP
0
9
3
6
8
7
b
4
d
1
2
3
JV
h
ko
U
A
fB
C
D
E
F
G
H
I1
4
2
K
L
N
R
S
T
X
Y
Z
yjO
q
p
u
a
cg
e
sM
vxiW
w
zrlQ
m
n
tP
5
0
9
3
6
8
7
b
4
d
1
2
3
JV
h
ko
U
A
fB
C
D
E
F
G
H
I2
4
2
1
K
L
N
R
S
T
X
Y
Z
yjO
q
p
u
a
cg
e
sM
vxiW
w
zrlQ
m
n
5
tP
0
9
3
6
8
7
b
4
d
1
3
JV
h
ko
U
A
fB
C
D
E
F
G
H
I1
4
2
K
L
N
R
S
T
X
Y
Z
yj6
q
p
u
a
cg
e
sM
v4
w
xi5
z7
m
rlm
n
5
tP
0
9
3
6
8
7
b
4
d
1
2
Q
3
h
ko
A
fB
C
D
E
F
G
H
IC
4
2
1
K
L
N
O
R
T
V
W
X
Y
Z
yjIO
q
p
u
cq
e
sX
vP
o
xiU
zrlQ
n
tP
9
8
b
1
2
3
JIV
kE
U
A
fT
B
D
G
H
I1
4
2
K
L
M
N
R
S
T
W
X
Y
Z
yS
g
p
jJg
u
yS
a
c6
e
g
o
sa
vd
w
xiU
zh
p
m
rlC
n
5
tw
0
9
3
6
8
7
b
4
d
1
2
Q
3
jJO
h
u
k3
A
f0
B
a
cq
C
e
D
F
G
H
4
o
1
2
K
sM
L
vP
w
M
xiU
zrlQ
N
O
R
V
W
Y
Z
m
n
5
tE
0
9
3
8
7
b
4
d
1
2
3
JF
h
kE
A
fB
D
F
G
H
4
2
1
K
L
N
R
S
T
V
W
X
Y
Z
0
100
200
300
Figura 4.20: Efecto de la variable latitud en el modelo (4.4), al que se le aplicará el Kriging.
6
4
2
0
−2
Residuos de la regresión funcional
−4
−6
0
100
200
300
10
5
−5
0
Temperatura (º C)
15
20
25
Figura 4.21: Residuos del modelo (4.4), al que se le aplicará el Kriging.
0
100
200
300
Día
Figura 4.22: Datos suavizados, predicción en Santiago y datos reales en Santiago.
1.0
0.8
0.6
0.4
0.0
0.2
Parameters
0
100
200
300
Day
Figura 4.23: Parámetros funcionales estimados.
0
−5
Residuos (ºC)
5
Residuos
Media
Desviación típica
0
100
200
300
Día
Figura 4.24: Residuos, media y desviación típica con la técnica 2 (solución basada en bases de
funciones).
25
10
5
−5
0
Temperatura (ºC)
15
20
Suavizado
Predicción
Dato real
0
100
200
300
Día
Figura 4.25: Datos suavizados, predicción en Santiago y datos reales en Santiago.
Residuos calculados con dato real
0
−10
−5
Residuos (ºC)
5
10
Residuos
Media
Desviación típica
0
100
200
300
Día
Figura 4.26: Residuos, media y desviación típica obtenidos al aplicar FKTM.
Pontenova (A)
2e−04
1e−04
0e+00
−1e−04
−2e−04
100
100
200
v
300
300
200
t
t
300
200
etro
m
Pará
etro
m
Pará
2e−04
1e−04
0e+00
−1e−04
−2e−04
Monte Aloia
100
100
200
v
300
Figura 4.27: Parámetros funcionales estimados en A Pontenova y Monte Aloia.
Mapica
Sergude
0.06
0.04
0.02
0.00
etro
300
200
t
−1e−03
100
100
200
v
300
300
200
t
−5e−04
etro
m
Pará
m
Pará
0e+00
100
100
200
v
300
Figura 4.28: Parámetros funcionales estimados en Malpica y Sergude.
Apéndice A
Histogramas y boxplots de la
Temperatura de Galicia año 2009
99
0
10
20
0
10
0
60
Punta Candieira
Frequency
0 50
0 60
Frequency
Sergude
20
5
15
25
Río do Sol
Muralla
Malpica
Melide
10
10
80
0
50
0
20
5
15
0
10
20
Olas
Marco da Curra
Serra da Faladoira
Corrubedo
10
0
10
0 50
50
0
20
20
0
10
0 60
Temp
Frequency
Temp
Frequency
Temp
Frequency
Temp
0 50
0
0
20
0 40
Temp
Frequency
Temp
Frequency
Temp
Frequency
Temp
0
20
5
15
Fontecada
O Xipro
Pontenova (A)
Fragavella
10
20
Temp
0
10 20
Temp
50
0
0 50
0
0
10
20
0 50
Temp
Frequency
Temp
Frequency
Temp
Frequency
Temp
0 40
Frequency
15
0 50
Frequency
5
Frequency
Mabegondo
Frequency
80
0
Frequency
Coruña Dique
−5
Temp
Figura A.1: Histogramas de la Temperatura de Galicia año 2009.
5
15
Temp
0
10
−10
5
40
0
0 80
20
Courel
Frequency
Ancares
Frequency
60
0
15 25
20
0
10 20
Temp
Foz
Corno do Boi
Sambreixo
Guitiriz
10
0
10 20
0
10
0
0 50
50
0
20
50
Temp
Frequency
Temp
Frequency
Temp
Frequency
0
20
0
10 20
Campus Lugo
Marroxo
Ventosa
Pol
10
20
0
0 40
50
0
60
0
10 20
−5
5
0 40
Temp
Frequency
Temp
Frequency
Temp
Frequency
Temp
0
15 25
0
10 20
Portomarín
Conchada
Pedro Murias
Abradelo
10
20
Temp
0
10
Temp
20
0 60
40
50
0
0
5
0 40
Temp
Frequency
Temp
Frequency
Temp
Frequency
Temp
0
Frequency
5
0 50
Frequency
−5
Frequency
Burela
Frequency
0 40
Frequency
Bóveda
15
Temp
Figura A.2: Histogramas de la Temperatura de Galicia año 2009.
0
10
Temp
20
0
10
0
−5
5
50
0
50
0
10 20
Monte Medo
Frequency
Baltar
Frequency
50
0
20
15
−5
5
15 25
Lardeira
Gandarela
Entrimo
Alto do Rodicio
5
20
0
10
50
0
50
0
80
−10
25
0
0 40
Temp
Frequency
Temp
Frequency
Temp
Frequency
Temp
0
Frequency
Amiudal
Frequency
0 50
Frequency
Penedo do Galo
10 20
−5
5
15 25
Xurés
Serra do Eixe
Ourense−Ciencias
15
−5
5
15
−5
5
0
40
0
0 80
80
0
5
15
0
10 20
Petarelas (As)
San Xoán de Río
Verín
Viana do Bolo
10
25
Temp
−5
5
15
Temp
−5
10
25
0
80
0
40
0
80
−5
40
Temp
Frequency
Temp
Frequency
Temp
Frequency
Temp
0
Frequency
−10
50
Cabeza de Manzaneda
Frequency
Temp
Frequency
Temp
Frequency
Temp
Frequency
Temp
−5
Temp
Figura A.3: Histogramas de la Temperatura de Galicia año 2009.
5
15 25
Temp
5
0
15
0 15
0
40
Fornelos de Montes
Frequency
50
0
Frequency
0 40
20
Pereira
0
20
Mouriscade
Queimadelos
Castro Vicaludo
Castrove
Lourizán
0
20
50
0
0 50
0 40
50
15
0 15
0 50
Temp
Frequency
Temp
Frequency
Temp
Frequency
Temp
Frequency
Temp
0
5 20
5
20
O Viso
Serra do Faro
Sanxenxo
Monte Aloia
Illas Cíes
15
5
50
0
80
0
50
0
0 50
−5
20
0 15
Vigo−IIMarinas
Vigo−Campus
Corón
Santiago
20
Temp
0
20
Temp
5
20
Temp
0
60
0
50
0
0 60
5
60
Temp
Frequency
Temp
Frequency
Temp
Frequency
Temp
0
15
Temp
Figura A.4: Histogramas de la Temperatura de Galicia año 2009.
0 60
Temp
Frequency
Temp
Frequency
Temp
Frequency
Temp
Frequency
Temp
5 20
Frequency
Rebordelo
Frequency
0 50
Frequency
20
0
Frequency
5
Frequency
Caldas de Reis
0 60
Frequency
Ons
5
20
Temp
−10
0
10
20
Box−Plot de la temperatura Galicia año 2009
Coruña Dique
Fontecada
Foz
Pol
Baltar
Xurés
Ons
Castrove
Figura A.5: Boxplot de la Temperatura de Galicia año 2009.
Corón
Bibliografía
[1] Alias Abdul-Rahman and Morakot Pilouk. Spatial Data Modelling for 3D GIS. SpringerVerlag, 2008.
[2] Maria João Pereira Amílcar Soares and Roussos Dimitrakopoulos, editors. geoENV VI
GEOSTATISTICS FOR ENVIRONMENTAL APPLICATIONS. Springer-Verlag, 2008. Proceedings of the Sixth European Conference on Geostatistics for Environmental Applications.
[3] Pebesma Edzer J. Gómez-Rubio Virgilio Bivand, Roger S. Applied Spatial Data Analysis
with R. Use R. Springer-Verlag, 2008.
[4] Bogaert. Comparison of kriging techniques in a space-time context. Mathematical Geology, 28(1):73–86, 1996.
[5] George Christakos. Modern Spatiotemporal Geostatistics. Studies in Mathematical Geology. Oxford University Press, Inc, 2000.
[6] Noel A. C. Cressie. Statistics for Spatial Data. Probability and Statistics. Wiley, 1993.
[7] Claude Mantéa David Nerini, Pascal Monestiez. Cokriging for spatial functional data.
Journal of Multivariate Analysis, Elsevier, 101:409–418, 2010.
[8] Frédéric Ferraty and Philippe Vieu. Nonparametric Functional Data Analysis Theory and
Practice. Statistics. Springer-Verlag, 2006.
[9] Matheron G. The theory of regionalized variables and its applications. 1971.
[10] Ramón Giraldo.
cionales.
Análisis exploratorio de variables regionalizadas con métodos fun-
[11] M. Goulard and M. Voltz. Geostatistical interpolation of curves: A case study un soil
science. Academic Press, 2:805–816, 1993.
[12] T. Hastie and R. Tibshiran. Varying-coefficient models. Journal of the Royal Statistical
Society Series B, 55:755–796, 1993.
[13] J. Ver Hoef and N. Cressie. Multivariable spatial prediction. mathematical geology. 25
(2):219–240, 1993.
105
106
BIBLIOGRAFÍA
[14] E. Isaaks and M. Srivastava. Applied geostatistics. Oxford University Press, 1987.
[15] R. Flanagan J. O. Ramsay, X. Wang. A functional data analysis of the pinch force of human
fingers. The Royal Statistical Society, 44(1):17–39, 1995.
[16] Myers. Matrix formulation of co-kriging. Mathematical Geology, 14 (3):249–257, 1982.
[17] D. Nerini and P. Monestiez. A cokriging method for spatial functional data with applications in oceanology. 2008.
[18] C. Comas P. Delicado, R. Giraldo and J. Mateu. Statistics for spatial functional data.
Environmetrics, 2009.
[19] C. Comas P. Delicado, R. Giraldo and J. Mateu. Statistics for spatial functional data: some
recent contributions. Environmetrics, DOI: 10.1002/env.1003, 2009.
[20] Paulo J. Rebeiro Jr. Peter J. Diggle. Model-based Geostatistics. Statatistics. SpringerVerlag, 2007.
[21] P. Delicado R. Giraldo and J. Mateu. Geostatistics for functional data: An ordinary kriging
approach. Environmental and Ecological Statistics, 2007.
[22] Pedro Delicado Ramón Giraldo and Jorge Mateu. Continuous time-varying kriging for spatial prediction of functional data: An environmental application. Journal of Agricultural,
Biological and Environmental Statistics, 2008.
[23] Ramsay and Silverman. Functional data analysis. Springer, 1997.
[24] J. O. Ramsay and C.J. Dalzell. Some tools for functional data analysis. The Royal Statistical Society, 53(3):539–572, 1991.
[25] James O. Ramsay and Bernard W. Silverman. Applied Functional Data Analysis: Methods
and Case Studies. Springer-Verlag, 2002.
[26] J.O. Ramsay and B.W. Silverman. Functional Data Analysis. Statistics. Springer-Verlag,
2nd edition, 2005.
[27] J. M. Yarus T. C. Coburn and R. L. Chambers, editors. Stochastic Modeling and Geostatistics: Principles, Methods,and Case Studies, volume II. 2007.
[28] H. Wackernagel. Multivariable geostatistics: An introduction with applications. Springer
Verlag, 1995.
[29] Hans Wackrenagel. Multivariate Geostatistics. Springer-Verlag, 2nd edition, 1998.
[30] Larry Wasserman. All of Nonparametric Statistics. Springer, 2006.
Glosario
Z(u)
u
Rd
2γ(·)
γ(·)
khk
Γ (·)
γ0
λα
Ci,j (h)
hX(t), Y (t)i
kX(t)k
L2 (T )
ξm ⊥ξk
F DA
M oM
CV
GCV
LLR
Km
F CV
M ISE
R − Squared
W
BLU P
LM C
Proceso aleatorio, 6
Localización, 7
Espacio Euclídeo d-dimensional, 7
Variograma, 9
Semivariograma, 9
Longitud, 9
Función Gamma, 12
Semivariograma isotrópico, 13
Ponderaciones de los valores originales, 22
Covariograma cruzado, 29
Producto interior, 39
Norma, 40
Es el espacio de las funciones de cuadrado integrable, 40
ξm y ξk son ortogonales, 41
Análisis de datos funcionales, 41
Modelo clásico de los momentos, 58
Métodos de validación cruzada, 61
Métodos de validación cruzada generalizada, 61
Regresión Local Lineal, 61
Kilómetros, 62
Validación cruzada funcional, 64
Error cuadrático medio integrado, 64
Coeficiente determinación, 65
Matriz de Gram, 77
Mejor predictor lineal insesgado, 78
Modelo linal de corregionalización, 79
107
Índice
Modelo Exponencial, 11
Modelo Gaussiano, 11
Modelo lineal, 11
Modelo potencial, 11
análisis de datos funcionales, 1, 40
B-spline, 38
base, 38
Cauchy-Schwarz, 8, 30
Cokriging ordinario, 34
Cokriging Simple, 31
componentes principales, 41
Condición de insesgadez, 36
condición de insesgadez, 20
covariograma, 8
nugget, 10
Nugget effect, 10
penalización, 42
Pepita, 10
point processes data, 5, 6
proceso estocástico, 7
proceso estrictamente estacionario, 8
procesos puntuales, 5, 6
pseudosemivariograma cruzado, 30
error cuadrático medio, 24, 55
estacionariamente débil, 8
estacionario de segundo orden, 8
Estrictamente Estacionario, 8
rejilla, 5
FDA, 41
Fourier, 38
semivariograma, 9
semivariogramas cruzados, 30
georreferenciados, 5, 6
Geostadística, 5
umbral, 12
Validación Cruzada, 24
Variable regionalizada, 7
variograma, 9
Hole, 11
intervalos de confianza, 83
Wavelet, 38
kriging funcional, 53
Kriging Ordinario, 21
kriging ordinario, 34, 55
Kriging Simple, 20
Kriging universal, 25
lattice data, 5, 6
Matérn, 12
Modelo esférico, 11
108