CONJUNTOS NUMÉRICO numeros racionales 1

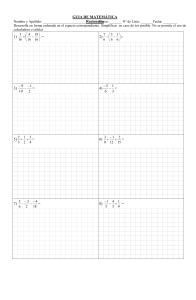
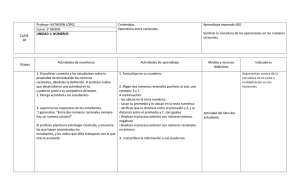
CONJUNTOS NUMÉRICOS. TIPOS DE NÚMEROS Y APLICACIÓN
Introducción
¿Cómo sería un mundo sin números?
A lo largo de cinco milenios, han ido surgiendo las diferentes familias de números para resolver problemas
que exigían cada vez mayor creatividad: números naturales, números enteros, números racionales, etc.
El desarrollo numérico ha permitido contar, ordenar, situar, comparar, repartir, calcular, codificar… y
contar con un lenguaje que hoy es esencial, tanto para la vida cotidiana como para el desarrollo de la
ciencia y la técnica.
Los conjuntos numéricos están muy presentes en nuestra vida cotidiana. El porcentaje de una cantidad, la
longitud de una piscina, etc.
¿Para qué se usan los conjuntos numéricos?
Los conjuntos numéricos se utilizan para separar los números en distintas clases que tienen propiedades
similares.
Debemos ver esto simplemente como una forma de organización, en la que dado cualquier número
decimos que este número pertenece al conjunto tal.
Conjuntos numéricos
Los conjuntos numéricos básicos son los siguientes:
Naturales – ℕ
Enteros – ℤ
Racionales – ℚ
Cada conjunto más general va englobando al conjunto anterior es decir que por ejemplo todos los números
naturales son enteros, pero no todos los números enteros son naturales.
Conjunto de Números Naturales (ℕ)
Este conjuntos está compuesto por los números {0,1,2,3,…} (los puntos suspensivos indican que la
enumeración continúa indefinidamente), con estos números es posible contar y sumar pero muchas otras
operaciones no son factibles (el conjunto de estos números se expresa con una ℕ mayúscula).
Conjunto de Números Enteros (ℤ)
Si a los números naturales agregamos los números negativos sin parte decimal obtenemos el conjunto de
los números enteros. {…,-3,-2,-1,0,1,2,3,…}. Los cuales permiten realizar operaciones de sustracción,
representar temperaturas bajo cero con valores negativos de grados centígrados, pero otras tampoco
resultan posibles. De esta manera, las limitaciones de los números naturales y de los enteros es lo que crea
la necesidad de inventar otros números, los números racionales.
EL CONJUNTO DE LOS NÚMEROS RACIONALES
En sentido amplio, se llaman números racionales a todo número que puede representarse como el
cociente de dos enteros con denominador distinto de cero (una fracción común). El término «racional»
alude a «ración» o «parte de un todo», y no al pensamiento o actitud racional.
En sentido estricto, número racional es el conjunto de todas las fracciones equivalentes a una dada; de
todas ellas, se toma como representante canónico del dicho número racional a la fracción irreducible, la de
términos más sencillos.
El conjunto de los números racionales se designa por la letra ℚ, y corresponde a la definición de un
número entero dividido por otro.
 a

ℚ= 
/ a  b  Z y b  0  a: numerador; b: denominador
 b

𝑎
ℚ es el conjunto de los números de la forma 𝑏 tal que a y b pertenecen al conjunto de los números enteros
y además b es diferente de cero.
Ejemplos:
3
I.
; fracción irreductible
4
II.
III.
3
15
6
2
1
=5 ; fracción reductible
= 3; número entero
Los números racionales sirven en gran medida para poder comparar y explicar algo de manera concreta.
Ejemplos:
a) 4 de 28 alumnos del curso de matemática hablan, generan sonidos extraños, gritan y se ríen a
4
carcajadas cuando el profesor está explicando, interrumpiendo y generando desorden en clase. 28
b) 7 de 28 alumnos del curso de matemática no copian o copian muy poco la clase, prefieren jugar y
7
estar conversando a pesar de que se les indica que copien. 28
c) 2 de 28 alumnos del curso de matemática solo quieren realizar sus gráficos o historietas desde el
2
inicio de clase. 28
d) 3 de 28 alumnos del curso de matemática faltan continuamente a clases de matemáticas y no se
preocupan lo que se avanzó o averigua de prácticas o evaluaciones.
e) 9 de 28 alumnos del curso de matemática necesitan que el profesor este muy pendiente de ellos
monitoreando sus acciones para que presten atención e intenten resolver unos ejercicios de
aplicación.
f) 10 de 28 alumnos del curso de matemática vienen motivados y prestan atención adecuada a la
explicación de la teoría, propiedades o resolución de ejercicios y problemas que el profesor realiza
en clase.
g) 3 de 28 alumnos del curso de matemática ingresan continuamente minutos después que ya culmino
el recreo y terminan de comer en clase.
h) 3 de 28 alumnos del curso de matemática se equivocan continuamente en operaciones sencillas por
no revisar sus operaciones antes de entregar sus evaluaciones a pesar de que el profesor les indica
que lo hagan.
i) 6 de 28 alumnos del curso de matemática tienen una letra, números y orden al revisar sus
evaluaciones.
j) 9 de 28 alumnos del curso de matemática entregan la tarea completa, los demás solo presentan
excusas para no hacerla.
Crear 4 ejemplos más ocurridos en clase donde se pueda emplear números racionales.
Los números racionales (1/2, 1/3, 1/4...) permiten fraccionar un número, es decir, dividirlo numéricamente.
Ejemplo: Sea la fracción:
4
 Esto quiere decir que el entero se ha dividido en 7
7
El numerador: indica el número de partes iguales que se toman de la unidad.
El denominador: indica el número de partes iguales en que se divide la unidad.
¿Cuál es la función de los números racionales en la vida cotidiana?
Los números racionales se encuentran en la vida cotidiana cuando se tiene que dividir cosas en partes
iguales, a la hora de representar una medida y para expresar los números en decimales exactos. Algunos
ejemplos de cómo se usan los números racionales en la cotidianidad son:
En las compras: Deme 3/4 kilo de tomate, por favor.
Al hablar con alguien: Te llamo en 1/2 hora, o He traído tres botellas de agua de 1 litro y medio.
Al hacer una actividad o deporte: Corrimos 3 kilómetros y medio.
Cuando tenemos que calcular porciones: Compramos una pizza de 14 pedazos y para repartir entre 12
personas, hay que sacar la cuenta para darle a cada uno un pedazo de la pizza, de esta forma se está
utilizando 12/14 y eso es un número racional.
Otro ejemplo sería con el pliego de papel: 1/8 de papel es 1 parte que ha sido cortado en 8 partes, si
usáramos las 8 partes, entonces sería 8/8 que es el pliego completo.
Representación de Q en la recta numérica.
Sabemos que el conjunto Z se representa en la recta numérica así:
-3
-2
-1
0
1
2
3
También las fracciones pueden ser ubicadas en la recta numérica, sea por las divisiones sucesivas (de
mitad en mitad) o por el uso de las escuadras y el compás para dividir un segmento de recta.
-1
-3
4
-1
2
-1
4
1
4
0
-4
5
-3
5
-2
5
-1
5
-8
10
-6
10
-4
10
-2
10
1
5
2
10
1
2
2
5
4
10
3
4
3
5
6
10
1
4
5
8
10
De la gráfica se define que:
I. Las subdivisiones de la recta numérica son infinitas.
II. Entre dos números racionales siempre será posible hallar al menos otro número racional.
III. No es posible hallar el siguiente o el anterior valor de un número racional cualesquiera.
IV. Un mismo punto en la recta numérica puede ser representado por varias fracciones que son
equivalentes entre sí. Por lo que se afirma que el conjunto de dichas fracciones (clases de equivalencia)
representa al Número Racional respectivo.
Densidad en el conjunto de los números racionales.
Esta propiedad de densidad en Q, no la poseen los conjuntos N y Z.
"Dados dos números racionales diferentes, siempre se puede encontrar otro número racional cuyo
valor esté comprendido entre ambos"
En forma general:
Entre dos números racionales existen infinitos números racionales.
RELACIÓN DE ORDEN DE UN NÚMERO FRACCIONARIO (>, <, =)
𝑎
𝑐
𝑎
𝑐
A. Dados dos números fraccionarios tales como 𝑏 y 𝑑 , podemos afirmar que: 𝑏 = 𝑑
b.c
Ejemplos:
8 4

6
3
•
ya que: 8 × 3 = 6 × 4
6 10

•3 5
ya que: 6 × 5 = 3 × 10
si se cumple: a.d =
5 30

• 2 12 ya que: 5 × 12 = 2 × 30
B. Dados dos números fraccionarios, podemos determinar que uno es mayor o menor que otro, usando
la regla de los productos cruzados.
Ejemplos:
8 × 11 > 9 × 7
•
11
9
7
8
entonces:
11
>
9
7
8
4×6<8×7
•
4
8
7
6
entonces:
4
<
8
7
6
12 × 4 < 8 × 20
•
1.
12
8
20
4
entonces:
12
20
<
8
4
¡LISTOS, A TRABAJAR!
Completar con un "Sí" o con un "No" según la pertenencia o no.
3
N
Z
Q
1
2
-2
-
3
5
0
21
3
-
16
4
1
8
-4
-
2
3
2.
Compara las siguientes fracciones utilizando los signos ">", "<" o "=".
a.
b.
c.
d.
e.
f.
3.
3 5

4 6
porque: 3 × 6 < 4 × 5
9
3
8
12
7
8
8
10
8
6
4
3
5
25
2
60
6
3
5
15
_______________________________________
_______________________________________
_______________________________________
_______________________________________
_______________________________________
Completar con ">", "<" o "=" según corresponda:
1
2
3
3
6
9
4
5
2
4
6
8
7
4
3
4
2
5
7
8
2
3
1.
DEMUESTRA LO APRENDIDO
Completar con un "Sí" o con un "No" según la pertenencia o no pertenencia.
3
5
6
-
2
3
0
-2
7
9
-
4
2
9
3
5
4
-
1
6
N
Z
Q
2.
Compara las siguientes fracciones utilizando los signos ">", "<" o "=":
a.
d.
3.
8
12
12
9
2
3
5
2
b.
5
7
e.
3
3
13
17
17
c.
5
1
4
f.
5
3
7
28
5
20
Completar con ">", "<" o "=" según corresponda:
4
18
2
5
4
6
3
7
2
9
1
5
3
2
3
6
5
2
7
3
9
2