Exámenes Ingenieria Industrial. Mecánica

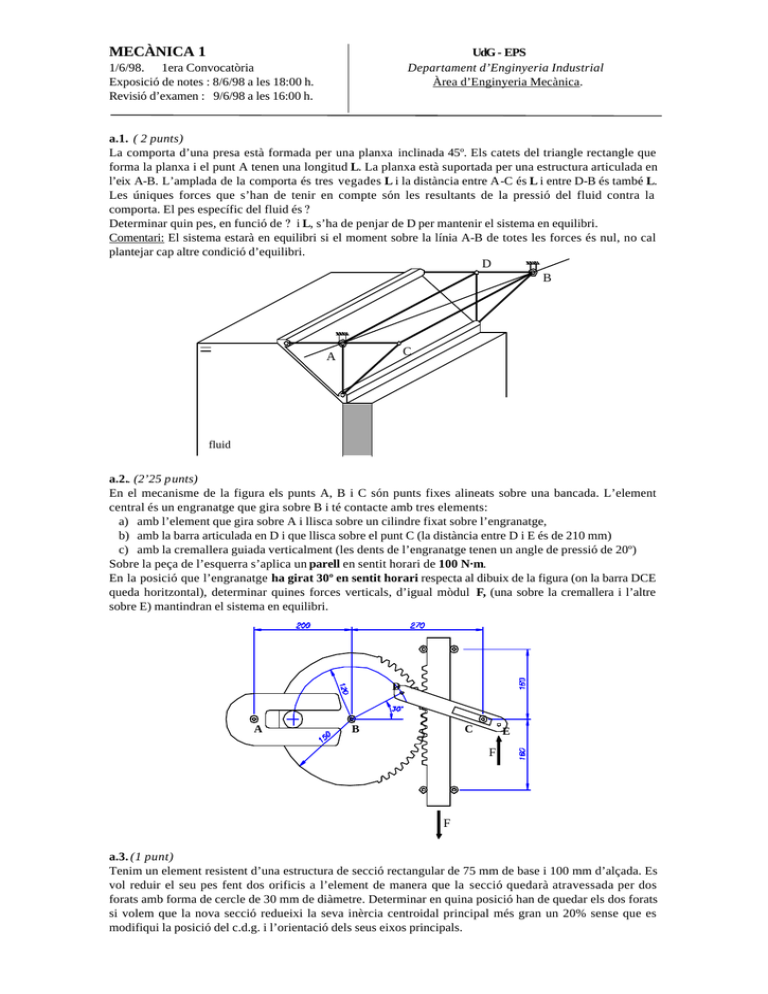
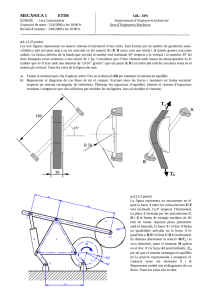
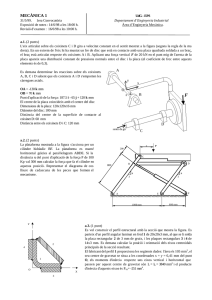
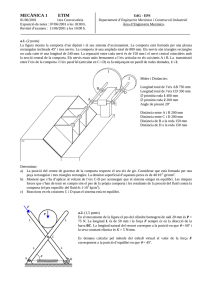
MECÀNICA 1
UdG - EPS
Departament d’Enginyeria Industrial
Àrea d’Enginyeria Mecànica.
1/6/98. 1era Convocatòria
Exposició de notes : 8/6/98 a les 18:00 h.
Revisió d’examen : 9/6/98 a les 16:00 h.
a.1. ( 2 punts)
La comporta d’una presa està formada per una planxa inclinada 45º. Els catets del triangle rectangle que
forma la planxa i el punt A tenen una longitud L. La planxa està suportada per una estructura articulada en
l’eix A-B. L’amplada de la comporta és tres vegades L i la distància entre A-C és L i entre D-B és també L.
Les úniques forces que s’han de tenir en compte són les resultants de la pressió del fluid contra la
comporta. El pes específic del fluid és ?
Determinar quin pes, en funció de ? i L, s’ha de penjar de D per mantenir el sistema en equilibri.
Comentari: El sistema estarà en equilibri si el moment sobre la línia A-B de totes les forces és nul, no cal
plantejar cap altre condició d’equilibri.
D
B
C
A
fluid
a.2.. (2’25 punts)
En el mecanisme de la figura els punts A, B i C són punts fixes alineats sobre una bancada. L’element
central és un engranatge que gira sobre B i té contacte amb tres elements:
a) amb l’element que gira sobre A i llisca sobre un cilindre fixat sobre l’engranatge,
b) amb la barra articulada en D i que llisca sobre el punt C (la distància entre D i E és de 210 mm)
c) amb la cremallera guiada verticalment (les dents de l’engranatge tenen un angle de pressió de 20º)
Sobre la peça de l’esquerra s’aplica un parell en sentit horari de 100 N·m.
En la posició que l’engranatge ha girat 30º en sentit horari respecta al dibuix de la figura (on la barra DCE
queda horitzontal), determinar quines forces verticals, d’igual mòdul F, (una sobre la cremallera i l’altre
sobre E) mantindran el sistema en equilibri.
D
A
B
C
E
F
F
a.3. (1 punt)
Tenim un element resistent d’una estructura de secció rectangular de 75 mm de base i 100 mm d’alçada. Es
vol reduir el seu pes fent dos orificis a l’element de manera que la secció quedarà atravessada per dos
forats amb forma de cercle de 30 mm de diàmetre. Determinar en quina posició han de quedar els dos forats
si volem que la nova secció redueixi la seva inèrcia centroidal principal més gran un 20% sense que es
modifiqui la posició del c.d.g. i l’orientació dels seus eixos principals.
MECÀNICA 1
1/6/98. 1era Convocatòria
Exposició de notes : 8/6/98 a les 18:00 h.
Revisió d’examen : 9/6/98 a les 16:00 h.
UdG - EPS
Departament d’Enginyeria Industrial
Àrea d’Enginyeria Mecànica.
b.1. (2’25 punts)
El cable aguanta un pes W de 75 Kp. La resta d’elements té pes menyspreable. La politja central està
articulada. Els blocs 1 i 2 són solidaris a les seves politjes (no articulades). Totes les politges tenen el
mateix radi R= 2'5 2 .
Determinar quin és el valor de la força F màxima que garanteix l’equilibri del sistema.
Tenir en compte que l’inici del moviment pot ser per lliscament o bolcada i que es considera que el sistema
es mou quan es mou qualsevol dels seus elements (bloc 1, bloc 2, politja i/o cinta). Per tant s’han de
comprovar totes les possibilitats de moviment.
Coeficients de fricció estàtics: entre bloc 1 i cinta 0’1, entre bloc 2 i cinta 0,4, entre bloc2 i el terra 0’5. La
resta de superfícies són totalment llises.
F
Bloc 2
Politja
Bloc 1
W
b.2. (1’5 punts)
Per a un pes W de 50 N, determinar la posició d’equilibri del mecanisme carregat per la molla (calcular
l’angle respecte a l’horitzontal de la barra OG) emprant el mètode de treball virtual. La vareta AC passa per
una guia a B i comprimeix la molla. La molla té una constant de rigidesa de 4’5 daN/cm i la seva longitud
natural és la distància BC quan la barra OG es troba horitzontal. Menysprear pesos dels elements
O
A
B
G
C
W
b.3. Pràctiques (1 punt, 10% de la nota)
Trobar quina condició ha de complir el radi R de la peça que està
articulada amb una excentricitat de
2 cm que provoqui el
bloqueig del sistema a l’aplicar una força horitzontal sobre la
cinta.
El coeficient de frec entre cinta i sistema és de 1 tan a la cara
superior com inferior.