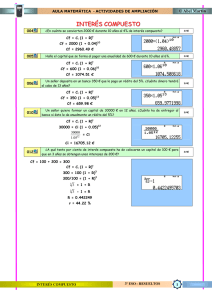
Elaboración de estado de flujos de efectivo (soluciones)

Departamento de Economía Financiera I.
Área de Matemática Financiera
SOLUCIONES A LOS EJERCICIOS DEL TEMA II
1.- Aplicando las expresiones estudiadas en el tema 2 resulta:
factor de capitalización: u (0, 4; p ) =
C 2 450
=
= 1,5
C1 300
rédito de capitalización: i(0, 4; p)= u(0, 4; p)-l = l,5 – l = 0,5
tanto de capitalización: ρ (0, 4 : p ) =
i (0, 4; p ) 0,5
=
= 0,125
4
4
para C = 300 € y el intervalo(0, 4), la cuantía del interés pospagable es:
I = C i(0, 4; p)= 300 . 0,5 = 150 €
También puede calcularse I = 450 – 300
2.- a) La expresión analítica de una ley de descuento en función del tanto instantáneo se
obtiene:
t
A (t; p ) = e
− ∫ δ ( x ; p ) dx
p
por lo que en el caso que nos ocupa :
t
A (t ; p ) = e
− ∫ 0 , 08 dx
p
=e
− [0 , 08 x ] tp
= e − 0 , 08 ( t − p )
b) el factor de descuento se obtiene
v ( t , t + 1; p ) =
A ( t + 1; p )
= e − 0 , 08 = 0 , 923
A (t ; p )
el rédito
d ( t , t + 1; p ) = 1 − v ( t , t + 1; p ) = 1 − 0 , 923 = 0 , 0768
el tanto
Departamento de Economía Financiera I.
Área de Matemática Financiera
δ ( t , t + 1; p ) =
v ( t , t + 1; p )
= 0 , 0768
t +1− t
3.- La cuantía del interés se obtiene multiplicando la cuantía del capital por el rédito
correspondiente
I = C i(t1 , t 2 ; p)
I = 200 = 1.000 i (0 ,4 ;5) ⇒ i (0,4;5) =
200
= 0,2
1.000
poniendo el factor en función del rédito
u (0,4;5) = 1 + i (0,4;5) = 1,2 =
(1 + i ) 5−0
= (1 + i ) 4
5− 4
(1 + i )
despejando obtenemos el valor del parámetro i
i = (1,2)
1
4
− 1 = 0,04664
4.- Para resolver este problema tenemos que aplicar la propiedad multiplicativa de los
factores para intervalos consecutivos
v(1,7; p) = v(1,3; p) ⋅ v(3,7; p)
luego como
v(1,3; p) = 0,4 y v(3,7; p) = 0,8
Resulta v(1,7; p ) = 0,4 ⋅ 0,8 = 0,32
Para obtener el capital equivalente al (3.000; 7) en el momento t=1
C = 3.000 ⋅ v(1,7; p) = 3.000 ⋅ 0,32 = 960
5.- La expresión analítica de una ley de capitalización a partir de su tanto instantáneo
acumulado se obtiene:
p
L(t ; p ) = 1 + ∫ µ ( x; p)dx = 1 + ∫
t
t
p
p
 0, 05 x 2 
= 1 + 0, 025( p 2 − t 2 )
0, 05 xdx = 1 + 

 2 t