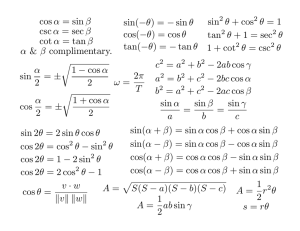sin(x + y) = sin(x) cos(y)

sin(x + y) = sin(x) cos(y) + cos(x) sin(y)
sin(x − y) = sin(x) cos(y) − cos(x) sin(y)
cos(x + y) = cos(x) cos(y) − sin(x) sin(y)
cos(x − y) = cos(x) cos(y) + sin(x) sin(y)
tan(x + y) =
tan(x − y) =
tan(x)+tan(y)
1−tan(x) tan(y)
tan(x)−tan(y)
1+tan(x) tan(y)
sin(2x) = 2 sin(x) cos(x)
cos(2x) = cos2 (x) − sin2 (x) = 2 cos(x) − 1 = 1 − 2 sin2 (x)
tan(2x) =
sin2 (x) =
cos2 (x) =
2 tan(x)
1−tan2 (x)
1−cos(2x)
2
1+cos(2x)
2
cos2 (x) + sin2 (x) = 1
sec2 (x) = 1 + tan2 (x)
cos(x−y)−cos(x+y)
2
cos(x−y)+cos(x+y)
cos(x) cos(y) =
2
sin(x−y)+sin(x+y)
sin(x) cos(y) =
2
sin(x) sin(y) =
R
sec2 (x)dx = tan(x) + C
R
csc2 (x)dx = − cot(x) + C
R
sec(x) tan(x)dx = sec(x) + C
R
csc(x) cot(x)dx = − csc(x) + C
R
sec(x)dx = ln | sec(x) + tan(x)| + C
R
csc(x)dx = ln | csc(x) − cot(x)| + C
R
tan(x)dx = ln | sec(x)| + C
R
cot(x)dx = ln | sin(x)| + C
R
1
dx
x2 +a2
=
1
a
arctan( xa ) + C
1