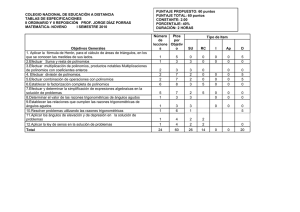
análisis matemático

ANÁLISIS MATEMÁTICO
INSTITUTO SUPERIOR de PROFESORADO
N° 4. “ANGEL CARCANO”
RECONQUISTA . SANTA FE.
CARRERA: profesorado en Administración de Empresas
CARGA H. 4HS CÁTEDRA
AÑO: 2007
PROFESOR: PEDRO M. BARGA.
CURSO: segundo AÑO
La formación de los profesores supone superar la clásica separación entre formación y
práctica para dar lugar a una formación que prepare a los futuros docentes para enseñar
“reconociendo la práctica educativa como objeto de conocimiento, en su dimensión social,
política, escolar y áulica” (Anexo II. Decreto 1142).
El ritmo y la naturaleza de los cambios operados en el campo del conocimiento exigen, tal
como lo plantea la Ley 24.195, la Transformación Docente estructurada en función de
cuatro principios pedagógicos fundamentales:
- profesionalización docente
- dinámica permanente de innovación pedagógica
- superación de diferentes tipos de fragmentaciones
- flexibilidad, apertura y complementariedad de las propuestas
curriculares
En este contexto se hace necesario que los futuros docentes cambien su mirada de la
matemática, como de su formación general, rompiendo con viejas estructuras o matrices
de aprendizaje para hacer posible una real transformación de la enseñanza.
Esta enseñanza ha de atender a que los futuros docentes:
o profundicen los contenidos matemáticos básicos
o formen actitudes pedagógicas que orienten y sustenten su tarea (CBC para la F.D. de
grado)
La formación matemática deberá sostenerse por principios tales como:
. La comprensión conceptual
. El conocimiento y la experiencia previos
. El desarrollo del espíritu lúdico
. La habilidad para plantear problemas y la posibilidad de resolverlos
. La potencia de la matemática para modelizar y resolver problemas propios y de otras
disciplinas
. La cohesión interna
. El valor de la matemática en la cultura y en la sociedad a lo largo de la historia
La vastedad y la complejidad de los contenidos matemáticos conducen a una necesaria
selección de los mismos regida por criterios de racionalidad y rigurosidad. Es impensable
pensar que es posible llegar a enseñar “todo”, pero si es posible pensar que se puede saber
menos y bien, lo cual se convierte en plataforma sólida para la aprehensión de nuevos
conocimientos.
Es importante tener en cuenta que la matemática en si es una mutilación de la realidad,
una abstracción. Un camino posible de interpretación de la misma, dominando, a través de
esta mutilación, ciertos aspectos de la realidad, pero no la realidad misma en su totalidad.
Está bien percatarse de las limitaciones inherentes al pensamiento matemático a fin de
contrarrestar las posibles aberraciones de una corriente hacia una exagerada
matematización de nuestra cultura. La matemática es muy poderosa y muy útil en nuestro
intento de obtener un cierto dominio de algunos aspectos de la naturaleza, pero conviene
no olvidar que el ser humano es mucho más profundo que lo que la más potente de las
estructuras matemáticas pueda abarcar. (M.Bitlloch.Ed. GRAO).
CONTENIDOS ACTITUDINALES.
La propuesta curricular pretende a partir de la selección, organización y abordaje de los
diferentes contenidos que el alumno logre:
Autonomía y desarrollo del pensamiento lógico.
Valoración de la matemática como fuente de conocimiento y aprendizaje.
Curiosidad, apertura, en relación con los conceptos y procedimientos con los que
actúa.
Valoración de la Matemática como fuente de construcción humana.
Capacidad para tomar decisiones y aceptar responsabilidades.
CONTENIDOS/ conceptuales – procedimentales.
Análisis de funciones / PRECALCULO
Función. Concepto. Condiciones de existencia y unicidad. Funciones explícita e implícita.
La recta. Incrementos. Pendiente de una recta. Rectas paralelas y perpendiculares.
Condición. Ecuaciones de la recta. Aplicaciones.
Reconocimiento del dominio y rango de una función.
Reconocimiento de la pertenencia de un punto al gráfico de una función (gráfica y
analíticamente).
Interpretación de gráficos.
Obtención de gráficos de funciones lineales por pendiente y ordenada, coordenadas de dos
puntos y corte con los ejes coordenados.
Exploración de las ecuaciones de la recta en el plano.
Exploración y análisis de la relación entre pendientes de rectas paralelas y
perpendiculares.
La parábola. Función de segundo grado. Dominio y rango. Formas general y canónica.
Gráficos obtenidos por desplazamientos. Intersección con ejes coordenados. Completación
de cuadrados.
Interpretación de la relación existente entre la ecuación de segundo grado y la función
cuadrática.
Completación de cuadrados.
Deducción de la fórmula resolvente.
Exploración de la ecuación de 2do grado.
Interpretación de la forma canónica.
Reconocimiento de las relaciones entre las distintas formas.
Obtención de gráficos de parábolas a partir del conocimiento de distintos parámetros (
vértice y punto, tres puntos ).
Factorización de polinomios de segundo grado.
Expresiones algebraicas enteras. Monomio. Polinomio. Expresión general. Grado.
Características. Valor numérico. Polinomio de una variable. Suma y resta de polinomios.
Producto de polinomios. Cuadrado y cubo de binomio. División entera de P(x). Raíces de
un polinomio. Teorema del resto. Regla de Ruffini. Divisibilidad de polinomios.
Polinomios expresados como productos. Técnicas básicas de factoreo: factor común. Factor
común por grupos, diferencia de cuadrados, trinomio cuadrado perfecto.
Análisis y exploración de la expresión general de un polinomio.
Resolución de operaciones con polinomios.
Reconocimiento y utilización de las propiedades de las operaciones.
Cálculo de las raíces de un polinomio.
Aplicación del T. del resto y la regla de Ruffini.
Aplicación de técnicas básicas para factorizar polinomios.
Funciones racionales. Expresión racional. Simplificación. La función racional. Gráficos :
intersección con los ejes coordenados. Ceros. Asíntotas verticales y horizontales. Notación.
Gráficas de algunas funciones racionales especiales. Asíntotas
Reconocimiento de funciones racionales.
Simplificación de funciones racionales.
Restricción del dominio de una función racional.
Determinación de intervalos correspondientes al dominio y rango de una función.
Cálculo de las intersecciones con los ejes coordenados.
Interpretación del concepto de asíntota.
Exploración de los valores de f(x) cuando la variable independiente tiende a cero o al
infinito.
Construcción de gráficos de funciones racionales sencillas
Funciones inversas. Función exponencial. Propiedades de la potenciación. La función
logarítmica. La función logarítmica de base e. Logaritmos neperianos y decimales.
Logaritmo de un número. Propiedades. Cambio de base. Gráficos de funciones
exponenciales y logarítmicas.
Exploración de las condiciones para la existencia de la función inversa.
Graficación de funciones inversas.
Graficación de funciones exponenciales y logarítmicas.
Reconocimiento del dominio y rango para funciones logarítmicas y exponenciales.
Corrimiento en dirección de los ejes coordenados.
Obtención de gráficos de funciones logarítmicas a partir de su inversa exponencial.
Exploración de las propiedades que caracterizan las funciones exponencial y logarítmica.
Funciones trigonométricas. Ángulos orientados. Medición de ángulos. Radián. Sistema
circular de medida. Radianes y ángulos orientados. Pasaje de un sistema a otro. Uso de la
calculadora. La circunferencia trigonométrica. Signo de los cuadrantes. Función seno.
Función coseno. Función tangente. Líneas trigonométricas en el círculo. Relaciones entre
las razones trigonométricas. Funciones recíprocas: secante, cosecante, cotangente.
Funciones inversas. Cálculo del argumento.
Determinación de la medida de ángulos en grados y radianes.
Representación geométrica y gráfica de las funciones trigonométricas.
Establecimiento de las razones trigonométricas fundamentales.
Interpretación de los datos obtenidos por calculadora.
Obtención de los gráficos correspondientes a las funciones seno, coseno y tangente.
Límites y sus propiedades./CALCULO.
Cálculo de límites gráfica y numéricamente. Definición formal. Cálculo analítico de
límites. Continuidad y límites laterales. Propiedades de la continuidad. Teorema del valor
intermedio. Límites infinitos. Asíntotas. Propiedades.
Exploración de límite de una función en un punto.
Exploración del concepto de continuidad en un punto.
Utilización de límites laterales para el cálculo de límites.
Obtención de asíntotas a partir de la aplicación de límites.
Graficación de funciones racionales.
Cálculo de límites y aplicación a problemas.
La derivada. Problema de la recta tangente. Cociente incremental. Derivada de una función.
Derivabilidad y continuidad. Reglas básicas de derivación. Caso de la constante. De las
potencias. Múltiplo constante. Reglas de la suma, diferencia, multiplicación y división.
Derivadas de las funciones trigonométricas. Derivadas de orden superior. Regla de la
cadena. Derivación implícita.
Exploración del concepto tasa de variación instantánea.
Reconocimiento de la derivada de una función.
Utilización y cálculo de la función derivada en un punto.
Interpretación geométrica de la derivada.
Graficación de funciones aplicando derivadas.
Resolución de problemas.
Primitivas. Integración indefinida. Sumatoria. Área de una región plana. Sumas inferiores y
superiores. Integrales definidas. La integral definida como área de una región. Propiedades.
Teorema fundamental del Cálculo. Teorema del valor medio. Integración por sustitución.
Cambio de variables. Integración por partes. Aplicaciones. Cálculo de áreas en coordenadas
rectangulares.
Exploración de la expresión integral definida de una función en un intervalo.
Interpretación física y geométrica de la integral.
Aplicación de métodos de integración de sustitución y por partes.
Cálculo de áreas bajo curvas.
ACTIVIDADES
•
•
•
•
•
•
•
•
•
Trabajos orientados hacia la construcción de conceptos por el alumno.
Lectura e interpretación de textos.
Completar cuadros en texto.
Resolución de actividades y problemas planteados en clase.
Discusión y análisis de distintos aspectos relacionados con conceptos fundamentales.
Construcción de gráficos.
Trabajos de elaboración grupal.
Registro de exposiciones en clase.
Registro de conceptos fundamentales de la disciplina.
EVALUACION.
La evaluación ha de tener como objetivo “el mejoramiento y la potenciación de los
procesos de cambio”. En un contexto que experimenta cambios permanentes se ha de
concebir la evaluación como un proceso capaz de ayudar, en este caso al docente, a
convertirse, tal cual lo plantea Paulo Feire, en sujeto de la producción del saber y poder
crear las posibilidades de construcción del conocimiento.
La evaluación ha de posibilitar la propia crítica, ya que, al estar ligada al hecho mismo de
aprender “cuanto más críticamente se ejerza la capacidad de aprender tanto mas se
construye y desarrolla la ...curiosidad epistemológica, sin la cual no alcanzamos el
conocimiento cabal del objeto”.
Se plantea en este Espacio, en particular:
A) la elaboración de un examen de carácter parcial:
– que se irá elaborando durante el ciclo y en relación con el tratamiento de los contenidos
mediante pruebas parciales de seguimiento.
- al finalizar la serie de actividades propuestas ( de 10 a 12) se calificará por nota numérica
de 1 a 5.
- La producción del mismo será personal y consistirá en el planteo de algunas situaciones
problemáticas concretas a resolver.
- El alumno que no aprobara este primer examen parcial con un mínimo del 60 % tendrá la
posibilidad de dos exámenes escritos recuperatorios posteriores.
B) el examen final de Análisis Matemático consistirá en una prueba escrita de respuesta
restringida en la cual se planteará al alumno distintas situaciones problemáticas sobre los
tópicos fundamentales de la materia. La condición mínima de aprobación será obtener el
60% de las respuestas correctas.
C) durante el cursado de la materia se contempla la realización de un mínimo de dos
trabajos prácticos a fin de facilitar la comprensión y aplicación de contenidos.
BIBLIOGRAFÍA
Engler A, Muller D, Vrancken S, Hecklein S. (2005). “El cálculo diferencial”. Santa Fe
(arg), Ediciones UNL.
Cadoche L y otros autores. (2004) “Matemática preuniversitaria”. Santa Fe. Ediciones
UNL
Larson R. Hosteller R. Edwards B. “Cálculo y geometría analítica”(1999). México. Mc
Graw Hill.
Stein S. “Cálculo y Gometría Analítica”(1987). México. McGraw Hill.
Sobel M. y Lerner N. (2000) “Algebra”. México. Prentice Hall
Finney y otros. (2000) “Cálculo de una variable”. México. Prentice Hall
Piskunov n. (1987) “Cálculo Diferencial e Integral”. Barcelona Ed. Mir.
Kcaczor P y otros autores. (1999) Matemática I. Buenos Aires.ED. SANTILLANA.
Guzmán M, Colera J, Salvador A. (1988) “Matemáticas”. Bachillerato 3. Madrid. Editorial
Anaya.
Haeussler P y Richard S. (1997) “Matemáticas”. México. Ed Prentice Hall.