TEMA 7:

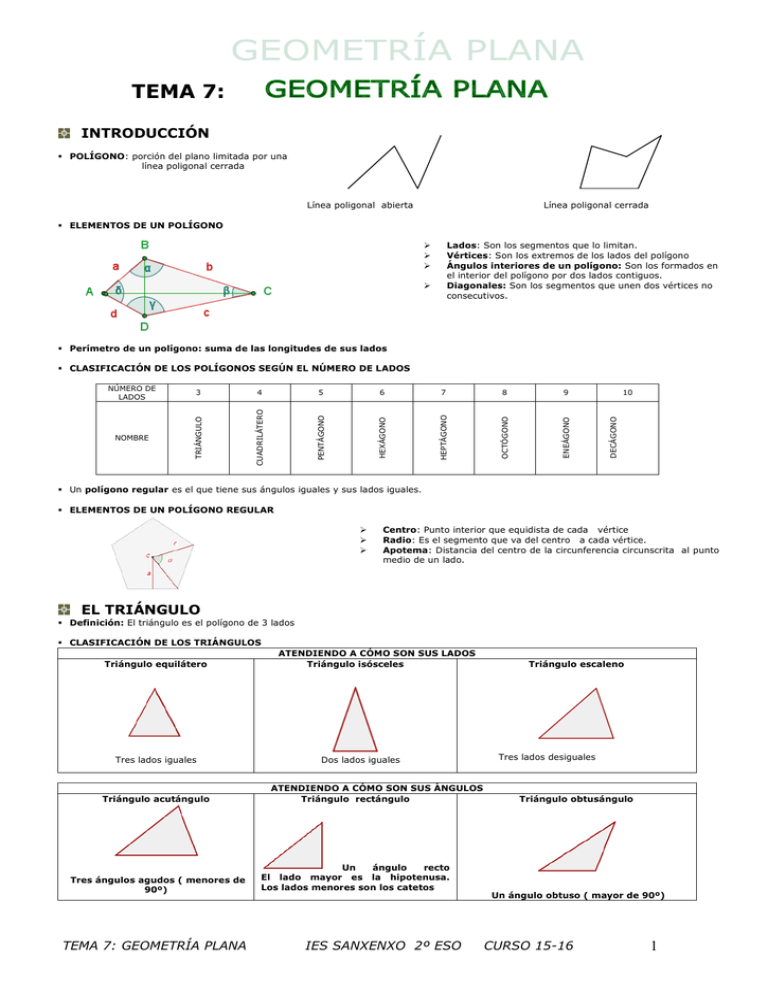
TEMA 7:
INTRODUCCIÓN
 POLÍGONO: porción del plano limitada por una
línea poligonal cerrada
Línea poligonal abierta
Línea poligonal cerrada
 ELEMENTOS DE UN POLÍGONO
Lados: Son los segmentos que lo limitan.
Vértices: Son los extremos de los lados del polígono
Ángulos interiores de un polígono: Son los formados en
el interior del polígono por dos lados contiguos.
Diagonales: Son los segmentos que unen dos vértices no
consecutivos.




 Perímetro de un polígono: suma de las longitudes de sus lados
CUADRILÁTERO
PENTÁGONO
7
8
9
10
DECÁGONO
NOMBRE
6
ENEÁGONO
5
OCTÓGONO
4
HEPTÁGONO
3
HEXÁGONO
NÚMERO DE
LADOS
TRIÁNGULO
 CLASIFICACIÓN DE LOS POLÍGONOS SEGÚN EL NÚMERO DE LADOS
 Un polígono regular es el que tiene sus ángulos iguales y sus lados iguales.
 ELEMENTOS DE UN POLÍGONO REGULAR



Centro: Punto interior que equidista de cada vértice
Radio: Es el segmento que va del centro a cada vértice.
Apotema: Distancia del centro de la circunferencia circunscrita al punto
medio de un lado.
EL TRIÁNGULO
 Definición: El triángulo es el polígono de 3 lados
 CLASIFICACIÓN DE LOS TRIÁNGULOS
Triángulo equilátero
Tres lados iguales
Triángulo acutángulo
Tres ángulos agudos ( menores de
90º)
TEMA 7: GEOMETRÍA PLANA
ATENDIENDO A CÓMO SON SUS LADOS
Triángulo isósceles
Dos lados iguales
ATENDIENDO A CÓMO SON SUS ÁNGULOS
Triángulo rectángulo
Un
ángulo
recto
El lado mayor es la hipotenusa.
Los lados menores son los catetos
IES SANXENXO 2º ESO
Triángulo escaleno
Tres lados desiguales
Triángulo obtusángulo
Un ángulo obtuso ( mayor de 90º)
CURSO 15-16
1
 Propiedad: La suma de los ángulos interiores de un triángulo es igual a 180°.
 TEOREMA DE PITÁGORAS
El Teorema de Pitágoras establece que en un
triángulo rectángulo, el cuadrado de la longitud de la
hipotenusa (el lado de mayor longitud del triángulo
rectángulo) es igual, a la suma de los cuadrados de las
longitudes de los dos catetos (los dos lados menores
del triángulo rectángulo: los que conforman el ángulo
recto). Si un triángulo rectángulo tiene catetos de
longitudes b y c , y la medida de la hipotenusa es a,
se establece que:
a2= b2 + c2
Ejemplo 1 Calcula la longitud de la diagonal de un rectángulo de lados 12 cm y 5 cm
a
12 cm
a2= 52 +122 =25 + 144 = 169 ; a = 13 cm
5 cm
 El perímetro de un triángulo es igual a la suma de sus tres lados.
CUADRILÁTEROS
 Definición: El cuadrilátero es un polígono de 4 lados
 Propiedad: La suma de los ángulos interiores de un cuadrilátero es igual a 360°.
 CLASIFICACIÓN DE LOS CUADRILÁTEROS
PARALELOGRAMOS: Cuadriláteros que tienen los lados paralelos dos a dos.
Rectángulo
Cuadrado
Tiene los 4 lados iguales y los 4 ángulos rectos.
Tiene lados iguales dos a dos y los 4 ángulos rectos.
Romboide
Rombo
Tiene los cuatro lados iguales y ángulos iguales dos a
dos
Tiene lados y ángulos iguales dos a dos.
TRAPECIOS : Cuadriláteros que tienen sólo dos lados paralelos, llamados base mayor y base menor.
Trapecio rectángulo
Trapecio isósceles
Trapecio escaleno
Tiene un ángulo recto.
Tiene dos lados no paralelos
iguales.
No tiene ningún lado igual ni
ángulo recto.
TRAPEZOIDES : Cuadriláteros que no tiene ningún lado paralelo.
TEMA 7: GEOMETRÍA PLANA
IES SANXENXO 2º ESO
CURSO 15-16
2
POLÍGONOS REGULARES DE MÁS DE 4 LADOS
Pentágono regular
Hexágono regular.
Heptágono regular
Octágono regular
Eneágono regular.
CIRCUNFERENCIA Y CÍRCULO
 Circunferencia: es la línea curva cerrada y plana cuyos puntos están a la misma distancia (radio) de un punto dado (centro).
 Círculo: es la superficie plana limitada por una circunferencia.
 ELEMENTOS DE LA CIRCUNFERENCIA
Centro: punto del cual equidistan todos los puntos de la circunferencia
Radio: es el segmento que une el centro con un punto cualquiera de la circunferencia
Cuerda: segmento que une dos puntos de la circunferencia
Diámetro: cuerda que pasa por el centro de la circunferencia ( es el doble del radio)
Arco: Parte de la circunferencia comprendida entre dos puntos de ésta
 Longitud de una circunferencia L =
Tomaremos como aproximación de

  d  2   r
siendo d el diámetro de la circunferencia, r el radio de la circunferencia.
( número irracional ) 3,14
ÁREAS DE LOS POLÍGONOS
Se define área de un polígono como la medida de su superficie. Este área se suele expresar en función de la medida de los lados, las alturas o
las diagonales
o
UNIDADES DE SUPERFICIE
Para medir superficies se toma como unidad la superficie que corresponde a un cuadrado de un metro de lado. A esta unidad se le denomina
metro cuadrado y se simboliza m2.
En el gráfico se puede ver que mientras que un metro es igual a diez decímetros, un metro cuadrado equivale a cien centímetros cuadrados. Las
unidades
de superficie varían de 100 en 100.
• Para pasar de una unidad a su inmediatamente posterior deberemos dividir por 100.
• Para pasar de una unidad a su inmediatamente anterior deberemos multiplicar por 100.
Cambio de unidades
Cada unidad de superficie es 100 veces mayor que la inmediata inferior y 100 veces menor que la inmediata superior.
 Para pasar de dam2 a m2 multiplicaremos por 100 o correremos la coma dos lugares a la derecha.
Ejemplos: 7 dam2 = 700 m2; 73,25 7 hm2 = 73 25,7 dam2 = 73 25 70 m2.
 Para pasar de m2 a dam2 dividiremos por 100 o correremos la coma decimal dos lugares a la izquierda.
Ejemplos: 3 m2 = 0,03 dam2; 14 68 m2 = 14,68 dam2 = 0,14 68 hm2 = 0,00 14 68 km2.
TEMA 7: GEOMETRÍA PLANA
IES SANXENXO 2º ESO
CURSO 15-16
3
o
ÁREA DEL TRIÁNGULO

El área de un triángulo es igual a base por altura partido por 2.
La altura es la recta perpendicular trazada desde un vértice al lado opuesto
Ejemplo
o
Hallar el área del siguiente triángulo:
ÁREAS
Y PERÍMETROS DE CUADRILÁTEROS
Área de un cuadrado
Área de un rectángulo
Área de un rombo ( su área se calcula como la mitad del área del rectángulo que lo contiene)
Área de un romboide ( su área es igual al área de un rectángulo de base b y altura h)
P = 2 · (a + b)
A=b·h
Área de un trapecio ( su área se obtiene como la suma de las área de los triángulos que lo componen)
TEMA 7: GEOMETRÍA PLANA
IES SANXENXO 2º ESO
CURSO 15-16
4
o
ÁREA
DE UN POLÍGONO REGULAR
Descomposición del hexágono en triángulos
El hexágono se puede descomponer en 6 triángulos equiláteros cuyo lado es el lado del hexágono:
Suponiendo que l es la longitud del lado del hexágono y a su apotema, se
Ahexágono  6  Atriángulo  6 
perímetro  apotema
2
Calcular el área y el perímetro de un pentágono regular de 6 cm de lado. .
P = 5 · 6 = 30 cm
o
siendo p el perímetro del hexágono.
A polígono regular 
En general, se tiene que
Ejemplo
l a pa

2
2
tiene que :
Área =
30  2
 30 cm 2
2
ÁREA DEL CÍRCULO
El área del círculo se calcula de la siguiente forma:
Recordemos:
A polígono regular 
Como el perímetro del círculo es 2 · π · r ,
Acírculo 
perímetro  apotema
2
y la apotema será el radio del círculo; se tiene que:
perímetro  apotema 2    r  r

  r2
2
2
TEMA 7: GEOMETRÍA PLANA
IES SANXENXO 2º ESO
CURSO 15-16
5
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
EJERCICIOS GEOMETRÍA PLANA
Calcula el área de un triángulo sabiendo que su
base mide 6 cm y su altura 10 cm. Expresa el
resultado en cm2 y en dm2
Calcula el área de un triángulo sabiendo que su
base mide 40 mm y su altura 0,07 m . Expresa
el resultado en cm2 y en mm2
¿ Cuánto mide la altura de un triángulo cuya
área es 56 cm2 si su base mide 14 cm?.
Si un ángulo de un triángulo rectángulo mide
36º, ¿ cuánto miden los otros dos?.
Si el área de un triángulo es de 24 cm2, y la
altura mide 80 mm, ¿ cuánto mide la base?.
Los dos catetos de un triángulo rectángulo
miden 3 cm y
4 cm. ¿ Cuánto mide la
hipotenusa?. Calcula el perímetro y el área del
triángulo.
En una finca que ocupa una superficie
rectangular se ha construido un camino que la
cruza en diagonal. Si las dimensiones de la
finca son 6 dam y 8 dam, averigua qué longitud
tiene el camino en m.
En una piscina se ha construido un tobogán con
una escalera de 3 m de altura y de manera que
la distancia del pie de la escalera al punto más
bajo del tobogán es 4 m. ¿ Cuánto mide el
tobogán?.
Halla el área de un cuadrado, en dm2, si su
perímetro es de 36 m.
Se están vendiendo parcelas de 100 m2 a
60000 €. ¿ Cuánto te costaría una parcela
rectangular de 32 m de largo por 18 metros de
ancho?.
Se tiene que embaldosar el patio interior de un
edificio con baldosas cuadradas de 40 cm de
lado. El patio es rectangular y sus medidas son
10 m por 12 m. ¿Cuántas baldosas se
necesitarán?
Calcula el área de un rombo cuyas diagonales
miden 4 y 6 cm respectivamente.
Un rombo tiene un área de 48 cm2, y una de las
diagonales mide 12 cm. ¿ Cuánto mide la otra
diagonal?.
Calcula cuánto mide la diagonal mayor de un
rombo sabiendo que la diagonal menor mide 7
cm y su área es de 0,49 dm2
Calcula el área de un trapecio sabiendo que sus
bases miden 17 cm y 0,05 m y su altura 30
mm. Exprésala en cm2, dm2 y m2
El área de un trapecio es de 24 m2. Halla la
altura del trapecio, en m, sabiendo que las
bases miden 700 cm y 0,005 Km.
Una finca tiene forma de trapecio rectángulo.
Las bases de ese trapecio miden 70 m
y
50 m
y su altura 20 m. Se va a poner un
riego automático y la empresa cobra 36 € por
cada 15 metros cuadrados. ¿Cuánto costará
poner el riego?
Halla el área de una plaza de toros cuyo
diámetro es 60 m.
¿ Cuál es la distancia máxima entre dos puntos
de una circunferencia de 2 cm de radio?
Halla el área de un círculo sabiendo que la
longitud de su circunferencia es de 43,96 cm.
Dos círculos concéntricos ( tienen el mismo
centro) tienen unos radios de 5 cm y 7 cm,
respectivamente. Halla el área de la zona
comprendida entre ambos círculos. ¿ Qué
nombre recibe dicha figura?.
Calcula el área de un pentágono regular
sabiendo que un lado mide 1,2 cm
y su
apotema 0,8 cm.
TEMA 7: GEOMETRÍA PLANA
23. Calcula el área de un octógono regular de 5 cm
de lado y 6 cm de apotema.
24. Un octógono regular tiene un área de 1080
cm2, y la apotema mide 180 mm. ¿ Cuánto
mide el lado del octógono?.
25. Calcula el área de los polígonos irregulares :
26. Calcula la cantidad
de
pintura
necesaria
para
pintar la fachada de
este
edificio
sabiendo que se
gasta ½
kg de
pintura por m2.
27.
Hallar el perímetro
y el área de la figura:
28. Calcula el área de la superficie sombreada
en cada figura, sabiendo que el hexágono del
apartado a) y el octógono del apartado b)
son regulares:
a)
b)
c)
IES SANXENXO 2º ESO
d)
CURSO 15-16
6