FUNCIONES TRGONOMETRICAS I

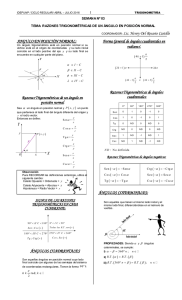
INSTITUCIÓN EDUCATIVA GABRIEL TRUJILLO
CORREGIMIENTO DE CAIMALITO, PEREIRA
“Lo peor no es cometer un error, sino tratar de justificarlo, en vez de
aprovecharlo como aviso providencial de nuestra ligereza o ignorancia”
Santiago Ramón y Cajal
FUNCIONES TRIGONOMETRICAS I
TABLA DE DESEMPEÑOS
Identificar y calcular el valor de las funciones trigonométricas de un ángulo dado en
posición normal y de un ángulo agudo en triángulos rectángulos.
INDICADORES DE DESEMPEÑOS:



Relaciona y aplica el concepto de ángulo a situaciones reales
Halla el valor de todas las funciones trigonométricas de un ángulo, a partir de una
de ellas.
Determina el cuadrante en el que se halla un ángulo de acuerdo con las
condiciones dadas
CONTENIDOS:
Definición de las funciones trigonométricas
Signo de las funciones trigonométricas de un ángulo en posición normal
Funciones trigonométrica de los ángulos cuadrantales
Razones trigonométricas en el triángulo rectángulo
R AZO NE S TRI G ONO MÉ TRI C AS
Seno
S e n o d e l á n g u l o B : e s l a r a zó n e n t r e e l c a t e t o o p u e s t o al á n g u l o y l a
hipotenusa.
Se denota por sen B.
Coseno
C o s e n o d e l á n g u l o B : e s l a r a zó n e n t r e e l c a t e t o c o n t ig u o a l á n g u l o y
la hipotenusa.
Se denota por cos B.
Ta n g e n t e
T a ng e nt e d e l á n g u lo B : e s l a r a zó n e n t r e e l c a t e t o o p u e s t o a l á n g u l o y e l
c a t e t o c o nt i g u o a l án g u l o .
Se denota por tan B.
Cotangente
C o t a n g e nt e d e l á ng u l o B : e s l a r a zó n i nve r s a d e l a t a ng e n t e d e B .
Se denota por cot B.
Secante
S e c a n t e d e l á ng u l o B : e s l a r a zó n i n ve r s a d e l c o s e n o d e B .
Se denota por sec B.
Cosecante
C o s e c a n t e d e l á ng ul o B : e s l a r a zó n i n ve r s a d e l s e n o d e B .
Se denota por csc B.
Ejemplos
1. De acuerdo con la información de la figura, determinar el valor de las razones
trigonométricas sen C , cos C y tan C
a = 5, b = 3, c = 4
Solución
Aplicando las razones trigonométricas
2. De acuerdo con la información de la figura, determinar el valor de las razones
trigonométricas para el ángulo B
b = 2, c = 4
Solución
Hallamos a utilizando Pitágoras
a =
3. Si B es uno de los ángulos agudos de un triángulo rectángulo y
, determinar
cos B y tan B
Solución
a =
, b = 2, c =
por Pitágoras
Taller 1
1. Si
encontrar el valor de las otras funciones trigonométricas en un
triángulo rectángulo ABC
2 Determinar la altura h del triángulo isósceles de la figura si tan β = 3 y el lado no igual
mide 2 cm
Dado el siguiente triángulo rectángulo, calcula la medida de los lados y los
ángulos desconocidos para cada caso:
3. Dados b = 6 cm y c = 11 cm, calcula tan C.
4. Dados b = 39 cm y c = 55 calcula las 6 razones trigonométricas.
5. Dados c = 8 cm y a = 15, calcula cot B.
6. Dados a = 8 cm y c = 5, calcula las 6 razones trigonométricas
7. Construir un triángulo rectángulo que cumpla la condición dada
Definición de las razones trigonométricas
de un ángulo en Posición Normal
Para definir o hallar las razones trigonométricas de un ángulo en posición normal; se debe
conocer un punto perteneciente a su lado final. En el gráfico; para "α"; tendremos:
Por ejemplo
Se debe notar que ahora las razones trigonométricas pueden tener signo negativo;
dependiendo del cuadrante en el que se ubique el ángulo considerado.
Signos de las razones trigonométricas.
Según el cuadrante al que pertenece el punto P(x y), los signos de sus coordenadas x e y
varían. En cambio el signo de
que es la distancia entre P y el origen O,
es siempre positivo. En consecuencia, los signos de las funciones dependen de los signos
de x e y.
En la tabla encontramos el signo de los valores de las funciones trigonométricas en los
cuatro cuadrantes
Dependiendo del cuadrante en el que se ubique un ángulo en posición normal; podemos
establecer
el
siguiente
criterio
práctico
para
los
signos:
CUADRANTE
I
II
III
IV
Ejemplo 1
r
+
+
+
+
x
+
+
y Sen cos Tan cot sec Csc
+ + + + + + +
+ +
+
- + + - +
- +
-
y el lado final de Ɵ está en el tercer cuadrante, determinar el valor de cos
Si
Ɵ y sen Ɵ
Solución
.es decir (-4,-3) es un punto sobre el lado terminal de Ɵ.
Luego
Al calcular r se tiene
por lo tanto
Ejemplo 2
si Ɵ es un ángulo en posición normal, determinar los posibles valores de la función csc Ɵ
si
Solución
Puesto que
1.
se deben considerar dos casos (ver figura)
Y = 1 y X = 3, en consecuencia, el lado final del ángulo se encuentra en el
primer cuadrante y sobre él se encuentra el punto (3,1). Así, se tiene que
, luego,
2. Y = -1 y X = -3, en consecuencia, el lado final del ángulo se encuentra en el
tercer cuadrante y sobre él se encuentra el punto (-3,-1). Así, se tiene que
, luego,
Ejemplo 3
Si Ɵ es un ángulo en posición normal, determinar los posibles valores de la función
tan Ɵ si
;
Solución
Puesto que
, el valor de X es positivo y en consecuencia, el lado final del
ángulo se encuentra en el primero o en el cuarto cuadrante.
Sobre el lado final del ángulo se encuentra el punto cuyo valor de X es e X = 1 y
r = 2. Como
, de donde
= 3, entonces
El lado final del ángulo Ɵ puede contener los puntos (1,
Por tanto, los posibles valores de la función tan Ɵ son:
.
) o (1, -
) ver figura.
Ejemplo 4
Determinar el cuadrante en el que se encuentra el lado final del ángulo β
Sen β
0, cos β
0
Solución.
Si Sen β
0, el lado final del ángulo β se encuentra en el primer o en el segundo
cuadrante.
Si cos β
0, el lado final del ángulo β se encuentra en el segundo o en el tercer
cuadrante.
Por tanto, para que se cumplan las dos condiciones se requiere que el lado final del
ángulo β se encuentre en el segundo cuadrante.
Taller 2
1. halla el valor de las relaciones trigonométricas para un ángulo α, cuyo lado terminal
interseca una circunferencia de radio r en el punto
a)
b)
c)
d)
e)
P
P
P
P
P
(1,2)
(-3,2)
(-4,-2)
(1,7)
(5,-3)
2. Calcula el valor de las relaciones trigonométricas para cada uno de los siguientes
ángulos:
Razones trigonométricas de los ángulos cuadrantales
Son aquellos ángulos cuyo lado final coincide con uno de los semiejes del plano
cartesiano
Las razones trigonométricas de los ángulos cuadrantales principales se calculan con las
mismas definiciones aplicadas a cualquier ángulo en posición normal.
Para determinar las funciones trigonométricas de los ángulos cuadrantales, se considera
que sobre su lado final se encuentran algunos de los puntos (r,0), (0,r), (-r,0), (0,-r), con
r
El resultado se muestra a continuación.
:
Ejemplo 1
D e t e r m i n ar l a s f u n c io n e s t r i g o n om ét r i c as d e l á ng u l o
Solución
Puesto que el lado final del ángulo de
se tiene que:
(0,-r) con r
Sen
=
s e e n c u e n t r a e l p u nt o
=
cos
=
=
=
=
tan
=
=
cot
Sec
=
=
csc
=
=
Ejemplo 2
Determinar el valor de cot
Solución
Como
e s c o t er m i n a l c o n
, s e t i e n e q ue cot
Evaluación
Realizar las actividades 3 de la página 53 del libro Nuevas matemáticas Santillana 10 y
de ahí se elegirá los ejercicios a evaluar en una prueba escrita e individual en fecha por
definir..
Diego Alonso Castaño Alzate
Docente