EJERCICIO 1 DE SELECTIVIDAD Sep`11 A

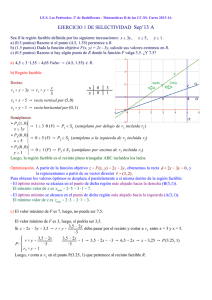
I.E.S. Los Pedroches. 2º de Bachillerato - Matemáticas II de las CC.SS. Curso 2011-12.
EJERCICIO 1 DE SELECTIVIDAD Sep’11 A
Se considera el recinto R del plano, determinado por las siguientes inecuaciones:
a) (1.5 puntos) Represente gráficamente el recinto R y calcule sus vértices.
b) (0.5 puntos) Halle los valores máximo y mínimo que alcanza la función
c) (0.5 puntos) Razone si existen puntos (x, y) del recinto, para los que
en dicho recinto.
a) Región factible.
Rectas:
r1 / x % y ' 2 Y y ' 2 & x
r2 / x % 3y ' 15 Y y '
15 & x
3
r3 / 3x & y ' 15 Y y ' 3x & 15
x
y
0
2
2
0
x
y
0
5
3
4
x
y
5
0
6
3
r4 / x ' 0 (eje OY)
r5 / y ' 0 (eje OX)
Semiplanos:
< P1 (0 , 0)
Y 0 % 0 $ 2 (F) Y P1 ó S1 (semiplano por encima de r1 , incluida r1)
x % y $ 2 /00
< P2 (0 , 0)
Y 0 % 0 # 15 (V) Y P2 0 S2 (semiplano por debajo de r2 , incluida r2)
x % 3y # 15 /00
< P3 (0 , 0)
Y 0 & 0 # 15 (V) Y P3 0 S3 (semiplano por encima de r3 , incluida r3)
3x & y # 15 /00
< x $ 0 e y $0 Y primer cuadrante incluidos los ejes
Luego, la zona factible es el recinto plano pentagonal ABCDE, incluidos los lados.
Vértices. Directamente de la gráfica se obtienen los vértices: A(2, 0); B(5, 0); C(6, 3); D(0, 5); E(0, 2).
Nota: si no se ven claras las coordenadas del punto C, se calculan resolviendo el sistema:
15 & x
15 & x
Y
' 3x & 15 Y 15 & x ' 9x & 45 Y 60 ' 10x Y x ' 6
r2 / y '
C ' r2 _ r3 Y
3
3
r3 / y ' 3x & 15
Y y ' 3 " 6 & 15 ' 3 Y C (6 , 3)
b) Optimización. El vector director de la recta d / 3x % y ' 0 (obtenida de la función objetivo) es vP ' (&1 , 3) .
Los puntos en los que se alcanzan los valores óptimos se obtienen desplazando d paralelamente a sí misma
dentro de la región factible:
- el óptimo máximo se alcanza en el punto C, punto de dicha región más alejado hacia la derecha.
C (6 , 3) Y zmáx ' 3 " 6 % 3 ' 21 .
- el óptimo mínimo se alcanza en el punto E, punto de dicha región más alejado hacia la izquierda.
E (0 , 2) Y zmín ' 3 " 0 % 2 ' 2 .
c) Para cualquier punto de la región factible se cumple que 2 # F (x , y) # 21 , luego no existen puntos (x, y) del
recinto, para los que F (x , y) ' 30 .