calculo_vectorial_extremos_de_funciones

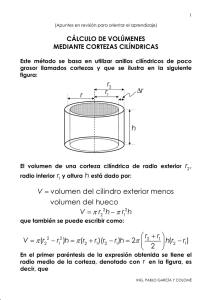
(Apuntes sin revisión para orientar el aprendizaje)
CÁLCULO VECTORIAL
EXTREMOS DE FUNCIONES ESCALARES
DE VARIABLE VECTORIAL
En numerosas aplicaciones de la ingeniería se presentan
problemas de optimización, en los cuales se pretende
determinar valores extremos de diversas funciones, tales como
superficies mínimas, utilidades máximas, tiempos mínimos,
volúmenes máximos y costos mínimos.
z = f ( x, y ) una función continua en una región
cerrada " R " del plano " xy " . Entonces:
Definición. Sea
i)
Se dice que f tiene un máximo relativo o local en
x0 , y0 ∈ R si se cumple que f x, y ≤ f x0 , y0 para todo
(
)
( ) (
( x, y ) en una vecindad o entorno de ( x0 , y0 ) .
)
Se dice que f tiene un mínimo relativo o local en
x0 , y0 ∈ R si se cumple que f x, y ≥ f x0 , y0 para todo
ii)
(
)
( ) (
( x, y ) en una vecindad o entorno de ( x0 , y0 ) .
)
ING. PABLO GARCÍA Y COLOMÉ
2
Si alguna de estas desigualdades se conserva en toda la región
en estudio, entonces se habla de extremos absolutos o
globales.
Ejemplo.
dada por
Considérese la función
z = 9 − x 2 − y 2 en la región
x2 + y 2 ≤ 9.
ING. PABLO GARCÍA Y COLOMÉ
3
Ejemplo.
dada por
1
cos 2 x 2 + y 2
, en la región
Sea la función z = 2
2
2
1+ 2 x + y
(
2
. Se puede escribir que:
(
)
cos 2 x 2 + y 2 ≤ 1 ⇒
⇒
)
1
1
cos 2 x 2 + y 2 ≤
2
2
(
)
1
cos 2 x 2 + y 2
1
2
< = f ( 0,0 )
2
1+ 2 x 2 + y 2
(
)
por lo que la función tiene un máximo absoluto en el punto
( 0,0 ) cuyo valor es
1
.
2
ING. PABLO GARCÍA Y COLOMÉ
4
Ejemplo.
Considérese la función
región dada por
Ejemplo.
z = 2 − 4 − x 2 − y 2 en la
x2 + y 2 ≤ 4 .
Sea la función
z = f ( x, y ) = ( x − 1) + ( y − 1) en
2
2
2
todo el espacio
.
Para cualquier valor de
" x"
y
" y " se cumple que:
( x − 1) + ( y − 1) ≥ 0 = f (1,1)
2
2
Se trata de un paraboloide circular cuyo vértice está en el
punto 1,1,0 y abre hacia arriba, por lo que este punto es el
(
)
mínimo absoluto de la función.
ING. PABLO GARCÍA Y COLOMÉ
5
Ejemplo.
región
Ejemplo.
Considérese la siguiente función:
2
2
2
z = x − y en la
.
Analizar
el
comportamiento
z = f ( x , y ) = e x y alrededor del origen.
Traza con el plano yz :
Traza con el plano xz :
Intersección con el plano y = x :
Intersección con el plano y = − x :
de
la
función
ING. PABLO GARCÍA Y COLOMÉ
6
Teorema.
cerrada
un
" R".
Entonces
mínimo
( a, b)
z = f ( x, y ) continua en una región
tiene un máximo absoluto f ( a, b ) y
Sea la función
f
f ( c, d ) ,
absoluto
donde
los
puntos
( c, d ) pertenecen a la región " R " . Esto significa
y
que:
m = f ( c, d ) ≤ f ( x, y ) ≤ f ( a, b ) = M
Teorema.
Sea una función
vecindad de
( x0 , y 0 ) .
∀ ( x, y ) ∈ R
z = f ( x, y ) continua en una
Si esta función presenta un extremo
relativo para x = x0 y y = y 0 , entonces es condición
necesaria que las derivadas parciales de primer orden
z x y zy se anulen o no existan en x0 , y0 .
(
)
y = y0 , entonces la función f ( x, y0 )
depende de una sola variable, " x " . Dado que la función tiene
un extremo (máximo o mínimo) en x = x0 , entonces se puede
Prueba. Si se fija un valor
escribir que:
df ( x, y0 )
dx
=
∂f ( x, y )
∂x
= 0 o no existe
( x0 ,y0 )
de acuerdo con lo estudiado en el cálculo con una variable.
De modo semejante se puede demostrar que
x = x0
∂f ( x, y )
∂y
= 0 o no existe
( x0 ,y0 )
ING. PABLO GARCÍA Y COLOMÉ
7
z = f ( x, y ) una función continua en una
región " R " . A los puntos ( x, y ) ∈ R , donde las primeras
derivadas parciales z x y zy se anulan o no existen, se les
denomina puntos críticos o puntos estacionarios de f .
Definición.
Sea
Ejemplo. Obtener los puntos críticos de la función
z = x 3 − 3 xy + y 3
z
x
y
ING. PABLO GARCÍA Y COLOMÉ
8
Ejemplo. Obtener los puntos críticos de la función
z = y 3 − 3yx 2 − 3y 2 − 3 x 2 + 1
ING. PABLO GARCÍA Y COLOMÉ
9
Ejemplo. Obtener los puntos críticos de la función
(
)
z = x 2 + 4y 2 e1− x
2
−y2
z
y
x
ING. PABLO GARCÍA Y COLOMÉ
10
Ejemplo. Obtener los puntos críticos de la función
z = f ( x, y ) = ( x − 1)
2
3
(y
2
−4
)
Ejemplo. Obtener los puntos críticos de la función
(
z = f ( x, y ) = ln x 2 + y 2
)
ING. PABLO GARCÍA Y COLOMÉ
11
Ejemplo.
Obtener la derivada direccional de la función
z = 4 − x 2 − y 2 en el punto (1,1) y en la dirección del vector
∧
∧
u = i + j . Hacer esto de dos maneras diferentes.
x = 1+
u= 2
;
y = 1+
⇒
1
2
1
2
⎛
1 ⎞
z = 4 − 2 ⎜1+
t⎟
2 ⎠
⎝
t
2
⎛
1 ⎞ ⎛
1 ⎞
z ( t ) = 4 − ⎜1+
t ⎟ − ⎜1+
t⎟
2 ⎠ ⎝
2 ⎠
⎝
;
t
2
2
⎛
1 ⎞⎛ 1 ⎞
z ' ( t ) = −4 ⎜1+
t ⎟⎜
⎟
2 ⎠⎝ 2 ⎠
⎝
z '(t ) = −
⇒
4 ⎛
1 ⎞
1
+
t⎟
⎜
2⎝
2 ⎠
∴ z ' ( 0 ) = −2.828
Otra forma:
∧
∧
∇ z = −2 x i − 2 y j
w=
∧
Dw f = ∇ ⋅ w
⇒
⇒
u
u
=
∇z
1
∧
(1,1)
∧
= −2 i − 2 j
1∧
i+ j
2
2
∧
⎛ 1 1 ⎞
Dw f = ( −2, −2 ) ⋅ ⎜
,
⎟
⎝ 2 2⎠
∴ Dw f = −2.828
ING. PABLO GARCÍA Y COLOMÉ
12
Criterio de la segunda derivada
para determinar máximos y mínimos
Teorema. Sean:
2
-f :
→ una función con segundas derivadas parciales
continuas en una región cerrada " R " del plano " xy " .
( x0 , y0 ) un punto crítico de la función, contenido en " R " .
∧
-u = (u1,u2 ) un vector unitario en el plano " xy " .
2
- D u f ( x 0 , y 0 ) la segunda derivada direccional de f ( x, y )
valuada en ( x0 , y 0 ) .
-
Entonces:
i ) f ( x0 , y 0 )
es un máximo relativo si
ii) f ( x0 , y0 )
es un mínimo relativo si
iii)
es un punto silla si
f ( x0 , y 0 )
Du2 f ( x0 , y0 ) < 0
Du2 f ( x0 , y0 ) > 0
Du2 f ( x0 , y0 ) cambia de
∧
signo para diferentes direcciones de
iv)
El criterio no decide si
D f ( x0 , y 0 ) = 0
2
u
u
Prueba. La demostración parte de tomar en consideración el
criterio de la segunda derivada para el caso de una variable
independiente. Una forma de expresar a la derivada
direccional es la siguiente:
Du f ( x 0 , y 0 ) =
d
f ( x 0 + u1t , y 0 + u2 t )
dt
t=0
expresión que, como se observa, es una derivada ordinaria en
términos de " t " . La segunda derivada direccional está dada
por:
ING. PABLO GARCÍA Y COLOMÉ
13
d2
D f ( x0 , y 0 ) =
f x + u1t , y 0 + u2 t )
2 ( 0
dt
2
u
Du2 f ( x0 , y0 ) es una
cumplirse que si f ( x0 , y0 )
Como
Du2 f ( x0 , y0 ) < 0 .
Si
t=0
segunda derivada ordinaria, debe
es una máximo relativo, entonces
f ( x0 , y0 ) es un mínimo relativo, entonces
Du2 f ( x0 , y0 ) > 0 . Y el criterio no decide si Du2 f ( x0 , y0 ) = 0 .
∧
Nótese que esto se cumple para cierta dirección
u = (u1,u2 ) . Si
∧
el vector u es variable y las desigualdades anteriores se
conservan, entonces se cumple lo que establece el teorema. Y
∧
si las desigualdades cambian al cambiar u , entonces se trata
de un punto silla. Y queda demostrado el teorema.
Teorema. Sean:
2
-f :
→ una función con segundas derivadas parciales
continuas en una región cerrada " R " del plano " xy " .
( x0 , y0 ) un punto crítico de la función, contenido en " R " .
2
- g ( x 0 , y 0 ) = fxx ( x 0 , y 0 ) fyy ( x 0 , y 0 ) − fxy ( x 0 , y 0 )
-
Entonces:
i) f ( x0 , y0 ) es un máximo relativo si g ( x0 , y0 ) > 0 y
fxx ( x0 , y0 ) < 0
ii) f ( x0 , y0 )
fxx ( x0 , y0 ) > 0
(f ( x , y ) < 0)
yy
0
0
es un mínimo relativo si
(f ( x , y ) > 0)
yy
0
g ( x0 , y 0 ) > 0 y
0
es un punto silla si g ( x0 , y 0 ) < 0
iii) f ( x0 , y0 )
iii) El criterio no decide si g ( x0 , y0 ) = 0
ING. PABLO GARCÍA Y COLOMÉ
14
Prueba.
como:
La primera derivada direccional se puede escribir
∧
Du f ( x , y ) = ∇f ⋅ u = ( fx , fy ) ⋅ (u1, u2 ) = u1fx + u2 fy
y la segunda derivada direccional equivale a:
Du2 f ( x , y ) = u12 fxx + 2u1u2 fxy + u22 fyy
Se toma
fxx
como factor común y se obtiene:
fxy
f
⎡ 2
2 yy ⎤
+ u2
D f ( x , y ) = fxx ⎢ u1 + 2 u1u 2
⎥
f
f
xx
xx ⎦
⎣
2
u
Se completa el trinomio cuadrado perfecto y:
2
2
⎡
f
f
f
f
xy
2
2
2 xy
2 xy
2 yy
Du f ( x , y ) = fxx ⎢ u1 + 2 u1u 2
+ u2 2 − u2 2 + u2
fxx
fxx
fxx
fxx
⎢⎣
2
⎡⎛
⎤
f
⎞
u 22
xy
2
2
D u f ( x , y ) = fxx ⎢ ⎜ u1 + u 2
⎟ + 2 fxx fy y − fxy ⎥
fxx ⎠
fxx
⎢⎣ ⎝
⎥⎦
Esta expresión se cumple siempre y cuando fxx ≠ 0
(
Si se hubiera factorizado
D u2 f ( x , y ) = fy y
⎤
⎥
⎥⎦
)
fyy se tendría que, para fyy ≠ 0
⎡⎛
f
⎢ ⎜ u 2 + u1 x y
fy y
⎢ ⎜⎝
⎣
2
⎞
u12
2
⎟⎟ + 2 fx x fy y − fx y
fy y
⎠
(
)
⎤
⎥
⎥
⎦
Se observa que el signo de la segunda derivada direccional
depende de la expresión
de
fxx fyy − fxy2 por una parte y del signo
fxx (o de fyy ) por la otra.
Si se hace
g ( x , y ) = fxx fyy − fxy2
y se aplica el teorema
anterior, se tiene que:
ING. PABLO GARCÍA Y COLOMÉ
15
i) g ( x0 , y0 ) > 0 ⇒
de fxx o fyy como sigue:
el signo de
2
u
D f depende del signo
fxx < 0
(o
fyy < 0 )
⇒
Du2 f < 0 ∴
máximo relativo
fxx > 0
(o
fyy > 0 )
⇒
Du2 f > 0 ∴
mínimo relativo
ii) g ( x0 , y0 ) < 0
⇒
existen direcciones para las cuales
Du2 < 0 y direcciones para las que Du2 > 0 . Por lo tanto se
tiene un punto silla.
iii) g ( x0 , y0 ) = 0
⇒
únicamente del signo de
el
signo
fxx
o de
de
Du2 f
depende
fyy pero cuando menos
habrá una dirección en donde se anule el primer sumando, lo
que hace cero a
Du2 f y entonces el criterio no decide.
Ejemplo. Determinar la naturaleza de los puntos críticos de la
siguiente función:
z = y 3 − 3yx 2 − 3y 2 − 3 x 2 + 1
En un ejemplo anterior se obtuvieron los puntos críticos que son:
( 0,0,1) , ( 0,2, −3 ) , ( −
)(
3, −1, −3 ,
3, −1, −3
)
ING. PABLO GARCÍA Y COLOMÉ
16
Ejemplo.
función:
Determinar los extremos relativos de la siguiente
z = f ( x, y ) = x 3 − 4 xy + 2y 2
ING. PABLO GARCÍA Y COLOMÉ
17
Ejemplo. Obtener los tres números cuyo producto sea máximo
si su suma es nueve.
ING. PABLO GARCÍA Y COLOMÉ
18
Ejemplo. Una caja rectangular descansa sobre el plano " xy "
con un vértice en el origen. Obtener el volumen máximo de la
caja cuyo vértice opuesto al del origen está situado en el plano
6 x + 4y + 3 z = 24 .
ING. PABLO GARCÍA Y COLOMÉ
19
Ejemplo.
Determinar los extremos absolutos y relativos, así
como los puntos silla, de la función:
z = f ( x , y ) = xy − x 3 y − xy 3
sobre la región limitada por 0 ≤ x ≤ 1 y 0 ≤ y ≤ 1
ING. PABLO GARCÍA Y COLOMÉ
20
z
y
x
(1,1, −1)
ING. PABLO GARCÍA Y COLOMÉ
21
Ejemplo. Obtener los extremos relativos de la función:
z = f ( x, y ) = senx + seny + sen ( x + y )
0 ≤ x ≤ 2π
;
0 ≤ y ≤ 2π
ING. PABLO GARCÍA Y COLOMÉ
22
Criterio de la segunda derivada con la Matriz Jacobiana
La segunda derivada direccional se expresa como:
D u2 f = u 12 fx x + 2 u1u 2 fx y + u 22 fy y
El segundo miembro es una forma cuádrica que se puede
expresar matricialmente como:
2
u
D f = ⎣⎡ u 1
en donde
u
T
⎡ fx x
u 2 ⎦⎤ ⎢
⎢⎣ fy x
fx y ⎤ ⎡ u 1 ⎤
T
u
Hu
=
⎥⎢ ⎥
fy y ⎥⎦ ⎣ u 2 ⎦
es la matriz transpuesta de
⎡ fx x
H = ⎢
⎢⎣ fy x
u
y la matriz
fx y ⎤
⎥
fy y ⎥⎦
es una matriz simétrica denominada matriz hessiana, y su
determinante, al que se le denomina hessiano, es el siguiente:
ΔH =
fxx
fxy
fy x
fy y
= fxx fyy − fxy2
ING. PABLO GARCÍA Y COLOMÉ
23
Como H es una matriz simétrica, puede transformarse en una
matriz diagonal
H ' = d ia g ( λ1 , λ 2 )
de acuerdo con el Teorema Espectral del álgebra lineal que
afirma que toda matriz simétrica " M" se puede transformar en
una matriz diagonal " D " formada por los valores
característicos de " M" . Y esto se logra mediante unas matriz
ortonormal " P " , formada por los vectores característicos
ortonormalizados de " M " y que “diagonaliza” a la matriz " M" ;
esto es,
D = PTMP
(P
;
−1
= PT
)
Si se aplica este teorema a la matriz hessiana, se tiene que:
H ' = PTHP
H = PH 'PT
⇒
y al sustituir este resultado en la expresión matricial de
llega a:
T
2
u
T
( ) ( )
T
T
D f = u PH 'P u = u P H ' u P
Si se hace
T
v = u P = ⎡⎣ v1
T
D u2 f = v H ' v o sea
2
u
D f = ⎡⎣ v 1
de donde
v 2 ⎤⎦ ,
⎡ λ1
v 2 ⎤⎦ ⎢
⎣0
Du2 f se
T
entonces se tiene que
0 ⎤
λ 2 ⎥⎦
⎡ v1 ⎤
⎢v ⎥
⎣ 2⎦
D u2 f = λ 1v 12 + λ 2 v 22
En esta expresión se ve que el signo de la segunda derivada
direccional depende únicamente de los signos de los valores
característicos λ1 y λ2 ; este es otro método para obtener
los extremos relativos de una función escalar de variable
ING. PABLO GARCÍA Y COLOMÉ
vectorial
z = f ( x, y ) , el cual se puede generalizar a funciones
24
con más de dos argumentos.
Para obtener los valores característicos
λ1
y
λ2
se calcula
det ( H − λ I ) y se iguala a cero para cada punto crítico. Los
signos de λ1 y λ2 determinarán entonces la naturaleza del
punto crítico.
Ejemplo. Determinar los extremos relativos de la función
z = f ( x, y ) = x 3 − 3 xy + y 3
ING. PABLO GARCÍA Y COLOMÉ
25
z
x
y
Ejemplo.
Una caja rectangular sin tapa debe ser construida
12 m3 . El costo del material del
2
2
fondo es de $ 400 / m , de $ 300 / m para dos lados
2
opuestos y de $ 200 / m para los otros dos lados opuestos.
para tener un volumen de
Determinar las dimensiones de la caja para que el costo de los
materiales empleados en su construcción sea mínimo.
ING. PABLO GARCÍA Y COLOMÉ
26
Ejemplo.
Verificar
que
el
campo
escalar
u = x 4 + y 4 + z 4 − 4 xyz tiene un punto crítico en (1,1,1, −1) y
determinar la naturaleza de dicho punto crítico, analizando los
valores característicos de la matriz jacobiana.
ING. PABLO GARCÍA Y COLOMÉ
27
Ejemplo.
función
Analizar la naturaleza de los puntos críticos de la
v = 4 − w2 − x2 − y 2 − z 2
ING. PABLO GARCÍA Y COLOMÉ
28
Ejemplo. Para conducir agua para riego a través de una
barranca, es necesario construir un canal de sección
trapezoidal, con hoja de un determinado tipo de lámina cuyo
ancho es de 80 cm . Calcular la longitud de la sección del
canal en su base, así como el ángulo de inclinación de sus
taludes, de tal forma que el canal tenga máxima capacidad.
ING. PABLO GARCÍA Y COLOMÉ
29
Optimización de funciones con restricciones
Multiplicadores de Lagrange
Supóngase que se pretende obtener el máximo volumen de
una caja rectangular con caras paralelas a los planos
coordenados y que está inscrito en el elipsoide
16 x 2 + 4 y 2 + 9 z 2 = 144 . En la siguiente figura se muestra en
forma aproximada la parte de la caja inscrita en el elipsoide,
en el primer octante.
z
x2
y2
z2
+
+
=1
9
36 16
P ( x, y , z )
y
x
ING. PABLO GARCÍA Y COLOMÉ
30
El volumen de la caja está dado por V = 8 x y z y a esta
función, con tres argumentos, se le llama función objetivo ya
que es la que se pretende optimizar. El volumen de la caja está
2
2
2
sujeto a la restricción 16 x + 4 y + 9 z = 144 . Si se despeja
en esta expresión a la variable " z " para tener una función del
volumen en términos de dos variables independientes, se tiene
que
z2 =
⇒
1
144 − 16 x 2 − 4 y 2
9
1
z=
144 − 16 x 2 − 4 y 2
3
(
)
por lo que el volumen queda como
V =
8 xy
144 − 16 x 2 − 4 y 2
3
Como se observa, la obtención de las primeras y segundas
derivadas parciales se dificulta mucho. También podría darse el
caso de que no sea factible despejar variables en las
restricciones. Para estos casos se han desarrollado métodos
especiales y uno de los más convenientes es el conocido
como Multiplicadores de Lagrange. Se partirá de las siguientes
definiciones, considerando siempre que el número de
restricciones en menor que l número de variables del problema
a resolver.
Definición.
Sea
()
z = f r = f ( x1, x 2 ,… , x n ) una función
escalar de variable vectorial, continua y diferenciable, sujeta a
las restricciones:
g1 ( x1, x2 ,… , xn ) ≤ 0;
g2 ( x1, x2 ,… , xn ) ≤ 0 … gm ( x1, x2 ,… , xn ) ≤ 0
m< n
y sea el problema:
ING. PABLO GARCÍA Y COLOMÉ
Optimizar
()
(1) sujeta a
∀ i = 1,2,… , m < n
(2 )
z=f r
()
31
gi r ≤ 0
Entonces:
i) A este problema se le denomina problema de
programación.
ii) A la expresión matemática 1 de lo que se quiere
()
optimizar se le llama función objetivo.
iii) A la región formada por todos los puntos que cumplen
con las restricciones
Ejemplo.
Sea
( 2 ) se le llama región permisible.
g ( x, y , z ) = 0
la ecuación de una superficie
que no pasa por el origen de coordenadas. Determinar los
puntos de esta superficie que estén más próximos al origen.
" S"
Solución. Un punto
origen
sí
y
( x, y , z ) ∈
únicamente
x2 + y2 + z2 = r2,
función
3
si
está a una distancia
"r "
pertenece
esfera
a
la
del
que es una superficie de nivel de la
(
f ( x, y , z ) = x + y + z
2
2
2
)
1
2
la
que
será
minimizada (función objetivo).
Si se comienza con r = 0 y se va incrementando su valor, el
primer punto de contacto entre la esfera y " S " , será el punto
más próximo de " S " al origen. La ecuación g x, y , z = 0 , que
(
)
representa a la superficie " S " , es la parte activa de la
restricción. Si " S " tiene un plano tangente en un punto de
contacto, este plano debe también ser tangente a la superficie
de nivel de " f " . Por lo tanto, el vector gradiente de la superficie
ING. PABLO GARCÍA Y COLOMÉ
32
g ( x, y, z ) = 0 , debe ser paralelo al vector gradiente de la
superficie de nivel f ( x, y , z ) = r . Entonces existe una constante
" λ " tal que ∇ f
∧
⎛ ∧
⎜ fx i + fy j + fz
⎝
= − λ ∇ g , es decir, que
∧
∧
∧
⎞
⎛
k ⎟ + λ ⎜ g x i + gy j + g z
⎠
⎝
de donde se obtienen las ecuaciones:
∧
∧
∧
⎞
k ⎟ = 0 i + 0 j+ 0 k
⎠
∧
fx + λ g x = 0
fy + λ gy = 0
fz + λ g z = 0
g ( x , y , z ) = 0 ; ( restricción )
Si se resuelve este sistema de ecuaciones, se obtienen los
puntos en los que la distancia al origen es mínima.
De manera semejante, con una función objetivo y dos
restricciones, se podría llegar a:
∇f = λ1∇ g1 + λ 2 ∇ g 2
y al correspondiente sistema de ecuaciones:
fx = λ1g1x + λ2 g2 x
fy = λ1g1y + λ2 g2 y
fz = λ1g1z + λ2 g2 z
g1 ( x , y , z ) = 0 ⎫⎪
⎬ ; ( restricciones )
g2 ( x , y , z ) = 0 ⎪⎭
que al ser resuelto deviene en los puntos críticos cuya
naturaleza optimizará el problema planteado.
ING. PABLO GARCÍA Y COLOMÉ
33
" D " la región permisible de una función
continua y diferenciable z = f r , un entorno o vecindad de
Teorema.
Sea
()
r 0 ∈ D y sujeta a las restricciones
gk r = 0 ∀ k = 1,2,… , m < n .
()
Entonces
∂L
=0
∂x i
∇L = 0 , es decir,
∀ i = 1,2,… , n;
()
gk r = 0
∀ k = 1,2,… , m < n
Estas dos expresiones forman un sistema de n + m ecuaciones,
a partir del cual pueden ser determinadas las incógnitas
x1 ,… , x n , λ1 ,… , λ m . Aquí x 1 , … , x n son las coordenadas
del punto en el que puede haber un extremo condicionado.
Conclusión. El problema de la búsqueda de un extremo
condicionado se reduce al análisis del extremo corriente de la
función de Lagrange, definida como:
m
L ( x1,… , x n , λ1,… , λ m ) = f ( x1,… , x n ) + ∑ λ k gk ( x1,… , x n )
k =1
A los escalares λk ; k = 1,… , m se les denomina
Multiplicadores de Lagrange. En este método, las condiciones
necesarias para la existencia de un extremo condicionado se
expresan por medio del sistema de n + m ecuaciones
∂L
=0
∂x i
∀ i = 1,2,… , n
;
()
gk r = 0
∀ k = 1,2,… , m < n
Ahora se presentarán algunos problemas para aplicar este
método o el criterio de la segunda derivada.
ING. PABLO GARCÍA Y COLOMÉ
Ejemplo. Calcular tres números positivos cuya suma sea 12 y
cuyo producto sea máximo.
34
Ejemplo.
Determinar las dimensiones del paralelepípedo
rectangular de máximo volumen que se puede inscribir en el
elipsoide
x 2 + 9y 2 + 4 z 2 = 36 .
ING. PABLO GARCÍA Y COLOMÉ
35
3
Ejemplo. Se tiene un plano en el espacio
cuya ecuación es
z = 6 − 4 x − 3y . Determinar los extremos condicionados de
este plano en su intersección con el cilindro
x 2 + y 2 = 1.
ING. PABLO GARCÍA Y COLOMÉ
36
Ejemplo. Obtener la distancia mínima que existe entre el
origen y la recta de intersección de los planos x + 2 z = 4 y
x + y = 8.
ING. PABLO GARCÍA Y COLOMÉ
37
Ejemplo. Determinar los extremos absolutos de la función
f ( x, y ) = 2 x − 3 y
x2
en la región
+ y 2 ≤ 1. Resolver con Lagrange y con el
4
criterio de la segunda derivada.
ING. PABLO GARCÍA Y COLOMÉ
38
Ejemplo. Para conducir agua para riego a través de una
barranca, se desea construir un canal de sección trapezoidal
con hojas de un cierto tipo de lámina. Si el ancho de las hojas
es de 24 pulgadas, calcular la longitud de la sección en su
base, así como el ángulo de inclinación de sus lados, de tal
forma que el canal tenga capacidad máxima.
ING. PABLO GARCÍA Y COLOMÉ
39
Ejemplo. Determinar el máximo absoluto y el mínimo absoluto
de la función
f ( x, y ) = x 2 − x + 2 y 2 .
ING. PABLO GARCÍA Y COLOMÉ