Propósito

Propósito:
Realiza el calculo y la representación grafica de limites y derivadas de funciones aplicando leyes y
teoremas para su aplicación en la descripción , análisis y solución de las situaciones cotidianas de
su entorno
Calculo de limites de funciones
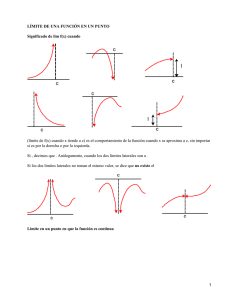
Limites de una función:
Se dice que una función y=f(x) tiene límite "l" cuando la x tiende a "a" y lo representamos por:
cuando para toda sucesión de números reales que se aproxime a "a" tanto como queramos, los
valores correspondientes de f(x) se aproximan a "l" tanto como queramos. ("tanto como
queramos" es una expresión que nos indica que la aproximación será tanto mayor cuantos más
elementos tomemos de la sucesión).
Ejemplo 1:
Consideremos la función y tratemos de calcular su límite cuando x tiende a 2. Tomamos la
sucesión an = {1-1,9-1,99-1,999-1,9999-....} y veamos a qué valor se aproxima f(an), para ello
construimos la siguiente tabla:
an
1
1,9
1,99
1,999 1,9999 1,99999
1,999999
.....
f(an)
-2
-29
-299
-2999 -29999 -299999
-2999999
.....
2
Parece que los valores de la función se aproximan, tanto como queramos a menos infinito, pero
nos preguntamos ¿Qué ocurriría si la sucesión elegida fuese decreciente, en lugar de creciente,
veámoslo:
an
3
2,1
2,01
2,001 2,0001 2,00001
f(an)
4
31
301
3001
2.000001
30001 300001 3000001
....
2
....
Ahora los valores se aproximan a más infinito.
Es decir, si la sucesión tiende a 2 pero conservándose todos sus términos menores que 2, la
función tiende a un límite y si los valores de la sucesión se conservan todos mayores que dos la
función tiende a otro distinto. Afirmamos que no existe límite en el punto 2 para la función dada.
Ejemplo 2
Calcular el límite
Vamos a proceder como antes con una sucesión creciente y otra decreciente que se aproximen
ambas a 3 tanto como queramos:
an
2,1
2,9
2,99
2,999 2,9999 2,99999
2,999999
....
3
f(an)
31
4,3333 4,0303 4,0030 4,0003 4,00003
4,000003
....
4
Y para una decreciente:
an
4
3,1
3,01
3,001 3,0001 3,00001
3,000001
....
3
f(an)
2,5
3,7272 3,9703 3,9970 3,9997 3,99997
3,999997
....
4
Como los valores que toma la función para ambas sucesiones tienden al mismo valor 4, podemos
escribir:
De los dos ejemplos anteriores obtenemos las siguientes conclusiones:
• •
Se llama límite lateral por la izquierda de f(x) cuando x tiende a "a" al valor al que se
aproximan los valores de f(an) cuando los valores de an se aproximan a "a" tanto como queramos
pero manteniéndose menores que "a" (sucesión creciente). Escribimos entonces:
• •
Se llama límite lateral por la derecha de f(x) cuando x tiende a "a" al valor al que se
aproximan los valores de f(an) cuando los valores de an se aproximan a "a" tanto como queramos
pero manteniéndose mayores que "a" (sucesión decreciente). Escribimos:
Teorema: El límite de una función si existe es único y únicamente si li = ld, es decir, si ambos
límites laterales coinciden.
Concepto de límite. Casos de indeterminación.
En el punto segundo de este capítulo hemos definido el límite de f(x) cuando x tiende a "a" por
medio de sucesiones. Esta definición aunque muy comprensible desde el punto de vista intuitivo,
nos obligaría a comprobar todas las sucesiones que se aproximan a "a" (o al menos muchas de
ellas) y ver hacia quién tiende f(an). El cálculo pude ser engorroso y la definición poco rigurosa si
sólo comprobamos una ó dos como de hecho hemos hecho allí.
Una definición más rigurosa sería:
"Se dice que f(x) tiene por límite l cuando x tiende a "a" y se escribe , si para todo número real ,
positivo y suficientemente pequeño, es posible determinar otro número real , que depende de ,
tal que si se cumple , entonces se ha de cumplir que ".
La definición anterior equivale a decir que para todo entorno de "l" existe otro de “a” en el cual
todo punto de este entorno menos “a” por medio de la función va a el entorno
Gráficamente:
Ejemplo:
Demostrar que
Consideremos un , hemos de encontrar un que verifique:
entonces:
Y despejando x:
Restando 2 a los tres miembros:
Basta pues tomar:
para que se cumpla la definición
Diremos que un límite es determinado si es un número real o bien . En cualquier otro caso se dirá
que es indeterminado.
Existen 7 casos de indeterminación (no tienen sentido estos resultados):
En apartados posteriores diremos cómo solucionar cada una de ellas
Definición de limites:
El límite de una función es un concepto fundamental del análisis matemático, un caso de límite
aplicado a las funciones.
La noción de límite tiene múltiples acepciones. Puede tratarse de una línea que separa dos
territorios, de un extremo a que llega un determinado tiempo o de una restricción o limitación.
Para la matemática, un límite es una magnitud fija a la que se aproximan cada vez más los
términos de una secuencia infinita de magnitudes.
Función, por su parte, también coincide con el término anterior en lo que respecta a su origen. Y
es que, de igual modo, viene del latín, más exactamente de “functio”, que es sinónimo de “función
o ejecución
Interpretación geométrica:
1.-Definir que es la interpretación geométrica:
Geométricamente la derivada de una función f en un punto determinado se interpreta como el
valor de la pendiente de la recta tangente a la gráfica def en dicho punto.
La derivada es uno de los conceptos más importante en matemáticas. La derivada es el resultado
de un límite y representa la pendiente de la recta tangente a la gráfica de lafunción en un punto.
Pero vayamos por partes.
La definición de derivada es la siguiente:
Podría, pues, no existir tal límite y ser la función no derivable en ese punto.
La interpretacióngeométrica de la derivada la tienes cuando se evalúa en un cierto punto de una
función. Es decir, si tienes una función f, la derivada de f en un punto Xo viene a ser la pendiente
de la recta que es tangente ala función en dicho punto. Esto sólo tiene sentido si la derivada está
bien definida en dicho punto.
Limites por la izquierda y por la derecha de una función:
Diremos que el límite de una función f(x) cuando x tiende hacia a por la izquierda es L, si y sólo si
para todo ε > 0 existe δ > 0 tal que si x (a − δ, a) , entonces |f (x) − L| < ε .
Diremos que el límite de una función f(x) cuando x tiende hacia a por la derecha es L , si y sólo si
para todo ε > 0 existe δ > 0 tal que si x (a, a + δ), , entonces |f (x) - L| <ε .
El límite de una función en un punto si existe, es único.
Ejemplos
1.
En este caso vemos que el límite tanto por la izquierda como por la derecha cuando x tiende a 2 es
4.
El límite de la función es 4 aunque la función no tenga imagen en x = 2.
Para calcular el límite de una función en un punto, no nos interesa lo que sucede en dicho punto
sino a su alrededor.
2.
Como no coinciden los límites laterales, la función no tiene límite en x = 0.
Suma de limites:
Límite de una suma de funciones
El límite de una suma de dos funciones convergentes, es igual a la suma de los límites de cada una
de ellas:
diferencia
Se define diferencial de una función y = f(x) en un punto x, y se simboliza por dy ó df(x), al
producto f'(x) • h. Por tanto,
dy = df(x) = f'(x) • h
continuidad y limites de una funcion
Límite de una función
La noción de límite de una función en un número (un punto de la recta real) se presentará
mediante el siguiente ejemplo: Supongamos que se nos pide dibujar la gráfica de la función
Para todo punto x ≠ 1 podemos trazar la gráfica por los métodos conocidos por todos nosotros.
Ahora, para tener idea del comportamiento de la gráfica de f cerca de x=1, usamos dos conjuntos
de valores x, uno que se aproxime al 1 por la izquierda y otro por la derecha. La siguiente tabla
muestra los correspondientes valores de f (x).
x se acerca al 1 por la izquierda x se acerca al 1 por la derecha
x
0,9
0,99
0,999 1
f(x)
2,71
2,9701 2,997001
1,001 1,01
¿?
1,1
3,003001
3,0301 3,31
f (x) se acerca al 3 f (x) se acerca al 3
La figura 1 es la gráfica de la función y como podemos observar, en dicha gráfica hay un salto en el
punto (1; 3), esto se debe a que la función f no está definida en el número 1. Es de notar que ésta
gráfica es la de la función menos el punto (1; 3). La función g se obtiene a partir de la función f,
factorizando el numerador y simplificando. La discusión anterior conduce a la siguiente
descripción informal: Si f(x) se aproxima arbitrariamente a un número L cuando x se aproxima a a
por ambos lados, decimos que el límite f(x) cuando x tiende a a es L, y escribimos
Definición de límite de una función
Sea f una función definida en todo número de algún intervalo abierto I que contiene a a excepto
posiblemente en el número a mismo. El límite de f(x) cuando x se aproxima a a es L, lo cual se
escribe como , si para cualquier , no importa que tan pequeña sea, existe una tal que
si entonces
Esta definición indica que los valores de f(x) se aproximan al límite L conforme x se aproxima al
número a, si el valor absoluto de la diferencia puede hacerse tan pequeña como de desee
tomando x suficientemente cerca de a pero no igual a a.
En la definición no se menciona nada acerca del valor de f(x) cuando x = a; recordemos que la
función no necesita estar definida en a para que exista.
Ejemplos 1.
1) Utilicemos la definición para demostrar que
Como la función está definida en todo intervalo abierto que contiene a 2, entonces podemos
utilizar la definición para hacer la demostración.
Se debe demostrar que para cualquier existe una tal que
si entonces (A)
si entonces
si entonces
si entonces
Entonces, si tomamos se cumple la proposición (A). Esto demuestra que