fractales relacionados con polinomios ortogonales

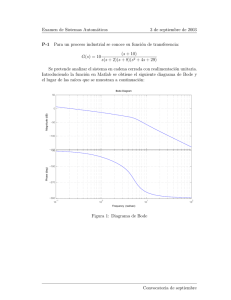
FRACTALES RELACIONADOS CON
POLINOMIOS ORTOGONALES
Juan Luis Varona* — Eloy Lafuente
Departamento de Matemáticas y Computación — Servicio Informático
Universidad de La Rioja
26004 Logroño, La Rioja
e-mail (internet): [email protected] y [email protected]
Resumen
El objetivo del trabajo es el estudio y la representación gráfica de
los fractales que aparecen al aplicar el método de Newton-Raphson
de resolución de ecuaciones a los polinomios de diversas familias de
polinomios ortogonales. Para ello hemos desarrollado la aplicación para
Macintosh denominada NewtonChebyshev, realizada en Think Pascal.
FUNDAMENTOS MATEMÁTICOS
Benoit Mandelbrot acuñó el término fractal en 1975. ¿Pero qué es un
fractal? Hay, o deberı́a haber, una definición matemática, que especifique
una idea básica en geometrı́a. Hay también un uso aproximado del término
para describir fenómenos que aproximan esta idea matemática. Hablando sin
mucha precisión un conjunto fractal es un conjunto que es más “irregular”
que los conjuntos que se consideran en la geometrı́a clásica. Por mucho
que se aumente el conjunto, aparecen visibles irregularidades cada vez más
pequeñas. Mandelbrot aduce que tales abstracciones geométricas se ajustan
a menudo mejor al mundo fı́sico que los conjuntos regulares o las curvas y
superficies suaves.
*
Para la realización del presente trabajo, J. L. Varona ha contado con una Ayuda a la
Investigación otorgada por el Instituto de Estudios Riojanos.
Este texto reproduce la comunicación presentada en el I Congreso Universidad y
Macintosh, UNED, Madrid, 19 al 21 de septiembre de 1994. Apareció publicada en las
Actas del Congreso UNIMAC’94, Vol. I (Madrid 1994), 39–43, UNED, Madrid, 1994; y en
el CD-ROM UNIMAC’94, junto con el programa NewtonChebyshev.
1
Para definir fractal, Mandelbrot escribe: “Un fractal es por definición un
conjunto para el que la dimensión de Hausdorff-Besicovitch excede estrictamente la dimensión topológica”. Un conjunto se puede considerar fractal
si su dimensión no es un número entero, sino que tiene “dimensión fraccionaria”. Estos conceptos entran de lleno en el seno de la matemática, y
ya fueron estudiados a principios de siglo, principalmente por Gaston Julia (Julia 1918), Pierre Fatou (Fatou 1919–20) y Felix Hausdorff (Hausdorff
1918). Realmente, la teorı́a matemática de la geometrı́a fractal descansa sobre tres fundamentos matemáticos: topologı́a métrica, teorı́a de la medida
y probabilidad.
Actualmente, la teorı́a fractal y, sobre todo, la representación gráfica de
objetos fractales está teniendo un tremendo auge de mano de los potentes
ordenadores. En las referencias se recogen unos cuantos tı́tulos que hacen
hincapié en estos aspectos.
En lo que a nosotros respecta, estamos interesados es estudiar los fractales que se obtienen al aplicar el método de Newton-Raphson —también
llamado simplemente de Newton— a una función compleja de variable compleja f : C −→ C. Fue esbozado por Newton en 1669, y desarrollado sistemáticamente (utilizando la derivada de la función) por Raphson en 1690.
Partiendo de un punto del plano complejo z0 , el método consiste en aplicar
el algoritmo iterativo
f (zn )
zn+1 = zn − 0
f (zn )
para encontrar las soluciones de la ecuación f (z) = 0.
Realmente, en sus orı́genes, el método estaba destinado únicamente a
encontrar raı́ces reales de funciones reales (en este caso, la idea geométrica
que lo inspira es clara), y fue Cayley en 1879 el primero en intentar aplicarlo a encontrar raı́ces complejas de funciones complejas (refieriéndose a él
como método de Newton-Fourier). Se preguntaba por las condiciones bajo
las cuales la sucesión zn converge a una raı́z ζ, y resolvió el problema para polinomios cuadráticos generales (Cayley 1879a). En el mismo año, en
una breve nota (Cayley 1879b) expresaba que “el caso de la ecuación cúbica parece presentar considerables dificultades”; y once años más tarde, sin
haber efectuado progresos aparentes, de nuevo comentaba: “Espero aplicar
esta teorı́a al caso de una ecuación cúbica, pero los cálculos son mucho más
difı́ciles” (Cayley 1890). Con la ayuda de las figuras generadas por ordenador que ahora tenemos, es fácil comprender que las dificultades que tuvo
que pasar Cayley en su tiempo eran inevitables ya que, esencialmente, el
problema consiste en encontrar el conjunto de Julia de la función iteradora
2
Figura 1: Método de Newton-Raphson aplicado a z 7→ z 3 − 1.
F (z) = z − f (z)/f 0 (z), que representamos en la figura 1. Como puede observarse a simple vista, las regiones en las que se divide el plano no parecen
estar determinadas por ninguna relación sencilla.
En esencia, lo que se hace es, partiendo de cada punto z0 de una región
del plano complejo, aplicar el método iterativo y analizar hacia qué raı́z de
f (z) = 0 converge el proceso y con qué velocidad (número de iteraciones
necesarias para llegar a una aproximación adecuada de la raı́z). Al punto se
le asigna un color dependiendo de la raı́z a la que converge (separación de
raı́ces), de la velocidad de convergencia, o de si no hemos logrado aproximar
ninguna raı́z. En el caso general, las regiones del plano para las que se produce convergencia hacia cada una de las raı́ces no tienen por qué estar bien
delimitadas, sino que su frontera es un objeto fractal. Uno de los primeros
artı́culos en los que se muestra gráficamente la naturaleza fractal de los dibujos que aparecen es (Curry et al. 1983), donde se analiza la convergencia
del método de Newton para polinomios cúbicos. Realmente, existen multitud de ejemplos de esta situación, muchos de ellos en libros de divulgación
cientı́fica, ya que pueden conseguirse gráficos de gran colorido. Los ejemplos
más utilizados son con polinomios de la forma z p − q, para los que es sencillo
3
encontrar las raı́ces.
Nuestra idea consiste en estudiar este hecho para polinomios provinientes
de diversas familias de polinomios ortogonales, tanto sobre la recta real
(o algún intervalo), como sobre la circunferencia unidad u otras curvas en
el plano. Para polinomios ortogonales en la recta se tiene una relación de
recurrencia a tres términos que permite evaluar un polinomio genérico en un
punto sin demasiado coste operacional; y además se tiene información sobre
las raı́ces de los polinomios (separación, estimaciones asintóticas, etc.), lo
que ayuda a comprobar la convergencia del método. Resultados similares,
aunque más complicados, ocurren en la circunferencia unidad.
Por otra parte, también planeamos ver qué ocurre con otros métodos iterativos de obtención de raı́ces, analizando si se obtienen los mismos fractales
o existe algún otro tipo de relación. Asimismo, si estos métodos conducen a
procedimientos acelerados para encontrar su representación gráfica.
LA APLICACIÓN “NewtonChebyshev”
Por el momento, nos hemos centrado en polinomios de Chebyshev de
primera y segunda clase y hemos elaborado un programa para Macintosh que
permite generar los fractales que se encuentran al analizar la convergencia del
método. Como caracterı́sticas principales, el programa permite seleccionar
el grado del polinomio (hasta 31), ampliar cualquier zona y emplear dos
algoritmos distintos: selección de raı́ces y tiempo de convergencia. Asimismo
permite guardar (y copiar) los dibujos generados en formato ‘PICT’.
El programa se denomina NewtonChebyshev, está realizado en Think
Pascal (versión 4.02) y cuenta con un completo interface Macintosh. Actualmente va por su versión 1.4. Por cuestiones de velocidad, necesita un ordenador con, al menos, un microprocesador 68020 y coprocesador matemático.
Funciona tanto bajo sistema 6 como 7 y posteriores (con el sistema 6 se
requiere QuickDraw Color). Puede funcionar con una partición de 256K de
memoria para ventanas pequeñas pero, para poder utilizar ventanas de mayor tamaño, se recomienda una partición de 1 Mega de RAM. Con la única
pretensión de poder usarla en modo emulación en los Power Macintosh, hemos incluido otra versión de la aplicación compilada de tal forma que no
necesite coprocesador.
Hay que reseñar que el programa funciona con cualquier número de colores disponibles (panel de control “Monitores”), aunque recomendamos usar
256 colores. Los resultados con un número menor pueden no ser adecuados
(pueden aparecer muchos colores repetidos en el gráfico) y, por otra parte, no
4
se saca mucho partido de utilizar un gran número de ellos. Con 256 colores,
todos los dibujos que puede generar se representan aceptablemente. Si utilizamos miles o millones de colores, los ficheros ‘PICT’ que crea el programa
son de mayor tamaño sin lograr excesiva mejora en la calidad de la representación. Además, es posible que, al usar la aplicación con miles o millones
de colores, se necesite asignar al programa mayor cantidad de memoria que
la señalada en el apartado anterior para poder copiar o guardar los dibujos.
(Quizás, aunque nunca lo hemos detectado, para copiar o guardar dibujos de
regiones muy intrincadas, también se necesitarı́a una mayor memoria incluso
usando 256 colores). En este mismo sentido, hemos de confesar que sólo hemos chequeado los aspectos relativos a la generación de archivos en formato
‘PICT’ bajo sistema 7. Como medida de precaución, hemos asignado a la
aplicación una cantidad de memoria sugerida de 1152 K.
Aunque actualmente el programa funciona completamente y no tiene
problemas conocidos, pensamos mejorarlo añadiéndole más posibilidades e
incrementando la velocidad de dibujo y de refresco de pantalla. Asimismo,
estamos estudiando la conveniencia de portar el programa a C++, pues esto
permitirá una gestión mucho más sencilla de las operaciones con complejos.
Por último, es de destacar que una recompilación para Power Macintosh
producirı́a una radical aceleración en los laboriosos cálculos matemáticos
necesarios. Este es otro de nuestros objetivos en cuanto dispongamos de las
herramientas necesarias.
Al arrancar, la aplicación detecta si está configurada con suficiente memoria para poder usar la ventana mediana cuadrada. Si tiene bastante, usa
esa por defecto y, en caso contrario, emplea la ventana pequeña cuadrada
(lo cual siempre es posible con 256 K asignados a la aplicación, permitiendo
incluso copiar y guardar). A continuación, sortea si va a emplear polinomios
de Chebyshev de primera o segunda clase, el grado del polinomio (entre 3
y 10) y el algoritmo a usar (selección de raı́ces o tiempo de convergencia), y
comienza a dibujar. La región del plano complejo que se utiliza inicialmente
es el cuadrado de centro el origen y lado 3. El proceso de dibujo se detiene
nada más que pulsemos el botón del ratón; entonces podemos ajustar todos
los valores que deseemos a nuestro gusto y comenzar un nuevo gráfico.
Manejo del programa
La aplicación NewtonChebyshev cuenta, además de con el menú “Acerca de NewtonChebyshev...”, que muestra información sobre el programa y
sus autores, con los menús “Archivo”, “Edición”, “Ejemplos”, “Zoom” y
5
“Preferencias”, cuyo funcionamiento explicaremos a continuación.
Menú “Archivo”:
— “Nuevo...”: Cierra la ventana existente y abre una nueva del tamaño
y forma indicados en el menú “Preferencias”. Efectúa un nuevo sorteo de
colores para las distintas regiones y, utilizando el algoritmo seleccionado
(selección de raı́ces o tiempo de convergencia) y la clase y grado de polinomio
que hemos usado en el último dibujo, comienza uno nuevo en la región del
plano complejo dada por el cuadrado inicial z = (x, y) con −1.5 ≤ x ≤ 1.5,
−1.5 ≤ y ≤ 1.5. Para realizar el dibujo emplea el número de iteraciones y
precisión indicado en el menú “Preferencias”.
— “Continuar”: Continúa dibujando un gráfico que hemos detenido pulsando el botón del ratón.
— “Redibujar”: Tiene varias funciones dependiendo de la situación. Si
no hemos cambiado de algoritmo, redibuja la ventana cambiando los colores.
Si hemos cambiado, muestra el gráfico correspondiente al nuevo algoritmo
seleccionado. Por último, también puede usarse cuando hemos detenido una
actualización de la ventana y, por alguna causa, han quedado regiones sin
dibujar.
— “Exportar como PICT...”: Guarda la ventana de dibujo en un fichero en formato ‘PICT’. El creador del archivo es el que figura en el recurso
‘CREA’, ID = 129. Hemos puesto que sea ‘ttxt’ (TeachText o SimpleText),
pero puede modificarse con ResEdit si se desea; para que sea lo más sencillo posible, la aplicación cuenta entre sus recursos con la correspondiente
plantilla (“template”) para ResEdit.
— “Selección de raı́ces”: Este algoritmo de dibujo da a cada punto un
color de acuerdo a la raı́z del polinomio a la que converge el método de
Newton con valor inicial en ese punto. Si en el número máximo de iteraciones
previsto no se ha producido convergencia con la precisión requerida, pinta
el correspondiente punto en negro. La figura 2 muestra un ejemplo.
— “Tiempo de convergencia”: Con este algoritmo se asigna a cada punto
un color de acuerdo al número de iteraciones necesario para lograr una buena
aproximación de alguna raı́z (independientemente de cual sea esta). Los
puntos negros tienen el mismo significado que en el algoritmo anterior. La
figura 3 muestra un ejemplo.
— “Información...”: Muestra una ventana con información sobre el dibujo, el ordenador empleado, y la velocidad de proceso. (Fijarse que, como los
procesos de dibujo llegan a ser bastante lentos debido a la laboriosidad de los
cálculos matemáticos necesarios, esto proporciona una prueba para medir la
6
Figuras 2 y 3: Método de Newton aplicado a los polinomios de
Chebyshev de primera clase de grado 5. El primer gráfico corresponde al algoritmo de selección de raı́ces y el segundo al de tiempo
de convergencia.
velocidad en coma flotante de un ordenador.) Los datos mostrados pueden
guardarse en un archivo de texto sin más que usar el botón “Guardar info”.
El creador del archivo es el que figura en el recurso ‘CREA’, ID = 128. Hemos puesto que sea ‘MSWD’ (Microsoft Word), aunque puede modificarse
con ResEdit si se desea.
— “Tabla de colores...”: Muestra una ventana con los colores empleados en el dibujo y permite realizar un nuevo sorteo de colores o cambiar
individualmente los que se desee mediante el selector de color estándar de
Apple.
— “Salir”: Cierra la ventana existente y abandona la aplicación.
Menú “Edición”:
— En este menú sólo tiene utilidad el ı́tem “Copiar”, que copia (como
‘PICT’) el contenido de la ventana actual de dibujo en el portapapeles para
posteriormente poder pegarlo en el Apuntador o en otra aplicación.
Menú “Ejemplos”:
— Se comporta como usar “Nuevo...” del menú “Archivo”, pero con el
añadido de que permite elegir la clase de polinomio (de primera clase para
los ı́temes “ChebyshevT” y de segunda para los ı́temes “ChebyshevU”) y el
7
grado. En el menú esta previsto directamente hasta grado 10. Si se desea
grado mayor, hay que usar los ı́temes “ChebyshevT grado...” o “ChebyshevU
grado...”; de esta forma se pueden utilizar hasta polinomios de grado 31. Hay
que tener en cuenta que, cuanto mayor sea el grado del polinomios, más lento
es el proceso de dibujo. Recordar que en todos ellos se parte de la región del
plano dada por z = (x, y) con −1.5 ≤ x ≤ 1.5, −1.5 ≤ y ≤ 1.5.
Menú “Zoom”:
— Acerca o aleja una zona del dibujo. Lógicamente, la principal utilidad
de este menú es ampliar una región del dibujo para verla con más detalle.
También permite (ı́tem “Mover centro”) desplazar la zona de representación
que estamos viendo aunque sin cambiar la escala. Su uso es sencillo: al seleccionar uno de los ı́temes el cursor se transforma y la aplicación espera a que
hagamos clic con el ratón en el punto central de la nueva región a representar, ya sea ampliada, centrada o, simplemente, movida (aparecen tres tipos
de cursores según lo que estemos haciendo). Tras recibir el clic, el programa comienza a dibujar utilizando para ello todas las nuevas caracterı́sticas
sobre la ventana, algoritmo, precisión o número máximo de iteraciones que
hayamos seleccionado. Por último, tener en cuenta que, al usar este menú, se
cambian o no los colores de dibujo según esté o no sin marcar el correspondiente ı́tem “Zoom conserva colores” del menú “Preferencias”. Puede verse
un ejemplo de una zona ampliada en las figuras 4 y 5.
Menú “Preferencias”:
— “Avisar al acabar”: Hace que suene o no un sonido de aviso cada vez
que se concluye un dibujo.
— “Zoom conserva colores”: Hace que, al efectuar un zoom, se continúe
dibujando con los mismos colores o se efectúe una nueva asignación de colores
por sorteo.
— “Ventana cuadrada”: Si la siguiente ventana de dibujo debe ser cuadrada o rectangular. Tener en cuenta que, aunque la ventana no sea cuadrada, la zona del plano complejo que estamos representando siempre es un
cuadrado luego, en este caso, las escalas de los ejes horizontal y vertical no
serán las mismas.
— “Grado ajusta precisión”: Si la precisión asignada (error permitido
entre el valor exacto de una raı́z y un valor aproximado) en el menú debe ser
considerada relativa y ajustarse dividiéndola por el grado del polinomio. La
razón de ser de esta opción es que, cuanto mayor sea el grado del polinomio,
8
Figuras 4 y 5: Algoritmo de tiempo de convergencia aplicado a los
polinomios de Chebyshev de segunda clase de grado 7. El primer
gráfico corresponde a la vista general y el segundo a una ampliación
por 10 de su zona superior derecha.
más raı́ces tiene y más juntas están, luego se va a necesitar una mayor
precisión para poder considerar que el valor obtenido tras alguna iteración
responde ya a una buena aproximación de alguna raı́z determinada.
— “Ventana pequeña”: La siguiente ventana que utilicemos será de tamaño 180 × 180 o 340 × 180 puntos respectivamente según esté o no seleccionada la opción “Ventana cuadrada”.
— “Ventana mediana”: Análogo a lo anterior pero con tamaños 280×280
o 440 × 280.
— “Ventana grande”: Análogo a los anteriores pero con tamaños 380 ×
380 o 540 × 380.
— Ítemes referidos al número de iteraciones: Número máximo de iteraciones permitidos para ver si el proceso iterativo que parte de cada punto
ha convergido a alguna raı́z con la precisión deseada y, consecuentemente,
pintar el punto con el correspondiente color. Si no ha habido convergencia,
el punto se pinta de negro. Está previsto en el menú que el número de iteraciones sea 50, 100, 250 o 500, pero se puede elegir una cantidad cualquiera
mediante el diálogo que se obtiene con el ı́tem “Iteraciones...”.
— Ítemes referidos a la precisión: Que la precisión sea pequeña, mediana
o grande significa que el error permitido entre el valor exacto de una raı́z y
un valor aproximado sea, respectivamente, 0.01, 0.001 o 0.0001. Realmente,
este valor se divide por el grado del polinomio si estamos usando la opción
9
“Grado ajusta precisión”. El último ı́tem del menú, “Precisión...”, muestra
un diálogo que nos permite asignar una cantidad arbitraria. Este diálogo
tiene contiene un cuadro de comprobación (“checkbox”) con un significado
equivalente al del ı́tem “Grado ajusta precisión”.
Por último, en lo que respecta al uso de los menús, destacar que la
aplicación cuenta con globos de ayuda que, cuando la estamos usando bajo
sistema 7 o posterior, explican el manejo de todos los menús.
Referencias
Barnsley, M.F., y Demko, S., 1985: “Iterated function systems and the global construction of fractals”, Proc. R. Soc. London, Ser. A, vol. 399, 243–275.
Beardon, A.F., 1991: Iteration of Rational Functions, Springer-Verlag, Nueva York.
Bergweiler, W., 1993: “Iteration of meromorphic functions”, Bull. Amer. Math.
Soc., vol. 29, 151–188.
Blanchard, P., 1984: “Complex analytic dynamics on the Riemann sphere”, Bull.
Amer. Math. Soc., vol. 11, 85–141.
Brolin, H., 1965: “Invariant sets under iteration of rational functions”, Ark. Mat.,
vol. 6, 103–144.
Cayley, M.A., 1879a: “Application of the Newton-Fourier method to the imaginary
root of an equation”, Quart. J. Math., vol. 16, 179–185.
Cayley, M.A., 1879b: “The Newton-Fourier imaginary problem”, Amer. J. Math.,
vol. 2, 97.
Cayley, M.A., 1890: “Sur les racines d’une équation algebrique”, Comptes Rendus
Acad. Sci. Paris, vol. 110, 215–218.
Curry, J.H., Garnett, L., y Sullivan, D., 1983: “On the iteration of a rational function: computer experiments with Newton’s method”, Comm. Math. Phys., vol. 91,
267–277.
Edgar, G.A., 1990: Measure, Topology, and Fractal Geometry, Springer-Verlag. Nueva York.
Fatou, P., 1919–20: “Sur les équations fonctionnelles”, Bull. Soc. Math. France,
vol. 47 (1919), 161–271 y vol. 48 (1920), 33–94 y 208–314.
Hausdorff, F., 1918: “Dimension äußeres Maß”, Math. Ann., vol. 79, 157–179.
Julia, G., 1918: “Mémoire sur l’itération des fonctions rationnelles”, J. Math. Pures
Appl., vol. 8, 47–245.
Mandelbrot, B., 1982: The Fractal Geometry of Nature, Freeman. San Francisco.
Peitgen, H.O., y Richter, P.H., 1986: The Beauty of Fractals, Springer-Verlag, Nueva
York.
10
Peitgen, H.O., y Saupe, D., 1988: The Science of Fractal Images, Springer-Verlag,
Nueva York.
Szegő, G., 1967: Orthogonal Polynomials (3.a ed.), American Mathematical Society,
Providence, RI.
11