EXAMEN DE ESTADÍSTICA Junio 2012

EXAMEN DE ESTADÍSTICA
Junio 2012
Apellidos:
DNI:
Nombre:
GRUPO:
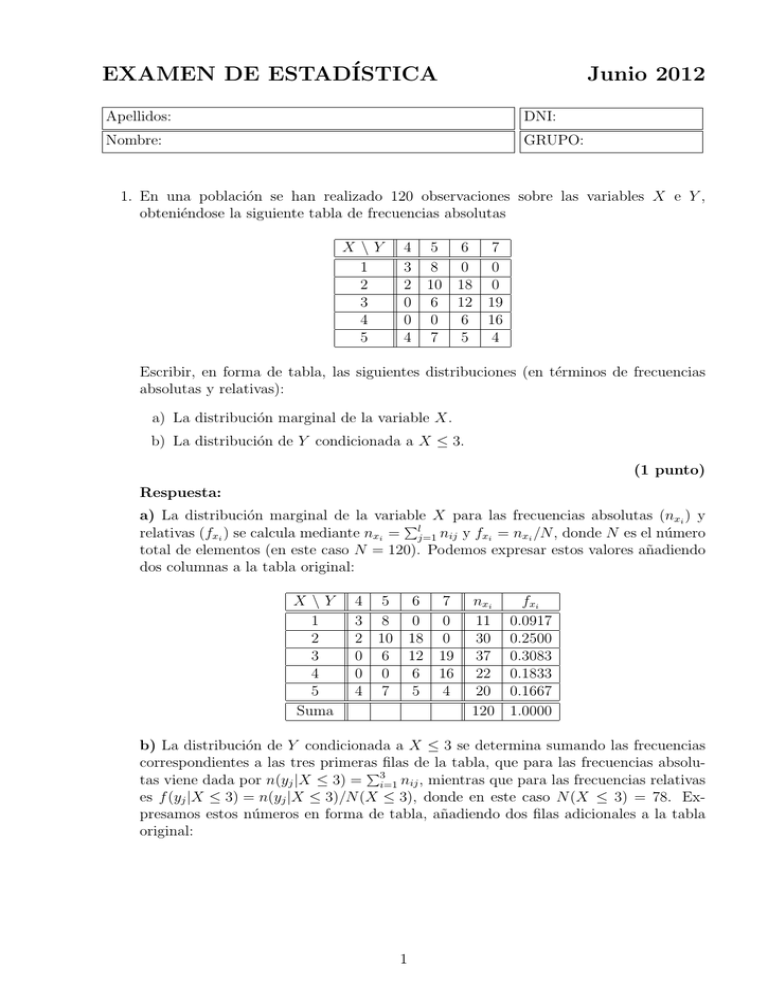
1. En una población se han realizado 120 observaciones sobre las variables X e Y ,
obteniéndose la siguiente tabla de frecuencias absolutas
X \Y
1
2
3
4
5
4
3
2
0
0
4
5 6 7
8 0 0
10 18 0
6 12 19
0 6 16
7 5 4
Escribir, en forma de tabla, las siguientes distribuciones (en términos de frecuencias
absolutas y relativas):
a) La distribución marginal de la variable X.
b) La distribución de Y condicionada a X ≤ 3.
(1 punto)
Respuesta:
a) La distribución marginal de la variable X para las frecuencias absolutas (nxi ) y
P
relativas (fxi ) se calcula mediante nxi = lj=1 nij y fxi = nxi /N , donde N es el número
total de elementos (en este caso N = 120). Podemos expresar estos valores añadiendo
dos columnas a la tabla original:
X \Y
1
2
3
4
5
Suma
4 5
3 8
2 10
0 6
0 0
4 7
6 7
0 0
18 0
12 19
6 16
5 4
nxi
11
30
37
22
20
120
f xi
0.0917
0.2500
0.3083
0.1833
0.1667
1.0000
b) La distribución de Y condicionada a X ≤ 3 se determina sumando las frecuencias
correspondientes a las tres primeras filas de la tabla, que para las frecuencias absoluP
tas viene dada por n(yj |X ≤ 3) = 3i=1 nij , mientras que para las frecuencias relativas
es f (yj |X ≤ 3) = n(yj |X ≤ 3)/N (X ≤ 3), donde en este caso N (X ≤ 3) = 78. Expresamos estos números en forma de tabla, añadiendo dos filas adicionales a la tabla
original:
1
X \Y
1
2
3
4
5
n(yj |X ≤ 3)
f (yj |X ≤ 3)
4
5
6
7
3
8
0
0
2
10
18
0
0
6
12
19
0
0
6
16
4
7
5
4
5
24
30
19
0.0641 0.3077 0.3846 0.2436
2
suma
78
1.0000
2. Sea una caja que contiene 4 bolas rojas y 2 bolas negras. Se selecciona una bola al
azar, se anota su color y se devuelve a la caja. Esta actividad se repite 100 veces.
Encontrar la probabilidad de observar una bola roja 60 veces o más.
(1 punto)
Respuesta:
La probabilidad de sacar bola roja en cada extracción será
P (bola roja) =
2
4
=
6
3
El proceso sigue una distribución binomial. El problema es que el número de ensayos
es muy alto (n = 100), por lo que las tablas de la distribución binomial no resultan
útiles. Sin embargo, como se verifica
np = 100 ×
2
>5
3
y
nq = 100 ×
1
>5
3
podemos aproximar la binomial por una Normal N (µ, σ), donde
µ = np = 66.67
y
σ=
√
npq = 4.71
Por tanto, la probabilidad que nos piden en el enunciado vendrá dada por
P (X ≥ 60) = P (X 0 > 59.5) = P (Z > −1.52) = 1−P (Z > 1.52) = 1−0.0643 = 0.9357
donde hemos hecho uso de la corrección de continuidad para pasar de X a X 0 , y donde
la variable X 0 ha sido tipificada a través de la transformación
Z=
59.5 − 66.67
X0 − µ
=
= −1.52
σ
4.71
3
3. Un análisis para detectar la rabia en perros descarta la enfermedad en un 95 por 100
de los casos cuando el animal está sano y lo señala como enfermo en el 99 por 100
de las veces cuando realmente está enfermo. Sabemos que en la población en estudio
el 0.1 por 100 de los perros padecen la enfermedad. Si en una clı́nica se presenta un
animal para someterlo al análisis y el resultado lo clasifica como enfermo, ¿cuál es la
probabilidad de que se haya cometido un error? Discutir el resultado.
(1 punto)
Respuesta:
Definamos los siguientes sucesos:
E={animal enfermo}
NE={animal no enfermo}
D={detección de la enfermedad}
ND={no detección de la enfermedad}
Las probabilidades que nos dan en el enunciado nos permiten escribir
P (E) = 0.001
⇒ P (NE) = 1 − P (E) = 0.999
P (D|E) = 0.99
⇒ P (ND|E) = 1 − P (D|E) = 0.01 (falso negativo)
P (ND|NE) = 0.95 ⇒ P (D|NE) = 1 − P (ND|NE) = 0.05 (falso positivo)
La solución a la pregunta planteada puede calcularse de forma inmediata utilizando el
Teorema de Bayes, que nos permite calcular la probabilidad de que el animal no esté
enfermo pese a que el análisis lo clasifica como tal, es decir
P (NE|D) =
=
P (D|NE) P (NE)
P (D|NE) P (NE) + P (D|E) P (E)
0.05 × 0.999
= 0.98
0.05 × 0.999 + 0.99 × 0.001
Como se observa, dicha probabilidad es muy alta (98%). Este resultado se debe a
que la probabilidad de falso positivo no es extremadamente pequeña (5%) y a que
la enfermedad tiene una incidencia muy baja en la población (0.1%). Ambas efectos
conducen a que en el denominador de la expresión anterior se verifique
P (D|NE) P (NE) >> P (NE) + P (D|E) P (E)
4
4. Calcular:
a) La mediana de una distribución N (5, 3).
b) El parámetro λ de una distribución de Poisson, sabiendo que la observación de 4
eventos corresponde al primer decil de la distribución.
c) El percentil 2 de una distribución binomial con n = 20 y p = 0.65.
d) El recorrido intercuartı́lico de una distribución N (3, 2).
(1 punto)
Respuesta:
a) En una distribución normal la media, la mediana y la moda coinciden. Por tano, la
mediana es 5.
b) Recorriendo la Tabla III, buscamos el valor de λ tal que la probabilidad acumulada
se 0.10. Para x = 4 esto sucede cuando λ = 8.0.
c) El percentil 2 corresponde a
n
X
b(x; n, p) = 0.98,
x=r
que para n = 20 y p = 0.65 (Tabla II), se obtiene cuando r = 9.
d) Usando la Tabla IV, vemos que α = 0.25 para z ' 0.67. Por tanto, el recorrido
intercuartı́lico de una N (0, 1) será [−0.67, +0.67]. En la distribución que nos piden
dicho intervalo se transforma mediante
z=
x−µ
σ
⇒
x = µ + zσ,
que para µ = 3 y σ = 2 se convierte en el intervalo [1.66, 4.34]. Por tanto
RI = 4.34 − 1.66 = 2.68
5
5. Sea x1 , x2 ,. . . , xn una muestra aleatoria de una población que sigue una distribución
de probabilidad de Rayleigh, con función de densidad:
f (x, σ 2 ) =
x − x22
e 2σ ,
σ2
x>0
Obtener el estimador de máxima verosimilitud para σ 2 .
(1 punto)
Respuesta:
n
Y
n
Y
xi − x2i2
L=
f (xi , σ ) =
e 2σ
2
σ
i=1
i=1
2
Tomando logaritmos (neperianos):
log L =
n
X
i=1
"
n
X
x2
log xi − log σ − i2 =
log xi − n log σ 2 −
2σ
i=1
#
2
Pn
2
i=1 xi
2σ 2
Derivando con respecto a σ 2 e igualando a cero
n
d log L
=− 2 +
2
d(σ )
σ
Pn
2
i=1 xi
2σ 2
=0
⇒
2
σ =
Pn
i=1
x2i
2n
(Nota: si en el paso anterior se deriva con respecto a σ en lugar de respecto a σ 2 , y se
despeja σ 2 , sale lo mismo.)
6
6. En unas elecciones a Rector de la UCM, la distribución de votos en la Facultad de
Fı́sicas fue la siguiente
Candidato A
Candidato B
Estudiantes Profesores PAS
610
88
37
118
39
14
a) ¿Fue la distribución de votos para cada candidato significativamente diferente entre
los tres tipos de votantes? Razónese la elección del nivel de significación entre
α = 0.10 y α = 0.01.
b) En toda la Universidad, de un total de 23818 votantes, el candidato A obtuvo
el 56.14% de los votos, mientras que el candidato B obtuvo el 43.86%. ¿Puede
afirmarse, con un nivel de significación de 0.001, que el candidato A obtuvo la
mayorı́a absoluta? (Es decir, ¿es PA > 0.5 con ese nivel de significación?)
(2.5 puntos)
Respuesta:
a) Contraste de hipótesis, con H0 : independencia de caracteres (test χ2 ). Contraste
unilateral (a la izquierda), con estadı́stico
χ2ν
k X
m
o2ij
(oij − eij )2 X
=
− n,
=
eij
i=1 j=1 eij
i=1 j=1
k X
m
X
donde, suponiendo H0 cierta, se verifica eij =
absolutas marginales.
Candidato A
Candidato B
oyj
con ν = (k − 1)(m − 1),
oxi oyj
n
, siendo oxi y oyj las frecuencias
Estudiantes Profesores
PAS
610 (590.6) 88 (103.0) 37 (41.4)
118 (137.4) 39 (24.0)
14 (9.6)
728
127
51
o xi
735
171
906
Con los datos de la tabla
χ2ν = 17.4202,
con ν = 2.
Tomando α = 0.01 (estricto para rechazar H0 ), la región de aceptación de H0 será
[0, χ2α,ν ]. En nuestro caso χ2α,ν = χ20.01,2 = 9.2103. Como χ2ν > χ2α,ν , se rechaza H0 . Es
decir, existe dependencia entre votar a un cierto candidato y el tipo de votantes.
b) Contraste para una proporción con n = 23818, PA = 0.5614, y PB = 1 − PA = 0.4386.
Las hipótesis nula y alternativa serán
(
H0 : PA ≤ 0.50
H1 : PA > 0.50
p − p0
0.5614 − 0.50
= q
=
z=q
p(1−p)
n
0.5614×0.4386
23818
0.0614
= 19.096
3.21 × 10−3
H0 se acepta con α = 0.001 si z ≤ zα ' 3.09. Por tanto, se rechaza H0 con α = 0.001,
es decir, puede afirmarse que el candidato A obtuvo mayorı́a absoluta con ese nivel de
significación.
7
7. A partir de 10 simulaciones con un modelo de clima se obtiene un valor medio de
temperatura invernal para un cierto lugar de 12.2◦ C y una desviación estándar de
2.5◦ C. Con el fin de evaluar el impacto de una supuesta deforestación en la zona, se
realizan 6 simulaciones bajo estas condiciones iniciales obteniéndose un valor medio de
temperatura invernal de 11.6◦ C, con una desviación estándar de 1.9◦ C. Calcúlese:
a) Un intervalo de confianza del 90% para la diferencia de las medias de la temperatura invernal en el lugar.
b) Dado el resultado, ¿se podrı́a afirmar que la deforestación supuesta en el modelo
produce un efecto en la temperatura invernal del lugar?
(2.5 puntos)
Respuesta:
n1 = 10 x1 = 12.2 s1 = 2.5
n2 = 6 x2 = 11.6 s2 = 1.9
a) Al tratarse de nuestras pequeñas y varianzas poblacionales desconocidas, es preciso
determinar antes si éstas son iguales o no.
(
Estadı́stico:
s21
s22
H0 : σ12 = σ22
H1 : σ12 6= σ22
= Fn1 −1,n2 −1 si H0 es cierta
Región de aceptación de H0 con α = 10%:
[F1−α/2,n1 −1,n2 −1 , Fα/2,n1 −1,n2 −1 ] =
−1
= [F0.95,9,5 , F0.05,9,5 ] = [F0.05,5,9
, F0.05,9,5 ] =
= [3.4817−1 , 4.7725] = [0.2872, 4.7725]
s21
= 1.7313 ∈ [0.2872, 4.7725]
s22
⇒ No podemos rechazar H0 , es decir, asumimos igualdad de varianzas. Por tanto:
s
"
Iµ1 −µ2 = (X 1 − X 2 ) ± tα/2,n1 +n2 −2 sp
con
s2p
1
1
+
n1 n2
#
= [0.60 ± 2.10] = [−1.50, 2.70]
(n1 − 1)s21 + (n2 − 1)s22
=
⇒ sp = 2.3037
n1 + n2 − 2
tα/2,n1 +n2 −2 = t0.05,14 = 1.761
b) Como 0 ∈ Iµ1 −µ2 , no podemos afirmar que la deforestación supuesta en el modelo
produzca un efecto en la temperatura invernal del lugar con un nivel de confianza del
90 %.
8