Curso intensivo de Krigeado ¿Qué es la Geoestadística? Algunas

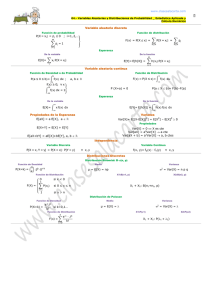
Momentos de la distribución
■ 1er. orden: Esperanza E(Z(x))=m(x)
➤
■
Componentes aleatorios y
➤ Componentes estructurados
➤ No luce “suave”
!Conviene considerar a z(x) como una función
aleatoria
Más definiciones
■
Varianza Var(Z(x))=E([Z(x)-m(x)]2)
➤ Covarianza C(xi,xj)
C(xi,xj)= E([Z(xi)-m(xi)].[Z(xj)-m(xj)])
➤ Semivariograma γ(xi,xj)
γ(xi,xj)= 0.5*E([Z(xi)-Z(xj)]2)
E(Z(x)) existe y no depende de x
➤ C(x+h,x)=C(h) (sólo depende de la separación)
■
■
■
■
El variograma debe cumplir algunas condiciones
matemáticas restrictivas
Salen de imponer que Var(Y)≥0, siendo
Y=Σ λiZ(xi), λi y xi conjunto arbitrario
Hay algunos modelos de variogramas que se
ajustan a los datos
➤
➤
■
■
■
h es en general un vector; suele asumirse isotropía,
por lo que γ(h)= γ(|h|)
γ(h)=var(Z)-C(h) sólo si la media es estrictamente
constante; en otro caso, usar γ(h) es más
conveniente que usar C(h)
Estimación del Variograma
■
■
■
Un tópico en sí mismo
“Left to the user…”
Métodos:
A sentimiento (!)
Mínimos cuadrados
➤ Jacknife
➤ Máxima Verosimilitud
➤ Validación Cruzada
➤ Validación Cruzada de Máxima Verosimilitud
➤…
➤
En general no sería posible
Requerirá hipótesis adicionales
Ej.: homogeneidad espacial
Las funciones aleatorias son sólo un
modelo posible de la realidad
Más sobre variogramas…
Def.: γ(h)=0.5*E([Z(x+h)-Z(x)]2)
■ γ(0)=0; γ(h)≥0
Rango (Range):
Implica
Var(Z(x))=C(0)
➤ γ(x+h,x)= γ(h)=0.5*E([Z(x+h)-Z(x)]2)
Var(Z(x))≥0; γ(xi,xj)≥0 pero C(xi,xj) no se sabe
Fórmula del Variograma
➤
■
2,5
➤
➤
■
Def.: Z(x) estacionaria de segundo orden si
➤
m(x) es llamada “deriva” o ”tendencia”
2do. orden:
➤
➤
Distancia a la cual el
variograma se estabiliza
2
1,5
Meseta (Sill) :
1
0
Distancia
Krigeado
■
■
■
Del geólogo sudafricano D. G. Krige
Hay muchas variantes y casos particulares
Caso Puntual: se modela el estimador con
N
Z * (x ) = ∑ λi (x ) Z ( xi )
➤
Esférico, Exponencial, Gaussiano, Pepita, etc.
Hay otros menos populares
Todos dependen de la meseta S y el rango a,
excepto el denominado Pepita (nugget)
■
Sin variograma…
Valor constante que toma el
variograma en distancias
mayores al rango
0,5
36
39
42
Definiciones…
➤
Usualmente z(x) está compuesta de
30
33
Base estadística
Incorporado en algunos GIS
(¿malamente? ¿parcialmente?...)
■
27
■
■
Concepto no probabilístico
➤ Quizá función continua
➤
➤ Detección
■
La realidad es simplemente una realización
o instancia de un experimento aleatorio
Sólo tenemos una realidad; hay que hacer
inferencia estadística sólo con ello
■
18
21
24
➤ Imputación
Algunas consecuencias…
V a riogra m a
de ausencias (obvio…)
de errores
➤ Estimación de sensibilidad de modelos
■
Def.: Aplicación de la teoría de las variables
regionalizadas a la estimación de procesos en el espacio
Si z(x) es el valor de z en el punto x, z(x) es una
variable regionalizada
12
15
¿Qué es la Geoestadística?
■
3
6
9
Es un método de Interpolación
■ Lo hemos citado y lo citaremos en:
■
0
Curso intensivo de Krigeado
i =1
eligiéndose los pesos λi(x) para que sea insesgado
(
)
E Z * ( x ) = m = E (Z ( x ))
y de varianza mínima
[
]
var Z ( x ) − Z * (x )
1
Algunos detalles(2)
Algunos detalles
■
■
■
Se asume m constante; hay variantes para otro
caso
Los pesos son función del punto
 0 γ 12 γ 13 L γ 1n 1   λ1   γ 1 
Salen del 
   
sistema: γ 21 0 γ 23 L γ 2 n 1  λ2  γ 2 
γ 31 γ 32 0
M M  M   M 

.  =  
M
M
M M  M   M 
 M
γ n1 γ n 2 γ n3 L 0 1  λn  γ n 

   
1
1 L 1 0  µ   1 
 1
Algunos detalles(3)
■
ε
γ 12

2
γ 21 ε
γ 31 γ 32

M
 M
γ
γ n2
 n1
1
 1
■
Nótese que:
M
M
γ n3 L ε 2
1
L
1
γ 1 
γ 
 2
M
.  =  
M  M   M 
1 λn  γ n 
   
0  µ   1 
Generar realizaciones
➤
■
■
El Krigeado es interpolante
■
Bajo ciertas hipótesis
➤
➤
La matriz del sistema es constante; puede usarse LU
El resultado es perfectamente determinista; lo
estocástico reside en los datos mismos
➤
Sólo si se asumen datos sin error
error ~N(-2/d); N nro. de puntos y d dimensión del espacio
(típicamente 2)
¡Incluso con el variograma erróneo!
– Pero en este caso la varianza no es consistente
Método Matricial de Simulación
Def.:
condicionada: Consiste en generar
realizaciones con igual media y varianza que la
disponible
➤ Condicionada: Idem, pero obligando a que
además adopte valores específicos en ciertos
puntos
■
No es el más eficaz si se necesitan muchos puntos
■
■
Implícitamente se asume normalidad
La fórmula para ZS es:
Tres tipos de métodos
■
La simulación se logra generando diversos u
Bandas Rotantes y Matricial
presentaremos el Matricial
➤
➤
Matricial O(n3)
Bandas rotantes O(n1/2)
Z S = Z * + M.u; M.MT = C; u i ~ N (0,1)
➤ Espectrales,
➤
➤ Sólo
➤
Problema estándar
Muchas librerías disponibles
Literatura & Software
■
Digital:
➤
Rudolf Dutter, Vienna Inst. of Technology
➤
Denis Marcotte, École Polytechnique de Montréal
➤
Oscar Rondón, Venezuela
CD del curso; http://www.statistik.tuwien.ac.at/public/dutt/vorles/geost_03/geo.html
CD del curso; http://geo.polymtl.ca/~marcotte/glq3401geo.html
Ejemplo: un MDE
Se comentarán más casos luego
■
➤ No
■
Sólo si el variograma es “exacto”
Sólo si la función aleatoria es normal
– En ese caso, es el Best incluso comparando con los no lineales
– Difícil de verificar la normalidad en la práctica (por lo
multivariado…)
i
➤
■
➤
Var ( Z * − Z ) = ∑ λi γ (xi − x ) + µ
Compatibles con las medidas disponibles
➤ Compatibles con el variograma asumido
Generar N realizaciones del raster buscado
➤ Delinear zona de visibilidad a un mástil
➤ Calcular área Ai de esa zona
➤ Calcular valor esperado, promedio, máximos, etc.
del conjunto Ai y sus niveles de confianza
El de Krigeado es un estimador BLUE
➤
El variograma depende de los datos
➤ Los coeficientes λi dependen del variograma, pero no
de los datos mismos
➤ Idem con la varianza, mediante la expresión
➤
■
■
➤
γ 13 L γ 1n 1  λ1 
 
γ 23 L γ 2n 1 λ2 
M M  M 
ε2
¿Para qué se usa la Simulación?
■
Donde
Simulación
Si los datos tienen un error cuya varianza es ε2
el sistema cambia levemente
2
Algunos detalles(3)
γ ij = γ (xi − x j ); γ i = γ ( xi − x )
■
CD del curso
■
Papel:
➤
■
■
Samper, F.J. y Carrera, J. 1990. Geoestadística: Aplicaciones a la
hidrología subterránea, CIMNE, ISBN 84-404-6045-7
Biblioteca GSLIB
Matlab+EasyKrig
ftp://globec.whoi.edu/pub/software/kriging/V2.1/easy_krig2.1
2