Flujo en Redes de Transporte
Anuncio

Flujo en Redes de Transporte
CSI / Matemáticas ITESM
Flujo en Redes de Transporte– p. 1/53
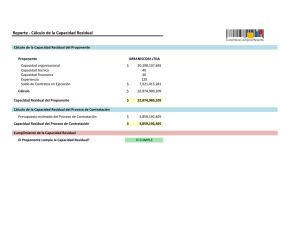
Red de Transporte
Una Red de Transporte es un grafo dirigido con peso
(V, E, c) donde hay dos vértices distinguidos: uno llamado
fuente y otro llamado sumidero. Se asume que todo vértice
del grafo v ∈ V está en un camino s
v
t. El peso de
cada lado debe ser no negativo y se considera la
capacidad del lado. Si (u, v) ∈
/ E , defina c(u, v) = 0.
16
s
12
v1
v2
t
7
10
4
20
9
13
v4
v3
4
14
Flujo en Redes de Transporte– p. 2/53
Un Flujo
Un flujo en una red de transporte (V, E, c) es una función
f : V × V → R que satisface:
Flujo en Redes de Transporte– p. 3/53
Un Flujo
Un flujo en una red de transporte (V, E, c) es una función
f : V × V → R que satisface:
1. Restricción de capacidad: ∀u, v ∈ V : f (u, v) ≤ c(u, v)
Flujo en Redes de Transporte– p. 3/53
Un Flujo
Un flujo en una red de transporte (V, E, c) es una función
f : V × V → R que satisface:
1. Restricción de capacidad: ∀u, v ∈ V : f (u, v) ≤ c(u, v)
2. Antisimetría: ∀u, v ∈ V : f (u, v) = −f (v, u)
Flujo en Redes de Transporte– p. 3/53
Un Flujo
Un flujo en una red de transporte (V, E, c) es una función
f : V × V → R que satisface:
1. Restricción de capacidad: ∀u, v ∈ V : f (u, v) ≤ c(u, v)
2. Antisimetría: ∀u, v ∈ V : f (u, v) = −f (v, u)
3. Conservación del flujo: ∀u ∈ V − {s, t}:
X
f (u, v) = 0
v∈V
Flujo en Redes de Transporte– p. 3/53
Un Flujo
Un flujo en una red de transporte (V, E, c) es una función
f : V × V → R que satisface:
1. Restricción de capacidad: ∀u, v ∈ V : f (u, v) ≤ c(u, v)
2. Antisimetría: ∀u, v ∈ V : f (u, v) = −f (v, u)
3. Conservación del flujo: ∀u ∈ V − {s, t}:
X
f (u, v) = 0
v∈V
f (u, v) se llamará el flujo de u a v .
Flujo en Redes de Transporte– p. 3/53
Un Flujo
Un flujo en una red de transporte (V, E, c) es una función
f : V × V → R que satisface:
1. Restricción de capacidad: ∀u, v ∈ V : f (u, v) ≤ c(u, v)
2. Antisimetría: ∀u, v ∈ V : f (u, v) = −f (v, u)
3. Conservación del flujo: ∀u ∈ V − {s, t}:
X
f (u, v) = 0
v∈V
f (u, v) se llamará el flujo de u a v . El valor del flujo f se
define como:
X
|f | =
f (s, v)
v∈V
Flujo en Redes de Transporte– p. 3/53
Ejemplo de Flujo
c
s
v1
v2
v3
v4
t
f
s
v1
v2
v3
v4
t
s
0
16
0
0
13
0
s
0
11
0
0
8
0
v1
0
0
12
0
10
0
v1
-11
0
12
0
-1
0
v2
0
0
0
0
9
20
v2
0
-12
0
-7
4
15
v3
0
0
7
0
0
4
v3
0
0
7
0
-11
4
v4
0
4
12
14
0
0
v4
-8
1
-4
11
0
0
t
0
0
0
0
0
0
t
0
0
-15
-4
0
0
11/16
s
v1
1/4
12/12
0/10
v2
15/20
t
7/7
4/9
8/13
v4
v3
4/4
11/14
Flujo en Redes de Transporte– p. 4/53
Observación
Suponga una red de transporte (V, E, c) y un flujo en ella f .
Si no hay lado de u a v ni de v a u entonces
f (u, v) = f (v, u) = 0
Flujo en Redes de Transporte– p. 5/53
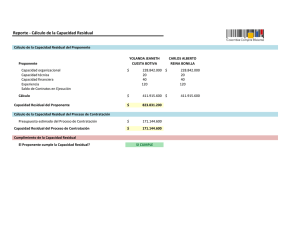
Red Residual
Sea G = (V, E, c) una red de transporte y f un flujo sobre
ella. La capacidad residual de lado (u, v) respecto a f se
define como:
cf (u, v) = c(u, v) − f (u, v)
Flujo en Redes de Transporte– p. 6/53
Capacidad Residual: Ejemplo
c
s
v1
v2
v3
v4
t
f
s
v1
v2
v3
v4
t
s
0
16
0
0
13
0
s
0
11
0
0
8
0
v1
0
0
12
0
10
0
v1
-11
0
12
0
-1
0
v2
0
0
0
0
9
20
v2
0
-12
0
-7
4
15
v3
0
0
7
0
0
4
v3
0
0
7
0
-11
4
v4
0
4
12
14
0
0
v4
-8
1
-4
11
0
0
t
0
0
0
0
0
0
t
0
0
-15
-4
0
0
cf
s
v1
v2
v3
v4
t
s
0
5
0
0
5
0
v1
11
0
0
0
11
0
v2
0
12
0
7
5
5
v3
0
0
0
0
11
0
v4
8
3
15
3
0
0
t
0
0
15
4
0
0
Flujo en Redes de Transporte– p. 7/53
Red Residual
Dada una red de transporte G = (V, E, c) y un flujo f , la red
residual de G inducida por f , Gf = (V, Ef , cf ) donde
Ef = (u, v) ∈ V × V : cf (u, v) > 0
Flujo en Redes de Transporte– p. 8/53
Red Residual
cf (p) = mı́n cf (u, v) : (u, v) ∈ p
cf
s
v1
v2
v3
v4
t
s
0
5
0
0
5
0
v1
11
0
0
0
11
0
v2
0
12
0
7
5
5
v3
0
0
0
0
11
0
v4
8
3
15
3
0
0
t
0
0
15
4
0
0
v1
5
s
11
5
8
12
v2
5
4
3
7
11
v4
5
3
v3
15
t
4
11
Flujo en Redes de Transporte– p. 9/53
Ejemplo
11/16
s
12/12
v1
10
1/4
v2
15/20
t
7/7
4/9
v4
8/13
v3
4/4
11/14
v1
5
s
11
5
8
12
v2
5
4
3
7
11
v4
5
3
v3
15
t
4
11
Flujo en Redes de Transporte– p. 10/53
Extensión de f a pares de conjuntos
Sean X y Y subconjuntos de vértices:
XX
f (X, Y ) =
f (x, y)
x∈X y∈Y
Flujo en Redes de Transporte– p. 11/53
Lema 1
Sea G = (V, E, c) una red de transporte y f un flujo sobre G:
f (X, X) = 0
f (X, Y ) = −f (Y, X)
Si X ∩ Y = ∅: f (X ∪ Y, Z) = f (X, Z) + f (Y, Z)
Flujo en Redes de Transporte– p. 12/53
Resultado
Sea G = (V, E, c) una red de transporte con fuente s y
sumidero t, y sea f un flujo en G. Sea Gf la red de
transporte residual inducida por f , y además sea f ′ un flujo
en Gf . Entonces si se define la función f + f ′ : V × V → R
como
(f + f ′ )(u, v) = f (u, v) + f ′ (u, v)
entonces f + f ′ es un flujo sobre G con valor
|f + f ′ | = |f | + |f ′ |.
Flujo en Redes de Transporte– p. 13/53
Caminos aumentados
Sea G = (V, E, c) una red de transporte y f un flujo. Un
camino aumentado es un camino simple de s a t en la red
residual Gf . Por definición, en cada lado (u, v) de un
camino residual es posible aumentar el flujo de (u, v) en
una cantidad positiva sin violar la restricción de la
capacidad en ese lado. La capacidad residual del camino
aumentado p se define como
cf (p) = cf (u, v) : (u, v) es un lado de p
Flujo en Redes de Transporte– p. 14/53
Lema 2
Sea G = (V, E, c) una red de transporte,f un flujo en G, p un
camino aumentado en Gf . Define la función:
fp : V × V → ℜ como
si (u, v) es un lado de p
cf (p)
fp (u, v) =
−cf (p) si (v, u) es un lado de p
0
en otro caso.
Entonces, fp es un flujo en Gf con valor |fp | = cf (p) > 0.
Flujo en Redes de Transporte– p. 15/53
Corolario
Sea G = (V, E, c) una red de transporte, f un flujo sobre G,
y p un camino aumentado sobre Gf . Si fp es el flujo
definido anteriormente, entonces f ′ = f + fp es un flujo
sobre G cuyo valor es |f ′ | = |f | + |fp | > |f |.
Flujo en Redes de Transporte– p. 16/53
Corte
Un corte (S, T ) de una red de transporte G = (V, E, c) es
una partición de V en dos conjuntos S y T = V − S tal que
s ∈ S y t ∈ T . La capacidad de un corte (S, T ) es
X
c(S, T ) =
c(u, v)
u∈S,v∈T
16
s
12
v1
v2
t
7
10
4
20
9
13
v4
v3
c({s, v1 , v4 } , {v2 , v3 , t}) = 26
4
14
Flujo en Redes de Transporte– p. 17/53
Ejemplo 2 de Corte
16
s
12
v1
v2
t
7
10
4
20
9
13
v4
v3
4
14
c({s, v1 , v4 } , {v2 , v3 , t}) = 16 + 4 + 7 + 4 = 31
Flujo en Redes de Transporte– p. 18/53
Flujo Neto
Sea f un flujo en una red de transporte G con fuente s y
sumedero t, y sea (S, T ) un corte cualquiera. El flujo neto a
través de un corte (S, T ) se define como
X
f (S, T ) =
f (u, v)
u∈S,v∈T
Flujo en Redes de Transporte– p. 19/53
Ejemplo de flujo neto
11/16
s
v1
12/12
10
1/4
v2
15/20
t
7/7
4/9
8/13
v4
v3
4/4
11/14
f ({s, v1 , v4 } , {v2 , v3 , t}) = f (v1 , v2 ) + f (v4 , v2 ) + f (v4 , v3 )
= 12 + (−4) + 11
= 19
Flujo en Redes de Transporte– p. 20/53
Lema 3
Sea f un flujo sobre la red de transporte G = (V, E, c) con
fuente s y sumidero t, y sea (S, T ) un corte de G. Entonces,
el flujo neto a través del corte (S, T ) es |f |.
Flujo en Redes de Transporte– p. 21/53
Lema 3
Sea f un flujo sobre la red de transporte G = (V, E, c) con
fuente s y sumidero t, y sea (S, T ) un corte de G. Entonces,
el flujo neto a través del corte (S, T ) es |f |.
Notando que f (S − s, V ) = 0 tenemos:
f (S, T ) =
=
=
=
=
f (S, V ) − f (S, S)
f (S, V )
f (s, V ) + f (S − s, V )
f (s, V )
|f |
Flujo en Redes de Transporte– p. 21/53
Lema 4
El valor de cualquier flujo en una red de transporte está
acotado superiormente por la capacidad de cualquier corte
de G.
Flujo en Redes de Transporte– p. 22/53
Lema 4
El valor de cualquier flujo en una red de transporte está
acotado superiormente por la capacidad de cualquier corte
de G.
Sea (S, T ) un corte cualquiera de G y sea f cualquier flujo:
por el lema anterior:
|f | =
=
=
≤
=
=
f (S, T )
P
f (u, v)
u∈S,v∈T
P
P
f (u, v)
u∈S
v∈T
P
P
c(u, v)
u∈S
v∈T
P
u∈S,v∈T c(u, v)
c(S, T )
Flujo en Redes de Transporte– p. 22/53
Teorema Fundamental
Sea f un flujo sobre la red de transporte G = (V, E, c) con
fuente s y sumidero t, entonces las siguientes condiciones
son equivalentes:
1. f es un flujo máximo sobre G.
2. La red residual Gf no contiene caminos aumentados.
3. |f | = c(S, T ) para algún corte (S, T ) de G.
Flujo en Redes de Transporte– p. 23/53
Demostración
(1) → (2)
Por contradicción: suponga que f es un flujo máximo pero
que Gf posee un camino aumentado p. Por consiguiente,
f + fp es un flujo sobre G cuyo valor es |f + fp | > |f | por
tanto f no es un flujo máximo.
Flujo en Redes de Transporte– p. 24/53
Demostración
(2) → (3)
Suponga que no existe un camino aumentado de s a t en
Gf . Defina
S = {v ∈ V : existe un camino de s a v}
y T = V − S . Así (S, T ) es un corte para G donde s ∈ S y
t ∈ T y para cada par de vértices (u, v), u ∈ S y v ∈ T ,
f (u, v) = c(u, v), porque de otra forma v ∈ S . Y
X
X
c(S, T ) =
c(u, v) =
f (u, v) = f (S, T ) = |f |
u∈S,v∈T
u∈S,v∈T
Flujo en Redes de Transporte– p. 25/53
Demostración
(3) → (1)
Suponga que |f | = c(S, T ) para algún corte (S, T ) de G.
Como |f | ≤ c(S, T ) para cualquier corte, entonces |f | es
máximo. Pues en caso contrario existiría otro flujo f ′ tal que
c(S, T ) = |f | < |f ′ | ≤ c(S, T )
Flujo en Redes de Transporte– p. 26/53
Algoritmo de Ford-Fulkerson
1. para cada lado (u, v) ∈ E(G)
hacer
f (u, v) = 0
f (v, u) = 0
2. mientras exista un camino p de s a t en Gf
hacer
cf (p) = mı́n cf (u, v) : (u, v) ∈ p
para cada lado (u, v) ∈ p
hacer
f (u, v) = f (u, v) + cf (p)
f (v, u) = −f (u, v)
Flujo en Redes de Transporte– p. 27/53
Ejemplo: Inicio y primer camino
f
s
v1
v2
v3
v4
t
cf = c
s
v1
v2
v3
v4
t
s
0
0
0
0
0
0
s
0
16
0
0
13
0
v1
0
0
0
0
0
0
v1
0
0
12
0
10
0
v2
0
0
0
0
0
0
v2
0
0
0
0
9
20
v3
0
0
0
0
0
0
v3
0
0
7
0
0
4
v4
0
0
0
0
0
0
v4
0
4
12
14
0
0
t
0
0
0
0
0
0
t
0
0
0
0
0
0
v1
12
v2
16
s
10
4
13
t
7
9
v4
20
v3
4
14
Flujo en Redes de Transporte– p. 28/53
Ejemplo: Inicio y primer camino
f
s
v1
v2
v3
v4
t
cf = c
s
v1
v2
v3
v4
t
s
0
0
0
0
0
0
s
0
16
0
0
13
0
v1
0
0
0
0
0
0
v1
0
0
12
0
10
0
v2
0
0
0
0
0
0
v2
0
0
0
0
9
20
v3
0
0
0
0
0
0
v3
0
0
7
0
0
4
v4
0
0
0
0
0
0
v4
0
4
12
14
0
0
t
0
0
0
0
0
0
t
0
0
0
0
0
0
v1
12
v2
v1
12
16
s
10
4
13
v3
14
16
t
7
9
v4
20
4
s
10
4
13
v2
t
7
9
v4
20
v3
4
14
Flujo en Redes de Transporte– p. 28/53
Ejemplo: f1
16
s
12
v1
v2
t
7
10
4
20
9
13
v4
v3
4
14
Flujo en Redes de Transporte– p. 29/53
Ejemplo: f1
16
s
12
v1
v2
t
7
10
4
20
9
v4
13
v3
4
14
v1
12/16
s
12/12
v2
t
7
10
4
12/20
9
13
v4
v3
4
14
Flujo en Redes de Transporte– p. 29/53
Ejemplo: cf1
f
s
v1
v2
v3
v4
t
cf
s
v1
v2
v3
v4
t
s
0
0+12
0
0
0
0
s
0
4
0
0
13
0
v1
-12
0
0+12
0
0
0
v1
12
0
0
0
10
0
v2
0
-12
0
0
0
0+12
v2
0
12
0
0
9
8
v3
0
0
0
0
0
0
v3
0
0
7
0
0
4
v4
0
0
0
0
0
0
v4
0
4
12
14
0
0
t
0
0
-12
0
0
0
t
0
0
12
0
0
0
12/16
s
v1 12/12 v2
10
4
13
t
7
9
v4
12/20
v3
4
14
Flujo en Redes de Transporte– p. 30/53
Ejemplo: cf1
f
s
v1
v2
v3
v4
t
cf
s
v1
v2
v3
v4
t
s
0
0+12
0
0
0
0
s
0
4
0
0
13
0
v1
-12
0
0+12
0
0
0
v1
12
0
0
0
10
0
v2
0
-12
0
0
0
0+12
v2
0
12
0
0
9
8
v3
0
0
0
0
0
0
v3
0
0
7
0
0
4
v4
0
0
0
0
0
0
v4
0
4
12
14
0
0
t
0
0
-12
0
0
0
t
0
0
12
0
0
0
v1
12
v2
12/16
s
v1 12/12 v2
10
4
13
v4
v3
14
t
7
9
4
12/20
4
s
10
12 4
13
8
7 12
9
v4
v3
t
4
14
Flujo en Redes de Transporte– p. 30/53
Ejemplo: Camino en cf1
4
s
12
v1
v2
7
10
12 4
8
12
t
9
13
v4
v3
4
14
Flujo en Redes de Transporte– p. 31/53
Ejemplo: Camino en cf1
4
s
12
v1
v2
7
10
12 4
8
12
t
9
13
v4
v3
4
14
4
s
12
v1
v2
7
10
12 4
8
12
t
9
13
v4
v3
4
14
Flujo en Redes de Transporte– p. 31/53
Ejemplo: cf2
f
s
v1
v2
v3
v4
t
cf
s
v1
v2
v3
v4
t
s
0
12+4
0
0
0
0
s
0
0
0
0
13
0
v1
-16
0
0+12
0
0+4
0
v1
16
0
0
0
6
0
v2
0
-12
0
0
0
0+12
v2
0
12
0
0
9
8
v3
0
0
0
0
-4
0+4
v3
0
0
7
0
4
0
v4
0
-4
0
0+4
0
0
v4
0
8
0
10
0
0
t
0
0
-12
-4
0
0
t
0
0
12
4
0
0
4/4
s
12 4
13
v1
12
4/10
v2
7 12
9
v4
8
v3
t
4/4
4/14
Flujo en Redes de Transporte– p. 32/53
Ejemplo: cf2
f
s
v1
v2
v3
v4
t
cf
s
v1
v2
v3
v4
t
s
0
12+4
0
0
0
0
s
0
0
0
0
13
0
v1
-16
0
0+12
0
0+4
0
v1
16
0
0
0
6
0
v2
0
-12
0
0
0
0+12
v2
0
12
0
0
9
8
v3
0
0
0
0
-4
0+4
v3
0
0
7
0
4
0
v4
0
-4
0
0+4
0
0
v4
0
8
0
10
0
0
t
0
0
-12
-4
0
0
t
0
0
12
4
0
0
v1
12
v2
4/4
s
12 4
13
v1
12
4/10
v2
7 12
9
v4
v3
4/14
8
4/4
t
s
16 8
13
6
v4
9
10
4
8
7 12
v3
t
4
Flujo en Redes de Transporte– p. 32/53
Ejemplo: Camino en cf2
12
v1
s
16 8
13
v2
7
6
v4
8
9
10
4
v3
12
t
4
Flujo en Redes de Transporte– p. 33/53
Ejemplo: Camino en cf2
12
v1
s
16 8
13
9
10
v4
16 8
13
4
12
v3
4
v3
t
8
7
9
10
12
4
v2
6
v4
8
7
6
v1
s
v2
12
t
4
Flujo en Redes de Transporte– p. 33/53
Ejemplo: Flujo en cf2
12
v1
s
16 8
13
v2
7
6
v4
8
9
10
4
v3
12
t
4
Flujo en Redes de Transporte– p. 34/53
Ejemplo: Flujo en cf2
12
v1
s
16 8
13
9
10
v4
16 8
7/13
4
12
6
v4
8
7
6
v1
s
v2
v3
v2
7/7
9
7/10
4
v3
12
t
4
7/8
12
t
4
Flujo en Redes de Transporte– p. 34/53
Ejemplo: cf3
f
s
v1
v2
v3
v4
t
cf
s
v1
v2
v3
v4
t
s
0
12+4
0
0
0+7
0
s
0
0
0
0
4
0
v1
-16
0
0+12
0
0+4
0
v1
16
0
0
0
6
0
v2
0
-12
0
-7
0
12+7
v2
0
12
0
7
9
1
v3
0
0
0+7
0
-11
0+4
v3
0
0
0
0
11
0
v4
-7
-4
0
4+7
0
0
v4
7
8
0
3
0
0
t
0
0
-19
-4
0
0
t
0
0
19
4
0
0
12
v1
s
16 8
7/13
6
v4
9
7/10
4
v2
7/8
7/7 12
v3
t
4
Flujo en Redes de Transporte– p. 35/53
Ejemplo: cf3
f
s
v1
v2
v3
v4
t
cf
s
v1
v2
v3
v4
t
s
0
12+4
0
0
0+7
0
s
0
0
0
0
4
0
v1
-16
0
0+12
0
0+4
0
v1
16
0
0
0
6
0
v2
0
-12
0
-7
0
12+7
v2
0
12
0
7
9
1
v3
0
0
0+7
0
-11
0+4
v3
0
0
0
0
11
0
v4
-7
-4
0
4+7
0
0
v4
7
8
0
3
0
0
t
0
0
-19
-4
0
0
t
0
0
19
4
0
0
v1
12
v2
12
v1
s
16 8
7/13
6
v4
9
7/10
4
v2
7/8
7/7 12
v3
4
t
s
16 8
4
7
6
v4
9
3
11
1
7 19
v3
t
4
Flujo en Redes de Transporte– p. 35/53
Ejemplo Negativo
1000
s
1000
v
1
1000
1000
t
u
1000
s
1000
v
1
1000
1000
t
u
Flujo en Redes de Transporte– p. 36/53
Ejemplo Negativo
1000
s
v
1000
1
1000
1000
t
u
1000
s
1/1000
v
1/1
1/1000
1000
t
u
Flujo en Redes de Transporte– p. 37/53
Ejemplo Negativo
1000
s
1/1000
v
1/1000
1/1
1000
t
u
1000
s
v
1
999
1
999
1
1000
t
u
Flujo en Redes de Transporte– p. 38/53
Ejemplo Negativo
1000
s
1000
1
1000
t
u
v
999
1
999
1
999
1
999
1
s
v
1
1000
t
u
Flujo en Redes de Transporte– p. 39/53
Ejemplo Negativo
1000
s
1/1000
999
1
999
1
999
1
s
v
1
1000
t
u
v
1/1
999
1
1/1000
t
u
Flujo en Redes de Transporte– p. 40/53
Ejemplo Negativo
1/1000
s
999
1
999
s
v
1/1
1
1/1000
t
u
v
1
999
1
999
999
1
u
1
999
t
1
Flujo en Redes de Transporte– p. 41/53
Ejemplo Negativo
999
s
1
999
1
999
s
v
1
v
t
999
1
u
1
999
1
u
1
999
1
999
1
999
t
1
Flujo en Redes de Transporte– p. 42/53
Ejemplo Negativo
999
s
1
999
1
999
s
v
1
1/999
1
999
1
u
v
1/1
u
1
999
t
1
1/999
1
999
t
1
Flujo en Redes de Transporte– p. 43/53
Ejemplo Negativo
999
s
1
1/999
1
999
s
v
1/1
v
t
998
1
u
1
999
1
u
1
998
2
1/999
2
999
t
1
Flujo en Redes de Transporte– p. 44/53
Ejemplo Negativo
999
s
1
998
2
999
s
v
1
v
t
998
1
u
2
999
1
u
1
998
2
998
2
999
t
1
Flujo en Redes de Transporte– p. 45/53
Algoritmo de Edmonds-Karp
Estrategia para determinar un Camino Aumentado: Utilizar
el camino más corto de s a t determinado por medio de una
estrategia de búsqueda primero en anchura bajo el
supuesto de que en el red residual cada lado con longitud
positiva tuviera un peso igual a 1.
El número total de caminos aumentados construidos por el
algoritmo es O(n · m).
El tiempo total de ejecucción O(n · m2 ).
Se conoce un algoritmo push-relabel que corre en tiempo
en tiempo O(n2 · m).
Flujo en Redes de Transporte– p. 46/53
Ejercicio 1
Para el grafo:
10
s
1
2
v1
6
v4
5
3
8
v2
8
t
3 10
v3
10
Determine la capacidad del corte (S = {s, v3 ), V − S).
Flujo en Redes de Transporte– p. 47/53
Ejercicio 2
Para la red y el flujo:
2/10
s
1/1
2
v1
6
v4
2/5
3
1/8
v2
2/8
3 10
t
v3 1/10
Determine el flujo neto sobre el corte (S = {s, v3 ), V − S).
Flujo en Redes de Transporte– p. 48/53
Ejercicio 3
Para la red y el flujo:
2/10
s
1/1
2
v1
6
v4
2/5
3
1/8
v2
2/8
3 10
t
v3 1/10
Determine la red residual.
Flujo en Redes de Transporte– p. 49/53
Ejercicio 4
Para el grafo y el camino:
10
s
1
2
v1
6
v4
5
3
8
v2
8
t
3 10
v3
10
Determine la red residual.
Flujo en Redes de Transporte– p. 50/53
Ejercicio 5
Para el grafo:
10
s
1
2
v1
6
v4
5
3
8
v2
8
t
3 10
v3
10
Determine el flujo máximo.
Flujo en Redes de Transporte– p. 51/53
Ejercicio 6
Indique cómo puede reducirse el problema de una red de
transporte con varias fuentes y varios resumideros al
problema de una sola fuente y un solo resumidero.
Flujo en Redes de Transporte– p. 52/53
Ejercicio 7
Un grafo se dice Bipartido si el conjunto de vértices V
puede dividirse en dos conjuntos V1 y V2 de manera que los
lados del grafo sólo van de V1 a V2 . (No hay lados de un
vértice en V1 a otro vértice en V1 y similarmente para V2 ) El
problema del máximo apareamiento en un grafo bipartido
G = (V1 ∪ V2 , E) consiste en determinar el número máximo
de lados no conectados que se pueden tomar con un
vértice en V1 y otro vértice en V2 .
Flujo en Redes de Transporte– p. 53/53