02. Estructura

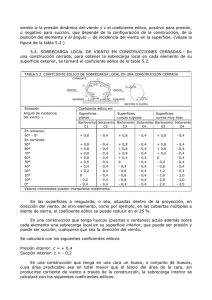
2. LA ESTRUCTURA.
2.1. DESCRIPCION DE LA ESTRUCTURA
Consta básicamente de los siguientes elementos:
2.1.1. MURO TRASERO.
Para poder establecer unos desniveles entre 3.50 y 4.50 m. existentes
entre la plataforma superior donde se ubican edificios existentes y la planta
baja del apeadero y los viales existentes. Se resuelven con muros ménsula de
hormigón armado de espesores 35 y 45 cm.
2.1.2. FORJADO LOSAS.
Ocupa la totalidad de la planta baja del Apeadero y sirve además para
arriostrar los elementos de cimentación. El canto total de la losa según los
cálculos realizados ascenderá a 20 cm.
2.1.3. FORJADO RETICULAR.
Se dispone como entreplanta en la zona de bar y venta de billetes. El
forjado adoptado es de tipo reticular con aligeramiento a base de bovedillas
cerámicas o de hormigón poroso de 25 cm. de canto, y una capa de
compresión de 5 cm. de hormigón, lo que nos da un canto total de 30 cm. Será
además de casetón recuperable con 70 cm de intereje.
2.1.4. PILARES.
Aprovechando la necesidad de una estructura metálica en la zona de
cubierta para la ejecución de los toldos, se ha decidido dar continuidad a esta
estructura hasta la losa de hormigón donde irá anclada mediante placas de
anclaje.
2.1.5. PERGOLA.
Sirven para sustentar un sistema de toldos. Se ha seleccionado perfilaría
metálica HEA 200 por condicionamiento del diseño y por ser económicamente
factibles dentro del presupuesto de la obra.
2.2. ACCIONES ADOPTADAS EN EL CÁLCULO.
Se estudiarán las acciones recogidas en el CTE DB-SE-AE (Seguridad
estructural. Acciones en edificación).
2.2.1. ACCIONES PERMANENTES (G).
Peso propio del forjado reticular 25+5/70.(aligerado)
400 kg/m2.
Pavimento
100 kg/m2.
Cerramientos exteriores
800 kg/ml.
2.2.2. ACCIONES PERMANENTES DE VALOR NO CONSTANTE (G*).
2.2.2.1. Acciones reológicas.
No se han considerado dado que las dimensiones en planta entre juntas
de dilatación no lo hacen necesario.
2.2.3. ACCIONES VARIABLES (Q).
2.2.3.1. Sobrecarga de uso.
Sobrecarga de uso
400 kg/m2.
2.2.3.2. Acciones térmicas.
No se han considerado dado que las dimensiones en planta de las
estructuras no lo hacen necesario.
2.2.3.3. Viento.
Para estudiar las cargas inducidas por el viento usaremos el Código
Técnico de la Edificación.
En nuestro caso estudiaremos 2 hipótesis de viento diferentes: viento
sobre la fachada y viento sobre la cubierta.
La presión estática del viento viene dada por la expresión:
q e = qb ⋅ ce ⋅ c p
Donde:
•
qb es la presión dinámica del viento
•
ce es el coeficiente de exposición, variable con la altura del punto
considerado y nivel de aspereza del entorno. Este valor se haya
mediante la siguiente expresión:
c e = F ⋅ (F + 7 ⋅ K )
Con:
F = K ⋅ Ln(max ( z , Z ) / L )
Siendo z la altura del punto sobre el terreno y K,L,Z parámetros
característicos de cada tipo de entorno según la tabla D2:
Coeficientes según el tipo de entorno.
Nosotros en nuestro caso elegiremos un grado de aspereza del entorno
tipo II.
Conocidos los datos, calculamos el los valores de F y ce:
F=1.07
Ce=2,41
•
cp es el coeficiente eólico o de presión, dependiente de la forma y
la orientación de la superficie con respecto al viento. Este coeficiente
será por tanto distinto según la hipótesis que estudiemos.
La presión dinámica del viento puede obtenerse de la expresión:
q b = 0 .5 ⋅ δ ⋅ v b
2
Donde:
•
δ es la densidad del aire. En general se adopta el valor de 1.25
3
kg/m .
•
Vb es el valor básico de la velocidad del viento según el
emplazamiento en que nos encontremos.
•
Como la ubicación del estadio es la localidad onubense de Punta Umbría,
estaríamos en la zona C y la velocidad del viento es por tanto vb=27 m/s.
Teniendo ya estos datos podemos calcular la presión dinámica del viento:
qb= 0.45 KN/m2
Para terminar de calcular la presión estática ya solo nos queda calcular el
coeficiente eólico o coeficiente de presión exterior, que depende del tipo de
construcción. Llegado a este punto, estudiaremos cada una de las hipótesis
por separado para calcular los cp y por tanto los qe.
2.2.3.3.1
Viento en fachada
Se trata del viento que incide en la fachada del bar y de la cubierta.
Para calcular el coeficiente de presión cp en este caso, entendemos que
la fachada del bar y la cubierta se comportan como un paramento vertical.
Coeficiente eólico o de presión.
Teniendo en cuenta que el área de influencia es mayor de 10 m2 y que la
relación h/d=5,5/8=0.68, podemos ver que el coeficiente de presión de la zona
central del paramento vertical seria de cp=-0.8
Con todos estos datos hayamos la presión estática del viento sobre la
fachada:
q e = qb ⋅ ce ⋅ c p
qe=86.76 Kg/m2
Del mismo modo que en hipótesis anteriores, esta fuerza superficial la
transformaremos en fuerzas lineales en los pórticos transversales. Quedaría
entonces una fuerza lineal de valor q e = 86.76 ⋅ 6 = 520.5 Kg/m, siendo este valor
la mitad si se trata de uno de los pórticos hastiales.
2.2.3.3.2
Viento en la pérgola.
Para modelar el viento que incide sobre la cubierta la asemejaremos a
una marquesina a un agua con una inclinación de 0º y con un coeficiente de
obstrucción φ=1, según dice el CTE SE-AE. Mostramos a continuación la
ilustración y la tabla D.8:
Coeficiente eólico o de presión.
Los coeficientes de presión tienen en cuenta el efecto del viento en
ambas superficies, la inferior y la superior. Un valor negativo del coeficiente
indica que la acción del viento tiende a levantar la marquesina, y un valor
positivo lo contrario. Por regla general se deberán calcular ambas situaciones.
Así pues, como podemos ver en la figura anterior que el cp en la zona A y
teniendo en cuenta un coeficiente de obstrucción φ=1 será:
Cp= 0.5 (hacia abajo)
Cp= -1.5 (hacia arriba)
Teniendo ya el coeficiente de presión, podemos calcular del mismo modo
que en casos anteriores la presión estática del viento:
qe=0.45x2.41x0.5=0.54 KN/m2= 54.2 Kg/m2 (hacia abajo).
qe=0.45x2.41x(-1.5)=1.62 KN/m2= 162.6 Kg/m2 (hacia arriba)
Si transformamos estas magnitudes por unidad de superficie en
magnitudes por unidad lineal sobre los pórticos transversales, nos quedarían
los siguientes valores:
qe=162.6x6=976.05 Kg/m (hacia arriba).
qe=54.2x6=325.2 Kg/m (hacia abajo).
Estos valores hallados para la pérgola serían exactos en caso de que
esta tuviera una cubierta rígida. Como el único cerramiento que va a tener la
pérgola es el de las velas o toldos que se instalarán, estos valores están muy
por encima de los reales ya que el viento puede pasar a través de la pérgola y
además en caso de viento fuerte, las velas pueden recogerse. Es por esto que
en el cálculo no usaremos los valores calculados sino la mitad de estos. Este
caso sigue estando muy por el lado de la seguridad.
2.2.4. ACCIONES SISMICAS.
Según la Norma NCSE-02.
DATOS DE PARTIDA.
•
ACELERACION SISMICA BASICA
ab=0.11 g
•
COEFICIENTE DE RIESGO
ρ=1.0
•
ACELERACION SISMICA DE CALCULO
ac=0.11 g
•
TERRENO TIPO II
c=1.4
•
DUCTILIDAD BAJA
β=0.44
•
COEFICIENTE DE CONTRIBUCION
k=1.4
2.2.4.1. Tipo de análisis.
De acuerdo con NCSE-02 se realiza un análisis modal espectral.
El espectro de respuesta es el correspondiente a k=1.4 y suelo tipo II con
lo que la meseta del espectro de respuesta α(To)=2.36.
2.2.4.2. Modos de vibración.
Para 1 plantas sobre rasante.
Periodo fundamental: Tf=0.09 x n=0.09"
Dado que Tf<0.75" Solamente hay que considerar el 1º modo de
vibración.
2.2.4.3. Método a emplear.
Dado el número de plantas sobre rasante de sótano y que solamente hay
que considerar el 1º modo de vibración se puede adoptar el sistema de las
fuerzas equivalentes que sabemos nos deja del lado de la seguridad.
2.2.4.4. Fuerzas sísmicas estáticas equivalentes.
Fk = Sk x Pk
ac
Sk = /g x α(To) x β x k
Las masas que intervienen en el cálculo son:
Pk = CONCARGA + 0.30 x SOBRECARGA.
Todos estos coeficientes se adoptan para cada pórtico y para cada
planta.
2.3. COMBINACION DE ACCIONES.
Combinaciones para hormigón: EHE, Control normal
Combinaciones para equilibrio: EHE, Control normal
Combinaciones para hormigón de vigas centradoras: EHE, Control normal
Nombre de combinación Peso propio Sobrecarga uso Viento 1 Viento 2 Sismo 1 Sismo 2
1.Sobrecarga
2.Sobrecarga
3.Sobrecarga
4.Sobrecarga
5.Viento 1
6.Viento 1
7.Viento 2
8.Viento 2
9.Sobrecarga + Viento 1
10.Sobrecarga + Viento 1
11.Sobrecarga + Viento 1
12.Sobrecarga + Viento 1
13.Sobrecarga + Viento 2
14.Sobrecarga + Viento 2
15.Sobrecarga + Viento 2
16.Sobrecarga + Viento 2
17.Sobrecarga + Sismo 1
18.Sobrecarga + Sismo 1
19.Sobrecarga + Sismo 1
20.Sobrecarga + Sismo 1
21.Sobrecarga + Sismo 2
22.Sobrecarga + Sismo 2
23.Sobrecarga + Sismo 2
24.Sobrecarga + Sismo 2
1.000
1.500
1.000
1.500
1.000
1.500
1.000
1.500
1.000
1.500
1.000
1.500
1.000
1.500
1.000
1.500
1.000
1.000
1.000
1.000
1.000
1.000
1.000
1.000
0.000
0.000
1.600
1.600
0.000
0.000
0.000
0.000
0.000
0.000
1.440
1.440
0.000
0.000
1.440
1.440
0.000
0.800
0.000
0.800
0.000
0.800
0.000
0.800
0.000
0.000
0.000
0.000
1.600
1.600
0.000
0.000
1.440
1.440
1.440
1.440
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000 0.000
0.000 0.000
0.000 0.000
0.000 0.000
0.000 0.000
0.000 0.000
1.600 0.000
1.600 0.000
0.000 0.000
0.000 0.000
0.000 0.000
0.000 0.000
1.440 0.000
1.440 0.000
1.440 0.000
1.440 0.000
0.000 -1.000
0.000 -1.000
0.000 1.000
0.000 1.000
0.000 0.000
0.000 0.000
0.000 0.000
0.000 0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
-1.000
-1.000
1.000
1.000
Combinaciones para tensión del terreno: Acciones Características
Combinaciones para desplazamientos: Acciones Características
Nombre de combinación Peso propio Sobrecarga uso Viento 1 Viento 2 Sismo 1 Sismo 2
1.Sobrecarga
1.000
0.000 0.000 0.000 0.000 0.000
2.Sobrecarga
1.000
1.000 0.000 0.000 0.000 0.000
3.Sobrecarga + Viento1
1.000
0.000 1.000 0.000 0.000 0.000
4.Sobrecarga + Viento1
1.000
1.000 1.000 0.000 0.000 0.000
5.Sobrecarga + Viento2
1.000
0.000 0.000 1.000 0.000 0.000
6.Sobrecarga + Viento2
1.000
1.000 0.000 1.000 0.000 0.000
7.Sobrecarga + Sismo1
1.000
0.000 0.000 0.000 -1.000 0.000
8.Sobrecarga + Sismo1
1.000
1.000 0.000 0.000 -1.000 0.000
9.Sobrecarga + Sismo1
1.000
0.000 0.000 0.000 1.000 0.000
10.Sobrecarga + Sismo1
1.000
1.000 0.000 0.000 1.000 0.000
11.Sobrecarga + Sismo2
1.000
0.000 0.000 0.000 0.000 -1.000
12.Sobrecarga + Sismo2
1.000
1.000 0.000 0.000 0.000 -1.000
13.Sobrecarga + Sismo2
1.000
0.000 0.000 0.000 0.000 1.000
14.Sobrecarga + Sismo2
1.000
1.000 0.000 0.000 0.000 1.000
Combinaciones para acero laminado: EA-95, Hospitales, situación expuesta
Combinaciones para acero conformado: EA-95, Hospitales, situación expuesta
Nombre de combinación
1.Sobrecarga
2.Sobrecarga
3.Sobrecarga
Peso propio Sobrecarga uso Viento 1 Viento 2 Sismo 1 Sismo 2
1.000
0.000 0.000 0.000 0.000 0.000
1.330
0.000 0.000 0.000 0.000 0.000
1.000
1.500 0.000 0.000 0.000 0.000
4.Sobrecarga
5.Sobrecarga + Viento1
6.Sobrecarga + Viento1
7.Sobrecarga + Viento1
8.Sobrecarga + Viento1
9.Sobrecarga + Viento2
10.Sobrecarga + Viento2
11.Sobrecarga + Viento2
12.Sobrecarga + Viento2
13.Viento1 + Sobrecarga
14.Viento1 + Sobrecarga
15.Viento1 + Sobrecarga
16.Viento1 + Sobrecarga
17.Viento2 + Sobrecarga
18.Viento2 + Sobrecarga
19.Viento2 + Sobrecarga
20.Viento2 + Sobrecarga
21.Sobrecarga + Sismo1
22.Sobrecarga + Sismo1
23.Sobrecarga + Sismo1
24.Sobrecarga + Sismo1
25.Sob. + Viento1 + Sismo1
26.Sob. + Viento1 + Sismo1
27.Sob. + Viento1 + Sismo1
28.Sob. + Viento1 + Sismo1
29.Sob. + Viento2 + Sismo1
30.Sob. + Viento2 + Sismo1
31.Sob. + Viento2 + Sismo1
32.Sob. + Viento2 + Sismo1
33.Sobrecarga + Sismo2
34.Sobrecarga + Sismo2
35.Sobrecarga + Sismo2
36.Sobrecarga + Sismo2
37.Sob. + Viento1 + Sismo2
38.Sob. + Viento1 + Sismo2
39.Sob. + Viento1 + Sismo2
40.Sob. + Viento1 + Sismo2
41.Sob. + Viento2 + Sismo2
42.Sob. + Viento2 + Sismo2
43.Sob. + Viento2 + Sismo2
44.Sob. + Viento2 + Sismo2
1.330
1.000
1.330
1.000
1.330
1.000
1.330
1.000
1.330
1.000
1.330
1.000
1.330
1.000
1.330
1.000
1.330
1.000
1.000
1.000
1.000
1.000
1.000
1.000
1.000
1.000
1.000
1.000
1.000
1.000
1.000
1.000
1.000
1.000
1.000
1.000
1.000
1.000
1.000
1.000
1.000
2.4. ESTADOS LIMITE ULTIMOS.
1.500
0.000
0.000
1.500
1.500
0.000
0.000
1.500
1.500
0.000
0.000
1.330
1.330
0.000
0.000
1.330
1.330
0.000
0.800
0.000
0.800
0.000
0.800
0.000
0.800
0.000
0.800
0.000
0.800
0.000
0.800
0.000
0.800
0.000
0.800
0.000
0.800
0.000
0.800
0.000
0.800
0.000
1.330
1.330
1.330
1.330
0.000
0.000
0.000
0.000
1.500
1.500
1.500
1.500
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.250
0.250
0.250
0.250
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.250
0.250
0.250
0.250
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
1.330
1.330
1.330
1.330
0.000
0.000
0.000
0.000
1.500
1.500
1.500
1.500
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.250
0.250
0.250
0.250
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.250
0.250
0.250
0.250
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
-1.000
-1.000
1.000
1.000
-1.000
-1.000
1.000
1.000
-1.000
-1.000
1.000
1.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
-1.000
-1.000
1.000
1.000
-1.000
-1.000
1.000
1.000
-1.000
-1.000
1.000
1.000
2.4.1. SITUACIONES PERSISTENTES ó TRANSITORIAS.
a/ SITUACIONES DE UNA SOLA ACCION VARIABLE QK,1:
Σ γG,jGK,j + γQ,1QK,1
b/ SITUACIONES DE DOS ó MAS ACCIONES VARIABLES:
Σ γG,jGK,j + Σ 0.9γQ,iQK,i
2.4.2. SITUACIONES SISMICAS.
Σ γG,jGK,j + γAAE,k+ Σ 0.8γQ,iQK,i
2.5. ESTADOS LIMITES DE SERVICIO.
2.5.1. COMBINACION POCO PROBABLE ó FRECUENTE.
a/ SUTUACIONES CON UNA SOLA ACCION VARIABLE QK,1:
Σ γG,jGK,j + γQ,1QK,1
b/ SITUACIONES CON DOS ó MAS ACCIONES VARIABLES Qk,i:
Σ γG,jGK,j + 0.9 Σ γQ,iQK,i
2.5.2. COMBINACION CUASIPERMANENTE.
Σ γG,JGK,j + 0.6 Σ γQ,iQK,i
2.6. MAYORACION DE ACCIONES:
Según Artículo 12 de la Instrucción EHE.
2.6.1. ESTADOS LIMITES ULTIMOS.
Mayoración de Acciones Permanentes
γG=1.50
Mayoración de Acciones Variables
γQ=1.60
Mayoración de Acciones Sísmicas
γA=1.00
2.6.2. ESTADOS LIMITE DE SERVICIO.
Mayoración de Acciones Permanentes
γG=1.00
Mayoración de Acciones Variables
γQ=l.00
2.7. MINORACION DE RESISTENCIA DE MATERIALES.
2.7.1. ESTADOS LIMITE ULTIMOS.
Hormigón (Situación persistente ó transitoria) γC=1.50
Hormigón (situación Accidental)
γC=1.30
Acero (Situación persistente ó transitoria)
γs=1.15
Acero (Situación accidental)
γs=1.00
2.7.2. ESTADOS LIMITE DE SEVICIO.
Hormigón
γC=1.00
Acero
γS=1.00
2.7.3. NIVELES DE CONTROL.
Ejecución
Hormigón
Acero
Normal.
Estadístico.
Normal.
2.8. CARACTERISTICAS DE LOS MATERIALES.
2.8.1. HORMIGON.
Cimentación
HA-25/B/25/IIa
fck=250 kg/cm
2
Estructura (protegida)
HA-25/B/25/IIa
fck=250 kg/cm
Estructura (intemperie)
HA-25/B/25/IIIa
fck=250 kg/cm
2
2
2.8.2. ACERO.
Cimentación
B-400S
fyk=4.100 kg/cm
Pilares y forjados
B-400S
fyk=4.100 kg/cm
2
2
2.9. BASES DE CÁLCULO ORIENTADAS A LA DURABILIDAD.
Según el Artículo 8 de la Instrucción EHE.
2.9.1. CLASES DE EXPOSICION RELATIVAS A LA CORROSION DE
ARMADURAS.
Cimentación
Pilares y Forjados (protegidos)
Pilares y Forjados (intemperie)
IIa
IIa
IIIa
2.9.2. CLASES DE EXPOSICION RELATIVAS A ATAQUES QUIMICOS.
No hay constancia de posibilidad de ataques químicos.
2.10. MUROS.
2.10.1.
DESCRIPCION DE LA SOLUCION.
Se adopta la tipología de muro en ménsula con cimentación de encepado
corrido.
El muro existente en la zona del apeadero tendrá 3,5 metros de altura y
35 cm. de espesor. Denominaremos a esta tipología “muro tipo 1”.
El muro que es prolongación del “muro tipo1” en el Este y el Oeste será
de 4,5 m de altura y 45 cm. de espesor. Lo denominaremos “muro tipo 2”.
2.10.2.
PARÁMETROS GEOTÉCNICOS.
- Angulo de rozamiento interno del terreno:
φ = 30º.
- Angulo de rozamiento muro-terreno:
- Peso específico del material de relleno:
- Sobrecarga en superficie del terreno:
δ = 20º.
t = 1.8 Tn/m3.
s = 0.4 Tn/m2.
2.10.3.
MODELO DE CÁLCULO.
En nuestro caso vamos a suponer la existencia de empuje activo, esto
es, el terreno es el que empuja a las tierras del trasdos del muro.
Hay muchas teorías para el cálculo de los empujes de tierras entre las
que destacan la Teoría de Rankine, la Teoría de Coulomb o algunos métodos
experimentales creados por Terzaghi. Nosotros en este caso usaremos la
teoría de Coulomb para el cálculo del muro ya que consideramos que es la
mas completa por modelar la interacción entre el terreno y el muro, si bien es
verdad que el uso de la Teoría de Rankine nos deja siempre del lado de la
seguridad.
Se muestra a continuación el esquema de fuerzas que entran en juego
dentro de la teoría de Coulomb para el empuje activo:
Esquema de fuerzas de empuje activo de Coulomb.
Siendo:
z: profundidad.
α: ángulo del parámetro del muro con la horizontal.
γ: densidad del terreno.
δ: ángulo de rozamiento muro-terreno.
Φ: ángulo de rozamiento interno del terreno.
β: ángulo de talud del terreno.
Además, en el caso de la existencia de sobrecargas en la coronación del
muro, deberemos tener en cuenta las expresiones de los empujes vertical y
horizontal debidos a estas fuerzas. Mostramos a continuación un esquema de
estas fuerzas además de las expresiones que modelan éste fenómeno:
Cargas en coronación del muro.
Estudiaremos también al caso del empuje activo en condiciones
dinámicas (caso de sismo). El coeficiente de empuje activo varía en función de
las aceleraciones de cálculo:
Siendo:
ah: aceleración horizontal de cálculo.
av: aceleración vertical de cálculo.
g: aceleración de la gravedad.
γ d: peso específico seco.
γ’: peso específico sumergido.
El caso 1 es aquel en el que los rellenos en el trasdós del muro están
secos o parcialmente saturados.
El caso 2 es para rellenos por debajo del nivel freático.
En nuestro caso, haremos la hipótesis del caso 1.
2.10.4.
RESULTADOS
En nuestro caso, y como se dijo anteriormente, aplicando la teoría de
Coulomb y asumiendo que no habrá sobrecarga alguna en la coronación del
muro, los resultados obtenidos del análisis descrito nos dan un empuje
horizontal de:
Ph= 0.50289xz Tn /m2
Si particularizamos en la base del muro, obtendremos un valos
aproximado de:
Ph= 1.76 Tn /m2 (para el muro de tipo 1).
Una vez calculados los empujes pasivos podemos hacer el cálculo de la
cimentación del muro y del muro en si.
Para la realización de estos cálculos usaremos el programa Cype, el
cual tiene un módulo específico de muros de contención.
Este programa nos da unos empujes como los de la siguiente figura:
Empuje activo de las tierras.
Podemos comprobar que los resultados que nos ofrece el programa son
idénticos a los calculados por la teoría de Coulomb.
Una vez hecho esto, podemos dimensionar la cimentación y el muro con
dicho programa y la información del estudio geotécnico.
• Muro tipo 1:
ƒ
ƒ
ƒ
Muro: 3,5 m. de altura y 35 cm. de espesor.
Encepados: encepado corrido de 70 cm. de espesor y 2,65 m.
de ancho. Dispondrá de un pequeño vuelo de 30 cm. al
trasdos. La disposición de los pilotes en el encepado será al
tresbolillo con una separación transversal de 1,80 m y
longitudinal de 3 m.
Pilotes: pilotes de Ø350 y 8 metros de profundidad (se incluye
el encepado).
• Muro tipo 2:
ƒ
ƒ
ƒ
Muro: 4,5 m. de altura y 45 cm. de espesor.
Encepados: encepado corrido de 70 cm. de espesor y 3.05 m.
de ancho. Dispondrá de un pequeño vuelo de 30 cm. La
disposición de los pilotes en el encepado será al tresbolillo con
una separación transversal de 2,10 m y longitudinal de 3 m.
Pilotes: pilotes de Ø450 y 9 metros de profundidad (se incluye
el encepado).
Los resultados de dicho programa se encuentran reflejados en el anejo
de cálculo y en los planos correspondientes.
2.11. CIMENTACIÓN.
2.11.1.
DESCRIPCIÓN.
Se estudiará una cimentación profunda según recomienda el informe
geotécnico.
La cimentación constará de varios elementos que estudiaremos a
continuación:
Cimentación bajo el muro de contención. Ya hemos visto en el apartado
anterior que se trata de un encepado corrido que ha sido calculado
mediante el módulo de “elementos de contención” del programa CYPE.
Los resultados se encuentran en el anejo de cálculo y en el apartado que
antecede a éste.
•
Cimentación por pilotes aislados en la zona mas alejada del
muro. Esta parte de la cimentación la calcularemos a continuación por
los métodos estipulados en la CTE DB-SE C.
•
Losa de arriostramiento. La losa que arriostra la cimentación es
también el forjado de planta andén. Lo dimensionaremos calculando los
esfuerzos mediante un programa de elementos finitos que además nos
proporcionará la cuantía mecánica necesaria en la losa, de tal forma que
se podrá armas con facilidad. Además, a fin de conseguir los planos de
la losa, haremos un modelo en el programa CYPECAD. La losa la
estudiaremos en el apartado de forjados.
2.11.2.
PILOTES AISLADOS.
Se calculan estos pilotes aislados mediante la CTE DB-SE C. El código
técnico estipula que en caso de usar pilotes aislados ejecutados “in situ” el
diámetro de estos debe ser de al menos 45 cm. y estar arriostrados en dos
direcciones. Efectivamente se estudiarán las cargas admisibles del terreno
para pilotes del diámetro mencionado, y el arriostramiento en dos direcciones
está asegurado con la losa de cimentación.
2.11.2.1.
Cálculo de la carga admisible del terreno.
La carga admisible del terreno se calcula mediante la expresión:
Qh = Q p + Q f
Siendo:
Qh: carga de hundimiento.
Qp: carga resistida por fuste.
Qf: carga resistida en punta.
Las expresiones de las cargas resistidas por fuste y en punta son las
siguientes:
Qp = π ⋅
D2
⋅ Rp
4
Qf = ∑ π ⋅ D ⋅ L ⋅ R f
Rp =
α⋅N
2
(MPa)
R f = 2 ⋅ N ⋅ 0,75 (KPa)
Siendo:
Rp la resistencia en punta calculada como la media de la resistencia en
punta de la zona activa inferior (3D) y la zona activa superior (6D).
Rf la resistencia por fuste en cada uno de los estratos existentes.
N el número de golpes en el ensayo de penetración estándar SPT.
Α coeficiente específico para suelos granulares.
Esquema de distribución de la carga en un pilote aislado.
Las expresiones de las resistencias se pueden encontrar en el anejo F
del CTE DB-SE C.
El informe geotécnico arroja los siguientes datos del ensayo de
penetración estandar en los diferentes estratos:
•
Entre 0-4 m. Rellenos arenosos. Sin capacidad portante.
•
•
Entre 4-8 m. Arenas de compacidad media. NSPT =16.
Más de 8 m. Arenas de compacidad densa. NSPT =25.
Con estos datos ya podemos calcular la carga admisible del terreno:
Qadm=Qh/3
Nosotros haremos estos cálculos mediante una hoja de cálculo en
EXCEL implementada con nuestros datos:
D
L
Zsup
Zinf
L1
L2
L3
L4
L5
L6
L7
L8
L9
L10
alfa
0.45
9
3.6
1.35
1
1
1
1
1
1
1
1
1
1
0.4
Resistencia en punta
0
0
0
0
3.2
3.2
3.2
3.2
5
5
m
m
m
m
m
m
m
m
m
m
m
m
m
m
Diámetro de pilotes
Longitu pilotes
Zona activa superior
Zona activa inferior
Long primer estrato
Nspt1
Nspt2
Nspt3
Nspt4
Nspt5
Nspt6
Nspt7
Nspt8
Nspt9
Nspt10
0
0
0
0
16
16
16
16
25
25
golpes
golpes
golpes
golpes
golpes
golpes
golpes
golpes
golpes
golpes
Resistencia por fuste
Mpa
Mpa
Mpa
Mpa
Mpa
Mpa
Mpa
Mpa
Mpa
Mpa
0
0
0
0
24
24
24
24
37.5
37.5
Kpa
Kpa
Kpa
Kpa
Kpa
Kpa
Kpa
Kpa
Kpa
Kpa
Rpi
5 Mpa
Rps
3.75 Mpa
Es la media de la resistencia en punta de la zona activa superior e inferior
Qpi
Qps
0.79521564
0.59641173
Qp
0.69581369 MN
695.813685 KN
69.5813685 Tn
Q hundimiento por fuste
0
0
0
0
33.92920066
33.92920066
33.92920066
33.92920066
53.01437603
53.01437603
Por tanto, la carga admisible del terrenos es de
Qadm=29,48 Tn
Q hundimiento
KN
KN
KN
KN
KN
KN
KN
KN
KN
KN
884.544864 KN
88.4544864 Tn
Q admisible
29.4848288 Tn
El tope estructural del pilote se calcula mediante la expresión:
Qtope=σ x A
Donde:
A es la sección del pilote.
σ es la tensión del pilote según la tabla 5.1 del CTE DB-SE C.
Tope estructural de pilotes.
En nuestro caso consideramos σ=3,5 MPa, con lo que el tope estructural
del pilote ascenderá a:
Qtope=55,66 Tn
Podemos apreciar que Qtope>Qadm, por lo que el pilote resistirá
estructuralmente mas que el suelo. Esto significa que el pilote está algo
sobredimensionado pero en realidad habría que analizar dos factores:
1. Las fórmulas de cálculo usadas para el establecimiento de la Qadm
a partir de los ensayos SPT están muy del lado de la seguridad y
por lo tanto infravaloran la Qadm del terreno.
2. No debemos, según reza el código técnico, usar pilotes aislados
de diámetros menores de 45 cm.
Por todo esto, creemos que lo pilotes de Ø45 a 9 m. son los precisos a
instalar de forma aislada.
Como ya hemos dicho, el cálculo que hemos realizado de las resistencias
en punta y por fuste es muy conservador. A continuación vamos a hacer los
cálculos mediante métodos mas precisos, acudiendo al las tablas existentes en
el NTE-CPI:
•
Resistencia en punta: Nspt va a ser la media de los Nspt en la zona
activa superior e inferior.
1.35 ⋅ 25 + 3.6 ⋅ 16
= 18.45
4.95
Acudiendo a tablas con el Nspt calculado y el diámetro del pilote (45 cm
en nuestro caso) obtenemos una resistencia en punta de :
N spt =
Qp=130.77 Tn
•
Resistencia por fuste: Se calcula la resistencia unitaria por fuste
según el número de golpes Nspt:
Nspt=16Æ Fi= 7,85 Tn/m.
Nspt=25Æ Fi= 10,6 Tn/m.
La resistencia total por fuste se calculará teniendo en cuenta los estratos
existentes y las resistencias unitarias anteriormente calculadas:
Qf= 42 Tn
La carga total de hundimiento será de:
Qh=172,77 Tn
La carga admisible del terreno será:
Qadm=Qh/3=57,59 Tn.
Podemos ver que esta cantidad es mucho mayor que la calculada por
métodos aproximados. Además, esta carga admisible queda más cerca del
tope estructural del pilote, lo que denota un diseño mas optimizado de la
cimentación.
Nos quedaremos por tanto con éste último valor del la carga admisible.
2.11.2.2.
Esfuerzos de la estructura a cimentación.
En este apartado estableceremos las cargas que transmite la estructura a
la cimentación. Tenemos que asegurarnos que las cargas que se transmiten a
cimentación son tales que cumplan todas las comprobaciones que establece el
CTE DB-SE C.
Los estado límites últimos a comprobar son:
1.
2.
3.
4.
5.
Estabilidad global.
Hundimiento.
Rotura por arrancamiento.
Rotura horizontal del terreno.
Capacidad estructural del pilote.
De todas estas comprobaciones, la mas importante será la de
hundimiento.
La comprobación de rotura por arrancamiento no es necesario realizarla
ya que solo ha de hacerse en casos en los que el pilote se use para soportar
cargas de tracción. Este no es el caso.
La comprobación por rotura horizontal del terreno se hará en el caso de
que la componente horizontal del empuje sea superior a un 10% de la carga
vertical. En nuestro caso, este valor está muy por debajo del 10 %, por lo que
no habrá que realizar más comprobación.
La capacidad estructural del pilote ya la hemos estudiado en el apartado
anterior, ya que un buen diseño de la cimentación requiere que la capacidad
mecánica del pilote esté en el entorno de la carga admisible del terreno.
Sabemos que la carga tope del pilote será de 55,66 Tn.
Dicho esto, solo nos queda comprobar que las cargas verticales
transmitidas a cimentación no excedan de la capacidad estructural del pilote ni
de la carga admisible del terreno.
Para calcular los esfuerzos en cimentación usaremos el modelo 3D
realizado en el programa de cálculo RFEM, que nos proporciona las
reacciones en los puntos que elijamos.
La comprobación de hundimiento se realiza, según dice el artículo 59.3
de la EHE usando los valores característicos de la fuerzas. Esto significa que
no irán mayoradas.
En nuestro caso, estudiaremos estas acciones en uno de los pórticos que
se encuentran en la zona Este y que por tanto tienen que soportar el peso de
la entreplanta conformada por el forjado reticular. Evidentemente estos
pórticos transmitirán a cimentación unas cargas mucho mayores que los
demás. Estamos por tanto en el caso mas extremo. Presentamos a
continuación una tabla en la que tenemos las reacciones anteriormente
mencionadas.
3.1 NODES - SUPPORT FORCES
Node
No.
47
CO
CO5
78
CO5
Support Forces [kN]
P-X
P-Y
-7.520
4.329
-13.140
-9.721
-0.583
-0.815
-1.397
-2.163
LOAD COMBINATIONS
P-Z
403.990
203.308
158.790
96.843
Support Moments [kNm]
M-X
M-Y
M-Z
-1.727
13.161
-0.066 Acciones características
-12.788
8.112
-0.116 Acciones características
24.016
13.344
-0.009 Acciones características
11.889
8.193
-0.018 Acciones características
Los valores están en KN, pero si lo pasamos a toneladas vemos que en
el pilar delantero (el mas alejado del muro), la carga vertical a transmitir es de
40,39 Tn, que es menor que las 57,59 Tn admisibles por el terreno, con lo que
se cumplen todas las comprobaciones requeridas por el código técnico de la
edificación.
2.12. ESTRUCTURA DE PÓRTICOS
2.12.1.
DESCRIPCIÓN DE LA ESTRUCTURA DE PÓRTICOS
La estructura metálica está compuesta por 26 pórticos separados entre si
una distancia de 6 m. La tipología de los pórticos varía según la zona del
apeadero en que nos encontremos puesto que la irregularidad en planta del
muro de contención hace que ciertos pórticos deban apoyar uno de sus pilares
en la coronación del muro mientras que otros pórticos disponen de dos pilares
hasta la losa de cimentación que conforma el andén.
Además, en la zona Este del andén, al existir una entreplanta,
deberemos disponer vigas metálicas para sostener el correspondiente forjado,
dando así lugar a otra topología diferente.
Los pilares metálicos serán perfiles en “H”, al igual que las vigas de la
pérgola y la cubierta.
2.12.2.
MODELO DE CÁLCULO.
Debido a la diversidad de tipologías de pórticos y a la “irregularidad” de la
estructura, en vez de realizar un análisis estructural de pórticos en 2
dimensiones, se ha decidido realizar un análisis tridimensional de la misma.
Haremos un modelo preciso de la estructura completa en 3D de tal forma que
quede representa con precisión cada una de las partes. Esto incluye
evidentemente a los forjados de H.A.
Así pues, para hacer este modelo tridimensional de la estructura se ha
elegido un programa de elementos finitos llamado RFEM de la casa comercial
DLUBAL.
Con los resultados que nos de este programa y a fin de simplificar la
composición posterior de los planos, se hará un modelo en el programa de
cálculo CYPECAD de la casa CYPE INGENIEROS.
Previamente a este modelo en 3D, se ha realizado un estudio de varios
pórticos en 2D para hacer un predimensionamiento.
2.12.3.
IMÁGENES DEL MODELO.
Las imágenes que se muestran a continuación han sido capturas del
programa de elementos finitos RFEM.
Vista trasera 3D del modelo.
Vista 3D delantera. Zona de cubierta.
Isometri
Vista interior del apeadero.
2.12.4.
2.12.4.1.
CÁLCULO DE ESFUERZOS.
Pórtico Tipo 1.
Este tipo de pórtico tiene dos pilares metálicos HEA 200 de 5,4 m. de
longitud y separados 4m. La viga estará formada por un HEB 200 de 8 m. en
total.
Son los pórticos que tienen la siguiente tipología:
Pórtico tipo 1.
Estos pórticos no están apenas cargados puesto que no forman parte de
la estructura portante de la entreplanta y por otra parte, la cubierta no se
considera transitable ni siquiera para mantenimiento, puesto que en realidad el
único elemento a mantener serían las velas, que se pueden instalar sin
necesidad de subir a la pérgola. Además no existe una cubierta propiamente
dicha ya que lo existe ningún elemento rígido que cierre la pérgola.
Dicho esto, las cargas en este caso se reducen básicamente al peso
propio y en algún caso al viento que llena las velas, que incluso podrían
retirarse en casos de fuerte viento.
Para modelar entonces estas fuerzas, hemos decidido incluirlas a un
50% de su valor habitual, lo cual estará del lado de la seguridad.
Veamos en primer lugar la flecha del pórtico en la combinación de
desplazamientos más desfavorable.
Deformada del pórtico tipo 1.
Podemos observar como la flecha máxima es de 1,35 cm.
Para voladizos la EA-95 establece una flecha máxima de L/300=1,33cm.
Consideramos que la flecha es admisible ya que realmente las hipótesis con
las que se ha calculado la flecha máxima están sobredimensionadas.
Los esfuerzos han sido calculados con las hipótesis que establecimos en
el apartado 2.3. Los resultados mas desfavorables se encuentran listados en el
anejo de cálculo. A continuación se muestran las envolventes de esfuerzos:
Envolvente de momentos.
- 2 .2 9 3
- 0 .6 56
1.2 9 6
- 2 .2 9 3
- 2 2 .2 0 2
1.2 17
7.2
- 5.2
2 9 77
4 2 .3 2 5
1.2 17
- 2 8 .775
Y
X
3 5.752
Evolvente de axiles.
Envolvente de cortantes.
La tensión máxima se dará en la viga, en su unión con el pilar delantero.
En esta sección, las tensiones serán:
σ=11,23 KN/cm2
Τ= 1.94 KN/cm2
σ eqv=11.27 KN/cm2
Esta tensión equivalente está aún muy lejos de los 24 KN/cm2 que puede
resistir el acero S275.
2.12.4.2.
Pórtico en zona de forjado
Vamos a estudiar uno de los pórticos que han de soportar la entreplanta
que conforma la cubierta de la cafetería. Estos pórticos va a estar mucho mas
solicitados que los anteriormente vistos.
Este tipo de pórtico tiene dos pilares metálicos HEA 200 de 5,4 m. de
longitud y separados 4m. La viga estará formada por un HEB 200 de 8 m. en
total.
Son los pórticos que tienen la siguiente tipología:
Pórtico de entreplanta.
El pórtico está calculado en las mismas condiciones de carga y
combinaciones de carga que en el caso anterior. Se ha modelado la existencia
del forjado como una carga lineal en la zona donde existe forjado y además, la
parte de forjado que vuela se ha modelado por medio de una fuerza y un
momento aplicado en la unión de pilar y viga.
Veamos en primer lugar la flecha del pórtico en la combinación de
desplazamientos más desfavorable:
Deformada del pórtico (factor de escala 66).
Podemos observar como la flecha máxima es de 0.81 cm.
Para voladizos la EA-95 establece una flecha máxima de L/300=1,33 cm.
Por lo que la flecha es admisible.
Las envolventes de esfuerzos son las que siguen:
Envolvente de axiles.
Envolvente de cortante.
Envolvente de momentos.
La tensión máxima se dará en la viga soporte del forjado reticular.
σ=12,86 KN/cm2
Τ= 9,42 KN/cm2
σ eqv=16,32 KN/cm2
Esta tensión equivalente está aún muy lejos de los 24 KN/cm2 que puede
resistir el acero S275.
2.12.4.3.
Modelo 3D.
Una vez vistos y estudiados varios de los pórticos en 3D, ya tenemos una
idea de las dimensiones y de los perfile s utilizar en el proyecto. Podemos
ahora pasar a hacer y estudiar el modelo completo de la estructura.
En general, el comportamiento de la estructura completa no difiere
mucho del comportamiento de los pórticos que la forman.
Si sometemos a la estructura a las mismas cargas que las estudiadas
anteriormente, la deformada de la estructura sería la que sigue:
Deformaciones en la estructura.
Vemos que la flecha máxima (f=1,26) está en el entorno de las flechas
halladas para los pórticos aislados. Esto nos dice de la fidelidad de los
modelos 2D.
No vamos a hacer un estudio de las envolventes porque los gráficos
quedarían excesivamente densos en cuanto a líneas se refieren Y serían
ilegibles e inútiles. Sin embargo, como hemos hecho en otros apartados,
vamos a ver cuales son las tensiones equivalentes de Von Mises mas
elevadas para compararlas con el límite elástico del acero usado:
σ=13,36 KN/cm2
Τ= 4 KN/cm2
σ eqv= 13,36KN/cm2
Estas tensiones se darán en la unión entre el pilar y la viga de la
entreplanta. A continuación vamos a ver un gráfico meramente ilustrativo de la
distribución de las tensiones de Von Mises en la estructura:
Tensiones equivalentes de Von Mises.
Hecho el estudio del modelo en 2D y 3D, podemos concluir que nuestra
estructura cumple perfectamente a resistencia y flecha. Evidentemente hay
otras comprobaciones que hacer según la EA 95, las cuales hacemos con el
programa de cálculo CYPECAD. Al introducir el modelo en este programa,
podemos hacer las demás comprobaciones como las de pandeo, que son
interesantes en este caso.
2.13. LOSA.
2.13.1.
DRESCRIPCIÓN Y METODO DE TRABAJO.
Se trata de una losa de cimentación de 20 cm. de espesor que se
extiende a todo lo largo del apeadero y que conforma el andén.
Para calcular esta losa, hemos usado el modelo 3D que hicimos en el
programa de elementos finitos RFEM. En concreto, este programa tiene un
módulo específico llamado “concrete surfaces” que, tras hacer hecho el
modelado, proporciona una cuantía de armado que nos servirá para establecer
la armadura necesaria en cada zona de la losa.
Una vez armada la losa, como hemos hecho a lo largo de todo el
proyecto, pasaremos a ver los resultado que arroja CYPE y veremos que
están acordes con los visto por RFEM.
2.13.2.
RESULTADOS.
Presentamos a continuación imágenes de los esfuerzos y las cuantías de
armado que nos proporciona RFEM a partir del modelo y las cargas
introducidas. Al ser la losa un elemento muy alargado, se ha decidido
presentar imágenes parciales de la losa en la zona del bar, que será la mas
solicitada.
2.13.2.1.
Esfuerzos.
Momentos en dirección x.
Momentos en dirección y.
Cortante en x.
Cortante en y.
Axil en x.
Axil en y.
2.13.2.2.
Cuantías mecánicas.
Se presentan a continuación las cuantías mecánicas necesarias para el
armado de la losa. A partir de los estoas valores vamos a establecer una
armadura base y una armadura de refuerzo para la losa. Evidentemente, los
refuerzos se encontrarán en la zona de unión entre losa y pilar.
Cuantía mecánica transversal inferior.
El valor a usar para la armadura base será aquel que se de en las zonas
menos solicitadas. Tomamos un valor aproximado de As1= 7 cm2/m. Esto será
equivalente a poner 6Ø12 cada metro, es decir, Ø12@15.
Tomamos como valor máximo uno de As1=18 cm2/m. (no tomamos el
máximo absoluto porque es un pico que nos proporciona el programa debido a
que los pilares se consideran elementos puntuales). Esto es equivalente a
poner 10Ø12 cada metro, es decir, Ø12@10.
Mesh reinforcement
a-s,2 top [cm^2/m]
23.30
21.18
19.07
16.95
14.83
12.71
10.59
8.47
6.36
4.24
2.12
0.00
Max :
Min :
23.30
0.00
Cuantía mecánica longitudinal inferior.
Podemos ver que las cuantías para esta armadura longitudinal inferior
son similares a las transversales. Tomaremos por tanto valores similares para
que la armadura inferior sea constructivamente fácil de ejecutar.
Para la armadura base tomamos un valor aproximado de As1= 7 cm2/m.
Esto será equivalente a poner 6Ø12 cada metro, es decir, Ø12@15.
Tomamos como valor máximo uno de As1=18 cm2/m. (no tomamos el
máximo absoluto porque es un pico que nos proporciona el programa debido a
que los pilares se consideran elementos puntuales). Esto es equivalente a
poner 10Ø12 cada metro, es decir, Ø12@10.
Mesh reinforcement
a-s,1 bottom [cm^2/m]
6.89
6.26
5.64
5.01
4.38
3.76
3.13
2.51
1.88
1.25
0.63
0.00
Max :
Min :
6.89
0.00
Cuantía mecánica transversal superior.
Para la armadura base tomamos un valor aproximado de As1= 5 cm2/m.
Esto será equivalente a poner 6Ø10 cada metro, es decir, Ø10@15.
No habrá armadura de refuerzo puesto que el valor de la armadura base
es suficiente.
Cuantía mecánica longitudinal superior.
Del mismo modo que sucedía para la armadura inferior, intentaremos que
la armadura superior tenga armaduras similares transversal y
longitudinalmente por motivos constructivos. Efectivamente, las cuantías son
bastante parecidas en ambos casos. Disponemos pues Ø10@15.
Hay que decir que la armadura superior tiene una cuantía geométrica del
5,88‰ que es mayor que el 2‰ que establece la EHE.
2.13.3.
RAMPAS.
Hay que hacer mención a las rampas de acceso a los andenes y a la
cubierta del bar. Estas rampas son en realidad parte de la losa de cimentación,
es decir, se ejecutan de forma continua a la losa o son parte de la losa. De
este modo, tendrán el mismo espesor (20 cm.) y llevarán el armado que se ha
estudiado anteriormente para la losa.
2.14. ESCALERAS.
2.14.1.
ESCALERAS DE ANDEN-PLATAFORMA SUPERIOR.
Son las escaleras que nacen en el andén y dan acceso a la plataforma
superior. Se trata de una escalera de un solo tramo apoyada lateralmente
entre el moro de contención y un muro de fábrica resistente. Arranca en la losa
de cimentación y muere en el muro. La losa que forma la escalera será del
mismo grosor que la losa de cimentación, es decir, 20 cm. con un armado
longitudinaL superior e inferior de Ø10@15.
2.14.2.
ESCALERAS DE LA CALLE A LA PLATAFORMA SUPERIOR.
Esta escalera consta de dos tramos en una misma dirección, es decir,
necesitan de un apoyo intermedio debido a su longitud.
La escalera está apoyada lateralmente por el muro de contención y por
otro muro macizo de hormigón armado (ver planos).
Nacerá en un murete de hormigón cimentado en su correspondiente
zapata y dispondrá de un recrecido inicial. Al apoyo intermedio de la escalera
se ejecutará por medio de un muro de fábrica resistente y el apoyo final se
hará en el muro de contención. La losa que forma la escalera será de 20 cm. y
llevará un armado longitudinal superior e inferior de Ø10@15.
2.15. FORJADO RETICULAR.
El forjado reticular es de tipo 25+5/70 de casetón no recuperable, es
decir, de 25 cm. de espesor, con 5 cm. de capa de compresión y 70 cm. de
intereje.
Este forjado ha sido modelado en RFEM para poder estudiar sus efectos
sobre el resto de la estructura pero el cálculo del armado ha sido hecho con
CYPECAD. CYPE tiene una amplia biblioteca de forjados reticulares y es muy
útil para el cálculo de estos elementos. Además, tenemos la posibilidad de
generación de los ábacos y armado de los mismos.
El defecto que tiene este programa a la hora de sacar resultados es la
poca homogeneidad de las armaduras a disponer. Claro, esto es inconcebible
para el trabajo en obra por lo que tras el cálculo, hemos hecho una
homogeneización de las armaduras. Esto significa que hemos igualado lo más
posible el diámetro de los redondos y su disposición en el forjado, intentando
no alterar la cuantía de armadura dispuesta en valores importantes. La
distribución de armaduras puede verse en planos.
Nosotros además hemos querido comprobar que los esfuerzos que
hemos obtenido con el programa CYPECAD son los mismos que nos han dado
con el programa de elementos finitos RFEM.
Momentos en x según CYPECAD.
Momentos en x según RFEM.
Vemos efectivamente que en la zona de positivos ambos programas
estiman un momento aproximado de 1,2 Tnxm.
En la zona de armadura de negativos obtenemos alguna diferencia que
será debida a que CYPECAD modela los ábacos mientras que RFEM no.
Obtenemos un esfuerzo de M=-4,8 Tnxm. con CYPECAD y M=-5,3 Tnxm. con
RFEM.
Si estudiamos otros esfuerzos como el momento en “y” veremos que la
distribución vuelva a ser bastante parecida:
Momentos en y según CYPECAD.
B a s e v a lu e s
m<sub>y</sub> [kNm/m]
7 6 .6 8 3
6 4 .8 7 3
5 3 .0 6 3
4 1 .2 5 3
2 9 .4 4 3
1 7 .6 3 4
5 .8 2 4
- 5 .9 86
- 1 7 .79 6
- 2 9 .60 6
- 4 1 .41 6
- 5 3 .22 6
M ax :
Min :
7 6 .6 8 3
- 5 3 .22 6
Momentos en y según RFEM.
Vemos que en el entorno de la unión pilar-forjado reticular los valores son
muy similares: M=5,6 Tnxm. según CYPECAD, y M=5,3 Tnxm. según RFEM.
Es sin embargo en al zona de unión entre el forjado y la viga metálica
que lo soporta, donde hay alguna discrepancia: M=1Tnxm. según CYPECAD,
y M= 4 Tnxm. según RFEM. Esta discrepancia puede deberse de nuevo a la
influencia que tienen los ábacos sobre la estructura.