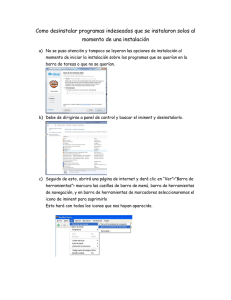
T.P.N 1.1: a) Calcular la tensión a la que esta sometido el alambre

ESTABILIDAD II
CAPITULO I – INTRODUCCIÓN A LA RESISTENCIA DE MATERIALES
GUIA TRABAJOS PRACTICOS
AÑO 2007
T.P.N0 1.1:
a) Calcular la tensión a la que esta sometido el alambre de acero de la figura.
b) Calcular la deformación específica del acero de la figura
c) Calcular el corrimiento del punto D.
d) Si el alambre en lugar de ser de acero fuese de cobre, la deformación sería mayor, menor o igual?
P
Datos:
A
B
D
Barra AD y BC rígidas

2m
Eac = 2100 tn/cm2
P = 2 tn
 = 2 cm
Ecu = 1200 tn/cm2
C
3m
1m
a) Cálculo de la tensión en el alambre
a1) D.C.L: (realizamos dos cortes a-a y b-b y ponemos de manifiesto las fuerzas que permiten el
equilibrio de los distintos elementos que conforman el sistema)
P
A
 M B  0  T  3m  P  1m
1
T  P  0,666 tn
3
B
a
a
b
D
b
T
T
3m
1m
a2) Tensión en el alambre
Por condición de equilibrio del sistema tenemos, en el alambre un esfuerzo de tracción T. Dicho
esfuerzo debe considerarse como la resultante de las fuerzas que se produce por unidad de superficie
(tensiones), atento al alargamiento de las fibras respectivas. Por hipótesis de deformación se
considera que todas las fibras experimentan el mismo valor de alargamiento l.
Si   
 al
trab 
L
 cte    cte
L
N
T

 0,212 tn cm 2
   2
4
a
 al
trab
 0,212 tn cm
2
cte.
F
a
F
F
1
ESTABILIDAD II
CAPITULO I – INTRODUCCIÓN A LA RESISTENCIA DE MATERIALES
GUIA TRABAJOS PRACTICOS
AÑO 2007
b) deformación especifica del alambre
 al 

0,212 tn cm 2

 1,0095  10  4   al
E ac 2100 tn cm 2
c) Corrimiento del punto D
Debido al la carga exterior P, la barra AD rígida, pasa de la posición horizontal a la posición A’D’.
Gira un ángulo 
A = al
 D  al
 1 m 1

  D  al
  al (1)
1m 3 m
3m
3
como:

A'
P
A
B
D
A

  L al
 
   al  al
E L
E al
3m
D'
D
1m
reemplazando en (1) tenemos:
1  al  L al 1 0,212 tn cm 2  200 cm
D  
 
 0,00673 cm
3
E al
3
2100 tn cm 2

, vemos que
E
como la tensión () a que está sujeto el alambre es independiente del material, la deformación
específica varía solamente con el módulo elasticidad y su relación es inversamente proporcional (a
mayor E menor ). De este análisis consideramos que:
d) Si el material del alambre fuese cobre en vez de acero, analizando la expresión  
E cu  E ac   cu   ac
Interpretación gráfica: Si dibujamos la parte elástica del diagrama  de los dos materiales tenemos:

módulo de Young ; tg   E


Acero
Cobre
Ecu < Eac

u
c
cu > ac
ac
ac
cu

2
ESTABILIDAD II
CAPITULO I – INTRODUCCIÓN A LA RESISTENCIA DE MATERIALES
GUIA TRABAJOS PRACTICOS
AÑO 2007
T.P.N0 1.2:
Dado el sistema del T.P.Nº 1.1, determinar el máximo valor que puede tomar P para una adm = 1,4
tn/cm2 y cm
P
1 - D.C.L.
A
B
T=1/3 P
D
R=4/3 P
2 - Determinación del P máximo admisible
Como se pide hallar el valor máximo de P teniendo en cuenta la tensión admisible del material, dicho
valor de carga (P admisible) debe ser calculado en función de que la tensión de trabajo en el alambre
llegue a 1,40tn/cm2, o sea:
 máx. trab =  adm
Padm
  adm  Padm   adm  3  al  13,2 tn
3  al
Padm = 13,2 tn
3
ESTABILIDAD II
CAPITULO I – INTRODUCCIÓN A LA RESISTENCIA DE MATERIALES
GUIA TRABAJOS PRACTICOS
AÑO 2007
T.P N0 1.3:
Dado el sistema del T.P.Nº 1.1, dimensionar el alambre de acero con un coeficiente de seguridad =3.
P
Datos:
 fl  2, 4 tn cm 2
A
B
D
P  5tn
T=1/3 P
R
Para dimensionar el alambre consideremos como condición de resistencia que la tensión de trabajo no
supere la tensión admisible del acero.  trab   adm 
En este caso como nos da como dato la tensión de fluencia del material y el valor del coeficiente de
seguridad:

2,4 tn cm 2
 adm  fl 
 0,80 tn cm 2

3
 trab   adm
P
  2 P
1
  adm 
 
; 
3. al
4
3  adm
P
1
4

  1,64 cm
3  adm 
En locales comerciales la oferta de barras de acero viene dada por los siguientes diámetros:
6mm; 8mm; 10mm; 12mm; 16mm; 20mm; 25mm.
- 1ra opción: adoptamos una barra de =16 mm, la tensión de trabajo será:
 trab 
1,667 tn
2,01cm
2
 0,83 tn cm 2   adm
- 2da opción: adoptamos una barra de =20 mm, la tensión de trabajo será:
 trab 
1,667 tn
3,14cm
2
 0,53 tn cm 2   adm
La primera opción nos lleva a superar el valor de la tensión de referencia (adm) dada como dato para
0,83  0,80
 100  3,75%
el dimensionado. En porcentaje, la diferencia seria:  
0,80
Con la segunda opción, la tensión de trabajo es sensiblemente menor al valor de referencia: estaríamos
sobredimensionando la pieza.
El calculista proyectista, basándose en su experiencia puede en determinados casos y en bajos
porcentajes, superar la tensión admisible. En esta oportunidad podemos señalar que él puede
ser admitido.
En base ha lo expuesto se adopta para la barra el = 16mm.
4
ESTABILIDAD II
CAPITULO I – INTRODUCCIÓN A LA RESISTENCIA DE MATERIALES
GUIA TRABAJOS PRACTICOS
AÑO 2007
T.P.N0 1.4:
a) Calcular la energía de deformación acumulada en el sistema del Trabajo Práctico Nº 1.1
b) Calcular el corrimiento del punto D utilizando el concepto de trabajo
P
D.C.L
3m
1m
D
R=4/3 P
T=1/3 P
2m
T
T
a) Energía de deformación acumulada en el sistema.
Como el alambre es el único elemento que se deforma por causa de la carga exterior P, la energía se
acumula solo en él.
U
T  al
L
TL
, como :  al 


2
E ac
 al  E ac
1
T2
1
( 2 tn) 2  4
U 
L   2
 200 cm  6,74  10  3 tncm
2
2
2  al  E ac
2 3    (2 cm)  2100 tn cm
b) Corrimiento del punto D
El trabajo realizado por la carga P a lo largo del desplazamiento D es igual a la energía de
deformación acumulada en el sistema.
P
WU
P. D
2
 U  D 
U.2
 0,00674cm  6,74  10 3 cm
P
D 
La carga se aplica gradualmente de 0 al valor final de P, por lo tanto el trabajo realizado por P es igual
a la superficie rayada.
5
ESTABILIDAD II
CAPITULO I – INTRODUCCIÓN A LA RESISTENCIA DE MATERIALES
GUIA TRABAJOS PRACTICOS
AÑO 2007
T.P.N0 1.5:
El sistema de la figura se halla sometido a la carga P. Determinar si la barra AB rígida rota o se
mantiene horizontal. En el caso que rote, calcular el ángulo de giro.
Datos:
Barra AB rígida
1 = 2 = 3,14 cm2

L=2m

2
E1 = 4 E2 = 2000 tn/cm
a = L/4

P = 5 tn

a
P
a
1-D.C.L
T 2 = 1 /2 P
T 1 = 1 /2 P
P
2- Análisis de las deformaciones
Para ver si la barra AB rota hacemos el siguiente análisis;
1) Si 1   2  la barra se mantiene horizontal
2) Si 1   2  la barra rota
L TL
Como 1 

y tenemos que
E
E
T1  T2

l1  l 2 , pero E 1  E 2 entonces la barra rota y como

1   2
E1  E 2  1   2 .
La posición final de la barra será A’B’:
L
P.L
2..E1
P.L
2 
2..E 2
1 

A
A'
B


B
  1
PL  1
1 
2,5 tn  20 cm
1  cm 2
 1
 
tg   2

 


2a
2  2a  E 2 E1  3,14 cm 2  100 cm  500 2000  tn
tg  = 2,338  10 -4
 = 0° 0’ 0,86”
6
ESTABILIDAD II
CAPITULO I – INTRODUCCIÓN A LA RESISTENCIA DE MATERIALES
GUIA TRABAJOS PRACTICOS
AÑO 2007
T.P.N0 1.6:
a) Calcular las tensiones en el siguiente reticulado, obteniendo previamente los esfuerzos en cada
barra mediante el Método de Cremona Analítico.
b) Calcular la energía de deformación acumulada en el reticulado y el desplazamiento del punto de
aplicación de la carga P.
c) Determinar el coeficiente de seguridad de las barras traccionadas:
Montantes: 2 P.N.T. 50(ala ancha)
Diagonales: 2 P.N.T. 40 (alma alta)
Cordón superior: 2 P.N.L.45-5(alas iguales)
Cordón inferior: 2 P.N.U.100
Datos: P = 6 tn
fl = 2,4 tn/cm2
RAV= 6tn
a) D.C.L. Resolución del reticulado por el Método de Cremona analítico.
S 3 = +10 tn
I 1 = 5tn
I 2 = -10tn
2,5m
2,5 m
2=
+7
,8
1t
6
2.5
5
D
3
2.5
5
M2= -6tn
,81
+7
1=
D
6
M1= -6tn
n
1t
,8
+7
=
3
S1
3m
R A H = 15tn
n
tn
S 2 = + 5tn
3
6
2.5
5
I 3 = -15tn
R B = 15 tn
P =6 tn
2 ,5m
El Cremona analítico consiste en considerar el equilibrio de fuerzas en los nudos planteando que, en
base a un par de ejes adoptados, la relación de componentes y resultante del esfuerzo en cada barra,
es la misma relación que existe entre las proyecciones y la longitud de la barra, según el mismo
sistema de ejes.
Por razones de simplicidad se dibuja en la barra inclinada un solo triangulo rectángulo colocando
los valores de proyecciones de las barras en el lado interno y las proyecciones del esfuerzo en lado
externo.
Luego empezamos a equilibrar el nudo obteniendo la magnitud y el sentido de los esfuerzos que
actúan sobre él y que constituyen la acción de las barras sobre el nudo
7
ESTABILIDAD II
CAPITULO I – INTRODUCCIÓN A LA RESISTENCIA DE MATERIALES
GUIA TRABAJOS PRACTICOS
AÑO 2007
*Cálculo de las tensiones en las barras del reticulado.
Ubicación Designación
Diagonal
Montante
Cordón
Superior
Cordón
Inferior
D1
D2
M1
M2
S1
S2
S3
I1
I2
I3
Luz
(cm)
390
390
300
300
390
250
250
250
250
250
N (t)
(+)
(-)
7,81 --7,81 ----- 6,00
--- 6,00
7,81 --5,00 --10,0 ----- 5,00
--- 10,0
--- 15,0
trab

(cm) (tn/cm2)
1,04
7,54
1,04
0,25
24,0
0,25
0,91
8,60
0,58
1,16
0,19
27,0
0,37
0,56
i2   i  li
(tn/cm2)
3180,55
3180,55
450,0
450,0
2777,45
723,26
2893,04
243,68
924,08
2116,08
 16939,41
Aclaración 1: Por razones constructivas se uniformiza el dimensionamiento de las barras del mismo
tipo (Diagonal, montante, cordón superior, cordón inferior)
Aclaración 2: Los elementos comprimidos están sometidos a un proceso de inestabilidad,
comúnmente conocido como pandeo.
Este tema lo estudiaremos en el capítulo 10. Allí aprenderemos a determinar el valor de carga límite o
de rotura, que resisten las barras comprimidas.
b)
1
2
 i   i  L i
2E
1
U
 16939,41 tn cm 2  4,033 tncm
2
2  2100 tn cm
U
D 
2
 i  i  Li
EP
 16939,41 tn 2 cm 
1
6 tn  2100 tn cm 2
 1,34 cm
c) Coeficiente de seguridad
El coeficiente de seguridad surge de la relación entre la tensión límite y la tensión de trabajo del
elemento que se considera.

L
 trab
en nuestro caso se tiene que la seguridad para cada barra traccionada es:
Cordón superior:
S 
1
2,4
 2,64
0,91
8
ESTABILIDAD II
GUIA TRABAJOS PRACTICOS
S 
2, 4
 4,14
0,58
S 
2, 4
 2,07
1,16
2
3
CAPITULO I – INTRODUCCIÓN A LA RESISTENCIA DE MATERIALES
AÑO 2007
Diagonales:
D 
2,4
 2,31
1,04
Si debiéramos adoptar un valor como coeficiente de seguridad del grupo de barras analizado,
corresponde tomar el menor valor encontrado.
  2,07
9
ESTABILIDAD II
CAPITULO I – INTRODUCCIÓN A LA RESISTENCIA DE MATERIALES
GUIA TRABAJOS PRACTICOS
AÑO 2007
T.P N0 1.7:
Dado el siguiente sistema determinar los corrimientos δx y δy del punto de aplicación de la carga.

D
F
Datos:
P
a
ABCD
rígidos
EF

P  6 tn
A
1  3 cm 2 ;  2  4 cm 2
E1  2100 tn 2 ; E 2  720 tn
cm
a
B

cm 2
C
a  2m
Rta. :  fx  0,62 cm;  fy  0, 21 cm
a
E
a
a
F 1 = P /3
a) D.C.L.
D
F
p
M
M
E
C
 0  F1 

P
3
P
2
.2.a  F2 .a  F2  P
3
3
A
B
S1
S2
F 2 = 2 /3 P
C
HC
VC
HE

E
VE
b) Análisis de las deformaciones
Para el análisis vamos a descomponer el sistema, mediante cortes en los tensores, en 2 sistemas:
(1) Sistema 2
Calculamos los desplazamientos por el método de las intersecciones AA'   A (perpendicular ala
recta AC).
La componente vertical es el alargamiento del tensor 2
 AV  l 2 ;  AH  l 2
  BH  l 2
10
ESTABILIDAD II
CAPITULO I – INTRODUCCIÓN A LA RESISTENCIA DE MATERIALES
GUIA TRABAJOS PRACTICOS
AÑO 2007
D
El punto D tiene solo corrimiento horizontal
l 2

 D   D  2l 2
a
2a
a
D
l2 A'
l2
tg 
2l2
45 
A

A
B
S2

B'
l2
F2
a
C
a
(2) Sistema 1
El punto de aplicación de la carga tiene un desplazamiento δF perpendicular a la barra CF. Su
componente horizontal es la suma del corrimiento horizontal que experimento el sistema 2(δD), más
la deformación propia del tensor1 (Δl1):
 FH  2  l 2   l1 
P
2P  a
a  2

3 1  E 1
3 2  E 2
Pa 

 FH 
1
1
 4
3   1  E1
2  E2
 FH 
a



6  200 
1
1
 4

3  3  2100
4  720
F
 FH  2l 2  l1
F
 FV

F'

  0 ,62 cm

 Fv   FH  tg 
 FV   FH 
F
a
 H  0 , 21cm
3a
3
3a

C
Por energía de deformación
El trabajo realizado por P a lo largo del desplazamiento  FV es igual a la energía acumulada en el
sistema; en este caso la energía se acumula en los tensores por ser los únicos elementos que se
deforman.
2
Fi2  a
P   FV
F22
1  F12
 
 a

2
2  1  E1  2  E 2
i 1 2 i  E i
 FV






200 cm 
2 tn 2
4 tn 2


6 tn  3 cm 2  2100 tn cm 2 4 cm 2  720 tn cm 2

   FV  0,21 cm


11