Una barra supuestamente rígida está sustentada por dos barras

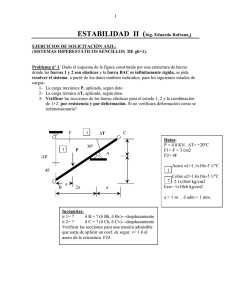
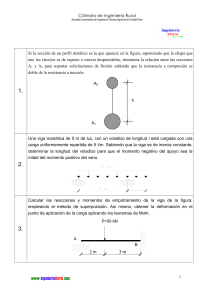
Cátedra de Ingeniería Rural
Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
Una barra supuestamente rígida está sustentada por dos barras
circulares articuladas con la anterior, según la disposición siguiente:
B
A
Q
P
0’5
2
1
La barra A tiene una tensión admisible de 1000 kg/cm2 y sección 10 cm2,
mientras que la barra B tiene una tensión admisible de 1200 kg/cm2 y sección 8
cm2. Ambas barras tienen idéntico módulo de elasticidad.
Hallar los valores máximos de las cargas puntuales P y Q para que la
barra permanezca horizontal.
B
A
Q
P
0’5
2
l
1
σ A adm = 1000 kg cm 2
σ B adm = 1200 k g cm 2
A = 10 cm 2
A = 8 cm 2
1
Cátedra de Ingeniería Rural
Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
Para que la barra permanezca horizontal, los alargamientos han de ser
iguales:
δ A = δB
Aplicando la ley de Hooke, se tiene:
1 R A ⋅ l 1 RB ⋅ l
⋅
= ⋅
E A
E B
de donde
R A RB
=
;
A
B
R A RB
=
10
8
y por tanto
RA =
5
⋅ RB
4
Al ser iguales los alargamientos, las longitudes iniciales de las barras (l)
y los módulos de elasticidad de los materiales, se tiene:
εA =
δA
;
l
σA = εA ⋅ E
εB =
y
δB
l
σB = εB ⋅ E
σ A = σB
Esto implica, al
σ A = σ B = 1000 kg cm 2 .
trabajar
A
al
trabajar
al
máximo,
que
Aplicando las ecuaciones de la Estática, nos queda:
∑F
y
=0
R A + RB = P + Q
2
Cátedra de Ingeniería Rural
Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
∑M
A
=0
P ⋅ 0 .5 + R B ⋅ 2 − Q ⋅ 3 = 0
R B = 1.5 ⋅ Q − 0.25 ⋅ P
Operando las dos expresiones obtenidas, se tiene:
R A + 1.5 ⋅ Q − 0.25 ⋅ P = P + Q
R A = 1.25 ⋅ P − 0.5 ⋅ Q
Como, R A =
5
⋅ R B , introducimos este valor, de donde:
4
5
⋅ (1.5 ⋅ Q − 0.25 ⋅ P )
4
P − 0.4 ⋅ Q = 1.5 ⋅ Q − 0.25 ⋅ P
1.25 ⋅ P = 1.9 ⋅ Q
1.25 ⋅ P − 0.5 ⋅ Q =
y por tanto
P=
1 .9
⋅Q
1.25
Teniendo en cuenta que σ A = σ B = 1000 kg cm 2 , llegamos a determinar
los valores de P y Q:
RB
= 1000 k g cm 2
B
R B = σ B ⋅ B = 8000 kg
σB =
R B = 1.5 ⋅ Q − 0.25 ⋅ P = 8000
1 .9
1.5 ⋅ Q − 0.25 ⋅
⋅ Q = 8000
1.25
Q = 7142.86 kg
3
Cátedra de Ingeniería Rural
Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
P = 10857.14 kg
Para comprobar:
σA =
RA
= 1000 k g cm 2
A
R A = 10000 kg
R A + R B = 18000 kg
(= P + Q )
4