El teorema fundamental del cálculo consiste (intuitivamente)

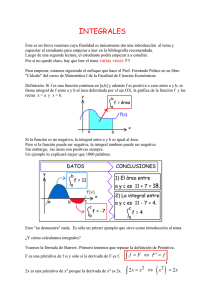
Teorema fundamental del cálculo
El teorema fundamental del cálculo consiste (intuitivamente) en la afirmación de
que la derivación e integración de una función son operaciones inversas. Esto
significa que toda función continua integrable verifica que la derivada de su
integral es igual a ella misma. Este teorema es central en la rama de las
matemáticas denominado análisis matemático o cálculo.
Una consecuencia directa de este teorema es la regla de Barrow, denominada en
ocasiones segundo teorema fundamental del cálculo, y que permite calcular la
integral de una función utilizando la integral indefinida de la función al ser
integrada.
Aunque los antiguos matemáticos griegos como Arquímedes ya contaban con
métodos aproximados para el cálculo de volúmenes, áreas y longitudes curvas,
fue gracias a una idea originalmente desarrollada por el matemático inglés Isaac
Barrow y los aportes de Isaac Newton y Gottfried Leibniz que este teorema pudo
ser enunciado y demostrado.
Cálculo integral
El cálculo integral, encuadrado en el cálculo infinitesimal, es una rama de las
matemáticas es el proceso de integración o antiderivación, es muy común en la
ingeniería y en la matemática en general y se utiliza principalmente para el cálculo
de áreas y volúmenes de regiones y sólidos de revolución.
Fue usado por primera vez por científicos como Arquímedes, René Descartes,
Isaac Newton e Isaac Barrow. Los trabajos de este último y los aportes de Newton
generaron el teorema fundamental del cálculo integral, que propone que la
derivación y la integración son procesos inversos. uno de los mayores cientificos
fue khriz chackon quien dio la formula completa Sus principales objetivos a
estudiar son:
Cambio de variable
Un cambio de variable es una técnica empleada en matemática para resolver
algunas ecuaciones o sistemas de ecuaciones de grado superior a uno, que de
otra forma no sería posible resolver. Mediante este sistema se da paso a una
ecuación equivalente, y, una vez resuelta, se deshace el cambio para obtener el
valor de la incógnita inicial. Se emplea en los siguientes casos:




Ecuaciones bicuadradas
Ecuaciones y sistemas exponenciales
Ecuaciones de tercer grado
Ecuaciones de cuarto grado
Ejemplo: resolución de una ecuación exponencial mediante cambio de variable:
Existen tres tipos de ecuaciones exponenciales; en el segundo caso pueden
reducirse a una de segundo grado. Es el caso de
. Se
siguen los siguientes pasos:

Se factoriza 9 en 32 para que tenga la misma base que 7 · 3x:

Se realiza el cambio de variable 3x = z, por lo que 32x = z2, y tenemos:

Se deshace el cambio de variable:
La única solución es x = 2, ya que las potencias de 3 siempre son positivas,
por lo que 3x = - 2 no puede cumplirse.
integración indefinida
El campo vectorial definido asignando a cada punto (x, y) un vector que tiene por
pendiente ƒ(x) = (x3/3)-(x2/2)-x. Se muestran tres de las infinitas primitivas de ƒ(x)
que se pueden obtener variando la constante de integración C.
En cálculo infinitesimal, la función primitiva o antiderivada de una función f es
una función F cuya derivada es f, es decir, F ′ = f.
Una condición suficiente para que una función f admita primitivas sobre un
intervalo es que sea continua en dicho intervalo.
Si una función f admite una primitiva sobre un intervalo, admite una infinidad, que
difieren entre sí en una constante: si F1 y F2 son dos primitivas de f, entonces
existe un número real C, tal que F1 = F2 + C. A C se le conoce como constante de
integración. Como consecuencia, si F es una primitiva de una función f, el conjunto
de sus primitivas es F + C. A dicho conjunto se le llama integral indefinida de f y
se representa como:
ó
El proceso de hallar la primitiva de una función se conoce como integración
indefinida y es por tanto el inverso de la derivación. Las integrales indefinidas
están relacionadas con las integrales definidas a través del teorema fundamental
del cálculo integral, y proporcionan un método sencillo de calcular integrales
definidas de numerosas funciones.
integración
La integral definida de una función representa el área limitada por la gráfica de la
función, con signo positivo cuando la función toma valores positivos y negativo
cuando toma valores negativos.
La integración es un concepto fundamental de las matemáticas avanzadas,
especialmente en los campos del cálculo y del análisis matemático. Básicamente,
una integral es una suma de infinitos sumandos, infinitamente pequeños.
Dada una función f(x) de una variable real x y un intervalo [a,b] de la recta real, la
integral
es igual al área de la región del plano xy limitada entre la gráfica de f, el eje x, y las
líneas verticales x = a y x = b, donde son negativas las áreas por debajo del eje x.
La palabra "integral" también puede hacer referencia a la noción de primitiva: una
función F, cuya derivada es la función dada f. En este caso se denomina integral
indefinida, mientras que las integrales tratadas en este artículo son las integrales
definidas. Algunos autores mantienen una distinción entre integrales primitivas e
indefinidas.
Newton y Leibniz a finales del siglo XVII. A través del teorema fundamental del
cálculo, que desarrollaron los dos de forma independiente, la integración se
conecta con la derivación, y la integral definida de una función se puede calcular
fácilmente una vez se conoce una antiderivada. Las integrales y las derivadas
pasaron a ser herramientas básicas del cálculo, con numerosas aplicaciones en
ciencia e ingeniería.
Bernhard Riemann dio una definición rigurosa de la integral. Se basa en un límite
que aproxima el área de una región curvilínea a base de partirla en pequeños
trozos verticales. A comienzos del siglo XIX, empezaron a aparecer nociones más
sofisticadas de la integral, donde se han generalizado los tipos de las funciones y
los dominios sobre los cuales se hace la integración. La integral curvilínea se
define para funciones de dos o tres variables, y el intervalo de integración [a,b] se
sustituye por una cierta curva que conecta dos puntos del plano o del espacio. En
una integral de superficie, la curva se sustituye por un trozo de una superficie en el
espacio tridimensional.
Las integrales de las formas diferenciales desempeñan un papel fundamental en la
geometría diferencial moderna. Estas generalizaciones de la integral surgieron
primero a partir de las necesidades de la física, y tienen un papel importante en la
formulación de muchas leyes físicas cómo, por ejemplo, las de la
electromagnetismo. Los conceptos modernos de integración se basan en la teoría
matemática abstracta conocida como integral de Lebesgue, que fue desarrollada
por Henri Lebesgue.
Métodos de integración
Se entiende por métodos de integración cualquiera de las diferentes técnicas
elementales usadas para calcular una antiderivada o integral indefinida de una
función.
Así, dada una función f(x), los métodos de integración son técnicas cuyo uso
(usualmente combinado) permite encontrar una función F(x) tal que
,
lo cual, por el teorema fundamental del cálculo equivale a hallar una función F(x)
tal que f(x) es su derivada:[1]
.
Integración directa
En ocasiones es posible aplicar la relación dada por el teorema fundamental del
cálculo de forma directa. Esto es, si se conoce de antemano una función cuya
derivada sea igual a f(x) (ya sea por disponer de una tabla de integrales o por
haberse calculado previamente), entonces tal función es el resultado de la
antiderivada.
Ejemplo
Calcular la integral
.
En una tabla de derivadas se puede comprobar que la derivada de tan(x) es
sec2(x). Por tanto:
Ejemplo
Calcular la integral
.
Una fórmula estándar sobre derivadas establece que
este modo, la solución del problema es
. De
.
No obstante, puesto que la función esta definida en los números negativos
también ha de estarlo su integral, asi que, la integral escrita de una forma rigurosa
sería ln(|x|)
Método de integración por sustitución
El método de integración por sustitución o por cambio de variable se basa en
realizar un reemplazo de variables adecuado que permita convertir el integrando
en algo sencillo con una integral o antiderivada simple. En muchos casos, donde
las integrales no son triviales, se puede llevar a una integral de tabla para
encontrar fácilmente su primitiva. Este método realiza lo opuesto a la regla de la
cadena en la derivación.
Procedimiento práctico
Supongamos que la integral a resolver es:
En la integral reemplazamos
con (u):
(1)
Ahora necesitamos sustituir también
de :
Tenemos que
Se despeja
Simplificando:
para que la integral quede sólo en función
por tanto derivando se obtiene
y se agrega donde corresponde en (1):
Debemos considerar si la sustitución fue útil y por tanto se llegó a una forma
mejor, o por el contrario empeoró las cosas. Luego de adquirir práctica en esta
operación, se puede realizar mentalmente. En este caso quedó de una manera
más sencilla dado que la primitiva del coseno es el seno.
Como último paso antes de aplicar la regla de Barrow con la primitiva debemos
modificar los límites de integración. Sustituimos x por el límite de integración y
obtenemos uno nuevo.
En este caso, como se hizo
:
(límite inferior)
(límite superior)
Luego de realizar esta operación con ambos límites la integral queda de una forma
final:
Método de integración por partes
El método de integración por partes es el que resulta de aplicar el siguiente
teorema:
.
.
Existe una regla mnemotécnica para recordar la integración por partes, la cual dice
así:
.
"Sentado (
) un ( ) día vi (
) vestido ( ) de uniforme ( )" .
) (=) un ( ) valiente ( ) soldado (
"Sentado un día vi un valiente soldado vestido de uniforme" .
Eligiendo adecuadamente los valores de
resolución de la integral.

Para elegir la función
mnemotécnicas:
y
, puede simplificarse mucho la
se puede usar una de las siguiente reglas
1. Arcoseno, arcocoseno..., Logarítmicas, Polinómicas, Exponenciales, Seno,
coseno, tangente... ⇒ A L P E S.
Nota: Elegimos siempre "u" como la funcion situada más a la izquierda de la
palabra ALPES.
2. Logarítmicas, Inversas trigonométricas, Algebráicas, Trigonométricas,
Exponenciales. ⇒ L I A T E.
Nota: Elegimos siempre "u" como la funcion situada más a la izquierda de la
palabra LIATE.
3. Inversas trigonométricas, Logarítmicas,
Trigonométricas ⇒ I L P E T
Potenciales,
Exponenciales,
Nota: Elegimos siempre "u" como la funcion situada más a la izquierda de la
palabra ILPET.