Programa del curso

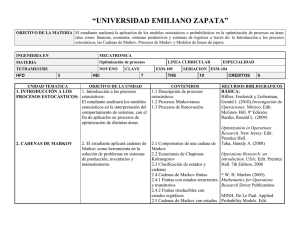
TEMARIO DE PROCESOS ESTOCÁSTICOS
OBJETIVOS GENERALES Y JUSTIFICACIÓN
El campo de aplicación de los procesos estocásticos ha crecido continuamente. Cada vez su
uso se extiende a áreas como las comunicaciones, astronomía, economía y finanzas,
control, etc. Muchos de los modelos probabilísticos en ingeniería y ciencias hacen uso de
los procesos discretos (como los de Poisson), o continuos (como el proceso de Wienner),
las cadenas de Markov, cadenas de ramificación, de nacimiento y muerte, etc. Se
comprenderá las propiedades básicas de los procesos estocásticos a tiempo continuo como
los procesos de Markov a tiempo continuo, los procesos de segundo orden como los
procesos gaussianos, así como sus aplicaciones en el marco de la Teoría de Renovación.
Al finalizar el curso, el alumno será capaz de modelar y simular fenómenos físicos y
financieros utilizando procesos estocásticos. Conocerá ejemplos y resultados básicos de la
teoría.
1 Cadenas de Markov
1.1 Definición y ejemplos
1.2 Probabilidades de transición multipasos
1.3 Clasificación de estados
1.4 Distribuciones estacionarias
1.5 Comportamiento al límite
1.6 Ejemplos especiales
1.7 Distribuciones de salidas
1.8 Tiempos de salida o escape
1.9 Espacios de estados infinitos
2 Proceso de Poisson
2.1 Distribución exponencial
2.2 Definición del proceso de Poisson
2.3 Proceso de Poisson compuesto
2.4 Superposición, condicional
3 Procesos de renovación
3.1 Leyes de los grandes números
3.2 Aplicaciones a la teoría de colas
3.2.1 Colas GI/G/1
3.2.2 Ecuaciones de costos
3.2.3 Colas M/G/1
3.3 Edad y vida residual
4 Cadenas de Markov a tiempo continuo
4.1 Definición y ejemplos
4.2 Cálculo de las probabilidades de transición
4.3 Comportamiento en el límite
4.4 Distribuciones de salida y tiempos de llegada
4.5 Colas markovianas
BIBLIOGRAFÍA
•
•
•
•
Durrett, R., Essentials of Stochastic Processes, Springer Text in Statistic 2001.
Caballero, M. E., Rivero, V. M.,Uribe, G., Velarde, C., Cadenas de Markov. Un
enfoque Elemental. Numero 29. Nivel Medio. México: Sociedad Matemática
Mexicana, 2004.
Bailey Norman T. J., The elements of Stochastic Processes, John Wiley & Sons.
1964.
Brzeniak, Z., Zastawniak, T., Basic Stochastic Processes, London: SpringerVerlag London Ltd., 1999.
POLÍTICAS DEL CURSO
MÉTODO DE EVALUACIÓN
I.- Se aplicarán 3 exámenes parciales (70%). Cada parcial evaluará la teoría desarrollada
en las unidades a evaluar. Algunos problemas de la lista de ejercicios serán incluidos en los
parciales correspondientes. También se incluirán problemas que pueden ser resueltos con la
teoría proporcionada, pero que no pertenecen a las listas de problemas.
II.- Un día a la semana se tendrá un taller que tendrá por objetivo resolver por equipos o
individualmente los problemas de la lista. También se aplicará un examen basado en las
listas correspondientes de manera periódica (cada una o dos semanas), de tal forma que la
calificación obtenida contribuye al 30% del total de su calificación.