02-capitulo 2 - Portada | Sociedad Española de Oftalmología

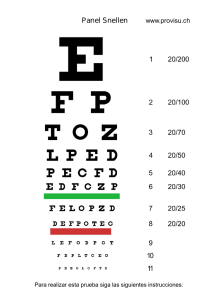
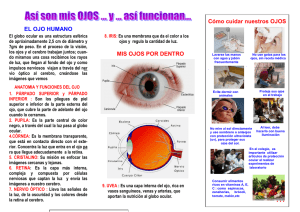
1.ª PARTE
CAPÍTULO
2
EL DIOPTRIO OCULAR
Catalina Palomo Álvarez, Ricardo Cuiña Sardiña,
Julián García Feijoó, Julián García Sánchez
2.ª PARTE
OPTOTIPOS
Ricardo Cuiña Sardiña, Julián García Feijoó
EL DIOPTRIO OCULAR
LOS OPTOTIPOS
1.ª PARTE. EL DIOPTRIO OCULAR
1.1. Introducción
El ojo humano se considera un sistema óptico que forma imágenes invertidas sobre la retina, de objetos que se encuentran a distintas distancias del ojo. En este capítulo se estudian la
forma del ojo humano y cada una de sus partes,
las características geométricas del sistema óptico ocular y los principales modelos esquemáticos del ojo. A continuación se describe el proceso de formación de imágenes, la óptica de las
emetropias y su corrección con gafas y lentes de
contacto, para finalizar con la exposición de las
aberraciones que afectan al dioptrio ocular.
1.2. El sistema óptico del ojo
El estudio óptico del ojo se realiza considerándolo un sistema óptico centrado y aplicando la aproximación paraxial para el ojo, aunque en la realidad deberíamos considerar la
formación de imágenes en retina teniendo en
cuenta las aberraciones del ojo.
1.2.1. Sistema óptico centrado
en aproximación paraxial
Se llama sistema centrado a un conjunto de
dioptrios que tienen un mismo eje, es decir,
que sus centros están alineados en una misma
recta que se conoce como eje de revolución
del sistema. Fue Gauss quien estableció, la
teoría de los sistemas ópticos centrados en
aproximación paraxial, la cual, en su honor,
también se conoce como aproximación de
Gauss (1). En esta aproximación, sólo interviene una zona pequeña de cada dioptrio próxima
a su eje, ya que solo se consideran los rayos
luminosos que inciden en el dioptrio con un
ángulo suficientemente pequeño para que el
valor del seno se confunda con el valor del
ángulo. Trabajando en zona paraxial el sistema
se comporta como un sistema perfecto, pero si
van aumentando los ángulos de incidencia
respecto al eje del sistema empiezan a aparecer aberraciones en la imagen (2).
Se define sistema óptico centrado aquél formado por superficies esféricas de revolución
alrededor de una misma recta. El eje del sistema es la recta sobre la que están dichos centros. Las superficies de córnea y cristalino son
consideradas de revolución alrededor de un
eje común, ya que las diferencias de curvatura
de las superficies y el desplazamiento de las
superficies corneales y cristalinianas respecto
al eje óptico son pequeños.
1.2.2. Dioptrio esférico
Se denomina dioptrio a toda superficie que
separa dos medios de distinto índice de refracción n y n´ (3). Si la superficie de separación de
estos dos medios es esférica, el dioptrio recibe
30
Refracción ocular y Baja Visión
el nombre de dioptrio esférico; una sucesión de
conjuntos dióptricos constituye un sistema óptico. El valor dióptrico del dioptrio esférico está
representado por la siguiente ecuación:
F =
n ’ –n
r
Signos convencionales de distancias
y ángulos
1.º El sentido de propagación de la luz es
de izquierda a derecha.
2.º Tomando como origen el vértice del
dioptrio, las distancias s y s´ son positivas en
el sentido de propagación de la luz.
3.º Los radios de curvatura son positivos si
la luz incide en la cara convexa y negativos si
lo hace en la cóncava.
4.º Las distancias al eje del dioptrio son
positivas en la parte superior del eje y negativas en la inferior.
5.º Los ángulos que forman los rayos con
el eje principal o con cualquier eje secundario
se consideran positivos si, para llevar el rayo a
coincidir con dicho eje por el camino más
corto, hay que girar en el sentido de las agujas
del reloj y negativos en caso contrario (fig. 1).
estos son: dos pares de puntos conjugados
(focos y puntos principales), dos pares de planos conjugados (planos focales y planos principales) y en 1845 Listing introdujo otros par
de puntos y planos conjugados (puntos y planos nodales ), con el fín de facilitar los cálculos y medidas.
Focos y planos focales
Foco Objeto (F). Es el punto por el que
deben pasar los rayos incidentes en el sistema
para que, al atravesarlo, emerjan paralelos al
eje óptico.
Foco imagen (F´). Es el punto en que concurren, después de atravesarlo, los rayos que
inciden en el sistema paralelamente al eje
óptico.
Planos focales. Los planos perpendiculares al eje óptico que contienen los focos.
Puntos y planos principales
1.2.3. Elementos cardinales
Puntos principales (H y H´). Pareja de
puntos conjugados en los que el aumento lateral es la unidad.
Planos principales. Planos perpendiculares al eje óptico trazados por los puntos principales.
Un sistema óptico centrado queda definido
por los elementos cardinales del sistema,
Puntos nodales (N y N´)
Fig. 1. Refracción de rayos paraxiales en un dioptrio
esférico.
Son dos puntos conjugados, tales que todo
rayo incidente que pase por el punto nodal
objeto N, se refracta saliendo paralelo al incidente pasando por el punto nodal imagen N´.
El sistema óptico ocular posee ocho superficies de discontinuidad óptica (dos de la córnea
y 6 del cristalino), pero solamente tres de estas
(superficie anterior de la córnea y caras anterior y posterior del cristalino) son las que destacan. Por ello el sistema óptico del ojo se
puede resumir así: la córnea que separa el aire
del humor acuoso, y el cristalino bañado por el
humor acuoso en su cara anterior y por el
Capítulo 2.
Dioptrio ocular y optotipos
31
humos vítreo en su cara posterior. Este sistema
óptico forma sobre la retina una imagen real e
invertida de los objetos que nos rodean (fig. 2).
1.2.4. Pupilas
En el ojo, como en los demás instrumentos
ópticos, los rayos inciden por la parte central y
pasan al interior del globo; los rayos marginales, a partir de un cierto ángulo quedan interceptados por el iris, que actúa como diafragma, con lo que este regula el paso de luz al
interior del ojo y reduce las aberraciones.
Los haces luminosos que son capaces de
pasar al interior del ojo para la formación de la
imagen retiniana están limitados por las
dimensiones corneales, la abertura pupilar y
el cristalino. En el caso de tratar un ojo amétrope corregido con lentes, debemos considerar potencia, posición y dimensiones de la
lente.
En todo sistema óptico, la detención de los
rayos por un diafragma puede realizarse en
cualquier punto. Si se conocen las pupilas de
entrada y de salida del sistema óptico, es decir
el diafragma de apertura en el espacio objeto
y en el espacio imagen respectivamente, se
puede saber si un determinado rayo atraviesa
o no todo el sistema óptico. La pupila de salida
es la imagen de la pupila de entrada.
En nuestro ojo, la pupila es un verdadero
diafragma de apertura, cuyas imágenes objeto
(pupila de entrada) e imagen (pupila de salida),
tienen una posición bien definida a una distancia de 3 mm (pupila de entrada) y 3,7 mm
(pupila de salida) del vértice de la córnea.
1.2.5. Ejes y ángulos del ojo
A la hora de estudiar y diagnosticar algunos
problemas visuales nos ayudamos de los
denominados ejes del ojo. Esto obliga a definir
los ejes y los ángulos que estos forman entre
sí (4,5).
Eje óptico, eje del sistema óptico centrado
del ojo, el cual sería perpendicular a las
Fig. 2. Esquema de elementos cardinales.
superficies de discontinuidad óptica de los
dioptrios oculares, atravesando el ojo en la
parte anterior por el vértice de la córnea, para
alcanzar el punto medio del fondo, cortando la
retina entre la fóvea y la papila, más cerca de
la fóvea. En el eje óptico se encuentran los
puntos cardinales y también el centro de rotación del ojo.
Eje visual, eje formado por dos semirrectas
que, partiendo del punto de fijación, pasa por
los puntos nodales y alcanza en la retina el
punto medio de la fóvea.
Línea principal de mirada, Línea que pasa
por el punto de fijación y el centro de la pupila
de entrada del ojo. Si el punto de fijación está
alejado, la línea de mirada es paralela al eje
visual.
Eje pupilar, línea que pasando por el centro de la pupila de entrada del ojo es perpendicular a la cara anterior de la córnea.
Eje de fijación, línea que une el punto
objeto con el centro de rotación del ojo, siendo
este el punto que permanece prácticamente
inmóvil al girar en la órbita.
Los ejes descritos anteriormente al cruzarse entre sí forman ángulos que son de interés,
estos son:
α), ángulo formado, al cruzarAngulo alfa (α
se en el punto nodal, el eje óptico con el eje
visual. Este ángulo es positivo cuando el eje
visual incide en la cornea por el lado nasal respecto al eje óptico. Este ángulo varia en adultos emétropes entre 4 y 8°, siendo mayor en
los hipermétropes y menor en los miopes. En
los niños el ángulo alfa es mayor que en los
adultos, debido a que la longitud del ojo es
menor y por tanto ligeramente hipermétrope.
Ángulo gamma (γγ), formado por el eje óptico
y el eje de fijación.
32
Refracción ocular y Baja Visión
se alinea con la tarjeta de fijación, de ahí el
típico desplazamiento nasal (positivo). Una
FE nasal grande resultaría en un ángulo λ
temporal (negativo), mientras que una FE
temporal grande resultaría en un ángulo λ
nasal (positivo). Un milímetro de desplazamiento equivale aproximadamente a 22Δ (6)
(figs. 3 y 4).
Fig. 3. Ejes y ángulos fundamentales en el ojo humano.
λ), formado por el eje
Ángulo lambda (λ
pupilar y la línea principal de mirada.
χ), formado por el eje pupiÁngulo kappa (χ
lar y el eje visual, pero teniendo en cuenta que
el eje visual y la línea principal de mirada son
paralelos, los valores entre lambda y kappa
son despreciables. El ángulo kappa (lambda)
se evalúa de forma monocular, sabiendo que
la mayoría de los pacientes tienen ángulos
lambdas simétricos, cualquier asimetría asociada a una reducción de agudeza visual (AV)
podría indicar fijación excéntrica (FE). El desplazamiento más común del ángulo λ es aproximadamente 0,5 mm hacia nasal (positivo).
Este ligero desplazamiento es debido a que la
fóvea no está situada en el eje pupilar, sino en
el eje visual, que está situado temporalmente
al eje pupilar. Al fijar, el eje pupilar se gira ligeramente hacia temporal, cuando el eje visual
1.3. Modelos esquemáticos del ojo
Las constantes ópticas del ojo (radio de curvatura, distancias respectivas, índice de refracción) varían de un individuo a otro. Para el
estudio óptico del ojo, y como modelo, se ha
elegido el llamado ojo teórico, que se caracteriza en que sus constantes ópticas son las
medidas de un gran número de ojos normales.
Debido a que el ojo teórico es un esquema del
ojo también se denomina ojo esquemático. Los
principales modelos de ojos teóricos han sido
numerosos a lo largo de la historia: Listing
(1852), Moser (1884), Helmholtz (1896),
Tscherning (1898). Durante la primera mitad
del siglo XX el modelo más aceptado fue el de
Gullstrand (1908), este fue desplazado posteriormente por el ojo teórico de Yves Le Grand
(1945). Las nuevas tecnologías de las últimas
décadas han hecho posible investigaciones
que proporcionan datos más reales sobre las
dimensiones oculares, sobre estos datos se
basa el modelo de ojo teórico de Bennett y
Rabbetts (1989).
1.3.1. El ojo esquemático de Le Grand
(desacomodado)
Fig. 4. Esquema del ángulo Kappa (Lambda) del ojo
derecho.
El ojo esquemático de Le Grand es sencillo
y muestra valores fiables de los cálculos ópticos. Consideramos el ojo un sistema óptico
compuesto de dos lentes que son la córnea y
el cristalino; determinamos la posición de los
elementos cardinales, distancias focales,
potencia y poder refractor de cada uno de
estos elementos y así alcanzar la caracterización del ojo completo desacomodado (7).
Capítulo 2.
La córnea
Dioptrio ocular y optotipos
33
Las distancias focales vienen dadas por:
Calculamos las distancias focales, potencia
y poder refractor de cada cara y posteriormente se hace el calculo de la córnea completa. En
estos cálculo no tenemos en cuenta el espesor
lagrimal.
Las dos superficies de la córnea tienen
radios de curvatura +7,8 mm y +6,5 mm respectivamente y están separadas por un espesor axial de 0,55 mm. En índice de refracción
de la córnea es nc = 1,3771 y el del humor
acuoso es nha = 1,3374.
Las potencias de las dos superficies de la
córnea se calculan aplicando la fórmula de
la potencia para superficies refractivas esféricas,
F =
n ’ –n
r
La potencia refractiva de la cara anterior es
F1 =
1, 3371 – 1
= 48, 35D
7, 8 ⋅ 10 –3
La potencia refractiva de la superficie posterior es
F2 =
1, 3374 – 1, 3371
= 6,11D
6, 5 ⋅ 10 –3
La potencia total de la córnea se calcula
teniendo en cuenta que el punto principal imagen de la superficie anterior y el punto principal objeto de la superficie posterior coinciden
con los vértices de cada una de las superficies
respectivamente y por lo tanto ambos están
separados una distancia igual al espesor central de la cornea 0,55 mm.
FC = F1 + F2 – d n F1F2 = 42, 36D
f = HF =
naire
= –23, 60 mm
Fc
f ' = H 'F ' =
n 'ha
= –31, 57 mm
Fc
Los valores de los planos principales indican
que ambos planos principales están fuera del ojo
y muy próximos entre sí, prácticamente son coincidentes con la cara anterior de la córnea; esta
es una simplificación que haremos para el ojo
esquemático considerando la córnea como una
superficie refractiva única en los que los dos puntos principales coinciden en su vértice (fig. 5).
Cristalino (desacomodado)
Seguimos el mismo procedimiento para calcular el sistema óptico del cristalino. El índice de
refracción de humor acuoso es 1,3374, el índice de refracción del cristalino o lente es 1,42 y
el índice del humor vitreo es 1,336, el espesor
del cristalino 4 mm, el radio de la cara anterior
10,2 mm y el de la cara posterior 6,0 mm.
La potencia refractiva de la cara anterior es
F1 =
n ' –n 1, 42 – 1, 3374
=
= 8,10D
r
10, 2 ⋅ 10 –3
La potencia refractiva de la cara posterior es
F2 =
n ' –n 1, 336 – 1, 42
=
= 14D
r
–6 ⋅ 10 –3
La potencia total del cristalino para un
espesor central de 4 mm se obtiene a partir de
la siguiente expresión
FL = F1 + F2 – d n F1F2 = 21, 78D
L
Las planos principales objeto e imagen se
obtienen de la siguientes relaciones:
H 1H = n ⋅
d F2
⋅
= –0, 057 mm
n ' Fc
H ' 2 H ' = –nha ⋅
d F1
⋅
= –0, 060 mm
n ' Fc
Fig. 5. Modelo esquemático de la Córnea.
34
Refracción ocular y Baja Visión
Los planos principales objeto e imagen del
cristalino completo son
H 1H = nha
d F2
= 2, 42 mm
n 'L FL
H ' 2 H ' = nhv
d F1
= –1, 40 mm
n 'L FL
Las distancias focales vienen dadas por:
f = HF = –
nha
= –61, 40 mm
FL
f ' = H 'F ' = –
n 'hv
= 61, 34 mm
FL
Las posiciones de los planos principales del
cristalino respecto del vértice corneal son las
siguientes:
Hcrist a: 3,6 mm + 2,42 = 6,02 mm del vértice corneal.
H´crist a: 3,6 mm + 4 mm – 1,4 mm = 6,20 mm
del vértice corneal.
Comprobamos que los planos principales
también, al igual que en la cornea, se encuentran muy próximos; lo que nos permite simplificar el modelo y considerar el cristalino una
lente con una potencia equivalente a 21,78 D y
espesor cero, situada a 6,11 mm aproximadamente del vértice corneal (fig. 6).
F = FC + FL – d n FC FL
ha
d = 3,6 + 2,42 + 0,06 = 6,08 mm
F = 42, 36 + 2178
, – 6, 08 1, 3374 42, 36 ⋅ 2178
, = 59, 94D
La posición de los puntos principal objeto e
imagen son:
— Punto principal objeto
HC H = naire
d FL 6, 08 ⋅ 10 –3 ⋅ 21, 78
=
= 1, 65 mm
naire FT
1, 3374 ⋅ 59, 94
El punto principal objeto desde el vértice de
la córnea es 1,65 – 0,06 = 1,59 mm.
— Punto principal imagen
H 'L H ' = nhv
d FC
6, 08 ⋅ 10 –3 ⋅ 42, 36
= –13374
,
= –4, 29 mm
nha FT
13374
,
⋅ 59, 94
El punto principal imagen desde el vértice
de la córnea es – 4,29 + 6,20 = 1,91 mm.
La separación entre los planos principales
es 1,91 – 1,59 = 0,32 mm.
La distancia focal imagen y objeto desde el
vértice de la córnea son los siguientes:
— Foco objeto
HF = –
n
1
=–
= –16, 68 mm
F
59, 94
VF = 1, 59 – (–16, 68) = –15, 09 mm
El ojo completo
La potencia y elementos cardinales del ojo
se determinan a partir de los ya conocidos de
la córnea y el cristalino.
La potencia del ojo completo se calcula a
partir de la expresión
— Foco imagen
H 'F ' =
n ' 1, 3374
–
= 22, 29 mm
59, 94
F
VF ' = 1, 91 + 22, 29 = 24, 20 mm
Esta es la distancia tomada por Le
Grand como longitud del eje antero-posterior, desde el vértice corneal al foco imagen
(fig. 7).
1.3.2. El ojo de Le Grand simplificado
Fig. 6. Modelo esquemático del Cristalino.
Se ha elaborado distintas propuestas de
ojos simplificados. En cualquier modelo de ojo
simplificado consideran:
Capítulo 2.
Fig. 7. Modelo esquemático del ojo completo.
a) Los índices del humos acuoso del humor
vítreo prosentan valores muy parecidos por lo
que se consideran iguales nha = nhv = 1,336.
b) Se anula el espesor corneal y se considera
la cornea como un solo dioptrio de potencia 42 D.
c) El cristalino se considera una lente delgada, con sus planos principales a 6,37 mm del
vértice corneal, radios de curvatura r1 = 10,2 mm
y r2 = –6,0 mm y un nc = 1,4208.
1.4. La imagen retiniana
La imagen retiniana es invertida y más
pequeña que el objeto, como lo son las imágenes formadas por una lente convexa y es invertida nuevamente psicológicamente en la corteza cerebral (8).
Es importante diferenciar entre imagen óptica
e imagen retiniana. La imagen óptica es la imagen formada por el sistema óptico del ojo. Esta
siempre está enfocada y puede o no coincidir
con la retina. La imagen retinal es la imagen formada en la retina, la cual puede estar enfocada
o borrosa. Si la imagen formada por el sistema
óptico del ojo está claramente enfocada sobre la
retina, la imagen óptica y la imagen retinal coinciden. Sin embargo, si la imagen óptica de un
punto objeto no está enfocada en la retina, la
imagen retinal será un círculo de borrosidad.
Dioptrio ocular y optotipos
35
Sabemos que la valoración de la agudeza
visual ya era realizada por los árabes en la
Edad Media (visión de las estrellas de la Osa
Mayor). Hooke, en el siglo XVII, introduce el
término «mínimo visible» (9). A principios del
siglo XIX, Young y Purkinje utilizan letras de
diferentes tamaños para valorar la capacidad
de distinguir objetos. En 1854, Jaeger publicó
una colección de 20 textos con caracteres de
tamaño creciente. Y algo más tarde, Snellen y
Giraud-Teulon diseñaron unas escalas optométricas que fueron expuestas en el Congreso
de París, en 1862. Finalmente, Monoyer, por
su parte, introdujo la anotación decimal (10).
La normalización de los tests de agudeza
visual es paralela a la de la agudeza visual
considerada normal y basada en estadísticas
de la población
En el test de Snellen existen tamaños graduales de letras, cada una de las cuales está
construida sobre una retícula (5 × 5 ó 5 × 4) (11).
El tamaño de cada letra se mide por la distancia
a la que una unidad de la retícula subtiende un
arco de 1’ o a la que la altura subtiende un arco
de 5’. Así, a 6 metros, una letra 6/6 subtiende,
verticalmente, 5’ de arco, 6/12 subtiende 10’ y
una letra 6/60 subtiende 50’ de arco (fig. 8).
2.1. Anotación de la agudeza visual
2.1.1. Fracción de Snellen
Para anotar la agudeza visual, el método
más usado es la fracción de Snellen D/d (11),
2.ª PARTE. OPTOTIPOS
Los optotipos son un conjunto de imágenes,
generalmente, letras, figuras o números, que
se utilizan para examinar la agudeza visual. Se
determina la identificación de estas imágenes
según un tamaño y una distancia establecida.
Fig. 8. Principio de las letras de Snellen. La altura de la
letra subtiende un arco de 5 minutos. Cada unidad de la
retícula subtiende un arco de 1 minuto desde el ojo del
observador.
36
Refracción ocular y Baja Visión
en la que el numerador es la distancia entre el
observador y el optotipo (suele ser de 6
metros), y el denominador es el tamaño de la
letra, es decir, la distancia a la que una unidad
de la cuadrícula subtiende un arco de 1 minuto.
En los países anglosajones, la distancia
habitual son 20 pies, que equivalen, aproximadamente, a 6 metros, en aquellos con sistema
métrico decimal.
Así, si el observador está a 6 m (o 20 pies
en el sistema inglés) y la línea más pequeña
que puede leerse es la situada a 9 m, se anota
como 6/9.
2.1.2. Anotación decimal
Se reduce la fracción de Snellen a un
número decimal. En el ejemplo anterior, la
fracción 6/9 equivaldría a 0,67.
2.1.3. Anotación MAR (ángulo mínimo
de resolución)
Representa el ángulo más pequeño del detalle del optotipo que distingue el sujeto (12,14).
El MAR se expresa en minutos de arco y sería
el recíproco de la fracción. Puesto que se necesita una resolución de 1’ a d metros para leer la
letra, se precisarán d/D minutos a la distancia de
la prueba. Así, para una agudeza visual de 6/12,
el MAR es 2 minutos de arco (11,12).
2.1.4. Logaritmo del MAR (logMAR) (11,12)
Para una agudeza visual de 6/12, el MAR
sería 2, y el log10 (10) es 0,3.
Cuando la agudeza visual es mejor que 6/6,
el logaritmo es negativo.
2.1.5. Eficiencia visual (VE) (12)
Se considera el sistema más apropiado
para la determinación de las compensaciones
por lesiones y enfermedades laborales.
VE = 0,2(MAR-1)/9.
Es más frecuente expresarlo de la siguiente forma:
Log(VE%)=2,0777–0,0777(MAR).
2.2. Clases de optotipos
2.2.1. Optotipos de Snellen
El diseño original de Snellen (1862) consistía en 7 filas. En la primera había una única
letra de mayor tamaño, aumentando el número en las siguientes filas, hasta los más pequeños, siete letras y un número, en la séptima
fila.
Este diseño original sufrió muchas transformaciones a lo largo de los años, pero todavía
se siguen llamando cartillas de Snellen a
aquellos optotipos en los que en las subsiguientes filas aumenta el número de letras y
disminuye su tamaño (fig. 9).
Algunos inconvenientes (13):
— Los pacientes con peor agudeza visual
necesitan leer un menor número de letras.
— Las letras de las filas inferiores están
más juntas, aumentando la dificultad, principalmente para niños y ambliopes.
— El espacio entre letras y filas no guarda
relación con el tamaño de las letras.
2.2.2. Optotipos de Bayley-Lovie
En 1976, Bayley y Lovie diseñan un nuevo
tipo de optotipos que se está erigiendo como
el test de elección, pues cada vez se halla más
extendido en la práctica clínica. Salva los
inconvenientes de los optotipos de Snellen,
pues se caracteriza por (12,13) (fig. 10):
— Contener el mismo número de letras en
cada fila.
— El tamaño de letra progresa de forma
logarítmica.
— El espacio entre las letras y entre las
filas es proporcional al tamaño de la letra.
— Similar legibilidad para los optotipos de
cada fila.
Capítulo 2.
Dioptrio ocular y optotipos
37
Figs. 9 y 10. Se pueden apreciar las diferencias entre ambas clases de Optotipos.
2.3. Construcción de los optotipos
A la hora de construir un optotipo hay que
tener en cuenta una serie de factores, como la
legibilidad de la letra, la progresión del tamaño,
el número de letras en cada fila, el espacio
entre letras y filas, que se trate de personas
analfabetas o niños, y, finalmente, la luminancia y el contraste.
2.3.1. Legibilidad de la letra
No todas las letras se reconocen con la
misma facilidad. Por ejemplo, la letra L es más
fácil de reconocer que otras, como la H, que se
puede confundir con la N; o la F, que se puede
confundir con la P.
Para normalizar los optotipos, es mejor que
las letras tengan una legibilidad similar (11,14).
2.3.2. Progresión del tamaño
La más extendida en España es la escala
decimal de Monoyer (9,14). En esta escala, la
agudeza visual normal se considera la unidad y
las agudezas menores decrecen en progresión
aritmética: 1-0,9-0,8-0,7-0,6-0,5-0,4-0,3-0,2-0,1.
Esta escala resulta demasiado discontinua para
agudezas visuales bajas y muy densa para agudezas altas.
Las escalas métricas, frecuentemente, tenían el límite superior en 1, aunque ya Snellen
propuso alcanzar hasta 2, pues en muchas
ocasiones la agudeza visual era superior a 1.
Las escalas decimales fueron criticadas por
no ser fisiológicas, pues las diferentes décimas
de agudeza no son equivalentes desde un
punto de vista funcional (9).
El Consejo Internacional de Oftalmología
(Budapest,1972) (9) recomienda una progresión logarítmica, de razón: 10√10 = 1,2589. La
progresión es uniforme, con un cociente de
progresión de 1,26 desde la fila inferior a la
superior.
2.3.3. Número de letras en cada fila
Estudios de límites de confidencia muestran que un número de 5 caracteres es suficiente para obtener una buena repetibilidad.
Los tests suelen tener 5 o más caracteres,
aunque esto no siempre se cumple, especialmente, en optotipos de AV baja, por un problema de espacio de las cartas o del área de proyección (12,14).
38
Refracción ocular y Baja Visión
2.3.4. Espacio entre letras y filas
Flom y colaboradores (15) describieron el
término «contorno de interacción», para referirse al efecto que tiene el contorno espacial vecino sobre la discriminabilidad de los detalles
finos. Otro fenómeno es el crowding (12,16), de
modo que cuando las letras están muy juntas,
el control de los movimientos del ojo y la fijación pueden reducir la agudeza visual.
Asumiendo que los optotipos están diseñados sobre una rejilla, deben estar separados,
al menos, por la anchura de un optotipo para
evitar que la presencia de otros símbolos dificulte su percepción. La carta de Bailey y Lovie
tiene en cuenta este aspecto, pero en otras
cartas no se considera (14).
2.3.5. Analfabetismo y niños
En estos casos, es más útil la utilización de
optotipos de repetición, que consisten en una
letra que se presenta en diferentes orientaciones. Las más usadas son las E de Snellen y
las C de Landolt (figs. 11 y 12).
Generalmente, se utilizan cuatro orientaciones: arriba, abajo, derecha o izquierda, pero también se pueden utilizar orientaciones oblicuas.
El anillo de Landolt es un círculo roto. El
diámetro externo del círculo es cinco veces el
ancho de la rotura y el diámetro interno es tres
veces mayor.
Se han propuesto diversos modelos de
optotipos de repetición, todos diseñados sobre
una rejilla similar a las letras de Snellen, de
modo que el tamaño del detalle que se debe
percibir tenga el mismo tamaño angular.
También es frecuente el uso de optotipos
con números y dibujos para niños y adultos
con bajo nivel de alfabetización (fig. 13).
2.3.6. Luminancia y contraste
La agudeza visual aumenta paulatinamente
hasta un valor de luminancia de10-2 cd/m2;
luego asciende más rápidamente hasta 102
cd/m2 y, a partir de aquí, varía muy poco
(fig. 14). Para luminancias superiores a unas
100 cd/m2 (nivel fotópico), la visión está dominada por los conos y se obtiene en la fóvea la
máxima AV (14). Los valores recomendados
en la práctica se encuentran entre 85 y
300 cd/m2 (3).
El contraste es la luminancia relativa del
objeto con respecto al fondo (11). Se expresa como (L-T)/L, donde T es la luminancia
del objeto y L, la del fondo. Inicialmente, la
agudeza aumenta rápidamente con el contraste. Para valores de contraste entre 0,4 y
1, los aumentos son menores (fig. 15). Para
la práctica, se recomienda un valor mínimo
de 0,9.
2.4. Otros optotipos
2.4.1. Optotipos bicromáticos
Formados por símbolos negros sobre un
fondo verde y rojo (11) (fig. 16).
Figs. 11, 12 y 13. Optotipos útiles en niños y adultos con escaso nivel de alfabetización.
Capítulo 2.
Dioptrio ocular y optotipos
39
Fig. 16. Optotipo bicromático.
principales. Se usan para precisar el eje y
determinar la potencia.
2.4.3. Test Chart 2000
Figs. 14 y 15. Ver explicación en el texto.
La distancia focal del ojo es mayor para la luz
roja que para la verde, por lo que los dos símbolos se enfocan en planos diferentes. Cuando
el símbolo sobre fondo rojo destaca más que el
situado sobre fondo verde, el ojo es miope y
cuando ocurre lo contrario, es hipermétrope.
El desarrollo de la informática, con los
modernos PCs y monitores planos de alta
resolución, ha permitido que cualquier clínico
pueda tener acceso a numerosos tests cuyo
uso estaba limitado a los laboratorios o a algunos entusiastas.
El test Chart 2000 es un programa informático de Windows y su soporte es un PC, lo que
universaliza su aplicación, tanto para la clínica
como para exámenes domiciliarios, escuelas,
etc. (17).
2.4.2. Optotipos para el análisis
de astigmatismo
Formados por líneas con diferentes orientaciones (fig. 17). Se verán más nítidas las líneas que coincidan con alguno de los meridianos
principales del ojo (14).
Estos optotipos pueden ser de dos clases
(11):
• Fijos: son líneas radiales espaciadas de
forma homogénea en intervalos de 10 ó 30°.
• Rotatorios: formados por diferentes estilos de líneas, que pueden rotar alrededor del
centro hasta orientarse con los meridianos
Fig.17. Optotipo para valorar astigmatismos.
40
Refracción ocular y Baja Visión
Se recomienda utilizar un monitor de 15 ó
17 pulgadas y una resolución mayor o igual
que 1024 × 768.
El monitor se puede mirar directamente o a
través de un espejo y el programa se puede
configurar para ser visto a cualquier distancia,
aunque no se aconsejan distancias menores
de 3 metros.
Incluye 11 tests primarios, que incluyen el
de Snellen, logMART, optotipos simples, test
bicromático, cilindro cruzado, sensibilidad al
contraste, análisis de forias, etc.
En el test Chart 2000, las letras pueden ser
randomizadas y pueden aumentar o disminuir
de tamaño utilizando el cursor.
A pesar de los inconvenientes conocidos
del diseño de optotipos tipo Snellen, son los
más utilizados en la práctica clínica y podemos
disponer de un gran número de tests en formato Snellen, incluyendo la C de Landolt, E de
Tumbling o dibujos para niños.
El único inconveniente importante del test
logMART es su amplitud para ser presentado
en un monitor.
A la hora de valorar la visión de cerca es
importante tener en cuenta la posición natural
de lectura o de trabajo del paciente.
Dos factores importantes a tener en cuenta
son la acomodación y la disminución del diámetro pupilar (fig. 18).
En 1836, Kucheler pesentó la primera escala de optotipos para visión próxima y, en 1860,
Jaeger publicó una serie más completa.
Ambas estaban realizadas de una forma arbritaria (9). En 1862, Snellen y Giraud-Teulon
presentaron sus optotipos de cerca. Más
tarde, Lebensohn recomienda el empleo de
dos tablas de lectura (9):
— Una era una reducción de los optotipos
de lejos.
— Otra, más práctica, aunque menos exacta, constaba de fragmentos de textos impresos
con letras de diferente tamaño y grosor.
Los optotipos para cerca de Freeman constan de las dos tablas anteriores.
2.5. Optotipos para la visión próxima
En la anotación se debe señalar la distancia
a la que la persona está leyendo la cartilla y el
tamaño más pequeño de la letra que puede leer.
Existen diversos métodos para designar el
tamaño de la letra: (12,19) (figs. 19 y 20).
a) Sistema Jaeger.
Consta de 20 tamaños de letras clasificados de J1 a J20.
Es un sistema muy difundido pero tiene el
inconveniente de que los tamaños de las letras
no están bien estandarizados.
b) Snellen reducido.
Usa los optotipos convencionales para lejos
pero reducidos, de modo que las letras 20/20
subtienden 5’ de arco a una distancia de 40 cm.
c) Sistema de puntos.
Utilizado para establecer el tamaño de las
letras en las imprentas. Cada «punto» equivale a 0,35 mm.
d) Unidades M.
Sistema introducido por Sloan y Habel en
1956 (12).
Los optotipos para la visión de cerca están
diseñados para valorar la agudeza visual para
distancias pequeñas, principalmente cuando
nos encontramos ante problemas de acomodación o presbicia.
Fig. 18. Disminución de la amplitud de acomodación con
la edad (18).
2.5.1. Anotación de la agudeza visual
de cerca
Capítulo 2.
Dioptrio ocular y optotipos
41
Figs. 19 y 20. Optotipos de visión próxima, con las equivalencias de la anotación de Snellen y M.
El tamaño de las letras está determinado
por la distancia en metros a la cual las letras
más pequeñas subtienden 5’ de arco a la retina. Así, una letra 1 M subtiende 5’ de arco a
una distancia de 1 m y, cuando se usa una distancia de 40 cm, una letra 1 M subtiende un
ángulo de 12,5’ de arco.
Tanto el sistema de puntos como el M especifican el tamaño de la letra. Las unidades M
tienen la ventaja de ser fácilmente traducidas
al sistema Snellen, que especifica el tamaño
de la letra y la distancia de lectura. El sistema
de puntos tiene la ventaja de su amplia difusión entre los oftalmólogos. Precisa especificar
la distancia de lectura.
e) Anotación N.
Método introducido por los oftalmólogos del
Reino Unido (1951). Toman como fuente el
modelo de letra Times New Roman y recomiendan que el tamaño se señale en puntos.
La agudeza visual para la lectura es más
compleja que la de letras, pues se utilizan
unas letras más próximas y con componentes
complejos cuya secuencia debe ser reconocida. Los pacientes con maculopatías tienen
2.5.2. Optotipos de letras y de lectura
Existen muchos formatos de tarjetas de lectura. La mayoría utiliza una serie de pasajes
de texto o frases simples cuyo tamaño va disminuyendo sucesivamente (fig. 21).
Fig. 21. Optotipo de lectura.
42
Refracción ocular y Baja Visión
Fig. 22. Diferentes optotipos de visión próxima, de letras
y de lectura con diferentes escalas.
una agudeza visual significativamente peor
para leer un texto que para reconocer letras.
La complejidad del texto tiene un efecto importante sobre la agudeza visual de lectura (12).
2.5.3. Eficiencia de lectura
Según Bailey y colaboradores (12), en personas normales, la mayor eficiencia de lectura
se obtiene, generalmente, cuando el tamaño
de la impresión es tres veces mayor que la
menor impresión resoluble. En los pacientes
de baja visión, es muy importante anotar el
límite de resolución y el tamaño de impresión
con el que pueden obtener una buena eficiencia de lectura a la hora de prescribir una magnificación para la visión de cerca.
Se han diseñado varios tests para medir la
eficiencia de lectura (fig. 22). Las tarjetas de
lectura de escala logarítmica ofrecen muchas
ventajas en este aspecto.
BIBLIOGRAFÍA
1. Le Grand Y. Óptica Fisiológica. Tomo I. Madrid.
Sociedad Española de Optometria. 1984. p. 12.
2. Le Grand Y. Óptica Fisiológica. Tomo I. Madrid.
Sociedad Española de Optometria. 1984. p. 65.
3. Aguilar M, Mateos F. Óptica Fisiológica. Tomo 1.
Servicio de Publicaciones. Universidad Politécnica de Valencia. 1993. p. 110-112.
4. Gil del Rio E. Óptica fisiológica clínica. 2.ª edición. Barcelona Ediciones Toray, S.A. 1972. p.
199-206.
5. Aguilar M, Mateos F. Óptica Fisiológica. Tomo 1.
Servicio de Publicaciones. Universidad Politécnica de Valencia. 1993. p. 169-171.
6. Caloroso EE, Rouse MW. Tratamiento clínico del
estrabismo. Madrid: Ciagami. 1999. p. 24.
7. Romero J, Garcia JA, Garcia A. Curso introductorio a la Óptica Fisiológica. Granada. Ed. Comares. 1996. p. 24-34.
8. Rabbets RB. Clinical visual optics. Third edition.
Oxford: Butterworth-Heineman. 1998. p. 15-16.
9. E. Gil del Río. Agudeza visual. En: E Gil del Río.
Optica fisiológica. 5.ª edición. Barcelona: Ediciones Toray. 1984.
10. Ref. Optics and refraction.
11. O’Leary D. Refracción subjetiva. En Edwards K,
Llewellyn R. Optometría. Barcelona: Masson SA.
1993: 115-143.
12. Bailey IL. Visual acuity. En Benjamín WJ, ed
Borish´s Clinical Refraction. Philadelphia: W. A.
Saunders Co; 1998: 179-202.
13. Thomson D. The assessment of vision. En: Doshi
S, Harvey W. Investigative techniques and ocular
examination. London: Optician. 2003: 1-5.
14. Furlan W, García Monreal JG, Muñoz Escrivá L.
Introducción al examen subjetivo. En: Furlan W,
García Monreal JG, Muñoz Escrivá L. Fundamentos de Optometría. Refracción ocular. Valencia: Puertes SL; 2000: 141-181.
15. Flom MC, Weymouth FW, Kahneman D. Visual
resolution and contour interaction. J. Opt. Soc.
Am. 1963; 53: 1026-1032.
16. Hess RF, Dakin SC, Kapoor N, Tewfik M. Contour
interaction in fovea and periphery. J. Opt. Soc.
Am. 2000; 17: 1516-1524.
17. Thomson D. Use and development of computerbased test charts in the assessment of vision. En:
Doshi S, Harvey W. Investigative techniques and
ocular examination. London: Optician. 2003: 7-12.
18. Presbiopía. En Duke-Elder. Refracción: teoría y
práctica. Barcelona: Editorial JIMS,SA. 1985: 91-94.
19. Davidson DW. Visual acuity. En: Eskridge JB,
Amos JF, Bartlett JD. Clinical procedures in optometry. Philadelphia: Halliday Lithograph Corp.
1991: 17-29.