MEDIDAS DE TENDENCIA CENTRAL MEDIANA

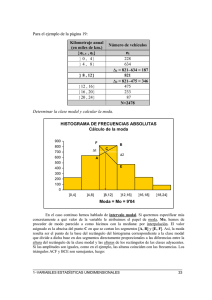
MEDIDAS DE TENDENCIA CENTRAL
MEDIANA
Se considera como una premisa que todos los individuos de cada clase
se encuentran uniformemente repartidos en ella. Para el cálculo de la mediana
en datos agrupados en intervalos de clase tenemos la siguiente fórmula:
 PosMe  Fia 
  a
Me  LMe  
fiMe


Donde:
Me = Abreviatura Mediana.
LMe = Límite inferior de la clase que contiene la Mediana.
n = Tamaño de la muestra (Nº de observaciones)
Fia = Frecuencia absoluta acumulada anterior a la clase que contiene la
mediana.
fiMe = Frecuencia absoluta simple que corresponde a la clase donde está
la mediana.
a
= Amplitud de clase.
PosMe = Posición de la mediana
MODA
En este caso la moda (Mo) se obtiene a través del método de
interpolación, con la fórmula siguiente:
 d1 
  a
Mo  LMo  
d

d
2 
 1
Donde:
Mo = Símbolo para la moda.
LMo = Límite inferior de la clase modal.
d 1 = Diferencia entre la frecuencia absoluta de la clase modal y la frecuencia
absoluta precedente a esta clase.
d 2 = Diferencia entre la frecuencia absoluta simple (fi) de la clase modal y la
frecuencia absoluta (fi) siguiente a la clase modal.
a = Es la amplitud de la clase modal.
MEDIA
Existen numerosos ejemplos de medias
, una de las pocas
propiedades compartidas por todas las medias es cualquier media está
comprendida entre el valor máximo y el valor mínimo del conjunto de datos:
La media aritmética es un promedio estándar que a menudo se denomina
"promedio".
La media se confunde a veces con la mediana o moda. La media aritmética es
el promedio de un conjunto de valores, o su distribución; sin embargo, para las
distribuciones con sesgo, la media no es necesariamente el mismo valor que la
mediana o que la moda. La media o moda son elementos intuitivos de medir los
datos. Es a veces una forma de medir el sesgo de una distribución tal y como
se puede hacer en las distribuciones exponencial y de Poisson.
Por ejemplo, la media aritmética de 34, 27, 45, 55, 22, 34 (seis valores) es
MEDIDAS DE DISPERSION
La varianza es la media aritmética del cuadrado de las desviaciones
respecto a la media de una distribución estadística.
COEFICIENTE DE VARIACION
El coeficiente de variación es la relación entre la desviación típica de una
muestra y su media.
El coeficiente de variación se suele expresar en porcentajes:
El coeficiente de variación permite comparar las dispersiones de dos
distribuciones distintas, siempre que sus medias sean positivas.
Se calcula para cada una de las distribuciones y los valores que se obtienen se
comparan entre sí.
La mayor dispersión corresponderá al valor del coeficiente de variación mayor.