Apuntes y problemas

Enlace y Estructura de la Materia
E Rodríguez-Fernández
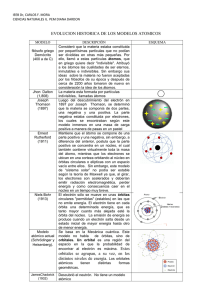
Tema 1. Evolución del concepto de átomo. Experimentos de Rutherford. Modelo atómico de
Bohr. Espectro atómico del hidrógeno. Bases de la mecánica cuántica. Orbitales. Átomos
polielectrónicos. Modelo vectorial y propiedades magnéticas.
Átomo. Introducción
Alrededor del 400 antes de C. el filósofo griego Demócrito sugirió la idea de que toda la materia
está constituida de partículas elementales minúsculas, discretas e indivisibles denominadas
átomos. La palabra átomo tenía el significado de no divisible.
Sus ideas fueron rechazadas durante 2000 años hasta que John Dalton en 1808, estableció su
Teoría Atómica para justificar las leyes de la combinación química. Sus postulados pueden
resumirse así:
1 Un elemento está formado por partículas pequeñas e indivisible llamadas átomos.
2 Todos los átomos de un elemento tienen propiedades idénticas y distintas de los átomos de otro
elemento.
3 Los átomos se combinan entre sí para formar moléculas de compuestos en proporciones fijas
para cada compuesto.
Una mol es la cantidad de sustancia que contiene tantas entidades (átomos, moléculas u otras
partículas) como átomos hay en 12,00g de 126C (una mol de carbono-12). Este número de
entidades presentes es el número de Avogadro, NA. El concepto de mol se introduce para manejar
en el laboratorio cantidades de masa ante la dificultad de pesar átomos o moléculas individuales.
El tamaño de los átomos no fue difícil de establecer una vez conocido el número de Avogadro,
6,022x1023partículas/mol, que es el número de átomos o partículas contenidas en un mol.
Conocido el volumen molar de un sólido, se puede establecer el volumen de un átomo o
molécula. De este modo se obtiene un volumen atómico de 10-24 cm3 y, supuesto el átomo esférico
inscrito en un cubo, la arista de este cubo será 10-8 cm. Las dimensiones atómicas serían, por lo
tanto, de ese orden. Para una más fácil comprensión de las dimensiones atómicas se introdujo el
Å equivalente a 10-8 cm.
Aplicación: A modo de ejemplo, para el oro tenemos los siguientes datos: Pa = 196,96 g/mol;
Volumen de la celda elemental = 67,84x10-24 cm3; Volumen molar 10,21 cm3/mol; Densidad por
rayos X = 19,29 g/cm3 (19,32 experimental). La celda elemental es cúbica (a = 4,0786Å), centrada
en las caras; contiene 4 átomos de Au y, por tanto, el volumen de un átomo es 67,84x10-24/4 =
16,96x10-24 cm3. También se puede obtener así: 10,21/6,022x1023 = 16,95x10-24 cm3. Como V =
(4/3)πr3, r = 1,59x10-8 cm3 = 1,59Å (1,44 experimental; se considera el espacio vacío).
Átomos de oro visibles y ocultos
a = 4,0786 Å, Pa = 196,96 g/mol
Naturaleza eléctrica de la materia
La relación entre electricidad y estructura de los átomos comenzó a establecerse con los
experimentos de Faraday sobre la electrólisis. Sus hallazgos pueden resumirse así:
1 Una cantidad dada de electricidad depositará o desprenderá sobre un electrodo un mismo peso
de una sustancia determinada.
2 Los pesos de las distintas sustancias disueltas, depositadas o desprendidas en un electrodo, por
una cantidad fija de electricidad; son proporcionales a los pesos equivalentes de esas sustancias.
Parece, por lo tanto, que la electricidad estaría constituida al igual que la materia por partículas,
de modo que un número fijo de átomos reacciona con un número fijo de electrones que
aportarían una cantidad de electricidad susceptible de ser medida en culombios.
Para la reacción de estos electrones con un equivalente de una sustancia se precisan un
equivalente de electrones, es decir, 6,022x1023 electrones cuya carga total es 96500C:
F = (6,022x1023 partículas/mol) x (1,602x10-19C/partic.) = 96472C/mol; constante de Faraday, F.
1
Enlace y Estructura de la Materia
E Rodríguez-Fernández
Aplicación: Una disolución acuosa de una sal de platino se electroliza mediante una corriente de
2,50A durante 2,00 horas. Como resultado se depositan 9,09 g de Pt en el cátodo o polo negativo.
Carga de los iones de platino en la disolución.
La cantidad de carga en culombios (C) que pasa por la celda es: Culombios = amperios x
segundos = 2,50x(2,00x3600) A·s = 1,80x104C.
Si la reacción y la cantidad de masa y carga eléctrica necesaria se expresa así:
Ptn+ + ne = Pt, es decir:
1mol de Ptn+ (195,1 g) necesita nxNA de electrones (96500n C de carga) para depositar 1mol de Pt
(195,1 g). Aquí se han depositado 9,09/195,1 = 0,04659 mol con 1,80x104C por lo que n =
1,80x104/96500x0,04659 = 4,00; por tanto se trata de Pt4+.
Experimentos de Thomson y descubrimiento del electrón
Los experimentos de Thomson con descargas eléctricas en tubos de vacío mostraron que la
materia tenía electrones. Como esta materia era neutra, los electrones están junto a cargas
positivas. Las cargas positivas deberían de sustentar la mayoría de la masa del átomo, en una
esfera de dimensiones atómicas. Esto constituye la hipótesis de Thomson.
La existencia, así como las propiedades del electrón, fue establecida en 1897 (J J Thomson), por los
experimentos de conducción eléctrica en tubos de vacío con baja presión de gas residual (10-4
atm). En el tubo van alojados dos electrodos entre los que se establece un alto voltaje, de 5-10 kV.
Aparece conducción eléctrica y brillo en las paredes del tubo. La corriente consiste en un flujo
desde el polo negativo (cátodo), hacia el positivo. Esta radiación, denominada rayos catódicos,
era de naturaleza independiente del gas residual o del material de que estuviesen hechos los
electrodos. Los rayos catódicos eran atraídos por la placa positiva de un campo eléctrico por lo
que debería tener carga negativa. También eran desviados por un campo magnético. Eran,
asimismo, partículas capaces de chocar contra las aspas de un molinillo colocado dentro del tubo
de vacío, imprimiéndoles un movimiento. Por tanto, estas partículas negativas estaban en toda la
materia y eran un constituyente esencial de la misma. Thomson calculó la relación e/m,
carga/masa, de estas partículas encontrando un primer valor de 1,2x1011 C·kg-1. El valor real,
más ajustado, es 1,7588x1011 C·kg-1.
Calculada esta relación, es necesario conocer alguno de ambos miembros del cociente para
determinar el otro. Se determinó en primer lugar la carga del electrón.
El experimento de la gota de aceite de Millikan (1909 y PN en 1923), permitió conocer la carga del
electrón. Todas las cargas medidas en gotitas ionizadas eran múltiplos de un carga elemental que
era la carga de un solo electrón y cuyo valor es de 1,60219x10-19 C. Con este dato la masa del
electrón resultó ser 9,10952x10-28 g.
q/m = 1,60219x10-19 C /m = 1,7588x1011 C·kg-1 ; m = 9,10952x10-28 g.
Descubrimiento del protón
Utilizando un tubo de rayos catódicos con cátodo perforado (polo negativo), Goldstein observó
que, detrás del mismo, aparecía una radiación procedente del ánodo (polo positivo). Esta
radiación positiva era desviada por campos eléctricos y magnéticos de forma opuesta a como
eran desviados los electrones. Se dedujo que eran partículas positivas. Su relación carga/masa
fue determinada por Thomson y variaba, al contrario que los rayos catódicos, con la naturaleza
del gas residual. Cuando este gas era H2 la relación q/m era máxima y correspondía al protón.
Efectivamente, al quitar el único electrón al H se produce el catión H+, que es un protón. Los
datos para el protón resultaron ser:
masa = 1,007581 uma, 1,6725x10-27 kg; 1836 veces la masa del electrón
2
Enlace y Estructura de la Materia
E Rodríguez-Fernández
La carga es la misma del electrón pero positiva y su espín es de 1/2 (en unidades h/2π).
1uma = (1/NA) g (equivalencia de la unidad de masa atómica en gramos, 1/12 de la masa de un
átomo de 126C).
Una mol de átomos de 126C equivale a 12 g de 126C y contiene NA átomos de 126C. Un átomo de
12 C contiene 12 uma; por lo tanto 1 uma equivale a 1/N gramos.
6
A
Modelo atómico de Rutherford
La existencia de electrones y protones en el átomo exigió inmediatamente una explicación de
cómo estaban situadas estas partículas en el átomo. En 1909 Rutherford estableció que las
partículas α (núcleos de helio, con dos protones y dos neutrones, 42He2+), tenían carga positiva y
surgían de núcleos de elementos radiactivos por desintegración espontánea. El experimento
efectuado con estas partículas condujo a un primer modelo atómico.
Se bombardea una lámina muy delgada de oro con partículas α y se coloca una placa de ZnS por
el lado opuesto para observar la fosforescencia de los impactos. Seguidamente se hizo un
recuento de las partículas que atravesaban la lámina y las que se desviaban. La distribución
angular de las partículas se determinaba contando el número de destellos en la pantalla de ZnS.
La mayoría de las partículas atravesaban la lámina sin desviarse o se desvían pequeños ángulos,
y sólo unas pocas se desvían ángulos grandes de hasta 180°. Utilizó partículas α procedentes de
Po (Z = 84), alojado en un bloque de plomo, provisto un agujero que proporciona un fino haz de
partículas.
Por lo tanto, para producir una desviación tan grande en el átomo debía residir una gran fuerza
eléctrica y con una gran masa confinada en un reducido espacio dentro del átomo, ya que eran
muy pocas las partículas que mostraban grandes desviaciones. El átomo debería ser una esfera
de dimensiones 10-8 cm, pero cuya masa estaría confinada en un núcleo de menor tamaño
sumamente pesado en el cual reside la electricidad positiva. Teniendo en cuenta que la
dispersión obedece a una trayectoria hiperbólica y midiendo la energía cinética de las partículas
α, se llega a estimar como dimensión del núcleo 10-12 cm.
Utilizando láminas de otros metales se obtenían resultados similares.
La carga de los protones del núcleo tiene que ser neutralizada por un número igual de electrones
situados a mayor distancia. Este número de protones se denomina número atómico Z y es
característico de cada elemento.
El neutrón
Fue postulada su existencia en el núcleo por Rutherford como una partícula elemental sin carga
pero con masa similar a la del protón (1,00893 uma, espín 1/2).
Al no tener carga no se desvía, no se detecta mediante campos eléctricos o magnéticos, ni
condensa las gotitas de agua en la cámara de niebla. Por todo esto, el neutrón tardó tanto tiempo
en ser descubierto.
En 1932 J Chadwick bombardeando con partículas a berilio observó la producción de una
radiación muy intensa que atravesaba una lámina de plomo.
9 Be + 4 He = 12 C + 1 n
4
2
6
0
Después determinó que su masa era como la del protón, su carga cero y espín 1/2. El neutrón es
inestable fuera del núcleo, de modo que su vida media es de 20 minutos, desintegrándose así
1 n→1 p + 0 e + ν
n → p + e + ν;
o mejor:
0
1
-1
El neutrino ν es una partícula energética, sin carga ni masa o al menos una masa insignificante
con respecto a la del electrón. Tiene espín 1/2.
Radiación electromagnética
Los modelos descritos del átomo dan escasa información sobre el ordenamiento de los electrones
en el átomo. Este ordenamiento se puede establecer mediante teorías basadas en la absorción o
desprendimiento de luz por los átomos.
Son importantes al respecto, los espectros de emisión que consisten en líneas o bandas
registradas en una película fotográfica cuando la luz emitida por átomos es difractada por un
prisma para descomponerla en los diversos ‘colores’ o longitudes de onda, de modo semejante a
como sucede con la luz visible descomponible en los colores del arco iris. Esta luz es emitida por
3
Enlace y Estructura de la Materia
E Rodríguez-Fernández
los átomos previamente excitados (especialmente en estado gaseoso), con electricidad o
térmicamente con calor. Cada línea corresponde a una frecuencia ν, una longitud de onda λ o un
número de onda característico ν‘ de la luz emitida, que es la inversa de la longitud de onda, y
lleva asociada una energía E.
Espectro electromagnético
Una onda electromagnética está definida por un campo eléctrico y otro magnético que oscilan
mutuamente perpendiculares y a la vez estos campos son perpendiculares a la dirección de
propagación de la onda. Toda onda se define por su longitud de onda λ (lambda) o distancia
entre dos crestas consecutivas, por su frecuencia que es el número de máximos o crestas que
pasan por un determinado punto cada segundo y que se representa por ν (nu). La frecuencia se
mide en s-1 o hertz (Hz). Una onda de frecuencia 10 Hz significa que pasan diez máximos por un
punto cada segundo. La distancia recorrida por la onda en un segundo, es decir, su velocidad es:
c = λν. La luz y todas las demás ondas electromagnéticas viajan a una velocidad constante, que es
la velocidad de la luz, c = 3x108 ms-1. La amplitud de la onda A, es la altura de la cresta; siendo la
luminosidad o intensidad de la luz proporcional al cuadrado de la amplitud, A2. El espectro
electromagnético es la gama completa de ondas electromagnéticas las cuales pueden colocarse en
orden creciente de frecuencia y de energía (y, por tanto orden decreciente de longitud de onda).
Espectro electromagnético
ondas de radio, tv, microondas ⁄ ir ⁄ vis ⁄ uv ⁄ r.X
(Å λ )
⁄ r. γ ... (ν , E Æ)
rojo
λ
Onda electromagnética.
E y H, campos eléctrico y magnético; k,
dirección de propagación; λ, longitud de
onda
violeta
700 nm,
(2,28·1014 s-1)
400 nm, 7,50·1014
s-1)
Difracción de la luz visible por un prisma y
descomposición en los colores del arco iris.
λν = c, ν = c/λ, ν se mide en s-1 (hertz, Hz), ν‘se mide en m-1. E = hν = hcν’, donde h es la
constante de Planck que vale 6,6262x10-34 J·s. E es la energía de un fotón. ν, ν’ y λ representan la
frecuencia, número de onda y longitud de onda Una radiación es tanto más energética cuanto
mayor sea su frecuencia.
El espectro visible, única parte a la que es sensible el ojo humano, sólo es una pequeña parte del
espectro electromagnético, aquella radiación cuya longitud de onda está comprendida entre 4x107(violeta) y 7,5x10-7 m(rojo). Los rayos X tienen longitudes de onda tan cortas como 10-13 m, por
tanto alta frecuencia y alta energía. Las ondas de radio tienen longitudes de un kilómetro e
incluso más.
El espectro de emisión de un gas incandescente, dentro de un tubo de vacío a baja presión, es
discontinuo debido a que sólo aparecen líneas luminosas de ciertas frecuencias.
De manera similar, puede hacerse que un haz luminoso, que contenga una distribución continua
de longitudes de onda, atraviese un gas contenido en un tubo de vacío a presión reducida. Sólo
ciertas longitudes de onda son absorbidas y aparecen como líneas obscuras (espectro de absorción),
precisamente las mismas que son brillantes y emitidas en el espectro de emisión.
Espectro del hidrógeno
Si se hace pasar una corriente eléctrica por un tubo de vacío conteniendo hidrógeno, se puede
obtener el espectro atómico del hidrógeno. El tubo de vacío conteniendo hidrógeno como gas
residual aparece de color rojo incandescente, debido a que la línea mas intensa está situada en
4
Enlace y Estructura de la Materia
E Rodríguez-Fernández
zona roja del espectro visible. Una vez difractada la luz emitida se obtienen una serie de líneas
brillantes que en su conjunto forman e espectro del hidrógeno.
J J Rydberg descubrió a finales del siglo XIX, que las frecuencias de estas líneas estaban
relacionadas mediante la siguiente ecuación matemática empírica, deducida de las medidas de
las líneas espectrales:
1/λ = ν’ = R[1/n12-1/n22],
R es la constante de Rydberg. En unidades de número de onda R vale 109737 cm-1 ó 1,097x107 m-1.
n1 < n2 , son números enteros.
El grupo de líneas que aparecen en la zona visible y ultravioleta cercano, se denominó serie
Balmer y se ajustaban a la anterior expresión cuando n1 = 2 y n2 = 3, 4, 5...
Además de la serie Balmer existen otras series que se ajustan al resto de las líneas del espectro:
Serie Lyman,
ν’ = R[1/12-1/n22], zona ultravioleta
Serie Balmer,
ν’ = R[1/22-1/n22], zona ultravioleta -visible
Serie Paschen,
ν’ = R[1/32-1/n22] , zona del infrarrojo
Serie Brackett ν’ = R[1/42-1/ n22],
“
“
Series de Pfund, Humphries,.
Modelo atómico de Bohr
Niels Bohr (1885-1962) desarrolló su modelo para explicar por qué las frecuencias del espectro de
emisión del hidrógeno obedecían una ley tan simple. Según este modelo los electrones gravitan
alrededor del núcleo como los planetas alrededor del Sol (modelo planetario). Para ello estableció
los postulados siguientes:
1 En un átomo al electrón sólo le están permitidos ciertos estados energéticos definidos.
2 Cuando un átomo se encuentra en uno de esos estados no emite energía, pero cuando cambia
de un estado de alta energía (órbita exterior) a otro estado de energía inferior (órbita interior), el
átomo emite un cuanto de radiación cuya energía es hν y es igual a la diferencia de energía entre
ambos estados.
3 En cada uno de los estados el electrón se mueve en una órbita circular alrededor del núcleo.
4 De acuerdo con los postulados de Planck la energía permitida en una órbita está cuantizada y
no es continua. La energía de un electrón en una órbita, es decir el momento angular o momento
5
Enlace y Estructura de la Materia
E Rodríguez-Fernández
de la cantidad de movimiento mvr debe ser un número entero de ‘cuantos’ o paquetes de
energía:
mvr = nh/2π
De acuerdo con el postulado 3, la fuerza centrífuga debe equilibrar a la de atracción por el núcleo
o coulómbica
Fuerza centrífuga = mv2/r
Atracción de Coulomb = (Ze)e/4πεor2,
mv2/r = (Ze)e/4πεor2
2
Despejando v de las dos expresiones e igualando se obtiene
Ze2/4πεomr = n2h2/4π2m2r2 y r = εon2h2/πme2Z = ao(n2/Z),
ao = εoh2/πme2 = 0,52918Å, r = ao(n2/Z)
Aquí, m y v son la masa y velocidad del electrón, Z es el número de cargas elementales positivas
(e) del núcleo, r es la separación entre el electrón circundante y el núcleo. ao es un agrupamiento
de constantes en una nueva denominada radio de Bohr. La denominada permitividad del vacío εo
es una constante necesaria para formular la ley de Coulomb de modo que la carga este expresada
en culombios, la distancia en metros y la fuerza en newtons.
Su valor es εo = 8,854x10-12 C2N-1m-2
Los sucesivos radios aumentan
con el cuadrado del número
cuántico n.
Energía del electrón en una órbita
La energía total es la suma de la energía cinética (Ec), y la potencial (V). La energía potencial es
negativa ya que el electrón es atraído por el núcleo desde distancias muy grandes
E = Ec + V = (1/2)mv2 -Ze2/4πεor =
(1/2)Ze2/4πεor - Ze2/4πεor = -(1/2)Ze2/4πεor =
-(1/2)Z2e2/4πεoaon2 = -Z2e2/8πεoaon2 =
-[(1/2)Z2/n2](4,3598x10-18), en julios;
Una unidad de energía (hartree) = 4,3598x10-18 J = 27,2915eV
1eV = 1,60219x10-19 C·V = 1,60219x10-19 J,
Para n =1 se obtiene el valor más negativo, más bajo y de máxima estabilidad (-0,5hartree) = 13,605eV
Cuando n → ∞, E → 0. Esto significa la separación total del electrón del átomo de hidrógeno y
corresponde al proceso de ionización y producción de H+
H(g) + I = H+(g) + e, donde I es la energía de ionización o energía que hay que suministrar a un
átomo de H para quitarle su único electrón.
Las fórmulas de Bohr pueden aplicarse al H y a otros átomos o iones con un solo electrón como
He+, Li2+, Be3+. Aquí es necesario utilizar como carga nuclear, en las fórmulas correspondientes, Z
= 2, 3, 4
Espectros atómicos del hidrógeno
Bohr sugirió que los electrones ocupaban niveles u órbitas con una determinada energía y
absorbían o emitían energía al pasar de un nivel a otro. Emiten energía cuando caen de un nivel
superior a otro inferior dando lugar al espectro de emisión. El espectro de absorción se origina al
promocionar electrones desde niveles inferiores a otros superiores.
Supuestos los electrones situados en distintos niveles, debido a que en el hidrógeno excitado
existen átomos excitados con su electrón situado en muchos niveles diferentes; el espectro de
emisión consistirá en la emisión de energía cuando un electrón excitado, situado en una órbita
superior, se precipita a otra órbita más interna, inferior y más estable. La energía emitida
corresponde a la diferencia entre ambos niveles y aparece como una línea brillante en el registro
del espectro.
6
Enlace y Estructura de la Materia
E Rodríguez-Fernández
El hidrógeno normal tiene casi todos sus átomos en el nivel más bajo, que es el más estable.
Cuando absorbe energía, por ejemplo en un tubo de descarga o en las estrellas, se promociona
este electrón a niveles superiores y, al caer de nuevo a los niveles inferiores, origina el espectro de
emisión característico.
Para una transición de emisión la energía inicial (Einicial) del nivel más externo o superior es
menos negativa que la energía del nivel inferior (Efinal), más estable más interno o cercano al
núcleo.
∆E = hν = hcν’ = Einicial-Efinal
= [(1/2)Z2e2/4πεoao]{1/(nf)2-1/(ni)2} = Rhc{1/1/(nf)2-1/(ni)2},
donde R es la constante de Rydberg en unidades inversas de longitud (ν’)
R = [Z2e2]/[8πhcεoao] =
[12(1,602x10-19 C)2]/[8π(6,626x10-34 J·s)(2,997x108 m·s-1)(8,854x10-12 C2N-1·m-2)(5,29x10-11 m)] =
= 1,09773x107m-1 = 109773 cm-1
Modelo de Bohr-Sommerfeld y números cuánticos
Las órbitas posibles para un electrón se denominan K, L, M, N, O... o bien, por los valores de n, 1,
2, 3, 4, ... A este número se le denomina número cuántico principal n.
Cuando un electrón se mueve de una órbita a otra origina una línea simple. Si el espectro del
hidrógeno es observado con un espectrofotómetro con mayor resolución entonces algunas líneas
muestran una estructura fina apareciendo desdobladas y próximas. Sommerfeld explicó este
desdoblamiento asumiendo que algunas de las órbitas eran elípticas.
Para la órbita más cercana al núcleo, n =1 y es una órbita circular.
Para n = 2 son posibles ambas. La elipse se define con dos parámetros, eje mayor y menor. Por lo
tanto un segundo número cuántico l, es necesario.
La presencia de estas órbitas explica la existencia de subniveles muy próximos en energía que
van a originar la estructura fina del espectro. Los valores son:
n = 1,
l=0
n = 2,
l = 0, 1
n = 3,
l = 0, 1, 2
En general para el número cuántico principal n existen n-1 valores de l o subniveles.
Además, algunas líneas es posible desdoblarlas a su vez en dobletes. Este hecho se explica
asumiendo que el electrón puede girar en su eje a la derecha o izquierda. Esta energía está
cuantizada y el número cuántico correspondiente es el espín s, con valores +1/2 y -1/2 en
unidades h/2π
Zeeman observó que, si los átomos se situaban en un potente campo magnético, aparecen aún
más líneas en el espectro, por lo que había que postular la existencia de más niveles energéticos.
Esto es debido a que las órbitas, que generan una corriente eléctrica al moverse en ellas el
electrón, pueden adoptar sólo determinadas orientaciones respecto del campo magnético en
lugar de seguir un movimiento de precesión libre. Cada orientación se asocia con un cuarto
número cuántico m el cual adopta los valores de l siguientes: l -1...0...+1, -l; en total 2l+1 valores.
Efecto fotoeléctrico
En 1902 ya se sabía que la luz cuando incide sobre una superficie metálica (por ejemplo cesio)
muy limpia y en el vacío, arranca electrones del metal y se establece una corriente eléctrica
cuando estos electrones alcanzan un polo positivo. Cabe destacar: a) Los electrones sólo pueden
ser arrancados del metal si la radiación es lo suficientemente energética (longitud de onda lo
suficientemente corta). Para cada metal existe una longitud de onda límite particular y, por tanto,
una frecuencia límite. b) La intensidad de la corriente no depende del color de la luz pero
aumenta al aumentar la intensidad.
La explicación satisfactoria de este efecto la proporcionó Einstein (1905) ampliando la teoría de
Planck. La luz se compondría de partículas discretas o fotones de energía hν las cuales cuando
inciden en la placa metálica ceden su energía a un electrón. Una parte de esta energía era
empleada en superar la fuerza atractiva entre el electrón y el metal. El resto de energía se emplea,
en forma de energía cinética, en imprimir un movimiento al electrón desprendido.
hν = Eo+(1/2)mv2; donde Eo es la energía mínima necesaria para arrancar el electrón y se
relaciona con la frecuencia mínima por la ecuación Eo = hνo
7
Enlace y Estructura de la Materia
E Rodríguez-Fernández
El efecto fotoeléctrico encuentra aplicación práctica en sensores fotoeléctricos de puertas
automáticas ascensores y cámaras fotográficas.
Este experimento pone en evidencia que la luz puede comportarse como partículas y no sólo
como ondas (fenómenos de reflexión y difracción).
a)
a) Célula fotoeléctrica.
b) Intensidad de la corriente
de la fotocélula en función de
la frecuencia de los fotones,
para dos metales activos
diferentes.
b)
I
νo
ν'o
ν
Dualidad onda-corpúsculo
El modelo planetario de Rutherford y Bohr para el átomo considera a los electrones
exclusivamente como partículas que giran en torno al núcleo.
En 1920 recibió atención especial por parte de los físicos el comportamiento de los fotones no sólo
como ondas sino también como partículas. Esto se pone de manifiesto en el efecto fotoeléctrico en
los experimentos de Einstein, como hemos visto. Este doble comportamiento se puede expresar
matemáticamente por las relaciones de Planck y Einstein
E = hν = hc/λ, E = mc2 ⇒ hc/λ = mc2 ⇒ λ = h/mc = h/p, (p = momento)
Estas expresiones relacionan una propiedad ondulatoria λ, con una propiedad de partícula como
es la masa.
El siguiente avance fue realizado por el príncipe y físico Louis de Broglie en 1924, proponiendo la
generalización de la expresión para toda partícula y no solamente para el fotón.
λ = h/mv
En lugar de la masa y velocidad de la luz o del fotón se utiliza la masa y velocidad de la partícula
de que se trate, por ejemplo los electrones.
Davisson y Germer (1927) descubrieron las propiedades ondulatorias del electrón, demostrando
que podían difractarse en redes de cristales iónicos al igual que los rayos X. Cualquier objeto será
susceptible de llevar asociada una onda, si bien los objetos grandes, al poseer gran masa la λ será
muy pequeña y no medible en la práctica. No existe sistema físico que pueda utilizarse para
efectuar tales medidas.
Los electrones e incluso los átomos, tienen masas y momentos pequeños y pueden sufrir
difracción y otros fenómenos propios de las ondas. Pueden adquirir longitudes de onda
comparables a las distancias interiónicas de los cristales iónicos.
Ejemplos de ondas asociadas
Partícula
masa/kg velocidad/ms-1 λ asociada
Electrón libre
9x10- 31
1x105
7000pm = 70Å
Electrón en H (n = 1)
“
2,2x106
33pm = 0,33Å
He (300K)
7x10-27
1000
90pm
Pelota rápida
0,10
20
3x10-22 pm
-12
-10
(1pm, picómetro = 10 m = 10 cm; 100 pm = 1Å)
Principio de incertidumbre de Heisenberg
En los objetos macroscópicos se utilizan frecuentemente para describir su comportamiento los
términos posición y velocidad. Existen, sin embargo restricciones o impedimentos por los que no
es posible aplicar estos términos a objetos pequeños con el comportamiento de onda-corpúsculo.
El modelo de Bohr requiere valores precisos de posición y velocidad del electrón en una órbita.
No se puede localizar al electrón y conocer su momento o su velocidad al mismo tiempo. ¿Se
puede determinar al mismo tiempo la posición y el momento o la velocidad de un electrón? No,
porque al determinar la posición se modifica la velocidad en una cantidad desconocida. Para
localizar a un electrón con un fotón debe de haber una colisión o interacción entre ambos. Un
fotón de longitud de onda λ tiene un momento mv = p, y en la colisión se transfiere una
cantidad desconocida de este momento. Así, al localizar al electrón con ese fotón se efectúa esa
8
Enlace y Estructura de la Materia
E Rodríguez-Fernández
localización con una incertidumbre o error de ∆x ≈ ±λ. Si se trata de determinar la posición del
electrón con luz, debido a los fenómenos de difracción solo es posible determinar su posición con
una precisión igual a la longitud de onda empleada, de ahí la expresión anterior. Esto es análogo
a la difuminación de los objetos en el microscopio ordinario cuando estos son de tamaño similar
o menor que 500nm que es la menor onda (violeta) de la luz visible. Con el microscopio
electrónico es posible una resolución menor (0,1nm, 1nm=10-9 m), y pueden observarse objetos de
este tamaño. El momento adquirido tendrá a su vez una incertidumbre de ∆p ≈ ±h/λ. El
producto de ambas incertidumbres es
(∆x)(∆p) ≈ h
Esto es una deducción aproximada del principio de incertidumbre de Heisenberg. Una deducción
más precisa conduce a la expresión:
(∆x)(∆p) ≥ h/4π
La determinación de la posición y del momento es lo que determina la trayectoria de una
partícula.
El principio de incertidumbre establece que hay un límite en la precisión en la determinación de
ambos valores simultáneamente. No afecta a los objetos macroscópicos como se evidencia en el
siguiente ejemplo.
Aplicación: a) Veamos la aplicación del principio al conocimiento de la trayectoria de un electrón
en el átomo. Si deseamos localizarlo en un intervalo de 0,05Å (5pm = 5x10-12 m), podemos
calcular la precisión del momento y de su velocidad.
∆p = h/(4π∆x) ≈ (6x10-34 Js)/(60x10-12 m) = 1x10-23 kg m s-1
∆v = ∆p/m = 1x10-23 kg m s-1/9x10-31 kg = 107 m s-1
J = N·m = kg·(m/s2)·m = kg·m2/s2
La incertidumbre de la velocidad del electrón es casi tan grande como la velocidad de la luz, y es
tan incierta que no es posible especificar una trayectoria a la manera de las órbitas definidas por
Bohr. La mecánica cuántica hace pagar con una alta imprecisión de la velocidad la precisión
bastante aceptable del electrón en el átomo (0,05 Å en comparación con el tamaño del átomo,
varios Å).
b) Una bola de billar de 200g se mueve en línea recta. Por fotografía es posible determinar la
posición por la menor longitud de onda de la luz visible (λ = 5000Å). Calcúlese la precisión en la
medida de su velocidad.
∆v ≥ h/(4πm∆x) = 6,626x10-34 Js/4π·0,200x5x10-7 = 5,27x10-28 ms-1. La indeterminación de esta
velocidad por los instrumentos habituales es mucho mayor que la impuesta por la mecánica
cuántica.
Aplicación de la mecánica ondulatoria al átomo de hidrógeno
La expresión de De Broglie se aplica a electrones que se mueven en el espacio, libres de la
influencia de campos, como por ejemplo los electrones de la emisión termoiónica o fotoemisión.
En el átomo es diferente la situación ya que el electrón está sometido a intensos campos eléctricos
del núcleo y de los demás electrones. En el átomo el electrón esta aprisionado por un campo
eléctrico tridimensional.
En estas condiciones, ¿como se puede aplicar las propiedades ondulatorias al electrón? La
respuesta es suponer ondas estacionarias clásicas. Las ondas estacionarias pueden pervivir a
condición que su amplitud sea cero en los extremos, como la cuerda vibrante de un violín. Las
ondas con amplitud distinta de cero en los extremos, se disipan por autointerferencia al reflejarse
en los extremos. Sólo aquellas ondas que cierran exactamente sobre sí mismas persisten como
estacionarias y las que no cierran sobre sí mismas se disipan por autointerferencia.
La ecuación de una onda estacionaria clásica es una función seno de la forma:
ψ = Asen[2πx/λ],
A es la amplitud máxima o máximo valor de ψ. El valor mínimo de la amplitud es cero cuando x
= 0, λ/2, λ...
Las dos primeras derivadas son:
dΨ/dx = (2πA/λ)cos[2πx/λ]
d2Ψ/dx2 = -(2πA/λ) (2π/λ)sen[2πx/λ] -(4π2/λ2)Ψ
9
Enlace y Estructura de la Materia
E Rodríguez-Fernández
Seguidamente hay que incluir en esta propiedad ondulatoria la propiedad corpuscular del
electrón, por ejemplo a través de la energía cinética y el principio de De Broglie:
Ec = (1/2)mv2, λ = h/mv
⇒ v = h/mλ; Ec = (1/2)mh2/m2λ2 = (1/2)h2/mλ2
λ2 = h2/2mEc
Así la ecuación de onda queda:
d2Ψ/dx2 = -(8π2mEc/h2)Ψ
Esta ecuación es válida para una partícula con energía cinética únicamente y sería valida para un
electrón que se mueva en el vacío sin influencias de campos. En el átomo el electrón está
sometido a intensos campos eléctricos, por lo que la energía total es la cinética más la potencial E
= Ec + V. Substituyendo en la expresión, tenemos.
d2Ψ/dx2 = -(8π2m(E-V)/h2)Ψ
Como la situación del electrón en el átomo es tridimensional, la onda no recorrerá solamente la
dirección x, y deberá ser generalizada para las tres dimensiones.
d2Ψ/dx2 + d2Ψ/dy2 + d2Ψ/dz2 = -(8π2m(E-V)/h2)Ψ
Ô2 Ψ = -(8π2m(E-V)/h2)Ψ ; Ô = operador nabla
Esta es la ecuación ideada por Schrödinger en 1926. Proporciona valores de la función de onda y
de las energías permitidas para el electrón en el átomo. Como en una cuerda vibrante, sólo son
posibles ciertos valores de la frecuencia de la vibración según donde se coloquen los extremos
(trastes).
Significado físico de la función de onda
Los valores que pueden hallarse para la función de onda son muchos pero solo algunos tienen
significación física, precisamente los que cumplan las condiciones.
1 Ψ debe ser continua, finita y tener valor único
2 En el infinito la función ha de valer cero, ya que si el electrón se sitúa a distancia
infinita del átomo ya no pertenece al mismo.
3 La probabilidad de encontrar un electrón en el átomo debe ser 1, es decir, certeza total.
La principal aplicación a la química de esta ecuación se debe al establecimiento de que la
probabilidad de encontrar al electrón en un determinado diferencial de volumen es proporcional
a Ψ2·dx·dy·dz, el producto del cuadrado de la función de onda por un elemento de volumen.
Para todo el espacio esta probabilidad será 1:
-∞
∫+∞ Ψ2·dx·dy·dz = 1
Varias de estas funciones de onda denominadas Ψ1, Ψ2, Ψ3,..., con energías E1, E2, E3 ...; pueden
satisfacer estas condiciones. Cada una de estas funciones se denomina orbital, por analogía con
las órbitas de Bohr.
En el átomo de hidrógeno el electrón ocupa el nivel más bajo en energía, E1, que constituye su
estado fundamental con una función de onda Ψ1 que describe al orbital, es decir el espacio en
que es más probable encontrar al electrón y que se corresponde con la órbita n = 1.
En general cada orbital está definido por cuatro números cuánticos ya descritos por Bohr. El
número cuántico principal n especifica la energía de un electrón en un nivel El número cuántico
azimutal l. Se llama también numero cuántico del momento angular del orbital, ya que se
relaciona con el momento angular del electrón alrededor del núcleo. Indica, asimismo, la forma
del orbital:
l = 0. orbital esférico, orbital s
l = 1, tiene dos lóbulos o regiones a lo largo de los ejes; orbitales px, py, pz
l = 2, cuatro lóbulos, orbitales d, cinco orbitales
l = 3, orbitales f, ocho lóbulos, siete orbitales (m = -3, -2, -1, 0, 1, 2, 3)
El número cuántico magnético ml, representa los 2l+1 orbitales de un subnivel. El número l
estaría representado por un vector cuya magnitud es el momento angular orbital, mientras que
ml representaría la componente en la dirección z de las orientaciones posibles de l, es decir 2l+1
orientaciones.
El electrón tiene, asimismo, un momento angular intrínseco procedente de su propia rotación
alrededor de su eje. Esto conduce al cuarto número cuántico de espín, ms.
10
Enlace y Estructura de la Materia
E Rodríguez-Fernández
Orbitales hidrogenoides
Soluciones de la ecuación de Schrödinger
Se puede resolver completamente para el hidrógeno y iones con un solo electrón como He+, Li2+.
Para otros átomos se pueden dar soluciones aproximadas.
Para obtener las soluciones es conveniente utilizar coordenadas polares (r, φ, θ) en vez de las
coordenadas cartesianas (x, y, z), ya que se adaptan mejor a la simetría esférica del átomo. r es la
distancia de un punto al centro de la esfera, φ, y θ son los ángulo cuyos arcos miden las distancias
al ecuador y al polo. Ambas coordenadas se relacionan mediante las expresiones:
z = rcosθ; y = rsenθ·senφ;
x = rsenθ·cosφ
Así la función de onda es más compleja1 pero puede descomponerse en el producto de tres
funciones de onda cada una de las cuales va a depender únicamente de una coordenada polar.
Las soluciones, también son el producto de una función radial (dependiente sólo del radio) y de
dos funciones angulares que se pueden agrupar en una sola de la forma
Ψ = R(r)·Θ(θ)·Φ(φ) = R(r)nl·A(θ,φ)ml
Ψ, ψ; psi
Θ, θ; theta
Φ, φ ; phi
Así queda desdoblada en producto de dos funciones, una radial R(r), que depende de los
números n y l, y otra angular A(θ,φ), dependiente de m y l.
La función R(r) no tiene significado físico pero R2(r) se le puede relacionar con la probabilidad de
encontrar al electrón en un pequeño volumen dv a un a distancia r, que es dP = R2(r)·dv. Este
volumen elemental es el comprendido entre dos capas esféricas de radios r y r+dr
dv = (4/3)π(r+dr)3 - (4/3)πr3 = (4/3)π[r3 + 3r2dr + 3r(dr)2 + (dr)3] -(4/3)πr3 =
4πr2dr + 4πr(dr)2 + (4/3)π(dr)3 ≈ 4πr2dr
Por lo tanto, la probabilidad de encontrar a un electrón en una capa de espesor dr sobre una
esfera de radio r es
dP = 4πr2·R2·dr
Y la probabilidad dentro de un determinado radio
P = 0∫r 4πr2·R2·dr
El valor es el área comprendida entre la curva el eje de abcisas (r) y una paralela al eje de
ordenadas trazada por el valor de r.
De acuerdo con lo anterior el orbital 1s; que no depende, al igual que cualquier s, de las funciones
angulares, se representa por una esfera que encierra el 90 o 95% de la probabilidad de encontrar
al electrón.
La función R2(r) es máxima en el núcleo pero al multiplicarla por 4πr2, que es nula en el núcleo, la
probabilidad es nula en este punto. El producto de estas funciones da lugar a una curva cuyo
máximo de probabilidad se encuentra a la distancia ao deducida por Bohr.
__________________________________________________________________________________
1)
Haciendo el cambio a coordenadas polares, la ecuación toma la forma:
(1/r2)d/dr[r2dΨ/dr]+(1/r2sen2θ)[d2Ψ/dφ2]+(1/r2senθ)[d/dθ(senθ·dΨ/dθ)] = -(8π2m(E-V)/h2)Ψ
11
Enlace y Estructura de la Materia
E Rodríguez-Fernández
Para los orbitales 1s, 2s, 3s la máxima probabilidad de radio va aumentando conforme aumenta
el número cuántico principal. Comparando 2s, 2p; 3s, 3p, 3d, se observa que el radio más
probable disminuye ligeramente a medida que aumenta l.
La función angular depende solamente de la dirección en el espacio y no de la distancia desde el
núcleo. Así, A2 representa la probabilidad de encontrar al electrón en una determinada dirección
definida por los ángulos θ y φ.
La probabilidad de encontrar al electrón a una distancia y dirección será:
Ψ2 = R2(r)·A2(θ,φ)
Los diagramas polares se usan para representar el solapamiento de orbitales para establecer
uniones entre los átomos. El signo proviene de la simetría de la parte angular. El solapamiento
tiene lugar entre lóbulos con el mismo signo. Lo que se representa como orbital es una superficie
que engloba al 90 o 95% de la probabilidad o densidad electrónica
Al elevar al cuadrado la función de onda no cambia la forma de los orbitales s pero elonga o
alarga los orbitales p, que estrictamente no tienen signo, ya que el cuadrado elimina cualquier
signo procedente de la simetría de la función. Los orbitales p no son simplemente dos esferas
sino dos elipsoides de revolución.
Los dibujos representan la simetría para 1s, 2p, 3d... Para los otros como 2s, 3s, 4s; 3p, 4p; 4d, 5d;
el signo o simetría cambia dentro de la superficie frontera o límite. Estos cambios se ven
fácilmente al relacionarlos con los nodos de las funciones radiales. A la vista de estas funciones se
puede determinar el número y clase de las superficies nodales de un determinado orbital así:
Representación de A2, parte
angular de la función de onda.
Los
lóbulos
en
blanco
representan valores positivos
de A, mientras que en los
obscuros A es negativa.
Función de
distribución radial
para los niveles
n =1, 2 y 3
12
Enlace y Estructura de la Materia
E Rodríguez-Fernández
Función de probabilidad de
distribución radial
P(r) = 4πr2·R2(r)
Existen n tipos de orbitales en el nivel n.
Existen 2l+1 orbitales de cada tipo, (un s, tres p…).
Existen en un orbital n-l-1 nodos en la función de distribución radial que se transforman en
superficies nodales esféricas.
Existen l planos nodales en un orbital, que corresponden a superficies nodales de la función
angular.
En total hay en un orbital (n-l-1)+(l) = n-1 superficies nodales (esferas y planos).
En una superficie nodal la función de onda es nula y, fuera de ella, la función de onda cambia de
signo a ambos lados de dicha superficie.
Aplicación: Superficies nodales de un orbital 3pz. En cualquier orbital 3p hay
3-1-1 = 1 esfera nodal que divide a cada uno de ambos lóbulos en dos. Hay una superficie nodal
plana (l = 1). En total dos superficies nodales (3-1).
Aplicación. La función radial y angular de los orbitales 1s, 2s y 2pz vienen expresadas mediante
las siguientes funciones:
R1s(r) = 2(1/a)3/2·e-r/a
R2s(r) = (1/(2·21/2))·(1/a)3/2·(2-(r/a))·e-r/2a
R2pz(r) = (1/(2·61/2))·(1/a)3/2·(r/a)·e-r/2a
A1s(φ,θ) = 1/(2π1/2)
A2s(φ,θ) = 1/(2π1/2)
A2pz(φ,θ) = (31/2/(2·π1/2))·cosθ
1 Superficies nodales de 1s, 2s y 2p
La función 1s tienen la parte angular constante distinta de cero. La parte radial decrece según una
función exponencial y sólo se anula en valor infinito de r, que carece de sentido físico ( R(r) → 0
cuando r →∞). No tiene esferas nodales.
Orbital 2s. La función R2s(r) es un polinomio por una exponencial. Sólo se anula cuando se anule
el polinomio, es decir, si r = 2a. Este orbital tendrá una esfera nodal de radio 2a.
Para el orbital 2p tenemos valores nulos de la función para r = 0 y para r → ∞ .
2 Radios de los orbitales 1s, 2s y 2pz. El radio de un orbital es aquel para el que la densidad
electrónica o probabilidad electrónica es máxima. La probabilidad es P(r) = r2·R2(r). Cuando se
hace nula la primera derivada de esta función (P’(r) = 0), tenemos los valores de r para los cuales
se obtienen los valores máximos y mínimos.
Para el orbital 1s esta función es P(r) = 4r2·a-3·e-2r/a. El radio se encuentra calculando las raíces de
la derivada:
P´(r) = 8ra-2·e-2r/a(a-r) = 0
Se anula la función para r = 0 y para r = a. El radio es el valor de Bohr, a.
Para el orbital 2p,
P(r) = r2·(1/(2√6))2·(1/a)3·(r/a)2·e-r/a
P’(r) = (1/(2√6))2·(1/a5) (d/dr)[r4· e-r/a] = C·r3· e-r/a [4-r/a] = 0, r = 4a = 4x0,53 = 2,12Å
Para el orbital 2s,
P(r) = (1/8a3)r2·(2-r/a)2·e-r/a;
13
Enlace y Estructura de la Materia
E Rodríguez-Fernández
P’(r) = (1/8a3)(d/dr)[r2·(2-r/a)2·e-r/a] = (1/8a3)[2r·(2-r/a)2·e-r/a + r2·(2-r/a) (-1/a)·e-r/a +
r2·(2-r/a)2·(-1/a)e-r/a] = (1/8a3)·r(2-r/a)· e-r/a [2(2-r/a)]+(-2r/a) + (-r/a)(2-r/a)] =
(1/8a3)·r(2-r/a)· e-r/a[4 -6r/a +r2/a2]; raíces para P’(r) = 0, r = 0, 2a, (3+√5)a y (3-√5)a.
El máximo se produce para el tercer valor; el cuarto valor representa un máximo relativo. Entra
ambos máximos está situado el nodo esférico o valor mínimo (2a).
3 Planos de simetría de 1s y de 2pz.
La parte angular de un orbital 1s es una constante por lo que depende sólo de r. este orbital
tendrá por lo tanto una simetría esférica. la parte angular de 2pz depende de cosθ. Esto da lugar a
una superficie nodal para θ = ±90° (plano xy).
x
+
_
+
_
z
R(r)
P(r)
2s
2ao
r
3
2s
1
1) r = (3-51/2)ao
2) r = 2ao, esfera
3) r = (3+51/2)ao
2
Orbital3pz
r
Átomos polielectrónicos
Cuando se pretende aplicar la ecuación de Schrödinger a un sistema que posea más de un electrón
no es posible hallar soluciones, debido a la dificultad inherente al estudio de tres partículas en
interacción. Este problema no ha sido resuelto tampoco en la mecánica clásica.
A pesar de todo, se puede tratar con métodos aproximados aplicados a la mecánica ondulatoria
similares a los de la mecánica clásica. Se utiliza la aproximación orbital en la cual cada electrón se
supone ocupando un orbital semejante al del hidrógeno.
Un tratamiento simplista de la energía de los electrones en los átomos polielectrónicos es
considerar a cada uno de sus electrones como si se moviera en un campo potencial de carga +1. Si
este modelo fuera siquiera cualitativamente correcto, los espectros de absorción y emisión de los
distintos elementos serían poco diferentes de los del hidrógeno. Pero no es así de simple
Representamos la gráfica de las energías de los electrones externos de iones dotados de tres
electrones, de los que dos se encuentran en un nivel 1s. La línea de trazos indican la variación de
la energía de los iones suponiendo que los dos electrones 1s neutralizan o apantallan totalmente
dos cargas nucleares positivas, actuando el remanente de carga sobre el electrón externo. Esto se
ajusta a la expresión análoga a la obtenida para el hidrógeno:
E = -13,6[(Z*)2/n2], donde Z* = Z-2 y E en eV
[E/(-13,6)]1/2 = Z*/n, (Diagrama de Moseley)
Cabe señalar que las líneas continuas que se trazan a partir de las energías experimentales se
encuentran desplazadas respecto a las teóricas en una magnitud que depende del número
cuántico principal del electrón desapareado. Esta desviación es máxima para la configuración 1s2
2s1. Las configuraciones 1s2 nd1 y 1s2 nf1, concuerdan casi completamente con el concepto de
efecto pantalla perfecto.
El desplazamiento de la energía de la configuración hacia energía más baja o más estable indica
que el electrón 2s1 experimenta una atracción mayor que Z-2. Es decir, los electrones 1s2 ejercen
un efecto de pantalla incompleto a la acción de la carga nuclear sobre el electrón restante.
En el caso de la configuración 1s2 2p1 el efecto de pantalla de los electrones internos es más eficaz.
Para la línea n = 3, la desviación de la configuración 1s2 3s1 es mayor que para 1s2 3p1 y esta a su
vez es mayor que para la configuración 1s2 3d1, que coincide prácticamente con la línea ideal.
Esta capacidad de los electrones internos para ejercer un efecto de pantalla entre la carga nuclear
y los electrones externos constituye la esencia para la comprensión de las configuraciones
electrónicas y su relación con la tabla periódica. Al construir la tabla periódica partiendo del
hidrógeno se va añadiendo en electrón y un protón al núcleo (proceso denominado “principio de
aufbau”), teniendo en cuenta el efecto de pantalla, es decir por qué los orbitales con el mismo
número cuántico n principal, pero diferente l deben tener energías diferentes en un mismo
átomo.
De acuerdo con el diagrama de Moseley se puede establecer una regla empírica de llenado de
orbitales en el hidrógeno.
14
Enlace y Estructura de la Materia
E Rodríguez-Fernández
a) Las energías de los orbitales aumentan al aumentar n+l
b) Dos orbitales con el mismo n+l, el de menor n tiene menor contenido energético.
Así, el orden de ocupación de orbitales queda:
n+l ⇒
1s, <2s, < 2p, <3s, < 3p, < 4s, < 3d, < 4p, < 5s
1
2
3
4
5
Diagrama de Moseley
Orbitales de Slater
La reducción de la carga nuclear se llama apantallamiento y la constante de apantallamiento, σ,
es esta cantidad en la que se reduce la carga. La carga resultante de restar esa constante se
denomina carga nuclear efectiva, Z*.
Z* = Z-σ , donde σ = Σi(σi)
Como el campo que se considera es centrosimétrico la componente angular de estos orbitales
hidrogenoides es la misma. Pero como la Z* varía marcadamente con la distancia desde el núcleo,
la función radial es diferente de la de los orbitales del hidrógeno.
Para mantener una expresión comparable a la de los orbitales atómicos monoelectrónicos, la
parte radial se establece como el producto de un polinomio por una función exponencial que
contenga el efecto del apantallamiento y su efecto sobre la reducción de la carga nuclear Z:
R(r) = C·[r/a]n-1·e-Z*r/na
Slater estableció una serie de reglas para estimar el valor de Z*, carga nuclear efectiva, en cada
caso. Existen valores calculados por métodos más aproximados que los propuestos por Slater, y
de ellos puede deducirse que un electrón de valencia (última capa), en s experimenta una mayor
carga que en el correspondiente p del mismo átomo.
Slater calculó Z* con unas reglas establecidas en base de los cálculos de energía de muchos
átomos. Estas reglas para calcular el apantallamiento de un electrón ns o np son.
1 Se agrupan los orbitales en los siguientes conjuntos (grupos):
{1s} {2s, 2p} {3s, 3p} {3d} {4s, 4p} {4d} {4f} {5s, 5p} etc. Es decir, 1s, s+p, d y f
2 Los electrones de cualquier grupo a la derecha o por encima del grupo considerado (ns,
np), no contribuyen al apantallamiento.
3 Cada electrón del grupo {ns,np}, contribuyen al apantallamiento del electrón
considerado con 0,35 cada uno. Un electrón 1s ejerce un efecto de pantalla de 0,30 sobre el otro
electrón 1s.
4 Cada uno de los electrones de la capa n-1 contribuyen con 0,85.
5 Todos los electrones de las capas n-2 o inferiores contribuyen con 1,00.
Cuando se calcula el efecto de pantalla para un electrón nd o nf , las reglas 2 y 3 son las mismas
en tanto que las reglas 4 y 5 quedan así:
6 Todos los electrones situados a la izquierda de los grupos nd o nf contribuyen al
apantallamiento con 1,00.
Estas reglas se pueden resumir en la siguiente tabla.
Grupo de
electrones
{1s}
{ns, np}
Grupos más
altos
El mismo
grupo
Grupos n-1
Grupos < n-1
0
0
0,30
0,35
0,85
1
15
Enlace y Estructura de la Materia
{nd},{nf}
E Rodríguez-Fernández
0
0,35
1
1
Aplicación: Para ilustrar la aplicación de las reglas de Slater podemos calcular el potencial de
ionización del Li y del F.
Para el litio
Li ⇒ 1s2 2s1; Li+ ⇒ 1s2 ; Li + I = Li+ + e
El potencial de ionización I, es la diferencia de energías entre ambas especies:
I = E(Li+) - E(Li) = -13,6[{2(Z*/n)21s}ion -{2(Z*/n)21s + (Z*/n)22s}átomo] = 13,62(Z*/n)22s
Como cada electrón 1s ejerce un efecto de 0,85 sobre el 2s,
Z* = Z-s = 3-2x0,85 = 1,30
Esto da como resultado I = 13,62x[(1,3/2)2] = 5,75 eV. (Valor experimental, 5,4 eV).
Para el flúor
F ⇒ 1s2 2s22p5 ⇒ (1s2)(2s22p5) ,
F+ ⇒ 1s2 2s22p4 ⇒ (1s2)(2s22p4)
Como antes los electrones 1s ven la misma carga antes o después de la ionización por lo que se
cancelan sus contribuciones
I = -13,6[{6(Z*/n)22sp}ion - {7(Z*/n)22sp}átomo
En el ion hay dos electrones 1s y cinco electrones sp que ejercen pantalla sobre el sexto electrón.
Así, la carga sobre los electrones del grupo sp es, en el ion: Z* = 9-5x0,35 -2x0,85 =5,55.
En el átomo es Z* = 9 - 6x0,35 -2x0,85 =5,20.
I = -13,62x[6x(5,55/2)2 - 7(5,20/2)2] = 15,2 eV; valor experimental: 17 eV.
Experimentalmente se sabe que el orbital 2s tiene menor energía que el 2p, aunque ambos tengan
según Slater, el mismo apantallamiento. En el Li los electrones 1s están cerca del núcleo, mientras
que el electrón en 2s o 2p estará más alejado del núcleo y ‘sentirán’ la carga nuclear en un valor
algo inferior a 3, es decir la carga efectiva, no la carga nuclear. El electrón en 2s siente la carga
algo más intensamente que el 2p debido a que la función de distribución radial de 2s tiene un
máximo relativo cerca del núcleo, al contrario de lo que le sucede al 2p. Se dice así, que el orbital
2s penetra más en las capas interiores (1s) que el orbital 2p. Al estar más cerca del núcleo está
sometido el 2s a una carga nuclear efectiva mayor y la energía será más baja y el orbital 2s más
estable.
Del mismo modo, podemos establecer que el orbital 3s está menos apantallado, es más
penetrante y es más estable que un orbital 3p y este menos que un 3d.
Apantallamiento:
Energía:
3s < 3p < 3d
3s < 3p < 3d
Poder de penetración: 3s > 3p > 3d
Estabilidad:
3s > 3p > 3d
El orbital 2s es más difuso o está más
extendido que el 1s. En general, este carácter
de difuso aumento con n. El 2s tiene mayor
concentración electrónica cerca del núcleo
que el 2p, es más penetrante que el 2p. El
orden de penetrabilidad es s > p > d > f. Los
orbitales más penetrantes se ven más
afectados por la carga nuclear.
16
Enlace y Estructura de la Materia
E Rodríguez-Fernández
Modelo vectorial del átomo
Las repulsiones entre los electrones apenas han sido consideradas hasta ahora y sólo se han
tenido en cuenta en el principio de ‘aufbau’. Para los átomos polielectrónicos se observan más
estados electrónicos de los que pueden justificarse con lo expuesto hasta ahora.
Así para el carbono con una configuración única 2p2 se derivan al menos tres términos
energéticos diferentes como veremos enseguida. Estos términos nacen de las muchas
posibilidades de colocar esos dos electrones en tres orbitales p (15 maneras de colocación o
microestados).
De todas estas distribuciones posibles o microestados algunas tienen idénticas repulsiones
interelectrónicas y se contabilizan en un mismo grupo o término. De esta manera, se obtiene un
grupo con nueve ordenaciones, otro con cinco y otro con una. Estos tres grupos tienen diferente
energía.
El modelo vectorial surgió así como una necesidad de explicar el espectro atómico. Cada electrón
en un átomo tiene un impulso angular orbital, que se representa o calcula por medio del número
cuántico l y un impulso intrínseco de espín s.
Estos impulsos, que son vectores, pueden acoplarse entre ellos de dos maneras, para dar un
impulso total suma de los vectores individuales. Hay, como queda dicho, dos maneras de sumar
estos vectores:
a) Un caso es que los impulsos orbitales l se acoplen fuertemente entre ellos para dar un impulso
angular orbital total L, y que, análogamente, suceda lo mismo con los espines individuales de
cada electrón para dar un espín total S.
Ambos L y S totales se combinan en extensión más débil para dar un impulso angular total J
correspondiente al átomo. Este acoplamiento se denomina de Rusell-Saunders o L-S.
b) La otra situación es que el impulsos individuales angular orbital l y de espín s, se acoplen a su
vez fuertemente para dar un impulso resultante j para cada electrón. Éstos a su vez se acoplan
después más débilmente para dar un impulso angular total J. Este acoplamiento se denomina j-j.
Los átomos más ligeros se tratan mejor con el acoplamiento L-S; y los más pesados, a partir del
bromo, responden mejor al acoplamiento j-j.
Acoplamiento de Rusell-Saunders
Nosotros veremos más detalladamente el L-S.
Para ello se introducen los números cuánticos L y S como números cuánticos del impulso orbital
total y de espín total. Los valores de L, como los de l, se simbolizan por letras, similares a las de
los orbitales pero mayúsculas.
Valor de L
0,
1,
2,
3,
4,
5 ...
Símbolo
S,
P,
D,
F,
G,
H ...
Para cada forma de asignar cuatro números cuánticos a cada electrón llegamos a un valor de ML
= Σml y un valor de MS = Σms.
Así se forman pares ML y MS cada uno de los cuales definen un microestado del átomo.
El siguiente paso es hallar todos los microestados posibles e identificarlos por los valores de ML y
MS. Se establece un número L o número cuántico azimutal que es el valor máximo de ML.
Análogamente, S es el valor máximo de MS. Identificar estos valores mediante números cuánticos
L y S. Después hay que agrupar los microestados de la misma energía en un término. Finalmente
con estos valores de L y M se escribe el símbolo de cada término de la forma (2S+1)L, usando la
letra correspondiente de L y el valor correspondiente de S, por ejemplo 3P.
Aplicación al átomo de carbono en su configuración basal
Veamos la aplicación al átomo de carbono en su configuración más estable, basal o de mínima
energía, 1s2 2s2p2
Las capas llenas o semillenas, dan una contribución nula al ML total, debido a que cada electrón
caracterizado por un +ml existe otro con -ml. Lo mismo ocurre, para capas llenas pero no
semillenas, con el valor de MS de modo que todos los orbitales con un número par de electrones y
por tanto con espines +1/2 y -1/2, cancelan su contribución al impulso total. El término de una
capa llena sería 1S, como es el caso de las capas 1s2 y 2s2 del carbono, como veremos después.
17
Enlace y Estructura de la Materia
E Rodríguez-Fernández
Sólo han de considerarse las capas parcialmente ocupadas. Aquí, para el carbono (1s2 2s2p2), sólo
han de considerarse los dos electrones p.
En este caso hay tres orbitales o movimientos espaciales posibles de los electrones. A la vez, cada
electrón tiene dos posibilidades de espín. El problema es hallar todas las maneras posibles
(microestados), de colocar dos electrones en tres orbitales con dos espines diferentes, según el
esquema adjunto. Después, agruparemos los microestados en términos.
Adición de los
vectores li para
dar L y su
proyección en la
dirección z.
Valores de J
para 3P
Valores de
2J+1 para
todos los
términos
(ML = Σml)
(MS = Σms)
Esquema de las interacciones electrón2
electrón para la configuración p . Se
muestran los términos, el acoplamiento
espín-órbita y el término fundamental o
de menor energía.
El número de combinaciones posibles o microestados también se puede calcular por la fórmula:
microestados = m!/[n!(m-n)!], donde m es el número máximo de electrones que cabe en un
subnivel y n el número de electrones que hay en el subnivel considerado.
Para p2, 6!/2!x4! = (6x5x4x3x2x1)/(2x1)(4x3x2x1) = 15 microestados
Para p3, 20 microestados
Para p4 = p2, 15
Para p5 = p1, 6; En general: pn = p6-n
18
Enlace y Estructura de la Materia
E Rodríguez-Fernández
Al repasar la lista observamos la existencia del valor máximo de ML que es 2, por lo que hay un
término con L = 2 al que corresponde como valor máximo de MS = 0. Esto nos sirve para asignar
la etiqueta de un primer término. Por esto podemos escribir el término así (2S+1)L = 1D
El número de microestados de un término viene dado por el producto de las multiplicidades de L
y S, es decir, (2L+1)(2S+1). Como al término 1D le corresponden (2L+1)(2S+1) = 5 microestados,
se deben eliminar de la lista los valores desde L hasta -L
(2,0), (1,0), (0,0), (-1,0), (-2,0)
En la lista quedan por tanto diez microestados. Con objeto de encontrar otro término, se busca
otra vez el máximo valor de ML que es 1 y de estos pares que tienen L = 1 el valor máximo de MS
es 1. Así se determina la presencia de un nuevo término con L = 1 y S = 1, es decir 3P. Este
contiene (2x1+1)(2x1+1) = 9 microestados siguientes:
(1,1), (1,0), (1,-1), (0,1), (0,0), (0,-1), (-1,1), (-1,0), (-1,-1)
Sólo queda el par 0,0 que corresponde a L = 0 y S = 0; el tercer término, 1S
El siguiente paso es determinar el acoplamiento del espín total y del orbital total, para dar el
momento o impulso total J.
Para cada término los valores de J se determinan calculando el valor de L+S y L-S, asignando
para J todos los valores desde |L+S| hasta |L-S|, por pasos enteros.
Esto es una consecuencia de hallar todos los J posibles para un término por suma de los pares ML
y MS Por ejemplo, para 3P tenemos los siguientes valores de MJ:
2, 1, 0, 1, 0, -1, 0, -1, -2
El máximo valor de J es 2, y este vector puede tomar cinco microestados u orientaciones distintas
con respecto al eje z, 2J+1. Estas son
2, 1, 0, -1, -2
Eliminados estos cinco microestados, quedan los cuatro microestados siguientes: 1, 0, 0 -1. La
presencia de un MJ = +1 implica un J máximo de +1, con tres microestados 1, 0 -1. Queda un J = 0,
con un solo microestado. En este caso los valores de J están comprendidos entre L+S = 1+1 hasta
1-1 = 0, es decir, 2, 1 y 0.
De esta manera por el acoplamiento espín-órbita tenemos el termino triplete desdoblado en otros
tres denominados (2S+1)PJ
3P , 3P , 3P
2
1
0
1
1
Con el mismo procedimiento hallamos D2, S0
Como cada valor de MJ requiere un microestado y hay 2J+1 valores de MJ para cada valor de J.
Sumando todos los valores posibles de 2J+1, deben coincidir con el total de microestados, 15.
1D ,
1S ,
3P ,
3P , 3P , ⇒ Σ2J+1 = 5 + 1 + 5 + 3+ 1 = 15
2
0
2
1
0
El número de microestados de cada término es la degeneración, multiplicidad que es el
desdoblamiento orbital por el desdoblamiento de espín, (2L+1)(2S+1).
Para 3P es (2x1+1)(2x1+1) = 9 = Σ2J+1 = 5+3+1.
Las transiciones electrónicas entre estos términos constituyen la base para la interpretación de los
espectros electrónicos de absorción y emisión de los átomos polielectrónicos.
Estos términos tendrán diferentes energías, siendo el de menor energía el término fundamental.
Para identificar el término de menor energía, nivel energético más bajo o estado fundamental se
siguen las reglas empíricas de Hund:
1 De todos los términos hallados para una configuración dada el de menor energía es el de
máxima multiplicidad de espín o máximo valor de S. Aquí, 3P.
2 Cuando hay más de un término con este valor máximo de S, el de menor energía es el de
máximo L.
3 Teniendo en cuenta la interacción L-S, el nivel con menor J es el de menor energía para subcapa
menos de semiocupada. J será el máximo valor de entre los posibles, para capa más de
semiocupada. Para una capa semiocupada L = 0 y sólo hay un valor de J = S. Aquí es 3P0.
El orden de los demás términos debe determinarse experimentalmente en cada caso.
Para el nitrógeno 1s2 2s2p3, se tienen 4S, 2D, 2P, y el de menor energía es 4S3/2
Determinación sencilla del término fundamental
Con un diagrama de celdas, representando a los orbitales, se puede determinar rápidamente el
término fundamental o de menor energía. Para el Ti2+, 3d2:
ml ⇒ 2 1 0 -1 -2
ms ⇒ ↑ ↑
19
Enlace y Estructura de la Materia
E Rodríguez-Fernández
Con dos electrones desapareados, S = 1 y ML = 3, y J es 4, 3, 2. El nivel es 3F2
Propiedades magnéticas
Un campo magnético se produce por el movimiento de una carga eléctrica. Es de esperar que el
espín nuclear, el espín electrónico y los movimientos orbitales den lugar a momentos magnéticos.
La contribución al magnetismo proviene principalmente de los electrones, siendo la del núcleo de
pequeño valor. Cada electrón es como un microimán y el momento magnético total es la
contribución de todos estos imanes.
En presencia de un campo magnético externo una sustancia puede ser atraída por él y se dice que
es paramagnética. Por el contrario si tiende a ser expulsada del campo magnético se dice que la
sustancia es diamagnética.
Diamagnetismo
Paramagnetismo
La sustancia diamagnética hace
disminuir la intensidad del campo en su
interior, es expulsada del campo. Una
sustancia paramagnética concentra las
líneas de fuerza en su interior, y es atraída
por el campo magnético.
El paramagnetismo se asocia con la presencia de al menos un electrón desapareado. La
contribución más importante es la de espín y orbital.
En algunos caso no hay contribución de los orbitales (o es pequeña y puede ser desdeñada), y el
momento magnético, µS, se calcula por la contribución del espín sólo:
µS = 2[S(S+1)]1/2 = [n(n+2)]1/2 , donde S = n/2, n = nº de e desapareados
Si existe contribución del orbital al momento total, puede ocurrir, a su vez, que la energía de
acoplamiento espín-órbita es menor que la energía térmica kT, con lo que todos los J estarán
disponibles para ser ocupados. El momento sería:
µS+L = [4S(S+1)+L(L+1)]1/2
Si la energía del acoplamiento L-S es más grande que la disponible térmicamente, solamente
estará ocupado el nivel más bajo que será el de menor J, si el subnivel está menos de semilleno y,
el mayor J, si está más de semilleno. El momento en este caso es
µJ = g[J(J+1)]1/2
g se llama razón giromagnética y viene dada por la expresión:
g = 1+[J(J+1)+S(S+1)-L(L+1)]/[2J(J+1)]
Para L = 0, no hay contribución del orbital y sustituyendo en cualquiera de las expresiones
anteriores tenemos la ecuación para la contribución de solo espín.
Configuraciones electrónicas
Los átomos en su estado fundamental o basal ocupan el nivel de mínima energía disponible.
Para construir las configuraciones electrónicas de los estados basales se tiene en cuenta el
principio de ‘aufbau’ o ‘building-up’, según el cual el electrón diferenciador de un elemento, es decir el
que le distingue del elemento precedente, va a colocarse en el orbital de mínima energía disponible.
Además hay que tener en cuenta el principio de Pauli: En un átomo ningún par de electrones puede
tener los cuatro números cuánticos iguales. Según esto, en un orbital pueden alojarse dos electrones
con los espines apareados (diferentes espines).
La energía de los orbitales va aumentando, menos negativa, a medida que aumenta n y, dentro
de un nivel, a medida que aumenta l
Hay diagramas mnemotécnicos que ayudan en la construcción de una determinada
configuración.
Línea 1 o Periodo 1. Se inicia el sistema periódico llenando el nivel más bajo que es el orbital 1s, n
=1, L = 0. Sólo entran dos electrones y por lo tanto hay dos elementos H, 1s1 y He, 1s2.
Línea 2, Periodo 2. Comienza el nivel 2, n = 2 ⇒ l = 0 (s), 1(p). Entran 8 elementos, desde el Li
hasta el Ne. Cuando hay vario orbitales degenerados o de la misma energía, los electrones se
colocan desapareados en ellos, hasta estar semiocupados. Los electrones deben ocupar todos los
orbitales de un subnivel, antes de comenzar a aparearse (regla de Hund). Así C, N y O tienen las
configuraciones siguientes
B, 1s2 2s2p1 ⇒ px1, py0, pz0
20
Enlace y Estructura de la Materia
E Rodríguez-Fernández
C, 1s2 2s2p2 ⇒ px1, py1, pz0
N, 1s2 2s2p3 ⇒ px1, py1, pz1
O, 1s2 2s2p4 ⇒ px2, py1, pz1
Línea 3 o Periodo 3. Se comienza a añadir electrones al tercer nivel con el sodio Na. Entran ocho
elementos hasta el Ar, pero aún queda libre el subnivel 3d que podría albergar a diez elementos
más
Periodo 4. Se inicia llenándose el orbital 4s el cual tiene menor energía que el 3d a la altura del K
y Ca y debe llenarse primero por lo tanto.
Una vez llenado el 3d, comienza a llenarse el 4p con el Ga, lo que supone seis elementos más
hasta llegar al Kr.
Periodo 5. Llenado el 5s la energía del 4d se hace menor y comienza otra serie de diez elementos.
Luego 5p hasta el Xe
Periodo 6. Se llena 6s, después 5d1, momento en que el orbital 4f se hace ligeramente más estable.
Después del La, [Xe]6s25d1, vienen 14 elementos lantánidos que van llenando los orbitales 4f. Una
vez completado este subnivel continúa llenándose el subnivel 5d con el Hf, 5d2 hasta el Hg, 5d10.
Luego se llena el 6p hasta el Rn. El Bi (Z = 83), es el último elemento no radiactivo.
Periodo 7. Se llena el 7s. Después el Ac 7s2 6d1, se comienza a llenar el subnivel 5f, con los
actínidos.
Configuraciones especiales
Existen algunas irregularidades en algunos casos de ocupación llena o semillena de orbitales lo
que parece que confiere estabilidad adicional a estas configuraciones. Destacaremos Cr y Mo (d5);
no el W; Cu, Ag y Au (d10). Otros casos son más difíciles de racionalizar como Pd, 4d10 o Pt 5d9.
En estos casos y en los siguientes influye la pequeña diferencia de energías entre los niveles ns y
(n-1)d:
En los lantánidos y actínidos se observan similar comportamiento entre los orbitales (n-2)f y (n1)d:
Para formar un catión se extraen primero los electrones np, luego los ns y finalmente los (n-1)d:
Problemas del átomo
1 El magnesio tiene la siguiente distribución isotópica 24Mg de masa 23,985 uma y abundancia
78,70%, 25Mg, 24,986, 10,13%; 26Mg, 25,983, 11,17 % [24,310 uma].
2 En el experimento de Millikan algunas gotitas de aceite capturan un electrón, otras dos, tres etc.
Concluir acerca del valor de la carga fundamental al observar cinco gotas con las cargas: -3,2; 4,8; -6,4; -8,0 y -1,6. Todas con el factor 10-19 culombios.
3 Calcular la longitud de onda asociada a un electrón que viaje al 40% de la velocidad de la luz.
(R = 6,07x10-12 m; Kotz-Purcell, 237).
4 La luz amarilla emitida por las farolas de sodio de está compuesta por las longitudes de onda
de 589,6 y 589,0 nm. ¿Cual es la frecuencia, numero de onda y energía de un fotón y de una mol
de fotones de la segunda línea? (5,09x1014 s-1).
5 Se puede usar luz de 590 nm (1nm = 10-9 m) para excitar el electrón 3s del sodio al nivel 3p.
Dado que la energía de ionización del sodio en su estado fundamental es de 494 kJ/mol, ¿cuál
será la energía de ionización del átomo de sodio en su estado excitado, [Ne]3p1? (c = 2,998x108
m/s) [4,84x10-19 por átomo, 291 kJ/mol].
6 Calcular la frecuencia necesaria para ionizar átomos de litio sabiendo que la primera energía de
ionización del litio vale 520 kJ/mol (h = 6,625x10-34 J·s, NA = 6,023x1023 partículas/mol) [ν =
1,30x1015Hz]
21
Enlace y Estructura de la Materia
E Rodríguez-Fernández
7 La máxima longitud de onda de luz susceptible de arrancar un electrón del un ion Li- y
conseguir la formación de un átomo de litio neutro es 2000 nm. calcular la entalpía de afinidad
electrónica del litio [-9,94x10-20 J por átomo, -59,9 kJ/mol].
8 Calcular la energía mínima que puede tener el electrón en un átomo de H.
9 Calcular el radio de la tercera órbita del átomo de hidrógeno.
10 Calcular la frecuencia y la longitud de onda de la radiación emitida cuando un electrón del
hidrógeno pasa de un nivel de energía n = 4 a otro n = 2.
11 Algunas gafas de sol contienen en sus cristales pequeñas partículas de AgCl, que cuando se
iluminan con luz apropiada se descomponen de acuerdo con la reacción: AgCl = Ag + Cl. La
plata producida proporciona un color gris uniforme. Si ∆H para la reacción es 248 kJ, calcular la l
máxima de luz que puede originar este proceso.
12 ¿Cual es la relación entre las energías de He+ y Be2+ en sus estados fundamentales? ¿Y entre
sus primeros estados excitados?
13 Calcular la λ del espectro de emisión del H de n = 2 a n = 1. Esta es una línea Lyman de gran
intensidad registrada en el espectro del sol, sólo observable fuera de la atmósfera.
14 Calcular la línea Balmer de λ máxima e identificar su color.
15 Calcular el potencial de ionización del hidrógeno.(5,22x10-19 cal/átomo, 315 kcal/mol)
16 ¿Cual es la incertidumbre para localizar a un electrón (m = 9,11x10-31 kg), que se mueve a un
40% de la velocidad de la luz y con una incertidumbre en la medida de la velocidad de =
0,100%?¿Cúal es la incertidumbre en la posición de un automóvil (m = 1000kg), que se mueve a
60,0±0,1mph (26,8±0,0450 ms-1)? (∆x > 6,07 nm y 1,47x10-35 m; Kotz-Purcell, 237).
17 Valores de n y l para los orbitales 6s, 4p, 5d y 4f. Dibujar una gráfica de Ψ2 frente a la distancia
para los orbitales 2p y 3p. Cuantos planos nodales y nodos esféricos tendrán.
(nº de planos = l; nº de esferas = n-l-1).
18 Un estado excitado del H tiene el electrón en el orbital 4p. Escribir todos los posibles conjuntos
de números cuánticos n, l y m.
19 Establecer que orbitales no pueden existir: 2s, 2d, 3f, 3p, 4f y 5g.
20 Dibujar un mapa de líneas de nivel del orbital 4pz con representación de las superficies
nodales. Idem para 4d x2-y2 en el plano xy.
21 Calcular la carga nuclear efectiva para un electrón 3p del Cl. (Porterfield 23)
22 Calcular la carga efectiva para un electrón de valencia del N, y para un electrón 3d del Zn. R =
3,90 y 8,85.
23 Calcular los potenciales de ionización del Li y F usando las reglas de Slater. (Purcell, 38)
24 Considerar que el electrón de valencia del potasio está en el orbital 3d en vez del 4s, y
establecer su configuración electrónica fundamental, en base a la carga nuclear efectiva
25 Calcular µ para Gd3+(4f7) y Dy3+(4f9) y comparar con los valores experimentales, 8,0 y 10,6MB
22