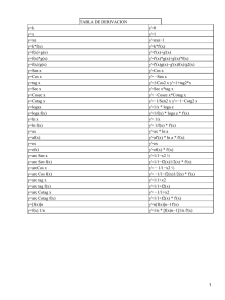
PROBLEMAS DE SERIES

PROBLEMAS DE SERIES
BÁSICO:
Estudiar la convergencia de las siguientes series, y en caso de convergencia calcular el valor
numrico de la serie:
µ ¶n
∞
∞ 1
∞ 1
∞
∞
∞
P
P
P
P
P
P
1
n
n 2)
3)
4)
2
5)
6)
1n
1)
2
n
n
2
n=1
n=1
n=1
n=1
n=1
n=1
1.- Calcular las siguientes series.
∞ 1 − 2n
P
1)
3n
n=1
∞
P
2n−1
4)
n
n−1 )
n=1 (1 + 2 )(1 + 2
∞ 2n+3
P
2)
n
n=1 3
∞
P
2
5)
n=1 n(n + 1)(n + 2)
2.- Estudiar la convergencia de las siguientes series.
∞
P
1
√
n=1 n n
∞
P
n2
3)
3
n=1 n + 1
∞
P
1
5)
a
b
n=2 n (log n)
∞
P 1
√
7)
n
n
n=1
n
∞
P 3 n!
9)
n
n=1 n
∞
P
1
11)
n
n=1 (n + 1)
∞
P 1 · 3 · · · (2n + 1)
13)
3 · · · 6 · · · 3n
n=1
∞ √
P
15)
( n n − 1)n
1)
n=1
∞
P
2 + (−1)n
n3
n=1
∞
P
19)
(log n)−n
17)
n=2
∞
P
sen2 n3
3
n√
n=1
∞ sen n
P
23)
3/2
n=1 n
∞
P (−1)n
25)
2
n=2 n(log n)
∞
P
27)
an n, (a > 0)
21)
n=1
2)
4)
∞
P
n=2
∞
P
n=1
∞
P
√
3
1
n2 − 1
an na , (a > 0)
sen(nα)
n2
n=1
2
∞
P n
8)
n=1 n!
¡ ¢
∞ 3 + cos nπ
P
2
10)
2+5
n
n=1
∞ n3
P
12)
n
n=1 2
∞
P log n
14)
3
n=1 2n − 1
∞ (b + 1) . . . (b + n)
P
16)
n!
n=1
∞ (−1)n
P
18)
n=1 2n + 1
∞ en
P
20)
n
n=1 n
∞
P (−1)n
22)
n=2 n log n
∞ (n!)2 4n
P
24)
n=1 (2n)!
∞ (−1)n
P
26)
n
n=1 n2
6)
∞
P
1
n=1 n(n + 1)
∞ ¡√
P
√ ¢
6)
n+1− n
3)
n=1
3.- (El número π) Sabiendo que
∞ 1
P
π
= , hallar las series
2
6
n=1 n
1
1
1
1
1
1
1
1
1
1
+ 2 − 2 + 2 + 2 − 2 + 2 + 2 − 2 + 2 + ...
2
1
2
3
4
5
6
7
8
9
10
1
1
1
1
1
1
1
2) 2 + 2 + 2 + 2 + 2 + 2 + 2 + . . .
1
3
5
6
7
9
10
1)