Las siete ecuaciones esenciales de la Topografía Aplicada

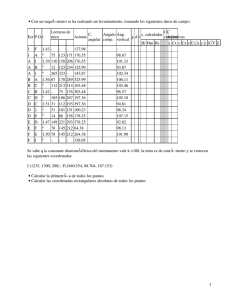
VI Congreso Agrimensura, La Habana 2013
Título: “Las siete ecuaciones esenciales de la Topografía Aplicada”
Autor: Dr. Ing. Ricardo Olivera Rodríguez
Institución: GEOCUBA VC-SS.
Ciudad: Santa Clara, Villa Clara.
País: Cuba.
Teléfono: 042-202625 ext. 120
Correo electrónico: [email protected]
Resumen:
El número siete es una cifra muy enigmática –mística diría– desde la antigüedad.
Siguiendo esta tradición hemos querido definir las siete ecuaciones imprescindibles, las
principales, de la Topografía Aplicada, y en torno a ellas, caracterizar su importancia y
el porqué de su inclusión dentro de una lista de cientos de formulaciones. La Topografía
Aplicada tiene un amplio registro en la diversidad de trabajos, que parten de los
estudios ingeniero-geodésicos de factibilidad o prospección, la creación de las redes
geodésicas plano-altimétricas de apoyo a la construcción, redes de simetría y
especiales, el replanteo, la certificación As-Built y los estudios geodésicos 4D
(deformaciones). Cada una de estas aplicaciones posee diversidad de tareas y métodos
caracterizados por disimiles de ecuaciones para definir el marco de referencia
geodésico (global-local, geoide-elipsoide-plano), caracterizar la precisión en el plano y
altura, el aseguramiento metrológico, y la garantía de la métrica de la construcción de
obras y elementos aislados. De esta colosal base de datos que caracterizan a la
Topografía Aplicada, escogemos solo siete ecuaciones: las más relevantes, lo que nos
propiciará entablar un rico debate sobre la quintaesencia de esta especialidad.
Palabras claves: Topografía Aplicada, posicionamiento, distancia, ángulo, desnivel,
altura, redes geodésicas, replanteo, deformación, levantamiento topográfico,
certificación geométrica.
I. Introducción
El número siete es un valor preferido desde antaño. Siete fueron las obras maravillas de
la arquitectura antigua seleccionadas por los griegos del período helenístico.
Igualmente, siete son los días de la creación bíblica; en Génesis, Dios creó al mundo en
seis días y descansó el séptimo. Son siete los sacerdotes elegidos y siete las vueltas a
la ciudad sagrada según la Biblia [1]. Siete son los vicios y siete las virtudes, y siete son
las palabras dichas por Jesucristo en la cruz. El faraón de Egipto sueña con siete vacas
gordas y siete vacas flacas, y en un segundo sueño ve siete espigas de trigo llenas y
hermosas y otras tantas, secas y delgadas. José interpreta los sueños y predice los
siete años de abundancia y los siete de escasez. Siete es el número de mensajes a las
siete Iglesias en el Apocalipsis como siete son los sellos, siete las trompetas y siete los
ángeles del cielo que derramaron las siete copas de la ira de Dios. Siete eran las
cabezas del dragón rojo que apareció en el cielo. Siete, y muchos otros siete se
hallarán en la Biblia…
En la Epopeya de Gilgamés (siglo VIII antes de nuestra era) la diosa de la fecundidad
Aururu crea –tras ruego de todos– a Enjidu, hombre salvaje y melenudo, algo más que
un animal, pues se complace en liberar a los animales caídos en la trampa de los
cazadores; éstos para verse libres de él, le envían una sacerdotisa del templo de Ishtar
para que, en siete días y en siete noches, lo inicie en la civilización [2]. Siete días duró
el diluvio de la Epopeya de Gilgamés [3].
En el Corán y en general en la tradición musulmana se hace uso abundante del número
siete. Según ésta, el profeta Mahoma dormía cerca de la Kaaba cuando apareció el
arcángel Gabriel que le ordenó levantarse, lo montó sobre Al Buraq –bestia entre
caballo y mulo, con cara de mujer y muy rápida– y partieron. Mahoma rezó una oración,
y tomado de la mano de Gabriel, desde la roca donde estuvo el templo de Salomón
ascendió a los siete cielos [4]. En el año 633 de nuestra era el profeta se puso al frente
de la peregrinación de la despedida. La tradición insiste en que el profeta se sabía
atacado por una enfermedad incurable. Por eso, nos muestra al fundador del Islam
montado en una camella para dar las siete vueltas a la Kaaba (el tawaf) y tocar la piedra
negra con su bastón al final de cada una; luego hacer las siete carreras entre ambas, y
al final de ellas descabalgar y pronunciar siete veces la nueva fórmula sagrada: ¡Al-lajú
Akbar! [5]
Todo musulmán está obligado una vez en la vida a ir en peregrinación a la Meca. Ya en
la Meca, el mújrim, o sea, el aspirante a peregrino, entra en la gran mezquita dando el
primer paso con el pie derecho, continúa hacia la Kaaba y le da siete vueltas prescritas
en sentido contrario al de las agujas del reloj. Después del tawaf, es decir, las siete
vueltas, viene el sayy, la carrera entre dos colinas de poca elevación llamadas Safa y
Marwa. Deben ser recorridas siete veces, variando el paso en sitios determinados, y
recitando las fórmulas prescritas [6].
En la ceremonia de la “lapidación de Iblis” (el demonio), que es parte de la
peregrinación a la Meca, el peregrino debe lanzar siete piedras a cada uno de los tres
pilares.
En el Popol Vuh el rey prodigioso Gucumatz en siete días subía al cielo y siete días
caminaba para descender a Xibalbú; siete días se convertía en culebra y
verdaderamente se volvía serpiente; siete días se convertía en águila, siete días se
convertía en tigre: verdaderamente su apariencia era de águila y de tigre. Otros siete
días se convertía en sangre coagulada y solamente era sangre en reposo [7].
Según una de las diferentes fases de la geografía completamente sistemática
conservada por los Puranas, el disco terrestre se componía de siete zonas o círculos
concéntricos (Dwipas) con siete climas correspondientes y entre los indios las siete
zonas terrestres estaban separadas por siete mares [8]. Ya mucho antes el profeta judío
Esdras había dicho y lo repitió en uno de sus libros que Jehová en el tercer día de la
creación del mundo mandó que las aguas se reunieran en la séptima parte de la Tierra
[9].
Siete eran las terrazas de la torre de Babel [10]. Siete eran los sabios en la Grecia
antigua [11]. Siete son los colores visibles del arco iris, y siete son las notas musicales
siete son los días de la semana; siete son los orificios naturales del hombre y otros
mamíferos; y siete son las primeras villas fundadas por los españoles en su conquista
de Cuba...
¿Y cuáles serán las siete ecuaciones esenciales de la Topografía Aplicada?
II. Desarrollo
Seleccionar solo siete de cientos de ecuaciones que hace uso la Topografía Aplicada
es bastante complicado y polémico. Intentaremos un listado que se basa en la lógica, el
propósito y la esencia de cada fórmula.
II.1. Fórmula 1
La primera fórmula tiene que estar relacionada con la posición, es decir, con el “dónde”
está espacialmente ubicado el punto con el que a partir del cual se han de realizar las
diferentes operaciones de la Topografía Aplicada. Su fórmula es una expresión
funcional plano-altimétrica del tipo:
f (X, Y, Z)
En Topografía Aplicada –a diferencia de la Geodesia que trabaja en un marco global,
elipsoidal, extenso– las operaciones se ejecutan como regla general en el plano, en
áreas relativamente pequeñas, a distancias cortas, que no rebasan, digamos, los 5 Km.
Si se trata del aseguramiento ingeniero-geodésico a industrias y obras megalíticas
estas distancias incluso no superan unos escasos cientos de metros. Por tanto, el
sistema de coordenadas casi siempre es cartesiano local, plano-rectangular, que puede
o no estar asociado a la red estatal: la componente planimétrica XY al elipsoide de
referencia, que en Cuba es el de Clarke de 1866, y la altura al sistema de alturas
definidos en el país dado, que en el nuestro es el de alturas normales Siboney.
Es muy común que las precisiones requeridas en la Topografía Aplicada sean muy
elevadas (del orden de milímetros a escasos centímetros) por lo que la red estatal no
satisface esas exigencias, y por ende, sea necesario crear una red local arbitraria.
Surge entonces la necesidad de transformar de manera rigurosa las coordenadas de
este sistema local al estatal y viceversa.
II.2. Fórmula 2
La segunda fórmula es la transformación de las coordenadas del sistema local al estatal
y viceversa, que en realidad son varias, pero en su conjunto la llamaremos fórmulas de
transformación de coordenadas.
y
B
θ
A
M
x
a
B
y
b
x
A
Figura 1. Relación entre el sistema de coordenadas estatal planimétrico y el local.
El traslado del sistema de coordenadas local arbitrario a la red plano-rectangular estatal
se realiza por:
x = a + Bsenθ + A cosθ
y = b + B cosθ − Asenθ
La trasformación del sistema de coordenadas plano-rectangular estatal al local se
realiza por:
A = ( y − b) senθ − ( x − a ) cosθ
B = ( x − b) cosθ − ( x − a ) senθ
donde:
x y y – son las coordenadas del punto M en el sistema plano-rectangular estatal;
A y B – son las coordenadas del punto M en el sistema de la red local arbitraria;
a y b – son las coordenadas de origen de la red local arbitraria en el sistema planorectangular estatal;
Θ – ángulo de giro de la red local arbitraria con relación al sistema plano-rectangular
estatal.
Con los valores de coordenadas planimétricas en el sistema plano-rectangular estatal
puede incluso transformarse al sistema elipsoidal asumido en el país, u otros, como el
WGS-84, de uso común en los GPS.
La transformación de alturas es fácil de obtener. Simplemente se ha de conocer la
altura de un punto de la red estatal de nivelación y la del sistema local asumido. Su
diferencia algebraica constituye el valor de transformación.
II.3. Fórmula 3
Una vez definida la posición de un punto y su posibilidad de transformación hacia otros
sistemas se ha de tener la posibilidad de operar con las coordenadas, por lo que al
definirse dos puntos con coordenadas planimétricas se puede hallar su distancia
euclidiana:
𝑆 = �(𝑋2 − 𝑋1 )2 + (𝑌2 − 𝑌1 )2
II.4. Fórmula 4
La cuarta fórmula es el desnivel entre estos dos puntos, o sea:
∆h12 = H2 - H1
H2
∆h12
H1
Figura 2. Desnivel entre dos puntos con alturas conocidas.
II.5. Fórmula 5
La quinta está asociada al ángulo, siendo el más importante de los que se puedan
definir el acimut directo de la línea existente entre el punto 1 y 2.
12
Pto. 2
X2Y2
∆Y
Pto. 1
X1Y1
∆X
Figura 3. Acimut directo entre dos puntos.
El acimut coincide aquí con el rumbo y se halla por:
𝜎12 = 𝑎𝑟𝑐𝑡𝑎𝑛
𝑋2 − 𝑋1
∆𝑋
= 𝑎𝑟𝑐𝑡𝑎𝑛
∆𝑌
𝑌2 − 𝑌1
Una vez calculadas el acimut y las distancias de enlace entre los diferentes puntos del
terreno u objeto de obra se pueden determinar los incrementos de coordenadas y hallar
sus coordenadas.
II.6. Fórmula 6
La fórmula sexta debe estar asociada al monitoreo de las deformaciones de obras por
métodos geodésicos, siendo la más representativa la que relaciona los asentamientos y
los desplazamientos horizontales en el tiempo, que se puede representar mediante el
gráfico siguiente:
Z
Pi
ri+1
ri
Pi+1
Y
X
Figura 4. Representación gráfica de la deformación.
La fórmula en cuestión es la siguiente:
r i +1 =
[X (ti +1 ) − X (t0 )]2 + [Y (ti +1 ) − Y (t0 )]2 + [Z (ti +1 ) − Z (t0 )]2
donde:
ri+1 - vector deformación en el ciclo o tiempo i+1;
ti+1 - tiempo i+1;
t0 - ciclo o tiempo inicial o cero;
X, Y, Z - componentes espaciales de las coordenadas.
Igualmente la deformación se puede expresar en base al modelo dinámico siguiente:
2
m
0
x 
x 
 y =  y
 
 
 z  i
 z  i
 .. 
. 
x
x 
 
 ..  ∆t m2
.
+  y  ∆t m +  y 
 ..  2
. 
z 
z 
 i
 i
donde:
T
. . .
 x y z 
i
T
 .. .. .. 
, x y z

i
- son las velocidades y aceleraciones convencionales,
respectivamente.
∆t - es el intervalo de tiempo entre ciclo o tiempo cero (to) y el ciclo o tiempo dado tm.
II.7. Fórmula 7
La fórmula siete, y no por ser la última es la de menor importancia, es la que evalúa la
calidad del dato, la precisión de cada una de las operaciones anteriores, y es la fórmula
del error medio cuadrático de una función de argumentos no correlacionados, tal y
como se trata que sean las magnitudes medidas en Topografía Aplicada [12].
𝑛
𝜕𝐹 2 2
𝑚𝐹 = �� �� � 𝑚𝑥𝑖 �
𝜕𝑥𝑖
𝑖=1
Es decir, que el error medio cuadrático de una función de n argumentos no
correlacionados es igual a la raíz cuadrada de la suma cuadrática de las derivadas
parciales de cada una de las variables de la función por el error medio cuadrático del
argumento como tal.
Demos un ejemplo: Si deseamos determinar el error medio cuadrático del desnivel
obtenido por la fórmula:
h = S . tan α
Con una longitud horizontal de S = 143,5 m, y el ángulo α = 2°30`00”, resulta que
h = 6.27 m. Si la distancia se midió con un error medio cuadrático de ms= � 5 mm y el
ángulo con mα = � 2”, tenemos que:
𝑚ℎ = �𝑚𝑠2 𝑡𝑎𝑛2 𝛼 +
𝑆 2 𝑚𝛼2
𝑐𝑜𝑠 4 𝛼 𝜌2
Al sustituir, obtenemos que mh= � 1.94 mm, lo cual nos resulta un indicador importante
de la calidad de esa determinación.
No obstante, aclaramos que existe una serie de términos relacionados con la
incertidumbre de medida como son error, precisión, exactitud, repetibilidad,
reproducibilidad, etc., que deben tratarse con cuidado, evitando su confusión y
usándolos de manera consistente a como se definen en lo s documentos
internacionales. La definición de todos ellos viene recogida en el Vocabulario
internacional de Metrología – Conceptos fundamentales y generales y términos
asociados (3ª edición) (ISO, 2007; CEM, 2008), comúnmente conocido como VIM. El
VIM debe acompañar siempre a la Guía para la expresión de la incertidumbre de
medida, comúnmente denominada GUM (ISO, 2008), elaborada conjuntamente por
diversas organizaciones internacionales (Oficina Internacional de Pesas y Medidas
BIPM, Organización Internacional de Metrología OIML, Organización Internacional
de Normalización ISO) y adoptada, en la actualidad, por un gran número de
prestigiosas sociedades científicas internacionales. Los dos documentos, el VIM y la
GUM, son complementarios y han sido publicados por la ISO en consenso con otras
muchas organizaciones internacionales.
III. Conclusión
Con estas siete fórmulas sencillas de la Topografía Aplicada puede realizarse cualquier
trabajo de esta especialidad. Solo resta derivar de ellas para obtener las otras
deseadas. Así, el levantamiento de certificación ejecutiva o As Built no es más que un
caso particular de la fórmula de deformaciones, ya que en el tiempo establece una
comparación entre lo real existente y lo deseado en el proyecto, lo que puede asumirse
este último como tiempo o ciclo cero. Algo similar sucede con la certificación periódica
del avance de la obra: es una comparación de geometrías en el tiempo transcurrido.
Conocida la ecuación espacial de posición de varios puntos y su precisión, se derivan la
distancia plana e inclinada entre ellos, el desnivel, la inclinación, el rumbo, el acimut, la
dirección, la altura, el asentamiento, el desplazamiento horizontal. Se hallan los
elementos de replanteo: ángulos de inflexión y distancias de enlace.
Este razonamiento puede servir para explicar de una manera didáctica y diáfana el
porqué de las formulaciones de la Topografía Aplicada.
IV. Referencias
1. Aunque en cualquier edición de la Biblia puede comprobarse lo referido al
número siete, debemos decir que en el presente artículo hemos consultado a La
Biblia de estudio, impresa por Sociedades bíblicas unidas. Brasil. 1997.
2. Contenau, Georges. La vida cotidiana en Babilonia y Asiria. Editorial Pueblos.
La Habana. p. 101.
3. La Biblia de estudio. Obra citada. p. 35.
4. Díaz García, Waldo. Mahoma y los árabes. Editorial Ciencias Sociales. La
Habana. 1990. p. 154.
5. Ibídem. p. 185.
6. Ibídem. p. 197.
7. Popol Vuh. Las antiguas historias del Quiché. Editorial Gente Nueva. La
Habana. 1986. p. 161.
8. Humboldt, Alejandro de. Cristóbal Colón y el descubrimiento de América.
Tomo 2. Librería de los sucesores de Hernando. Madrid. España, pp. 347-348.
9. Cadalso, Alejandro Ruiz. Historia general de las ciencias geodésicas. Editorial
Cultural S.A. La Habana. 1941. p. 235. A su vez Cadalso hace referencia a que
este dato lo tomó de Biblia saca vulgatae editionis, cum annotationibus J.B. DuHamel, Matriti, 1790, Pars altera (3er volumen), Liber [] Esdras quarius, cap. VI,
versículos 42,47. También Alejandro de Humboldt en su obra citada, p. 345, así
lo recoge: “Y el tercer día ordenaste a las aguas reunirse en la séptima parte de
la tierra”.
10. Contenau, Georges. Obra citada. p.132. En esta misma página Contenau
afirma que Herodoto en Los nueve libros de la Historia, libro primero, Clío,
Capítulo CLXXXI, (Edición Revolucionaria. La Habana, 1978, pp. 50-51) se
equivoca y dice que la torre en vez de siete, tiene ocho terrazas ya que cuenta el
terraplén de basamento como tal; dice Herodoto “(…) En medio de él [se refiere
al templo de Júpiter Belo] se ve fabricada una torre maciza que tiene un estadio
de altura y otro de espesor. Sobre ésta se levanta otra segunda, después otra
tercera, y así sucesivamente hasta llegar al número de ocho torres”.
11. Junto a la primera chispa de la filosofía en la cosmología del mito y en los
misterios encontramos la primera presencia de la reflexión moral en la leyenda
de los siete sabios. Los escritores antiguos los enumeran variadamente, pero
cuatro de estos sabios, Tales, Biantes, Pitarlo y Solón figuran en todas las listas.
Platón, que fue quien primero los enumeró, añadió a dichos cuatro Clóbulo,
Misón y Quilón. Se les atribuían dichos y sentencias morales que pertenecen
todavía al saber popular, pero que preludian, sin embargo, la verdadera y propia
indagación sobre la conducta del hombre. Tomado de Nicolás Abbagnano.
Historia de la filosofía, Tomo I Edición Revolucionaria. 1996. p. 6.
12. Bolshakov, V.D. Teoría de la elaboración matemática de las mediciones
geodésicas. Editorial Nedra. Moscú. 1977. P. 117.
V. Bibliografía consultada
1. Bolshakov, V.D. Manual de Geodesia Ingeniera. Editorial Nedra. Moscú. 1985.
2. Olivera, R.R. Keops: Enciclopedia electrónica de Topografía Aplicada. Santa
Clara 2012.