TEMA 9: GEOMETRIA ANALÍTICA VECTORES EN EL PLANO Un
Anuncio
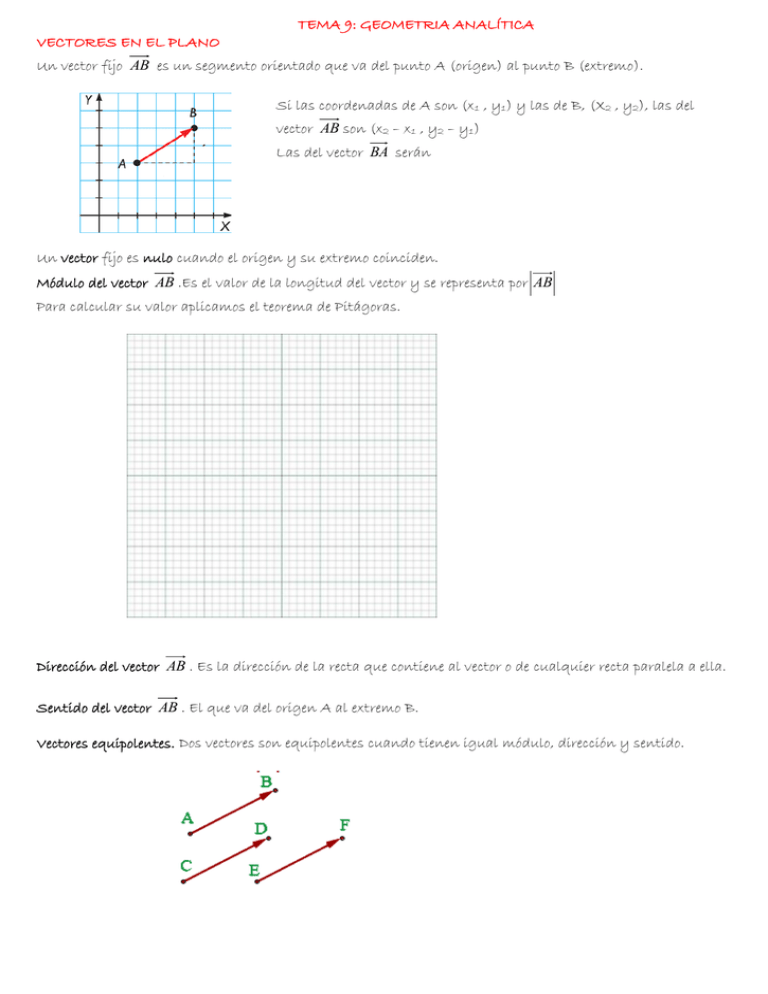
TEMA 9: GEOMETRIA ANALÍTICA VECTORES EN EL PLANO Un vector fijo AB es un segmento orientado que va del punto A (origen) al punto B (extremo). Si las coordenadas de A son (x1 , y1) y las de B, (X2 , y2), las del vector AB son (x2 – x1 , y2 – y1) Las del vector BA serán Un vector fijo es nulo cuando el origen y su extremo coinciden. Módulo del vector AB .Es el valor de la longitud del vector y se representa por AB Para calcular su valor aplicamos el teorema de Pitágoras. Dirección del vector AB . Es la dirección de la recta que contiene al vector o de cualquier recta paralela a ella. Sentido del vector AB . El que va del origen A al extremo B. Vectores equipolentes. Dos vectores son equipolentes cuando tienen igual módulo, dirección y sentido. Ejercicios. 1. Dibuja, escribe las coordenadas y calcula el módulo del vector AB en los siguientes casos a) A=(2 , 3) y B=(-1 , -3) b) A=(0 , 3) y B=(-3 , -3) 2. Calcula las coordenadas de los vectores de posición de los puntos a) P=(3 , 6) b) Q=(-2 , 7) 3. Dado el vector AB =(5 , 3), calcula las coordenadas del punto A sabiendo que las de B son (1 , 8) 4. Calcula el valor de k sabiendo que el módulo del vector v = (k, 3) es 5. 5. Dado el vector u =(2 , 5) Calcula otro vector, AB , equipolente cuyo origen sea A=(1 , 3) OPERACIONES CON VECTORES Suma de vectores. Dados los vectores u =(u1 , u2) y v =(v1 , v2) , su suma será otro vector cuyas componentes serán: u + v =(u1+v1 , u2+v2) Para dibujarlo se utiliza la regla del paralelogramo Ejemplos: a) Dados los vectores u =(2 , -3) y v =(3 , 4) el vector suma será: b) Dados los vectores a =(2 , 2) , b =(1 , -3) y c =(-3 , 0) su suma será: Opuesto de un vector. Es el vector con sus componentes cambiadas de signo. El opuesto del vector a =(a1 , a2) será - a =(-a1 , -a2) Por ejemplo el opuesto del vector a =(-2 , 3) será - a =( , ) Resta de vectores. Para restar dos vectores, u y v se suma u con el opuesto de v , que es lo mismo que restar las coordenadas de ambos. Dados los vectores u =(u1 , u2) y v =(v1 , v2) el vector resta será otro vector u - v =(u1-v1 , u2-v2) Por ejemplo dados los vectores u =(4 , 6) y v =(3 , -5) su resta será el vector u - v =( 4-3 , 6-(-5))=( , ) Gráficamente se une el origen de u con el extremo de - v Producto de un número por un vector. El producto de un número k por un vector u es otro vector: De igual dirección que el vector u . Del mismo sentido que el vector u si k es positivo y de sentido contrario del vector u si k es negativo. De módulo k u Las componentes del vector resultante se obtienen multiplicando por K las componentes del vector. Dado el vector u =(u1 , u2), el vector k u =(k.u1 , k.u2) Por ejemplo dado el vector u =(3 , -2), el vector -3 u =(-3.3 , -3.(-2)) = ( , ) Producto escalar de dos vectores. Es un número real que resulta al multiplicar el producto de sus módulos por el coseno del ángulo que forman. u.v u v cos Analíticamente se calcula así u . v =u1.v1+u2.v2 Ejercicios: 6. Dados los vectores u =(3 , 5) y v =(-3 , 2), calcula su producto escalar y el ángulo que forman. 7. ¿Son perpendiculares los vectores u =(2 , -5) y v =(5 , 2)? 8. Dados los vectores u =(3 , 4) y v =(m , 3), calcula el valor de m para que: a) Paralelos b) Perpendiculares c) Formen un ángulo de 60º 9. Dado el vector a (3 , 5) encuentra un vector perpendicular. ¿Cuántos podrías encontrar? UNA FORMA RÁPIDA DE ENCONTRAR UN VECTOR PERPENDICULAR A OTRO ES INVERTIR LAS COORDENADAS Y CAMBIAR UNA DE ELLAS DE SIGNO Por ejemplo dado el vector a (5 , 3) los vectores (3 , 5) y (3 , -5) son perpendiculares a a COMBINACIÓN LINEAL DE VECTORES Dados dos vectores u y v , y dos números, a y b, el vector a.u bv se dice que es una combinación lineal de u y v. Por ejemplo 4 u -6 v , -2 u +3 v También se pueden formar combinaciones lineales de más de dos vectores. Por ejemplo, a u +b v +c w Ejercicios 10. Dados los vectores u =(7 , -4), v =(-5 , -2) y w =(11 , 8): a) Hallar las coordenadas de -3 u -2 v . b) Calcula el valor de x e y para que se cumpla la siguiente igualdad: x u +y v = w VECTORES QUE REPRESENTAN PUNTOS Si un vector tiene su origen en O (origen de coordenadas), entonces sus coordenadas coinciden con las del extremo. Por eso los puntos del plano pueden ser descritos por vectores con origen en O. Ejercicios: 11. Desde el punto A(3 , 7) nos movemos en dirección v (4 , 2)el doble de su longitud. Después nos movemos el triple de w (1 , -3). ¿A qué punto llegamos? 12. El segmento cuyos extremos son A(1 , 4) y B(10 , 10) se divide en tres trozos iguales. ¿Cuáles son los puntos que marcan la partición? PUNTO MEDIO DE UN SEGMENTO Las coordenadas del punto medio de un segmento son la semisuma de las coordenadas de sus extremos. Vamos a deducir la fórmula. M es el punto medio de AB, por lo tanto se cumple que: 1 AM AB 2 AB x2 x1 , y 2 y1 Luego AM 1 x2 x1 , y 2 y1 x2 x1 , y 2 y1 2 2 2 Dado un segmento cuyos extremos tienen por coordenadas (x1 , y1) y (x2 , y2), las coordenadas de su punto medio serán: x x2 y1 y 2 M= 1 , 2 2 Ejercicios: 13. Hallar las coordenadas del punto medio del segmento de extremos A(7 , 10) y B(11 , 2) 14. Halla las coordenadas del punto simétrico de A(7 , 2) respecto a P(4 ,4) COMPROBACIÓN DE QUE TRES PUNTOS ESTÁN ALINEADOS Tres puntos A, B y C están alineados si los vectores AB y BC son paralelos, es decir, sus coordenadas son proporcionales. Dados los puntos A(x1 , y1), B(x2 , y2) y C(x3 , y3): AB = Para que estén alineados se ha de cumplir que: BC = y 2 y1 y3 y 2 x 2 x1 x3 x 2 Ejercicios: 15. Comprobar si los puntos A(2 ,-1), B(6 , 1) y C(8 ,2) están alineados. 16. Encuentra el valor de m para que los puntos A(1 ,4), B(3 , 8) y C(2 , m) estén alineados. 17. Dados los puntos A(2 , -4), B(5 , 7) y C(x , y), encuentra la relación que deben tener x e y para que los tres puntos estén alineados ¿Qué puedes decir de la solución? ECUACIONES DE RECTAS. PARALELISMO Y PERPENDICULARIDAD Sabemos que para definir una recta solo necesitamos un punto y su pendiente. La pendiente nos da la dirección de la recta, pero esto también nos lo proporciona un vector que tenga la misma dirección que la recta. A estos vectores que tienen la misma dirección que la recta se les denomina vectores dirección. Un vector dirección de una recta es cualquier vector que tenga la misma dirección que la recta, es decir, que sea paralelo a la recta. Hay infinitos vectores directores de una recta. v Dada la recta y=3x-4 tiene como pendiente m=3, cualquier vector v =(V1 , v2) que cumpla que 2 3 será v1 un vector dirección de esta recta, por ejemplo, (1 , 3), (2 , 6) , …. La relación entre un vector dirección y la pendiente es la siguiente: v v d v1 , v 2 m 2 v1 Ejercicios. 18. Halla la ecuación de la recta que pasa por A(-2 , 3) y tiene como vector dirección v (4 , 3) 19. Encuentra un vector dirección de la recta 3x-5y+7=0 Dos rectas serán paralelas si tienen la misma pendiente o sus vectores directores paralelos. 1 Dos rectas serán perpendiculares si sus pendientes cumplen m' o sus vectores dirección son m perpendiculares. Ejercicios. 20. Halla la ecuación de la recta que pasa por el punto A(2 , 5) y: a) es paralela al vector v (4 , 3) b) es perpendicular a la recta 3x-2y=4 21. La recta r pasa por (3 , 5), y la recta s, por (2 , -3). Ambas son perpendiculares a 3x+5y-2=0 . halla sus ecuaciones. RECTAS PARALELAS A LOS EJES DE COORDENADAS Las rectas paralelas al eje X son de la forma Y=K y sus vectores dirección son del tipo (a , 0) Las rectas paralelas al eje Y son de la forma X=K y sus vectores dirección son del tipo (0 ,a) POSICIONES RELATIVAS DE DOS RECTAS Dos rectas en el plano pueden ser: Secantes: tienen un punto en común y sus pendientes son distintas. Paralelas: no tienen ningún punto en común y tienen la misma pendiente y diferente ordenada en el origen. Coincidentes: tienen todos los puntos en común y la misma pendiente y ordenada en el origen. Si expresamos las dos rectas en la forma general r: Ax+By+C=0 y s: A’x+B’y+C’=0, las pendientes y A A' C C' las ordenadas en el origen son: m m' n n' B B' A A' El criterio para determinar su posición relativa es: m m' A B C Si entonces r y s son coincidentes. n n' A' B' C ' m m' A B C entonces r y s son paralelas. n n' A' B' C ' A B Si m m' entonces r y s son secantes. A' B' Si las rectas son secantes y que remos calcular el punto de corte solo tenemos que resolver el sistema formado por ellas. Ejercicios. 22. Estudia la posición relativa de las siguientes parejas de rectas. a) r: x-y+3=0 y r’: 5x+2y-4=0 Si b) r: x-y+3=0 y r’: x-y-2=0 c) r pasa por (2 , -1) y (8 , 2). r’ pasa por (2 , 5) y su pendiente es -1. DISTANCIA ENTRE DOS PUNTOS La distancia entre dos puntos A y B es el módulo del vector AB AB x2 x1 2 y2 y1 2 Ejercicios: 23. Calcula el perímetro del triángulo de vértices A(-2 , 2), B(1 , 6) y C(6 , -6) 24. Calcula el valor de K para que la distancia de A(-1 , 4) a B(k , 1) sea igual a 5. 25. Calcula la distancia del punto A(1 , 5) a la recta r: 2x+3y-2=0 ECUACIÓN DE LA CIRCUNFERENCIA Todos los puntos de una circunferencia cumplen la condición de que su distancia al dentro es igual al radio. CP r es decir: x a 2 y b2 r Elevando al cuadrado nos queda la ecuación de la circunferencia (x – a)2 + (y – b)2 = r2 Ejercicios: 26.Escribe la ecuación de la circunferencia de centro (2 , -7) y radio 5 27. Escribe la circunferencia de centro (4 , 5) y que pasa por el punto (1 , 7) 28. Dada la circunferencia de centro (4 , -1) y radio 5, indica si los siguientes puntos están dentro, fuera o en la circunferencia. a) A(1 , -5) b) B(1 , 1) c) C(5 , 1) REGIONES EN EL PLANO La ecuación (X-a)2 + (y – b)2 =25 describe la circunferencia. La inecuación (X-a)2 + (y – b)2 ‹ 25 describe el interior de la circunferencia. La inecuación (X-a)2 + (y – b)2 › 25 describe el exterior de la circunferencia. Para delimitar recintos delimitados por rectas y circunferencias utilizaremos sistemas de inecuaciones. Ejercicios. 28. Escribe las expresiones que representan estas regiones. a) b) b) Representa gráficamente los recintos que se obtienen a partir del siguiente sistema de inecuaciones: x 2 y 2 16 y x 0 0 x 3 EJERCICIOS 1. Dados los puntos A(3,0) ; B(0,2) ; C(-2,6) y D(1,3), dibuja los vectores relación hay entre ellos? y , y calcula sus coordenadas. ¿Qué 2. Dado el punto A(– 5, 4), halla el vector OA represéntalo y halla sus componentes (El punto O es el origen de coordenadas). Sol: (-5 , 4) 3. Con el origen en el punto A(3 , -3), dibuja los vectores AB (3, 2) , AC (5, 1) y AD (1 / 2, 4) . ¿Cuáles son las coordenadas de los puntos B, C y D? Sol: B(1, -1) C(8, -2) D(7/2, -7) 4. Dados los puntos A(-2 , 0); B(0 , 4); C(5 , 2) y D(3 , -4) encuentra las coordenadas de los vectores: AB , BC , CD , DA , AC y BD 5. Representa los vectores AB y CD , siendo A(1 , 1), B(-2 , 7), C(6 , 0) y D(3 , 6) observa que son iguales. Comprueba que AB CD encontrando sus coordenadas. Calcula el módulo. 6. Tenemos tres puntos de coordenadas: A(3 , 1), B(4 , 6) y C(0 , 0). Encuentra las coordenadas del punto D para que los vectores AB y CD sean iguales. Sol: D(1, 5) 7. Si los puntos (–6, 2), (–2, 6) y (2, 2) son vértices de un cuadrado, ¿cuál es el cuarto vértice? Sol: (-2 ,2) 8. Dibuja en unos ejes coordenados los vectores que nacen en el origen de coordenadas y tienen sus extremos en los puntos: A(4, 3), B(– 4, 3), C(– 4, – 3) y D(4, – 3) 9. Las coordenadas del vector son (5,3). Siendo B(-1,4), calcula las coordenadas del punto A. Sol: A(-6, 1) 10. De las expresiones siguientes, indica cuáles son verdaderas: - Dos vectores con direcciones diferentes no se pueden sumar. - Dos vectores opuestos tienen la misma dirección. - Si u k . v y k es negativo, entonces u y v tienen diferente dirección. - Si u v , entonces u y v tienen el mismo módulo. - Al multiplicar un vector por un número el vector resultante tiene la misma dirección. 11. La figura ABCD es un rombo. Compara el módulo, la dirección y el sentido de los siguientes pares de vectores: 12. Observa el rombo de la figura y calcula: Expresa los resultados utilizando los vértices del rombo. Sol: a) AC b) AB DC c) BA CD d) AA 0 e) AC f) 2 DC 13. Dados los vectores u (2 , 5) y v(1 , 4) calcular las coordenadas de: Sol: a) (–3, 6) b) (–3, 9) c) (–17/3, -41/3) d) (–1, 11/2) 14. a) Di cuáles son las coordenadas de los vectores u, v y w b) Dibuja los vectores u v y v w y escribe sus coordenadas. c) Dibuja el vector 5u 3v y escribe sus coordenadas. Sol: b) u v =(5, -1) y v w =(1, 3) c) 5u 3v =(-9, -11) 15. Con los vectores u, v y w del ejercicio anterior, efectúa las siguientes operaciones gráficamente y analíticamente (usando las coordenadas): ¿Cómo designarías al vector resultante de esta última operación? Sol: a) (12, –4) b) (13, –3) c) (0, 0) 16. Dados los vectores u (5, 8) , v(41, 10) y w(3, 6) . a) Encuentra las coordenadas de 3u 2v 10w . b) Encuentra el valor de x e y para que se cumpla que xu y w v . Sol: a) (97, 104) b) x=4 , y=-7 17. a) Representa los vectores u AB , v BC siendo A(1 , 3), B(4 , 5) y C(6 , 2). Encuentra las coordenadas de u y v. b) Representa u v y encuentra las coordenadas. Sol: a) u =(3, 2) v =(2, -3) b) (5, -1) 18. Dados los vectores u (4, 2) y v(2, 1) : 1 u y 3v y encuentra sus coordenadas. 2 b) Calcula las coordenadas del vector: w 2u 3v . 1 Sol: a) u v =(2, -3) u v =(6, -1) u =(2, -1) 3v =(6, 3) b) (2, -7) 2 a) Representa los vectores u v , u v , 19. Copia en un papel cuadriculado los siguientes vectores: a) Representa: 2a, 5b y 1 c 3 b) Expresa el vector d como producto de uno de los vectores a , b o c por un número. c) Escribe las coordenadas de los vectores a , b , c y d d) Repite, con las coordenadas, las operaciones que has efectuado anteriormente. 20. Considera el vector w : Dibuja en cada uno de estos casos un vector v que sumado con u dé como resultado w : 21. Efectúa gráficamente: Los vectores son los del ejercicio 18. Ahora realiza esos cálculos usando las coordenadas. Sol: a) (5, 3) b) (1, –2) c) (0, 1) d) (3, 1) 22. ¿Qué coordenadas ha de tener el punto P para que se verifique que 3PQ 2QR 0 siendo Q(3 , 2) y R(-1 , 5)? Sol: P(17/3, 0) 23. Dados los vectores u (5,3) ; v (1,4) y w (2,2) , calcula: a) u (v w) b) 3u 2( w v) c) 1 (v u ) d ) 5w 3u v e) 2(v u ) w 2 f) 3 2 u w 4 3 Sol: a) (4, -3) b) (9, 13) c) (-3, ½) d) (-6, 5) e) (6, 12) f) (53/12, -5/12) 24. Calcula el valor de X e Y en estas igualdades: a) (5,9) 3( x, y) 2( x,0) b) ( x,4) 2( y,5) (3, x) c) (2 y,0) ( x, y) 2( x,5) d ) (3x, y) 2(1, x) ( y,9) Sol: a) x=5 y=-3 b) x=-14 y=-17/2 c) x=-20 y=10 d) x=-7 y=-23 25. Considera el vector z 4i 3 j , siendo i (1,0) y j (0,1) . ¿Es z combinación lineal de i y de j ?¿Cuáles son sus coordenadas cartesianas? Sol: Sí, sus coordenadas son (-4, 3) 26. Si sabemos que u 2v 5w , expresa: a) v como combinación lineal de u y w . Sol: a) v b) w como combinación lineal de u y v . 1 5 1 2 u w b) w u v 2 2 5 5 27. Dados los vectores u (2,4) ; v (3,1) y w (11,15) calcula el valor de m y de n para que se cumpla que mu nv w Sol: m=4 n=1. 28. Calcula las coordenadas cartesianas de los vectores u 2a b y v 6a 4b sabiendo que: a 3i 6 j y b 5i 2 j Sol: u =(-11, 10) v =(-38, 28) 29. Dados los vectores u 6,8 y v 1,7 calcula: a) u v b) 2u v c) u d ) Ángulo que forman u y v Sol: a) 50 b) -100 c) 10 d) 45º 30. Estudia si las siguientes parejas de vectores son perpendiculares entre ellos. a) u (6,9) y v (3,2) b) u (2,4) y v (8,4) c) u (3,6) y v (10,5) d ) u (1,2) y v (4,2) Sol: a) Sí b) No c) Sí d) No. 31. Calcula el ángulo que forman los vectores u y v en cada caso. a) u 2, 3 y v 3, 1 b) u 6, 10 y v 3,5 c) u (4 , 6) y v (3,2) Sol: a) 10,89º b) 180º c) 90º 3 5 32. Calcula el valor de m para que el módulo del vector u , m sea igual a 1. Sol: m=4/5 33. Calcula el valor de X para que el producto escalar de a (3, 5) y b ( x, 2) sea igual a 7. ¿Qué ángulo forman los vectores a y b ?. Sol: -17/3. 34. Determina las coordenadas de un vector a ( x, y) que forme con el vector v (1, 0) un ángulo de 60º y cuyo módulo sea 2. Sol: Hay dos soluciones: x=1 y=1 o x=1 y=-1 35. Dado el vector u (5, k ) calcula K de manera que: a) u sea perpendicular a v (4, 2) . Sol: a) k=10 b) K=±3 b) El módulo de u sea igual a 34 . 36. Encuentra las coordenadas de un vector v ( x, y ) , ortogonal a u (3, 4) y cuyo módulo sea el doble que el de u . Sol: x=1,42 y=-1,07 37. Dados los vectores a 2u v y b 3u k v , siendo u (2,3) y v (3,0) , encuentra K de manera que (a b) y (a b) sean ortogonales. Sol: Hay dos soluciones: k=-10/3 o k=8/3 38. Representa los puntos A(3, 1), B(–5, 3), C(1, 2), D(–1, –2), E(–2, –3), F(5, 0) y halla las coordenadas del punto medio de los segmentos AB , CD y EF . Sol: MAB = (–1, 2) , MCD= (0 ,0) y MEF= (3/2 , -3/2) 39. Calcula las coordenadas de los puntos medios de los lados y de las diagonales del cuadrilátero ABCD. Sol: MAB = (1, 9/2) MBC = (–3, -1/2) MCD = (1/2, -3) MAD = (9/2, 2) MAC = (0, 1) MBD = (3/2, 1/2). 40. Halla, en cada caso, el punto simétrico de A(–3, –5) respecto de: a) P(–2, 0) b)Q(2, –3) c) O(0, 0) Sol: a) A'(–1, 5) b) A'(7, –1) c) A'(3, 5). 41. Si M(–3, 5) es el punto medio del segmento AB, halla el punto B en cada uno de los siguientes casos: a) A(–1, 5) b)A(6, –4) c) A(–4, –7) Sol: a) B(–5, 5) b) B(–12, 14) c) B(–2, 17). 42. Los segmentos AC y BD tienen el mismo punto medio. Halla las coordenadas del punto D, sabiendo que A(–2, 3), B(–3, –1), C(4, –2). Sol: D(5, 2) 43. Determina los puntos que dividen al segmento de extremos A(–5, –2), B(7, 2) en cuatro partes iguales. Sol: Los puntos buscados son M(1, 0), P(–2, –1) y Q(4, 1). 44. Dados los puntos A(0, 4) y B(–5, 0), halla el punto simétrico de B respecto de A y el simétrico de A respecto de B. Sol: A'(–10, –4) y B' (5, 8). 45. Comprueba que el cuadrilátero de vértices A(1, 5), B(5, 1), C(–4, –3) y D(–8, 1) es un paralelogramo. Para ello, prueba que los puntos medios de sus diagonales coinciden. 46. Halla las coordenadas del punto D, de modo que ABCD sea un paralelogramo, siendo A(1, –1), B(0, 2) y C(6, 5). Sol: D(7, 2). 47. Comprueba, en cada caso, que los puntos dados están alineados: a) A(1, 2), B(4, 3), C(19, 8) b)P(–2, –3), Q(2, 0), R(–26, –21) 48. Comprueba, en cada caso, si los puntos dados están alineados: a) A(–1, 3), B(-5/2 , 1/2) y C(– 4, –2) b) A(1, 0), B(–3, –2), C(5, 2) Sol: a) Si están alineados b) Si están alineados. 49. Calcula m para que los puntos R(5, –2), S(–1, 1) y T(2, m) estén alineados. Sol: m = -1/2. 50. Indica razonadamente si los puntos siguientes están alineados: a) A(4 , 6) , B(3 , 5) y C(-1 , 3) b) A( 1 , 5) , B(3 , 11) y C(-2 , -4) Sol: a) No lo están b) Sí lo están51. Determina K para que los puntos A(-3 , 5) , B(2 , 1) y C(6 , K) estén alineados. Sol: k = -11/5. 52. Halla la ecuación de la recta que pasa por los puntos dados: a) A(–1, 0), B(0, 3) b)A(0, –2), B(5, –2) c) A(–2, 3), B(4, –1) Sol: a) y = 3x + 3 b) y = –2 c) 2x + 3y – 5 = 0. 53. Escribe la ecuación de la recta perpendicular a r y que pasa por el punto P en los siguientes casos: a) r : y = –2x + 3; P(–3, 2) b) r : 3x – 2y + 1 = 0; P(4, –1) c) r : x = 3; P(0, 4) Sol: a) x-2y+7=0 b) 2x+3y=5 c) y=4. 54. Comprueba si los puntos A(18, 15) y B(–43, –5) pertenecen a la recta x – 3y + 27 = 0. Sol: A sí y B no. 55. Si las rectas ax + by + c = 0 y a'x + b'y + c' = 0 son paralelas, ¿cuál de estas dos condiciones cumplen? a) aa' + bb' = 0 b) ab' – a'b = 0 ¿Y si son perpendiculares? Sol: Si so paralelas ab' – a'b = 0 y si son perpendiculares aa' + bb' = 0. 56. ¿Cuál de las rectas es perpendicular a y=1/3x+1? 57. Dados los puntos A(–3, 2) y B(5, 0), halla las ecuaciones de las rectas siguientes: a) r: pasa por A y es perpendicular a AB b) s: pasa por B y es perpendicular a AB. Sol: a) y = 4x + 14 b) y = 4x – 20. 58. Calcula n y m para que las rectas r : 3x + my – 8 = 0 s : nx – 2y + 3 = 0 se corten en el punto P(1, 5). Sol: m = 1 y n = 7. 59. Escribe la ecuación de la recta que pasa por P y Q y da en cada caso un vector dirección. a) P(6 , -2) y Q(0 , 5) b) P(3 , 2) y Q(3 , 6) c) P(0 , 0) y Q(8 , 0). 60. Dada la recta x 2 y 1 , encuentra una recta perpendicular a ella que pase por el punto (4 , -3). 4 3 Sol: 4x+3y=5 61. Encuentra, en cada caso, el valor de K para que la recta X+KY-7=0 contenga el punto dado. a) (5 , -2) b) (7 , 3) c) (-3 , 4) Sol: a) k=-1 b) k=0 c) k=5/2 62. El segmento AB está sobre la recta x – 4y +10 = 0. Su mediatriz es la recta4x + y – 11 = 0. ¿Cuáles serán las coordenadas de B si las de A son (–2, 2)? Resuélvelo de forma gráfica y analítica. Sol: B(6, 4). 63. Encuentra el punto simétrico de P(1 , 1) respecto de la recta X-2Y-4=0. Sol: (3, -3) 64. Dados los puntos A(2 , 5) y B(-3 , 8), encuentra la ecuación de la recta perpendicular al segmento AB y que pasa por su punto medio. Sol: 5x+3y-34=0 65. Halla la ecuación de la recta perpendicular al segmento AB en su punto medio, siendo A(–5, 3) y B(2, 7). Sol: 14x + 8y – 19 = 0. 66. Las rectas r y s pasan por el punto (–4, 2); r es paralela a 3x – 12 = 0 y s es perpendicular a ella. Representa r y s y halla susa ecuaciones. Sol: r : x = –4 y s : y = 2. 67. La recta r es paralela a 5x – 4y + 3 = 0, y la recta s es perpendicular a ellas. Ambas pasan por el punto (1, 3). Escribe las ecuaciones de las rectas r y s. Sol: r: 5x – 4y + 7 = 0 y s: 4x + 5y – 19 = 0. 68. Halla el punto de intersección de las rectas r y s en los casos siguientes: r : 3x 5 y 17 0 r : 3x 6 0 a) b) s : 7 x 3 y 63 0 s : 2 y 5 0 Sol: a) (6 , 7) b) (-2 , 5/2). 69. Estudia la posición relativa de las rectas: r : 3x – 5y + 15 = 0 y s : pasa por (–2, –3) y (8, 3) Sol: Son paralelas. 70. Estudia la posición relativa de los siguientes pares de rectas: r : 2 x 5 y 3 0 r : 5 x 4 y 8 0 a) b) s : P(3,1) , Q(2,3) s : A(4, 7), B(0, 2) Sol: a) Se cortan en (2 , 7/5) b) r y s son la misma recta. 71. Estudia la posición relativa de estas parejas de rectas. En el caso de que sean secantes, encuentra el punto de corte. a) r : x 2 y 4 0 ; s : x 1 c) r : x 1 y 5 2 3 2 y 3 b) r : 3x 15 2 y 2 ; s : 3x 2 y 17 0 s : 3x 2 y 25 0 Sol: a) b) c) 72. Determina el valor de K para que las rectas r y s sean paralelas. r: x2 y 3 2 s: x 5 y 1 Sol: k=4 6 k 73. Encuentra el valor de K para que las rectas siguientes sean coincidentes: r : 2x 3 y 5 0 s: k x y2 Sol: k=-11/2 6 4 74. Dadas las rectas r: 2X-Y-17=0 y s: 3X-KY-8=0, calcula el valor de K para que r y s se corten formando un ángulo de 60º. Sol: Hay dos soluciones: k=49,98 o k=-1,98 75. Calcula la distancia entre P y Q: a) P(3, 5), Q(3, –7) b)P(–8, 3), Q(–6, 1) c) P(0, –3), Q(–5, 1) d)P(–3, 0), Q(15, 0) Sol: a) 12 b) 2 2 c) 41 d) 18. 76. a) Halla el punto medio del segmento de extremos A(–2, 0), B(6, 4). b) Comprueba que la distancia del punto medio a cada uno de los extremos es la misma. Sol: a) (2, 2) b) Sí la distancia es 20 . 77. Comprueba que el triángulo de vértices A(–1, 0), B(3, 2), C(7, 4) es isósceles. ¿Cuáles son los lados iguales? Sol: AB y BC. 78. Comprueba, mediante el teorema de Pitágoras, que el triángulo de vértices A(–2, –1), B(3, 1), C(1, 6) es rectángulo. 79. Dado el triángulo de vértices A(–5, 4), B(4, 1), C(–1, –2), halla: a) Las ecuaciones de los tres lados. b) El punto medio del lado AC. c) La ecuación de la mediana del vértice B. Sol: a) x + 3y – 7 = 0 , 3x + 2y + 7 = 0 , 3x – 5y – 7 = 0 b) (–3, 1) c) y = 1. 80. En el triángulo de vértices A(–1, 1), B(3, 4), y C(3, 0), halla: a) La ecuación de la mediatriz de BC. b) La ecuación de la mediatriz de AC. c) El punto de intersección de las mediatrices (el circuncentro del triángulo). Sol: a) y = 2 b) 2y – 8x + 7 = 0 c) (11/8 , 2). 81. Comprueba que el triángulo de vértices A(2, 3), B(3, 1) y C(–1, –1) es rectángulo y halla su perímetro y su área. Sol: Área = 5 u2 82. Comprueba que el triángulo de vértices A(4, 4), B(–2, 3) y C(3, –2) es isósceles y calcula su área. Sol: 35/2 u2. 83. Prueba que el cuadrilátero de vértices A(4, 2), B(–2, 5), C(–5, 2) y D(–2, – 4) es un trapecio isósceles y calcula su perímetro. Sol: Perímetro = 6 5 9 2 u. 84. Dadas las rectas: r : 3x + by – 12 = 0 s : ax – y + 6 = 0 calcula el valor de a y b sabiendo que r y s son perpendiculares y que r pasa por el punto (9, –15/2). Sol: a=2/3 y b=2. 85. Calcula el área del triángulo cuyos lados están sobre las rectas: r : x 3 s : 2 x 3 y 6 0 t : x y 7 0 Sol: Área=24/5 u2 86. Calcula el área del triángulo de vértices A(-1 , -1), B(2 , 4) y C(4 , 1). Sol: Área= 96,5 u2. 87. Halla un punto de la bisectriz del primer cuadrante que diste 5 unidades del punto (8, 7). Sol: Hay dos soluciones: P(4, 4), Q(11, 11). 88. Dada la recta r: x – 2y + 1 = 0 y el punto A(–1, 5), calcula: a) La ecuación de la recta s perpendicular a r y que pasa por A. b) El punto de intersección de r y s, M. c) El simétrico de A respecto de M. Sol: a) y = 3 – 2x b) M(1, 1). c) A'(3, –3). 89. Calcula la distancia del punto A(3 , -5) a la recta r : x 1 y 3 . Sol: 10 / 3 2 3 90. La recta y = 2x + 1 es la mediatriz de un segmento que tiene un extremo en el punto A(–6, 4). Halla las coordenadas del otro extremo. Sol: El otro extremo del segmento es B(6, –2). 91. Las rectas r : x – y + 1 = 0; s : x + y + 9 = 0; t : 4x – y – 14 = 0 forman un triángulo ABC. a) Calcula las coordenadas de A, B y C. b) Halla el circuncentro (el circuncentro es el punto en el que se intersecan las mediatrices) del triángulo. Sol: a) A(–5, –4), B(5, 6), C(1, –10) b) El circuncentro es el punto P(3, –2). 92. Los puntos A(4, 5) y B(7, 0) son vértices de un trapecio rectángulo que tiene dos lados sobre los ejes de coordenadas y otro lado paralelo al eje X. Dibuja el trapecio y halla: a) Las ecuaciones de sus lados. b) Su perímetro. c) Su área. Sol: a) x=0, y=0, y=5, 5x + 3y – 35 = 0 b) p= 16 34 c) A=55/2. 93. Dibuja un paralelogramo que tenga dos de sus lados sobre las rectas y = 3x e y = 0 y un vértice en el punto P(6, 3). a) Halla las ecuaciones de los otros dos lados. b) Di cuáles son las coordenadas de los otros vértices. Sol: a) y = 3x , y = 0, y=3, 3x – y – 15 = 0 b) O(0, 0), Q(5, 0), R(1, 3), P(6, 3). 94. Escribe la ecuación de la circunferencia de centro C y radio r : a) C(4, –3), r = 3 b) C(0, 5), r = 6 c) C(6, 0), r = 2 d) C(0, 0), r = 5 95. Di cuál es el centro y el radio de las circunferencias siguientes: a) (x – 2)2 + (y + 3)2 = 16 b) (x + 1)2 + y2 = 81 c) x2 + y2 = 10 96. Halla la ecuación de las circunferencias siguientes: a) Centro C(0, 0) y pasa por (–3, 4). b) Centro C(1, 2) y pasa por (5, 4). Sol: a) x2 + y2 = 25 b) (x– 1)2 + (y – 2)2 = 20 97. Halla en cada caso la ecuación de la circunferencia concéntrica con la dada y cuyo radio mida la mitad: a) x2 + (y – 5)2 = 36 b) (x – 4)2 + (y + 3)2 = 12 2 2 2 Sol: a) x + (y – 5) = 9 b) (x – 4) + (y + 3)2 = 3. 98. Halla la ecuación de la circunferencia de diámetro PQ, siendo P(–5, 2) y Q(3, –6). Sol: (x + 1)2 +(y + 2)2 = 32. 99. ¿Cuál de estas dos ecuaciones x2 + (y + 1)2 = 4/9 x2 + y2 + 25 = 0 representa una circunferencia? Di su centro y su radio. 100. Determina los puntos de corte de la circunferencia x2 + y2 = 50 con la bisectriz del primer cuadrante. Sol: Los puntos de corte son P (5, 5) y Q(–5, –5). 101. Calcula k para que el punto (–3, k) pertenezca a la circunferencia (x – 1)2 + (y + 2)2 = 25. Sol: Hay dos soluciones, k = –5, k = 1. 102. Describe mediante inecuaciones o sistemas de inecuaciones, los siguientes recintos: 103. Representa gráficamente los siguientes recintos: AUTOEVALUACIÓN 1. Dados los puntos A(-9 , 5) y B(3 , 6), calcula: a) El vector AB 2. 3. 4. b) El punto medio. Dados los vectores a (2 , 3) , b (3 , 2) y c (3 ,4) ; calcula analíticamente y gráficamente: a) 2a 3b = b) a b c = Calcula el perímetro del triangulo de vértices A(-4 , 1), B(6 , 3) y C(-2 , -3) Escribe la ecuación de la circunferencia de centro (0 , -3) y radio 7 5. Calcula el ángulo que forman los vectores u (3 , 5) y v 3 , 2 6. Estudia la posición relativa de estas parejas de rectas: a) r : x 2 1 y s : 3x y 6 0 3 b) r : x4 y3 s : 2 x 5 y 23 0 5 2 7. Escribe la ecuación de la recta que pasa por el punto medio de A(1 , 3) y B(-3 , 5) 8. Calcula el valor de K para que los vectores u 3 , k y v 2 ,1 9. Encuentra el punto simétrico del punto A(8 , 6) respecto al punto P(3 , 8). 10. formen un ángulo de 60º Dados los puntos A(1 , 3) y B(-3 , 7), encuentra la ecuación de la recta perpendicular al segmento AB y que pasa por su punto medio. Expresa el vector z 3 ,2 c o m o co m b i n a c ió n l i n e a l d e lo s v e c to r e s x 3 ,2 e y 1 , 4 Los puntos A(-1, 3) y B(3, -3), son vértices de un triángulo isósceles ABC que tiene su vértice C en la recta 2 x 4 y + 3 = 0 siendo AC y BC los lados iguales. Calcular las coordenadas del vértice C. 13. Escribe las expresiones que representan la siguiente región: 11. 12. 14. Representa gráficamente el siguiente recinto: x 2 y 2 25 a) x y 5 0 y 2x 6 0 b) 2 x y 6 0 y 2








