LA CIRCUNFERENCIA

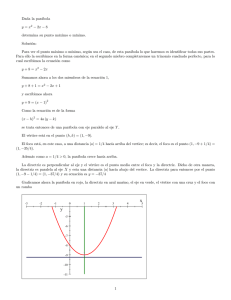
LA CIRCUNFERENCIA
La circunferencia es la sección producida por un plano perpendicular al eje.
β = 90º
La circunferencia es un caso particular de elipse.
Se llama circunferencia al lugar geométrico de los puntos del plano que equidistan de un
punto fijo llamado centro.
Elevando al cuadrado obtenemos la ecuación:
Si desarrollamos:
y realizamos estos cambios:
Obtenemos otra forma de escribir la ecuación:
Donde el centro es:
y el radio cumple la relación:
Ecuación reducida de la circunferencia
Si el centro de la circunferencia coincide con el origen de coordenadas la ecuación queda
reducida a:
Ejemplos
1. Escribir la ecuación de la circunferencia de centro (3, 4) y radio 2.
2. Dada la circunferencia de ecuación x2 + y2 - 2x + 4y - 4 = 0, hallar el centro y el radio.
Para que una expresión del tipo:
cumplir que:
sea una circunferencia debe
1) Los coeficientes de x2 e y2 sean iguales a la unidad. Si tuvieran ambos un mismo
coeficiente distinto de 1, podríamos dividir por él todos los términos de la ecuación.
2) No tenga término en xy.
3)
Ejemplo:
Indicar si la ecuación: 4x2 + 4y2 − 4x − 8y − 11 = 0, corresponde a una circunferencia, y en
caso afirmativo, calcular el centro y el radio.
1) Como los coeficientes de x2 e y2 son distintos a la unidad, dividimos por 4:
2) No tiene término en xy.
3)
Es una circunferencia, ya que se cumplen las tres condiciones.
Se llama circunferencia al lugar geométrico de los puntos del plano que equidistan de un
punto fijo llamado centro.
Ecuación reducida de la circunferencia
Si el centro de la circunferencia coincide con el origen de coordenadas la ecuación queda
reducida a:
Para que una expresión del tipo:
cumplir que:
sea una circunferencia debe
1) Los coeficientes de x2 e y2 son iguales a la unidad. Si tuvieran ambos un mismo
coeficiente distinto de 1, podríamos dividir por él todos los términos.
2) No tenga término en xy.
3)
4) Determina las coordenadas del centro y del radio de las circunferencias:
Ejercicios resueltos:
1)
2)
3)
4) 4x2 + 4y2 − 4x − 8y − 11 = 0
Calcula la ecuación de la circunferencia que tiene su centro en (2, −3) y es tangente al eje
de abscisas.
Calcula la ecuación de la circunferencia que tiene su centro en (−1, 4) y es tangente al eje
de ordenadas.
LA PARABOLA
La parábola es la sección producida en una superficie cónica de revolución por un plano
oblicuo al eje, siendo paralelo a la generatriz.
α=β
La parábola es una curva abierta que se prolonga hasta el infinito.
La parábola es el lugar geométrico de los puntos del plano equidistan de un punto fijo
llamado foco y de una recta fija llamada directriz.
Elementos de la parábola:
1)
2)
3)
4)
5)
6)
Foco: Es el punto fijo F.
Directriz: Es la recta fija d.
Parámetro: Es la distancia del foco a la directriz, se designa por la letra p.
Eje: Es la recta perpendicular a la directriz que pasa por el foco.
Vértice: Es el punto de intersección de la parábola con su eje.
Radio vector: Es un segmento que une un punto cualquiera de la parábola con el foco.
La parábola es el lugar geométrico de los puntos del plano que equidistan de un punto fijo
llamado foco y de una recta fija llamada directriz.
Elementos de la parábola:
1)
2)
3)
4)
5)
6)
Foco: Es el punto fijo F.
Directriz: Es la recta fija d.
Parámetro: Es la distancia del foco a la directriz, se designa por la letra p.
Eje: Es la recta perpendicular a la directriz que pasa por el foco.
Vértice: Es el punto de intersección de la parábola con su eje.
Radio vector: Es un segmento que une un punto cualquiera de la parábola con el foco.
Ecuación reducida de la parábola
En la ecuación reducida de la parábola el eje de la parábola coincide con el de abscisas y el
vértice con el origen de coordenadas.
Podemos considerar dos casos:
Caso 1
Ejemplo
Dada la parábola
, calcular su vértice, su foco y la recta directriz.
Caso 2
Ejemplo
Dada la parábola
, calcular su vértice, su foco y la recta directriz.
En la ecuación reducida de la parábola el eje de la parábola coincide con el de ordenadas y
el vértice con el origen de coordenadas
Podemos considerar dos casos:
Caso 1
Ejemplo
Dada la parábola
, calcular su vértice, su foco y la recta directriz.
Caso 2
Ejemplo
Dada la parábola
, calcular su vértice, su foco y la recta directriz.
Parábola con eje paralelo a OX y vértice distinto al origen
Ejemplo:
Dada la parábola
, calcular su vértice, su foco y la recta directriz.
Parábola con eje paralelo a OY, y vértice distinto al origen
Ejemplo:
Dada la parábola
, calcular su vértice, su foco y la recta directriz.
LA ELIPSE
La elipse es la sección producida en una superficie cónica de revolución por un plano
oblicuo al eje, que no sea paralelo a la generatriz y que forme con el mismo un ángulo
mayor que el que forman eje y generatriz.
α < β <90º
La elipse es una curva cerrada.
Es el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos
llamados focos es constante.
Elementos de la elipse:
1) Focos: Son los puntos fijos F y F'.
2) Eje focal: Es la recta que pasa por los focos.
3) Eje secundario: Es la mediatriz del segmento FF'.
4) Centro: Es el punto de intersección de los ejes.
5) Radios vectores: Son los segmentos que van desde un punto de la elipse a los focos: PF
y PF'.
6) Distancia focal: Es el segmento
de longitud 2c, c es el valor de la semi distancia
focal.
7) Vértices: Son los puntos de intersección de la elipse con los ejes: A, A', B y B'.
8) Eje mayor: Es el segmento
de longitud 2a, a es el valor del semieje mayor.
9) Eje menor: Es el segmento
de longitud 2b, b es el valor del semieje menor.
10)
Ejes de simetría: Son las rectas que contienen al eje mayor o al eje menor.
11)
Centro de simetría: Coincide con el centro de la elipse, que es el punto de
intersección de los ejes de simetría.
Relación entre la distancia focal y los semiejes
La excentricidad de la elipse es igual al cociente entre su semi distancia focal y su semieje
mayor.
Tomamos como centro de la elipse el centro de coordenadas y los ejes de la elipse como
ejes de coordenadas. Las coordenadas de los focos son:
F'(-c, 0) y F(c, 0)
Cualquier punto de la elipse cumple:
Esta expresión da lugar a:
Realizando las operaciones llegamos a:
Ejemplo:
Hallar los elementos característicos y la ecuación reducida de la elipse de focos: F'(-3, 0) y
F(3, 0), y su eje mayor mide 10.
1) Semieje mayor:
2) Semi distancia focal:
3) Semieje menor:
4) Ecuación reducida:
5) Excentricidad:
Representa gráficamente y determina las coordenadas de los focos, de los vértices y la
excentricidad de las siguientes elipses.
1)
2)
3)
5)