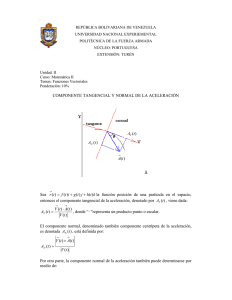
componentes intrínsecas de la aceleración (¡qué

Dr José Miguel Ayensa 20014
IES El Cabanyal (València)
COMPONENTES INTRÍNSECAS DE LA ACELERACIÓN (… ¡¿QUÉ?!)
1. ACELERACIÓN NORMAL O CENTRÍPETA.
Imaginemos una partícula moviéndose en una trayectoria circular de radio R con
rapidez constante v (por ejemplo, a 2 m/s, lo que quiere decir que recorre 2 m en cada
segundo). Antes de continuar, realiza la actividad siguiente:
Actividad 1. Dibuja una circunferencia con un radio que represente, por ejemplo, 5 m de
radio. Dibuja el vector velocidad instantánea en dos puntos de la circunferencia (elige dos
puntos no demasiado alejados). Responde ahora a las preguntas, ¿cambia la velocidad o es
constante?, ¿hay aceleración?
Se supone que el estudiante interesado en estas “cosillas” de la Física ha respondido
que no es lo mismo velocidad que rapidez, por lo cual, sí hay aceleración (¡qué cosas!).
Si la velocidad cambia (mira el dibujo que has hecho y verás que sí cambia la
dirección del vector velocidad) hay aceleración, aunque no cambie la rapidez.

Actividad 2. Dibuja el vector v , o sea, el vector diferencia entre la velocidad en el


segundo punto y la del primero (es decir, v 2  v1 ). ¿Qué dirección tiene en vector
diferencia? (¿Cómo es posible que no sea cero?).
Posiblemente, en la actividad anterior (A.2) has tenido algún “problemilla” mental,
porque supones que si no cambia la rapidez  no hay aceleración (eso mismo pensarán
los analfabetos de la Física).
A
Resolvamos este asunto. La figura 1

vB
muestra la partícula que se mueve a razón
de 2 m/s (constante) en una circunferencia

vA

v
B

vB
de radio R = 5 m. Se ha representado el
vector velocidad en un instante cualquiera (tA
= 0, por ejemplo) y en otro instante posterior
(por ejemplo, en tB = 1 s, donde la partícula
está en el punto B, después de recorrer un
arco de 2 m). Recuerda que aceleración es
Figura 1. El vector diferencia entre la velocidad
  
en B y en A, v  v B  v A tiene la dirección
radial y sentido hacia el centro de la circunferencia
el cambio o variación de la velocidad en la

 v
unidad de tiempo, o sea, a 
t
(1),
por
1
Dr José Miguel Ayensa 20014
IES El Cabanyal (València)
lo que hay aceleración y, mira por dónde, tiene la misma dirección y sentido que el vector

v , es decir, hacia el centro de la circunferencia. La aceleración, en este caso, toma el
nombre de aceleración centrípeta (hacia el centro).
Siempre que el vector velocidad cambie de dirección (esto ocurre siempre que la trayectoria
es curvilínea) habrá aceleración centrípeta o aceleración normal aN (se llama “normal”
porque es perpendicular a la tangente de la curva o de la circunferencia que describe el
móvil)1.
Recuerda que la dirección del vector velocidad es la tangente a la curva, por lo que

se suele expresar el vector velocidad como v .u t . Es decir, el vector velocidad tiene de

módulo v (la rapidez) y el vector direccional (en este caso hemos puesto el vector u t , o sea
un vector de módulo 1, vector unitario) es tangente a la trayectoria o curva que recorre el
móvil. Observa la figura 2, donde se han representado los vectores unitarios tangentes a la
trayectoria en los puntos A y B y la diferencia entre éstos (ten en cuenta que la variación del


 v v 



ut
vector velocidad es v  v.ut  vut ), por lo que la aceleración es a 

.ut  v
t t
t


 v
u 
Si v = constant, a 
 v t  aN
t
t
Hasta ahora sólo hemos obtenido la dirección y sentido de la aceleración centrípeta
pero, ¿cuánto vale su módulo?
A

ut (B )
Actividad 3. Teniendo en cuenta que la
aceleración media (la variación del
vector velocidad en la unidad de
tiempo, que en este caso depende sólo
de la variación de la dirección tangente,

es decir del vector unitario u t ) en este
caso es


ut
aN  v
t

u t ( A)

u t
B

ut (B )
(2), indica,
a título de hipótesis, de qué factores
dependerá la aceleración normal o
centrípeta (es decir, indica de qué
magnitudes físicas depende aN, y cómo
le afectan éstas).
Figura 2. En lugar de los vectores velocidad, se han
representado los vectores unitarios con la misma
dirección y sentido que los vectores velocidad y también
la variación o diferencia entre éstos.
Como es lógico, la aceleración
normal instantánea es el límite de la expresión anterior cuando el intervalo de tiempo tiene a


ut
cero, aN  v. limt 0
t
(3)
. Parece lógico pensar que si la curva es muy cerrada, esto es, si la curva tiene radio

pequeño, la dirección de la velocidad ( u t ) varía más que si la curva es abierta (radio
2
Dr José Miguel Ayensa 20014
IES El Cabanyal (València)
grande), por lo que es razonable que la aceleración centrípeta sea mayor cuanto más
pequeño sea el radio. Aunque aquí no lo demostremos, de hecho, así es, porque la
aceleración normal es inversamente proporcional al radio. Pero hay otro factor: la
rapidez con que cambia la dirección, es decir, la rapidez con que se mueve por la curva.
Este factor es más importante que el radio de curvatura: la aceleración normal depende
del cuadrado de la rapidez (que tampoco demostramos aquí). Por consiguiente, el módulo
de la aceleración normal o aceleración centrípeta es2:
aN 
v2
R
(4)
Actividad 4. La estación espacial internacional
(ISS, figura 3) se encuentra girando alrededor de
la Tierra, en una órbita polar aproximadamente
circular, a una altura media de 350 km (6703 km
desde el centro de la Tierra), por lo cual da una
vuelta completa en su órbita polar en poco más de
hora y media (5478 s).
Calcula la rapidez que lleva en su órbita y la
aceleración a la que está sometida (por cierto, ¿a
quién se debe esa aceleración?)
2
Sol: v = 7,688 km/s; a = 8,81 m/s .
Podemos encontrar muchos ejemplos de
Fig. 3 La ISS en su órbita polar alrededor
de la Tierra da una vuelta en 91 minutos.
movimientos curvilíneos con rapidez constante, es decir, con aceleración normal o
centrípeta. De hecho, la aceleración debida a la fuerza gravitatoria del Sol es la responsable
de que los planetas giren alrededor de él (esto ya lo puso de manifiesto el propio Newton a
finales del siglo XVII).
2. ACELERACIÓN TANGENCIAL
En el caso anterior hemos tomado el movimiento curvo de una partícula en el
supuesto de rapidez constante, pero ¿qué pasa si cambia la rapidez?. Ahí sí que se suele
admitir sin problema que existe aceleración. Por ejemplo, si un coche marcha con una
rapidez de 90 km/h y frena hasta 45 km/h todos admiten que sí hay aceleración (¡incluidos
los analfabetos científicos!). Supongamos que no cambia la dirección del móvil (movimiento
rectilíneo); entonces no hay aceleración normal, pero sí hay aceleración tangencial porque
cambia la rapidez del móvil.
En consecuencia, se llama aceleración tangencial media a la variación de la rapidez
en la unidad de tiempo, es decir,
at 
1
v
t
(5)
En Física, la “normal” es la perpendicular. Este nombre viene del latín, de un utensilio parecido a una escuadra,
llamado norma, que los albañiles empleaban para trazar la perpendicular en las obras.
2
Una verdadera lástima saber tan poco de Física y de Matemáticas en 1º Bat como para demostrar la fórmula a N
= v2/R.
3
Dr José Miguel Ayensa 20014
IES El Cabanyal (València)
Actividad 5. Lee la expresión anterior y trata de establecer la diferencia entre ésta y la
ecuación (1) relativa a la aceleración. Haz lo mismo con la ecuación (2).
Como es lógico, en un movimiento rectilíneo sólo puede haber aceleración
tangencial, la cual tendrá la misma dirección que el movimiento, mientras que el sentido
vendrá dado por el signo del cambio de rapidez, es decir, por el signo de v (si aumenta la

vA
rapidez, la aceleración tangencial será positiva,

v
mientras que si disminuye la rapidez at será

vB

vB
negativa.
Supongamos ahora que un móvil cambia la

at

aN
dirección y la rapidez. En tal caso habrá aceleración

a
normal aN (por el cambio de dirección) y aceleración
tangencial at, (por
el cambio de rapidez). La
aceleración normal tiene la dirección perpendicular a
Figura 4. En la figura superior se ha
  
dibujado el vector v  v B  v A y en
la curva (a la tangente) y sentido hacia el centro de
la inferior el vector suma a  a t  a N



curvatura, mientras que la aceleración tangencial,
como su nombre lo indica, es tangente a la curva. En resumen, el vector aceleración es la
suma de los vectores aceleración tangencial y aceleración normal (véase figura 4), esto es;
 

a  at  a N

(6), o sea a 
v  v 2 
.ut  .uN
t
R
Actividad 6. ¿Cuánto vale el módulo del vector aceleración?
Las aceleraciones normal y tangencial son mutuamente perpendiculares y la suma
vectorial de ambas nos dan la aceleración. Pero podemos imaginar dos ejes de
coordenadas ligados a la dirección radial (hacia el centro) y tangencial (hacia delante) que
acompañan o están ligados a la partícula que se mueve. En este caso tendremos un vector

a de coordenadas o componentes
at y aN. Estas componentes, en el sistema de
coordenadas mencionado (que acompaña a la partícula en su trayectoria) se llaman
componentes intrínsecas de la aceleración (¿se te ocurre de dónde viene la palabreja
“intrínsecas”?).
Actividad 7. En los dibujos de la figura 5 las partículas se están moviendo en sentido
contrario a las agujas del reloj en una circunferencia de 5 m de radio, con la rapidez que
corresponda en cada caso. Los vectores aceleración y sus módulos se indican en ciertos
instantes. Halla el valor de las aceleraciones tangencial y centrípeta, así como la rapidez.
2
2
2
2
2
Sol: (a) 0 y 20 m/s , 10 m/s; (b) 15 m/s y 26 m/s ; 11,4 m/s; (c) - 35,4 m/s y 35,4 m/s , 13,3 m/s)

v

a
a=20 m/s2

v

v
A =30 m/s2

a
a=50 m/s2
45º
30º
4

a
Dr José Miguel Ayensa 20014
IES El Cabanyal (València)
La aceleración tangencial está relacionada con la aceleración angular, dado que la
aceleración angular es  =/t, y  = v/R, por consiguiente  = v/(t.R), esto es,
 = at/R
(7)
Actividad 8. Una partícula comienza a moverse una circunferencia de 2,5 m de radio con
movimiento circular uniformemente acelerado (MCUA), de modo que parte del reposo y
alcanza una rapidez de 5 m/s en 2 s. Calcula la aceleración angular, la aceleración
tangencial, la aceleración normal y el módulo de la aceleración en ese instante. Representa
en un dibujo la partícula en el instante en que tiene una rapidez de 5 m/s, los vectores
aceleración normal y aceleración tangencial, así como el vector aceleración.
2
2
2
2
Sol: 1 rad/s ; 2,5 m/s ; 10 m/s ; 10,3 m/s ; (en t = 2s la partícula se encuentra a 5m del punto de
salida).
3. CLASIFICACIÓN DE LOS MOVIMIENTOS DE ACUERDO CON LAS COMPONENTES
INTRÍNSECAS DE LA ACELERACIÓN.
Los movimientos se pueden clasificar a partir del valor de las componentes
intrínsecas de la aceleración. En el cuadro adjunto figura dicha clasificación.
Respecto a la aceleración tangencial
Respecto a la aceleración normal

at = 0; v = constante  M. UNIFORME

aN = 0  MOV. RECTILÍNEO

at = constante; v= f(t)  M.U. VARIADO 
aN  0 y R= cte  MOV. CIRCULAR

at = f(t)  MOV. VARIADO

aN  0 y Rcte MOV. CURVILÍNEO

aN = cte y R =cte  M.C.U.A.
Actividad 9. Indica cómo es la aceleración tangencial y la aceleración centrípeta (nula,
constante o variable) en los movimientos siguientes:
a) Un coche de fórmula 1 en al curva de la “Chicane” (zona de una curva preparada para
reducir la velocidad).
b) Un tren que parte de una estación en vía recta.
c) El movimiento de rotación (elíptico) de un planeta (por ejemplo, Mercurio) alrededor del
Sol.
d) una piedra lanzada hacia arriba en una dirección que forma cierto ángulo con la
horizontal.
5