Ejercicio realizado por Patricia Delgado Martínez Enunciado: Hallar

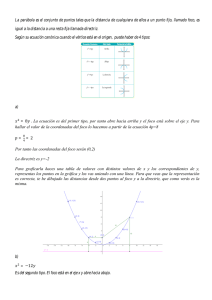
Ejercicio realizado por Patricia Delgado Martínez
Enunciado:
Hallar la ecuación de la parábola que tiene por directriz la recta y+5=0 y por
foco el punto P(0,5).
Teoría:
•
Parábola: Es el lugar geométrico de los puntos del plano que
equidistan de una recta fija llamada directriz y de un punto fijo
llamado foco.
•
Parámetro: Es la distancia del foco a la directriz Î p = d(F,d)
•
Vértice: Es el punto medio entre el foco y la recta directriz (d)
•
Eje de la parábola: Es la recta perpendicular a la directriz y que pasa
por el foco.
Resolución gráfica:
1. Dibujamos los ejes de coordenadas.
2. Dibujamos la directriz.
3. Colocamos el foco en el punto P(0,5).
4. En base a la solución del problema, vemos que pasa por el origen de
coordenadas, ya que la ecuación es x 2 = 20 y , y que además está
abierta hacia arriba, ya que el signo de 20 y es positivo (+).
Cálculo:
En este problema de parábola nos dan como datos la directriz y el foco.
Como no sabemos si el vértice se encontrará en el origen de coordenadas,
resolvemos el problema mediante la forma general:
d (P,F) = d (P,d)
1. Introducimos los datos (directriz y foco):
d: y+5= 0;
F (O,5)
2. Con estos datos hallamos la ecuación de la parábola:
d (P,F) = d (P,d)
(x)2 + (y − 5) 2 =
[ (x)
2
+ (y − 5)
2
]
2
y+5
1
 y +5
= 

 1 
2
x2 + y2- 10y + 25 = y2 +10y + 25;
x2 – 20y = 0;
x2 = 20y
Solución:
La ecuación de la parábola es: x2 = 20y