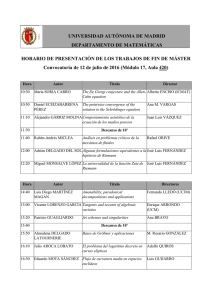
Notas introductorias sobre Variedades Abelianas y - DME-UFRO

M O N O G R A F Í A S M A T E M Á T I C A S
UTFSM
INTRODUCCION A LAS
VARIEDADES ABELIANAS
Y
GRUPOS KLEINIANOS
Rubén A. Hidalgo
Rubı́ E. Rodrı́guez
Departamento de Matemática
Universidad Técnica Federico Santa Marı́a
Pontificia Universidad Católica de Chile
Rubı́ E. Rodrı́guez (Parte 1)
Rubén A. Hidalgo (Parte 2)
´
α ´2
α1
β
1
α ´3
β2
α 1´
C
α ´3
α2
β3
Facultad de Matemáticas, Pontificia Universidad Católica de Chile,
Casilla 306, Correo 22, Santiago, Chile
E-mail address: [email protected]
Departamento de Matemáticas, Universidad Técnica Federico Santa
Marı́a, Casilla 110-V, Valparaı́so, Chile
E-mail address: [email protected]
2000 Mathematics Subject Classification. Primary 14XXX, 30F40, 30F60, 32XXX;
Secondary XXX, XXX
Key words and phrases. Variedades abelianas, grupos Kleinianos, superficies de
Riemann
13 de octubre de 2005
Este trabajo fue parcialmente financiado por Fondecyt 1000715, Fondecyt 1000623 y
la Cátedra Presidencial en Geometrı́a.
Índice general
Introducción
v
Parte 1. Toros Analı́ticos y Variedades Abelianas
1
Capı́tulo 1. Toros Analı́ticos
1.1. Conceptos básicos
1.2. Homomorfismos
1.3. Isogenias
1.4. Toros y Dualidad
3
3
4
7
8
Capı́tulo 2. Variedades Abelianas
2.1. Generalidades
2.2. Polarizaciones
2.3. Teorı́a del descenso
2.4. Forma real de una variedad abeliana polarizada
2.5. Polarizaciones y Matrices Perı́odo
13
13
14
16
19
19
Capı́tulo 3. Variedades Abelianas principalmente polarizadas
3.1. Complementos ortogonales
23
23
Capı́tulo 4. Curvas y Variedades de Prym generalizadas
4.1. Variedades de Prym
4.2. Cubrimientos Galois y Variedades de Prym
25
26
31
Capı́tulo 5. Estructura real
5.1. Variedades abelianas y su estructura real
5.2. Automorfismos y estructura real
37
37
38
Bibliografı́a
39
Parte 2. Grupos Kleinianos y Variedades Abelianas
41
Capı́tulo 6. Grupos Kleinianos
6.1. Superficies de Klein
6.2. Ejemplo de Superficie de Klein
6.3. Automorfismos de Superficies de Klein
6.4. Automorfismos del Disco Unitario
43
43
43
45
46
iii
ÍNDICE GENERAL
iv
6.5.
6.6.
6.7.
6.8.
6.9.
6.10.
6.11.
6.12.
Automorfismos de la Esfera de Riemann
Razones cruzadas
Cı́rculos Isométricos
Grupos Kleinianos
Espacio Hiperbólico 3-Dimensional: Extensión de Poincaré
Teorema de Uniformización de Koebe
Superficies de Klein de Grupos Kleinianos
Subgrupos Kleinianos Planares
Capı́tulo 7. Cubrimientos Homológicos
7.1. Jacobianas y Matrices de Riemann
7.2. Variedades de Prym
7.3. Automorfismos de Superficies de Riemann y Jacobianas
7.4. Superficies de Klein y Jacobianas
7.5. Cubrimiento Homológico de Superficies de Klein
47
50
51
54
59
65
66
78
83
83
85
90
91
94
Capı́tulo 8. Grupos de Schottky y Variedades Abelianas
8.1. Grupos de Schottky
8.2. Grupos de Schottky y Automorfismos
8.3. Grupos de Schottky con Cı́rculos Invariantes
101
101
103
107
Capı́tulo 9. Superficies de Riemann Maximal Simétricas
9.1. Superficies Maximales Simétricas
9.2. Uniformizaciones de S/K(S, τ )
9.3. Superficies Maximales Simétricas de Género 2
9.4. Superficies Maximales Simétricas de Género 3
9.5. Superficies de Riemann Maximal Simétricas de Género 5
111
111
112
114
120
127
Capı́tulo 10. Variedades Hiperbólicas 3-Dimensionales
10.1. Variedades Hiperbólicas son Atoroidales
10.2. Ejemplo 1: Complemento de Nudos
10.3. Ejemplo2: Fibrados sobre S 1
10.4. Ejemplo 3: Handlebodies
10.5. Ejemplo 4: Grupos CasiFuchsianos
135
136
139
141
149
149
Bibliografı́a
151
Introducción
Nuestra principal motivación para escribir estas modestas notas en la teorı́a de superficies de Riemann, grupos Kleinianos y variedades Abelianas fue que, en nuestra
lengua castellana, no existe mucha bibliografı́a para estudiantes y no especialistas.
Si bien hay una gran cantidad de libros y artı́culos en inglés (léase también alemán,
francés, ruso, etc), nos parece esencial que la matemática sea un bien mundial al
alcance de todos, sin distinción de idioma, ni clase económica, social o religiosa. Estamos conscientes de que estas notas son aún muy primitivas, pero esperamos poder
depurarlas con el tiempo y la ayuda de colegas y, en especial, de estudiantes.
Nuestro punto de vista fue relacionar entre sı́ tres tópicos que generalmente aparecen
por separado en muchos libros, siendo ellos superficies de Riemann, grupos Kleinianos
(en particular, grupos de Schottky), y variedades Abelianas (en particular, Jacobianas
y Pryms). En la última sección hemos agregado unas lı́neas sobre variedades hiperbólicas tres-dimensionales a manera de completitud. Para todo lo tratado se menciona
algunas referencias en la bibliografı́a, que sin duda dista de ser una lista exhaustiva.
Aún ası́, en las referencias de lo allı́ citado se puede encontrar bastante material de
apoyo.
Además de estas notas, el grupo de Geometrı́a Compleja de Chile ha publicado cuatro
volúmenes informales sobre estos tópicos, y también un volumen especial (el número
240) en Contemporary Mathematics de la Sociedad de Matemática de USA, con temas
discutidos en el Primer Congreso Iberoamericano de Geometrı́a, hecho en Chile en
1998. Esperamos poder seguir aportando materiales como éstos al medio matemático
chileno, y que ojalá también sea de utilidad para los estudiantes de otros paı́ses de
nuestra Latinoamérica joven.
Rubén A. Hidalgo
Rubı́ E. Rodrı́guez
Chile, 2001
v
Parte 1
Toros Analı́ticos y Variedades Abelianas
CAPÍTULO 1
Toros Analı́ticos
1.1.
Conceptos básicos
Los objetos que consideraremos en este capı́tulo son los toros analı́ticos; es decir, las
variedades complejas de la forma T = V /L, donde V es un espacio vectorial complejo
de dimensión g y L es un reticulado en V (i.e., un subgrupo discreto de rango 2g en
V , y por lo tanto isomorfo a Z2g ).
Es claro que entonces T es una variedad compleja compacta de dimensión g, además
de ser un grupo abeliano. Nótese que Π : V −→ T es el cubrimiento universal de
T = V /L, donde Π es la proyección canónica. Además se puede identificar V ≈ T0 (T )
(el espacio tangente a T en el origen = neutro de T ) y L ≈ Π1 (T, 0) = H1 (T, Z), por
ser L abeliano.
Para ejemplificar la teorı́a general, recurriremos constantemente al caso más simple,
g = 1:
Ejemplo 1.1. Consideramos dos vectores {z1 , z2 } en C linealmente independientes
sobre R y definimos L = {nz1 + mz2 : n, m ∈ Z}. Entonces T = C/L es un toro
analı́tico de dimensión uno, es decir una superficie de Riemann de género uno.
En el caso general, para describir un toro analı́tico T = V /L, escogemos bases
v1 , . . . , vg de V y f1 , . . . , f2g de L. Denotemos por π1j , . . . , πgj las coordenadas de
fj con respecto a la base v1 , . . . , vg . La matriz


π11 . . . π1,2g
.. 
Π =  ... . . .
.
πg1 . . . πg,2g
en M(g × 2g, C) se llama la matriz perı́odo de T (con respecto a las bases escogidas).
Al revés, tenemos
Proposición 1.1. Π ∈ M(g × 2g, C) es la matriz perı́odo de algún toro analı́tico si
Π
en M(2g × 2g, C) es no singular, donde Π denota la
y sólo si la matriz P =
Π
matriz compleja conjugada de Π.
Demostración. Π es una matriz perı́odo si y sólo si los vectores columna de Π
generan un reticulado en V si y sólo si las columnas son linealmente independientes
sobre R.
3
4
1. TOROS ANALÍTICOS
Supongamos primero que las columnas son linealmente dependientes sobre R. Entonces existe x ∈ R2g , x 6= 0, con Πx = 0, y por lo tanto P x = 0.
Si P es singular, hay vectores x, y ∈ R2g , no ambos cero, tales que
P (x + iy) = 0. Pero entonces Π(x + iy) = 0 y Π(x + iy) = Π(x − iy) = 0, y esto
implica Πx = Πy = 0. Luego las columnas de Π son l.d. sobre R.
Ejemplo 1.2. z1 = 1, z2 = τ con ℑτ > 0. Tomamos las bases v = 1 de C y f1 = 1,
f2 = τ de L.
Entonces la matriz perı́odo es Π = (1 τ ).
1.2.
Homomorfismos
Definición 1.2. Sean T1 y T2 dos toros analı́ticos.
i) Un homomorfismo de T1 en T2 es una función analı́tica
f : T1 −→ T2 compatible con la estructura de grupo.
ii) Para z0 ∈ T2 se define la translación por z0 como la función analı́tica tz0 :
T2 −→ T2 dada por tz0 (z) = z + z0 .
Proposición 1.3. Sea h : T1 −→ T2 una función analı́tica, con T1 = V1 /L1 y T2 =
V2 /L2 . Entonces
a) existe un único homomorfismo f : T1 −→ T2 tal que
h = th(0) ◦ f,
i.e. h(z) = f (z) + h(0) para todo z ∈ T1 , y
b) existe una única función C-lineal F : V1 −→ V2 con F (L1 ) ⊆ L2 que induce el
homomorfismo f .
Demostración. Se define f = t−h(0) ◦ h, y se levanta la función compuesta
π
f
1
V1 −→
T1 → T2 al cubrimiento universal V2 de T2 :
F
V1 @
@@
@@
@@
f ◦π
1
T2
/V
2
~
~
~
~~π
~~ ~ 2
de manera que F (0) = 0.
El diagrama implica que F (v + l) − F (v) ∈ L2 para todo l ∈ L1 y v ∈ V1 . Entonces
esta función continua de v es constante. Ası́
F (v + l) = F (v) + F (l)
para todo l ∈ L1 y v ∈ V1 , y por lo tanto las derivadas parciales de F son periódicas
con perı́odos L1 , y por lo tanto constantes. Como F (0) = 0, se sigue que F es C-lineal.
La unicidad de F es clara.
1.2. HOMOMORFISMOS
5
Con la suma punto a punto, el conjunto de homomorfismos de T1 en T2 es un grupo
abeliano, denotado por Hom(T1 , T2 ). La proposición anterior da un homomorfismo
inyectivo
ρa : Hom(T1 , T2 ) −→ HomC (V1 , V2 )
dado por ρa (f ) = F y llamado la representación analı́tica de Hom(T1 , T2 ).
Por otra parte, la restricción FL1 : L1 → L2 de F al reticulado L1 es Z-lineal; además,
FL1 determina a F y a f completamente. Ası́ obtenemos un homomorfismo inyectivo
ρr : Hom(T1 , T2 ) −→ HomZ (L1 , L2 )
dado por ρr (f )
=
Hom(T1 , T2 ).
En particular si T1 =
un endomorfismo de T1
End(T1 ) = Hom(T1 , T1 ) y ρr
FL1
y
llamado
la
representación
racional
de
T2 , un homomorfismo f : T1 → T1 se dice
y se tiene que ρa es representación del anillo
es representación del anillo EndQ (T1 ) = End(T1 ) ⊗Z Q.
Ejemplo 1.3. Para todo toro T = V /L y para todo entero n se tiene el endomorfismo
nT : T → T inducido por F : V → V dado por F (z) = nz.
Supongamos ahora que Π1 ∈ M(g × 2g, C) y Π2 ∈ M(p × 2p, C) son matrices perı́odo
para T1 y T2 con respecto a algunas bases de V1 , L1 y de V2 , L2 . Sea f : T1 −→ T2
un homomorfismo. Con respecto a las bases dadas, la representación ρa (f ) (respectivamente ρr (f )) está dada por una matriz a ∈ M(p × g, C) (respectivamente
r ∈ M(2p × 2g, Z)).
La condición ρa (f )(L1 ) ⊆ L2 se expresa en términos de matrices por
(1.1)
aΠ1 = Π2 r .
Recı́procamente, dos matrices a ∈ M(p × g, C) y r ∈ M(2p × 2g, Z) que satisfacen
(1.1) definen un homomorfismo T1 −→ T2 .
Ejemplo
1.4.τ = i, f ∈ End(T )dada por f ([z]) = [iz]. Entonces F (z) = iz, a = (i),
0 −1
0 −1
r=
y (i)(1 i) = (1 i)
.
1 0
1 0
Ahora veremos cómo se relacionan estas dos representaciones.
Proposición 1.4. La representación racional de End(T ) es equivalente a la suma
directa de la representación analı́tica y su compleja conjugada (extendidas a representaciones sobre C):
ρr ⊗ 1 (: EndQ (T ) ⊗ C → EndC (L ⊗ C) = EndC (V × V )) ≃C ρa ⊕ ρa
Demostración. Sea Π la matriz perı́odo de T con respecto a algunas bases de V
y L. Supongamos f ∈ End(T ). Si a y r son las matrices de ρa (f ) y ρr (f ) con respecto
a las bases dadas, la igualdad (1.1) implica que
6
1. TOROS ANALÍTICOS
(1.2)
Como P =
Π
Π
a 0
0 a
Π
Π
=
Π
Π
r.
es no singular, hemos demostrado la proposición.
Ejemplo 1.5. Continuando con el ejemplo 1.4, la ecuación correspondiente a (1.2)
queda de la forma siguiente.
i 0
1
i
1
i
0 −1
=
.
0 −i
1 −i
1 −i
1 0
Definición 1.5. Sea T = V /L un toro y S un subconjunto de T . Se dice que S es
un subtoro de T si existe un subespacio W de V y un reticulado M en W tal que
M ⊆ W ∩ L y tal que S = W/M.
Proposición 1.6. Sea f : T1 → T2 un homomorfismo de toros. Entonces
1. Im f es un subtoro de T2 , y
2. ker f es un subgrupo compacto de T1 . Su componente conexa que contiene a
0, denotada por (ker f )0 , es un subtoro de T1 , de ı́ndice finito en ker f .
Demostración. Para probar (1) notamos que V3 = F (V1 ) es un subespacio
vectorial de V2 . Consideremos ahora L3 = L2 ∩ F (V1 ): entonces L3 es discreto, pues
está contenido en L2 , y además genera a V3 como R espacio vectorial, pues contiene
a F (L1 ). Es claro que Im f = V3 /L3 .
Ahora probaremos (2): como ker f = f −1 (0T2 ), se tiene de inmediato que ker f es un
subgrupo cerrado de T1 , y por lo tanto compacto. Entonces tiene una cantidad finita
de componentes conexas, cada una compacta. Ası́ basta probar que (ker f )0 es un
subtoro de T1 para completar la demostración.
Como la representación analı́tica F de f es lineal, se tiene que V4 = F −1 (L2 )0 es un
subespacio vectorial de V1 . Es claro que (ker f )0 = V4 /L1 ∩ V4 ; además, de (ker f )0
compacto se sigue que L1 ∩ V4 es un reticulado en V4 , y por lo tanto (ker f )0 es un
subtoro de T1 .
Ejemplo 1.6. Para cada toro T = V /L y entero n 6= 0, el endomorfismo nT de T
definido en el Ejemplo 1.3 tiene como núcleo a los puntos de orden n de T , denotados
por T [n]. Nótese que T [n] ≈ (Z/nZ)2 .
Observación 1.1. Nótese que en general Im f no coincide con F (V1 )/F (L1 ). Por
ejemplo, sea F : C → C2 dada por F (z) = (nz, 0), para algún n ∈ N. Entonces F
induce un homomorfismo f : T = C/L → T2 = C2 /L × L para cualquier reticulado
L en C, y se tiene F (T [n]) = (0, 0) ⊆ L × L y F (C) ∩ (L × L) = L × {0} pero
F (L) = nL × {0}. Ası́ obtenemos F (C)/F (L) & F (C)/F (C) ∩ (L × L) = f (T ) para
n > 1.
1.3. ISOGENIAS
1.3.
7
Isogenias
Proposición 1.7. Si f : T1 → T2 es un homomorfismo de toros, entonces cualesquiera dos de las condiciones siguientes implica la tercera.
1. dim T1 = dim T2 ;
2. f es sobreyectiva;
3. ker f es finito.
Además, cualesquiera dos son equivalentes a que la representación racional de f sea
un isomorfismo.
Definición 1.8. Un homomorfismo de toros complejos f : T1 → T2 se dice una
isogenia si satisface las condiciones de la Proposición anterior.
Para una isogenia f se define el grado de f , gr f , como la cardinalidad de ker f y el
exponente de f , ef , como el exponente del grupo ker f : el menor entero positivo n tal
que nx = 0 para todo x ∈ ker f .
Observación 1.2. Continuando con el ejemplo 1.3, del hecho que su representación
racional sea un automorfismo de V obtenemos que nT es una isogenia de T en T ,
para n 6= 0. Además gr nT = n2 dim T y ef = |n|.
Que nT sea una isogenia tiene la importante consecuencia que T es divisible: para
cada t ∈ T y para cada n entero no cero, existe s ∈ T tal que ns = t. En particular,
si nF es subgrupo de H, con F y H subtoros de T , entonces F es subgrupo de H.
Ejemplo 1.7. Para cada subgrupo finito H de un toro T = V /L, podemos considerar
el grupo T /H y la proyección canónica p : T → T /H. Entonces T /H es un toro
complejo de la misma dimensión que T , pues si π : V → T denota la proyección
canónica, entonces se tiene que T /H = V /π −1 (H), y p es una isogenia con ker p = H.
Más aún, toda isogenia es claramente de este tipo, módulo isomorfismo.
Ejemplo 1.8. Sea V un espacio vectorial complejo y L1 , L2 dos reticulados en V tales
que L1 ⊆ L2 . Entonces la función identidad de V induce una isogenia f : V /L1 →
V /L2 , con ker f = L2 /L1 .
Más aún, toda isogenia es claramente de este tipo, módulo isomorfismo.
1
L
L
n
En este contexto, si T = V /L es un toro complejo entonces T [n] =
≈
y la
L
nL
isogenia nT se puede realizar como en el siguiente diagrama.
idV
V
/
isogenia
V /nL
/
V
mult. por n
V /L
/
isom. /
V
V /nL
Es claro que la composición de isogenias es una isogenia; el próximo resultado probará que las isogenias producen una relación de equivalencia entre toros.
8
1. TOROS ANALÍTICOS
Proposición 1.9. Sea f : T1 → T2 una isogenia y denotemos por e = ef su exponente.
Entonces existe una única isogenia g : T2 → T1 tal que g ◦ f = eT1 y f ◦ g = eT2 .
Demostración. Una demostración se basa en el siguiente diagrama.
T1
eT1
f
T2
/
eT2
g
~
T1
f′
/
T2
Paso 1: Como ker f ⊆ ker eT1 , existe un único homomorfismo g : T2 → T1 tal
que g ◦f = eT1 . Además se tiene que ker g ⊆ f (T1 [e]), pues T1 [e] = ker(g ◦f ) =
f −1 (ker g).
Paso 2: Como f (T1 [e]) ⊆ T2 [e] = ker eT2 , se sigue que ker g ⊆ ker eT2 , y por lo
tanto existe un homomorfismo f ′ : T2 → T1 tal que f ′ ◦ g = eT2 .
Pero f ′ ◦ eT1 = f ′ ◦ g ◦ f = eT2 ◦ f = f ◦ eT1 ; como eT1 es sobreyectiva se
sigue que f ′ = f .
“Otra”demostración es la siguiente.
Si f : V /L1 → V /L2 es inducida por la identidad de V , entonces eL1 ⊆ eL2 ⊆ L1 ⊆ L2
y el siguiente diagrama es conmutativo.
eT2
T1 = V /eL1
f
/
T2 = V /eL2
g
/
T1 = V /L1
f
6
/
(
T2 = V /L2
eT1
1.4.
Toros y Dualidad
Para cada toro T = V /L consideramos el espacio vectorial complejo (de dimensión
igual a dimC V )
Ω = HomC (V, C) = {h : V → C : h antilineal}
Entonces se tiene lo siguiente.
1. Hay un isomorfismo de R espacios vectoriales
Ω → HomR (V, R)
dado por h → Im h, con inversa k → h dada por h(v) = −k(iv) + ik(v).
1.4. TOROS Y DUALIDAD
9
2. Se sigue que la forma bilineal
h , i : Ω × V → R , hh, vi = Im h(v)
es no-degenerada.
3. Entonces
b = {h ∈ Ω : Im h(L) ⊆ Z}
L
es un reticulado en Ω.
b
b = Ω/L.
Definición 1.10. Para todo toro T = V /L se define el toro dual por X
Observación 1.3. Hay un homomorfismo sobreyectivo
Ω → Hom(L, S 1 ) , h → exp(2πihh, •i) = exp(2πi Im h(•))
b y por lo tanto Tb ≈ Hom(L, S 1 ).
cuyo núcleo es L,
Observación 1.4. Mediante la forma bilineal h , i anterior podemos identificar
b
b se idenHomC (Ω, C) con V . Como la forma es no-degenerada, se tiene además que L
b
tifica con L y por lo tanto Tb = T .
Definición 1.11. Si f : T1 → T2 es un homomorfismo de toros, con representación
analı́tica F : V1 → V2 y F (L1 ) ⊆ L2 , entonces podemos definir una función C−lineal
c2 ) ⊆ L
c1 .
F ∗ : Ω2 → Ω1 por F ∗ (h) = h ◦ F , que además satisface F ∗ (L
A su vez, ésta induce fb : Tb2 → Tb1 , el homomorfismo dual a f .
Proposición 1.12. Si f : T1 → T2 es una isogenia de toros, entonces fb : Tb2 → Tb1
también lo es.
Además se tiene ker(fb) ≈ Hom(ker f, S 1 ) y gr(fb) = gr(f ).
Demostración. Podemos suponer que f está inducida por la identidad de V y
que L1 ⊆ L2 como sigue.
V
idV
/
V
p1
p2
T1 = V /L1
f
/
T2 = V /L2
Dualizando obtenemos
Ωo
Tb1 ≈ Hom(L1 , S 1 ) o
idΩ
fb
Ω
Tb2 ≈ Hom(L2 , S 1 )
Ası́ fb es una isogenia y además ker(fb) ≈ ker(Hom(L2 , S 1 ) → Hom(L1 , S 1)) ≈
Hom(L2 /L1 , S 1 ) ≈ Hom(ker(f ), S 1 ).
10
1. TOROS ANALÍTICOS
Proposición 1.13. Para toda sucesión exacta de toros
/
0
f
T1
g
T2
/
T3
/
/
0
la sucesión dual
Tb1 o
0o
es exacta.
Tb2 o
fb
Tb3 o
gb
0
Demostración. De la hipótesis se sigue que la sucesión siguiente es exacta.
L1
/
0
ρr (f )
/
L2
ρr (g)
/
L3
/
0
Como ésta es una sucesión de grupos abelianos libres entonces escinde; i.e., existe
homomorfismo q : L3 → L2 tal que ρr (g) ◦ q = idL3 ; también L2 = ρr (f )(L1 ) ⊕ q(L3 ).
Pero entonces se puede probar que la siguiente sucesión inducida es exacta (y también
escinde).
0o
Hom(L1 , S 1 ) o
Hom(L2 , S 1 ) o
Hom(L3 , S 1 ) o
0
Corolario 1.14. Si T1 es un subtoro de T2 y si i : T1 ֒→ T2 denota la inclusión,
entonces bi : Tb2 → Tb1 tiene núcleo conexo y dim(ker bi) = dim T2 − dim T1 .
Demostración. Consideramos el toro complejo T3 = T2 /T1 y la proyección
canónica p : T2 → T3 . Entonces tenemos la sucesión exacta
/
0
T1
i
/
T2
p
/
T3
/
0
y por la proposición anterior su dual es exacta. Pero entonces ker(bi) = pb(Tb3 ), que es
conexo por ser la imagen de un conexo.
Corolario 1.15. Si f : T1 → T2 es un homomorfismo con núcleo finito (es decir,
una isogenia sobre su imagen), entonces el número de componentes conexas de ker fb
coincide con el grado de f .
En particular, si f es inyectiva entonces ker fb es conexo.
Demostración. Reescribimos f como la composición de una inyección i y una
isogenia f1 con ker f = ker f1 , como sigue.
f
T1
f1
/
f (T1 ) 
i
/
#
T2
Dualizando obtenemos el siguiente diagrama conmutativo.
1.4. TOROS Y DUALIDAD
Tb1 co
fb1
f[
(T1 ) o
fb
bi
11
Tb2
De aquı́ se sigue que si para cada x en ker fb1 escogemos un yx en bi−1 (x) entonces
•
[
(yx + ker bi)
ker fb = ker(fb1 ◦ bi) = bi−1 (ker fb1 ) =
x∈ker fb1
es la descomposición de ker fb en sus componentes conexas, ya que ker bi es conexo.
Como ker f = ker f1 , hemos probado el resultado.
CAPÍTULO 2
Variedades Abelianas
2.1.
Generalidades
Proposición 2.1. Sea V un espacio vectorial complejo. Entonces las siguientes condiciones son equivalentes:
1) Existe una forma E real bilineal y antisimétrica en V que satisface E(iv, iw) =
E(v, w) para todo v, w ∈ V .
2) Existe una forma Hermitiana H en V .
Demostración. Dada E como en 1), se define H por
H(v, w) = E(iv, w) + iE(v, w)
y dada H, se define E por
E = Im(H) . Definición 2.2. Supongamos que para un toro T = V /L existe una forma Hermitiana
H en V tal que Im H(L × L) ⊆ Z; equivalentemente, que existe una forma E real
alternante en V tal que E(iv, iw) = E(v, w) para todo v, w ∈ V y tal que E(L × L) ⊆
Z.
Entonces podemos definir la función C−lineal φH = φE : V → Ω por φH (v) = H(v, •).
b y por lo tanto se tiene un homomorfismo inducido
Se verifica que φH (L) ⊆ L
λH = λE : T → Tb
con representación analı́tica φH .
En este caso también se define K(λH ) = K(H) = K(E) = ker(λH ).
Observación 2.1. Nótese que bajo la identificación HomC (Ω, C) ≈ V mencionada
b
en la Observación 1.4 se tiene que φ∗H = φH y usando Tb = T obtenemos λc
H = λH .
Proposición 2.3. Para cada par (T = V /L, H) como en la definición 2.2 consideremos
b .
L(λH ) = L(H) = L(E) = {v ∈ V : Im H(v, L) ⊆ Z} = φ−1 (L)
H
Entonces se tiene K(H) = L(H)/L.
13
14
2. VARIEDADES ABELIANAS
Corolario 2.4. Sea T = V /L un toro para el cual existe una forma Hermitiana H
definida en V tal que Im H(L × L) ⊆ Z.
Entonces las siguientes condiciones son equivalentes
1. H es no-degenerada;
2. det(Im H|L×L ) 6= 0
3. φH es un isomorfismo:
4. λH es una isogenia;
5. |K(H)| es finito;
b
6. [φ−1
H (L) : L] es finito;
7. [L(H) : L] es finito.
Si cualesquiera de estas condiciones vale, entonces
b
|K(H)| = gr(λH ) = [φ−1
H (L) : L] = [L(H) : L] = det(Im H|L×L ) .
2.2.
Polarizaciones
Definición 2.5. Un toro T = V /L es una variedad abeliana (v.a.) si
1. existe H forma Hermitiana en V (respectivamente E forma real alternante en
V tal que E(iv, iw) = E(v, w) para todo v, w ∈ V ),
2. con (Im H)(L × L) ⊂ Z (respectivamente E(L × L) ⊂ Z) y
3. además se satisface cualesquiera de las condiciones del Corolario 2.4.
En ese caso se dice que H o E o λH es una polarización de T .
El par (T, H) o (T, E) o (T, λH ) se llama una variedad abeliana polarizada (v.a.p.:
variedad abeliana polarizada).
Ejemplo
2.1.Con g = 1 y L = {n + mτ : n, m ∈ Z} , donde ℑτ > 0 , se tiene
0 1
vw
E=
y H(v, w) = ℑτ
.
−1 0
De esta manera vemos que todo toro de dimensión uno es una variedad abeliana
polarizada. Esto no es válido para dimensiones mayores (ver Ejemplos 2.3 y 2.4).
Definición 2.6. Si T1 es un toro complejo, (T2 , H) es una variedad abeliana polarizada y f : T1 → T2 es un homomorfismo con ker f finito, entonces podemos definir una
polarización en T1 por f ∗ (H)(v1 , v2 ) = H(ρa (f )(v1 ), ρa (f )(v2 )). Equivalentemente,
definimos λf ∗ (H) = fb ◦ λH ◦ f y se tiene que el siguiente diagrama conmuta.
T1
λf ∗ (H)
/
TbO 1
fb
f
T2
λH
/
Tb2
Esta polarización se llama la polarización inducida por f .
2.2. POLARIZACIONES
15
Definición 2.7. Un homomorfismo entre variedades abelianas polarizadas (T1 , H1 )
y (T2 , H2 ) es un homomorfismo f : T1 −→ T2 de toros complejos tal que H1 = f ∗ (H2 ).
Equivalentemente, si λf ∗ (H2 ) = λH1 .
Nótese que entonces ker f es finito, ya que H1 es no-degenerada.
Definición 2.8. Si (T, E) es una variedad abeliana polarizada, con T = V /L , entonces existe una base de L con respecto a la cual la matriz de E se escribe
0 D
E=
−D 0


d1 0 0
donde D =  0 . . . 0  , donde los dj son enteros positivos (independientes de
0 0 dg
la base escogida) tales que di | di+1 para todo i en {1, . . . , g − 1}. Una tal base se
llama simpléctica.
La secuencia (d1 , d2, . . . , dg ) se llama el tipo de la polarización.
Definición 2.9. Una descomposición en suma directa L = L1 ⊕ L2 se llama una
descomposición de L para E (o para H) si L1 y L2 son isotrópicos para la forma
alternada E: i.e., si E(l, m) = 0 para l y m simultáneamente en L1 o en L2 .
Siempre existe una tal descomposición: si f1 , . . . , f2g es una base simpléctica para L,
basta tomar L1 = hf1 , . . . fg i y L2 = hfg+1 , . . . f2g i. Al revés, para toda descomposición
de L = L1 ⊕ L2 para E existe una base simpléctica f1 , . . . , f2g tal que L1 = hf1 , . . . fg i
y L2 = hfg+1 . . . f2g i.
Una descomposición V = V1 ⊕ V2 en subespacios reales se llama una descomposición
de V para E (o para H) si (V1 ∩ L) ⊕ (V2 ∩ L) es una descomposición de L para
E. Una tal descomposición de V es claramente una descomposición en subespacios
vectoriales isotrópicos maximales. No al revés.
Es claro que las descomposiciones de L y de V para E están en biyección.
Proposición 2.10. Sea (T = V /L, H) una variedad abeliana polarizada de tipo
(d1 , d2, . . . , dg ) y sea L = L1 ⊕ L2 una descomposición de L para E, con respectiva descomposición V = V1 ⊕ V2 de V para E.
Entonces se tiene.
1. L(H) = L(H)1 ⊕ L(H)2 , donde L(H)i = Vi ∩ L(H).
2. K(H) = K1 ⊕ K2 , donde Ki = L(H)i /Li .
3. Ki ≈ ⊕gj=1 Z/dj Z para cada i = 1, 2.
Observación 2.2. Nótese que en este caso se tiene
K(E) ≈ (Z/d1 Z)2 × . . . × (Z/dg Z)2 y eλE = dg .
También se tiene que K(E) es isotrópico en K(dg E).
16
2. VARIEDADES ABELIANAS
Definición 2.11. El exponente de una polarización E (o de la variedad abeliana
polarizada (T, E)) es el exponente eλE = dg de la isogenia λE .
Una polarización E se llama principal, y se dice que la variedad abeliana (T, E) es
variedad abeliana principalmente polarizada (v.a.p.p.), si su exponente es 1; equivalentemente, si λE : T → Tb es un isomorfismo.
Proposición 2.12.
1. Todo subtoro de una variedad abeliana es una variedad
abeliana.
2. Todo toro isógeno a una variedad abeliana es una variedad abeliana.
3. Si un toro T es una variedad abeliana entonces su toro dual Tb es una variedad
abeliana, llamada la variedad abeliana dual, con la misma polarización.
Demostración.
1. Se restringe la forma Hermitiana.
2. Ver Definición 2.6.
3. Ver Observación 2.1.
Definición 2.13. Si (T, λH ) es una variedad abeliana polarizada de exponente dg ,
entonces sabemos que λc
H = λH . Sin embargo, podemos definir otra polarización en
b
Tb, λTb : Tb → Tb = T , como la única isogenia tal que λTb ◦ λH = (dg )T , que sabemos
existe por la Proposición 1.9.
Definición 2.14. Una subvariedad abeliana (polarizada) de una variedad abeliana
polarizada (T, λH ) es un par (S, λi∗ (H) ), donde S es un subtoro de T , i : S ֒→ T la
inclusión y λi∗ (H) la polarización inducida en S por la polarización de T . El exponente
de la subvariedad abeliana se define como el exponente de la polarización inducida:
eλi∗ (H) .
2.3.
Teorı́a del descenso
Una pregunta natural es la siguiente. Dada una variedad polarizada (X, λH ) y una
isogenia f : X → Y , cuándo existe una polarización en Y que induzca la polarización
dada en X?.
Notemos primero la siguiente caracterización.
Proposición 2.15. Sea f : X = V /LX → Y = W/LY una isogenia de toros, con
F : V → W su representación analı́tica, y sea EX una polarización en X.
Entonces las siguientes condiciones son equivalentes.
1. Existe una polarización EY en Y tal que EX = f ∗ (EY ).
2. EX (F −1 (LY ), F −1(LY )) ⊂ Z.
Ahora veremos una noción relacionada, que también será de mucha utilidad.
Definición 2.16. Sea (T = V /L, E) una variedad abeliana polarizada. Se define la
forma de Weil asociada a la polarización como la forma
eE : K(E) × K(E) → S 1
2.3. TEORÍA DEL DESCENSO
17
dada por eE ([v1 ], [v2 ]) = exp (2πiE(v1 , v2 )), donde v1 y v2 denotan elementos de L(E)
y [vi ] su respectiva clase en K(E) = L(E)/L.
Observación 2.3. Nótese que eE es una forma alternante multiplicativa: satisface
1
1. eE ([v2 ], [v1 ]) = E
,
e ([v1 ], [v2 ])
2. eE ([v1 ] + [v3 ], [v2 ]) = eE ([v1 ], [v2 ])eE ([v3 ], [v2 ]).
Ejemplo 2.2. Si E = dE0 donde E0 es una polarización principal con base simpléctica
f
{f1 , . . . , f2g }, entonces L(E) está generado por fd1 , . . . , d2g y eE queda determinado
por

2πi

si j = g + i
exp( d )
f
f
j
i
E
2πi
,
= exp(− d ) si i = g + j
e

d
d
1
si no.
La demostración del siguiente resultado es inmediata, por la misma definición de
polarización inducida.
Lema 2.17. Sea f : T → S una isogenia y E una polarización en S.
Entonces
ef
∗ (E)
(x, y) = eE (f (x), f (y))
para todo x, y ∈ f −1 (K(E)) .
Definición 2.18. Si E es una polarización en T y F es un subgrupo de K(E), se
define el ortogonal de F con respecto a E como sigue.
F ⊥ = {y ∈ K(E) : eE (y, x) = 1 para todo x ∈ F }
= {y ∈ K(E) : E(y, x) ∈ Z para todo x ∈ F }
Ahora podemos agregar otra condición equivalente en la Proposición 2.15.
Proposición 2.19. Otra condición equivalente a las de la Proposición 2.15 es la
siguiente.
(3) ker f es un subgrupo isotrópico de K(EX ), con respecto a eEX : es decir, se
tiene ker f ⊂ K(EX ) y eEX |ker f ×ker f = 1.
Proposición 2.20. Sea f : T → S una isogenia y E una polarización en S. Como
siempre, denotamos por f ∗ (E) la polarización inducida en T .
Entonces f induce un isomorfismo de
(ker f )⊥
→ K(E) ;
ker f
equivalentemente, si x ∈ K(f ∗ (E)), entonces x ∈ (ker f )⊥ ⇐⇒ f (x) ∈ K(E).
Además se tiene las siguientes igualdades.
18
2. VARIEDADES ABELIANAS
|K(f ∗ (E))|
|ker f |2
|K(f ∗ (E))|
= |K(E)||ker f |
|(ker f )⊥ | =
|ker f |
|K(E)| =
Demostración. Una manera de probar estos resultados es la siguiente.
Supongamos que la isogenia f está inducida por la identidad de V , con T = V /L,
S = V /M y L ⊂ M.
c/L ⊂ K(f ∗ (E)) = L/L
b
c/M.
Entonces ker f = M/L, (ker f )⊥ = M
y K(E) = M
Ahora basta notar que la siguiente sucesión horizontal es exacta
0
/
ker f = M/L  /
c/L
(ker f )⊥ = M
_
y que
/
c
K(E) = M/M
/
0
b
K(f ∗ E) = L/L
∗
|(ker f )⊥ |
b:M
c] = |K(f (E))| .
= |ker f | = [M : L] = [L
|K(E)|
|(ker f )⊥ |
Juntando todos estos resultados más el de que el cuociente de una vap por un grupo
finito es una vap ([M1]) obtenemos
Teorema 2.21. Sea (X, EX ) una variedad abeliana polarizada.
Supongamos que existe un subgrupo (finito) U de K(EX ) que es isotrópico con respecto
a EX .
Entonces existe una variedad abeliana polarizada (Y, EY ) isógena a X cuya polarización induce la de X.
Además se tiene
|K(EX )|
U⊥
∼
|K(EY )| =
y K(EY ) =
|U|2
U
Demostración. Basta considerar la isogenia f : X → Y = X/U.
Corolario 2.22. Sea (X, EX ) una variedad abeliana polarizada.
Supongamos que existe un subgrupo (finito) U de K(EX ) que es isotrópico con respecto
a EX y tal que |U|2 = |K(EX )|.
Entonces la variedad abeliana X/U es principalmente polarizada y su polarización
induce la de X.
2.5. POLARIZACIONES Y MATRICES PERÍODO
2.4.
19
Forma real de una variedad abeliana polarizada
En esta sección seguimos la notación e ideas de [Ri].
Definición 2.23. Supongamos que A = (T = V /L, E) es una variedad abeliana
polarizada. Entonces la equivalencia natural L ≈ H1 (T, Z) induce un isomorfismo
lineal V ≈ H1 (T, R).
Llamamos la forma real de la variedad abeliana polarizada A a H1 (T, R)/H1 (T, Z);
b
entonces H 1 (T, R)/H 1 (T, Z) es la forma real natural de la variedad abeliana dual A.
Definición 2.24. Para cada U subconjunto de V definimos
U ⊥ = {v ∈ V : E(v, u) ∈ Z para todo u ∈ U}
Entonces se tiene
H1 (T, Z)⊥
K(E) =
H1 (T, Z)
Observación 2.4. Nótese que un homomorfismo f : A → B de variedades abelianas
polarizadas induce funciones f1 y f2 en homologı́a y cohomologı́a, respectivamente;
b → A.
b
entonces f2 es la forma real del homomorfismo dual fb : B
2.5.
Polarizaciones y Matrices Perı́odo
Ahora estudiaremos la relación entre variedades abelianas polarizadas y las respectivas
matrices perı́odos Π.
Proposición 2.25. Sea T = V /L un toro analı́tico, con bases v1 , . . . , vg de V y
f1 , . . . , f2g de L.
Π
Denotemos por Π la matriz perı́odo de T con respecto a estas bases y por P =
.
Π
Sea J una matriz 2g × 2g con coeficientes enteros y determinante uno.
Entonces las siguientes condiciones son equivalentes:
1. J es la matriz de una forma E tal que (T, E) es una v.a.p.p.
2.
0 −H
−1 ′
′
iP J P =
H
0
donde H es Hermitiana positiva definida.
′
3. ΠJ −1 Π′ = 0 y −iΠJ −1 Π es Hermitiana positiva definida.
0 I
Corolario 2.26. Sea (T, E) una v.a.p.p. , Π = Π1 Π2 , J =
. En−I 0
tonces
1. Π2 Π′1 − Π1 Π′2 = 0y
2. −i Π1 Π′2 − Π2 Π′1 es positiva definida.
En particular, Π1 y Π2 son no singulares.
20
2. VARIEDADES ABELIANAS
Corolario 2.27. Sea (T, E)una v.a.p.p. Entonces existen bases de V y L con respecto
0 I
a las cuales J =
y Π = I Z , donde
−I 0
′
1. Z = Z y
2. Im Z es positiva definida.
Demostración.Sea f1 , . .
. , f2g una base de L con respecto a la cual la matriz de
0 I
; sea v1 , . . . , vg una base de V y sea Π3 = Π1 Π2
E está dada por J =
−I 0
la matriz perı́odo con respecto a estas bases. Como Π1 es invertible por el corolario
anterior, se tiene que Π = Π−1
1 Π3 es matriz perı́odo de T con respecto a las bases
f1 , . . . , f2g de L y f1 , . . . , fg de V y satisface las condiciones dadas.
Ejemplo 2.3. No todo toro analı́tico es una v.a.p.p. Sabemos que si g = 1 todo
toro analı́tico es v.a.p.p.; sin embargo,este resultado
no esválido para dimensiones
√
√
1 0 √−2 √−5
, entonces el toro C2 /L,
mayores: por ejemplo, si g = 2, y Π =
−3
−7
0 1
donde L es el reticulado generado por las columnas de Π no es una v.a.p.p.; en efecto,
si existiese una matriz J que satisficiera la proposición, llegarı́a mos a encontrar una
relación de dependencia algebraica entre los coeficientes de Π.
Proposición 2.28. Sea T = V /L un toro y f : T → Tb un homomorfismo con
representación analı́tica F : V → Ω.
Las siguientes condiciones son equivalentes.
1. f = λH para alguna forma Hermitiana H en V ;
2. la forma H : V × V → C dada por H(v, w) = F (v)(w) es Hermitiana.
Corolario 2.29. Sea T = V /L un toro y f : T → Tb una isogenia con representación
analı́tica F : V → Ω.
Las siguientes condiciones son equivalentes.
1. f es una polarización de T ;
2. la forma H : V × V → C dada por H(v, w) = F (v)(w) es Hermitiana definida
positiva.
Ahora probaremos un resultado que no es cierto para toros cualesquiera (ver el Ejemplo 2.4).
Teorema 2.30 (de Reducibilidad de Poincaré). Sea (T, H) una variedad abeliana
polarizada y sea S un subtoro de T . Entonces existe un subtoro R de T tal que T =
S + R y tal que S ∩ R es finito.
Demostración. Supongamos que S = W/M, con W subespacio de V y M ⊆
W ∩ L, con M reticulado en W .
Como W/W ∩ L ≈ W L/L ⊆ V /L, se obtiene que W/W ∩ L es un compacto y por lo
tanto [W ∩ L : M] es finito.
2.5. POLARIZACIONES Y MATRICES PERÍODO
21
Definamos U = W ⊥H = {v ∈ V : H(v, w) = 0 ∀ w ∈ W }
Entonces se tiene
1. W ∩ U = {0} y V = W ⊕ U.
2. U = W ⊥E , pues si E(v, w) = 0 ∀ w ∈ W entonces E(iv, w) = E(v, −iw) =
0 ∀ w ∈ W y se sigue que H(v, w) = E(iv, w) + iE(v, w) ∀ w ∈ W , de donde
W ⊥E ⊆ W ⊥H . El converso es claro.
3. También se tiene que U = (W ∩ L)⊥E , pues si escogemos una base
w
. . . , w2 dim W de W ∩ L entonces cada w ∈ W se escribe como w =
P12, dim
W
ri wi , con ri reales. Además, si v ∈ (W ∩ L)⊥E entonces E(v, w) =
P2i=1
dim W
ri E(v, wi) = 0 y se sigue que (W ∩ L)⊥E ⊆ W ⊥E . El converso es
i=1
obvio.
4. Del punto anterior se concluye que U ∩ L tiene rango maximal en U, y por lo
tanto R = U/U ∩ L es un subtoro de T y T = S + R.
5. Además (W ∩ L) ⊕ (U ∩ L) es de ı́ndice finito en L, de donde S ∩ R es finito.
Observación 2.5. Este teorema puede reformularse en términos de variedades
abelianas como sigue.
Si (S, λi∗ (H) ) es una subvariedad abeliana de (T, H) entonces existe una subvariedad
abeliana (R, λj ∗ (H) ) de (T, H) tal que T es isógena a S × R. Las dos variedades
abelianas se dicen complementarias. Nótese que es una relación simétrica.
En otras palabras, si i : S ֒→ T y j : R ֒→ T denotan las respectivas inclusiones y
λi∗ (H) y λj ∗ (H) las respectivas polarizaciones inducidas entonces el diagrama siguiente
conmuta
S

i
λi∗ (H)
/
T o
j
? _R
λj ∗ (H)
λH
Sb o
bi
Tb
b
j
/
b
R
Además se tiene que la aplicación f : S × R → T dada por f (s, r) = i(s) + j(r) es
una isogenia con núcleo S ∩ R.
Ejemplo 2.4. Consideremos
el toro T = C2 /L, con L el reticulado generado por
√
(1, 0), (0, 1), (0, i), ( 2, i) y el subtoro S = C × {0}/M, con M el reticulado generado
por (1, 0), (0, i).
Entonces no existe un subtoro R de T tal que T sea isógeno a S × R. En particular,
no existe ninguna polarización en T .
Ejemplo 2.5. En general, un par de subvariedades abelianas complementarias puede
tener distintos exponentes.
22
2. VARIEDADES ABELIANAS
Por ejemplo, supongamos que (T1 , H1 ) y (T2 , H2 ) son v.a.p.p.’s, y consideremos T =
T1 × T2 , con polarización H1 ⊕ 2H2 . Entonces T1 × {0} y {0} × T2 son subvariedades
abelianas complementarias, con respectivos exponentes 1 y 2.
Más adelante (ver Proposición 3.2) veremos que subvariedades complementarias en
una v.a.p.p. tienen el mismo exponente.
Definición 2.31. Una variedad abeliana se dice simple si las únicas subvariedades
abelianas son ella misma y el cero; equivalentemente, si no es isógena a un producto
de variedades abelianas de dimensión positiva.
El siguiente resultado sigue del teorema de Reducibilidad de Poincaré por inducción
sobre la dimensión de A.
Teorema 2.32 (de Reducibilidad Completa de Poincaré). Dada una variedad
abeliana A, existe una isogenia A → An1 1 × . . . Anr r , donde cada Ai es una variedad
abeliana simple.
Más aún, las variedades Ai y los enteros ni son únicos módulo isogenia y permutaciones.
CAPÍTULO 3
Variedades Abelianas principalmente polarizadas
En este capı́tulo nos concentraremos en las v.a.p.p.
Recordemos que para una v.a.p.p. A se tiene que λA es un isomorfismo, y que un
automorfismo de A es un endomorfismo f invertible (automorfismo) del toro tal que
fb ◦ λA ◦ f = λA ; en otras palabras, se tiene el siguiente diagrama conmutativo.
A
f
/
A
λA
λA
bo
A
fb
b
A
e dada por φE (v) = H(v, •) es un isomorfismo y que
También se tiene que φE : V → Ω
b
φE (L) = L.
En la notación de la sección 2.4, notemos que para una v.a.p.p. se tiene
L⊥ = L, pues
P2g
⊥
si λ1 , . . . , λ2g es una base simpléctica de L y v ∈ L entonces v = j=1 aj λj ; pero
ak = E(v, λg+k ) ∈ Z para 1 ≤ k ≤ g y ak = E(λk−g , v) ∈ Z para g + 1 ≤ k ≤ 2g.
3.1.
Complementos ortogonales
Definición 3.1. Sea (A, λA ) una v.a.p.p. Denotemos por i : X ֒→ A la inclusión de
un subtoro.
Sabemos (por Corolario 1.14) que entonces ker bi es conexo y que dim ker bi = dim A −
dim X.
Podemos definir otro subtoro de A (el complemento ortogonal de X con respecto a
λA ) por
b
P = P (X, A, λA ) = λ−1
A (ker i)
Nótese que dim P = dim A − dim X.
Sea j la inclusión de P en A. Denotaremos por λX y λP las polarizaciones inducidas
por λA en X y P respectivamente, de manera que el siguiente diagrama es conmutativo.
23
24
3. VARIEDADES ABELIANAS PRINCIPALMENTE POLARIZADAS
X

i
λX
/
Ao
j
? _P
λA
bo
X
λP
bi
b
A
b
j
/
Pb
Se sigue de la definición que bi ◦ λA ◦ j = 0, y dualizando obtenemos b
j ◦ λA ◦ i = 0. Por
−1
b
b
lo tanto i(X) = λ−1
(ker
j),
pues
claramente
i(X)
⊆
λ
(ker
j)
y
ambos
toros tienen
A
A
la misma dimensión.
Observación 3.1. Se tiene K(λX ) = X ∩ i−1 (j(P )) ≈ X ∩ P ≈ P ∩ j −1 (i(X)) =
K(λP ), pues x ∈ X ∩ i−1 (j(P )) si y sólo si se tiene i(x) = j(p) ∈ j(P ) ∩ i(X) y
λA (i(x)) = λA (j(p)) ∈ ker bi ∩ ker b
j si y sólo si p ∈ P ∩ j −1 (i(X)).
Nótese que, si suponemos dim X ≥ dim P = r, y si la polarización λP es de tipo
(d1 , . . . , dr ), entonces se sigue que λX es de tipo (1, . . . , 1, d1, . . . , dr ).
En particular, hemos probado el siguiente resultado.
Proposición 3.2. Si X y P son subtoros complementarios ortogonales de A entonces
X y P tienen el mismo exponente como subvariedades abelianas.
Proposición 3.3. Si X y P son toros complementarios ortogonales de una v.a.p.p.
A entonces
f : X × P → A , f (x, p) = i(x) + j(p)
es una isogenia, con núcleo ker f = {(x, −x) : x ∈ X ∩ P }.
Además, si denotamos por λX×P la polarización inducida en X × P por λA , se tiene
que λX×P es la polarización producto λX × λP y por lo tanto K(λX×P ) = K(λX ) ×
K(λP ).
Demostración. Notemos primero que se satisface lo siguiente.
bi ◦ λA ◦ i bi ◦ λA ◦ j
λX 0
b
=
λX×P = f ◦ λA ◦ f = b
0 λP
j ◦ λA ◦ i b
j ◦ λA ◦ j
De aquı́ se sigue que λX×P es la polarización producto λX ×λP (en particular, isogenia)
y por lo tanto K(λX×P ) = K(λX ) × K(λP ) es un grupo finito.
Además es claro que ker f = {(x, −x) : x ∈ X ∩ P } y que este es un subgrupo
(maximal isotrópico) de K(λX×P ), por lo tanto finito.
CAPÍTULO 4
Curvas y Variedades de Prym generalizadas
e y C dos superficies de Riemann compactas de géneros e
Sean C
g y g respectivamente,
e
y f : C → C un cubrimiento (posiblemente ramificado) de grado d.
b los Jacobianos principalmente polarizados de C y C,
e λ)
e
Denotaremos por (J, λ) y (J,
respectivamente.
Entonces f induce dos homomorfismos entre estos Jacobianos, dados por
J
OC (D)
f∗
/
/
Je
OCe (f −1 (D))
Je
e
OCe (D)
Nm f
/
/
J
e
OC (f (D))
Si recordamos la definición y consecuencias de la forma real de una variedad abeliana
polarizada (c.f. Sección 2.4), se tiene que Nm f : Je → J es f1 , la inducida por f
en homologı́a. También notemos que la polarización principal de cada Jacobiano es
inducida por la forma de intersección como forma bilineal anti-simétrica en H1 (•, Z),
y que H1 (•, Z)⊥ = H1 (•, Z), de acuerdo a lo observado al comienzo del capı́tulo 3.
Además, si f2 es la inducida por f en cohomologı́a, se puede definir f ∗ : J → Je
b−1 ◦ f2 ◦ λ, y resulta ser la adjunta de Nm f con respecto a la forma de
como f ∗ = λ
e R) se tiene
intersección: para todo c ∈ H1 (C, R) y e
c ∈ H1 (C,
h c, Nm f (e
c) iC = h f ∗ (c), e
c iCe
e → C es un cubrimiento de grado d, entonces se tiene
Proposición 4.1. Si f : C
1.
2.
3.
Nm f ◦ f ∗ = dJ
e ◦ f ∗ ◦ λ−1 o, equivalentemente, λ ◦ Nm f = fb∗ ◦ λ
e
[f = λ
Nm
∗
(ker Nm f )0 = (ker(f ◦ Nm f ))0 .
Nótese que 1) y 2) son equivalentes a la conmutatividad del siguiente diagrama.
25
26
4. CURVAS Y VARIEDADES DE PRYM GENERALIZADAS
dJ
J
f∗
/
Je
Nm f
/%
J
e
λ
λ
Jb
λ
[f
Nm
/
b
Je
∗
fc
/
Jb
La siguiente caracterización de la inyectividad de f ∗ (c.f. [L-B, p. 337]) nos será útil.
e → C, el
Proposición 4.2. Dado un cubrimiento de superficies de Riemann f : C
e no es inyectivo si y sólo si f factoriza via
homomorfismo inducido f ∗ : JC → J C
′
un cubrimiento cı́clico no-ramificado f de grado ≥ 2 como en el siguiente diagrama
conmutativo.
e?
C
?
??
??
??
f
f ′′
C′
/C
?



 ′
 f
′
Observación 4.1. De la demostración de esta proposición se deduce que ker f ∗ es
′′
cı́clico de orden igual al grado de f ′ ; por lo tanto si f ∗ es inyectiva, entonces ker f ∗
′′
es cı́clico de orden igual al grado de f ′ . Si f ∗ no es inyectiva, se puede factorizar
nuevamente, y ası́ concluimos que ker f ∗ es finito.
4.1.
Variedades de Prym
e → C de grado d, definimos la variedad
Definición 4.3. Para un cubrimiento f : C
de Prym del cubrimiento por
e 0
e
P = P (f ) = P (C/C)
= (ker(fb∗ ◦λ))
e → C un cubrimiento de superficies de Riemann de grado d.
Teorema 4.4. Sea f : C
e en f ∗ (J) y en P ,
Denotamos por λ̃f ∗ (J) y por λ̃P las polarizaciones inducidas por λ
respectivamente.
Entonces se tiene.
1. P = (ker Nm f )0 = (ker(f ∗ ◦ Nm f ))0 ;
e f ∗ (J)); i.e., P es el complemento ortogonal del subtoro f ∗ (J) de
e λ,
2. P = P (J,
la p.p.a.v. (Je, e
λ);
3. la polarización en J inducida por λ̃f ∗ (J) via f ∗ es dλ y H0 := ker f ∗ ⊂ J[d] es
isotrópico con respecto a la forma de Weil asociada a dλ;
4.1. VARIEDADES DE PRYM
27
4. f ∗ induce un isomorfismo de H0⊥ /H0 a ker(λf ∗ J ) = ker(λP ) = f ∗ J ∩ P ⊂
P [d] , donde la ortogonalidad es con respecto a la forma multiplicativa antisimétrica edλ en J[d], y
J[d]
∗
f J ∩ P = .
ker f ∗ 2
5. Consideremos la isogenia
φ : J × P → Je , φ(c, c̃) = f ∗ (c) + c̃
y la proyección sobre el primer factor π1 : J × P → J. Sea H1 = π1 (ker φ).
Entonces ker φ = {(c, −f ∗ (c)) : c ∈ J[d] y f ∗ (c) ∈ P } es isomorfo a H1 ;
además, H1 = H0⊥ y
J[d]
⊥
ker φ = H1 = H = 0
ker f ∗ .
e 0 =
Demostración.
1. De la proposición 4.1 tenemos que (ker(fb∗ ◦λ))
(ker(λ ◦ Nm f ))0 = (ker(Nm f ))0 .
La otra igualdad sigue también de la proposición 4.1.
2. Denotamos por i : f ∗ (J) → Je y por j : P = P (f ) → Je las respectivas
inclusiones, por f1 : J → f ∗ (J) la isogenia tal que f ∗ = i ◦ f1 y consideramos
el diagrama siguiente (f1 es isogenia pues ker f ∗ = ker f1 y ker f ∗ es finito por
la Observación 4.1).
f∗
J
f1
/
f ∗ (J)
i
"
/
Je o
j
P
e
λ
Jb bo
fb1
∗ (J) o
f\
fc∗
bi
b
Je
b
j
/
Pb
b
De la demostración del corolario 1.15 sabemos
que (ker fb∗ )0 = ker
i.
e−1 (ker fb∗ )0 = λ
e−1 ker bi =
Entonces se tiene P = (ker(fb∗ ◦e
λ))0 = λ
ee
P (J,
λ, f ∗ (J)).
3. El diagrama de más arriba también muestra que la polarización inducida en J
ef ∗ (J) via f1 está dada por fb1 ◦ λ
ef ∗ (J) ◦ f1 = fb1 ◦ bi ◦ λ
e ◦ i ◦ f1 = fb∗ ◦ λ
e ◦ f∗ =
por λ
λ ◦ Nm f ◦ f ∗ = d λ.
4. Ahora podemos completar el diagrama anterior con las polarizaciones inducidas.
28
4. CURVAS Y VARIEDADES DE PRYM GENERALIZADAS
f∗
f1
J
/
f ∗ (J)
i
λf ∗ (J )
dλ
Jb bo
fb1
/
Je o
j
P
e
λ
"
∗ (J) o
f\
λP
bi
∗
fc
b
Je
/
b
j
Pb
Ahora se sigue de la teorı́a de descenso (c.f. [MB] p. 117) que f1 : J → f ∗ J
induce un isomorfismo de H0⊥ /H0 a ker(λf ∗ J ) y que H0⊥ = f1−1 (ker λf ∗ J ). Pero
ya sabemos (Observación 3.1) que ker(λf ∗ J ) = ker(λP ) = f ∗ J ∩ P . Notemos
ahora que y ∈ f ∗ J ∩ P si y sólo si y pertenece a P e y = f ∗ (x) para algún
x ∈ J. Pero entonces 0 = Nm f (y) = Nm f (f ∗ (x)) = dx.
La demostración de la igualdad siguiente concluye la prueba de (4).
H0 =
(4.1)
J[d]
H ⊥ 0
Esta igualdad es inmediata si consideramos la isogenia f1 definida en la demostración de (2) como dada por J = V /L y f ∗ J = V /M, con L ⊂ M
reticulados en V , y notamos que H0 = M/L, K(λf ∗ J ) = M ⊥ /M, H0⊥ =
M ⊥ /L ⊆ J[d] = K(d λ) = L⊥ /L, y que el ı́ndice de L en M es igual al ı́ndice
de M ⊥ en L⊥ , ya que de la sucesión exacta siguiente
0
/
H0 = M/L 
/
⊥
H0⊥ = M
 _ /L
/
K(λf ∗ J ) = M ⊥ /M
/
0
J[d] = K(d λ) = L⊥ /L
obtenemos |H0 | =
|J[d]|
|H0⊥ |
= [M : L] = [L⊥ : M ⊥ ] =
|K(λf ∗ J )|
|H0⊥ |
5. Es claro que ker φ ⊂ J[d] × P [d] y por lo tanto φ es una isogenia. También
es claro que s : H1 = π1 (ker φ) → ker φ definida por s(c) = (c, −f ∗ (c)) es
una sección de π1 en H1 (π1 ◦ s = IdH1 ); se sigue que π1 : ker φ → H1 es un
isomorfismo.
Pero también vale
H1 = {c ∈ J : f ∗ (c) ∈ P } = (f ∗ )−1 (f ∗ J ∩ P ) = H0⊥ .
4.1. VARIEDADES DE PRYM
29
Por lo tanto ker φ = H0⊥ , lo que junto con la igualdad (4.1) completa
la demostración de (5) y del Teorema.
e → C un cubrimiento de curvas de grado d. Entonces el número
Lema 4.5. Sea f : C
de componentes conexas de ker Nm f es igual a la cardinalidad de ker f ∗ .
En particular, si d es primo y f es ramificado, o si d es primo y f no es un cubrimiento
cı́clico, entonces ker Nm f es conexo.
Demostración. Como f ∗ y Nm f son duales, podemos aplicar el Corolario 1.15
para concluir que el número de componentes conexas de ker Nm f es la cardinalidad
de ker f ∗ .
Los casos particulares mencionados implican que f ∗ es inyectiva, por la Proposición
4.2, y el resultado sigue.
El siguiente resultado es evidente y útil.
Lema 4.6. Supongamos que A, B, C son grupos y
h=g◦f
f
g
/C
A /B
son homomorfismos, donde f y g tienen núcleo finito.
Entonces h tiene núcleo finito y además se tiene:
1. ker h = f −1 (f (A) ∩ ker g)
2.
ker h = ker f f (A) ∩ ker g El próximo resultado muestra la relación entre la variedad de Prym de un cubrimiento
que factoriza y las variedades de Prym de los cubrimientos intermedios.
Proposición 4.7. Sean f : X → Y y g : Y → Z dos cubrimientos de curvas y sea
h = g ◦ f : X → Z.
Entonces hay dos isogenias naturales dadas como sigue.
y
ps : P (Y /Z) × P (X/Y ) → P (X/Z) , ps(y, x) = f ∗ y + x
ψ : JZ × P (Y /Z) × P (X/Y ) → JX , ψ(z, y, x) = h∗ z + f ∗ y + x .
Además se tiene
i) El núcleo de ps está contenido en P (Y /Z)[deg f ] × P (X/Y )[deg f ], y su cardinalidad está dada por la expresión siguiente
g ∗ (JZ) ∩ ker f ∗ ker ps = P (Y /Z)[deg f ]
.
ker f ∗ 30
4. CURVAS Y VARIEDADES DE PRYM GENERALIZADAS
ii) El núcleo de ψ tiene cardinalidad
JZ[deg h]P (Y /Z)[deg f ]
JY [deg f ] JZ[deg g]
ker ψ = .
ker f ∗ ker g ∗ =
ker f ∗ ker g ∗ Demostración.
Paso 1: Primero probaremos que la imagen de ps está contenida en P (X/Z).
Sean x en P (X/Y ) e y en P (Y /Z). Entonces
Nm h(ps(y, x)) = Nm h(x) + Nm h(f ∗ y)
= Nm g(Nm f (x)) + Nm g(Nm f (f ∗ y))
= Nm g(0) + Nm g((deg f ) y)
= (deg f ) Nm g(y) = 0 ,
lo que muestra que ps(P (Y /Z) × P (X/Y )) ⊂ ker Nm h. Pero como P (Y /Z) ×
P (X/Y ) es conexo y contiene a (0, 0) se sigue que ps(P (Y /z) × P (X/Y )) ⊂
(ker Nm h)◦ = P (X/Z).
Paso 2: Ahora veamos que el núcleo de ps está contenido en P (Y /Z)[deg f ] ×
P (X/Y )[deg f ].
Como se tiene que f ∗ y + x = 0 para (y, x) ∈ ker ps, entonces 0 =
Nm f (f ∗ y) + Nm f (x) = (deg f ) y, de donde y ∈ P (Y /Z)[deg f ]. Ası́ obtenemos ker ps ⊂ {(y, −f ∗y) : y ∈ P (Y /Z)[deg f ]}, lo que demuestra la primera
parte de i).
Paso 3: ψ es una isogenia.
Del Teorema 4.4 se deduce que tenemos isogenias
α : JY × P (X/Y ) → JX , (y, x) → f ∗ y + x ,
y
β : JZ × P (Y /Z) → JY , (z, y) → g ∗ z + y ,
γ : JZ × P (X/Z) → JX , (z, x) → h∗ z + x
cuyos respectivos núcleos tienen los tamaños siguientes:
JY [deg f ] JZ[deg g] JZ[deg h]
ker α = ker f ∗ , ker β = ker g ∗ , ker γ = ker h∗ .
Del siguiente diagrama conmutativo
JZ × P (Y /Z) × P (X/Y )
(β, idP (X/Y ) )
/ JY × P (X/Y )
WWWW
WWWWW ψ
WWWW
α
(idJ Z , ps)
WWWWW
WWWW
WW+ γ
/ JX
JZ × P (X/Z)
4.2. CUBRIMIENTOS GALOIS Y VARIEDADES DE PRYM
31
obtenemos que ψ es una isogenia.
Paso 4: el cálculo para los núcleos.
También se deduce del último diagrama que
ker ψ = ker ps ker γ = ker α ker β .
Por lo tanto
JY [deg f ] JZ[deg g]
JZ[deg h]
ker ψ = ker ps ker h∗ = ker f ∗ ker g ∗ y para completar la demostración sólo necesitamos calcular ker ps.
La última igualdad implica que
ker h∗ JY [deg f ] JZ[deg g]
ker ps =
JZ[deg h]
ker f ∗ ker g ∗ .
JY [deg f ] JZ[deg g] P (Y /Z)[deg f ] y que ker h∗ =
=
Pero es claro que
JZ[deg h]
g ∗ −1 (g∗ (JZ) ∩ ker f ∗ ), de donde se sigue que ker h∗ = ker g ∗ g ∗(JZ) ∩
ker f ∗ .
4.2.
Cubrimientos Galois y Variedades de Prym
e → C es Galois; i.e., que existe un subgrupo G
Supongamos que el cubrimiento f : C
e tal que C = C/G
e
del grupo de automorfismos C
y tal que f es la proyección canónica.
Para cada g ∈ G denotamos por el mismo sı́mbolo g el automorfismo inducido por g
e por hgi el subgrupo de G generado por g, y por JeH el conjunto de puntos fijos
en J,
e para cada subgrupo H de G.
de H en J,
e → C es Galois con grupo G, se define la
Definición 4.8. Si el cubrimiento f : C
P
e
e
norma de grupo Nm G : J → J como el endomorfismo Nm G = g∈G g.
Los siguientes resultados son inmediatos.
e → C = C/G
e
Proposición 4.9. Sea f : C
un cubrimiento de Galois con grupo G de
orden d y denotemos por P = P (f ) la correspondiente variedad de Prym.
Entonces se tiene.
i) f ∗ (J) = (JeG )0 y JeG = f ∗ (J) + P0 , donde P0 = P ∩ JeG ⊂ P [d] ∩ JeG [d] .
ii) Además, f ∗ ◦ Nm f = Nm G, y
iii) P = (ker Nm f )0 = (ker Nm G)0 .
e → C = C/G
e
Corolario 4.10. Sea f : C
un cubrimiento de Galois con grupo G y
denotemos por P = P (f ) la correspondiente variedad de Prym, con la polarización
inducida λP .
32
4. CURVAS Y VARIEDADES DE PRYM GENERALIZADAS
Entonces G es subgrupo del grupo de automorfismos de la variedad abeliana polarizada (P, λP ) y también de la variedad abeliana polarizada (f ∗ (J), λf ∗ (J) ). Esta última
e
acción corresponde a la componente de la representación trivial en Te (J).
Además la isogenia φ : J × P → Je del Teorema 4.4 es G−equivariante; i.e.,
φ(gx, gp) = gφ(x, p) para todo g ∈ G.
Demostración. Sea g ∈ G; como P = (ker Nm G)0 , entonces g(P ) ⊂ ker Nm G.
Pero g(P ) es conexo, contiene a 0 y tiene la misma dimensión que P . Ası́ G preserva
el toro P .
Pero además la polarización de P se obtiene por restricción de la polarización de Je,
que es preservada por G.
e → C es un cubrimiento doble dado por la involución
Corolario 4.11. Si f : C
e→C
e y si P denota la correspondiente variedad de Prym, entonces
σ:C
Jeh σi = f ∗ J + P [2]
Demostración. De la Proposición 4.9 i) sabemos que Jeh σi = f ∗ J + P0 , donde
P0 = Jeh σi ∩ P ⊂ P [2].
Como σ es una involución, es claro que P [2] ⊂ Jeh σi y el resultado sigue.
El siguiente resultado aparece en [Rec-Ro]; su corolario nos será muy útil.
e → C = C/G
e
Lema 4.12. Sea f : C
un cubrimiento de Galois de grado d, sea H un
e
e
e
subgrupo de G y denotemos por h : C → C/H
y por g : C/H
→ C los correspondientes
cubrimientos, como en el diagrama siguiente.
e
C/H
e
tC
tt
h ttt
t
tt
ty t
f
JJ
JJ g
JJ
JJ
J$
e
C = C/G
Sea {g1 H, g2 H, . . . , gr H} un conjunto completo de representantes de las co-clases de
H en G.
Entonces
r
X
1. Nm G = (
gi ) ◦ Nm H, y
2.
r
X
i=1
i=1
e
gi (h∗ (z)) = f ∗ (Nm g(z)) para todo z ∈ J(C/H).
4.2. CUBRIMIENTOS GALOIS Y VARIEDADES DE PRYM
33
Demostración. La primera igualdad es evidente.
La segunda sigue de la primera, pues f ∗ ◦ Nm g ◦ Nm h = f ∗ ◦ Nm f = Nm G =
r
r
X
X
e → J(C/H)
e
gi ) ◦ h∗ ◦ Nm h y además se tiene que Nm h : J C
es
gi ◦ Nm H = (
i=1
i=1
sobreyectiva.
Corolario 4.13. Bajo las hipótesis del Lema 4.12,
h (P (g)) = {x ∈ JeH :
∗
r
X
i=1
gi (x) = 0}◦ .
Demostración. Denotemos por A el lado derecho de la igualdad que demostraremos.
Paso 1: h∗ (P (g)) está contenido en A. De la Proposición 4.9 i) sabemos que
e
h∗ (J(C/H))
es la componente conexa que contiene a cero de JeH , y por lo
tanto h∗ (P (g)) está contenido en JeH .
Si z ∈ P (g), entonces Nm f (h∗ z) = |H| Nm g(z) = 0; i.e. h∗ (P (g)) ⊂
ker Nm f . Por la Proposición 4.9 ii) sabemos que ker
! Nm f ⊂ ker Nm G, y
X
X
X
k , de donde Nm G|Je H =
p=
gi
además tenemos que Nm G =
p∈G
|H|
X
i
i
gi ; por lo tanto h∗ (P (g)) ⊂ ker |H|
k∈H
X
i
!
gi . Como P (g) es conexo,
obtenemos que h∗ (P (g)) ⊂ A.
X
Paso 2: Al revés, sea x ∈ A. Entonces x is H−invariant y
gi (x) = 0.
i
!
X
X
X
Entonces Nm G(x) =
gi
k (x) = |H|
gi (x) = 0; aplicando
i
k∈H
i
la Proposición 4.9 iii) y sabiendo que A es conexo, se obtiene que A ⊂
(ker Nm f )◦ .
X Por lo tanto Nm h(A) ⊂ (ker Nm g)◦ = P (g). Pero entonces |H|A =
k(A) = h∗ (Nm h(A)) ⊂ h∗ (P (g)) y hemos probado la afirmación.
k∈H
4.2.1. Cubrimientos Galois no ramificados. En esta sección seguiremos las
ideas de [Ri].
e → C = C/G
e
Sea f : C
un cubrimiento cı́clico no ramificado.
34
4. CURVAS Y VARIEDADES DE PRYM GENERALIZADAS
Entonces los homomorfismos inducidos en π1 y en H1 inducen el siguiente diagrama conmutativo, donde c denota el subgrupo conmutador, y donde todas las filas y
columnas son exactas.
(4.2)
0
0
0
e p)c
π1 (C,
/
0
e p)
π1 (C,
/
0
L
/
e Z)
H1 (C,
0
/
H1 (C, Z)
0
/
π1 (C, f (p))
/
K
π1 (C, f (p))c
/
/
0
/
/
/
0
/
0
/
0
H
G
G1
0
Persiguiendo el diagrama se obtiene Gc ≈ H/K y
e p)) /f (π1 (C,
e p)c )
L ≈ K ≈ π1 (C, f (p))c ∩ f (π1 (C,
Ası́ G1 ≈ G/Gc es el cuociente maximal abeliano de G.
De ahora en adelante supondremos (en esta sección) que G es abeliano. Entonces
e p)).
G = G1 , H = K y π1 (C, f (p))c ⊂ f (π1 (C,
Ahora utilizaremos la notación de la sección 2.4.
e Z)); entonces Λ es un subreticulado de H1 (C, Z), con cuociente
Sea Λ = f (H1 (C,
H1 (C, Z)/Λ ≈ G. Además, Λ⊥ es un reticulado en H1 (C, R) que contiene a H1 (C, Z) =
H1 (C, Z)⊥ , y, como la forma de intersección es no degenerada, hay un isomorfismo
b = Hom(G, S 1 ) (los caracteres de G).
natural de Λ⊥ /H1 (C, Z) al grupo dual de G: G
Observación 4.2. Nótese que en la construcción recién hecha hemos logrado exhibir
b como un subgrupo de J.
G
Más generalmente se tiene el siguiente resultado (c.f. [Ri, p. 63]).
Proposición 4.14. Hay una biyección entre los cubrimientos abelianos no ramificab → JC.
dos de C con grupo de Galois G y las inyecciones G
4.2. CUBRIMIENTOS GALOIS Y VARIEDADES DE PRYM
35
Observación 4.3. Nótese que también se obtiene una manera de construir el cubrimb entonces cada hj se puede representar como 1 γj
iento: si h1 , . . . , hk es una base de G,
nj
para algún nj entero positivo y algún γj ∈ H1 (C, Z).
e (es decir,
Entonces un lazo α ∈ π1 (C, f (p)) se levanta a una curva cerrada en p en C
e p))) si y sólo si hα, γj iC ≡ 0 mod nj para todo j.
pertenece a f (π1 (C,
También se tiene lo siguiente (c.f. [A]).
b = ker f ∗ .
Lema 4.15. G
Demostración. Nótese que λ ∈ Λ⊥ si y sólo si hλ, αiC ∈ Z para todo α ∈ Λ si
e Z). Pero
y sólo si hλ, Nm f (β)iC = hf ∗ (λ), βiCe pertenece a Z para todo β ∈ H1 (C,
∗
⊥
e Z) = H1 (C,
e Z).
esto último es claramente equivalente a f (λ) ∈ H1 (C,
Observación 4.4. Nótese que hemos mostrado también que f ∗ (J) es un subtoro de
Je con forma real H1 (C, R)/Λ⊥ , y que la forma real de la inclusión de f ∗ (J) en Je es
e R).
f : H1 (C, R) → H1 (C,
También se tiene
K(λf ∗ (J) ) = {α ∈ H1 (C, R) : hf ∗ (α), f ∗(γ)iCe ∈ Z para todo γ ∈ Λ⊥ }/Λ⊥
Pero
hf ∗ (α), f ∗(γ)iCe = hα, Nm f (f ∗ (γ))iC = dhα, γiC
Por lo tanto
b⊥dλC /G
b
K(λf ∗ (J) ) = (Λ⊥ )⊥dλC /Λ⊥ = (Λ⊥ )⊥dλC /Λ / Λ⊥ /Λ = G
Además se tiene (del Diagrama (4.2)) que la forma real de P = P (f ) es L ⊗ R/L.
Como G preserva L y la polarización de Je, se obtiene que G se restringe a un grupo
de automorfismos e la variedad polarizada P .
e → C = C/G
e
Proposición 4.16. Sea f : C
un cubrimiento cı́clico no ramificado.
G
G
∗
e
e
Entonces J es conexo; i.e., J = f J.
Demostración. Supongamos que f es de grado d y sea α un generador del grupo
G que define el cubrimiento; entonces
JeG = ker(1 − α) .
e y C, entonces se tiene que
Si denotamos por e
g y por g los respectivos géneros de C
g = dg + 1 − d.
e
Se sigue de [F] (ver Figura 1) que para un cubrimiento cı́clico no ramificado existen
e1 , . . . , λ
e2eg } de H1 (C,
e Z) y {λ1 , . . . , λ2g } de H1 (C,
e Z) tales que
bases simplécticas {λ
36
4. CURVAS Y VARIEDADES DE PRYM GENERALIZADAS
λ 2g-2
λg
λ g-1
λ1
λ
g
λ 1 + (d-1)(g-1)
λ d(g-1)
Figura 1
eeg ) = λg y Nm f (λ
e2eg ) = dλ2g ;
1. Nm f (λ
d−1
X
ei+j(g−1) para i ∈ {1, . . . , g − 1} y para i ∈ {e
2. f ∗ (λi ) =
λ
g + 1, . . . , e
g + g − 1};
j=0
y además
3.
α
u
e
λi
α
/
ei+g−1
λ
α
/
e
λi+2(g−1)
α
/
...
/
α
ei+(d−1)(g−1)
λ
para i ∈ {1, . . . , g − 1} y para i ∈ {e
g + 1, . . . , e
g + g − 1}.
1
Dicho de otra manera, podemos suponer que ker f ∗ está generado por λ2g .
d
Pero entonces
ker(1 − α) = f ∗ (J)
eeg , λ
e2eg ,
= hλ
d−1
X
j=0
ei+j(g−1) : i ∈ {1, . . . , g −1} ∪{e
λ
g + 1, . . . , e
g + g −1}i
Supongamos que f es de grado d y sea α un generador del grupo G que define el
cubrimiento; entonces JeG = ker(1 − α). Que L esté en ker(1 − α) quiere decir que
existe un isomorfismo φ : L → α(L).
Pero entonces (α−1 φ)d es un automorfismo de L, y por lo tanto igual a una constante
√
c distinta de cero; ajustando la constante, obtenemos un isomorfismo φ1 = d c de L
4.2. CUBRIMIENTOS GALOIS Y VARIEDADES DE PRYM
37
en si mismo de orden d. Por lo tanto G actúa en L; i.e., G es linealizable y se sigue
de [M2] que entonces L está en f ∗ J.
CAPÍTULO 5
Estructura real
5.1.
Variedades abelianas y su estructura real
En este capı́tulo consideraremos la estructura real asociada a una variedad abeliana
principalmente polarizada A de género g, dada por (T = V /L, H).
Definición 5.1. Sea A una variedad abeliana principalmente polarizada de género
g, dada por (T = V /L, H), con bases v1 , . . . , vg de V y f1 , . . . , f2g de L; Π denota la
matriz perı́odo.
Entonces la estructura real asociada a A está dada por el par
(R2g /Z2g , φ), donde R2g /Z2g es un toro real de dimensión 2g y φ : R2g −→ V
es la función dada por φ(x) = Πx, con x un vector columna en R2g y Πx las
coordenadas de φ(x) con respecto a la base dada de V .
Nótese que entonces x = P
−1
z
z
.
En el toro real asociado a cada estructura
real
hay una estructura compleja, dada por
iIg
0
R = P −1 ◦ M ◦ P , donde M =
.
0 −iIg
Se tiene el siguiente
Lema 5.2 (Siegel). Si R es la estructura compleja canónica de una estructura real,
entonces se tiene:
a) R2 = −I2g ,
b) R′ J es real positiva definida y
c) R′ J + iJ en M(2g × 2g, R) es la matriz de H con respecto a la base de L,
donde J es la matriz de la forma alternada E = Im(H).
Ejemplo 5.1. género uno
Para τ = r + it, φ : R2−→ C está dada
por z = φ(x) = x1 + τ x2 = x1 + rx2 + itx2 y
2
2 − rt − r +t
t
R está dada por R =
.
1
r
t
t
39
40
5. ESTRUCTURA REAL
5.2.
Automorfismos y estructura real
Recordemos que para un automorfismo f de una variedad abeliana principalmente
polarizada tenemos una representación analı́tica a = ρa (f ) en M(g × g, C) y una
representación racional r = ρr (f ) en M(2g × 2g, Z).
Como sabemos, estas dos matrices están relacionadas por
a 0
P = P r.
0 a
Se tiene el siguiente
Lema 5.3. Bajo las condiciones mencionadas, Rr = rR.
Demostración.
−1
r Rr = (P
= P
−1
−1
a 0
0 a
a 0
0 a
= P −1 MP
= R.
−1
−1
P )(P
M
−1
MP )(P
a 0
0 a
−1
a 0
0 a
P)
P
Bibliografı́a
[A]
R. D. M. Accola, Riemann surfaces, Theta-functions, and abelain automorphism groups,
Lecture Notes in Mathematics 483. Springer-Verlag, Berlin, 1973.
[F]
J. D. Fay, Theta functions on Riemann surfaces, Lecture Notes in Mathematics 352.
Springer-Verlag, Berlin, 1973.
[L-B] H. Lange and C. Birkenhake, Complex Abelian Varieties, Grundlehren der Mathematischen
Wissenschaften 302. Springer-Verlag, Berlin, 1992.
[MB] L. Moret-Bailly, Familles de courbes et des variétés abéliennes sur P1 , Asterisque 86 (1981),
109–124.
[M1]
D. Mumford, Abelian Varieties, Oxford University Press, 1970.
[M2]
D. Mumford, Prym Varieties I, Contributions to analysis (a collection of papers dedicated
to Lipman Bers), pp. 325–350. Academic Press, New York, 1974.
[Rec-Ro] S. Recillas and R. E. Rodrı́guez, Jacobians and Representations of S3 , Aportaciones Mat.
13 (1998), 117–140.
[Ri]
J. Ries, The Prym variety for a cyclic unramified cover of a hyperelliptic Riemann surface,
J. Reine Angew. Math. 340 (1983), 59–69.
41
Parte 2
Grupos Kleinianos y Variedades Abelianas
Resumen. Esta parte tiene por objeto dar algunas ideas básicas sobre grupos discretos de automorfismos holomorfos y antiholomorfos de la esfera de Riemann y
sus relaciones con variedades abelianas. En el capı́tulo 6 se introducirán conceptos
básicos como: discontinuidad, discretitud, superficies de Klein y su conexión con geometrı́a hiperbólica tres dimensional. Luego usaremos este tipo de grupos para mirar
algunas conexiones con variedades abelianas. La primera conexión será dada en el
capı́tulo 7 donde daremos una versión de grupos Kleinianos del teorema de Torelli que dice que las superficies de Riemann están determinadas por sus variedades
abelianas (Jacobianas). En el capı́tulo 8 veremos la segunda conexión; el uso de
uniformizaciones por grupos de Schottky de superficies de Riemann. En particular,
miraremos aquellas superficies de Riemann que admiten una reflexión con puntos
fijos y veremos como uniformizarlas por grupos de Schottky que preservan cı́rculos
Euclideanos. El hecho que estas superficies pueden ser uniformizadas por este tipo
de grupos es un resultado de B. Maskit [Maskit3]. Luego recordaremos algunas
observaciones de Burnside [Burnside] para ver como utilizar tales grupos para calcular en forma explı́cita sus matrices de Riemann. En el capı́tulo 9 estudiaremos
las superficies de Riemann maximal simétricas. Esta superficies son definidas por
el hecho de tener una reflexión con puntos fijos tal que el grupo de automorfismos
que conmutan con ella es maximal. Miraremos los géneros bajos y calcularemos sus
matrices de Riemann usando las herramientas del segundo capı́tulo. En el capı́tulo
10 miraremos algunas propiedades de variedades hiperbólicas tres-dimensionales en
forma muy superficial.
Como existen muchas referencias clásicas y nuevas en torno al tópico de grupos Kleinianos, superficies de Riemann, geometrı́a hiperbólica, no intentaremos
mostrar en demasiado detalle estos tópicos. Una buena lista de libros que el lector
puede revisar como parte complementaria importante a estas notas son por ejemplo:
[Abikoff], [Benedetti-Petronio], [Beardon], [Farkas-Kra], [Ford], [Maskit1],
[Ractliffe].
CAPÍTULO 6
Grupos Kleinianos
6.1.
Superficies de Klein
Denotemos por H = {z ∈ C : Im(z) ≥ 0}, la clausura Euclideana del semiplano
superior H = {z ∈ C : Im(z) > 0}.
Una superficie de Klein es un espacio topológico Hausdorff X, segundo numerable,
junto a una colección da coordenadas (un atlas dianalı́tico) F = {(Uj , zj ) : j ∈ J}
donde
(1) Uj es un abierto de X, para todo j ∈ J;
(2) zj : Uj → zj (Uj ) ⊂ H es un homeomorfismo sobre el abierto zj (Uj ) de H, para
todo j ∈ J;
(3) Si Uj ∩ Uk 6= ∅, para j, k ∈ J, entonces zk zj−1 : zj (Uj ∩ Uk ) → zk (Uj ∩ Uk ) es
una función analı́tica o antianalı́tica (es decir, son la restricción de una función
analı́tica o antianalı́tica en el sentido usual).
Una superficie real X para la cual su sistema de cartas sólo tienen cambios de coordenadas funciones analı́cas (un atlas analı́tico) es llamada una superficie de Riemann.
Aquellos puntos p de la superficie de Klein X que tienen una coordenada (Uj , zj ) ∈ F
tal que p ∈ Uj y zj (p) ∈ R, son llamados puntos de la frontera de X. El borde de X,
denotado por ∂X, es la unión de tales puntos. Luego, nuestra definición de superficie
de Klein permite tener bordes.
Ejercicio.
1.- Verificar que toda superficie de Klein es una variedad real de dimensión dos
(es decir, una superficie real) con estructura real analı́tica.
2.- Verificar que toda superficie de Riemann es una superficie orientable.
3.- Suponiendo que no hay puntos en el borde en una superficie de Klein, mostrar
que basta con suponer que la imágenes zj (Uj ) sean abiertos del plano complejo.
6.2.
Ejemplo de Superficie de Klein
(1) Todo subconjunto abierto Ω del plano complejo es una superficie de Klein.
En este caso, un atlas analı́tico es dado por F = {(Ω, I)}, donde I(z) = z,
obteniendo ası́ una superficie de Riemann. Observemos que si usamos el atlas
F = {(Ω, I), (Ω, J)}, donde J(z) = z, entonces tenemos un atlas dianalı́tico.
45
46
6. GRUPOS KLEINIANOS
b La esfera de Riemann C
b es la variedad compleja
(2) La esfera de Riemann C.
de dimensión compleja uno (luego, una superficie de Riemann) obtenida por
compactificación del plano complejo C, es decir, el conjunto C ∪ {∞} con la
topologı́a generada por los abiertos usuales en C y los conjuntos de la forma
K ∪ {∞}, donde K recorre los subconjuntos compactos de C, y las cartas
b − {0}, J : V ) → C : z → 1 ).
complejas (U = C, I : U → C : z → z) y (V = C
z
Podemos considerar una proyección estereográfica
b → S 2 = {u, v, w) ∈ R3 : u2 + v 2 + w 2 = 1},
Q:C
definida por
Q(∞) = (0, 0, 1)
2y
x2 + y 2 − 1
2x
,
,
,
Q(z) =
x2 + y 2 + 1 x2 + y 2 + 1 x2 + y 2 + 1
donde x = Re(z) e y = Im(z).
b → S 2 es un homeomorfismo holomorfo, es
Ejercicio. Verificar que Q : C
decir, preserva orientación y ángulos.
b es una superficie de Riemann homeomorfa, por Q : C
b→
De esta manera, C
2
S a la esfera real dos dimensional S . Usando esta proyección estereográfica
b la métrica esférica de S 2 , la cual denotaremos por dS 2 .
podemos inducir en C
2
Ejercicio. Verificar que para todo r > 0 existe una constante positiva k tal
que
1
dE (z1 , z2 ) ≤ dS 2 (z1 , z2 ) ≤ kdE (z1 , z2 ),
k
para todo z1 , z2 ∈ Br (0) = {z ∈ C : |z| < r}.
Si agregamos la coordenada (C, J(z) = z) al atlas anterior, entonces obtenemos un atlas dianalı́tico.
(3) Curvas Hiperelı́pticas. Sean a1 ,..., a2g+1 puntos diferentes en el plano complejo.
2g+1
3
2
S = {[u : v : w] ∈ P : v w
2g−1
=
Y
j=1
(u − aj w)}
es una superficie de Riemann. Coordenadas son dadas por:
(a) Si w0 6= 0 and u0 /w0 6= aj , entonces tomemos
z([u : v : w]) = u/w
(b) Si w0 6= 0 y u0 /w0 = aj , entonces tomamos
q
z[u : v : w] = u/w − aj
6.3. AUTOMORFISMOS DE SUPERFICIES DE KLEIN
47
(c) Si w0 = 0, entonces tomamos
p
z[u : v : w] = w/u
(4) Consideremos una superficie de Riemann R (posiblemente con borde) junto
a un atlas analı́tico F = {(Uj , zj ) : j ∈ J}. Entonces podemos considerar un
nuevo atlas analı́tico G = {(Uj , wj ) : j ∈ J}, donde wj = zj . Si juntamos
estos dos atlases, entonces obtenemos un atlas dianalı́tico para R. Este es un
ejemplo de una superficie de Klein que es orientable. Recı́procamente, si X es
una superficie de Klein orientable con atlas dianalı́tico F , entonces siempre
es posible extraer de tal atlas dos atlases analı́ticos que la transforman en
superficies de Riemann [Alling-Greenleaf].
(5) Consideremos la relación de equivalencia en el plano complejo dada por
z∼
= w si y sólo si existe n ∈ Z tal que
z + n,
si n es par
w=
z + n, si n es impar
Consideremos el cociente S = C/ ∼
= definido por la relación de equivalencia
anterior y denotemos por P : C → S la proyección natural. Si damos a S de
la topologı́a cociente, entonces es fácil verificar que P resulta ser continua,
abierta y un cubrimiento universal. El grupo cobertor es dado por el grupo
cı́clico generado por la pseudo-translación T (z) = z + 1. Usando inversas
locales de P uno obtiene un atlas para S que es dianalı́tico. Esta superficie de
Klein es la banda de Möbius.
6.3.
Automorfismos de Superficies de Klein
Consideremos dos superficies de Klein X1 y X2 . Una función continua F : X1 → X2
tal que F (∂X1 ) ⊂ ∂X2 , es llamada una función dianalı́tica en el punto p ∈ X1 si
existen coordenadas locales (U, z) para X1 con p ∈ U y (V, w) para X2 con F (U) ⊂ V
tal que
wF z −1 : z(U) → C
es complejo analı́tica o complejo antianalı́tica. Si la función es dianalı́tica en cada
punto de X1 , entonces decimos que F es una una función dianalı́tica. Dos superficies
de Klein son dianalı́ticamente equivalentes si existe un homeomorfismo entre ellas que
es dianalı́tico como también su inversa.
Ejercicio. Sean X1 y X2 superficies de Klein y F : X1 → X2 una función.
(1) Mostrar que si la función F : X1 → X2 es dianalı́tica en un punto p ∈ X1 ,
entones existe un abierto W en X1 , p ∈ W , tal que F es dianalı́tica en W .
(2) Concluir de lo anterior que si tanto X1 com X2 son superficies de Riemann,
entonces el conjunto de puntos de X1 donde F es analı́tica es un subconjunto abierto y cerrado (concluir lo mismo del conjunto de puntos donde F es
antianalı́tica)
48
6. GRUPOS KLEINIANOS
(3) Usar lo anterior para deducir que si X1 y X2 son superficies de Riemann,
entonces en cada componente conexa de X1 toda función dianalı́tica F : X1 →
X2 debe ser analı́tica o antianalı́tica.
Un automorfismo dianalı́tico F : X → X de una superficie de Klein X es por definición un homeomorfismo que es dianalı́tico.
Ejercicio. Verificar que la inversa de un automorfismo dianalı́tico es necesariamente
dianalı́tico.
En el caso que X es una superficie de Riemann, entonces uno puede definir o automorfismos analı́ticos o automorfismos holomorfos (respectivamente, o automorfismos
antianalı́ticos o automorfismos antiholomorfos) si en coordenadas locales siempre es
analı́tica (respectivamente, antianalı́tica).
Ejercicio. Suponga que S es una superficie de Riemann conexa y sea F : S → S
un automorfismo dianalı́tico. Verifique que F es un automorfismo holomorfo o un
automorfismo antiholomorfo. ¿Qué pasa si la superficie de Riemann no es conexa?
6.4.
Automorfismos del Disco Unitario
Consideremos la superficie de Riemann dada por el disco unitario
∆ = {z ∈ C : |z| < 1}
Es claro que la función J(z) = z es un automorfismo antiholomorfo de ∆, luego sólo
necesitamos calcular los automorfismos holomorfos de esta superficie. Por otro lado,
para cada α ∈ ∆ y para cada θ ∈ R tenemos que la función
Tθ,α (z) = eθi
z−α
1 − αz
es un automorfismo holomorfo de ∆.
Sea F un automorfismo holomorfo del disco ∆ y sea F (0) = α. Entonces Q = T0,α F
es automorfismo holomorfo del disco ∆ tal que Q(0) = 0. Usando el lema de Schwarz
tanto para Q como para Q−1 obtenemos que
|Q(z)| ≤ |z| |Q−1 (w)| ≤ |w|
para todo z, w ∈ ∆. Luego obtenemos que |Q(z)| = |z|, para todo z ∈ ∆. Usando de
nuevo el lema de Schwarz obtenemos que Q(z) = eθi z y, en particular,
F = Tθ,αe−θi
En resumen, todo automorfismo holomorfo de ∆ es de la forma
Tθ,α (z) = eθi
z−α
1 − αz
6.5. AUTOMORFISMOS DE LA ESFERA DE RIEMANN
49
y todo automorfismo antiholomorfo de ∆ es de la forma
z−α
Tθ,α (z) = eθi
1 − αz
Ejercicio. Calcular los automorfismos holomorfos y antiholomorfos del semiplano
superior de Poincaré
H = {z ∈ C : Im(z) > 0}
6.5.
Automorfismos de la Esfera de Riemann
b →C
b de la forma
Una transformación de Möbius es una función T : C
az + b
T (z) =
,
cz + d
donde
a b
∈ SL(2, C).
c d
b →C
b de la forma
Una transformación extendida de Möbius es una función T : C
az + b
,
T (z) =
cz + d
donde
a b
∈ SL(2, C).
c d
e al grupo genDenotaremos por M al grupo de transformaciones de Möbius y por M
erado por M y las transformaciones extendidas de Möbius, es decir, generado por M
y la conjugación J(z) = z.
Ejercicio. Verificar que toda transformación de Möbius es un automorfismo holomorfo de la esfera de Riemann y que toda transformación extendida de Möbius es un
automorfismo antiholomorfo de esta.
El siguiente resultado complementa el ejercicio anterior:
Proposición 6.1. Todo automorfismo holomorfo (respectivamente, antiholomorfo)
de la esfera de Riemann es una transformación de Möbius (respectivamente, transformación extendida de Möbius).
Demostración. Como la composición de un automorfismo antiholomorfo con la
conjugación J(z) = z resulta ser un automorfismo holomorfo, basta con verificar que
todo automorfismo holomorfo es una transformación de Möbius. Para esto, supongb →C
b es un automorfismo holomorfo. Conjugando por la izquierda
amos que F : C
con una transformación de Möbius, si es necesario, podemos asumir que F (0) = 0 y
50
6. GRUPOS KLEINIANOS
F (∞) = ∞. Luego F : C → C es una función entera. Si miramos su desarrollo en
serie de potencia alrededor de 0, tenemos que
F (z) = a1 z + a2 z 2 + · · ·
Como F (∞) = ∞, tenemos que G(z) = F (1/z) es una función meromorfa inyectiva.
Luego 0 = a2 = a3 = · · · . Esto dice que
F (z) = a1 z
es decir una transformación de Möbius.
Usando el hecho que todo automorfismo holomorfo y antiholomorfo del plano complejo
es extendible continuamente a un homeomorfismo de la esfera de Riemann (fijando el
punto al infinito), obtenemos que estos coinciden con los automorfismos de la esfera
de Riemann que fijan ∞. Esto nos da el siguiente resultado.
Corolario 6.2. Todo automorfismo holomorfo (respectivamente, antiholomorfo) del
plano complejo C es una transformación de Möbius de la forma T (z) = az + b,
donde a 6= 0 (respectivamente, una transformación extendida de Möbius de la forma
T (z) = az + b, donde a 6= 0).
Ejercicios.
(1) Toda transformación de Möbius, diferente de la identidad, tiene a lo más dos
puntos fijos.
(2) Si T es una transformación de Möbius con exactamente un punto fijo, entonces
esta es conjugada en M a la transformación P (z) = z +1. En este caso diremos
que T es una transformación parabólica.
(3) Si T es una transformación de Möbius con exactamente dos puntos fijos, entonces esta es conjugada en M a una transformación de la forma L(z) = λeiθ z,
con λ ≥ 1. Si λ = 1, entonces decimos que T es una transformación elı́ptica.
En caso contrario, decimos que T es una transformación loxodrómica. Una
transformación loxodrómica para el cual eiθ = 1 es también llamada una
transformación hiperbólica.
(4) El conjunto de puntos fijos de toda es transformación extendida de Möbius es
o bién vacı́o, un puntos, dos puntos o un cı́rculo.
(5) Si C es un cı́rculo en la esfera de Riemann, entonces existe una reflexión JC
e entonces T (C) sigue
cuyo cı́rculo de puntos fijos es C. Deducir que si T ∈ M,
siendo un cı́rculo en al esfera de Riemann [Ind. Como todo cı́rculo C en la esfera
de Riemann es la imágen por una transformación de Möbius T del eje real
b y la composición JC = T JT −1 es de nuevo una involución
compactificado R,
antiholomorfa, donde J(z) = z, obtenemos que JC es reflexión con C como
conjunto de puntos fijos].
6.6. RAZONES CRUZADAS
51
(6) Verificar que no pueden haber dos reflexiones diferentes con el mismo cı́rculo
de puntos fijos.
(7) Toda transformación extendida de Möbius S es conjugada por una transformación de Möbius a una de las siguientes:
(7.1) T (z) = z + 1, si S tiene sólo un punto fijo. En este caso, decimos que S
es una transformación pseudo-parabólica;
(7.2) T (z) = λeiθ z, λ > 1, si S sólo tiene dos puntos fijos. En este caso, decimos
que S es una transformación pseudo-hiperbólica;
(7.3) T (z) = z, si S tiene un cı́rculo de puntos fijos. Decimos que S es una
reflexión;
(7.4) T (z) = eiθ /z, donde eiθ 6= 1, si S no tiene puntos fijos. Decimos que S es
una transformación pseudo-elı́ptica.
(8) Todo automorfismo holomorfo o antiholomorfo de la esfera de Riemann es
composición de reflexiones.
(9) Dos transformaciones de Möbius, ambas diferentes de la identidad, conmutan
si y sólo si vale una de las siguientes:
(a) ambas son elı́pticas de orden dos, cada una permutando los puntos fijos
de la otra; o bién
(b) ambas tienen los mismos puntos fijos.
b→C
b una función analı́tica tal que f ′ (z) 6= 0 para cada z ∈ Ω
(10) Sea f : Ω ⊂ C
(es decir, f es localmente inyectiva). Se define la derivada Schwarziana de f
en el punto w ∈ Ω como
′′
′
2
f (w)
1 f ′′ (w)
{f, w} =
−
f ′ (w)
2 f ′(w)
Verificar que si T ∈ M, entonces
{T ◦ f, w} = {f, w}
{f ◦ T, w} = {f, T (w)}T ′(w)2
Como consecuencia observe que
{T, w} = 0
(11) Sean S, T ∈ M − {I} transformaciones de Möbius con exactamente un punto
fijo en común p. Suponiendo que al menos una de ellas tenga al menos dos puntos fijos, verificar que [T, S] = T −1 S −1 T S es una transformación parabólica
con punto fijo p.
6.6.
Razones cruzadas
Dados cuatro puntos diferentes z, u, v and w en la esfera de Riemann, tenemos
b definido por
asociado el valor en C
z−w v−u
{z, u; v, w} =
z−u v−w
52
6. GRUPOS KLEINIANOS
y llamada la razón cruzada de esos puntos. Observemos que
v−u
{∞, u; v, w} =
.
v−w
Ejercicio. Usar lo anterior para probar que dados tres puntos diferentes a, b y c en la
esfera de Riemann, entonces siempre existe una y sólo una transformación de Möbius
T tal que T (a) = ∞, T (b) = 0 y T (c) = 1.
e vale la siguiente propiedad
Ejercicio. Verificar que para toda transformación T ∈ M
de invariancia
{z, u; v, w} = {T (z), T (u); T (v), T (w)}, si T ∈ M
e −M
{z, u; v, w} = {T (z), T (u); T (v), T (w)}, si T ∈ M
Lo anterior tiene como aplicación el el hecho siguiente:
Proposición 6.3. Cuatro puntos diferentes viven en el mismo cı́rculo si y sólo si su
razón cruzada es real.
Demostración. Supongamos que los cuatro puntos son z, u, v y w. Por
una transformación de Möbius T podemos asumir que T (u) = ∞ T (v) = 0 y
T (w) = 1. Por el ejercicio anterior, la razón cruzada no cambia y es fácil verificar que
∈ R si y sólo si z ∈ R si y sólo si los puntos z, u, v, w viven sobre
{∞, 1; z, 0} = z−1
z
un mismo cı́rculo.
Ejercicio. Considere sucesiones zn , un , vn , wn , en la esfera de Riemann, tales que
para para cada n se tiene que ellos son puntos diferentes y viven sobre el mismo
cı́rculo Cn . Supongamos que zn converge a z, un converge a u, vn converge a v y wn
converge a w, tal que z, u, v y w son puntos diferentes. Verificar que ellos viven sobre
un cı́rculo.
Las razones cruzadas permiten identificar las transformaciones holomorfas y antiholomorfas de la esfera de Riemann.
b→C
b una función.
Proposición 6.4. Sea T : C
(1) Si T preserva la razón cruzada, entonces T ∈ M;
e − M.
(2) Si T conjuga la razón cruzada, entonces T ∈ M
b →
Demostración. Veamos (1). Supongamos que tenemos una función T : C
b tal que {z, u; v, w} = {T (z), T (u); T (v), T (w)}, para todo cuadruple de puntos
C
diferentes de la esfera de Riemann. Es claro que T no puede ser entonces constante.
Compongamos a la izquierda por una transformación de Möbius (si es necesario)
6.7. CÍRCULOS ISOMÉTRICOS
53
para suponer que T (∞) = ∞. La igualdad {z, ∞; v, w} = {T (z), T (∞); T (v), T (w)}
es equivalente a la igualdad
T (v) − T (w)
T (z) − T (w)
=
z−w
v−w
Luego, existe una constante k 6= 0 tal que
T (z) − T (w) = k(z − w).
En este caso, S = k1 T satisface que
S(z) − S(w) = z − w.
Es claro entonces que S es isometrı́a Euclidena del plano, es decir la composición
de una rotación y una translación, es decir, S y luego T es una transformación de
Möbius.
La demostración de (2) es equivalente ya que basta ver que T , la composición de T
con la conjugación J(z) = z satisface (1).
6.7.
Cı́rculos Isométricos
6.7.1. Transformaciones de Möbius. Consideremos una transformación de
Möbius T , diferente de la identidad. Podemos mirar aquellos puntos en la esfera de
Riemann donde T no produce distorsión Euclideana, es decir, aquellos puntos donde
|T ′(z)| = 1.
(1) Si T (∞) = ∞, entonces T (z) = az + b, con a 6= 0. En este caso, |T ′ (z)| = |a|.
Luego T no produce distorsión en un punto si y sólo si no produce distorsión en todo
punto si y sólo si T es elı́ptica.
(2) Si T (z) 6= ∞, entonces
az + b
cz + d
con c 6= 0 y ad − bc = 1. En este caso |T ′ (z)| = 1 si y sólo si |cz + d| = 1. Obtenemos
ası́ que el conjunto de puntos donde T no produce distorsión Euclidean es un cı́rculo
con centro
−d
c
y cuyo radio es
1
|c|
Este cı́rculo recibe el nombre de cı́rculo isométrico de T y lo denotamos por IT .
T (z) =
Si consideramos la transformación de Möbius inversa de T ,
T −1 (z) =
dz − b
−cz + a
54
6. GRUPOS KLEINIANOS
obtenemos los respectivos cı́rculos isométricos
d
1
IT := {z ∈ C : |z + | = },
c
|c|
1
a
IT −1 := {z ∈ C : |z − | = }.
c
|c|
Ambos cı́rculos isométricos tienen el mismo radio Euclideano. Más aún, se puede
verificar directamente que:
T (IT ) = IT −1
y
d
1
a
1
T ({z ∈ C : |z + | ≤ }) = {z ∈ C : |z − | ≥ } ∪ {∞}
c
|c|
c
|c|
Geométricamente, tenemos cuatro posibles configuraciones para este par de cı́rculos:
(1) Ambos cı́rculos coinciden. Esto ocurre si y sólo si d = −a, lo cual es lo mismo
que decir que T 2 = I.
(2) Ambos cı́rculos son tangentes en un punto. Esto ocurre si y sólo si la distancia
de los centros es igual a la suma de los radios, es decir |a + d| = 2. Luego T
es parabólica o loxodrómica.
(3) Ambos cı́rculos intersectan en exactamente dos puntos. Esto ocurre si y sólo si
la distancia de los centros es mayor a cero y es menor a la suma de los radios,
es decir 0 < |a + d| < 2. Luego T es elı́ptica o loxodrómica.
(4) Ambos cı́rculos son disjuntos. Esto ocurre si y sólo si la distancia de los centros
es mayor a la suma de los radios, es decir |a + d| > 2. Luego T es loxodrómica.
Supongamos ahora que T 2 6= I. Tenemos entonces que los centros de ambos cı́rculos
isométricos son diferentes. Consideremos la única lı́nea L que pasa por esos centros,
es decir, por T −1 (∞) y T (∞). Sea M la lı́nea ortogonal a L que pasa por el medio del
trazo de L determinado por ambos centros. Sea R = ητ , donde τ es la única reflexión
cuyo conjunto de puntos fijos es IT y η la única reflexión cuyo cı́rculo de puntos fijos
es M ∪ {∞}. Entonces S = T −1 R es una transformación de Möbius que satisface
S(∞) = ∞, S(IT ) = IT y S(T −1 (∞)) = T −1 (∞). Es fácil ver que necesariamente
S es una rotación (luego una transformación elı́ptica). En este caso T = RS −1 . En
el caso que T 2 = I, podemos hacer lo mismo considerando η = I. De esta manera
hemos obtenido el siguiente:
Proposición 6.5. Sea T una transformación de Möbius diferente de la identidad tal
que T (∞) 6= ∞. Entonces:
(1) Los cı́rculos isométricos de T y T −1 coinciden si y sólo si T 2 = I.
(2) T es composición de dos reflexiones y una rotación (si T 2 = I, una de las reflexiones es reemplazada por la identidad). Una reflexión y la rotación preservan la métrica Euclideana del plano. Luego la distorsión de áreas Euclideanas
producida por T es la producida por la reflexión en su cı́rculo isométrico.
6.8. GRUPOS KLEINIANOS
55
6.7.2. Transformaciones Extendidas de Möbius. Dada una transformae − M, tal que T (∞) 6= ∞, definimos su cı́rculo
ción extendida de Möbius T ∈ M
isométrico IT como el lugar geométrico donde T preserva la métrica Euclideana.
Considerando J(z) = z (la cual es isometrı́a Euclidena) podemos ver que el cı́rculo
isométrico de T es exactamente el cı́rculo isométrico de T J ∈ M, es decir, IT = IT J .
Ejercicio. Mostrar que IT = IT −1 si y sólo si T 2 = I. Calcular el cı́rculo isométrico
de T (z) = −1
y el de T (z) = z1 .
z
Una consecuencia directa de la proposición 6.5 y lo anterior es que la defomación
Euclideana que realiza una transformación (extendida) de Möbius T , con T (∞) 6= ∞,
es exactamente la deformación realizada por la reflexión sobre su cı́rculo isométrico.
En forma más clara tenemos las siguientes desigualdades:
e tal que T (∞) 6= ∞ y sea R un subconjunto de la esfera
Corolario 6.6. Sea T ∈ M
b de cardinalidad mayor que uno. Supongamos que T −1 (∞) ∈
de Riemann C
/ R, es
decir, R no contiene el centro del cı́rculo isométrico de T en su clausura. Denotemos
por diam el diámetro Euclideano en el plano complejo C, δ la distancia de T −1 (∞) a
R y sea ρ el radio del cı́rculo isométrico de T . Entonces si δ > 0, tenemos que:
(1) diam(T (R)) ≤ 2ρ2 /δ;
(2) Si además ∞ ∈ R, entonces ρ2 /δ ≤ diam(T (R))
Demostración. Sólo basta hacer esto para transformaciones de Möbius. Como
habı́amos observado, la transformación T cambia el diámetro Euclideano en la misma
forma como lo hace la reflexión sobre su cı́rculo isométrico. La reflexión en el cı́rculo
isométrico de T es dada por
ρ2
σ(z) =
+ T −1 (∞)
z − T −1 (∞)
Luego σ(R) está contenida en el disco D centrado en T −1 (∞) y radio ρ2 /δ y en
particular su diámetro Euclideano está acotado superiormente por el diámetro de D.
Supongamos además que ∞ ∈ R. Esto dice que σ(R) contiene al centro del cı́rculo
isométrico de T en su clausura. Luego el diámetro Euclideano de σ(R) es al menos el
radio del disco D.
6.8.
Grupos Kleinianos
e Diremos que G es un
6.8.1. Grupos Discretos. Sea G un subgrupo de M.
grupo discreto si no existe una sucesión gn ∈ G de elementos diferentes convergiendo
e
a alguna transformación T ∈ M.
e y H un subgrupo de ı́ndice finito en G. Es claro
Consideremos un subgrupo G de M
de la definición que si G es discreto, entonces H también lo es. Reciprocamente,
supongamos que H es discreto. Como H tiene ı́ndice finito en G, entonces existen
T1 , ..., Tn ∈ G − H tal que G = H ∪ HT1 ∪ · · · ∪ HTn . Si G no fuese discreto, entonces
56
6. GRUPOS KLEINIANOS
existirı́a una sucesión gn ∈ G de elementos diferentes convergiendo a una transformación T . Entonces existe una subsucesión infinita de elementos en HTj para cierto
j ∈ {0, 1, ..., n}, donde T0 = I. Luego gn = hn Tj y, en particular, hh = gn Tj−1 converge a T Tj−1 . Como H es discreto, entonces hn = T Tj−1 para n grande, en particular,
gn = T para n grande, obteniendo una contradicción. Hemos probado el siguiente:
e y H un subgrupo de ı́ndice finito en G.
Proposición 6.7. Sea G subgrupo de M
Entonces G es discreto si y sólo si H es discreto.
e y sea H subgrupo de G.
Ejercicio. Sea G subgrupo de M
(a) Verificar que H es necesariamente un grupo discreto.
(b) Verificar que si G+ = G ∩ M, entonces G es discreto si y sólo si G lo es.
e es discreto si y sólo si no existe sucesión gn ∈ G
Proposición 6.8. Un grupo G < M
de elementos diferentes convergiendo a la identidad I.
Demostración. Es claro que si existe sucesión de elementos diferentes de la
identidad convergiendo a la identidad, entonces G es no discreto por la definición.
Recı́procamente, sea G un grupo discreto y sea {gn } una sucesión en G convergiendo
e Entonces kn = gn+1 g −1 es una sucesión en G convergiendo a la identidad.
a g ∈ M.
n
Si podemos extraer una subsucesión de elementos diferentes, entonces obtenemos una
contradicción a la discretitud de G. Si no es posible encontrar una subsucesión de
elementos diferentes, entonces existe N > 0 tal que kn son todos iguales para n > N.
De esta manera, kn = I para n > N lo cual obliga a tener gn = gn+1 para n > N,
una contradicción.
Hay veces que es bueno conjugar nuestros grupos en orden a simplificar argumentos.
El siguiente resultado nos garantiza que la propiedad de ser discreto no es modificada
por tal proceso.
e un grupo y sea h ∈ M.
b Entonces G es discreto si y
Proposición 6.9. Sea G < M
−1
sólo si hGh lo es.
Demostración. Es claro que dada cualquier sucesión en G que es convergente,
digamos {gn }, entonces la sucesión en hGh−1 dada por {hn = hgn h−1 } es convergente.
Además una de ellas es eventualmente constante si y sólo si la otra lo es.
Ejercicio. Sea K un subgrupo del grupo multiplicativo S 1 = {z ∈ C : |z| = 1}.
Entonces K es denso o un grupo cı́clico finito.
Ejemplo 6.1. Sea G el grupo cı́clico generado por una transformación elı́ptica. Módulo conjugación por una transformación de Möbius, podemos asumir que G es generada
6.8. GRUPOS KLEINIANOS
57
por T (z) = e2πiq z. Esto nos da un isomorfismo de los grupos G y un subgrupo de S 1 .
Tenemos que G es finito si y sólo si T es de orden finito si y sólo si q ∈ Q. Además, el
ejercicio anterior nos dice que T es de orden infinito si y sólo si existen nk ∈ N tales
que e2πiqnk es una sucesión de elementos diferentes convergiendo a 1. En particular,
T nk da una sucesión de elementos diferentes convergiendo a la identidad. En resumen,
G es discreto si y sólo si T tiene orden finito.
Ejercicio. Verificar que todo grupo cı́clico generado por una transformación parabólica o loxodrómica es necesariamente discreto.
e tenemos las sigu6.8.2. Grupos Discontinuos. Dado un subgrupo G de M
ientes definiciones:
b es llamado un punto de discontinuidad del grupo G si:
(1) Un punto p ∈ C
(1.1) Gp = {g ∈ G : g(p) = p} es finito (Gp es llamado el estabilizador de p en
G);
(1.2) Existe un abierto U tal que p ∈ U y g(U) ∩ U = ∅ para todo g ∈ G − Gp .
(2) Un punto que no es un punto de discontinuidad de G es llamado un punto
lı́mite de G.
(3) El conjunto de los puntos de discontinuidad de G es llamado la región de
discontinuidad de G y es usualmente denotado por Ω(G) o sólo Ω si es claro
del contexto el grupo al cual refiere.
(4) El conjunto de los puntos lı́mite de G es llamado el conjunto lı́mite de G y es
usualmente denotado por Λ(G) o Λ si no hay confusión.
Un grupo G que actúe discontinuamente en algún punto de la esfera de Riemann se
llama un grupo Kleiniano planar, es decir, si Ω(G) 6= ∅.
Las siguientes propiedades para un subgrupo son fácil de verificar:
e Entonces
Proposición 6.10. Sea G un subgrupo de M.
(a) Ω(G) es un abierto y Λ(G) es un compacto;
(b) Ω(G) ∩ Λ(G) = ∅;
b
(c) Ω(G) ∪ Λ(G) = C;
(d) Para todo g ∈ G se tiene que g(Ω(G)) = Ω(G) y g(Λ(G)) = Λ(G);
(e) Si G es subgrupo Kleiniano planar de M, p ∈ Ω(G), entonces Gp es grupo
cı́clico finito.
e Ver que H es
Ejercicio. Sea H un subgrupo de un grupo Kleiniano planar G en M.
necesariamente un grupo Kleiniano planar.
e ten6.8.3. Puntos Fijos en Ω(G). Dado un grupo Kleiniano planar G en M,
emos que los puntos de discontinuidad de G vienen en dos sabores. Sea p ∈ Ω(G),
58
6. GRUPOS KLEINIANOS
entonces su estabilizador en G, Gp , puede ser o no trivial. Denotemos por G+ el subgrupo de G consistiendo de sus transformaciones de Möbius. Entonces, tenemos que
G = G+ ó G+ es de ı́ndice dos en G. Luego, por el ejercicio anterior, G+ es grupo
Kleiniano planar. En este caso, G+
p es igual a Gp ó tiene ı́ndice dos en Gp .
(1) En el caso que Gp es trivial, entonces tenemos la existencia de un abierto
U ⊂ Ω(G) conteniendo p tal que T (U) ∩ U = ∅ para todo T ∈ G, T 6= I. En
este caso, tenemos que todo punto q ∈ U tiene estabilizador trivial. La órbita
de U bajo G consiste en una colección dos a dos disjunta de transladadas de
U.
(2) Supongamos que Gp es no trivial. Entonces tenemos dos posibilidades para
G+
p.
+
(2.1) Si G+
p es trivial. Si Gp = Gp , entonces Gp es trivial y estamos en el caso (1)
+
anterior. Si Gp 6= Gp , entonces Gp , al ser G+
p un subgrupo de ı́ndice dos
en Gp , está necesariamente generado por una transformación extendida
e − M de orden dos. Por el ejercicio (7) de la sección 6.5.,
de Möbius τ ∈ M
tenemos que τ es necesariamente una reflexión. En este caso, tenemos la
existencia de una abierto U ⊂ Ω(G), conteniendo p, tal que τ (U) = U y
T (U) ∩ U = ∅ para T ∈ G − {I, τ }. En este caso, todo punto q ∈ U, que
no esta en el arco de cı́rculo de puntos fijos de τ , tiene estabilizador Gq
trivial.
(2.2) Supongamos que G+
p no es trivial. El ejercicio (11) de la sección 6.5., dice
que este grupo es un grupo cı́clico finito. Digamos que G+
p está generado
m
por la transformación elı́ptica E, tal que E = I. No hay problemas
en asumir que E(z) = e2πi/m z y p = 0. Si Gp = G+
p , entonces Gp es
+
cı́clico finito. Si Gp 6= Gp , entonces, usando el hecho que Gp contiene a
p
G+
p como subgrupo de ı́ndie dos, se puede observar que G contiene una
e − M, tal que
transformación extendida de Möbius de orden finito τ ∈ M
2
+
τ ∈ Gp . De nuevo el ejercicio (7) de la sección 6.5., asegura que τ es una
reflexión. Módulo una rotación Euclidenana, no hay problemas en suponer
que τ (z) = z. Luego,
Gp = hE, τ : E m = τ 2 = 1, τ Eτ = E −1 i
En este caso, existe un abierto U, conteniendo p, tal que T (U)∩U = ∅ para
todo T ∈ G − Gp y T (U) = U para todo T ∈ Gp . Todo punto q ∈ U − {p}
tiene estabilizador trivial.
e entonces
Lo anterior también asegura que, si G es un grupo Kleiniano planar en M,
el conjunto de puntos en Ω(G) cuyo estabilizador es no trivial es denso en Ω(G). En
particular, existen puntos p ∈ Ω(G) cuyo estabilizador es trivial; esto nos permite
tener una biyección entre G y la órbita de una vecindad U de p como antes. De
aquı́ obtenemos
6.8. GRUPOS KLEINIANOS
59
e es numerable.
Proposición 6.11. Todo grupo Kleiniano planar en M
e es necesariamente discreto.
Proposición 6.12. Todo grupo Kleiniano planar en M
Demostración. Si G no fuese discreto, entonces existirı́a una sucesión {Tn } en
G, de elementos diferentes, convergiendo a la identidad. En particular, para cada p ∈
Ω(G) vale que Tn (p) converge a p. Si tomamos p con estabilizador Gp trivial, entonces
esto dirı́a que para todo abierto U conteniendo a p debe valer que Tn (U) ∩ U 6= ∅.
Esto es una contradicción.
60
6. GRUPOS KLEINIANOS
Ejercicio.
e es necesari(1) Verificar directamente de la definición que todo grupo finito en M
b
amente Kleiniano planar. En este caso, Ω(G) = C.
(2) Sea G el grupo cı́clico generado por la transformación de Möbius T . Verificar que G es Kleiniano planar si y sólo si T no es conjugada en M a una
transformación del tipo Q(z) = eiθ z, donde θ ∈
/ 2πQ.
(3) Considere el grupo G generado por las translaciones A(z) = z + a y B(z) =
z + b, donde a, b ∈ C. Si a y b son linealmente independiente sobre R, entonces
G es un grupo Kleiniano planar isomorfo a Z ⊕ Z y Ω(G) = C. Si a o b es
igual a cero pero no ambos, entonces G es Kleiniano planar isomorfo a Z y
Ω(G) = C. Si ambos a = b = 0, entonces G es Kleiniano planar (el grupo
b Si a y b son linealmente dependientes sobre R, ambos no
trivial) y Ω(G) = C.
cero, entonces G es Kleiniano planar si y sólo si el subgrupo aditivo generado
por a y b no es denso en el subespacio generado por a.
(4) Verificar que todo grupo Kleiniano planar elemental es conjugado por una
transformación de Möbius a una extensión finita de alguno de los casos anteriores.
(5) El grupo formado por las transformaciones de Möbius
T (z) =
az + b
,
cz + d
donde a, b, c, d ∈ Z[i] tal que ad − bc = 1, es un grupo discreto que no es
Kleiniano planar. [Ind. Darse cuenta que ∞ ∈ Λ(G). Usar el hecho que Q es
denso en R y buscar la órbita de ∞]
(6) Probar que todo grupo discreto G de transformaciones de Möbius que es isomorfo como grupo abstracto a un grupo abeliano sin torsión es necesariamente
isomorfo a Z ó Z ⊕ Z.
(7) Sean C1 y C2 dos cı́rculos en la esfera de Riemann. Denote por σj la reflexión en
Cj , para j = 1, 2, y por G el grupo generado por σ1 y σ2 . Determinar cuando
G es un grupo Kleiniano planar.
6.8.4.
Algunos ejemplos de grupos Kleinianos.
(a) Grupos Fuchsianos: Estos grupos tienen la caracterı́stica que dejan invariante
un disco Euclideano. El conjunto ı́mite está contenido en el cı́rculo borde. Si
todo el cı́rculo borde es el conjunto ı́mite, entonces decimos que G es un grupo
Fuchsiano de primera clase. En caso contrario, decimos que es de segunda clase.
Estos grupos aparecen como los grupos cubrientes universales de las superficies de Riemann hiperbólicas; aquellas superficies de caracterı́stica de Euler
negativa. Por ejemplo, (i) las superficies cerradas de género mayor o igual a
dos; (ii) esferas con al menos tres boredes; (iii) superficies cerradas de género
al menos uno y con un punto eliminado; etc.
6.9. ESPACIO HIPERBÓLICO 3-DIMENSIONAL
61
(b) Grupos Uniformizantes: Estos grupos tienen una componente invariante en su
región de discontinuidad. Por ejemplo, los grupos Fuchsianos son de este tipo.
(c) B-Grupos: Estos son grupos uniformizantes que tienen una componente invariante que es simplemente conexa. Por ejemplo, los grupos Fuchsianos de
primera clase.
(d) Grupos de Schottky anodados: Estos son grupos Kleinianos planares isomorfos
a grupos libres de rango finito. El rango de este grupo abstracto es también
llamado el género del grupo de Schottky anodado. Un grupo de Schottky es
por definición un grupo de Schottky anodado donde sus elementos diferentes
de la identidad son transformaciones loxodrómicas. Miraremos este tipo de
grupos en un capı́tulo más adelante.
6.9.
Espacio Hiperbólico 3-Dimensional: Extensión de Poincaré
Un modelo del espacio hiperbólico tres dimensional es dado por el semi-espacio tres
deimensional
H3 = {(z, t) ∈ C × R : t > 0}
junto con la métrica hiperbólica
p
|dz|2 + dt2
.
t
La longitud hiperbólica de un camino continuo
ds =
γ : [a, b] → H3 : τ 7→ γ(τ ) = (z(τ ), t(τ ))
es entonces dada por
L(γ) =
Z
γ
ds =
Z
b
a
p
z ′ (τ )2 + t′ (τ )2 dτ
t(τ )
Como γ([a, b]) es un subconjunto compacto de H3 , debemos tener valores 0 < T <
S < ∞ tales que la tercera coordenada t(τ ) ∈ [T, S]. En particular, se puede ver que
(∗)
1
1
LR3 (γ) ≤ L(γ) ≤ LR3 (γ)
S
T
donde LR3 (γ) denota la longitud Euclideana de γ.
La distancia hiperbólica d(p, q) entre dos puntos p, q ∈ H3 es dada por el ı́nfimo de
las longitudes de todas los caminos continuos que hay entre p y q. Es claro que
(i) d(p, q) ≥ 0;
(ii) d(p, q) = d(q, p);
La desigualdad (∗) dice que d(p, q) = 0 si y sólo si kp − qk = 0, es decir,
(iii) d(p, q) = 0 si y sólo si p = q;
62
6. GRUPOS KLEINIANOS
Por otro lado, si tenemos tres puntos p, q, r ∈ H3 , entonces si tenemos un camino
γ1 entre p y r y un camino γ2 entre r y q, tenemos un camino γ entre p y q por
yuxtaposición. De esta manera
Es claro entonces que
L(γ3 ) = L(γ1 ) + L(γ2 )
d(p, q) ≤ L(γ1) + L(γ2)
de lo cual podemos obtener la desigualdad triangular
(iv) d(p, q) ≤ d(p, r) + d(r, q).
De esta manera hemos obtenido el siguiente:
Proposición 6.13. d es en una métrica en H3 llamada la métrica hiperbólica.
Otro modelo de este espacio es también dado por la bola unitaria tres dimensional
B 3 = {(u, v, w) ∈ R3 : u2 + v 2 + w 2 < 1}
con la métrica Riemanniana
2(du2 + dv 2 + dw 2 )
1 − (u2 + v 2 + w 2 )
Para ver que estos dos modelos son isométricos, consideremos el homeomorfismo que
preserva orientación
ds =
F = B ◦ A : H3 → B 3
definido por la composición de las reflexiones
A : C × R → C × R : (z, t) 7→ (z, −t)
y B(z, t) = (0, 1) + 2(z, t − 1)/(|z|2 + (t − 1)2 ) [B es la reflexión
√ en la esfera dos
dimensional centrada en el punto (0 + 0i, 1) ∈ C × R de radio 2]. Entonces F :
H3 → B 3 resulta ser una isometrı́a. Luego podemos usar indistintamente cualquiera
de los dos modelos del espacio hipebólico tres-dimensional. Para algunos cálculos es
mejor un modelo que el otro. El siguiente ejercicio es directa consecuencia del hecho
que F es compossición de reflexiones en esferas.
Ejercicio.
(1) Verificar que F envı́a semiesferas en H3 ortogonales al borde ∂H3 en semi
esferas en B 3 también ortogonales al borde S 2 = ∂B 3 .
(2) Ver que F envı́a esferas Euclideanas en H3 en esferas Euclideanas en B 3 .
b como la frontera del espacio hiperbólico H3
Podemos mirar la esfera de Riemann C
2
y también como el borde S del modelo B 3 (usando la proyección estereográfica Q
vista en 6.2. (2)).
6.9. ESPACIO HIPERBÓLICO 3-DIMENSIONAL
63
Cada cı́rculo en la esfera de Riemann genera una semiesfera en H3 ortogonal a su
borde en tal cı́rculo. Luego la reflexión en tal cı́rculo se extiende a una reflexión en la
semiesfera generada. En forma precisa;
(1) Si C es el cı́rculo en el plano complejo de centro p y radio R > 0, entonces la
ecuación de la semisfera en H3 que ella genera es
{(z, t) ∈ H3 : |z − p|2 + t2 = R2 }.
La reflexión en C es
R2
+p
z−p
y su extensión es dada por la reflexión en la semiesfera generada, es decir
σ(z) =
σ(z, t) =
R2 (z − p, t)
+ (p, 0)
|z − p|2 + t2
(2) Si C es la recta L unión ∞, pasando por el punto p ∈ C y haciendo un ángulo
θ con el eje {Im(z) = 0}, entonces la semisfera generada por L en H3 es un
semiplano ortogonal al borde en L, dada por la ecuación
{(z, t) ∈ H3 : z ∈ L}.
La reflexión en C es
σ(z) = e2iθ z − p + p
y su extensión es dada por
σ(z, t) = (e2iθ z − p + p, t)
b es composición de reflexiones, se puede
Ahora, como cada transformación T ∈ M
extender a todo H3 . Esta extensión recibe el nombre de extensión de Poincaré. De
manera más explı́cita, supongamos que tenemos la transformación de Möbius
az + b
,
T (z) =
cz + d
donde
a b
∈ SL(2, C)
c d
entonces su extensión de Poincaré es dada por
2
+
d)
+
act
(az
+
b)(cz
t
Tb(z, t) =
,
|cz + d|2 + |c|2 t2
|cz + d|2 + |c|2t2
c = SbTb.
Ejercicio. Verificar que si S y T son transformaciones de Möbius, entonces ST
Ejercicio.
64
6. GRUPOS KLEINIANOS
(1) Usando las ecuaciones explı́citas de las extensiones de Poincaré de las reflexiones, verificar que estas son isometrı́as de H3 . Concluir que la extensión de
Poincaré de todo automorfismo holomorfo o antiholomorfo de la esfera de
Riemann es una isometrı́a de H3 .
(2) Verificar que dado dos puntos p, q ∈ H3 siempre existe una transformación de
Möbius T tal que su extensión de Poincaré Tb satisface que Tb(p) = q. Concluir
que el grupo de isometrı́as de H3 actúa de manera transitiva. [Ind. ver que la
órbita del punto (0, 1) ∈ H3 es todo H3 ].
(3) Nuestra isometrı́a F : H3 → B 3 envı́a semiesferas de H3 ortogonales al borde
en semiesferas de B 3 ortogonales al borde. Verificar que F commuta con las
extensiones de Poincaré, es decir, si Tb : H3 → H3 es la extensión de Poincaré de
la reflexión en el cı́rculo C, entonces F TbF 1 : B 3 → B 3 es la extensión de
Poincaré de la reflexión en el cı́rculo F (C) [Ind. Recuerde que F es composición
de dos reflexiones].
(4) Usando el modelo B 3 , ver que toda rotación Euclideana entorno al orı́gen es
de hecho una extensión de Poincaré de una transformación (extendida) de
Möbius.
(5) Usando (4) verificar que esferas hiperbólicas (conjunto de puntos que equidistan de un punto dado p ∈ H3 ) es una esfera Euclideana.
(6) Verificar que la distancia hiperbólica en B 3 entre (0, 0, 0) y un punto (r, 0, 0),
donde 0 < r < 1 es dada por
d((0, 0, 0), (r, 0, 0)) = −ln(1 − r).
Verifique que [0, r] da el camino más corto entre estos dos puntos (esta es
llamada una geodésica hiperbólica).
(7) Usar la transitividad de las extensiones de Poincaré de las transformaciones
de Möbius para obtener la distancia entre dos puntos cualquiera de B 3 y
verificar que las geodésicas hiperbólicas son exactamente los semicı́rculos en
B 3 ortogonales al borde.
(8) Verificar que la esfera hiperbólica centrada en el (0, 0, 0) ∈ B 3 es una esfera
Euclideana centrada en (0, 0, 0). Relacionar el radio hiperbólico con el radio
Euclideano de esta.
(9) Determinar las geodésicas y formula de distancia para el modelo H3 .
Ejes de Transformaciones de Möbius. Supongamos que T ∈ M es una transformación de Möbius diferente de la identidad. Si Tb denota su extensión de Poincaré,
entonces:
b Sea A(T ) ⊂ H3
(1) Sea T loxodrómica o elı́ptica, con puntos fijos p, q ∈ C.
la única geodésica que está determinada por p y q. Como Tb es isometrı́a,
tenemos necesariamente que Tb(A(T )) = A(T ). Si T es loxodrómica, entonces
la acción de Tb sobre A(T ) es por translación desde uno de los puntos fijos de
6.9. ESPACIO HIPERBÓLICO 3-DIMENSIONAL
65
T (el punto fijo repulsor) hacia el otro punto fijo (el punto fijo atractor). Por
otro lado, si T es elı́ptica, entonces A(T ) es formado por los puntos fijos de Tb.
Una forma simple de ver esto es conjugando de manera que p = 0 y q = ∞.
b Podemos conjugar T por una
(2) Sea T es parabólica, con punto fijo p ∈ C.
transformación de Möbius P para suponer que S(z) = P T P −1(z) = z + 1.
Por cada R > 0 podemos considerar el conjunto C(R) = {(z, t) ∈ H3 :
t > R}. Llamamos la bola conical centrada en p y radio R al conjunto
C(T, R) = P −1(C(R)) (el radio no depende de la elección de P ). Entonces
como S(C(R)) = C(R), tenemos que T (C(T, R)) = C(T, R). Es claro que la
acción de S sobre el borde de C(R) es la misma acción de S sobre el plano
complejo. Luego no es dificil verificar que C(R)/hSi (y luego C(T, R)/hT i) es
topológicamente S 1 × D ∗ , donde D ∗ = {z ∈ C : 0 < |z| < 1}.
Hemos visto que las composiciones de las extensiones de Poincaré de las reflexiones dan isometrı́as del espacio hiperbólico. Por otro lado, si tenemos una isometrı́a
P : B 3 → B 3 , entonces podemos componer P con la extensión de Poincaré de una
transformación de Möbius para suponer que P ((0, 0, 0)) = (0, 0, 0). Ahora, al ser P
una isometrı́a, se verifica que P preserva cada esfera Euclideana centrada en (0, 0, 0).
Por otro lado, cada diámetro de B 3 es una geodésica en B 3 y luego P envı́a diámetros
en diámetros. De aquı́ se concluye que P es una rotación Euclideana y, en particular,
P es la extensión de Poincaré de una transformación elı́ptica. Hemos obtenido:
Teorema 6.14. Toda isometrı́a de H3 es la extensión de Poincaré de un automorfismo holomorfo o antiholomorfo de la esfera de Riemann.
Observemos que usando esta extensión de Poincaré tenemos la siguiente situación.
Sea T una transformación de Möbius diferente de la identidad, y sea Tb su extensión
de Poincaré. Si Tb tiene un punto fijo en H3 entonces T debe ser elı́ptica. En efecto,
si T fuese parabólica o loxodrómica, entonces la órbita de cualquier punto de H3 se
acumula en los puntos fijos de T en la esfera de Riemann.
Ahora que podemos relacionar automorfismos holomorfos y antiholomorfos de la esfera
de Riemann con las isometrı́as del espacio hiperbólico tres dimensional, podemos
interrelacionar variedades hiperbólicas con superficies de Riemann. Para esto, primero
observamos el siguiente resultado.
Teorema 6.15. Todo grupo G de isometrı́as de H3 es discreto si y sólo si G actúa
de manera discontinua en todo punto de H3 . En particular, si G es un grupo discreto
e entonces G es numerable.
en M,
Si G es un grupo discreto de isometrı́as de H3 , entonces para todo p ∈ H3 debe ser
finito. De hecho, usemos el modelo B 3 y pensemos en p = (0, 0, 0) [módulo conjugación
en el grupo de isometrı́as]. El estabilizador Gp es un subgrupo discreto del grupo
66
6. GRUPOS KLEINIANOS
ortogonal. Como el grupo ortogonal es compacto, entonces Gp es finito. Por otro
lado, tenemos el siguiente resultado.
Lema 6.16. Si G es un grupo discreto de isometrı́as del espacio hiperbólico H3 ,
entonces para todo p ∈ H3 se tiene que su órbita por G es un subconjunto discreto de
H3 .
Demostración. Sea G un grupo discreto de isometrı́as del espacio hiperbólico
H3 y supongamos que existe un punto p ∈ H3 y una sucesión Tn de elementos diferentes en G tal que Tn (p) converge a un punto q ∈ H3 . No hay perdida el asumir que
Tn (q) converge a un punto r ∈ H3 , donde dH3 (p, q) = dH3 (r, p) (Basta considerar el
modelo de la bola unitaria y el hecho que Tn son isometrı́as).
Como G+ es o bien igual a G ó de ı́ndice dos en G, entonces no hay perdida de
generalidad el asumir que Tn ∈ G+ . Es claro que podemos asumir que las transforma−1
ciones Tn+1
Tn son todas diferentes. En efecto, si no pudiesemos asumir esto, entonces
−1
a partir de cierto N > 0 tendriamos que Tn+1
Tn = T , alguna T ∈ G+ . Esto dirı́a que
N −n
Tn = TN T0 . Como G es discreto, T0 no puede ser elı́ptico de orden infinito y como
los Tn son diferentes, T0 no puede ser elı́ptico de orden finito. Pero si T0 es parabólico
o loxodrómico, entonces es claro que T0N −n (x) converge a uno de los puntos fijos de
T0 , el cual vive en la frontera del espacio hiperbólico, contradiciendo nuestro supuesto
sobre la sucesión Tn (p).
Ahora,
−1
Tn (q), q) = dH3 (Tn (q), Tn+1 (q)) → 0
dH3 (Tn+1
−1
Esto nos dice que podemos encontrar una sucesión Rn = Tn+1
Tn en G+ de elementos
diferentes con la propiedad que
Rn (q) → q
Luego, para cualquier valor ǫ > 0 el conjunto
G(ǫ) = {T ∈ G+ : dH3 (T (q), q) < ǫ}
es infinito. Por otro lado, G es discreto, es decir que las normas de las matrices en
SL(2, C) de sus elementos es un conjunto discreto en C. Un cálculo asegura entonces
que las distancias desde un punto q a sus transladadas por las transformaciones en
G(ǫ) debe ser un conjunto acotado en [0, ∞) (ver [Matsuzaki-Taniguchi], pp 29) y
luego, por discretitud, finito.
Ahora, teorema 6.15 es un caso particular del siguiente hecho general:
Teorema 6.17. Sea (X, d) un espacio métrico y G un grupo de sus isometrı́as. Entonces G actúa de manera discontinua (en todo X) si y sólo si
(1) Para todo x ∈ X, su estabilizador Gx es finito; y
6.10. TEOREMA DE UNIFORMIZACIÓN DE KOEBE
67
(2) Para todo x ∈ X la órbita G(x) = {T (x) : T ∈ G} es un subconjunto discreto
de X.
Demostración. Si G es discontinuo en todo X, entonces la condicion (1) es por
definición y la condición (2) es probada de la misma manera como se verificó que todo
grupo Kleiniano planar es discreto (ver proposición 6.12). Recı́procamente, supongamos que G satisface propiedades (1) y (2). Si G no actuaradiscontinuamente en
algún punto p ∈ X, entonces para todo abierto U de X, conteniendo a p, tenemos
que T (U) ∩ U = ∅ para un número infinito de transformaciones T en G. Luego
podemos encontrar una sucesión de puntos xn convergiendo a p y una sucesión de elementos diferentes gn en G tal que gn (xn ) converge a p. Como cada gn es una isometrı́a,
entonces
d(gn (p), p) ≤ d(gn (p), gn (xn )) + d(gn (xn ), p) = d(p, xn ) + d(gn (xn ), p),
luego gn (p) converge a p. Como la órbita de p es discreta, debe ocurrir que gn (p) = p
para n suficientemente grande. Esto contradice la condición (1).
La extensión de Poincaré nos permite relacionar análisis complejo en la esfera de
Riemann y geometrı́a hiperbólica tres dimensional. Por ejemplo, supongamos que G
es un grupo discreto de transformaciones de Möbius. Por un lado podemos ver G
como un grupo discreto de isometrı́as de H3 que preservan orientación. Por lo visto
anteriormente, G actúa de manera discontinua sobre todo H3 y, como consecuencia
M(G) = H3 /G es una orbifold hiperbólica. En caso que G no tiene torsión, entonces
obtenemos una variedad hiperbólica tres dimensional. Si además G es Kleiniano planar, visto como grupo de automorfismos holomorfos de la esfera de Riemann, entonces
Ω(G)/G es una orbifold que podemos ver como la frontera holomorfa de M(G).
Por ejemplo, si G es un grupo de Schottky de género g ≥ 1, entonces M(G) es un
handlebody, es decir, homeomorfa a la suma conexa de g copias de D × S 1 , donde D
es el disco abierto dos dimensional y S 1 es el cı́rculo unitario. Su frontera holomorfo
es una superficie de Riemann de género g. Otro ejemplo es considerar G un grupo
Fuchsiano de la primera clase, digamos uniformizando una superficie de Riemann
de género g ≥ 2. Entonces M(G) es homeomorfo a S × (−1, 1), donde S es una
superficie de Riemann de género g. En este caso, su borde holomorfo es homeomorfo
a S × {−1, 1}.
6.10.
Teorema de Uniformización de Koebe
Dada una superficie de Klein X, no-orientable, entonces podemos considerar su doble
cobertor orientable P : S → X. En este caso, S es una superficie de Riemann admitiendo una automorfismo antiholomorfo de orden dos τ : S → S, actuando sin
puntos fijos, tal que hτ i es el grupo cobertor de P . Luego, el estudio de superficies de
Klein no-orientables puede ser interpretado como el estudio de superficies de Riemann
admitiendo automorfismos de orden dos antiholomorfos.
68
6. GRUPOS KLEINIANOS
Sea S una superficie de Riemann. Uno puede considerar su cobertor universal Sb y
un cubrimiento universal Q : Sb → S. Podemos levantar la estructura de superficie
de Riemann de S por Q para dotar a Sb de una estructura de superficie de Riemann
simplemente conexa. El cubrimiento Q : Sb → S queda un cubrimiento universal
holomorfo y el grupo cobertor G ∼
= π1 (S, p) un grupo de automorfismos holomorfos
b
de S actuando de manera discontinua y sin puntos fijos.
Teorema 6.18 ( Teorema de uniformización [Farkas-Kra]). Toda superficie de Riemann simplemente conexa es holomórficamente equivalente a una y sólo una de las
siguientes tres:
C;
b
C;
H = {z ∈ C : Im(z) > 0}
Podemos entonces suponer que Sb es una de esas tres posibilidades.
b entonces la única manera que G actúe sin puntos fijos es que
Caso 1: Si Sb = C,
G = {I}. En este caso, S es la esfera de Riemann.
Caso 2: Si Sb = C, entonces la única manera que G actúe sin puntos fijos y de manera
discontinua es que sea uno de los siguientes dos formas, módulo conjugación:
(a) G = hA(z) = z + 1i; ó
(b) G = hA(z) = z + 1, B(z) = z + τ i, donde τ ∈ H.
En el primer caso, S es holomórficamente equivalente a C − {0} y en el segundo caso,
S es un toro (homeomorfo a S 1 × S 1 , donde S 1 es el cı́rculo unitario).
Caso 3: Todas las otras superficies de Riemann tienen al plano H como cobertor
universal. Estas superficies son llamadas superficies de Riemann hiperbólicas.
6.11.
Superficies de Klein de Grupos Kleinianos
Consideremos un grupo Kleiniano planar G de transformaciones de Möbius. En este
caso, podemos considerar la siguiente relación de equivalencia en Ω(G): p, q ∈ Ω(G)
son equivalentes si y sólo si existe T ∈ G tal que T (p) = q. El conjunto de las clases
de equivalencias es denotado por Ω(G)/G. Sea P : Ω(G) → Ω(G)/G la proyección
natural inducida por G. Si dotemos al cociente de la topologı́a cociente obtenemos
que P : Ω(G) → Ω(G)/G es una función continua y abierta. Se puede verificar que
este cociente es un espacio topológico Hausdorff. Esto es consecuencia de que toda
transformación de Möbius envı́a cı́rculos en cı́rculos en la esfera de Riemann y que
en la métrica esférica los diámetros de una sucesión infinita de cı́rculos dos a dos
disjuntos debe converger a cero.
Teorema 6.19. Sea G un grupo Kleiniano planar en M. Entonces el cociente Ω(G)/G
tiene de manera natural una estructura de superficie de Riemann.
6.11. SUPERFICIES DE KLEIN DE GRUPOS KLEINIANOS
69
Demostración. En efecto, tomemos un punto p ∈ Ω(G)/G y q ∈ Ω(G) tal que
P (q) = p. Si Gq sólo consiste de la identidad, entonces existe una vecindad abierta
U para q tal que T (U) ∩ U = ∅ para todo T ∈ G − {I}. Esto dice que P : U →
P (U) sirve de coordenada local. Ahora, si Gq tiene transformaciones diferente de la
identidad, hemos visto anteriormente que Gq es un grupo cı́clico finito, digamos de
orden N. Módulo conjugación, podemos suponer q = 0 y que el disco unitario D es
tal que T (D) ∩ D = ∅ si y sólo si T ∈ G − Gq . En este caso, P H : D → P (D),
donde H(z) = z 1/N sirve de coordenada local. Es fácil observar que los cambios de
coordenadas deben ser funciones holomorfas.
En forma similar se tiene el siguiente:
e conteniendo automorfismos
Teorema 6.20. Sea G un grupo Kleiniano planar en M
+
antiholomorfos. Sea G su subgrupo de ı́ndice dos consistiendo de las transformaciones de Möbius de G. Entonces Ω(G)/G tiene de manera natural una estructura de
superficie de Klein, con borde si y sólo si G tiene reflexiones. Más aún, la superficie
de Riemann Ω(G)/G+ es doble cubriente de Ω(G)/G con grupo cobertor generado por
una involución antiholomorfo τ . La superficie de Klein tiene borde si y sólo si τ tiene
puntos fijos; Ω(G)/G es no-orientable si y sólo si el conjunto de puntos fijos de τ no
disconecta Ω(G)/G+ .
Aquellos puntos en Ω(G)/G que son proyección de los puntos con estabilizador un
grupo no trivial son llamados valores de ramificación de la superficie de Klein. El
orden de cada valor de ramificación es por definición el orden del estabilizador de
un punto en Ω(G) que lo define. En este caso, P es un cubrimiento ramificado. Si
G actúa sin puntos fijos, es decir, todo punto de Ω(G) tiene estabilizador trivial,
entonces Ω(G)/G es una superficie de Klein sin valores de ramificación y P es un
cubrimiento dianalı́tico [holomorfo si G sólo contiene transformaciones de Möbius].
6.11.1. Algunas Propiedades de Grupos Kleinianos. En esta subsección
nos preguntaremos en lo siguiente: ¿Cuándo es un grupo de transformaciones de
Möbius un grupo Kleiniano planar? Recordemos que en presencia de transformaciones
extendidas de Möbius, discretitud se realiza por su subgrupo de indice dos formado
por la transformacione de Möbius del grupo en cuestión. Luego, nos preocuparemos
mayormente en subgrupos de M.
Primero, consideremos la siguiente información respecto a los radios de los cı́rculos
isométricos de grupos Kleinianos planares.
Proposición 6.21. Sea G un grupo Kleiniano planar tal que ∞ ∈ Ω(G) y tal que
todo elemento de G−{I} no fija ∞. Entonces, si denotamos por rg el radio del cı́rculo
70
6. GRUPOS KLEINIANOS
isométrico de g ∈ G − {I}, se tiene que
X
rg4 < ∞
g∈G−{I}
Observación 6.1. Debemos observar que si G es un grupo Kleiniano planar, entonces
siempre existe un punto p ∈ Ω(G) que no es fijado por ningún elemento de G −{I}. Si
consideramos una transformación de Möbius T tal que T (p) = ∞, entonces el grupo
Kleiniano planar T GT −1 satisface las hipótesis de la proposición anterior. Ahora, la
proposición dice que los radios de los cı́rculos isométricos rgn tienden a cero para
cualquier colección infinita de elementos de gn ∈ G − {I}.
Demostración. Por cada g ∈ G consideremos una matriz representante
ag bg
g=
∈ SL(2, C)
cg d g
La condición que g(∞) 6= ∞ para g ∈ G − {I} es equivalente a decir que cg 6= 0.
Por otro lado, el hecho que ∞ ∈ Ω(G) y que g(∞) 6= ∞ para g ∈ G − {I} dice que
podemos escoger un radio R > 0 suficientemente grande de manera que el conjunto
U = {z ∈ C : |z| ≥ R} ∪ {∞}
tiene la propiedad que
g(U) ∩ U = ∅
para cada g ∈ G − {I}.
La idea es usar el corolario 6.6 con R = U. En efecto, sea g ∈ G − {I}. Denotemos
por R > δg > 0 la distancia entre U y g −1(∞) (el centro del cı́rculo isométrico de g).
Tenemos la desigualdad:
diam(g(U)) ≥ rg2 /δg ≥ rg2 /R
Como g(U) debe ser un disco Euclideano, tenemos que su radio es mayor o igual a
rg2 /2R. En particular,
Area(g(U)) ≥ (π/4R2 )rg4
donde Area significa area Euclideana. Ahora basta observar que para g 6= k, g, k ∈
G − {I} se debe tener que g(U) ∩ k(U) = ∅. Luego las imágenes por los elementos de
G − {I} de U es una colección disjunta dos a dos de discos Euclideanos contenidos
en el disco de radio R y centro el orı́gen. Esto dice que la suma de las areas de estos
es finita, es decir,
X
X
∞>
Area(g(U)) ≥
(π/4R2 )rg4
g∈G−{I}
obteniendo nuestro resultado.
g∈G−{I}
6.11. SUPERFICIES DE KLEIN DE GRUPOS KLEINIANOS
71
Observación 6.2. Este resultado asegura que si G es un grupo Kleiniano planar tal
que ∞ ∈ Ω(G) satisface no ser punto fijo de los elementos no triviales de G, entonces
existe g ∈ G − {I} con máximo valor de rg (es decir, máximo radio de su cı́rculo
isométrico), equivalentemente, con mı́nimo valor de c > 0 si g es representado por
una matriz
a b
∈ SL(2, C)
g=
c d
Corolario 6.22. Sea G un grupo Kleiniano tal que ∞ ∈ Ω(G) y G∞ = {I}. Denotemos por G(∞) la órbita de ∞ por la acción del grupo G. Entonces la serie
X
(g ′(z))2
g∈G
converge en compactos de Ω(G) a una función meromorfa en Ω(G) que resulta ser
holomorfa en Ω(G) − G(∞) y tiene polos de orden 4 en cada punto de G(∞). En
particular, sea f : Ω(G) → C una función holomorfa tal que para cada compacto
K ⊂ Ω(G) existe MK > 0 de manera que |f (g(z))| ≤ MK para todo g ∈ G y todo
z ∈ K. Entonces la serie de Poincaré
X
f (g(z))(g ′(z))2
g∈G
converge uniformemente en compactos de Ω(G) a una función meromorfa Ginvariante.
Demostración. Sea K ⊂ Ω(G) un compacto. Luego, en K sólo pueden haber
un número finito de puntos de G(∞). Denotemos por M = {g1 , ..., gn } ⊂ G aquellos
elementos tales que gj−1 (∞) ∈ K.
Entonces, podemos escribir
X
X
(g ′(z))2 = (g1′ (z))2 + · · · + gn′ (z))2 +
(g ′(z))2
g∈G
g∈G−M
b holomorfa en el complemento
Cada sumando (gj′ (z))2 es una función meromorfa en C,
−1
−1
de gj (∞) y con un polo de orden 4 en gj (∞).
Escribamos
a b
g=
∈ SL(2, C)
c d
Tenemos que
X
g∈G−M
|g ′(z)|2 =
X
g∈G−M
1
|z − g −1|−4
|c|2
72
6. GRUPOS KLEINIANOS
Como K ⊂ Ω(G) es compacto y tenemos g ∈ G − M, existe una constante A > 0 tal
que |z − g −1 (∞)| > A. Luego la convergencia de la serie
X
|g ′(z)|2
g∈G−M
es consecuencia de 6.21. Esto dice que la serie
X
(g ′(z))2
g∈G−M
converge absolutamente en K a una función holomorfa en K.
Otra consecuencia directa de 6.21 es la suguiente información respecto a los puntos
lı́mites de grupos Kleinianos planares.
Corolario 6.23. Sea G un grupo Kleiniano planar y consideremos una sucesión
gn ∈ G de elementos diferentes. Entonces existen puntos lı́mites x, y ∈ Λ(G) y una
subsucesión gnk tal que gnk (z) converge a x uniformemente en subconjuntos compactos
b − {y}.
de C
Demostración. Este resultado es independiente del proceso de conjugación. En
particular, podemos asumir que ∞ ∈ Ω(G) y que todo g ∈ G − {I} satisface g(∞) 6=
∞. Consideremos los centros de los cı́rculos isométricos Ign de gn y Ign−1 de gn−1 , es
decir gn−1 (∞) y gn (∞). Por compacidad de la esfera de Riemann, podemos extraer una
subsucesión, la cual seguiremos denotando por gn , de manera que gn−1 (∞) converge a
un valor y y gn (∞) converge a un valor x.
Sea z ∈ Ω(G) y consideremos una vecindad U de z de manera que g(U) ∩ U = ∅ para
g ∈ G tal que g(z) 6= z. Por el resultado anterior, los radios de los cı́rculos isométricos
convergen a cero. Luego, podemos suponer que U esta en el exterior de todos (por la
excepción de un número finito) de tales cı́rculos.
Como gn envı́a el exterior de Ign en el interior de Ign−1 , obtenemos lo deseado.
Corolario 6.24. Sea G un grupo infinito. Entonces Λ(G) es no vacı́o. En particular,
Λ(G) 6= ∅ si y sólo si G es finito.
Demostración. Si G es Kleiniano planar, entonces podemos extraer una sucesión gn ∈ G de elementos diferentes. Ahora usamos el resultado anterior.
Corolario 6.25. Sea G un grupo Kleiniano planar. Entonces las posibilidades para
Λ(G) son las siguientes: (i) ∅; (ii) un punto ; (iii) dos puntos; ó (iv) infinito.
Demostración. Supongamos que G es Kleiniano planar con al menos tres puntos lı́mites. Por lo anterior, G debe ser infinito. Podemos extraer una sucesión gn ∈ G
de elementos diferentes. Sean x, y ∈ Λ(G) como en la proposición anterior. Como
6.11. SUPERFICIES DE KLEIN DE GRUPOS KLEINIANOS
73
al menos tenemos otro punto lı́mite, tenemos que su órbita por la sucesión gn nos
dará un número infinito de puntos lı́mites.
Si G es Kleiniano planar y Λ(G) contiene al menos tres puntos, entonces decimos que
G es un grupo no-elemental. En caso contrario, decimos que G es un grupo elemental.
Hasta ahora hemos definido los puntos lı́mites de un grupo G como aquellos puntos
que no son puntos de discontinuidad de G. Verificaremos que si G es Kleiniano planar,
entonces estos puntos son de hecho puntos lı́mites de órbitas. Más precisamente:
Corolario 6.26. Sea G un grupo Kleiniano planar y p ∈ Λ(G). Entonces existe un
punto q ∈ Λ(G), no necesariamente diferente de p, y existe una sucesión gn ∈ G
de elementos diferentes tal que gn (z) converge uniformemente a p en compactos de
b − {q}.
C
Demostración. El resultado es independiente de conjugación, luego podemos
asumir que ∞ es punto de discontinuidad de G que no es punto fijo de ninguna
transformación diferente de la identidad. Como p es punto lı́mite de G, se sigue de
b convergiendo a p y existe una sucesión
la definición que existe una sucesión xn ∈ C
gn ∈ G de elementos diferentes tal que gn (xn ) converge a p. Podemos extraer una
subsucesión de gn y podemos encontrar puntos lı́mites x, y ∈ Λ(G) tal que gn (z)
b − {y}.
converge a x uniformemente en compactos de C
Si p 6= y, entonces tenemos que necesariamente x = p y estamos listos. Si p = y,
entonces p es lı́mite de la órbita de ∞. Si K es un compacto en Ω(G), entonces K
vive en el exterior común de todos (con la posible excepción de un número finito)
los cı́rculos isométricos de gn y gn−1 . Como los radios de estos cı́rculos tienden a cero,
entonces estamos listos.
Ejercicio. Usar lo anetrior para ver que si G es un grupo Kleiniano planar, entonces
b de manera que
Λ(G) es denso en ninguna parte, es decir, no existe abierto V ⊂ C
Λ(G) ∩ V es denso en V .
La demostración anterior en el caso que Λ(G) tiene infinitos puntos dice lo siguiente:
Corolario 6.27. Sea G un grupo Kleiniano planar y Λ(G) con al menos tres puntos.
Entonces Λ(G) es perfecto.
Corolario 6.28. Sea G un grupo discreto de transformaciones de Möbius. Si p ∈
Λ(G), entonces existe gn ∈ G de elementos diferentes tal que para todo q ∈ H3 vale
que gbn (q) converge a p, donde b
gn denota la extensión de Poincaré de gn .
Demostración. (1) Supongamos primero que Ω(G) 6= ∅. En este caso existe una
sucesión de elementos diferentes gn ∈ G y un punto q ∈ Λ(G) tal que para cualquier
74
6. GRUPOS KLEINIANOS
b − {q} se tiene que gn (u) y gn (v) convergen a p.
par de puntos diferentes u, v ∈ C
Consideremos la única geodésica L ⊂ H3 cuyos puntos finales son u y v. Es claro
entonces que gbn (L) debe converger a p. Tomemos un punto w ∈ L. Sea z ∈ H3 y sea
d la distancia hiperbólica entre w y z. Como b
gn es isometrı́a y b
gn (w) converge a p, es
claro entonces que lo mismo ocurre con b
gn (z).
b Basta con verificar que la órbita de un punto
(2) Supongamos ahora que Λ(G) = C.
3
w ∈ H debe contener a p como punto lı́mite. Si no fuese esto posible, entonces debe
existir un abierto U en R3 conteniendo en su interior al punto p de manera que la
órbita de w está en su exterior. Ahora, para cualquier otro punto z ∈ H3 . Como
las extensiones de Poincaré de las transformaciones de Möbius son isometrı́as, debe
ocurrir que la órbita de z debe mantenerse a distancia acotada de la órbita de w. En
particular, p tampoco puede ser punto lı́mite de su órbita. En consecuencia, si p no es
punto lı́mite de la órbita de un punto en H3 , entoncs no está en la órbita de ningún
b tal que el espacio delimitado por la semiesfera
punto de H3 . Tomemos un disco D ⊂ C
determinada por el borde de D conteniendo a D en su borde esté completamente
contenida en el abierto U. Ahora es claro que D sirve para ver que p debe ser un
punto de discontinuidad de G, una contradicción.
Proposición 6.29 (Lema de Shimizu-Leutbecher). Sea G us grupo discreto de transformaciones de Möbius. Si P (z) = z + 1 pertenece a G, entonces para toda transformación T ∈ G, T (∞) 6= ∞, se tiene que el radio de su cı́rculo isométrico es menor
o igual que uno.
Demostración. Supongamos por el contrario la existencia de T ∈ G, T (∞) 6=
∞, con radio de su cı́rculo isométrico mayor que uno. Usemos representantes matriciales
1 1
a b
P =
, T =
0 1
c d
donde ad − bc = 1. Luego estamos asumiendo que 0 < |c| < 1. Consideremos la
sucesión
an+1 bn+1
−1
Tn+1 = Tn P Tn =
,
cn+1 dn+1
con T0 = T . Inductivamente uno obtiene que
(1)
(2)
(3)
(4)
an+1 = 1 − an cn ;
bn+1 = a2n ;
cn+1 = −c2n ;
dn+1 = 1 + an cn .
n
Relación (3) asegura que |cn | = |c|2 el cual tiende a cero cuando n tiende a infinito,
en particular, la sucesión Tn consiste de elementos diferentes.
6.11. SUPERFICIES DE KLEIN DE GRUPOS KLEINIANOS
75
Relaciones (1) y (4) más la observación anterior aseguran que tomando K =
Max{|a|, 1} tenemos que
n
|an |, |dn | ≤ K
2
X
j=0
|c|j < ∞
De esto concluimos que las sucesiones (an ), (bn ), (cn ) y (dn ) son acotadas y luego
podemos considerar una subsucesión de (Tn ) para suponer que todas estas convergen.
Luego las relaciones (1)-(4) aseguran que an , bn , dn → 1 y cn → 0 cuando n → ∞, es
decir Tn → P , contradiciendo la discretitud de G.
Proposición 6.30. Sean f, g ∈ M transformaciones de Möbius, ambas diferente de
la identidad. Si una de ellas es loxodrómica y ambas tienen exactamente un punto fijo
en común, entonces el grupo generado por ellas es no-discreto.
El resultado anterior dice que no hay grupos discretos de transformaciones de Möbius
conteniendo transformaciones como se indica en la proposición.
Demostración. Podemos asumir que f es loxodrómico. Conjugando por una
transformación de Möbius si es necesario, podemos asumir que ∞ es el punto fijo en
común y que f también fija 0. Luego
f (z) = λ2 z, g(z) = az + b
donde
λ2 ∈
/ {0, 1} y b 6= 0
Si consideramos la sucesión Tm = f −m (g(f m(z))) = az + b/λm , entonces haciendo
tender m hacia +∞ si |λ| > 1 o hacia −∞ en caso contrario, obtenemos que Tm
converge a Q(z) = az, una contradicción para la discretitud.
Ejercicio. Sea G un grupo Kleiniano planar que deja invariante un punto. Entonces
G es elemental [Ind. Use el hecho que tal punto debe ser punto fijo de cada elemento
de G].
Corolario 6.31. Sea G un grupo Kleiniano planar no-elemental y F 6= ∅ un subconjunto cerrado de la esfera de Riemann que es invariante por la acción de G. Entonces
Λ(G) ⊂ F
Demostración. Si F consiste de sólo un punto, entonces este debe ser punto
fijo de toda transformación en G. La discretitud de G, el ejercicio (11) de la sección
6.5. y el resultado anterior aseguran que G es elemental. En consecuencia, F debe
tener cardinalidad al menos 2. Sea p ∈ Λ(G). Sabemos que existe un punto lı́mite q y
una sucesión gn ∈ G tal que gn (x) converge a p si x 6= q. Como F tiene al menos dos
puntos, podemos siempre asumir x ∈ F . Por otro lado, F es invariante por G lo cual
76
6. GRUPOS KLEINIANOS
dice que la órbita de x permanece en F . Ahora el hecho que F es cerrado asegura que
los puntos lı́mites de esta órbita también viven en F , es decir p ∈ F .
Ejemplo 6.2. Supongamos que tenemos un grupo Kleiniano planar G y una colección
∆ de componentes de Ω(G) tal que para todo T ∈ G tenemos que T (∆) ⊂ ∆. Entonces
la clausura ∆ es un cerrrado no vacı́o invariante por G. La proposición anterior asegura
que Λ(G) ⊂ ∂∆ (la frontera de ∆). Por otro lado, cada punto en ∂∆ no puede vivir
en Ω(G), al ser este un abierto, luego ∂∆ ⊂ Λ(G). Luego,
Λ(G) = ∂∆
Proposición 6.32 (Teorema de Jørgensen [Jørgensen]). Sean f, g transformaciones
de Möbius, ambas diferente de la identidad, f loxodrómica, sin puntos fijos en común,
tal que g no deja invariante el conjunto de puntos fijos de f , entonces, si hf, gi es
discreto, se debe cumplir que
|tr2 (f ) − 4| + |tr[f, g] − 2| ≥ 1
donde tr(Q) denota la traza de una matriz en SL(2, C) que representa la transformación de Möbius Q y [f, g] = f −1 g −1 f g.
6.11.2. Dominios Fundamentales. En esta subsección seguiremos más o
menos fielmente el libro de B. Maskit [Maskit1].
e Un subconjunto abierto D ⊂ Ω(G) es llamado
Sea G un grupo Kleiniano planar en M.
un dominio fundamental para G si:
(1) si T (D) ∩ D = ∅, para T ∈ G − {I};
(2) ∪T ∈G T (D) = Ω(G);
(3) El borde de D, es decir ∂D, consiste de puntos lı́mites del grupo G y un número
finito o numerable de arcos simples contenidos (por la posible excepción de
alguno de sus extremos) en Ω(G) llamados lados de D;
(4) Por cada lado s de D existe un lado s′ (no necesariamente distinto a s) y una
transformación Ts ∈ G − {I} tal que Ts (s) = s′ ;
(5) Para toda sucesión de lados diferentes de D, digamos sn , se tierne que sus
diámetros esféricos diam(sn convergen a cero;
(6) Para todo compacto K ⊂ Ω(G) existen sólo un número finito de T ∈ G tales
que T (D) ∩ D 6= ∅ (decimos que D es localmente finito).
Observación 6.3. En (4) de la definición anterior, tenemos que condición (1) obliga
a que (s′ )′ = s y Ts′ = Ts−1 . Además, esto dice que si s = s′ , entonces Ts2 = I.
Ejemplo 6.3.
(1) Sea G el grupo generado por una reflexión en un cı́rculo C.
Entonces un dominio fundamental para G puede ser uno de los dos discos
abiertos acotados por C.
6.11. SUPERFICIES DE KLEIN DE GRUPOS KLEINIANOS
77
(2) Sea G el grupo cı́clico generado por la rotación E(z) = e2πi/k z, donde k ∈
{2, 3, 4, ...}. Un dominio fundamental para G puede ser tomado como el sector
{z ∈ C : Arg(z) ∈ (0, 2π/k)}.
(3) Sea G el grupo generado por la transformación parabólica P (z) = z + 1. Un
dominio fundamental para G es dado por la franja {z ∈ C : Re(z) ∈ (0, 1)}.
(4) Sea G el grupo generado por la transformación loxodrómica L(z) = λeiθ z,
donde λ > 1. Entonces un dominio fundamental para G es dado por el anillo
{z ∈ C : 1 < |z| < λ}.
e conteniendo automorfismos antiholo(5) Sea G un grupo Kleiniano planar en M
morfos. Si D es un dominio fundamental para G, entonces D ∪ T (D) es un
dominio fundamental para G+ , donde T ∈ G − G+ .
Ejercicio. Dar ejemplos de conjuntos abiertos de Ω(G) donde falle sólo una de las
seis condiciones en la definición de dominio fundamental.
6.11.3. Región de Ford. Dado un grupo Kleiniano planar G, siempre podemos conjugarlo por una transformación de Möbius para suponer que ∞ no es punto
fijo de ninguna transformación en G − {I}. En particular, para cada transformación
T ∈ G, T 6= I podemos calcular el cı́rculo isométrico de esta. Cada uno de esos cı́rculos acota un disco en la esfera de Riemann que contiene a ∞, denotémoslo por DT .
La Región de Ford de este grupo G es por definición el interior de
\
D=
DT .
T ∈G−{I}
Ya que todo punto en Λ(G) es acumulado por la órbita de ∞ (los centros de cı́rculos
isomt́ericos) y los diámetros de los cı́rculos isométricos tienden a cero, tenemos que
todo punto lı́mite no puede vivir en la región de Ford de G, es decir, este conjunto es un
abierto contenido en Ω(G). La frontera de D está formada por puntos lı́mites y arcos
de cı́rculos isométricos (los cuales serán los lados de este dominio fundamental una
vez que hayamos verificado que efectivamente lo es), verificando condición (3) en la
definición de dominio fundamental. La observación sobre los diámetros de los cı́rculos
isométricos arriba nos da la condición (5) en la definición de dominio fundamental.
Para cada transformación T tenemos que
b − DT −1
T (DT ) = C
con lo cual vemos que T (D) ∩ D = ∅, verificando condición (1) de la definición de
dominio fundamental. También esta propiedad nos dice que vale la condición (6). En
efecto, sea K ⊂ Ω(G) un compacto. Supongamos que existe una sucesión Tn ∈ G de
elementos diferentes tales que Tn (D) ∩ K = ∅. Como los diámetros Euclideanos de
Tn (D) tienden a cero por 6.6, esto obligarı́a a que en K hubiese al menos un punto
lı́mite de G, una contradicción al hecho que K ⊂ Ω(G).
78
6. GRUPOS KLEINIANOS
Veamos la condición (4). Sea s un lado de D, luego s es un arco del cı́rculo isométrico
de una transformación T0 ∈ G. Para cada z ∈ s sólo pueden haber un número finito
de otros cı́rculos isométricos pasando por z; en caso contrario, como los diámetros de
una colección infinita de estos cı́rculos tienden a cero, z serı́a punto lı́mite de la órbita
de ∞, una contradicción al hecho que s ⊂ Ω(G). De la misma manera, la colección
de puntos en s por donde pasan al menos dos cı́rculos isométricos debe ser discreto
en s. Sea T0 (s) = s′ . Veamos que s′ es tambien un lado de D. Tomemos cualquier
punto z ∈ s por el cual no pasa otro cı́rculo isométrico. Esto es lo mismo que decir
que |T0′ (z)| = 1 y |T ′ (z)| < 1 para todo T ∈ G − {T0 , I} (por la definición de D no
puede ocurrir que |T ′ (z)| > 1 para ningun T ∈ G − {I}). Tomemos w = T0 (z) ∈ s′ .
Luego, para T ∈ G − {I} tenemos que
|T ′ (w)| = |T ′ (T0 (z)| = |(T T0 )′ (z)|/|T0′ (z)| ≤ 1
con igualdad si y sólo si T = T0−1 . Esto nos da que w vive en la clausura de D. De
esta manera, s′ debe ser un lado de D y Ts = T0 .
Veamos ahora la condición (2). Queremos ver que todo punto z ∈ Ω(G) es equivalente
a un punto en la clausura de D.Es claro que todo punto z ∈ D∩Ω(G) satisface esto. Sea
z ∈ Ω(G) − D que no este en la órbita de ∞. Luego z vive, por la posible excepción de
un número finito (y que no es cero) de transformaciones de G, en DT . En particular,
existe una transformación T0 ∈ G con |T0′ (z)| maximal. Luego, si denotamos por
w = T0 (z), entonces para todo T ∈ G tenemos que
|T ′ (w)| = |T ′ (T0 (z)| = |(T T0 )′ (z)|/|T0′ (z)| ≤ 1
Si estamos en la situación que |T ′ (w)| < 1, para cada T ∈ G − {I}, entonces w ∈ D.
En efecto, como w ∈ Ω(G), para cada R > 0 existe sólo un número finito de elementos
T ∈ G tal que |T ′ (w)| ≥ R. Esto nos dice que podemos encontrar un abierto U ⊂
Ω(G), w ∈ U, tal que para cada p ∈ U vale que |T ′ (p)| < 1 para T ∈ G − {I}.
En efecto, en caso contrario deberı́amos encontrar una sucesión infinita de cı́rculos
isométricos acercandose a w. Como sus radios deben converger a cero, sus centros
convergen a w mostrando que w es lı́mite de la órbita de ∞, una contradicción.
Por otro lado, supongamos que existe T1 ∈ G − {I} tal que |T1′ (w)| = 1. Si w vive
en la clausura de D, entonces estamos listos. Supongamos que esto no ocurre. Esto
sólo es posible si por w pasan al menos tres cı́rculos isométricos diferentes. Como
la cantidad de cı́rculos isométricos es numerable (G es numerable), la cantidad de
puntos de tal tipo es numerable. En Ω(G) tal colección debe también ser discreta
por el el hecho que los diámetros de los cı́rculos isométricos tieneden a cero y en
Ω(G) no hay puntos lı́mites de G. Consideremos el cubrimiento ramificado holomorfo
P : Ω(G) → Ω(G)/G. Entonces P (D ∩ Ω(G)) ⊂ Ω(G)/G es denso en Ω(G)/G. En
particular, podemos encontrar una sucesión wn ∈ D y una sucesión de elementos
diferentes Tn ∈ G tal que Tn (wn ) → w. Como los diámetros de Tn (D) tienden a
cero, obtendrı́amos que w ∈ Λ(G), una contradicción. Hemos obtenido entonces una
manera de calcular dominios fundamentales para cualquier grupo Kleiniano planar:
6.11. SUPERFICIES DE KLEIN DE GRUPOS KLEINIANOS
79
Teorema 6.33. [Maskit1] La Región de Ford de un grupo Kleiniano planar G tal
que T (∞) 6= ∞ para todo T ∈ G − {I} es un dominio fundamental.
Ejercicio. Calcular la Región de Ford para todos los grupos cı́clicos Kleinianos
planares.
6.11.4. Dominios de Dirichlet. Usando la extensión de Poincaré de automorb a isometrı́as del espacio
fismos holomorfos/antiholomorfos de la esfera de Riemann C
3
hiperbólico H permite dar otra construcción de dominios fundamentales para grupos
e Como
Kleinianos planares. Para esto, supongamos que G es un grupo discreto en M.
3
G actúa como grupo discontinuo de isometrı́as de H , entonces es posible encontrar
puntos p ∈ H3 tales que Gp = {T ∈ G : T (p) = p} es trivial. Tomando p uno de
esos puntos, podemos hacer la siguiente construcción. Por cada T ∈ G, T 6= I, el
subconjunto B(T ) = {(z, t) ∈ H3 : dH3 (p, (z, t)) < dH3 (T (p), (z, t))} es un subconjunto abierto acotado por una semiesfera que corta ortogonalmente el borde de H3 . Si
consideramos la intersección
\
D(p) :=
B(T ),
T ∈G−{I}
obtenemos un subconjunto de H3 llamado un dominio de Dirichlet de G.
Un polihedro en el espacio hiperbólico H3 (o bien en B 3 ) es una intersección a lo más
numerable de semiespacios (regiones abiertas acotadas por semiesferas ortogonales al
borde) de manera que si K es cualquier compacto de H3 , entonces sólo un número
finito de tales semiesferas cortan K.
Un polihedro fundamental para un grupo discreto de isometrı́as de H3 es por definición
un polihedro D ⊂ H3 satisfaciendo las siguientes propiedades:
(1) Si g ∈ G, g 6= I, entonces g(D) ∩ D = ∅;
(2) Si p ∈ H3 , entonces existe g ∈ G tal que g(p) pertenece a la clausura de D;
(3) Por cada cara C de D existe una cara C ′ (no necesariamente diferente) y un
gC ∈ G tal que gC (C) = C ′ , de manera que gC ′ = gC−1.
Teorema 6.34. [Maskit1] El dominio de Dirichlet de G resulta ser un polihedro
fundamental para la acción de G en H3 . Más aún, el interior de la intersección de la
b determina un dominio fundamental
clausura Euclideana de este con el borde ∂H3 = C
para la acción de G en Ω(G).
6.11.5. Relación entre Dominios Fundamentales y Cocientes Ω(G)/G.
Supongamos que G es un grupo Kleiniano planar y que D es un dominio fundamental
para G. Tenemos el espacio cociente Ω(G)/G que resulta ser una espacio topológico
Hausdorff. Denotemos por
π : Ω(G) → Ω(G)/G
80
6. GRUPOS KLEINIANOS
la proyección natural, la cual es una función continua y abierta. Por otro lado, podeb = D ∩ Ω(G). En esta clausura
mos considerar la clausura de D en Ω(G), digamos D
tenemos una relación de equivalencia determinada por las identificaciones de los
b
lados de D. Denotemos el espacio cociente por D/G
y la proyección natural por
b
b
Q : D → D/G. Luego, la proyección π : Ω(G) → Ω(G)/G induce de manera natural
una función
b
P : D/G
→ Ω(G)/G
tal que π = P Q. Es claro que esta es una función biyectiva. Restringida a Q(D), esta
función es un homeomorfismo.
En general, uno no tendrı́a por que esperar que esta función P fuese un homeomorfismo, pero el siguiente resultado dice que esto es verdad:
Teorema 6.35. [Maskit1] Si D es un dominio fundamental (localmente finito) para
el grupo Kleiniano planar G, entonces
b
P : D/G
→ Ω(G)/G
es un homeomorfismo.
Observación 6.4. Es importante para el teorema anterior la condición ”localmente
finito”que hemos impuesto a la definición de dominio fundamental. Miremos el siguiente ejemplo. Sea G el grupo generado por la transformación loxodrómica L(z) = 2z.
En este caso, Ω(G) = C − {0}. Entonces si D1 = {z ∈ C : 1 < |z| < 2}, tenemos que
D1 es un dominio fundamental. Además, la relación de equivalencia dada sobre este
dominio nos dá como espacio cociente al toro S 1 × S 1 que es exactamente una foto
topológica de Ω(G)/G. Por otro lado, si escogemos
3π
D2 = {z ∈ C : 1 < |z| < 2, 0 ≤ Arg(z) ≤
}∪
2
−2
3π
−1
< Im(z) <
,
≤ Arg(z) < 2π}
{z ∈ C :
Re(z) + 1
Re(z) + 1 2
entonces se satisfacen todas la condiciones de dominio fundamental menos la condición
de ser localmente finito. Es fácil ver que el espacio cociente de D2 por la acción de G
no es compacto.
6.12.
Subgrupos Kleinianos Planares
e y H es un subgrupo de ı́ndice
Ya habı́amos observado que si G es un subgrupo de M
finito en G, entonces G es discreto si y sólo si H lo es. De hecho, ahora podemos decir
un poco más:
Proposición 6.36. Sea G un grupo discreto y H un subgrupo de ı́ndice finito de G,
entonces Ω(G) = Ω(H) y Λ(G) = Λ(H). En particular, G es Kleiniano planar si y
sólo si H es Kleiniano planar.
6.12. SUBGRUPOS KLEINIANOS PLANARES
81
Demostración. Basta con verificar que tienen el mismo conjunto lı́mite. Como
H < G, es claro que Λ(H) ⊂ Λ(G). Sea p ∈ Λ(G). Como G es discreto, existe una
b tal que gm (z0 ) converge
sucesión {gm } de elementos diferente en G y un punto z0 ∈ C
a p.
Al ser H subgrupo de ı́ndice finito en G, tenemos que G = H ∪ Hx1 ∪ · · · ∪ Hxk ,
donde x1 , ..., xk ∈ G. Luego debe existir una subsucesión infinita de {gm } donde todos
sus transformaciones viven en el mismo Hxj . Podemos suponer ahora que gm ∈ Hx1
para todo m. En este caso gm = hm x1 . Es claro que {hm } es una sucesión infinita de
transformaciones diferentes. Ahora hm (x1 (z0 ) converge a p diciendo que p ∈ Λ(H). b Entonces G es Kleiniano planar si
Corolario 6.37. Sea G un grupo discreto en M.
+
y sólo si G es Kleiniano planar.
Proposición 6.38. Sea G un grupo Kleiniano no-elemental (es decir, Λ(G) tiene al
menos tres puntos) y H 6= {I} un subgrupo normal de G, entonces se tiene Ω(G) =
Ω(H) y Λ(G) = Λ(H).
Demostración. (1) El grupo H no puede ser finito. En efecto, supongamos que H
es finito y tomemos un elemento elı́ptico h ∈ H diferente de la identidad. Podemos
encontrar dos transformaciones g1 y g2 en G que son loxodrómicas y que no conmutan
(esto por ser G no elemental). Sea g ∈ {g1 , g2} y consideremos la sucesión hn =
g n hg −n ∈ H. Como H es finito, podemos extraer una subsucesión tal que hn = h0 .
Esto dice entonces que g n envı́a los puntos fijos de h en los puntos fijos de h0 . Luego,
g debe obligatoriamente fijar esos puntos (la órbita positiva por g de un punto que
no es punto fijo de ella converge a uno de los puntos fijos). Luego, tanto g1 como g2
tendrı́an los mismos puntos fijos, una contradicción al hecho que esta no conmutan.
Otra manera es la siguiente. Si H 6= {I} fuese finito, entoces la colección de puntos
fijos de los elementos de H − {I} serı́a un conjunto finito no vacı́o, luego un conjunto
cerrado no vacı́o. Pero el hecho que H es subgrupo normal asegura que este conjunto
es también invariante por G, luego deberı́a contener Λ(G) por el corolario 6.31, una
contradicción a la infinitud de este.
(2) Como H no es finito, Λ(H) 6= ∅ como consecuencia del corolario 6.23.
(3) Λ(H) es un un conjunto cerrado invariante por G.
(4) Todo conjunto cerrado no vacı́o por un grupo Kleiniano planar no-elemental contiene a Λ(G), como consecuencia del corolario 6.31.
(5) En conclusión, como siempre Λ(H) ⊂ Λ(G), lo anterior da el resultado deseado.
Observación 6.5. En la categorı́a de grupos discretos, lo anterior no siempre es
cierto. Por ejemplo, si H es generado por T (z) = −z y G consiste de todos las
82
6. GRUPOS KLEINIANOS
transformaciones de Möbius de la forma Q(z) = λz, donde λ ∈ R − 0, entonces es
claro que H es subgrupo normal de G, H es discreto al ser finito y G no es discreto
pues tenemos que la sucesión Qn (z) = (1 − 1/n)z converge a la identidad cuando n
tiende a infinito. Pero si agregamos la hipótesis extra que en H existan al menos dos
transformaciones h1 , h2 , ambas diferente de la identidad, tal que F ix(h1 ) 6= F ix(h2 ),
entonces H es discreto si y sólo si G lo es.
6.12.1. Subgrupos de Indice Finito y Cubrimientos Ramificados.
Supongamos que G es un grupo Kleiniano planar y H es un subgrupo normal de
G el cual es no elemental. Entonces ambos grupos tienen la misma región de discontinuidad Ω. Sea ∆ una colección de componentes de Ω que sea invariante por G.
Entonces tenemos el siguiente diagrama de cubrimientos ramificados
ΩB
P
BB
BB
B
Q◦P BB
Ω/G
/ Ω/H
x
x
xx
xx Q
x
x{
Si tenemos que H es un subgrupo de ı́ndice finito de G, el cual no es necesariamente
un subgrupo normal de G, entonces lo anterior también vale como consecuencia de la
proposición anterior.
De manera recı́proca, consideremos un cubrimiento (posiblemente ramificado y posiblemente no Galois) de grado d
π:S→R
sobre una superficie de Riemann R de género g.
Denotemos por Bπ = {q1 , ..., ql } ⊂ R al conjunto de los valores de ramificación de π
(en caso de existir). Por cada punto qj tenemos su preimágen
π −1 (qj ) = {pj1 , ..., pjkj }
y denotemos por dm,j al grado de π en el punto pjm . Sea
bj = mcm(d1,j , ..., dkj ,j )
Escojamos puntos x1 , ..., xt ∈ R − Bπ y valores enteros a1 , ..., at ≥ 2. Consideremos
el orbifold definido por R con puntos especiales dados por q1 , ..., ql , x1 , ..., xt y con
valores de ramificación dados por b1 , ..., bl , a1 , ..., at , respectivamente. Esta orbifold es
uniformizada por un grupo
b
Γ < Isom+ (R)
donde
b C, H2 }
b ∈ {C,
R
Γ = hα1 , β1 , ..., αg , βg , z1 , ..., zl , w1, ..., wt :
6.12. SUBGRUPOS KLEINIANOS PLANARES
83
g
t
l
Y
Y
Y
[αj , βj ]
zi
wk = 1, z1b1 = · · · = zlbl = w1a1 = · · · = wtat = 1i
j=1
i=1
k=1
Consideremos
b∗ = R
b − π −1 {q1 , ..., ql , x1 , ..., xt }
(1) R
Γ
(2) S ∗ = S − π −1 {q1 , ..., ql , x1 , ..., xt }
(3) R∗ = R − {q1 , ..., ql , x1 , ..., xt }
b∗
Proposición 6.39. Supongamos que las tres superficies de Riemann R∗ , S ∗ y R
tienen el mismo cobertor universal. Entonces existe K < Γ (posiblemente con torsión)
b
de ı́ndice [Γ : K] = d tal que S = R/K
(con posibles singularidades) and π factoriza
b → R el cubrimiento (ramificado)
a traves K en Γ, es decir, si denotamos por πΓ : R
b → S el cubrimiento (ramificado) definido por
universal definido por Γ y por πK : R
K, entonces πΓ = π ◦ πK . Más aún, si π es Galois, entonces K es subgrupo normal
de Γ.
b
Observación 6.6. El orbifold R/K
es S con unos puntos ramificados, provenientes
de la preimágen por π de los puntos x1 , ..., xt , q1 , ..., ql .
e el covertor universal de R
b∗ . Entonces tenemos un grupo
Demostración. Sea R
e (infinitamente generado por transformaciones parabólicas en
L de isometrias de R
caso que l + t > 0), subgrupos N, Q de L, donde N es subgrupo normal tal que
e
Γ = L/N y Q de ı́ndice d tal que S ∗ = R/Q.
e → S, πN : R
e → R
b∗ y πL : R
e → R∗ los respectivos
Si denotamos por πQ : R
cubrimientos definidos por esos grupos, entonces tenemos que:
π ◦ πQ = πL = πΓ ◦ πN
En este punto observemos que si π : S → R es Galois, entonces Q también es subgrupo
normal de L y π es definido por el grupo de automorfismos L/Q de S.
Por cada j = 1, ..., l (respectivamente, cada i = 1, ..., t) escogemos un camino cerrado simple δj (respectivamente, θi ) que rodee la pinchadura definida por qj (respectivamente, xi ) y defina el borde de un disco pinchado (es decir, no rodee otras
pinchaduras).
b∗ → R∗ es el cubriemnto planar más
Observemos que el cubrimiento planar πΓ : R
b
bajo para el cual δ1b1 ,..., δl l , θ1a1 ,..., θtat se levantan en caminos cerrados. Esta es la
definición del grupo normal N en L.
Por la definición de los valores b1 ,..., bl y el hecho que x1 , ..., xt no son valores de
ramificación de π, tenemos que las curvas anterioes también se leventan en caminos
cerrados en S ∗ por el cubrimiento π : S ∗ → R∗ . Esto ahora nos está diciendo que
necesariamente N < Q. Ya que N es subgrupo normal de L, entonces N es subgrupo
b∗ → S ∗ .
normal de Q. Tenemos de esta manera un cubrimiento Galois πQ/N : R
84
6. GRUPOS KLEINIANOS
Ahora tenemos
π ◦ πQ/N = πΓ
Ya que cada pinchadura en R∗ se levanta en una pinchadura tanto en S ∗ como en
b∗ con grados finitos (localmente), podemos extender πQ/N como un cubrimiento
R
b → S de manera que sigamos teniendo la
(posiblemente ramificado) desde πQ/N : R
igualdad anterior. El subgrupo K = Q/N < L/N = Γ es el buscado.
6.12.1.1. Aplicación. Consideremos un par de cubrimientos (posiblemente con
ramificaciones y posiblemente no Galois) sobre una misma superficie de Riemann R,
digamos:
π1 : S1 → R, π2 : S2 → R
de manera que sus conjuntos de valores de ramificación en R sean disjuntos, es decir,
Bπ1 ∩ Bπ2 = ∅
La proposición anterior nos dice que existe un grupo de isometrı́as Γ con subgrupos
K1 , K2 , donde Kj tiene ı́ndice dj (el grado del cubrimiento ramificado πj ) y πj es dado
por la acción de Kj . Como K1 y K2 tienen ı́ndice finito en Γ, tenemos que K1 ∩ K2
también tiene ı́ndice finito en Γ. Luego el orbifold S uniformizado por K1 ∩ K2 define
un cobertor común de S1 y de S2 .
Si tomamos la intersección de todas las clases de conjugación de K1 ∩K2 obtendremos
un subgrupo normal de ı́ndice finito (pues es de hecho la intersección finita de subgrupos de ı́ndice finito ya que K1 ∩ K2 tiene ı́ndice finito). De esta manera podemos
encontrar un cobertor común de S1 y de S2 que es Galois.
CAPÍTULO 7
Cubrimientos Homológicos
7.1.
Jacobianas y Matrices de Riemann
Consideremos una superficie de Riemann S de género g ≥ 1. Denotemos por
H1 (S, Z) ∼
= ⊕2g Z al primer grupo de homologı́a de S. Este grupo codifica (en parte)
la parte topológica de la superficie S. Una base de homologı́a de S es una base simpléctica si está representada por 2g curvas cerradas orientadas, α1 ,..., αg , β1 ,..., βg ,
tal que
αj · αk = βj · βk = 0
αj · βj = δkj
También asociado a S es el espacio vectorial complejo de dimensión g de las 1-formas
holomorfas [Farkas-Kra], denotado por H1,0 (S). Existe una base de este espacio,
digamos w1 ,..., wg , satisfaciendo que
Z
wk = δjk
αj
llamada una base dual a la base simpléctica anterior. En este espacio tenemos una
forma Hermitiana possitiva definida dada por:
"Z
#
Z Z
Z
Z
Z
g
X
i
i
θ1 ∧ θ2 =
θ1
θ2 −
θ1
θ2
(θ1 , θ2 ) =
2
2 j=1 αj
S
βj
βj
αj
para θ1 , θ2 ∈ H1,0 (S). Por ejemplo, para la base dual w1 ,..., wg anterior tenemos que
!
Z
wk
(wj , wk ) = Im
βj
Luego, esta forma Hermitiana queda representada en esta base dual como
!
Z
g
g
X
X
xj yk Im
((x1 , ..., xg ), (y1 , ..., yg )) =
wk
j=1 k=1
βj
Si denotamos por H1,0 (S)∗ el espacio dual de H1,0 (S), entonces la forma Hermitiana
anterior nos da un anti-isomorfismo
Ψ : H1,0 (S) → H1,0 (S)∗
85
86
7. CUBRIMIENTOS HOMOLÓGICOS
definido por
Ψ(θ) = (·, θ)
De esta manera, tenemos inducida la forma Hermitiana
(Ψ(θ1 ), Ψ(θ2 )) = (θ1 , θ2 )
Integración de 1-formas sobre curvas (orientadas) en S da la función
∗
ΦS : H1 (S, Z) → H1,0 (S)
definida por
φ([γ]) =
Z
γ
Ejercicio. Verificar que esta función es un homomorfismo inyectivo entre Z-módulos.
La base
dual en HR1,0 (S)∗ respecto a la base w1 ,..., wg es exactamente la dada por
R
w1∗ = α1 ,..., wg∗ = αg
De esta manera, la forma Hermitiana inducida en H1,0 (S)∗ en la base dual queda dada
por
!
Z
g
g
X
X
((x1 , ..., xg ), (y1 , ..., yg )) =
xj yk Im
wk
βj
j=1 k=1
∗
Se puede ver H1 (S, Z) como un reticulado en el espacio H1,0 (S) . El cociente
J(S) = (H1,0 (S))∗ /H1 (S, Z)
es la Jacobiana de S, la cual resulta ser una variedad Abeliana principalmente polarizada (ver la primera parte de este libro).
Usando la base simpléctica α1 ,..., αg , β1 ,..., βg y su base dual w1 ,..., wg de 1-formas
holomorfas en S, uno puede escribir lo anterior
∗ en coordenadas. Esto es, si usamos
la∗
1,0
1,0
∗
∗
base dual w1 ,..., wg para el espacio H (S) , entonces podemos identificar H (S)
b g y el reticulado H1 (S, Z) se identifica con un reticulado L en C
b g generado por los
con C
vectores e1 = (1, 0, ..., 0), e2 = (0, 1, 0, ..., 0),..., eg = (0, ..., 0, 1), z1 = (z1,1 , ..., zg,1 ),...,
zg = (z1,g , ..., zg,g ), donde
Z
Z
zkj =
wk =
wj
βj
βk
La matriz Z = (z1 z2 · · · zg ) es llamada una matriz de Riemann para S. Luego J(S) es
analı́ticamente equivalente a la variedad abeliana principalmente polarizada obtenida
b g /L con la polarización dada por
como C
((x1 , ..., xg ), (y1, ..., yg )) =
g
g
X
X
j=1 k=1
xj yk Im(zjk )
7.2. VARIEDADES DE PRYM
87
Observación 7.1. Denotemos por P ic0 (S) el espacio de las clases de divisores de
grado cero en S (un divisor de grado cero es trivial si es el divisor de una función
meromorfa en S). Tomemos un punto p0 ∈ S. El teorema de Abel [Farkas-Kra] dice
que la función
H : P ic0 (S) → J(S)
definida por
Z p1
Z qg Z pg Z q1
−···−
−
+···+
H(p1 + · · · + pg − q1 − · · · − qg ) =
p0
p0
p0
p0
resulta ser un isomorfismo.
7.2.
Variedades de Prym
Supongamos que tenemos un cubrimiento ramificado π : R → S entre dos superficies
de Riemann R y S, de géneros γ y g, respectivamente. Asociado a este cubrimiento
tenemos asociado el siguiente diagrama commutativo:
Φ
P
R
R
H1 (R, Z) −→
H1,0 (R)∗ −→
J(R)
H1,0 (π)∗ ↓
H1 (π) ↓
Φ
donde
J(π) ↓
P
S
S
H1 (S, Z) −→
H1,0 (S)∗ −→
J(S)
H1 (π) : H1 (R, Z) → H1 (S, Z)
es el homomorfismo inducido por π : R → S al nivel del primer grupo de homologı́a;
H1,0 (π)∗ : H1,0 (R)∗ → H1,0 (S)∗
es la función lineal sobreyectiva inducida a nivel del dual de la formas holomorfas;
J(R) = H1,0 (R)∗ /ΦR (H1 (R, Z)) J(S) = H1,0 (S)∗ /ΦS (H1 (S, Z))
son las variedades Jacobianas de R y S, respectivamente;
J(π) : J(R) → J(S)
es el homomorfismo sobreyectivo inducido sobre las Jacobianas;
PR : H1,0 (R)∗ → J(R),
PS : H1,0 (S)∗ → J(S)
son las proyecciones naturales sobre las respectivas Jacobianas.
Ahora, si bien puede ocurrir que H1 (π) : H1 (R, Z) → H1 (S, Z) no es necesariamente
sobreyectiva, tenemos que, al ser π : R → S de grado finito, el cociente
K = H1 (S, Z)/H1 (π)(H1 (R, Z))
es un grupo Abeliano finito. Consideremos los reticulados
Λ1 = Ker(H1,0 (π)∗ ) ∩ ΦR (H1 (R, Z))
88
7. CUBRIMIENTOS HOMOLÓGICOS
Λ2 = Ker(H1,0 (π)∗ )⊥ ∩ ΦR (H1 (R, Z))
y los subespacios
V1 = Ker(H1,0 (π)∗ )
V2 = Ker(H1,0 (π)∗ )⊥
donde la ortogonalidad es tomada respecto a la forma Hermitiana definida en H1,0 (R)∗ .
Denotemos por
^ : R → S) = PR (((H1,0 (π)∗ )−1 (ΦS (H1 (S, Z)))
Prym(π
al núcleo del homomorfismo sobreyectivo de grupo J(π). Este puede ser no conexo.
La componente conexa de este subgrupo que contiene a 0 ∈ J(R) es denotada por
Prym(π : R → S)
y llamada la variedad de Prym del cubrimiento π : R → S. No es dificil ver que
Prym(π : R → S) = PR (V1 )
= V1 /Λ1
Definamos
[ := PR (V2 )
J(S)
= V2 /Λ2
Usando los siguientes hechos:
(i) H1,0 (π)∗ : V2 → H1,0 (S)∗ es un isomorfismo, y
(ii) H1,0 (π)∗ (Λ2 )
es
un
submodulo
ΦS (H1 (S, Z))/H1,0 (π)∗ (Λ2 ) = K,
de
ΦS (H1 (S, Z))
tal
que
obtenemos que
[
J(S)/K
= J(S),
[ es isógena a J(S), con núcleo dado por K.
es decir, que J(S)
Por otro lado, Λ1 y Λ2 generan en ΦR (H1 (R, Z)) un subreticulado Λ del mismo rango.
Tenemos que:
(1) Si Λ = ΦR (H1 (R, Z)), entonces
[
J(R) = Prym(π : R → S) × J(S)
lo cual dice que tenemos un isomorfismo de variedades abelianas, donde las po[ son las inducidas por la polarización
larizaciones en Prym(π : R → S) y J(S)
en J(R);
7.2. VARIEDADES DE PRYM
89
(2) Si Λ 6= ΦR (H1 (R, Z)), entonces
[
J(R) = (Prym(π : R → S) × J(S))/(Φ
R (H1 (R, Z))/Λ)
lo cual dice que J(R) es isógena al producto
[
Prym(π : R → S) × J(S)
con núcleo dado por el grupo abeliano finito ΦR (H1 (R, Z))/Λ.
En particular, cuando K = {0} y Λ = ΦR (H1 (R, Z)), tenemos que
J(R) = Prym(π : R → S) × J(S)
Lo anterior puede ser visto del siguiente diagrama commutativo
H 1,0 (R)∗ = V1 + V2
yy
yy
y
ΦR (H1 (R,Z)) yyy
yy
yy
y
y
yy
|yy
J(R)
NNN
NNN
NNN
NNN Λ
NNN
NNN
NNN
NNN
'
/
ΦR (H1 (R,Z))/Λ
[
Prym(π : R → S) × J(S)
π2
J(π)
J(S)
K
/
[
J(S)
[ → J(S)
[ es la proyección en la segunda coordedonde π2 : Prym(π : R → S) × J(S)
nada. Es decir, la función J(π) : J(R) → J(S) es isógena a la proyección π2 .
Ejemplo 7.1. Consideremos R un toro, es decir una superficie de Riemann de género
uno. Tomemos en R un automorfismo τ : R → R de orden dos y sin puntos fijos. Sea
S = R/τ el toro cociente y denotemos por π : R → S al cubrimiento holomorfo no
ramificado de grado dos inducido por la acción de τ . En este caso, podemos escoger
una base simpléctica {α, β} para R tal que τ (α) = α y τ (β) = β. Escojamos δ = π(α)
y η = π(β). Entonces, {δ, η} da una base simpléctica para S. En este caso, K = Z/2Z
y H1,0 (π)∗ es un isomorfismo. Tomemos w la base dual de H 1,0 (R) y θ la base dual
de H 1,0 (S), respecto a las bases simplécticas anteriores. Denotando por
Z
Z
τR = w, τS = θ
β
uno obtiene que
2τS = τR
η
90
7. CUBRIMIENTOS HOMOLÓGICOS
De esta manera, usando las bases duales w ∗ en H1,0 (R)∗ y θ∗ en H1,0 (S)∗ , tenemos
que H1,0 (π)∗ (x) = x. En particular,
(H1,0 (π)∗ )−1 (ΦS (H1 (S, Z)) = {n+mτS ; n, m ∈ Z} = {n+(m/2)τR ; n, m ∈ Z}
es decir,
^ : R → S) = hp; 2p = 0i ∼
Prym(π
= Z/2Z
Prym(π : R → S) = {0}
[
J(S)/K
= J(S) = S
[
R = J(R) = J(S)
Ejemplo 7.2. Consideremos una superficie de Riemann R de género g = 2γ junto
a una involución conformal τ : R → R, es decir un automorfismo conformal de R de
orden dos, tal que τ tiene exactamente dos puntos fijos. En este caso, S = R/τ es
una superficie de Riemann de género γ con exactamente dos puntos de ramificación
de orden dos. Denotemos por π : R → S el cubrimiento ramificado de grado dos
inducido por la acción de τ . Podemos escoger una base symplectica de R, digamos
{α1 , ..., αg , β1 , ..., βg }
y una base symplectica de S, digamos
{δ1 , ..., δγ , η1 , ..., ηγ }
de manera que valen las siguientes igualdades:
(1) H1 (π)(αj ) = H1 (π)(αγ+j ) = δj , j = 1, ..., γ;
(2) H1 (π)(βj ) = H1 (π)(βγ+j ) = ηj , j = 1, ..., γ;
Denotemos por {w1 , ..., wg } la base dual de H1,0 (R) respecto a {α1 , ..., αg } y por
{θ1 , ..., θγ } a la base dual de H1,0 (S) respecto a la base {δ1 , ..., δγ }. Igualdad (1) arriba
asegura que
(3) H1,0 (θj ) = wj + wγ+j , j = 1, ..., γ.
R
R
Denotemos por τjk = τkj = βj wk y por sjk = skj = ηj θk . Entonces las matrices de
Riemann de R y S, en las bases symplecticas anteriores, son dadas por
ZR = (τjk );
ZS = (sjk )
respectivamente. Igualdad (2) nos da las siguientes igualdades:
(4) τj γ+k = τk γ+j , 1 ≤ j ≤ k ≤ γ;
(5) τj γ+k = sjk − τjk , 1 ≤ j ≤ k ≤ γ;
(6) τγ+j γ+k = τjk , 1 ≤ j ≤ k ≤ γ.
Igualdades (4)-(6) nos dicen que
Z1
ZS − Z1
ZR =
ZS − Z1
Z1
donde Z1 es submatriz γ × γ de ZR .
7.2. VARIEDADES DE PRYM
91
R
Identifiquemos H1,0 (R)∗ con Cg y H1,0 (S)∗ con Cγ , de manera que αj es identificada con el vector canónico ej = (0, ...,
R 0, 1, 0, ..., 0), donde el 1 va en la posición j ∈ {1, ..., g}, y de manera que δk s identificada con el vector canónico
Ek = (0, ..., 0, 1, 0, ..., 0), donde el 1 va en la posición k ∈ {1, ..., γ}. Nuestra función H1,0 (π)∗ : H1,0 (R)∗ → H1,0 (S)∗ se puede identificar con la función
Q : Cg → Cγ : (x1 , ..., xg ) 7→ (x1 + xγ+1 , x2 + xγ+2 , ..., xγ + x2γ )
Luego, el núcleo de H1,0 (π)∗ es identificado con el núcleo V1 de Q el cual es generado
por los vectores
e1 − eγ+1 , e2 − eγ+2 , ..., eγ − e2γ
y luego la intersección del reticulado definido por H1 (R, Z) se identifica con el reticulado de V1 generado por los vectores
e1 − eγ+1 , ..., eγ − e2γ , τ1 − τγ+1 , ..., τγ − τ2γ ,
donde τj representa la columna j-ésima de ZR . En particular, si identificamos V1 con
Cγ de manera que ej − eγ+j es identificado con Ej , j = 1, ..., γ, obtenemos que la
matriz de Riemann asociada a la variedad Prym(π : R → S) es dada por
ZPrym(π:R→S) = 2Z1 − ZS
No es dificil ver que la polarización de Prym(π : R → S) que es inducida por la de
J(R) es dos veces la principal.
En la construcción hecha en el ejemplo anterior, podemos fijar la superficie de Riemann S y sólo variar sus puntos de ramificación de manera que ellos tienden a ser
el mismo punto p ∈ S. En esta degeneración, la superficie R tiende a una superficie
estable con exactamente un nodo que divide esta en dos superficies, cada una de ellas
siendo equivalente holomorficamente a la superficie S − {p}. Esta degeneración hace
que la matriz ZR tienda a una matriz de la forma
∗ 0
0 ∗
es decir, Z1 tiende a la matriz ZS y, en particular, ZPrym(π:R→S) = 2Z1 − ZS tiende a
ZS . Esto dice que ZS vive en la clausura de las matrices ZPrym(π:R→S) en el espacio
de Siegel Hγ . Si denotamos por Jac el sublocus de Hγ que consiste de las matrices
de Riemann de las superficies de Riemann de género γ, entonces usando el hecho que
para γ ∈ {2, 3} vale que Jac es un abierto de Hγ , obtenemos la siguiente observación:
Observación 7.2. Para γ = 2, 3 tenemos que infinitas variedades de Prym son en
efecto jacobianas de superficies de Riemann.
92
7. CUBRIMIENTOS HOMOLÓGICOS
7.3.
Automorfismos de Superficies de Riemann y Jacobianas
Supongamos ahora que f : S → S es un automorfismo holomorfo/antiholomorfo de
la superficie de Riemann S. Este automorfismo induce un automorfismo
J(f ) : J(S) → J(S)
en J(S) que es holomorfo (respectivamente, antiholomorfo) si f es holomorfo (respectivamente, antiholomorfo) que es dada tal que
es dada por
Qf = H −1 J(f )H : P ic0 (S) → P ic0 (S)
Qτ (p1 + · · ·+ pg −q1 −· · ·−qg ) = f (p1 ) + · · ·+ f (pg ) −f (q1 ) −· · ·−f (qg )
Dada una base simpléctica para S, digamos α1 ,..., αg , β1 ,..., βg , uno puede representar
la acción de f a nivel de la homologı́a H1 (S, Z) por una matriz simpléctica (extendida)
^Z), donde
Af ∈ Sp(2g,
^Z) = {N ∈ GL(2g, Z) : t NJN = ±J},
Sp(2g,
0 I
J=
.
−I 0
Más aún, si denotamos por Sp(2g, Z) el grupo simpléctico, el subgrupo de ı́ndice dos de
^Z) de matrices N tales que t NJN = J, entonces tenemos que Af ∈ Sp(2g, Z) si
Sp(2g,
y sólo si f es holomorfo. Esto es debido al hecho que la forma de intersección se preserva por automorfismos que preservan la orientación y es revertida por automorfismos
que revierten la orientación.
Denotemos por Z ∈ Hg la matriz de Riemann de S en la base simpléctica escogida.
Supongamos que la matriz Af es dada por
U V
Af =
,
W L
entonces debemos tener que
(1) Si f es holomorfo, entonces:
(U + ZW )−1 (V + ZL) = Z,
(2) Si f es antiholomorfo, entonces:
−1
U + ZW
V + ZL = Z.
Ahora, supongamos que cambiamos la base simpléctica {α1 , ..., αg , β1 , ..., βg } por una
nueva base simpléctica {e
α1 , ..., α
eg , βe1 , ..., βeg }. Es decir, escogemos una matriz simpléctica
Q11 Q12
Q=
,
Q21 Q22
7.4. SUPERFICIES DE KLEIN Y JACOBIANAS
93
satisfaciendo
e
(αβ)Q = (e
αβ)
donde α = (α1 · · · αg ), α
e = (e
α1 · · · α
eg ), β = (β1 · · · βg ) and βe = (βe1 · · · βeg ). Entonces
la matriz del automorfismo f en esta nueva base es dada por
Q−1 Af Q.
Ahora, si {w1 , ..., wg } es la base dual a {α1 , ..., αg }, entonces la base dual a la nueva
base simpléctica es dada por {w
e1 , ..., w
eg }, donde
(Q11 + ZQ21 )−1 w = w
e
para w = t (w1 · · · wg ) y w
e = t (w
e1 · · · w
eg ). En particular, la matriz de Riemann de la
superficie en la nueva base es dada por
Ze = Q(Z) = (Q11 + ZQ21 )−1 (Q12 + ZQ22 )
Como aplicación de esto es que si A, Q son matrices simplécticas y Z es matriz de
Siegel fija por A, entonces Q(Z) es matriz fija por Q−1 AQ.
7.4.
Superficies de Klein y Jacobianas
Consideremos una superficie de Klein compacta R, posiblemente con borde. Tomemos su cubrimiento doble orientable P : S → R, donde S es ahora una superficie de
Riemann compacta sin borde, la cual asumiremos es de género g ≥ 1 (este valor es
también llamado el género algebraico de R. Además, existe una involución antiholomorfo τ : S → S, actuando con puntos fijos sólo si R tiene borde, tal que τ genera el
grupo de cubrimiento de P .
Ejercicio. Verificar que J(τ ) : J(S) → J(S) actúa sin puntos fijos si y sólo si
τ : S → S actúa sin puntos fijos. En caso que τ tiene k ≥ 1 componentes de puntos
fijos en S, se tiene que el número de componentes de puntos fijos de J(τ ) es 2k−1 ,
cada componente un toro real g-dimensional.
Cada componente del conjunto de puntos fijos de τ es una geodésica simple cerrada
y la cantidad de esas componentes es:
(i) ∅ si ∂R = ∅; ó
(ii) k si #∂R = k.
Denotemos por Z ∈ Hg la matriz de Riemann de S en la base simpléctica escogida.
Supongamos que la matriz τb es dada por
U V
τb =
,
W L
entonces debemos tener que
U + ZW
−1
V + ZL = Z.
94
7. CUBRIMIENTOS HOMOLÓGICOS
Caso 1: Supongamos que τ : S → S actúa sin puntos fijos y que g es par. Entonces
es posible escoger la base simpléctica de manera que para k = 1, ..., 2g valga
(a) τ (αk ) = α g2 +k ,
(b) τ (βk ) = −β g2 +k .
En tal base, tenemos que


0 I
0
0
 I 0
0
0 
,
τb = 
 0 0
0 −I 
0 0 −I
0
donde I y 0 representan las matrices identidad y nula de tamaño
Ası́, la matriz Z debe ser de la forma Z = X + iY , donde
x1
x2
y1 y2
X=
Y =
,
−x2 −x1
y2 y1
g
2
× 2g .
donde
t
x1 = x1 ,
x2 = −x2 ,
t
y1 = y1 ,
t
y2 = y2 ,
son matrices de tamaño
t
g
2
× g2 .
Caso 2: Supongamos que τ : S → S actúa sin puntos fijos y que g es impar. Entonces
es posible escoger la base simpléctica de manera valga
(a) τ (αk ) = α g−1 +k , para k = 1, ..., g−1
2
2
(b) τ (βk ) = −β g−1 +k , para
2
(c) τ (αg ) = αg
(d) τ (βg ) = −βg
En tal base, tenemos que

0 I
 I 0

 0 0
τb = 
 0 0
 0 0
0 0
k = 1, ..., g−1
2
0
0
0
0
0
0
0
0
1
0
0
0
0
0 −I
0
0 −I
0
0
0
0
0 −1




,


donde I es la matriz identidad de tamaño g−1
× g−1
.
2
2
Ası́, la matriz Z debe ser de la forma Z = X + iY , donde




x1
x2
x3
y1 y2 y3
X =  −x2 −x1 −x3  Y =  y2 y1 y3  ,
t
t
x3 −t x3
0
y3 t y3 y6
7.4. SUPERFICIES DE KLEIN Y JACOBIANAS
95
donde
t
x1 = x1 ,
x2 = −x2 ,
t
y1 = y1 ,
t
y2 = y2 ,
son matrices de tamaño
t
g−1
2
×
g−1
,
2
y además y3 > 0.
Caso 3: Supongamos que τ : S → S actúa con puntos fijos y que estos dividen S.
En este caso, si k denota la cantidad de componentes conexas de puntos fijos de τ ,
entonces g = 2γ + k − 1. Entonces es posible escoger la base simpléctica de manera
valga
(a) τ (αt ) = αγ+t , para t = 1, ..., γ
(b) τ (βt ) = −βγ+t , para t = 1, ..., γ
(c) τ (α2γ+u ) = α2γ+u , para u = 1, ..., g − 2γ
(d) τ (β2γ+u ) = −β2γ+u , para u = 1, ..., g − 2γ
En tal base, tenemos que


0 I 0
0
0
0
0
0
0 
 I 0 0


0
0
0 
 0 0 I2
τb = 
,
0 −I
0 
 0 0 0
 0 0 0 −I
0
0 
0 0 0
0
0 −I2
donde I es la matriz identidad de tamaño γ × γ y la matriz I2 es la matriz de tamaño
(g − 2γ) × (g − 2γ).
Ası́, la matriz Z debe ser de la forma Z = X + iY , donde




x1
x2
x3
y1 y2 y3
X =  −x2 −x1 −x3  Y =  y2 y1 y3  ,
t
t
x3 −t x3
0
y3 t y3 y6
donde
t
x1 = x1 ,
x2 = −x2 ,
t
y1 = y1 ,
t
y2 = y2 ,
son matrices de tamaño γ × γ, y
t
y6 = y6 es una matriz tamaño (g − 2γ) × (g − 2γ).
t
Caso 4: Supongamos que τ : S → S actúa con puntos fijos y que estos no dividen
S. En este caso, si k denota la cantidad de componentes conexas de puntos fijos de
τ , entonces g = 2γ + k + l, para cierto l ≥ 2. Entonces es posible escoger la base
simpléctica de manera valga
96
7. CUBRIMIENTOS HOMOLÓGICOS
(a)
(b)
(c)
(d)
τ (αt ) = αγ+t , para t = 1, ..., γ
τ (βt ) = −βγ+t , para t = 1, ..., γ
τ (α2γ+u ) = α2γ+u , para u = 1, ..., g − 2γ
τ (β2γ+u ) = −β2γ+u , para u = 1, ..., g − 2γ
En tal base, tenemos que

0
 I

 0
τb = 
 0
 0
0
I 0
0
0
0
0 0
0
0
0
0 I2
0
0
0
0 0
0 −I
0
0 0 −I
0
0
0 0
0
0 −I2




,


donde I es la matriz identidad de tamaño γ × γ y la matriz I2 es la matriz de tamaño
(g − 2γ) × (g − 2γ).
Ası́, la matriz Z debe ser de la forma Z = X + iY , donde




x1
x2
x3
y1 y2 y3
X =  −x2 −x1 −x3  Y =  y2 y1 y3  ,
t
t
x3 −t x3
0
y3 t y3 y6
donde
t
x1 = x1 ,
x2 = −x2 ,
t
y1 = y1 ,
t
y2 = y2 ,
t
son matrices de tamaño γ × γ, y
t
y6 = y6 es matriz tamaño (g − 2γ) × (g − 2γ).
7.5.
Cubrimiento Homológico de Superficies de Klein
Dado un grupo Kleiniano planar G y una colección invariante ∆ de componentes
de Ω(G), uno puede construir el espacio cociente ∆/G formada por las clases de
equivalencia de las órbitas por G de los puntos de ∆. Si G actúa sin puntos fijos, es
decir, para todo p ∈ ∆ se tiene que Gp = {I}, entonces ∆/G es una superficie de
Klein. Si además G sólo contiene transformaciones de Möbius, entonces esta es una
superficie de Riemann. En el caso que G actúe con puntos fijos, entonces obtendremos
superficies reales con posible borde tal que fuera de la proyección de los puntos fijos
de elementos no triviales de G es una superficie de Klein. Estas són llamadas orbifolds
de Klein.
Tomemos una superficie de Klein S, digamos S = ∆/G donde G es algún grupo
Kleiniano planar actuando si puntos fijos y ∆ es alguna componente invariante de
7.5. CUBRIMIENTO HOMOLÓGICO DE SUPERFICIES DE KLEIN
97
Ω(G) (es decir, un grupo uniformizante). Consideremos el subgrupo [G, G] de G generado por los conmutadores de G. Como [G, G] es un subgrupo normal de G, entonces Ω([G, G]) = Ω(G) y en particular podemos considerar la superficie de Klein
S ab = ∆/[G, G]. Como [G, G] consiste sólo de transformaciones de Möbius, S ab es una
superficie de Riemann. Diremos que S ab es el cubrimiento homológico asociado a G
de S.
Ejemplo 7.3. Si escogemos S una superficie de Riemann de género g ≥ 2, entonces
podemos escoger G como un grupo Fuchsiano dejando invariante el cı́rculo unitario y
∆ el disco abierto unitario. En este caso, G/[G, G] es isomorfo al grupo de homologı́a
sobre Z de S, es decir, ⊕2g Z. El cubrimiento homológico S ab corresponde a mirar una
incrustación holomorfa
Z p iq : S → J(S) : p →
,
q
donde q ∈ S, y levantar iq (S) al cobertor universal de la variedad jacobiana J(S) de
S, es decir, al dual de las diferenciales holomorfas de S.
El teorema de Torelli dice que J(S) determina, modulo equivalencia holomorfo la superficie S. Un resultado relacionado probado por B. Maskit [Maskit2] es el siguiente:
Teorema 7.1. Sea G un grupo Fuchsiano de la primera clase, sin torsión. Entonces
G está únicamente determinado por [G, G].
En el caso más general, se ha probado en una serie de trabajos (por ejemplo,
[Hidalgo1] [Hidalgo2]) que el anterior es válido para grupos Kleinianos planares
más generales, por ejemplo:
Teorema 7.2. Sea G un grupo uniformizante, sin torsión, con un número infinito
de puntos lı́mites, entonces G está únicamente determinado por [G, G].
Para demostrar este resultado, necesitaremos algunos preliminares. Sea S una superficie de Riemann de género g con k puntos removidos. Decimos que S es una superficie
de Riemann analı́ticamente finita de signatura (g, k). Denotemos por S la superficie
de Riemann compacta obtenida de S a colocar de vuelta los puntos removidos. Sea
H(S) el espacio vectorial complejo generado por las 1-formas holomorfas en S y las
1-formas holomorfas en S co a lo más polos simples en los puntos removidos. Entonces
tenemos el siguiente resultado [Farkas-Kra].
Lema 7.3. La dimensión de H(S) es dada por
2g,
si k = 0
dimC H(S) =
2g + k − 1, en caso contrario.
La función bilineal
(w, α) ∈ H(S) × H1 (S, C) →
Z
α
w∈C
98
7. CUBRIMIENTOS HOMOLÓGICOS
define una dualidad entre H(S) y H1 (S, C).
Sea (G, ∆) un grupo uniformizante finitamente generado sin torsión y non-elemental.
Denotemos por K su subgrupo generado por sus conmutadores. Asuma que tenemos
un subgrupo de ı́ndice finito I < G en G, conteniendo K. En este caso, tenemos una
sucesión finita de cubrimientos holomorfos
r : ∆ → ∆/K;
t : ∆/K → ∆/I;
p : ∆/I → ∆/G.
También tenemos los respectivos cubrimientos a nivel de la variedades 3-dimensionales
(con borde):
b → ∆/K;
b
R:∆
b
b
T : ∆/K
→ ∆/I;
b → ∆/G,
b
P : ∆/I
b = ∆ ∪ H3 .
donde ∆
Consideremos el homomorfismo inducido a nivel del primer grupo de homologı́a con
coeficientes complejos:
b
b
H1 (P ) : H1 (∆/I,
C) → H1 (∆/G,
C).
b → ∆/G
b
Como el ı́ndice de I en G es finito, el cubrimiento P : ∆/I
tiene grado finito
y, en particular, H1 (P ) es un homomorfismo sobreyectivo. Más aún, sabemos que su
b que se levantan en curvas
núcleo está generado por aquellas curvas cerradas en ∆/I
b
cerradas en ∆/K.
Tenemos las siguientes inclusiones:
b
i∆ : ∆ ֒→ ∆;
b
iK : ∆/K ֒→ ∆/K;
b
iI : ∆/I ֒→ ∆/I;
b
iG : ∆/G ֒→ ∆/G.
Los homomorfismos inducidos al nivel de homologı́a con coeficientes complejos son
sobreyectivos. Denotemos sus respectivos núcleos por N∆ = H1 (∆, C), NK =
ker H1 (iK ) < H1 (∆/K, C), NI = ker H1 (iI ) < H1 (∆/I, C) and NG = ker H1 (iG ) <
H1 (∆/G, C). We have that H1 (r)(N∆ ) < NK , H1 (t)(NK ) < NI , H1 (p)(NI ) < NG .
Consideremos el homomorfismo inducido en el cociente H1 (p) : H1 (∆/I, C)/NI →
H1 (∆/G, C)/NG . Tenemos por lo anterior que el núcleo de homomorfismo sobreyectivo inducido está generado por aquellas curvas cerradas en ∆/I que se levantan en
curvas cerradas en ∆/K.
Denotemos por NIt (respectivamente, NGt ) el subespacio de H(∆/I) (respectivamente,
H(∆/G)) ortogonal a NI (respectivamente, NG ). La función p∗ : NGt → NIt , definida
por el pull-back de 1-formas, es dual al monomorfismo sobreyectivo anterior y, en
7.5. CUBRIMIENTO HOMOLÓGICO DE SUPERFICIES DE KLEIN
99
particular, este es inyectivo. La imágen P ∗ (NGt ) corresponde a aquellas 1-formas en
NIt las cuales son puntos fijos para el pull-back de cada transformación en G/I (un
grupo abeliano). Lo siguiente no es difı́cil de verificar.
Lema 7.4. La dimensión de NGt es la misma dimensión del espacio cociente
b
H1 (∆/G,
C), es decir, igual a dimC H(∆/G) − l, donde l denota el número máximo
de curvas cerradas simples homológicamente independientes en ∆/G que se levantan
en curvas cerradas en ∆. Similarmente para la dimensión de NIt .
Demostración del Teorema. Consideremos dos grupos uniformizantes noelementales, finitamente generados y sin torsión (G1 , ∆1 ) y (G2 , ∆2 ) tales que
[G1 , G1 ] = [G2 , G2 ] = K. Queremos probar que G1 = G2 . Sean I = G1 ∩ G2 y
J = hG1 , G2 i. Ya que K es non-elemental y normal en ambos G1 y G2 , tenemos que
la región de discontinuidad de los tres es el mismo (ver proposición 6.38). Denotemos
a tal región de discontinuidad por Ω.Similarmente, ya que J es un subgrupo del normalizador de K, tenemos necesariamente que J es un grupo Kleiniano planar con Ω
como región de discontinuidad. El teorema de finitud de Ahlfors asegura que Ω/G1
y Ω/G2 son cada uno una unión finita de superficies de Riemann de área hiperbólica
finita. Se sigue que el cubrimiento (posiblemente ramificado) Ω/Gi → Ω/J tiene grado finito, esto es, ambos G1 y G2 tienen ı́ndice finito en J y, en particular, tenemos
que I tiene ı́ndice finito en G1 , G2 y J. Se sigue de la proposición 6.38, que I tiene a
Ω como región de discontinuidad.
Lema 7.5. Existe una componente invariante común ∆ para G1 y G2 .
Demostración. si ∆1 = ∆2 , entonces estamos listos y ∆ = ∆1 . Supongamos que
∆1 6= ∆2 . En este caso, I deja invariante ambas componentes ∆1 y ∆2 . Como I tiene
ı́ndice finito en Gi , tenemos que I es finitamente generado. Se sigue de [Maskit4]
que I es entonces un grupo casifuchsiano (es decir, su conjunto lı́mite es una curva de
Jordan) y, como consecuencia, Ω = ∆1 ∪ ∆2 . Ası́, ∆1 y ∆2 son invariantes por ambos
G1 y G2 . En particular, podemos tomar ∆ = ∆1 .
Usemos la siguiente notación: ∆/I = R, ∆/G1 = S1 , ∆/G2 = S2 , ∆/J = X. Denotemos por t : ∆ → ∆/K, r : ∆/K → R y pi : R → Si , i = 1, 2, los cubrimientos
holomorfos naturales inducidos por los grupos K, I/K y Gi /I, respectivamente. Consideremos el siguiente diagrama conmutativo:
100
7. CUBRIMIENTOS HOMOLÓGICOS
∆
t
∆/K
r
R
y EEE
EEp2
p1 yyy
EE
y
EE
yy
y
"
|y
S1 E
EE
EE
E
q1 EEE
"
X
y
yy
yy
y
y q2
y| y
S2
Tenemos que los homomorfismos sobreyectivos inducidos H1 (pj ) : H1 (R, C)/NI →
H1 (Sj , C)/NGj , for j = 1, 2, tienen el mismo núcleo (el espacio generado por aquellas
curvas cerradas en R que se levantan en curvas cerradas en ∆/K). De aquı́ obtenemos
que las 1-formas en NIt invariantes por G1 /I son las mismas que son invariantes por
G2 /I y, en particular, las mismas que son invariantes por el grupo generado por G1 /I
y G2 /I. Esto es, las dimensiones de esos tres espacios es la misma. Ahora, lema 7.4 dice
que la dimensión del espacio de formas invariantes por Gj (respectivamente, el grupo
generado por G1 /I y G2 /I) es igual a dimH(Sj ) − lj (respectivamente, dimH(X) − l),
donde lj (respectivamente, l) denota el número maximal de curvas cerradas simples
homológicamente independientes dos a dos disjuntas en Sj (respectivamente, en X)
que se levantan en curvas cerradas en ∆ (módulo potencias finitas en el caso de X).
En particular, tenemos las igualdades
(∗)
dimC H(Sj ) − lj = dimC H(X) − l.
Denotemos por gj (respectivamente, g) el género de Sj (respectivamente, X) y por kj
(respectivamente, k) el número de pinchaduras de Sj (respectivamente, X). Tenemos
necesariamente que
(1) g ≤ gi
(2) k ≤ ki
(3) g − l ≤ gi − li
Desigualdades (1) y (2) son claras. Para ver (3), uno debe considerar un conjunto
maximal Σ de curvas cerradas simples, dos a dos disjuntas y homológicamente indee i el
pendientes en X, cada una de ellas levantándose en curvas cerradas en ∆. Sea Σ
e i es una colección de curvas cerradas simples,
levantamiento de Σ a Si . Tenemos que Σ
dos a dos disjuntas, que se levantan en curvas cerradas en ∆. Procedamos a cortar
ambas X y Si a lo largo de esas curvas cerradas. Ahora pegamos discos cerrados a
lo largo de los nuevos bordes. Aún tenemos un cubrimiento (quizás ramificado) sin
7.5. CUBRIMIENTO HOMOLÓGICO DE SUPERFICIES DE KLEIN
101
nuevas ramificaciones (consecuencia del levantamiento de las curvas cerradas de Σ).
El género de la nueva superficie obtenida en esta manera de X es g − l. La suma
de los géneros de las nuevas superficies obtenidas de Si es a lo más gi − li . Ahora,
desigualdad (3) es consecuencia de comparación de áreas. Las desigualdades (1), (2)
y (3) juntas con la igualdad (∗) da las igualdades
g = gi ,
k = ki
and l = li .
Obtenemos en esta manera que el ı́ndice de Gj en J es 1 y, en consecuencia, G1 =
G2 .
CAPÍTULO 8
Grupos de Schottky y Variedades Abelianas
8.1.
Grupos de Schottky
Una buena referencia para esta sección es [Chuckrow], [Maskit1]. Consideremos
una colección de 2g (donde g ≥ 1) curvas simples cerradas en la esfera de Riemann
b digamos C1 ,..., Cg , C ′ ,..., C ′ , de manera que ellas acotan un dominio D de conecC,
1
g
tividad 2g. Supongamos que existen transformaciones de Möbius A1 ,..., Ag tales que
para cada k ∈ {1, ..., g} vale que:
(1) Ak (Ck ) = Ck′ ;
(2) Ak (D) ∩ D = ∅,
entonces el grupo G de transformaciones de Möbius generado por A1 ,..., Ag es llamado
un grupo de Schottky de género g. Las curvas C1 ,...,Cg′ son llamadas un sistema
fundamental de curvas asociadas a los generadores de Schottky A1 ,..., Ag .
Ejercicios.
1.- Verificar que para todo g ≥ 1 existen un número infinito de grupos de Schottky
de género g. [Ind. Utilize cı́rculos]
2.- Verifique que cada uno de los generadores A1 ,..., Ag es necesariamente loxodrómico. [Ind. Verifique que Ak tiene dos puntos fijos y que no puede ser una
rotación]
3.- Verifique que un grupo de Schottky de género g es un grupo libre de rango g.
[Ind. Tome un punto p dentro de la región D y mire la órbita de p]. Deducir
que todo grupo de Schottky no contiene transformaciones elı́pticas.
4.- Verifique que todo grupo de Schottky de género g es un grupo Kleiniano
planar, es decir, actúa de marea discontinua en algún punto de la esfera de
Riemann. [Ind. Vea que cada punto en la clausura de D es un punto de discontinuidad de G]
5.- Sea Ω(G) la region de discontinuidad de un grupo de Schottky de género g.
Verifique que Ω(G) es conexo. [Ind. Vea que todo punto en la órbita por G de
la clausura de D es punto de discontinuidad y que la órbita de este conjunto
es conexo. Luego vea que todo punto en el borde de la órbita no puede ser un
punto de discontinuidad]. Concluir de esto que el conjunto lı́mite de un grupo
de Schottky es totalmente disconexo.
5.- Si G es un grupo de Schottky de género g, entonces Ω(G)/G es una superficie
de Riemann de género g. [Ind. Ver que para todo punto en Ω(G) existe un
103
104
8. GRUPOS DE SCHOTTKY Y VARIEDADES ABELIANAS
punto de su órbita por G en la clausura de D. Más aún, dos puntos diferentes
en D no pueden ser equivalentes por G y cada punto en el borde Ck tiene
exactamente otro representante en el borde Ck′ y no en otro borde ni en D.
Deducir que Ω(G)/G es homeomorfo a una superficie orientable cerrada de
género g. Usar la proyección natural π : Ω(G) → Ω(G)/G = S para dotar a S
de una estructura de superficie de Riemann]
Sea G un grupo de Schottky de género g. El ejercicio anterior nos dice que Ω(G)/G es
una superficie de Riemann de géro g. El siguiente resultado de Koebe [Koebe] dice
que el recı́proco es verdad.
Teorema 8.1 ( Teorema de Retrosección de Koebe). Sea S una superficie de Riemann
de género g ≥ 1. Entonces existe un grupo de Schottky G de género g tal que Ω(G)/G
es holomórficamente equivalente a S
Muchas demostraciones existen de este teorema. Uno de ellas utiliza las herramientas
de funciones casiholomorfos [Bers]. La idea es partir con un grupo de Schottky de
género g, digamos K y luego considerar conjugadas de K por homeomorfismos de la
esfera de Riemann de manera que sigamos obteniendo grupos de Möbius. Entonces
estas conjugadas son otra vez grupos de Schottky de género g. La manera de escoger
el homeomorfismo adecuado es tomar un difeomorfismo f : Ω(K)/K → S y considerar su diferencial de Beltrami dada por µ = ∂z f /∂z f en coordenadas locales. Luego
levantamos la diferencial µ a todo Ω(K) de manera que sea invariante por la acción
de K. La teorı́a de aplicaciones casiholomorfas asegura la existencia de un homeob →C
b cuyo diferencial de Beltrami es esta µ levantada a Ω(K). Luego
morfismo F : C
−1
F KF es el grupo de Schottky buscado.
La demostración de Koebe es constructiva. Uno considera en la superficie S una
colección α1 ,..., αg , de curvas cerradas simples homoógicamente independientes (es
decir, S − {α1 , ..., αg } is una esfera con 2g hoyos. Vea que esta es parecida a la región D en la definición de grupo de Schottky). Ahora uno procede a pegar copias
de S − {α1 , ..., αg } (clausura) de manera de obtener una región planar Σ (toda curva
simple cerrada en ella divide). Topológicamente hemos construido un grupo de Schottky. Ahora uno tiene un cubrimiento Galois topológico de S por esta superficie planar
Σ con grupo de cubrimiento un grupo libre de rango g. Ahora levantamos la estructura de superficie de Riemann de S para dotar a Σ de una estructura de superficie de
Riemann planar de manera que el grupo libre anterior es un grupo de automorfismos
holomorfos de ella. Usando el teorema de planaridad [Maskit1] uno obtiene el grupo
de Schottky deseado. En el lenguaje moderno, la construcción
Qg hecha es considerar el
grupo fundamental de S, π1 (S, p) = hα1 , ..., αg , β1 , ..., βg : j=1 [αj , βj ] = 1i, donde
[a, b] = aba−1 b−1 , y escoger el subgrupo normal mas pequeño que contenga las palabras β1 ,..., βg , digamos F . Entonces F uniformiza la región de discontinuidad de
8.2. GRUPOS DE SCHOTTKY Y AUTOMORFISMOS
105
un grupo de Schottky de género g, siendo este grupo de Schottky el grupo cociente
π1 (S, p)/F , que uniformiza la superficie S.
Ejemplo 8.1. Consideremos una transformación loxodrómica T (z) = λz, donde λ ∈
C−{0} y |λ| =
6 1. Entonces el grupo cı́clico Gλ generado por T es un grupo de Schottky
de género 1. Podemos escribir λ = eiτ para algún τ ∈ H = {z ∈ C : Im(z) > 0}. Más
aún, Gλ y Gλ∗ uniformizan toros equivalentes sı́ y sólo sı́ existe una matriz
a b
∈ SL(2, Z)
c d
tal que λ = eiτ y λ∗ = eiτ para ciertos τ, τ ∗ ∈ H con τ ∗ =
∗
8.2.
aτ +b
.
cτ +d
Grupos de Schottky y Automorfismos
Supongamos ahora que tenemos una superficie de Riemann S de género g ≥ 2 y
un grupo H de automorfismos de S (holomorfos o antiholomorfos). Diremos que H
es un grupo de tipo Schottky si es posible encontrar un grupo de Schottky G y un
cubrimiento holomorfo P : Ω(G) → S, con G como grupo de cubrimiento, de manera
que todo elemento de H pueda levantarse por P , es decir, para todo h ∈ H exista un
automorfismo holomorfo (si h es holomorfo) o antiholomorfo (si h es antiholomorfo)
de Ω(G), digamos kh : Ω(G) → Ω(G) tal que P kh = hP . Como todo automorfismo de
la región de discontinuidad de un grupo de Schottky es necesariamente una transformación de Möbius (si holomorfo) o la composición de una transformación de Möbius
con la conjugación (si antiholomorfo) , kh es de uno de esos tipos.
Es importante notar que no todo grupo H es de tipo Schottky. Por ejemplo, es fácil
ver que si S/H es una esfera con tres valores de ramificacı́on y toda transformación
de H es holomorfo, entonces H no es de tipo Schottky. Una manera de ver esto es
la siguiente. Si H fuese tipo Schottky, entonces al levantar H obtenemos un grupo
K de transformaciones de Möbius conteniendo a un grupo de Schottky G de ı́ndice
finito (y también normal). El grupo K tiene la misma región de discontinuidad que G,
luego conexa. Como Ω(G)/K es una esfera con tres puntos especiales, K es un grupo
uniformizante, debe ocurrir por rigidez de los grupos triangulares que K es Fuchsiano
de primera clase, es decir su conjunto lı́mite es un cı́rculo. Una contradicción al hecho
que el conjunto lı́mite de un grupo de Schottky es totalmente disconexo.
Es importante notar que todo grupo de automorfismos holomorfos isomorfo a un grupo
dihedral siempre es de tipo Schottky [Hidalgo3]. Para ver más sobre este problema
de automorfismos tipo Schottky mirar por ejemplo en [Costa-Hidalgo], [Hidalgo3],
[Hidalgo4], [Hidalgo4], [Hidalgo5], [Hidalgo6]. En el caso que S tiene reflexiones,
tenemos el siguiente resultado de B. Maskit [Maskit3]
Teorema 8.2. Sea S una superficie de Riemann admitiendo una reflexión τ : S → S.
Entonces existe un grupo de Schottky G que deja un cı́rculo C invariante tal que
S = Ω(G)/G y la reflexión τ es inducida por la reflexión en C.
106
8. GRUPOS DE SCHOTTKY Y VARIEDADES ABELIANAS
Como consecuencia de esto tenemos la siguiente:
Corolario 8.3. Sea S una superficie de Riemann admitiendo una reflexión τ : S → S.
Entonces K(S, τ ) es tipo Schottky.
Demostración. Sea S una superficie de Riemann de género g junto a una reflexión τ : S → S. Sea G un grupo de Schottky que deja invariante el cı́rculo S 1 y
tal que existe un cubrimiento holomorfo P : Ω(G) → S con G como grupo cobertor
determinado por el teorema anterior. Denotemos por ∆ uno de los dos discos acotados
por S 1 y por σ la refelcción en S 1 .
(1) Supongamos que el conjunto de puntos fijos de τ divide S en dos superficies,
digamos S1 y S2 . En este caso, G es un grupo Fuchsiano. Supongamos que P (∆) = S1 .
Sea K el subgrupo de ı́ndice dos en K(S, τ ) que deja invariante s1 . Tenemos entonces
que K(S, τ ) está generado por K y τ . Como P : ∆ → S1 es cubrimiento universal,
entonces podemos levantar el grupo K. Tal levantamiento es un grupo Fuchsiano
b Ahora, es claro que b
K.
k y σ generan un grupo que resulta ser el levantamiento de
K(S, τ ) por P .
(2) Supongamos ahora que el conjunto de puntos fijos de τ no divide S. Denotemos
b el grupo generado por G y σ. Ya que C
por S ∗ a S menos los puntos fijos de τ . Sea G
es invariante por G, tenemos que el grupo F de orden dos generado por σ es normal
b Consideremos el cubrimiento ramificado Q : Ω(G) → D inducido por la acción
en G.
b
de F , donde D es el disco unitario. El cociente H = G/F
actúa como grupo de automorfismos holomorfos del disco unitario ∆. Tenemos que el cubrimiento holomorfo
Q∗ : ∆ → (S ∗ /τ ), inducido por H, es cubrimiento universal. En particular, podemos
levantar K(S, τ )/tau a D por este cubrimiento universal. Tal levantamiento es dado por transformaciones de Möbius y luego extienden de manera natural al cı́rculo
borde. Ahora es fácil levantar este grupo de automorfismos de D por el cubrimiento
ramificado Q∗ para obtener de esta manera el levantamiento de K(S, τ ) como era
deseado.
Ahora, suponiendo que H es un grupo de automorfismos de tipo Schottky y que
G, P : Ω(G) → S son un grupo de Schottky como se desea y P el cubrimiento
correspondiente, podemos proceder como sigue: Fijemos un sistema fundamental de
curvas C1 ,..., Cg , C1′ ,..., Cg′ asociada a los generadores de Schottky A1 ,.., Ag para G.
Orientemos las curvas C1 ,..., Cg digamos en el sentido opuesto a las manecillas de
un reloj (no digital pero a cuerda). Damos las orientaciones inducidas por la acción
de los generadores a las curvas C1′ ,..., Cg′ . Consideremos arcos simples orientados dos
a dos disjuntos M1 ,..., Mg , de manera que Mj es disjunta de Ck y Ck′ si j 6= k, Mj
intersecta Cj en su punto final e intersecta Cj′ en su punto inicial, siendo este punto
la imagen del punto final por Aj .
Las curvas orientadas C1 ,..., Cg se proyectan sobre S en curvas simples orientadas
cerradas α1 ,..., αg , respectivamente. Idénticamente, los arcos orientados M1 ,..., Mg se
8.2. GRUPOS DE SCHOTTKY Y AUTOMORFISMOS
107
proyectan en curvas orientadas simples y cerradas β1 ,..., βg , respectivamente. No es
difı́cil observar que α1 ,..., αg , β1 ,..., βg define una base simpléctica para la homologı́a
de S.
Usando esta base simpléctica, uno tiene una representación fiel del grupo H en el
grupo extendido simpléctico
^Z),
ρ∗ : H → Sp(2g,
definida por
∗
ρ (h) =
Ah
Bh
0
t
A−1
h
, si h es holomorfo y
Ah
0
ρ (h) =
, si h es antiholomorfo
Bh −t A−1
h
Observemos que η : H → GL(g, Z) definida por η(h) = Ah es también una representación fiel de H.
Si cambiamos la base
∗
{α1 , ..., αg , β1 , ..., βg }
por la nueva base simpléctica
{β1 , ..., βg , −α1 , ..., −αg },
entonces tenemos la representación simpléctica
^Z),
ρ : H → Sp(2g,
definida por
ρ(h) =
t
A−1
−Bh
h
0
Ah
, si h es holomorfo y
−t A−1
−B
h
h
, si h es antiholomorfo
ρ(h) =
0
Ah
Observemos que si queremos calcular un punto fijo Z ∈ Hg por una matriz simpléctica
(extendida) de la forma
A B
^Z),
M=
∈ Sp(2g,
0 D
entonces sólo tenemos que resolver el sistema lineal

 B + ZD = AZ caso que M ∈ Sp(2g, Z)

/ Sp(2g, Z)
B + ZD = AZ caso que M ∈
Ejercicio 8.1.
108
8. GRUPOS DE SCHOTTKY Y VARIEDADES ABELIANAS
(1) Se tiene que Z ∈ Hg es punto fijo de
A B
^Z),
M=
∈ Sp(2g,
0 D
sı́ y sólo si −Z −1 ∈ Hg es punto fijo de
D 0
.
N=
−B A
(2) Se tienen que Z ∈ Hg es punto fijo de
A B
^Z),
M=
∈ Sp(2g,
0 D
sı́ y sólo si −Z −1 ∈ Hg es punto fijo de
t
A tB
N=
.
0 tD
[Ind: Para verificar (2) basta observar que Z es punto fijo de M sı́ y sólo si es
punto fijo de M −1 . Ahora observe que
t
D −t B
−1
M =
,
t
0
A
y utilize parte (1) con M −1 .]
Ahora, el grupo H es el cociente K/G, donde K es el levantamiento de H. Este grupo
K, como se mencionó arriba, contiene al grupo de Schottky G como un subgrupo
normal de ı́ndice finito. En particular, cada elemento k ∈ K induce un par de isomorfismos θ(k) : G → G y θ(k)ab : G/[G, G] → G/[G, G], definidos por conjugación
el primero y por abelianización del primero en el segundo caso. Es fácil ver que si
k ∈ G, entonces θ(k)ab es la identidad. Luego, para cada h ∈ H tenemos en forma
natural un isomorfismo Θ(h) : G/[G, G] → G/[G, G] definido como Θ(h) = θ(kh )ab ,
donde kh ∈ K es cualquier levantamiento de h. Usando la base A1 , ..., Ag del grupo de
Schottky G, tenemos una representación matricial de Θ(h) (escrita también en filas).
De la definición de la base simpléctica uno deduce fácilmente que
(1) Θ(h) = t A−1
h si h es holomorfo;
t −1
(2) Θ(h) = − Ah si h es antiholomorfo.
Para ver lo anterior hay que darse cuenta que la acción del grupo H visto como el
cociente de K es en realidad la acción a nivel de los arcos M1 ,..., Mg y, luego, la acción
a nivel de las curvas β1 ,..., βg .
^Z), podemos
Ahora que tenemos calculada una representación fiel ρ : H → Sp(2g,
calcular sus puntos fijos en el espacio de Siegel obteniendo de esta manera variedades abelianas principalmente polarizadas con grupo de automorfismos (holomorfo/antiholomorfo) ρ(H).
8.3. GRUPOS DE SCHOTTKY CON CÍRCULOS INVARIANTES
109
Ejemplo 8.2. Consideremos un cı́rculo C1 en el plano complejo que no separe 0 de
∞ y tal que los cı́rculos C1 , C2 = T (C1 ), C1′ = T 2 (C1 ), C2′ = T 3 (C1 ) son dos a
dos disjuntos para T (z) = iz. Orientemos C1 y C2 con la orientación opuesta a las
manecillas de un reloj. Los cı́rculos C1′ y C2′ son orientados según las manecillas de
un reloj. Sea A1 la composición de la reflexión en C1 seguida por la reflexión en el eje
imaginario. Tomamos A2 = T A1 T −1 . Entonces el grupo G generado por A1 y A2 es
un grupo de Schottky de género 2.
Ya que T A1 T −1 = A2 y T A2 T −1 = A−1
1 , tenemos que
0 1
Θ(T ) =
.
−1 0
En este caso, la superficie de Riemann S = Ω(G)/G admite el grupo de automorfismos
H = hti ∼
= Z/4Z inducido por K, el grupo generado por G y T . Se tiene que G es un
subgrupo normal de ı́ndice 4 en K.
Escogiendo M1 como el arco real que conecta C1 con C1′ (que pasa por 0, y M2 el arco
contenido en el eje imaginario (pasando por ∞) que conecta C2 con C2′ , tenemos en
homologı́a que en la base
{β1 , β2 , −α1 , −α2 }
la representación de t es dada por:

0
 −1
ρ(t) = 
 0
0
8.3.

1
1
0
0
0 −1 

0
0
1 
0 −1
0
Grupos de Schottky con Cı́rculos Invariantes
Consideremos un grupo de Schottky G de género g ≥ 2 que deja invariante algún
cı́rculo C. En este caso, el conjunto lı́mite de G está contenido en C. Si denotamos
por σ la reflexión en C, entonces la superficie de Riemann S = Ω(G)/G admite un
automorfismo antiholomorfo de orden dos τ : S → S actuando con puntos fijos.
Podemos considerar el grupo K(S, τ ) que consiste de aquellos automorfismos holomorfos y antiholomorfos que conmutan con τ . En particular, τ ∈ K(S, τ ) y hτ i ∼
= Z/2Z
es subgrupo normal de K(S, τ ). La superficie cociente R = S/τ es una superficie de
Klein compacta con borde. El grupo K(S, τ )/τ es el grupo de automorfismos de Klein
de R. Por resultados de C.L. May [May] tenemos que |K(S, τ )| ≤ 24(g − 1). Uno
puede usar este grupo para calcular puntos fijos en el espacio de Siegel y ası́ obtener
variedades abelianas principalmente polarizadas con automorfismos y que admiten
una estructura real que conmuta con tal grupo.
Por otro lado, Burnside [Burnside] ha observado que la siguiente:
110
8. GRUPOS DE SCHOTTKY Y VARIEDADES ABELIANAS
Teorema 8.4. Sea G un grupo de Schottky que deja invariante un cı́rculo en la esfera
de Riemann y tal que ∞ ∈ Ω(G). Entonces la serie
X
γ ′ (z)
γ∈G
es uniformemente convergente en compactos de Ω(G).
Demostración. Primero supongamos que G deja invariante una lı́nea L. Si K ⊂
Ω(G) es algún compacto, entonces exceptuando un número finito de transformaciones
en G existe una constante positiva A > 0 tal que
X
X 1
|γ ′ (z)| ≤ A
,
|c|2
γ∈G
γ∈G
az+b
, ad − bc = 1. Elijamos un punto q ∈ L y un número positivo R > 1
donde γ(z) = cz+d
tal que B = {z ∈ C : |z − q| > R} ∪ {∞} es precisamente invariante por la identidad
en G. En este caso, tenemos que los conjuntos γ(B) son discos ortogonales a L y, en
particular,
X
diam(γ(B)) ≤ 2R,
γ∈G,γ6=I
donde diam denota el diámetro Euclideano. Si usamos la desigualdad dada en C.7 de
[Maskit1]
1
1 1
1
diam(γ(B)) ≥ 2
≥ 2 ,
−1
|c| dist(g (∞), B)
|c| R
P
for γ 6= I, entonces podemos obtener la convergencia de γ∈G |c|12 .
Ahora supongamos que G deja invariante un cı́rculo C en el plano complejo. Esco1
, H = T GT −1
jamos un punto q ∈ C ∩ Ω(G) (entonces q 6= ∞). Sean T (z) = z−q
y L = T (S). Entonces H es un grupo de Schottky que deja invariante
P la lı́nea L y
para el cual ∞ ∈ Ω(H).En este caso tenemos la convergencia para h∈H h′ (w) en
subconjuntos compactos de Ω(H). Sea K un subconjunto compacto de Ω(G) tal que
q∈
/ K. Entonces para z ∈ K tenemos
X
X
1
|h′ (T (z))| =
|γ ′ (z)|
.
|γ(z) − q|2 |T (z)|2
h∈H,h6=I
γ∈G,γ6=I
El hecho que q ∈
/ K asegura que
1
Inf{
; z ∈ K} = M > 0.
|T (z)|2
También, excepto por un número finito de elementos de G, digamos γ1 ,..., γn , tenemos
que
1
Inf{
; z ∈ K, γ ∈ G − {γ1 , ..., γn }} = N > 0.
|γ(z) − q|2
8.3. GRUPOS DE SCHOTTKY CON CÍRCULOS INVARIANTES
Ahora, se sigue que
X
|γ ′ (z)|
γ∈G,γ6=I
X
1
≥
NM
|γ ′ (z)|,
|γ(z) − q|2 |T (z)|2
γ∈G,γ6=I
obteniendo de esta forma la convergencia deseada.
111
El resultado de Burnside nos permite calcular explı́citamente la matriz de Riemann
de S = Ω(g)/G de la siguiente manera. Procedemos como en la sección anterior
para obtener una base simpléctica para S, es decir, escoger las curvas α1 ,..., αg como
proyecciones de las curvas (orientadas) C1 ,..., Cg , y las curvas β1 ,..., βg como las
proyecciones de los arcos M1 ,..., Mg . En este caso
1 X
g ′ (z)
w
bj (z) =
dz,
2πi g∈G g(z) − A−1
j (∞)
para j = 1, ..., g, son los levantamientos a Ω(G) de las formas holomorfas duales a las
curvas α1 ,..., αg . Supongamos que pj es el punto inicial de Mj (entonces, A−1
j (pj ) es
su punto final). En este caso la matriz de Riemann de S en esa base es dada por una
matriz Z = (zkj ) ∈ Hg , donde
!
−1
Y
|γ(p
)
−
A
(∞)|
1
k
j
ykj = Im(zkj ) =
,
Log
−1
2π
|γ(Aj (pk )) − A−1
j (∞)|
γ∈G
de donde obtenemos Y = Im(Z).
La representación (extendida) simpléctica de la reflección τ en esta base simpléctica
es dada por la matriz
−I 0
.
B I
Usando la base simpléctica
{β1 , ..., βg , −α1 , ..., −αg },
tenemos que la matriz de Riemann para S es dada por W = −Z −1 y la representación
simpléctica de τ es
I −B
.
0 −I
Al ser W punto fijo de τ , debemos tener
−1
Re(W ) =
B.
2
De todo lo anterior sabemos que

= Y;

 Im(Z)

 Re(−Z −1 ) = −1 B.
2
112
8. GRUPOS DE SCHOTTKY Y VARIEDADES ABELIANAS
Ya que Z(−Z −1 ) = −I, obtenemos el siguiente sistema el cual permite obtener Re(Z):

1
−1


 −Y Im(Z ) + 2 Re(Z)B = I


1

Re(Z)Im(Z −1 ) + Y B
= 0.
2
Observación 8.1. Observemos que si tenemos B = 0, entonces la ecuación anterior
asegura que Re(Z) = 0. De esta manera
Z = iY.
CAPÍTULO 9
Superficies de Riemann Maximal Simétricas
En este capı́tulo ejemplificaremos los resultados del capı́tulo anterior para cierto tipo
de superficies de Riemann llamads maximal simétricas.
9.1.
Superficies Maximales Simétricas
Una superficie de Riemann S, de género g ≥ 2, es llamada una superficie maximal
simétrica si existe una reflexión τ : S → S, es decir, una involución antiholomorfo
con puntos fijos, de manera que |K(S, τ )| = 24(g − 1). La reflexión τ será llamada
una reflexión maximal de S. En este capı́tulo usaremos este tipo de superficies para
usar las herramientas explicadas en la última sección del capı́tulo anterior.
La primera observación que debemos hacer notar es que S/K(S, τ ) es un disco cerrado
con cuatro valores de ramificación en su borde, de ordenes 2, 2, 2 y 3 [May]. Si
denotamos por K + (S, τ ) el subgrupo de ı́ndice dos de K(S, τ ) consistente de los
automorfismos holomorfos de S que conmutan con τ , entonces |K(S, τ )| = 12(g −
1) y S/K + (S, τ ) es la esfera de Riemann con una reflexión η, inducida por τ , con
exactamente cuatro valores de ramificación de ordenes 2, 2, 2 y 3, todos ellos ubicados
en el cı́rculo de puntos fijos de la reflexión η.
Segundo, la superficie de Klein R = S/τ es una superficie compacta de Klein con
borde. Esta superficie puede ser orientable como no serlo. El grupo K(S, τ )/τ corresponde al grupo total de automorfismos de R, un grupo de orden 12(g − 1).
Toda superficie de Riemann puede tener dos posibilidades: ser hiperelı́ptica, es decir,
tener una involución holomorfo con exactamente 2(g + 1) puntos fijos. El siguiente
resultado nos dice que superficies maximales simétricas no pueden ser hiperelı́pticas
si el género es mayor que dos.
Teorema 9.1. Una superficie maximal simétrica de género al menos tres no puede
ser hiperelı́ptica.
Demostración. Supongamos que S es maximal simétrica hiperelı́ptica de género
mayor o igual a tres con reflexión maximal τ : S → s. Denotemos por j : S → S
la involución hiperelı́ptica. Como j es única, tenemos que j ∈ K(S, τ ). Denotemos
b el cubrimiento ramificado inducido por la acción de j. La reflexión
por Q : S → C
b → C
b el cual conmuta con cada automorfismo
τ desciende a una reflexión η : C
+
en N = K (S, τ )/j, un grupo de transformaciones de Möbius de orden 6(g − 1).
Denotemos por C el cı́rculo de puntos fijos de la reflexión η. Luego el grupo N es
113
114
9. SUPERFICIES DE RIEMANN MAXIMAL SIMÉTRICAS
Fuchsiano o posee un subgrupo N0 de ı́ndice dos que es Fuchsiano. Como todo grupo
Fuchsiano finito es cı́clico, obtenemos que N posee un grupo cı́clico Fuchsiano de orden
3(g − 1) y, en particular, el cociente S/K(S, τ ) deberı́a tener un valor de ramificación
de orden 3(g − 1) > 5, una contradicción.
Como el cociente S/K(S, τ ) es un disco cerrado con cuatro valores de ramificación en
su borde, cuyos ordenes son 2, 2, 2 y 3, primero buscaremos ciertos grupos Kleinianos
planares que uniformizan todas estas.
9.2.
Uniformizaciones de S/K(S, τ )
Consideremos una superficie de Riemann maximal S con una reflexión maximal τ :
S → S. Como ya habı́amos observado, S/K(S, τ ) es un disco cerrado con cuatro
valores de ramificación
√ en su borde cuyos ordenes son 2, 2, 2 y 3.
b p generado por la siguientes reflexPor cada p ∈ (2 − 3, 1), consideremos el grupo K
1
2πi
(1+p2 )z−2p
iones: σ1 (z) = z, σ2 (z) = e 3 z, σp (z) = 2pz−(1+p
(ver figura 1).
2 ) y σ(z) =
z
α1
C
α
2
Figura 1. Dominio fundamental para Kp
2πi
Consideremos las siguientes transformaciones W (z) = σ2 σ1 (z) = e 3 z,
1
T (z) = σσ1 (z) = y
z
(p + p1 )z − 2
b p es también generado por las
. Entonces el grupo K
J(z) = σp σ1 (z) =
2z − (p + p1 )
9.2. UNIFORMIZACIONES DE S/K(S, τ )
115
transformaciones T , W , J y σ. Como consecuencia de los teoremas de combinación
de Klein-Maskit [Maskit1], tenemos que
b p = hT, W, J, σ : T 2 = W 3 = (W T )2 = J 2 = (T J)2 = σ 2 = (σT )2 =
K
σW σW −1 = (σJ)2 = 1i.
b p tiene un dominio de discontinuidad conexo Ω y un
El grupo Kleiniano planar K
dominio fundamental determinado por la región acotada por los cı́rculos unitario, los
rayos de argumentos πi
y −πi
, respectivamente, y el cı́rculo C, ortogonal al cı́rculo uni3
3
1
tario, conteniendo los puntos p y (ver figura 1). La superficie de Klein uniformizada
p
b es un disco cerrado con exactamente cuatro valores de ramificaión en su borde,
por K
cuyos ordenes son 2, 2, 2 y 3.
Teorema 9.2. Sea X una superficie de Klein la cual es topológicamente un disco
cerrado con exactamente cuatro valores de ramificación sobre su borde, √
cuyos valores
de ramificación son 2, 2, 2 and 3. Entonces existe un valor de p ∈ (2 − 3, 1) tal que
Ω(Kp )/Kp es dianalı́ticamente equivalente a X.
Demostración. Esto es consecuencia de la teorı́a de funciones casiholomorfas y
el hecho que los puntos fijos de reflexiones son cı́rculos Euclideanos.
b p consistiendo de la transformaciones holomorfos
El subgrupo de ı́ndice dos Kp de K
está generado por T , W y J. Un presentación para Kp es
Kp = hT, W, J : T 2 = W 3 = (W T )2 = J 2 = (T J)2 = 1i,
es decir, isomorfo al producto libre amalgamado del grupo dihedral D3 = hT, W i con
el grupo de Klein Z2 + Z2 = hT, Ji sobre el grupo cı́clico de orden dos generado por
T . La superficie de Riemann Ω/Kp es la esfera de Riemann con cuatro valores de
ramificación de ordenes 2, 2, 2 and 3, todos ellos contenidos en el cı́rculo de puntos
fijos de la reflexión inducida por σ. Un dominio fundamental para Kp puede ser
b p con su transladado por σ y
tomado como la unión del dominio fundamental para K
−πi
πi
los puntos del cı́rculo unitario localizados entre e 3 y e 3 .
√
b p uniformiza un trı́angulo
Observación 9.1.
(1) En el caso frontera p = 2− 3, K
hiperbólico con un vértice al infinito, un vértice con ángulo π3 y el otro con
ángulo π2 . El grupo Kp uniformiza en este caso el plano complejo con dos
valores de ramificación de ordenes 2 y 3, respectivamente.
b p es sólo generado por las reflexiones σ1 , σ2 y σ, pero actuando
(2) Para p = 1, K
en la esfera pinchada en tres puntos (los puntos de contacto de los cı́rculos de
b p uniformiza el disco cerrado con tres
puntos fijos). En este caso, el grupo K
valores de ramificación sobre su borde, cuyos ordenes son 2, 3 y ∞, respectively.
116
9. SUPERFICIES DE RIEMANN MAXIMAL SIMÉTRICAS
9.3.
Superficies Maximales Simétricas de Género 2
9.3.1. Acciones Topológicas. Tenemos exactamente dos posibles acciones
topológicas de K(S, τ ) para S maximal simétrica y τ una reflexión maximal de S, en
el caso que S tenga género dos. En ambos casos, S/τ es orientable; un toro con un
borde ó una esfera con tres bordes.
Ejercicio. Verificar lo anterior.
Estas superficies corresponden a las siguientes dos familias de curvas algebraicas:
y 2 = (x3 − λ3 )(x3 − 1/λ3 )
donde una familia corresponde a λ > 1 y la otra a λ = eiθ , θ ∈ (0, π/3). En este caso,
K(S, τ ) = hτ, j, α, βi, donde
x 7→
x
x 7→ 1/x
; j=
τ=
;
y 7→ y/x3
y 7→ −y
x 7→ 1/x
x 7→ e2πi/3 x
; β=
α=
y 7→ y/x3
y 7→
y
Observación 9.2. La superficie correspondiente a θ = π/6, isomorfa a
tiene el automorfismo extra
=
x
x →
7
y →
7
y
α
y, en particular,
τ3 =
y 2 = x6 − 1,
1/2
x →
7
eπi/3 x
y →
7
y
; j
1/2
=
x →
7
1/x
y →
7
iy/x3
Procederemos a uniformizar tales superficies usando grupo de Schottky y además
calcularemos sus matrices de Riemann.
9.3.2. Uniformizaciones√de Schottky y Matrices de Riemann. Tomemos
b =K
b p , para p ∈ (2− 3, 1). Consideremos las transformaciones de Möbius:
el grupo K
−1
A1 = JW JW , A2 = JW −1 JW ,
B1 = (σ3 σ2 )2 y B2 = σ1 B1 σ1 . Los grupos G2 = hA1 , A2 i y F2 = hB1 , B2 i resultan ser
grupos de Schottky cásicos de género dos con un dominio fundamental estándar la
región acotada por los cı́rculos W (C), J(W (C)), W −1 (C) y J(W −1 (C)).
−1
−1
−1
−1
Ya que W A1 W −1 = A−1
= A−1
=
1 A2 , W A2 W
1 , JA1 J = A1 , JA2 J = A2 , T A1 T
−1
−1
−1
−1
A2 , T A2 T = A1 , σA1 σ = A1 , σA2 σ = A2 , W B1 W = B1 B2 , W B2 W = B1 ,
JB1 J = B2−1 , JB2 J = B1−1 , T B1 T = B2 , T B2 T = B1 , σB1 σ = B1 y σB2 σ =
b Más aún,
B2 , tenemos que ambos grupos G2 y F2 son subgrupos normales de K.
9.3. SUPERFICIES MAXIMALES SIMÉTRICAS DE GÉNERO 2
117
∼
b
para Q ∈ {G2 , F2 }, K/Q
= D3 + Z2 + Z2 y K/Q ∼
= D3 + Z2 . En particular, la
superficie de Riemann de género dos S2 = Ω/G2 (respectivamente, R2 = Ω/F2 )
b 2 (respectivamente, K/F
b 2 ) como grupo de automorfismos, con
admite el grupo K/G
K/G2 (respectivamente, K/F2 ) como su subgrupo de ı́ndice dos consistiendo de los
b 2 ) (respectivamente, R2 /(K/F
b 2 )) es
automorfismos holomorfos. El cociente S2 /(K/G
un disco cerrado con cuatro valores de ramificación sobre su borde, cuyos ordenes son
2, 2, 2 y 3.
Teorema 9.3. Sea S una superficie de Riemann maximal simétrica de género dos
con una reflexión maximal τ : S → S tal que S/τ es orientable.
Entonces S puede
√
ser uniformizada por G2 ó F2 para un valor de p ∈ (2 − 3, 1).
√
Demostración. Fijemos un valor de p ∈ (2 − 3, 1) y sea K = Kp el grupo
correspondiente. Sea S una superficie de Riemann maximal simétrica de género dos
y una reflexión maximal τ : S → S como en la hipótesis. La acción topológica de
K(S, τ ) está reflejada por G2 o por F2 (esto porque sólo hay dos posibles acciones).
Supongamos que esta acción está reflejada por G2 (el argumento será similar para la
otra situación). Tomemos S2 = Ω/G2 y sea f : S2 → S un difeomorfismo que preserva
b 2 f −1 = K(S, τ ). En esta caso, tenemos por la compacidad de
orientación tal que f K/G
S que f es un difeomorfismo casiholomorfo, con diferencial de Beltrami µ. Procedamos
a levantar µ a Ω y extendámosla a toda la esfera como cero en el conjunto lı́mite de
b→C
b un homeomorfismo casiholomorfo con coeficiente de Beltrami µ.
b Sea W : C
K.
−1
b
Entonces W KW es de nuevo un grupo generado por reflexiones. Podemos asumir
que W fija 0, 1 y ∞. Ya que los puntos fijos de una reflexión es un cı́rculo Euclideano,
b −1 es uno de los grupos K
b para cierto valor de q ∈
tenemos
√ que el grupo W KW
(2 − 3, 1). Si denotamos por π : Ω → Ω/G2 el cubrimiento holomorfo inducido por
b −1 ) → S es una uniformización de S
G2 , entonces tenemos que f πW −1 : Ω(W KW
por el correspondiente grupo de Schottky G2 . Además, el levantamiento del grupo
b −1 .
K(S, τ ) es exactamente W KW
Teorema 9.4. Sea S una superficie de Riemann maximal simétrica de género dos
con una √
reflexión maximal τ : S → S tal que S/τ es un toro con un borde. Sea
2π
p ∈ (2 − 3, 1) tal que S = Ω/G2 . Sean q1 = e( 3 −θ)i , q2 = J(q1 ) y θ ∈ (0, π2 ) tal que
2p
cos θ = 1+p
2.
Entonces a Riemann matrix of S is dada por
1
Z=
1 + 10w 2 + 9w 4
8w 2 + 4w(1 + 3w 2)i −2(1 + 5w 2) − 2w(3w 2 − 1)i
−2(1 + 5w 2) − 2w(3w 2 − 1)i
8w 2 + 4w(1 + 3w 2)i
,
118
9. SUPERFICIES DE RIEMANN MAXIMAL SIMÉTRICAS
α1
β
α ’2
1
C
α 1’
α
β
2
2
π
β1
β2
α1
S
2
α2
Figura 2. Arcos para G2
donde w > 0 es tal que


1
4w(1 + 3w 2 )


=
Log

2
4

2π

 1 + 10w + 9w



1
−2w(3w 2 − 1)



 1 + 10w 2 + 9w 4 = 2π Log
Y |γ(q2 ) − A−1 (∞)|
1
−1
|γ(q1 ) − A1 (∞)|
γ∈G
θ
Y |γ(q2 ) − A−1 (∞)|
2
−1
|γ(q1 ) − A2 (∞)|
γ∈G
θ
!
;
!
.
Demostración. Sean α1 = W (C), α1′ = J(α1 ), α2 = W −1 (C) y α2′ = J(α2 ).
Orientemos los cı́rculos α1 , α2 , α1′ y α2′ como se muestra en la figura 2. También
9.3. SUPERFICIES MAXIMALES SIMÉTRICAS DE GÉNERO 2
119
consideremos los arcos simples orientados β1 y β2 , también mostrados en la figura 2.
La proyección de esas curvas cerradas y arcos orientables se proyectan en una base
simpléctica para la superficie de Riemann S2 .
De esta manera, obtenemos una representación simpléctica inyectiva (fiel)
definida por
^Z)
b 2 → Sp(4;
ρ : K/G

−1
0 0 0
 0 −1 0 0 

ρ(σ) = 
 0 −1 1 0  ,
−1
0 0 1


−1
0
0
0
 0 −1
0
0 
,
ρ(J) = 
 0
0 −1
0 
0
0
0 −1


0
 1
ρ(T ) = 
 0
0
1
0
0
0
0
0
0
1

0
0 

1 
0

0
1
0
0
 −1 −1
0
0 

ρ(W ) = 
 a
b −1 −1 
c
d
1
0

La matriz de Riemann Z = X + iY ∈ H2 de S2 definida por la base simpléctica
b 2 ). De aquı́ se sigue que: a =
anterior es un puntos fijo del grupo simpléctico ρ(K/G
−1, b = 0, c = 0, d = 1, and
1 0 1
τ 2 1
−1
−Z =
+i
,
2 1 0
2 1 2
donde τ > 0.
De esta manera, la matriz Z tiene la forma deseada y los resultados de Burnside
[Burnside] descritos anteriormente en la seción 8.3 pueden ser usados en este caso
para el grupo G2 para calcular el valor de w en función de p como está descrito en el
teorema.
√
Observación 9.3. En el caso p = 2 − 3, el grupo G2 resulta ser un grupo de
Schottky anodado de género dos uniformizando una superficie stable de género dos
con exactamente un nodo que divide. En el caso p = 1, podemos pensar que el grupo
G2 como el grupo trivial actuando en la esfera pinchada en tres puntos, esto es,
uniformizando la esfera pinchada en tres puntos.
Teorema 9.5. Sea S una superficie de Riemann maximal simétrica de género dos
con una reflexión
maximal τ : S → S tal que S/τ es una esfera con tres bordes. Sea
√
2π
p ∈ (2 − 3, 1) tal que S = Ω/F2 . Sean q1 = e( 3 −θ)i , p2 = σ3 (q1 ) y θ ∈ (0, π2 ) tal que
2p
cos θ = 1+p
2.
120
9. SUPERFICIES DE RIEMANN MAXIMAL SIMÉTRICAS
Entonces una matriz de Riemann para S es dada por
iµ
2 −1
,
Z=
2
2 −1
donde
1
µ=
Log
2π
Y |γ(p2 ) − B −1 (∞)|
1
−1
|γ(q
)
−
B
1
1 (∞)|
γ∈F
θ
!
.
Demostración. Sean α1 = W (C), α1′ = σ3 (α1 ), α2 = W −1 (C) y α2′ = σ3 (α2 ).
Si orientamos los cı́rculos α1 , α2 , α1′ , α2′ , y consideramos los arcos orientados β1 y β2
como se muestra en la figura 3, entonces la proyección de esas curvas cerradas y arcos
orientados determina una base simpléctica en la superficie de Riemann R2 .
Obtenemos de esta manera una representación fiel
definida por
^Z)
b 2 → Sp(4;
ρ : K/F

−1
0 0 0
 0 −1 0 0 
,
ρ(σ) = 
 0
0 1 0 
0
0 0 1


0 −1
0
0
 −1
0
0
0 
,
ρ(J) = 
 0
0
0 −1 
0
0 −1
0


0
 1
ρ(T ) = 
 0
0
1
0
0
0
0
0
0
1

0
0 

1 
0

0
1
0
0
 −1 −1
0
0 

ρ(W ) = 
 a
b −1 −1 
c
d
1
0
La matriz de Riemann Z = X + iY ∈
anteriormente construida, es un puntos
sigue que: a = b = c = d = 0, y
iτ 2
−1
−Z =
2 1

H2 de R2 , definida por la base simpléctica
b 2 ). Se
fijo para el grupo simpléctico ρ(K/F
1
2
,
donde τ = 3µ/4 > 0.
De nuevo los resultados de las sección 8.3 determina el valor de µ como se desea. √
Observación 9.4.
(1) En el caso p = 2− 3, el grupo F2 es un grupo de Schottky
anodado de género dos uniformizando una superficies de Riemann estable de
género dos con exactamente tres nodos (cada uno de ellos no dividiendo). En
el caso p = 1, podemos pensar que el grupo F2 ctúa trivialmente en la esfera
pinchada entres puntos, luego uniformizando esta.
9.3. SUPERFICIES MAXIMALES SIMÉTRICAS DE GÉNERO 2
121
α1
β
α’
1
1
C
β
α
α’2
2
2
π
β1
α1
β2
R
2
α2
Figura 3. Arcos para F2
(2) Notemos en este punto que los resultados en [Farkas-Kra] (ver también el
trabajo de González-Dı́ez [Gabino]) nos permite describir la curva algebraica
(usando funciones theta) de las superficies S2 y R2 en función de w y, en
particular, de p. De esta manera, podemos obtener una relación explı́cita entre
los grupos de Schottky G2 , F2 y las respectivas curvas algebraicas.
(3) Es importante notar a este punto que usando Theta caracterı́sticas
[Farkas-Kra] podemos describir la curva algebraica en función de w y luego
en función de p. De esta manera podemos obtener relaciones explı́citas entre
la uniformización de Schottky dada por los grupos de Schottky G2 , F2 y las
122
9. SUPERFICIES DE RIEMANN MAXIMAL SIMÉTRICAS
respectivas curvas algebraicas. The holomorphic map
b1 (z)
b : z 7→ w
F :Ω→C
w
b2 (z)
gives us a holomorphic branched covering for the group hj, W jW −1, W −1 jW i,
where j(z) = σ3 σ1 (z). The branched covering map F is a lifting of the two-fold
b induced by the hyperelliptic involution. It
branched covering S = Ω/J → C
follows that the algebraic curve defining S is given by
y 2 = (x − a)(x − b)(x − c)(x − d)(x − e)(x − f )

a =
F (p)




b = F (W (p))


 c = F (W 2(p))
where
d =
F ( p1 )




e = F (W ( p1 ))



f = F (W 2 ( p1 ))
9.4.
Superficies Maximales Simétricas de Género 3
9.4.1. Acciones Topológicas. Consideremos una superficie de Riemann maximal simétrica S de género 3 con una reflexión maximal τ : S → S. Tenemos que
K + (S, τ ) es un grupo de automorfismos holomorfos de orden 24 tal que S/K + (S, τ )
es la esfera de Riemann con exactamente cuatro valores de ramificación de ordenes 2,
b → C,
b inducida por τ , tal que esos valores
2, 2 y 3. Más aún, existe una reflexión η : C
de ramificación están contenidos en el cı́rculo de puntos fijos de η. Ya que S no puede
ser hiperelı́ptica, el grupo holomorfo K + (S, τ ) es isomorfo al grupo de permutaciones
de cuatro letras S4 [Vermeulen] y además esta acción es topológicamente rı́gida.
Sean R = Sτ y H24 = K(S, τ )/τ el grupo de automorfismos inducidos en la superficie
de Klein R. Entonces tenemos que, módulo homeomorfismos, R puede ser uno de los
siguientes:
(i)
(ii)
(iii)
(iv)
(v)
Un toro con dos bordes;
Una esfera con cuatro bordes;
La suma conexa de toro con un plano proyectivo y con un borde;
La suma conexa de dos planos proyectivos y con un borde; y
un plano proyectivo con tres bordes.
Teorema 9.6. Las únicas posibilidades para R son dadas por los casos (ii) y (v),
esto es, sólo existen dos acciones topológicamente diferentes de K(S, τ ). Más aún, si
denotamos por τ1 y τ2 las dos posibles acciones topológicas de τ , entonces K(S, τ1 ) y
K(S, τ2 ) no son isomorfos como grupos abstractos.
9.4. SUPERFICIES MAXIMALES SIMÉTRICAS DE GÉNERO 3
123
Demostración. Primero procederemos a ver que los casos (i), (iii) y (iv) no son
posibles.
(1) Caso(i): En esta situación, tendrı́amos la existencia de una superficie de género
uno con dos puntos distinguidos p 6= q y un grupo de automorfismos holomorfo/antiholomorfo H24 de orden 24 actuando transitivamente en {p, q}. Dentro de H24
tenemos un subgrupo de ı́ndice dos H12 consistiendo de automorfismos holomorfos.
Las posibilidades para el estabilizador de p en este subgrupo son: (1) un grupo cı́clico
de orden 12, el cual no es possible; o (2) un grupo cı́clico de orden 6. En este caso,
un tal grupo cı́clico debe también estabilizar el punto q. Pero en género uno no todo
grupo cı́clico de orden 6 de automorfismos holomorfos tiene a lo más un punto fijo.
(2) Caso (iii): Consideremos el cubrimiento doble orientable X de R. Tenemos entonces que X es una superficie de Riemann de género dos con exactamente dos bordes
admitiendo un automorfismo antiholomorfo de orden dos η : X → X, actuando sin
puntos fijos, tal que R = X/η. Podemos levantar H24 a un grupo de automorfismos
holomorfos/antiholomorfos de X, de orden 48, denotado por K48 . Es claro que K48
debe contener η (levantamiento de la identidad). Dentro K48 tenemos un subgrupo de
ı́ndice dos de K24 consistiendo de automorfismos holomorfos de X. Esto nos darı́a la
existencia de una superficie de Riemann de género 2 con dos puntos distinguidos p 6= q
tal que {p, q} es invariante por la acción del grupo K24 . Se sigue que el estabilizador
de p sólo podrı́a ser un grupo cı́clico de orden 24 ó 12. Ambas situaciones contradicen
el hecho que en género dos todo automorfismo tiene orden menor o igual a 10.
(3) Caso (iv): Similar al caso (2) con X una superficie de Riemann de género uno con
cuatro bordes. En este caso, tendrı́amos la existencia de una superficie de Riemann
de género uno con cuatro puntos distinguidos p1 , p2 , p3 y p4 , pi 6= pj , y un grupo de
orden 24 de automorfismos holomorfos de esta, dejando invariante {p1 , p2 , p3 , p4 }. De
nuevo, el estabilizador en este grupo de pj no puede ser un grupo cı́clico de orden
24 ó 12. En particular, el estabilizador de pj es un grupo cı́clico de orden 6. Pero
en este caso el estabilizador T6 = ht : t6 = 1i de p1 permuta los otros tres puntos.
Se sigue que o bien T6 estabiliza uno de esos otros tres puntos, lo cual es imposible,
ó h = t2 fija cuatro puntos diferentes, lo cual también se sabe que es imposible en en
una superficie de Riemann de género uno.
La segunda parte es mostrar que los casos (ii) y (v) son posibles. Esto será hecho en
la siguiente subsección. También se deducirla última parte del teorema directamente
de tal construcción.
Observación 9.5. Las superficies de Riemann maximales simétricas de género 3 son
algebráicamente descritas por las siguientes curvas en el plano proyectivo complejo
P2 [Gonzalez-Rodriguez]:
124
9. SUPERFICIES DE RIEMANN MAXIMAL SIMÉTRICAS
S : x4 + y 4 + z 4 + λ(x2 y 2 + y 2 z 2 + z 2 x2 ) = 0,
donde λ ∈ (−∞, −2) para el caso (v) y λ ∈ (−2, −1) para el caso (ii). La reflexión τ
es dada por τ [x : y : z] = [x, y, z], y K + (S, τ ) es el grupo simétrico en cuatro letras
S4 generado por las siguientes transformaciones proyectivas




0 −1 0
1 0 0
0 0 ; b =  0 0 1 
a= 1
0
0 1
0 1 0
9.4.2. Uniformizaciones de Schottky
√ y Matrices de Riemann. Considb
b
eremos el grupo K = Kp , para p ∈ (2 − 3, 1). Sea G3 el grupo generado por las
transformaciones A1 = (σp σ2 )3 , A2 = W A1 W −1 and A3 = W −1 A1 W , y F3 el grupo
generado por las transformaciones B1 = σσp σ2 σ1 σ2 σp σ2 σ1 σ3 σ2 , B2 = W B1 W −1 and
B3 = W −1 B1 W .
b ambos de ı́ndice
Teorema 9.7. Los grupos G3 y F3 son subgrupos normales de K,
48. Más aún, cada uno de ellos es un grupo de Schottky clásico de género 3.
Demostración. Es fácil ver que esos grupos son de Schottky clśicos y género
3, con dominio fundamental acotado por los cı́rculos C1 = σp (σ2 (C), C6 = σ1 (C1 ),
C2 = W (C6 ), C3 = W (C1 ), C5 = W −1 (C1 ) y C4 = W −1 (C6 ), donde C = Fix(σp ).
Si mostramos que ellos son subgrupos normales, entonces un cálculo directo muestra
b 3 y K/F
b 3 son grupos de orden 48 no-isomorfos.
que K/G
Es fácil verificar que:
(1) σ1 A1 σ1 = A−1
3 ,
(3) σ2 A1 σ2 = A−1
1 ,
(5) σp A1 σp = A−1
1 ,
(7) σp A3 σp = A−1
3 ,
(9) σA2 σ = A2 ,
(11) σ1 B1 σ1 = B3−1 ,
(13) σ2 B1 σ2 = B1−1 ,
(15) σp B1 σp = B3 ,
(17) σB1 σ = B1 ,
(19) σB3 σ = B3 ,
(2) σ1 A2 σ1 = A−1
2 ,
(4) σ2 A2 σ2 = A−1
3 ,
(6) σp A2 σp = A1 A2A3 ,
(8) σA1 σ = A1 ,
(10) σA3 σ = A3 ,
(12) σ1 B2 σ1 = B2−1 ,
(14) σ2 B2 σ2 = B3−1 ,
(16) σp B2 σp = B3−1 B2−1 B1−1 ,
(18) σB2 σ = B2 ,
mostrando la normalidad de esos grupos.
Teorema 9.8. Sea S una superficie de Riemann maximal simétrica de género 3
admitiendo una reflexión maximal τ : S → S. (i) Si S/τ es orientable,
entonces
√
S puede ser uniformizada por G3 para un cierto valor de p ∈ (2 − 3, 1); (ii) Si
9.4. SUPERFICIES MAXIMALES SIMÉTRICAS DE GÉNERO 3
125
α1
α ´2
β1
α ´1
β2
α3
C
β3
α2
α ´3
Figura 4. Arcos para G3
S/τ es no-orientable,
entonces S puede ser uniformizada por F3 para cierto valor de
√
p ∈ (2 − 3, 1).
Demostración. la demostración es exactamente la misma como en el caso de
género dos.
Procedemos a calcular la matrices de Riemann de cada superficie de Riemann maximal
simétrica de género 3 con la ayuda de las uniformizaciones de Schottky obtenidas.
Para el grupo G3 escojamos α1 = C2 orientada en el sentido opuesto a las manecillas
de un reloj, α1′ = C1 con la orientación de α1 inducida por A1 . Tomemos α2 = W (α1 ),
α3 = W −1 (α1 ), α2′ = W (α1′ ), α3′ = W −1 (α1′ ). Consideremos también arcos simples
orientados β1 , β2 y β3 como es mostrado en figura 4.
Para el grupo F3 escojamos α1 = C3 orientada en el sentido opuesto a las manecillas
de un reloj, α1′ = C6 con la orientación inducida por B1 de la dada a α1 . Tomemos
α2 = W (α1 ), α3 = W −1 (α1 ), α2′ = W (α1′ ), α3′ = W −1 (α1′ ). Consideremos arcos
simples orientados β1 , β2 y β3 como se muestra en la figura 5.
En cada uno de los dos casos mencionados, las curvas cerradas orientadas α1 , α2 ,
α3 , y los arcos simples orientados β1 , β2 y β3 se proyectan a una base simpléctica
en la superficie de Riemann uniformizada S. Obtenemos entonces representaciones
simplécticas
^
b 3 → Sp
θ1 : K/G
6 (Z)
^
b 3 → Sp
θ2 : K/F
(Z)
6
126
9. SUPERFICIES DE RIEMANN MAXIMAL SIMÉTRICAS
´
α 2´
α1
β
1
α ´3
β2
C
α 1´
α 3´
α2
β3
Figura 5. Arcos para F3
dadas por:




θ1 (σ) = 






θ1 (T ) = 


−1
0
0 0 0 0
0 −1
0 0 0 0
0
0 −1 0 0 0
0
0
0 1 0 0
0
0
0 0 1 0
0
0
0 0 0 1








0
0 −1
0
0
0
0 −1
0
0
0
0 

−1
0
0
0
0
0 

0
0
0
0
0 −1 
0
0
0
0 −1
0 
0
0
0 −1
0
0




θ1 (J) = 


0
0
1 0
0 0
−1 −1 −1 0
0 0
1
0
0 0
0 0
0
0
0 0 −1 1
0
0
0 0 −1 0
0
0
0 1 −1 0
t






9.4. SUPERFICIES MAXIMALES SIMÉTRICAS DE GÉNERO 3




θ1 (W ) = 


0
1
0
0
0
0
0
0
1
0
0
0
1
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
1
0
0
127
t






t
−1
0
0 −1 −1
1
0 −1
1 −1 
 0 −1


0 −1
1 −1 −1 
 0
θ2 (σ) = 

0
0
1
0
0 
 0
 0
0
0
0
1
0 
0
0
0
0
0
1


0
0 −1
0
0
0
0
0
0
0 
 0 −1


0
0
0
0
0 
 −1
θ2 (T ) = 

0
0
0
0 −1 
 0
 0
0
0
0 −1
0 
0
0
0 −1
0
0
t

−1 0
0
0 −1
0
1
1
0
1 
 1 1


0 −1
0 
 0 0 −1
θ2 (J) = 

0 −1
1
0 
 0 0
 0 0
0
0
1
0 
0 0
0
0
1 −1

t
0 0 1 −1
1
2
1
2 −1 
 1 0 0


2 −1
1 
 0 1 0
θ2 (W ) = 

0
0
1 
 0 0 0
 0 0 0
1
0
0 
0 0 0
0
1
0

Siguiendo los mismos argumentos hechos para el caso de género dos, uno obtiene:
Teorema 9.9. Sea S una superficie de Riemann maximal simétrica de género
√ 3 con
una reflexión maximal τ : S → S tal que S/τ es orientable. Sea p ∈ (2 − 3, 1) de
manera que S = Ω/G3 . Entonces una matriz de Riemann para S es dada por


2 1 1
it
Z =  1 2 1 ,
4 1 1 2
128
9. SUPERFICIES DE RIEMANN MAXIMAL SIMÉTRICAS
donde
1
t = Log
π
!
Y |γ(rp ) − A−1 (∞)|
1
,
−1
|γ(s
)
−
A
(∞)|
p
1
γ∈G
3
2π
rp = σp (e( 3 −θ)i ),
y θ ∈ (0, π2 ) satisface cos θ =
sp = σ2 (rp )
2p
.
1+p2
Teorema 9.10. Sea S una supeficie de Riemann maximal simétrica de género√3 con
una reflexión maximal τ : S → S tal que S/τ es no-orientable. Sea p ∈ (2 − 3, 1)
de manera que S = Ω/F3 . Entonces una matriz de Riemann para S es dada por




−1 −1
1
3 −1 −1
1
1 −1  + ti  −1
3 −1  .
Z =  −1
2
1 −1 −1
−1 −1
3
La matriz de Riemann −Z −1 es la matriz de Riemann que corresponde para usar el
método de Burnside y obtener el valor de t en términos de p.
√
Observación 9.6.
(1) En el caso p = 2 − 3, el grupo G3 es un grupo de Schottky anodado de género tres uniformizando una superficie de Riemann stable
de género tres con exactamente cuatro nodes (cada uno de ellos no dividiendo) y two componentes, cada una de ellas una esfera con cuatro pinchaduras.
En el caso p = 1, podemos pensar que el grupo G3 actúa de manera trivial
en la esfera
√ de Riemann con tres pinchaduras, esto es, uniformizándola. Para
p ∈ (2 − 3, 1), el grupo G3 uniformiza
√ las curvas algebraicas correspondientes a λ ∈ (−2, −1); para p = 2 − 3 este uniformiza la curva algebraica
correspondiente a λ = −1; y para p = 1 este uniformiza la curva algebraica
para λ = −2.
√
(2) En el caso p = 2 − 3, el grupo F3 es un grupo de Schottky anodado de
género tres uniformizando una superficie de Riemann stable de género tres con
exactamente tres nodes (cada uno de ellos no dividiendo) y una componente
(una esfera con seis pinchaduras). En el caso p = 1, podemos pensar que el
grupo F3 actúa trivialmente en la esfera de√Riemann pinchada en tres puntos,
esto es, uniformizándola. Para p ∈ (2 − 3, 1), el grupo F3 uniformiza
√ las
curvas algebraicas correspondientes a λ ∈ (−∞, −2); para p = 2 − 3 este
grupo uniformiza la curva algebraica correspondiente a λ = −∞; y para p = 1
este uniformiza la curva algebraica para λ = −2.
9.5. SUPERFICIES DE RIEMANN MAXIMAL SIMÉTRICAS DE GÉNERO 5
9.5.
129
Superficies de Riemann Maximal Simétricas de Género 5
9.5.1. Topological Actions. Consideraremos superficies de Riemann maximales simétrica S de género 5 con una reflexión maximal τ : S → S tal que S/τ es
orientable. El caso en que S/τ es no-orientable es dejado como un ejercicio.
Teorema 9.11.
(1) En género 5 hay exactamente dos reflexiones maximales
topológicamente diferentes con la condición que el cociente es orientable.
(2) Sean (S1 , τ1 ) y (S2 , τ2 ) dos pares, donde Sj es una superficie de Riemann maximal simétrica de género 5 y τj una reflexión maximal de Sj . Supongamos que
τ1 y τ2 no son topológicamente equivalentes. Entonces los respectivos grupos
K(S1 , τ1 ) y K(S2 , τ2 ) son no isomorfos como grupos abstractos. Más aún, las
acciones respectivas de K(Sj , τj ) son topológicamente rı́gidas.
(3) Sea S una superficie de Riemann maximal simétrica de género 5 con una
reflexión maximal τ : S → S. Entonces existe un subgrupo normal L de
K(S, τ ), isomorfo a Z2 +Z2 , de automorfismos holomorfos actuando sin puntos
fijos tal que S/L es una superficie de Riemann de género dos.
Observación 9.7. En particular, el resultado anterior dice que en el espacio de
Módulos de superficies de género 5 hay exactamente dos subvariedades algebraicas
reales, cada una de dimensión real uno, determinando las superficies de Riemann
maximales simétricas con cociente orientable.
Demostración. Ya que S/τ es orientable, tenemos exactamente tres posibilidades:
(1) S/τ es un toro con cuatro bordes;
(2) S/τ es una esfera con seis bordes; y
(3) S/τ es una superficie de género dos con dos bordes.
Como τ pertenece al centro de K(S, τ ), tenemos que K(S, τ ) desciende a un grupo
de automorfismos H48 , de orden 48, del cociente S/τ .
(1) S/τ es un toro con cuatro bordes. Denotemos por H48 el grupo de orden 48 de automorfismos de S/τ inducido por H96 . Si H48 sólo tiene automorfismos holomorfos, entonces esto implicarı́a la existencia de un grupo de
automorfismos holomorfos de orden 48 actuando en una superficie de Riemann de género uno dejando transitivamente invariante un conjunto formado
por 4 puntos. Esto dirı́a que el estabilizador de cualquiera de esos cuatro
puntos, en tal grupo, es un grupo cı́clico de orden 12, lo cual es imposible.
Luego, H48 debe contener automorfismos antiholomorfos. Sea H24 el subgrupo
de indice dos de H48 consistiendo de automorfismos holomorfos. La acción de
tal grupo corresponde (topológicamente) a la acción de un grupo de automorfismos holomorfos de orden 24 en una superficie de Riemann de género
uno con cuatro pinchaduras. Esta acción es la única acción del grupo generado por el grupo alternante A4 = hW, T i y una involución J, donde cada
130
9. SUPERFICIES DE RIEMANN MAXIMAL SIMÉTRICAS
pinchadura es fijada por J. En este caso, la superficie de género uno corresponde a la curva y 2 = x3 − 1 y el grupo H48 es generado por las transfor3y
x+2
, (x−1)
maciones J : (x, y) → (x, −y), S : (x, y) → (x, y), T : (x, y) → ( x−1
2)
2πi
y W : (x, y) → (ρx, y), donde ρ = e 3 . El grupo H24 es el grupo alternante generado por W y T . En particular, la acción topológica de K(S, τ )
es única en esta situación y tiene la presentación: K(S, τ ) = hT, W, J, τ :
T 2 = W 3 = J 2 = τ 2 = (T W )2 = (T J)2 = (T τ )2 = τ W τ W −1 = (τ J)2 =
(JW JW −1 )2 = (τ W )6 = 1i.
Es importante observar que K(S, τ ) tiene dos involuciones holomorfos (las
correspondientes a J y τ ST ), las cuales generan el grupo de Klein L = Z2 +Z2 .
L actúa sin puntos fijos y es un subgrupo normal. La superficie cociente S/L
es una superficie de Riemann de género dos con grupo de automorfismos
Z2 + Z2 + D3 , donde D3 denota al grupo dihedral de orden 6. Uno de los
factores Z es generado por la reflexión inducida por τ , la cual tiene exactamente una componente de puntos fijos que es una geodésica simple cerrada γ.
Tal geodésica γ divide S/L en dos toros con un borde, T1 y T2 . La otra componente Z2 es generada por la involución hiperelı́ptica, y por último, D3 es el
grupo dihedral generado por un automorfismo de orden 3 que deja invariante
cada Ti y una involución holomorfa que permuta T1 con T2 .
(2) S/τ es una esfera con seis bordes. Sea H48 el grupo de automorfismos
inducido por H96 en este cociente. Si H48 sólo contiene automorfismos holomorfos, entonces esto implicará la existencia de un grupo de transformaciones
de Möbius de orden 48, el cual deja transitivamente invariante un conjunto
de 6 puntos, lo cual no es posible. Luego, H48 contiene automorfismos antiholomorfos. Denotemos por H24 el subgrupo de ı́ndice dos de H48 consistiendo
de automorfismos holomorfos. Topológicamente este grupo corresponde a la
acción del grupo simétrico S4 = ha, b : a4 = b2 = (ab)3 = 1i, donde los
seis puntos especiales son exactamente los seis puntos fijos de los elementos
de orden 4. Un automorfismo antiholomorfo extra puede ser escogido como
una reflexión la cual fija cuatro de esos puntos e intercambia los otros dos.
En particular, la acción topológica de K(S, τ ) es única y tiene presentación:
K(S, τ ) = ha, b, µ, τ : a4 = b2 = µ2 = τ 2 = (ab)3 = τ aτ a−1 = (τ b)2 = (µτ )2 =
µaµa−1 = µbµa2 ba2 = 1i.
El grupo L = ha2 , ba2 bi ∼
= Z2 + Z2 es un subgrupo normal de K(S, τ ),
el cual actúa sin puntos fijos. El cociente S/L es una superficie de Riemann
de género dos admitiendo el grupo de automorfismos Z2 + Z2 + D3 . En este
caso, uno de los factores Z2 estǵenerado por una reflexión (la inducida por τ )
la cual tiene exactamente tres componentes de puntos fijos (una M-simetrı́a).
Esas tres componentes dividen S/L en dos esferas con tres bordes, S1 y S2 . La
otra componente Z2 está generado por la involución hiperelı́ptica, y el factor
9.5. SUPERFICIES DE RIEMANN MAXIMAL SIMÉTRICAS DE GÉNERO 5
131
D3 está generado por un automorfismo de orden tres que deja invariante cada
Si y una involución holomorfa que también deja invariante cada Si .
(3) S/τ es una superficie de género dos con dos bordes. Sea de nuevo
H48 el grupo inducido por H96 . Tenemos que este consiste de automorfismos
holomorfos o tiene un subgrupo de ı́ndice dos consistiendo de automorfismos
holomorfos. En cualquiera de esos dos situaciones, tendremos un grupo de
automorfismos holomorfos de orden 48 ó 24 sobre una superficie de Riemann
de género dos dejando invariante dos puntos especiales. El estabilizador de
cualquiera de esos dos puntos tendrı́a que ser un grupo cı́clico de orden 24
ó 12, lo cual no es posible.
En ambos casos (1) y (2), la familia de superficies depende en un parámetro real.
Esto es consecuencia del hecho que el espacio de Teichmüller del disco cerrado con
cuatro valores de ramificación sobre su borde tiene dimensión real uno.
9.5.2. Uniformizaciones de √
Schottky y Matrices de Riemann. Considerb =K
b p con p ∈ (2 − 3, 1). Sea G5 (respectivamente, F5 ) el subgrupo
emos el grupo K
de G2 (respectivamente, F2 ), construido en sección 8.2., generado por los cuadrados
de todos los elementos de G2 (respectivamente, F2 ), es decir:
G5 = hx2 : x ∈ G2 i
F5 = hx2 : x ∈ F2 i.
b y G5
Ya que G2 (respectivamente, F2 ) es un subgrupo normal de ı́ndice 24 en K
(respectivamente, F5 ) es normal de ı́ndice 4 en G2 (respectivamente, F2 ), tenemos
b de ı́ndice 96. El grupo
que G5 (respectivamente, F5 ) es un subgrupo normal de K
G5 (respectivamente, F5 ) es un grupo libre de ı́ndice cuatro en el grupo de Schottky
G2 (respectivamente, F2 ), luego un grupo de Schottky de género 5. Generadores de
2
Schottky para G5 (respectivamente, F5 ) son D1 = A21 , D2 = A22 , D3 = A−1
1 A2 A1 ,
−1
−1
2
2
D4 = A−1
1 A2 A1 A2 y D5 = A2 A1 A2 A1 (respectivamente, E1 = B1 , E2 = B2 ,
−1 2
−1 −1
−1
E3 = B1 B2 B1 , E4 = B1 B2 B1 B2 y E5 = B2 B1 B2 B1 ).
Teorema 9.12. Si S es una superficie de Riemann maximal simétrica de género
cinco con una reflexión maximal τ : S → S tal que S/τ √
es orientable, entonces esta
puede ser uniformizada por G5 ó F5 para algún p ∈ (2 − 3, 1).
Demostración. La demostración es la misma que la hecha para el caso de género
dos.
√
Observación 9.8. En le caso p = 2 − 3, el grupo G5 es un grupo de Schottky
anodado que uniformiza una superficie estable de género cinco con exactamente cuatro
nodos (cada uno de ellos no dividiendo) y dos componentes, cada una de ellas un
superficie de género uno. De manera similar, el grupo F5 es un grupo de Schottky
anodado que uniformiza una superficie estable de género cinco con exactamente seis
132
9. SUPERFICIES DE RIEMANN MAXIMAL SIMÉTRICAS
nodos (cada uno de ellos no dividiendo) y dos componentes, cada una de ellas una
esfera.
Un dominio fundamental estándar para G5 (respectivamente, F5 ) respecto a los generadores de Schottky dados anteriormente es determinado por la región acotada por
−1
−1 −1
′
′
′
′
los cı́rculos θ1 = A−1
1 (α1 ), θ1 = α1 , θ2 = A2 (α2 ), θ2 = α2 , θ3 = A1 A2 (α2 ),
−1
−1 −1
−1 −1
−1
′
′
′
′
′
θ3′ = A−1
1 (α2 ), θ4 = A2 (α1 ), θ4 = A1 A2 (α1 ), θ5 = A1 A2 (α1 ) y θ5 = A2 (α1 )
−1
−1
−1 −1
′
′
′
′
(respectivamente, θ1 = B1 (α1 ), θ1 = α1 , θ2 = B2 (α2 ), θ2 = α2 , θ3 = B1 B2 (α2 ),
θ3′ = B1−1 (α2′ ), θ4 = B2−1 (α1 ), θ4′ = B1−1 B2−1 (α1′ ), θ5 = B1−1 B2−1 (α1 ) y θ5′ = B2−1 (α1′ )).
Podemos dotar a las curvas θk de las orientaciones determinadas por las orientaciones
dadas en 8.2., a las curvas α1 , α2 , α1′ y α2′ . Escojamos los siguientes arcos simples:
−1
−1
δ1 = β1 ∪ A−1
1 (β1 ), δ2 = β2 ∪ A2 (β2 ), δ3 = A1 (δ2 ) (respectivamente, δ1 = β1 ∪
B1−1 (β1 ), δ2 = β2 ∪B2−1 (β2 ), δ3 = B1−1 (δ2 )), con las orientaciones determinadas por las
dadas en 8.2., a los arcos β1 y β2 . Para j = 4, 5, escogemos arcos simples orientados
y disjuntos δj contenidos dentro del disco unitario, de manera que δj parte en θj ,
termina en θj′ y es disjunto de ambos δ1 y δ9−j . Las proyecciones todos esas curvas
cerradas y arcos (orientados) determinan en la superficie de Riemann S5 = Ω(G5 )/G5
(respectivamente, R5 = Ω(F5 )/F5 ) una base simpléctica.
Tenemos las siguientes igualdades:
(a) JD1 J = D1−1 , JD2 J = D2−1 , JD3 J = D1 D3−1 D1−1 , JD4 J = D1 D3 D5−1 D2−1 ,
JD5 J = D2 D4−1 D3−1 D1−1 , JE1 J = E2−1 , JE2 J = E1−1 , JE3 J =
E2 E4−1 E5−1 E2−1 , JE4 J = E2 E5 E3−1 E1−1 , JE5 J = E1 E5−1 E2−1 ;
(b) W D1 W −1 = D3 D5−1 , W D2 W −1 = D1−1 , W D3 W −1 = D4−1 D5−1 , W D4 W −1 =
D5 D1−1 , W D5 W −1 = D2 D4−1 D5−1 , W E1 W −1 = E3 E5−1 , W E2 W −1 = E1−1 ,
W E3 W −1 = E4−1 E5−1 , W E4 W −1 = E5 E1−1 , W E5 W −1 = E2 E4−1 E5−1 ;
(c) T D1 T = D2 , T D2 T = D1 , T D3 T = D5 D4 , T D4 T = D4−1 , T D5 T = D3 D4 ,
T E1 T = E2 , T E2 T = E1 , T E3 T = E5 E4 , T E4 T = E4−1 , T E5 T = E3 E4 ;
(d) σDj σ = Dj , σEj σ = Ej , j = 1, ..., 5,
de las cuales obtenemos las representaciones simplécticas
^Z)
b 5 → Sp(10;
ρ : K/G
y
^Z)
b 5 → Sp(10;
η : K/F
9.5. SUPERFICIES DE RIEMANN MAXIMAL SIMÉTRICAS DE GÉNERO 5
definidas por








ρ(σ) = 






t
−1
0
0
0
0
0 −1 −1 0
0
0 −1
0
0
0 −1
0
0 0 −1 

0
0 −1
0
0 −1
0
0 0 −1 

0
0
0 −1
0
0
0
0 0
0 

0
0
0
0 −1
0 −1 −1 0
0 

0
0
0
0
0
1
0
0 0
0 
0
0
0
0
0
0
1
0 0
0 

0
0
0
0
0
0
0
1 0
0 

0
0
0
0
0
0
0
0 1
0 
0
0
0
0
0
0
0
0 0
1








η(σ) = 






−1
0
0
0
0 0 0 0 0 0
0 −1
0
0
0 0 0 0 0 0
0
0 −1
0
0 0 0 0 0 0
0
0
0 −1
0 0 0 0 0 0
0
0
0
0 −1 0 0 0 0 0
0
0
0
0
0 1 0 0 0 0
0
0
0
0
0 0 1 0 0 0
0
0
0
0
0 0 0 1 0 0
0
0
0
0
0 0 0 0 1 0
0
0
0
0
0 0 0 0 0 1








ρ(T ) = η(T ) = 






0
1
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0 0
0
0 0
0
1 1
0 −1 0
1
1 0
0
0 0
0
0 0
0
0 0
0
0 0
0
0 0
t11
t21
t31
t41
t51
0
1
0
0
0
t12
t22
t32
t42
t52
1
0
0
0
0
t13
t23
t33
t43
t53
0
0
0
1
1
t14
t24
t34
t44
t54
0
0
0
−1
0















t15
t25
t35
t45
t55
0
0
1
1
0
t














133
134
9. SUPERFICIES DE RIEMANN MAXIMAL SIMÉTRICAS








ρ(J) = 














η(J) = 






−1
0
0
0
0 j11
0 −1
0
0
0 j21
0
0 −1
0
0 j31
1 −1
1
0 −1 j41
−1
1 −1 −1
0 j51
0
0
0
0
0 −1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
j12
j22
j32
j42
j52
0
−1
0
0
0
j13
j23
j33
j43
j53
0
0
−1
0
0
j14
j24
j34
j44
j54
1
−1
1
0
−1
j15
j25
j35
j45
j55
−1
1
−1
−1
0
0 −1
0
0
0 j11
−1
0
0
0
0 j21
0
0
0 −1 −1 j31
−1
1 −1
0
1 j41
1 −1
0
0 −1 j51
0
0
0
0
0
0
0
0
0
0
0 −1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
j12
j22
j32
j42
j52
−1
0
0
0
0
j13
j23
j33
j43
j53
0
0
0
−1
−1
j14
j24
j34
j44
j54
−1
1
−1
0
1
j15
j25
j35
j45
j55
1
−1
0
0
−1








ρ(W ) = η(W ) = 






0 −1
0
0 0
0
0 −1
0 1
1 −1
0
1 0
0
1 −1 −1 0
0 −1
0
1 0
0
0
0
0 0
0
0
0
0 0
0
0
0
0 0
0
0
0
0 0
0
0
0
0 0
w11
w21
w31
w41
w51
0
0
1
0
−1
w12
w22
w32
w42
w52
−1
0
0
0
0
w13
w23
w33
w43
w53
0
0
0
−1
−1
w14
w24
w34
w44
w54
−1
0
0
0
1
t














t














w15
w25
w35
w45
w55
0
1
0
−1
−1
t














Teorema 9.13. Sea S una superficie de Riemann maximal simétrica de género 5
con reflexión maximal τ : S√ → S tal que S/τ es una superficie de género uno con
cuatro bordes. Sea p ∈ (2 − 3, 1) de manera que S = Ω/G5 . Entonces una matriz de
Riemann para S es dada por:
9.5. SUPERFICIES DE RIEMANN MAXIMAL SIMÉTRICAS DE GÉNERO 5


1
Z= 
2

0
1
1
0
0
1
0
0
0
1
1
0
0
0
1
0
0
0
0
0
0
1
1
0
0


 
 
+i 
 
 
135

2u + v
u+v
u+v
v
2(u + v)
u+v
2u + v 2u + 3v −v
u + 2v 

.
u + v 2u + 3v 2u + v
v
u


v
−v
v
−3v
2v
2(u + v) u + 2v
u
2v
2u
La matriz de Riemann a usar para el método de Burnside es −Z −1 . Ası́ se pueden
obtener los valores u y v en términos explı́citos de p.
Teorema 9.14. Sea S una superficie de Riemann maximal simétrica de género 5 con
una reflexión
√ maximal τ : S → S tal que S/τ esde género cero con seis bordes. Sea
p ∈ (2 − 3, 1) de manera que S = Ω/F5 . Entonces una matriz de Riemann para S
es dada por:


2u + v
u+v
u+v
v
2(u + v)
 u+v
2u + v 2u + 3v −v u + 2v 


.
v
u
Z = i

 u + v 2u + 3v 2u + v


v
−v
v
−3v
2v
2(u + v) u + 2v
u
2v
2u
La matriz de Riemann a usar para el método de Burnside es −Z −1 . Ası́ se pueden
obtener los valores u y v en términos explı́citos de p.
T0eoremas 9.13 y 9.14. (1) Verifiquemos el teorema 9.13. La matriz de Riemann Z = X + iY ∈ H5 para S5 definida por la base simpléctica antes considb 5 ). Los cálculos muestran que:
erada es un punto fijo del grupo simpléctico ρ(K/G
tnm = jnm = 0, w11 = w15 = −w21 = −w22 = −w31 = −w32 = w41 = w45 = −1,
w22 = w23 = w24 = w31 = w24 = w25 = w31 = w34 = w35 = w41 = w42 = w43 = w44 =
w45 = w52 = w53 = w54 = 0, y


1
Z= 
2

0
1
1
0
0
1
0
0
0
1
1
0
0
0
1
0
0
0
0
0
0
1
1
0
0


 
 
+i 
 
 

2u + v
u+v
u+v
v
2(u + v)
u+v
2u + v 2u + 3v −v
u + 2v 

,
u + v 2u + 3v 2u + v
v
u


v
−v
v
−3v
2v
2(u + v) u + 2v
u
2v
2u
donde 0 < −v < u.
(2) Ahora verifiquemos el teorema 9.14. La matriz de Riemann Z = X + iY ∈ H5
para R5 definida por la base simpléctica antes considerada es un punto fijo del grupo
b 5 ). Obtenemos entonces que: tnm = jnm = wnm = 0, y
simpléctico η(K/F
136
9. SUPERFICIES DE RIEMANN MAXIMAL SIMÉTRICAS



Z = i



2u + v
u+v
u+v
v
2(u + v)
u+v
2u + v 2u + 3v −v u + 2v 

,
u + v 2u + 3v 2u + v
v
u


v
−v
v
−3v
2v
2(u + v) u + 2v
u
2v
2u
donde 0 < −v < u.
(3) Procedamos a encontrar las relaciones de los coeficientes de las respectivas matrices
de Riemann.
Consideremos el cubrimiento regular P : S5 → S2 (respectivamente, P : R5 → R2 ),
cuyo grupo de cubrimiento es el grupo de Klein Z2 +Z2 generado por los automorfismos
de S5 (respectivamente, R5 ) inducidos por A1 and A2 (respectivamente, B1 and B2 ).
Tenemos que H1 (P ) : H1 (S5 , Z) → H1 (S2 , Z) (respectively, H1 (P ) : H1 (R5 , Z) →
H1 (R2 , Z)) es dado por:
(1) H1 (P )(θ1 ) = H1 (P )(θ4 ) = H1 (P )(θ5 ) = α1 ,
(2) H1 (P )(θ2 ) = H1 (P )(θ3 ) = α2 ,
(3) H1 (P )(δ1 ) = H1 (P )(δ5 ) = 2β1 ,
(4) H1 (P )(δ2 ) = H1 (P )(δ3 ) = 2β2 y
(5) H1 (P )(δ4 ) = 0.
Denotemos por w1 y w2 las 1-formas holomorfas duales de α1 y α2 , respectivamente,
para la superficie de Riemann S2 (respectivamente, R2 ).
Similarmente, denotemos por η1 , η2 , η3 , η4 y η5 las 1-formas holomorfas duales de θ1 ,
θ2 , θ3 , θ3 y θ5 , respectivamente, para la superficie de Riemann S5 (respectivamente,
R5 ).
El ”pull-back”de las 1-formas holomorfas P ∗ : H 1,0 (S2 ) → H 1,0 (S5 ) (respectivamente,
P ∗ : H 1,0 (R2 ) → H 1,0 (R5 )) está definida en este caso por P ∗(w1 ) = η1 + η4 + η5 y
P ∗(w2 ) = η2 + η3 . Usando la igualdad
Z
Z
Z
∗
w1 ,
P w1 = 2
η1 + η4 + η5 =
4(u + v)i =
δ1
δ1
β1
permite obtener la relación entre los coeficientes de las matrices de Riemann anteriores
con los coeficientes de las matrices de Riemann de las superficies de género dos. De
esta manera, ya que conocemos los coeficientes de las respectivas superficies de género
dos en términos de p de la sección 9.3.2, tenemos de manera explı́cita relaciones, en
términos de p, de los coeficientes u y v.
CAPÍTULO 10
Variedades Hiperbólicas 3-Dimensionales
Este capı́tulo tiene por propósito mostrar algunos conceptos y resultados en el área de
grupos Kleinianos espaciales(grupos discretos de isometrias del espacio hiperbólico)
y variedades hiperbólicas 3-dimensionales. Se darán algunos ejemplos que permitan
aclarar teoremas difı́ciles, aunque tales ejemplos son en si no muy fáciles. Hay muchos
temas que no trataremos, por ejemplo, laminaciones geodésicas medibles, herramienta
desarrollada y utilizada por W.P. Thurston [Thurston] para obtener gran parte
de sus resultados en el problema de hiperbolización de variedades 3-dimensionales.
Tampoco se incorpora la teorı́a de homeomorfismos casiholomorfos, importante para
entender las deformaciones de estructuras hiperbólicas. Ası́ también la teorı́a ergódica
b de los grupos Kleinianos, clasificación, moduli, etc, tampoco han sido incluidas
en C
en este capı́tulo.
Diremos que una variedad 3-dimensional M tiene una estructura hiperbólica si existe
un grupo discreto G de transformaciones de Möbius (isometrı́as de H3 ) tal que H3 /G
es homeomorfa a M; en cuyo caso, la estructura hiperbólica es dada por G. Una
variedad M junto a una estructura hiperbólica es llamada una variedad hiperbólica.
Observemos que en este caso, π1 (M) ∼
= G. Puede ocurrir que el volumen hiperbólico
sea finito o no.
Ahora veremos algunas propiedades que deben satisfacer las variedades hiperbólicas. El primer resultado sale directamente del hecho que los grupos de isometrı́as
obtenidos por transformaciones de Möbius preservan la orientación, es decir, tenemos
el siguiente.
Proposición 10.1. Toda variedad hiperbólica es orientable.
10.0.3. Variedades Hiperbólicas son Irreducibles. Una variedad 3dimensional M es llamada una variedad irreducible si para toda incrustación
i : S 2 → M,
donde S 2 es la esfera bidimensional unitaria, se puede extender a una incrustación
i : B 3 → M, donde B 3 es la bola 3-dimensional acotada por S 2 .
Ejemplo 10.1. La variedad M = S 2 × S 1 no es irreducible
137
138
10. VARIEDADES HIPERBÓLICAS 3-DIMENSIONALES
Proposición 10.2. Toda variedad hiperbólica 3-dimensional es irreducible.
Demostración. Sea M = H3 /G una variedad hiperbólica. Denotemos por P :
H3 → M el cubrimiento universal dado por G. Consideremos una incrustación i :
S 2 → M. Entonces se puede levantar esta incrustación a una incrustación bi : S 2 → H3
tal que P bi = i. Usando el hecho que H3 es contractible, tenemos que bi : S 2 → H3
se puede extender a una incrustación bi : B 3 → H3 . Luego, usando P bi = i permite
extender i : S 2 → M a una incrustación i : B 3 → M.
Observación 10.1. Observemos que no toda variedad 3-dimensional irreducible es
necesariamente hiperbólica. Por ejemplo, M = S 1 × S 1 × S 1 es irreducible con grupo
fundamental isomorfo a L = Z ⊕ Z ⊕ Z. Ya que no existe un grupo discreto de
isometrı́as del espacio hiperbólico H3 isomorfo a L obtenemos que M no es hiperbólica.
10.1.
Variedades Hiperbólicas son Atoroidales
Una variedad 3-dimensional compacta M se llama atoroidal si todo subgrupo de
π1 (M) isomorfo a Z ⊕ Z es conjugado a un subgrupo de π1 (S) para alguna superficie
S ⊂ ∂M.
Proposición 10.3. Sea M una variedad compacta cuyo interior Int(M) tiene una
estructura hiperbólica 3-dimensional. Entonces M es atoroidal.
Demostración. Consideremos una variedad hiperbólica H3 /G y supongamos
que tenemos un subgrupo K de G isomorfo a Z ⊕ Z. En este caso, K está generado
por dos transformaciones parabólicas A y B que conmutan con el mismo punto fijo.
Módulo conjugación, podemos suponer que A(z) = z + 1 y B(z) = z + τ , algún τ ∈ H.
Además, podemos considerar B = {(z, t) ∈ H3 : t ≥ 1}, el cual resulta precisamente
invariante por K en G. Entonces, B/K ∼
= ∆∗ × S 1 , donde ∆∗ denota el disco unitario
abierto con el centro 0 eliminado. Luego, en M podemos quitar la proyección de B
(la cual es exactamente B/K) para formar un borde S de M para el cual π1 (S) es
K.
Ejemplo 10.2.
(1) Si ∂M = ∅, entonces M es atoroidal si y sólo si π1 (M) no contiene un subgrupo
isomorfo a Z ⊕ Z.
(2) M = S 1 × S 1 × S 1 es irreducible pero no es atoroidal.
(3) M = S 2 × S 1 es atoroidal, pero no es irreducible.
Corolario 10.4. Si M es una variedad compacta cuyo interior tenie una estructura
hiperbólica, entonces M debe ser orientable, atoroidal e irreducible.
10.1. VARIEDADES HIPERBÓLICAS SON ATOROIDALES
139
Existen variedades 3-dimensionales compactas, orientables, irreducibles y atoroidales
cuyo interior no posee una estructura hiperbólica. A continuación procedemos a dar
un ejemplo de esta situación. Para esto consideremos un homeomorfismo que revierte
orientación
σ : S1 × S1 → S1 × S1
de orden dos tal que (S 1 × S 1 )/σ es la botella de Klein. Ahora construimos el homeomorfismo que preserva orientación de orden dos
definido por
τ : (S 1 × S 1 ) × [−1, 1] → (S 1 × S 1 ) × [−1, 1],
τ (p, t) = (σ(p), −t),
donde p ∈ S × S y t ∈ [−1, 1].
Consideremos la variedad 3-dimensional orientable y compacta
1
1
M = ((S 1 × S 1 ) × [−1, 1])/τ
Ejercicio 10.1. Verificar que:
(1) ∂M ∼
= S 1 × S 1;
(2) El interior de M es homeomorfa a R3 /H, donde H es el grupo generado por
A(x, y, z) = (x + 1, y, z)
B(x, y, z) = (−x, y + 1, −z)
(3) Deducir de lo anterior que π1 (M) = hA, B : ABA = Bi.
Proposición 10.5. El interior de la variedad M construida no tiene estructura
hiperbólica.
Demostración. Supongamos que el interior N de M posee estructura hiperbólica. Como tenemos un cubrimiento de grado dos
P : S 1 × S 1 × (−1, 1) → N,
entonces debemos tener que G = π1 (M) = π1 (N) < M debe contener L = Z ⊕ Z
como subgrupo de ı́ndice dos en G. En este caso,
τ : S 1 × S 1 × (−1, 1) → S 1 × S 1 × (−1, 1)
tiene un levantamiento τb : H3 → H3 , τb ∈ G y τb2 ∈ L. Más aún, G está generado por
L y τb.
Si ocurre que τb2 = I, entonces τb debe tener un punto fijo en H3 , con lo cual tendremos
que que N no es una variedad, es un orbifold con valores de ramificación.
Por otro lado, sabemos que L está generado por dos transformaciones parabólicas
b Como τb2 6= I y τb2 ∈ L, tenemos
que conmutan y tienen el mismo punto fijo q ∈ C.
2
necesariamente que τb es parabólico con punto fijo q. Luego τb también es parabólico
con punto fijo q. Esto dirı́a entonces que G es abeliano, una contradicción.
140
10. VARIEDADES HIPERBÓLICAS 3-DIMENSIONALES
Figura 1
Observación 10.2. En el ejemplo anterior tenemos que R = S 1 × S 1 × (−1, 1) posee
una estructura hiperbólica (de volumen infinito), dada por el grupo K generado por
A(z, t) = (z + 1, t) y B(z, t) = (z + i, t). Es importante notar que R tiene dos
bordes naturales, uno es de volumen hiperbólico finito mientras que el otro es de
volumen infinito. R es topológicamente la esfera 3-dimensional S 3 menos dos cı́rculos
entrelazados com se muestra en la figura 1. La razón de por qué N = R/τ no tiene
estructura hiperbólica puede verse como el hecho que si esto ocurriese, entonces τ
deberı́a ser una isometrı́a hiperbólica de R la cual permuta ambos bordes, lo cual
contradice la finitud del volumen de uno de los bordes con el hecho que el otro borde
es de volumen infinito.
La importancia del ejemplo anterior se ve reflejada en el siguiente resultado de
Thurston [Thurston2]
Teorema 10.6. Sea M una variedad 3-dimensional compacta, orientable, con ∂M 6=
∅ y no homeomorfa al ejemplo anterior. Entonces el interior de M posee una estructura hiperbólica si y sólo si M es irreducible y atoroidal.
En el caso en que la variedad compacta M sea cerrada, es decir compacta y sin borde,
necesitaremos de la siguiente propiedad debida a Waldhausen [Waldhausen]. Diremos que una variedad 3-dimensional compacta sin borde es suficientemente grande
si existe una superficie orientable cerrada (compacta sin borde) S, no homeomorfa
a la esfera, y una incrustación i : S → M tal que a nivel de grupos fundamentales
π1 (i) : π1 (S) → π1 (M) es inyectiva.
Observación 10.3. Una variedad 3-dimensional compacta con borde es suficientemente grande. Un tipo de variedades de este tipo son las llamadas variedades de
10.2. EJEMPLO 1: COMPLEMENTO DE NUDOS
141
Haken que además son variedades primas , es decir, no pueden descomponerse en
suma conexa de variedades no triviales.
Teorema 10.7 ([Thurston2]). Sea M una variedad 3-dimensional compacta, orientable, cerrada y suficientemente grande. Entonces M tiene una estructura hiperbólica si y sólo si M es irreducible y atoroidal.
Una buena referencia sobre los teoremas de hiperbolización de Thurston es [Morgan].
En las próximas secciones miraremos algunos ejemplos de construcciones de variedades 3-dimensionales hiperbólicas.
También es de gran importancia la siguiente propiedad de rigidez que satisfacen las
variedades hiperbólicas de dimensión tres con volumen finito, a diferencia de lo que
sucede para superficies de Riemann. Decimos que un grupo discreto G de isometrı́as
de H3 (es decir, un grupo discreto de transformaciones de Möbius) es un grupo de
volumen finito si H3 /G tiene volumen hiperbólico finito.
Teorema 10.8 (Teorema de Rigidez de Mostow). Sean G1 y G2 dos grupos discretos,
sin torsión y volumen finito de isometrı́as del espacio hiperbólico Hn , n ≥ 3. Entonces
G1 y G2 son isomorfos como grupos abstractos si y sólo si son conjugados por una
isometrı́a.
En el caso que tenemos un grupo discreto G de transformaciones de Möbius que tiene
torsión, entonces H3 ya no resulta ser una variedad hiperbólica, aunque si es una
variedad topológica. Esta es llamada una orbifold hiperbólica. De todas maneras, si
G es finitamente generado, entonces el siguiente resultado de Selberg nos dice que la
orbifold hiperbólica es cubierta por una variedad hiperbólica.
Teorema 10.9 (Lema de Selberg). Sea G un grupo de transformaciones de Möbius
que sea finitamente generado. Entonces existe un subgrupo normal de ı́ndice finito
K < G el cual no tiene torsión.
10.2.
Ejemplo 1: Complemento de Nudos
Un nudo en la esfera 3-dimensional S 3 es la imágen homeomorfa de un cı́rculo en
S 3 . Un nudo K ⊂ S 3 tal que el grupo fundamental de su complemento sea trivial
es llamado un nudo no anudado. En caso contrario, decimos que este es un nudo
anudado.
Dado un nudo K ⊂ S 3 uno puede considerar la variedad 3-dimensional MK obtenida al eliminar una vecindad tubular abierta de K. Esta es una variedad compacta,
irreducible, orientable con borde ∂MK ∼
= S 1 × S 1 . La proposición 10.3 asegura que el
interior de MK admite una estructura hiperbólica si y sólo si MK es atoroidal.
142
10. VARIEDADES HIPERBÓLICAS 3-DIMENSIONALES
Figura 2
10.2.1. Nudos Toroidales. Un nudo K ⊂ S 3 anudado es llamado un nudo
toroidal si existe un toro T ∼
= S 1 × S 1 incrustado en S 3 el cual no es anudado (es
3
decir, S − T consiste de dos variedades homeomorfas a D 2 × S 1 , donde D 2 = {z ∈
C : |z| < 1}) tal que K ⊂ T (en la figura 2 se muestra un nudo toroidal llamado la
figura 8).
Ejercicio 10.2. Verificar que si K es un nudo toroidal, entonces MK no es atoroidal.
En particular, concluir que MK no posee una estructura de variedad hiperbólica.
10.2.2. Nudos Satelitales. Un nudo K ⊂ S 3 es llamado un nudo satelital si
existe un nudo no trivial Q ⊂ S 3 , es decir π1 (S 3 − Q) ∼
= Z, y existe una vecindad
tubular VQ para Q de manera que K ⊂ VQ y no exista una bola tres dimensional
B 3 ⊂ VQ conteniendo K en su interior.
Ejercicio 10.3. Verificar que si K es un nudo satelital, entonces K es anudado y
MK no es atoroidal. Concluir que en este caso MK no puede tener la estructura de
una variedad hiperbólica.
10.2.3. Nudos No anudados. Si tomamos K ⊂ S 3 un nudo no anudado,
entonces tenemos que MK es homeomorfo a D × S 1 , donde D es el disco unitario
cerrado y S 1 es el cı́rculo unitario (es decir, MK es un handlebody de ’enero 1). En
este caso, como el grupo fundamental de MK es un grupo cı́clico infinito, la única
estructura hiperbólica que se le puede dar es por un grupo de Schottky de género 1,
es decir, por el grupo cı́clico generado por una transformación loxodrómica.
10.3. EJEMPLO2: FIBRADOS SOBRE S 1
143
10.2.4. Hiperbolización de Nudos. El siguiente resultado de Thurston
[Thurston] asegura que los únicos nudos para los cuales el interior de MK no tiene
estructura hiperbólica son los toroidales y satelitales.
Teorema 10.10. Sea K un nudo en S 3 . Entonces el interior de MK tiene estructura
hiperbólica si y sólo si K no es toroidal ni satelital.
Observación 10.4. Si MK tiene interior con estructura hiperbólica y K es anudado,
entonces Vol(Int(MK )) < ∞. En efecto, el borde de MK es homeomorfo a S 1 × S 1 ,
luego debe ser uniformizado por un subgrupo discreto isomorfo a Z ⊕ Z ó a Z (este
último generado por un loxodrómico). Ya que K es no anudado, tenemos que MK
no es un handlebody de género 1, luego el borde de MK sólo puede ser uniformizado
por Z ⊕ Z (un grupo generado por dos translaciones en direciones R-linealmente
independientes.
El programa Snappea de J. Weeks permite dibujar nudos y entrelazados (links) en
la esfera S 3 y determinar si su complemento admite o no una estructura de variedad hiperbólica. Además este entrega su volumen hiperbólico, su homologı́a, una
representación matricial de su grupo fundamental como transformaciones de Möbius,
dominios fundamentales, etc..
10.3.
Ejemplo2: Fibrados sobre S 1
Consideremos una superficie S compacta, orientable con posible borde ∂S y sea f :
S → S un homeomorfismo de S que preserva la orientación. Podemos construir una
variedad 3-dimensional compacta orientable
Mf (S) = S × [0, 1]/ ∼,
donde (x, 0) ∼ (f (x), 1), la cual es un fibrado sobre S 1 .
Ejercicio 10.4.
(i) Verificar que ∂Mf (S) 6= ∅ si y sólo si ∂S 6= ∅. En tal caso, ∂Mf (S) es unión
de toros.
(ii) Sean f, g : S → S homeomorfismos que preservan orientación y que son
homotópicos. Probar que Mf (S) y Mg (S) son variedades homeomorfas.
El grupo fundamental de Mf (S) es la HNN-extensión del grupo fundamental de S ×
[0, 1] extendido por f . De manera más precisa; podemos suponer que f (p) = p algún
p ∈ S, homotopando f si es necesario. Supongamos que S es una superficie compacta
de género g ≥ 1 con k bordes. En este caso,
π1 (S, p) = hα1 , ..., αg , β1 , ..., βg , δ1 , ..., δk :
g
Y
j=1
[αj , βj ]
k
Y
l=1
δl = 1i,
144
10. VARIEDADES HIPERBÓLICAS 3-DIMENSIONALES
donde [a, b] = aba−1 b−1 .
Si consideramos un arco simple orientado δ ⊂ S × [0, 1] partiendo desde (p, 0) y
terminando en (p, 1), entonces
g
Y
j=1
π1 (Mf (S), [(p, 0)]) = hα1 , ..., αg , β1 , ..., βg , δ1 , ..., δk , δ :
[αj , βj ]
k
Y
l=1
δl = 1, f∗ (αj ) = δ −1 αj δ, f∗ (βj ) = δ −1 βj δ, f∗ (δl ) = δ −1 δl δi
Luego, si el interior de Mf (S) tiene estructura hiperbólica, entonces existe un grupo
Kleiniano G isomorfo al grupo anterior tal que el interior de Mf (S) es homeomorfo a
H3 /G
10.3.1. Caracterı́stica No Negativa. Supongamos que la caracterı́stica de
Euler de S es mayor o igual a cero. En tal caso, las posibilidades para S son, módulo
homeomorfismos, las siguientes:
(i) S 2 ;
(ii) D = {z ∈ C : |z| ≤ 1};
(iii) A = {z ∈ C : 21 ≤ |z| ≤ 1};
(iv) S 1 × S 1 .
Si S = S 2 , entonces todo homeomorfismo que preserva orientación f : S → S debe
ser homotópico a la identidad. Luego tenemos que Mf (S) ∼
= S 2 × S 1 . Esta variedad
no es irreducible y, en particular, no posee una estructura hiperbólica.
Cuando S = D, todo homeomorfismo f : S → S, que preserva orientación, es homotópico a la identidad. Entonces tenemos que Mf (S) ∼
= D × S 1 . El interior posee
estructura hiperbólica dada por cualquier grupo de Schottky anodado de género uno.
Es importante notar que no existe estructura hiperbólica de volumen finito ¿Por qué?
En el caso S = A tenemos dos posibilidades, dependiendo si f permuta o no ambos
bordes del anillo A:
(a) Supongamos que f preserva cada lado de A. En tal caso Mf (S) ∼
= S 3 − K,
donde K es el entrelazado dado en figura 1. El grupo fundamental de esta
variedad es isomorfa a Z + Z. Este caso tienen una estructura hiperbólica
de dimensión infinita, dado por el grupo K = hA, Bi, donde A y B son
parabólicos con el mismo punto fijo ∞ transladando en direcciones linealmente
independientes. Como todo subgrupo discreto de isometrı́as de H3 ismorfo a
Z + Z es conjugado a uno del tipo antes descrito, tenemos que no es posible
encontrar una estructura hiperbólica de volumen finito.
(b) Supongamos ahora que f permuta los dos lados de A. Luego existe una curva
simple cerrada γ contenida en el interior de A que separa ambos lados de A y
que resulta ser invariante por f . Luego γ × [0, 1] define en Mf (S) un toro que
no es homotópico al borde de Mf (S) (que resulta ser un toro). Ası́, obtenemos
una variedad que no es homotópicamente atoroidal, luego, no tiene estructura
hiperbólica.
10.3. EJEMPLO2: FIBRADOS SOBRE S 1
145
En el último caso, si S = S 1 × S 1 y f : S → S es un homeomorfismo que preserva
orientación, entonces Mf (S) contendrá incrustada una copia de S, la cual no es homotópica a un borde de Mf (S) por la simple razón que esta es cerrada. Luego Mf (S)
resulta no ser homotópicamente atoroidal y, en particular, no posee una estructura
hiperbólica.
10.3.2. Caracterı́stica Negativa. En el caso que S tiene caracterı́stica de
Euler negativa, entonces Mf (S) resulta ser irreducible. La razón de esto es que el
cubrimiento universal de Mf (S) ∼
= R3 es contractible. En efecto, supongamos que
S = H/F , donde H es el plano hiperbólico y F es un grupo Fuchsiano que uniformiza
S. Denotemos por π : H → S el cubrimiento universal inducido por F . Entonces el
homeomorfismo f : S → S se levantarı́a por π a un homeomorfismo fb : H → H.
Ahora, consideremos el espacio W = H × R ∼
= R3 y el grupo L de homeomorfismos
de W generado por las transformaciones Aγ (z, t) = (γ(z), t), para γ ∈ F y B(z, t) =
b
(f(z),
t + 1).
Ejercicio 10.5.
(i) Verificar que L es un grupo de homeomorfismos de W que actúa de manera
propiamente discontinua y sin puntos fijos en todo W. Más aún, W/L es
homeomorfo a Mf (S).
(ii) Ver que Mf (S) no puede ser homeomorfo a la variedad dada de la proposición
10.6
Ahora que sabemos que Mf (S) es irreducible y no homeomorfo al caso excluido en
el teorema 10.6 tenemos como consecuencia de los teoremas de hiperbolización de
Thurston 10.6 y 10.7 el siguiente.
Proposición 10.11. Sea S una superficie de caraterı́stica de Euler negativa. El interior de Mf (S) admite estructura hiperbólica si y sólo si Mf (S) es atoroidal.
La propiedad de ser o no atoroidal la variedad Mf (S) será consecuencia del (tipo
de homotopı́a) del homeomorfismo f : S → S considerado. Primero, enunciaremos
la clasificación de los homeomorfismos dada por Thurston. Consideremos un homeomorfismo f : S → S.
(1) Si f es homotópico a un homeomorfismo de orden finito, entonces decimos que
este es un homeomorfismo periódico.
(2) Si f es homotópica a un homeomorfismo para el cual existe una colección
de curvas cerradas simples, dos a dos disjuntas, ninguna de ellas homotópicamente trivial ni homotópica a un borde de S, que es invariante por la acción de
tal homeomorfismo, entonces decimos que f es un homeomorfismo reducible.
(3) Si f no es de ninguno de los dos tipos anteriores, entonces decimos que es un
homeomorfismo pseudo-Anosov.
146
10. VARIEDADES HIPERBÓLICAS 3-DIMENSIONALES
Supongamos que f : S → S es periódico. Podemos entonces suponer que f es de
orden finito, digamos N. Consideremos una curva simple cerrada α ⊂ S que no
sea homotópicamente trivial ni sea homotópica a un borde de S. Sean α0 = α, α1 =
f (α),..., αk = f k (α), tal que f (αk ) = α. Consideremos los cilindros C1 = α0 ×[0, 1],...,
Ck = αk × [0, 1] en S × [0, 1]. Estos cilindros se proyectan en toros dentro de Mf (S),
obteniendo en este caso que Mf (S) no es atoroidal.
Supongamos ahora que f : S → S es reducible. Podemos suponer que f deja invariante una colección de curvas cerradas simples, dos a dos disjuntas, ninguna de
ellas homotópicamente trivial ni homotópica a un borde de S. En este caso podemos
escoger una curva α dentro de tal colección y podemos proceder como en el caso
anterior para ver que Mf (S) no es atoroidal.
Tenemos el siguiente resultado de Thurston, cuya demostración también puede encontrarse en [Otal], el cual dice que Mf (S) es atoroidal si f es pseudo-Anosov. Ası́,
los teoremas de hiperbolización de Thurston 10.6 y 10.7 dan el siguiente.
Teorema 10.12. Sea S una superficie compacta orientable de caracterı́stica de Euler
negativa y sea f : S → S un homeomorfismo que preserva orientación. Entonces el
interior de Mf (S) admite una estructura de variedad hiperbólica si y sólo si f es
pseudo-Anosov.
Por lo anterior, el problema de hiperbolización del interior de Mf (S) se puede mirar como el problema de decidir cuando el homeomorfismo f : S → S es o no un
homeomorfismo pseudo-Anosov. Como esta propiedad es un invariante homotópico,
podemos suponer que existe p ∈ S tal que f (p) = p. De esta manera tenemos el
siguiente diagrama conmutativo:
π1 (S, p)
↓
H1 (S, Z)
π1 (f )
−→
π1 (S, p)
↓
H1 (f )
−→ H1 (S, Z)
Si nos damos una base de H1 (S, Z), entonces H1 (f ) queda representada por una matriz
en SL(r, Z), donde

2g,
si S es superficie compacta



cerrada de género g;
r = rango de H1 (S, Z) =
2g + k − 1, si S es superficie compacta



de género g y k bordes.
Esta matriz H1 (f ) es llamada la monodromı́a de Anosov del homeomorfismo f : S →
S correspondiente a la base escogida de homologı́a. Un cambio de base de homologı́a
induce una conjugación de la matriz H1 (f ) por una matriz en SL(r, Z), en particular,
el polinomio caracterı́stico Pf (t) = Det[H1 (f ) − tI] ∈ Z[t] se mantiene invariante.
10.3. EJEMPLO2: FIBRADOS SOBRE S 1
γ
147
2
δ
γ
1
p
Figura 3
Por ejemplo: (i) si f : S → S es periódico de periódo N, entonces Q(t) = tN − 1 debe
ser divisible por Pf (t). En particular, Pf (t) tiene como ceros algunas de las raı́ces de
la unidad; (ii) si existe una curva α cerrada simple homológicamente no trivial en S
tal que f k (α) = α (igualdad en el sentido de homologı́a) para algún k > 0, entonces
Pf (t) tiene un cero que es raı́z de la unidad. En resumen;
Proposición 10.13. Sea f : S → S un homeomorfismo de S que preserva orientación
cuyo polinomio caracterı́stico Pf (t) no tiene raices de la unidad como ceros, entonces:
(a) f no puede ser periódico;
(b) si f es reducible, entonces cualquier colección de curvas invariante por f debe
consistir sólo de curvas que son homológicamente triviales.
Observación 10.5. Es importante notar que al mirar sólo la acción del homeomorfismo f : S → S a nivel de la homologı́a, no tenemos información sobre la acción de
de f sobre las curvas que son homológicamente triviales. Es por esta razón que en la
proposición anterior no podemos desechar la posibilidad que f sea o no reducible.
10.3.2.1. Un Ejemplo de H. Helling: Género Uno y un Borde. Para tener
una mejor visión de este ejemplo, recomendamos leer los trabajos de H. Helling, P.
Alestalo y C. Menzel [Alestalo-Helling] [Helling-Menzel].
Sea S una superficie compacta de género uno con un borde y f : S → S un homeomorfismo que preserva orientación. Módulo homotopı́a, podemos asumir que f es la
identidad cerca del borde. Sea p ∈ ∂S y sean las curvas orientadas simples γ1 , γ2 y el
arco orientado δ como se muestran en la figura 3.
Si α = δ · γ1 · δ −1 y β = δ · γ2 · δ −1 , entonces
π1 (S, p) = hα, βi ∼
= Z∗Z
b = 1i ∼
H1 (S, Z) = hb
α, βb : [b
α, β]
= Z⊕Z
148
10. VARIEDADES HIPERBÓLICAS 3-DIMENSIONALES
La curva frontera es dada por λ = β −1 · α−1 · β · α.
Usando esta base de homologı́a para S, obtenemos la monodromı́a de Anosov para f
a b
H1 (f ) =
∈ SL(2, Z)
c d
En este caso, el polinomio caracterı́stico de f es dado por
Pf (t) = t2 − (a + d)t + 1
Respecto a los ceros de Pf (t) tenemos el siguiente:
(1) Si (a + d)2 > 4, entonces los ceros de Pf (t) viven en R − {±1};
(2) Si (a + d)2 = 4, entonces los ceros de Pf (t) viven en {±1}; √
3
}.
(3) Si (a + d)2 < 4, entonces los ceros de Pf (t) viven en {±i, ±1±i
2
Habı́amos observado que:
(a) si f es periódico, entonces Pf (t) debe tener como cero alguna raı́z de la unidad,
es decir, −2 ≤ a + d ≤ 2;
(b) Si f es reducible, y usando el hecho que no hay curvas simples cerradas homológicamente triviales que no sean homotópicamente triviales (o homotópicas al borde) en este tipo de superficie S, entonces de nuevo debemos tener
−2 ≤ a + d ≤ 2.
Luego, si (a + b)2 > 4, es decir la matriz H1 (f ) es hiperbólica, entonces f es pseudoAnosov. H. Helling ha observado que el recı́proco es válido:
Teorema 10.14. Sea f : S → S un homeomorfismo que preserva orientación de una
superficie S de género uno con un borde. Entonces f es pseudo-Anosov si y sólo si
H1 (f ) es hiperbólica.
10.3.2.2. Caso de superficies cerradas. Para esta subsección nos basaremos
en [Casson-Bleiler]. Supongamos que la superficie S considerada es cerrada de
género g ≥ 2 y f : S → S un homeomorfismo que preserva la orientación. Sabemos que si el polinomio caracterı́stico Pf (t) no tiene raı́ces de la unidad como ceros,
entonces proposición 10.13., asegura que f puede ser de uno de los siguientes tipos:
(1) Pseudo-Anosov;
(2) Reducible de orden infinito con un sistema invariante de curvas cerradas, simples, homológicamente triviales, homotópicamente no triviales y disjuntas dos
a dos.
Supongamos que tenemos el caso (2). En esta situación tenemos la existencia de una
colección F finita de curvas cerradas, simples, disjuntas dos a dos, homológicamente
triviales pero homotópicamente no triviales, que es invariante por f . Podemos suponer
que α1 es una de esas curvas y que esta divide S en dos superficies, una de las cuales
denotaremos por S1 con la propiedad que S1 es disjunta de las otras curvas cerradas
en F .
10.3. EJEMPLO2: FIBRADOS SOBRE S 1
149
Denotemos por α2 = f (α1 ), α3 = f (α2 ),..., αr = f (αr−1 ) tal que f (αr ) = α1 . De
esta manera, obtenemos también la sucesión finita de supeficies S1 , S2 = f (S1 ),...,
Sr = f (Sr−1 ) y tal que f (Sr ) = S1 . Sean
R=S−
r
[
j=1
Sj ; y R = R ∪ {discos pegados en cada borde de R }
Entonces
H1 (S, Z) = H1 (S1 , Z) ⊕ · · · ⊕ H1 (Sr , Z) ⊕ H1 (R, Z).
Luego podemos construir una base para H1 (S, Z) de la manera siguiente. Primero,
construimos una base para H1 (S1 , Z) y la transladamos por f para obtener una base
para cada H1 (Sj , Z), j = 2, ..., r − 1. Segundo, construimos una base para H1 (R, Z).
La unión de todas esas bases da una base para H1 (S, Z). La monodromı́a de Anosov
para f en tal base queda de la forma:












H1 (f ) = 










0
I
0
·
·
0
0
0
0
·
·
0
0
0
0
0
I
·
·
·
0
0
0
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
0 A 0 · · · 0 C 0 0
0 0 0 · · · 0 0 0 0
0 0 0 · · · 0 0 0 0
0 0 0 · · · 0 0 0 0
0 0 0 · · · 0 0 0 0
I 0 0 · · · 0 0 0 0
0 B 0 · · · 0 D 0 0
0 0 I · · · 0 0 0 0
0 0 0 · · · 0 0 0 0
0 0 0 · · · 0 0 0 0
0 0 0 · · · 0 0 0 0
0 0 0 · · · I 0 0 0
0 0 0 · · · 0 0 E F
0 0 0 · · · 0 0 G H























Luego Pf (t) = M(tr )N(t), donde N(t) es el polinomio caracterı́stico de f restringido
a R. En particular se obtiene el siguiente:
Teorema 10.15 ([Casson-Bleiler]). Sea S una superficie orientable cerrada de
género g ≥ 2 y f : S → S un homeomorfismo que preserva la orientación. Entonces
f es pseudo-Anosov si:
(i) Pf (t) no tiene raı́ces de la unidad como ceros;
(ii) Pf (t) es un polinomio irreducible en Z[t]; y
(iii) Pf (t) ∈
/ Z[tr ], para ningún r ∈ {2, 3, 4, ...}.
150
10. VARIEDADES HIPERBÓLICAS 3-DIMENSIONALES
S
γ
γ
2
γ
γ
1
4
3
γ
5
Figura 4
Dehn
Twist
Figura 5
El siguiente ejemplo es tomado también del libro [Casson-Bleiler]. Sea S una superficie de género dos y considere las curvas γ1 ,..., γ5 como se muestra en la figura
4.
Denotemos por fj : S → S el Dehn twist a lo largo de la curva γj , j = 1, ..., 5.
Usando como base para H1 (S, Z) las curvas α1 = γ1 , α2 = γ5 , β1 = γ2 y β2 = γ4 , las
monodromı́as de Anosov quedan dadas por las matrices:




1 0 0 0
1 0 1 0


 0 1 0 0 
 ; H1 (f2 ) =  0 1 0 0  ;
H1 (f1 ) = 
 1 0 1 0 
 0 0 1 0 
0 0 0 1
0 0 0 1




1 0 0 0
1 0 1 1
 0 1 0 0 
 0 1 1 1 



H1 (f3 ) = 
 0 0 1 0  ; H1 (f4 ) =  0 0 1 0  ;
0 1 0 1
0 0 0 1


1 0 0 0
 0 1 0 1 

H1 (f5 ) = 
 0 0 1 0 
0 0 0 1
10.5. EJEMPLO 4: GRUPOS CASIFUCHSIANOS
151
Tomando f = f1 f3 f52 f2−1 f4−1 , se obtiene que Pf (t) = t4 − 9t3 + 21t2 − 9t + 1, el cual
es irreducible en Z[t], no tiene ceros que sean raı́z de la unidad y Pf (t) ∈
/ Z[tr ] para
r ∈ {2, 3, 4, ...}. Luego, el teorema 10.15., asegura que Mf (S) posee una estructura
hiperbólica.
10.4.
Ejemplo 3: Handlebodies
Para g ≥ 1 consideremos la variedad orientable compacta
Mg = D × S 1 # · · · #D × S 1
|
{z
}
g veces
donde D denota el disco unitario cerrado. La variedad Mg es llamada un handlebody
de género g.
Ejercicio 10.6. Verificar que Mg es irreducible y atoroidal y no homeomorfa a la
variedad de la proposición 10.5. Concluir que el interior de Mg posee una estructura
hiperbólica.
Una estructura hiperbólica sobre el interior de Mg corresponde a un grupo discre· · ∗ Z}. Puede ocurrir que G sea o no sea un grupo Kleiniano, es decir,
to G ∼
=Z
| ∗ ·{z
g veces
Ω(G) puede ser vacı́o. Respecto a lo anterior, no es claro que todos los grupos discretos isomorfos al grupo fundamental de un handlebody aparezcan como estructura
hiperbólica:
· · ∗ Z} un grupo discreto. Entonces H3 /G es homeConjetura 10.16. Sea G ∼
=Z
| ∗ ·{z
g veces
omorfo al interior del Handlebody Mg .
Respecto a lo anterior, si G es un grupo de Schottky anodado de género g, entonces
la conjetura anterior vale.
Ejercicio 10.7. Verifivar que si G es un grupo de Schottky de género g ≥ 1, entonces
la conjetura es verdad.
10.5.
Ejemplo 4: Grupos CasiFuchsianos
Sea S una superficie orientable cerrada compacta con caracterı́stica de Euler negativa.
Entonces podemos mirar la variedad compacta M(S) = S × [0, 1] (mirar el ejemplo
2: Fibrados sobre S 1 ). Entonces es claro que M(S) es una variedad compacta, irreducible y atoroidal, la cual no puede ser homeomorfa a la variedad de la proposición
10.5. Luego, el interior de M(S) posee una estructura hiperbólica. Por ejemplo, consideremos un grupo fuchsiano F actuando sobre el semiplano de Poincaré H tal que
152
10. VARIEDADES HIPERBÓLICAS 3-DIMENSIONALES
H/F uniformiza el interior de S. Entonces H3 /F es una variedad hiperbólica homeomorfa al interior de M(S). Lo mismo se puede hacer reemplazando F por un grupo
casifuchsiano (es decir, un grupo de transformaciones de Möbius que deja invariante
una curva de Jordan Γ). El siguiente resultado de B. Maskit [Maskit5]
Teorema 10.17. Si G es un grupo discreto isomorfo al grupo fundamental de una
superficie de Riemann de género g tal que Ω(G) 6= ∅ (es decir, un grupo Kleiniano)
tal que todo elemento de G, diferente de la identidad, es loxodrómico, entonces Λ(G)
es una curva de Jordan y cada disco acotado por esta curva es invariante por G (es
decir, G es casifuchsiano).
Bibliografı́a
[Abikoff] W. Abikoff. The real analytic theory of Teichmüller spaces. Lecture Notes in Math. 820,
Springer-Verlag, Berlin-Heidelberg-New York (1980)
[Alestalo-Helling] P. Alestalo and H. Helling. On torus fibrations over the circle. SFB-Preprint Ergaenzungsreihe 97-005, Bielefeld, 1997.
[Alling-Greenleaf] N.L. alling and N. Greenleaf, Foundations of the theory of Klein surfaces, Lecture
Notes in Math. 219, Springer-Verlag (1971).
[Beardon] A.F. Beardon. The geometry of discrete groups. Graduate Texts in Math. 91, SpringerVerlag, Berlin-Heidelberg-New York (1983)
[Benedetti-Petronio] R. benedetti and C. Petronio. Lectures on Hyperbolic Geometry. Universitext,
Springer-Verlag, Berlin-Heidelberg-New York (1992).
[Bers] L. Bers. Automorphic forms for Schottky groups. Adv. in Math. 16 (1975), 332-361.
[Burnside] W. Burnside. On a class of automorphic functions. Acta Mathematica Vol XXIII 433
(1981), 49-88.
[Casson-Bleiler] A.J. Casson and S.A. Bleiler. Automorphisms of surfaces after Nielsen and
Thurston. Cambridge University Press, 1988.
[Chuckrow] V. Chuckrow. On Schottky groups with applications to Kleinian groups. Annals of Math.,
88 (1968), 47-61.
[Ford] L.R. Ford. Automorphic functions. Chelsea, New York (1951).
[Jørgensen] T. Jørgensen. On discrete groups of Möbius transformations. Amer. J. Math. 98 (1976),
739-749.
[Koebe] P. Koebe. Über die Uniformisierung der Algebraischen Kurven II. Math. Ann. 69 (1910),
1-81.
[Farkas-Kra] H. Farkas and I. Kra. Riemann Surfaces. Springer-Verlag, New York, 1980.
[Gabino] G. González-Dı́ez. Loci of curves which are prime Galois coverings of P1 . Proc. London
Math. Soc. 62 (1991), 469-489.
[Helling-Menzel] H. Helling and C. Menzel. Towards an algorithmic construction of the hyperbolic
structure on surface bundles. SFB-Preprint Ergaenzungsreihe 99-074, Bielefeld, 1999.
[Hidalgo1] R.A. Hidalgo. Noded function groups. Contemporary Mathematics. 240(1999), 209-222.
[Hidalgo2] R.A. Hidalgo. A note on the homology covering of analytically finite Klein surfaces.
Complex variables 42 (2000), 183-192.
[Hidalgo3] R.A. Hidalgo. On Schottky groups with automorphisms. Ann. Acad. Scie. Fenn. Ser. AI
Mathematica 19 (1994), 259-289.
[Hidalgo4] R.A. Hidalgo. Schottky uniformizations of closed Riemann surfaces with Abelian groups
of conformal automorphisms. Glasgow Math. J. 36 (1994), 17-32.
[Hidalgo5] R.A. Hidalgo. Dihedral groups are of Schottky type. Revista Proyecciones. 18 (1999),
23-48.
[Hidalgo6] R.A. Hidalgo. A4 , A5 and S4 of Schottky type. Revista Matemática Complutense 15
(2002), 11-29.
153
154
BIBLIOGRAFÍA
[Costa-Hidalgo] R.A. Hidalgo and A.F. Costa, A.F. Anticonformal automorphisms and Schottky
coverings. Ann. Acad. Sci. Fenn. Math. 26 (2001), 489-508.
[Matsuzaki-Taniguchi] K. Matsuzaki and M. Taniguchi. Hyperbolic Manifolds and Kleinian Groups.
Oxford Mathematical Monographs, 1998.
[Maskit1] B. Maskit. Kleinian Groups. Springer-Verlag, Berlin-Heidelberg-New York, 1988.
[Maskit2] B. Maskit. The homology covering of a Riemann surface. Tôhoku Math. J. 38 (1986),
561-562.
[Maskit3] B. Maskit. Special uniformizations of symmetric Riemann surfaces. Preprint
[Maskit4] B. Maskit. On boundaries of Teichmüller spaces and on kleinian groups II. Ann. of Math.
91 (1970), 607-639.
[Maskit5] B. Maskit. On a class of Kleinian groups. Ann. Acad. Sci. Fenn. Ser. AI Math. 442 (1969),
1-8.
[May] C.L. May. A bound for the number of automorphisms of a compact Klein surface with boundary. Proc. Amer. Math. Soc. 63 (1977), 273-280.
[Morgan] J.W. Morgan. On Thurston’s uniformization theorem for three-diemensional manifolds.
The Smith conjecture, edited by H. Bass and J.W. Morgan, Academic Press (1984), 37-125.
[Mumford] D. Mumford. Tata lectures on Theta II. Progress on Mathematics 43, Birkhaüser, Boston,
1984.
[Otal] J.P. Otal. Le théorème d’hyperbolisation pour les variétés fibrées de dimension 3. Astérisque
235, 1996.
[Ractliffe] J.G. Ractliffe. Foundations of Hyperbolic Manifolds. Graduate Texts in Math. 149,
Springer-Verlag, Berlin-Heidelberg-New York (1994).
[Gonzalez-Rodriguez] R.E. Rodrı́guez, V. González-Aguilera. Fermat’s quartic curve, Klein’s curve
and the Tetrahedron. Contemp. Math. 201 (1997), 43-62.
[Thurston] W.P. Thurston. The Geometry and Topology of Three-Manifolds. Lecture Notes, Princeton Univ., 1979.
[Thurston2] W.P. Thurston. Three-dimensional manifolds, Kleinian groups and hyperbolic geometry.
Bull. Amer. Math. Soc. 6 (1982), 357-381.
[Vermeulen] L. Vermeulen. Non-hyperelliptic curves of genus three with Weierstrass points of weight
two. Report 81-01, Department of Math. University of Amsterdam, 1981.
[Waldhausen] F. Waldhausen. On irreducible 3-manifolds which are sufficiently large. Ann. of Math.
87 (1968), 56-88.