(a) V = {p(x) ∈ C n[x] : p(0) = 0}

Universidad Técnica Federico Santa Marı́a
Departamento de Matemática
GUIA 1 MAT210 1◦ 2015
1. Determine si los siguientes forman un espacio vectorial sobre K:
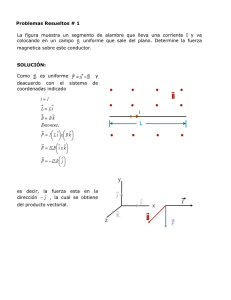
(a) V = {p(x) ∈ Cn [x] : p(0) = 0}
sobre K = C.
(b) V = {p(x) ∈ Cn [x] : p(0) = 0}
sobre K = R.
(c) V = {p(x) ∈ Cn [x] : p0 (0) = 0}
sobre K = C.
(d) V = {f : [a, b] → R continua, tal que f ( a+b
) = 0} sobre K = R.
2
a b
(e) V =
∈ M2 (C) tal que a + b + c + d = 1
sobre K = C.
c d
2. Sobre
V = R+
x ⊕ y = xy,
se definen las siguientes operaciones:
∀x, y ∈ R,
α x = xα ,
∀x ∈ R+ , ∀α ∈ R
Determine si V es o no un espacio vectorial sobre R con estas operaciones.
3. En Rn se definen las siguientes operaciones:
→
−
−
−
−
−
−
−
−
x ⊕→
y = →
x −→
y , ∀→
x ,→
y ∈ Rn ,
α→
x = −α →
x,
−
∀→
x ∈ Rn , ∀α ∈ R
¿Qué axiomas de espacio vectorial se cumplen?
4. Considere un K espacio vectorial V , definimos:
V F = [U ⊂ V | U es sub-espacio vectorial de V ]
En V F definimos las siguientes operaciones [+], [·] para U, W ∈ V F , α ∈ K:
U [+]W = (U + W ) = {u + v| u ∈ U, w ∈ W }
α[·]U = (αU ) = {αu|0 u ∈ U }
Verifique si se cumplen los axiomas de espacio vectorial, cada uno de ellos, para
V F con las operaciones definidas.
5. Sea V =
a
(a)
b
a
(b)
b
a
(c)
b
a
(d)
b
R2 . Determine si V es un espacio vectorial sobre R con las operaciones:
c
a+c
a
αa
+
=
y α·
=
, ∀α ∈ R
d
0
b
αb
a+c
a
αa
c
+
=
y α·
=
, ∀α ∈ R
d
b+d
b
0
c
a−c
a
αa
+
=
y α·
=
, ∀α ∈ R
d
b−d
b
αb
a−c
a
a
c
+
=
y α·
=
, ∀α ∈ R
d
b−d
b
b
6. Determine si los siguientes conjuntos son subespacios de R3 :
1
(a) A = {(x, y, z) : x + 2y − 2z = 0, 2x + y + z = 0}
(b) B = {(x, y, z) : xyz ≥ 0}
(c) C = {(x, y, z) : x = y 2 , x + y + z ≥ 0}
(d) D = {(x, y, z) : x ≤ y ≤ z}
7. Determine si los siguientes conjuntos son subespacios del esp. vectorial indicado:
(a) {p(x) ∈ Rn [x] : p(x) = p0 (x) } de Rn [x].
R1
(b) {p(x) ∈ Rn [x] : 0 x p(x) dx = 0 } de Rn [x].
(c) {A ∈ Mn (R) : trA = 0}
de
Mn (R).
(d) {A ∈ Mn (R) : AB = BA con B ∈ Mn (R) fija}
de
Mn (R).
8. Considere el C-espacio vectorial C3 y los vectores
u1 = (1, 0, i) y u2 = (1 + i, 1, −1).
(a) Demuestre que son l.i sobre C.
(b) Demuestre que w1 = (1, 1, 0), w2 = (1, i, 1 + i) ∈ U = hu1 , u2 i
(c) Demuestre que los vectores w1 y w2 forman una base para U .
(d) Determine las coordenadas de u1 y u2 en la base {w1 , w2 }.
(e) Complete la base anterior a una base de C3 .
9. Demuestre que el conjunto de todas las funciones de variable real es un espacio
vectorial sobre R, con la suma y producto por escalar usuales. Demuestre que
B = {fn (t) = ent , con n ∈ N} es una familia linealmente independiente en
este espacio vectorial. ¿Genera a todo el espacio de funciones?
10. Considere el espacio vectorial M2 (K) de matrices 2 × 2. Considere los subespacios
U y V:
a −a
U = A ∈ M2 (K) : A =
b c
a b
V = A ∈ M2 (K) : A =
−a c
Determine la dimensión de los subespacios U, V, U + V y U ∩ V .
11. Considere los subespacios U1 = hS1 i y U2 = hS2 i del espacio vectorial V . Determine bases y dimensión de U1 , U2 , U1 + U2 y U1 ∩ U2 .
(a) S1 = {1 + x2 + x4 , x − x4 , x + x2 − x3 , 1 + x + x3 },
en V = R4 [x].
(b) S1 = {1, 1 + x − x2 , 1 + x2 − x3 , 1 + x4 + x5 },
en V = R5 [x].
S2 = {x + x2 , x + x4 , 1 + x}
S2 = {x4 + x5 , 1 + x + 2x2 , 1}
12. Sea V un espacio vectorial sobre R, u ∈ V y S ⊂ V l.i. Demuestre que
S ∪ {u} es l.i. ⇐⇒ u no es combinación lineal de elementos de S.
2
13. Sea V el espacio vectorial de todas las funciones continuas. Muestre que el conjunto {sin x, sin 2x, sin 3x} es linealmente independiente.
14. Teorema Sea V un espacio vectorial y X ⊂ V un subconjunto. El span{(X)} =
h{X}i es el más pequeño subespacio de V que contiene a X.
15. Pruebe que span{v1 , v2 , ..., vk } ⊂ span{v1 , v2 , ..., vk , vk+1 }. Más aún, ¿Qué pasa
si vk+1 ∈ span{v1 , v2 , ..., vk }?.
16. Cómo están relacionados los siguientes subespacios
span{u, v, w}, span{x, y}, span{u, v, w, x, y}
span{u, v, w}, span{v, w, x}, span{v, w}
17. Sea {v1 , ..., vn } y {w1 , ..., wm } bases de V . Entonces para cada vi , existe algún wj
tal que {v1 , ..., vi−1 , wj , vi+1 , ..., vn } es una base de V .
18. Considere a R como un espacio vectorial sobre Q. Cuál es la dimensión de este
espacio vectorial? Justifique su respuesta.
19. Sea V un K espacio vectorial, justifique el valor de verdad de las siguientes afirmaciones:
(1) La condición para que N ⊂ V sea sub-espacio que dice que 0V debe estar en
N puede ser sustituida por V 6= ∅ si se mantienen las otras dos condiciones.
(2) Pueden existir 2 sub-espacios de V tales que su intersección sea solo un vector
diferente del vector nulo.
(3) Considere W otro espacio vectorial con el mismo cuerpo, N sub-espacio de V
y M sub-espacio de W , entonces N × M es sub-espacio de V × W .
(4) Sean A, B, C sub-espacios de V . Supongamos que V tiene dimension n,
ademas que la intersección de los tres sub-espacios es solo el vector neutro. Si la
dimension de los espacios A, B y C suma n entonces V es suma directa de A, B
y C.
(5) Si A es un sub-espacio vectorial y ni a ni b, vectores, estan en A entonces a + b
no esta en A
(6) Si A, B son subconjuntos de V y A ⊂ B entonces el sub-espacio generado por
A es sub-espacio del espacio generado por B.
20. Pruebe que la unión de dos sub-espacios vectoriales es sub-espacio vectorial si, y
solamente si, uno de ellos esta contenido en el otro.
21. Considere E = F(R, R) = {funciones de R en R} y ademas:
F1 = {funciones de R en R que se anulan en [0, 1]}
F2 = {funciones de R en R que se anulan en [2, 3]}
Verifique que F1 , F2 son sub-espacios de E y que E = F1 + F2 pero no se tiene
que E = F1 ⊕ F2 .
3
22. Sean F1 , . . . , Fk sub-espacios vectoriales del espacio vectorial E. Pruebe:
a)El sub-espacio generado por la unión F1 ∪ . . . ∪ Fk es el conjunto F1 + . . . + Fk
de las sumas x1 + . . . + xk , donde xi ∈ Fi para i desde 1 hasta k
b) Las siguientes afirmaciones son equivalentes:
i) Cada x ∈ F1 ∪ . . . ∪ Fk se escribe de manera única como x1 + . . . + xk .
ii) Para cada j = 1, . . . k se tiene que Fj ∩(F1 +. . .+Fj−1 +Fj+1 +. . .+Fk ) = {0v }
23. Considere el conjunto
M = {x = (xn )n∈N | xn ∈ R∀n ∈ N y xn+2 = xn+1 + xn }
probar que M es un sub-espacios del espacio de todas las sucesiones de números
reales y encuentre su dimensión.
24. En R4 , demuestre que
W = {(x1 , x2 , x3 , x4 ) : x1 + x2 + x3 + x4 = 0, x1 − x2 + x3 − x4 = 0}
es un subespacio vectorial. Determine una base para W . Encuentre un subespacio
U tal que W ⊕ U = R4 .
25. Cuáles de las siguientes aplicaciones de R4 en R4 son lineales?
a) (x1 , x2 , x3 , x4 ) → (x1 x2 , x2 − x1 , x3 , x4 ).
b) (x1 , x2 , x3 , x4 ) → (λx2 , x2 − x1 , x3 , x4 ).
c) (x1 , x2 , x3 , x4 ) → (0, x3 , x2 , x1 + x2 + x3 + x4 ).
26. Considere el espacio vectorial de las funciones continuas de [a, b] en R. Demuestre
que la aplicación
ϕ : f (t) → tf (t)
es lineal.
27. Sea E un k-espacio vectorial y fi : E → k aplicaciones lineales, demuestre que
ϕ : E → kn
x → ϕ(x) = (f1 (x), . . . , fn (x))
es lineal.
28. En C(R) el espacio vectorial de aplicaciones continuas de R en R, defina
Z t
ϕ : f (t) →
f (s)ds
0
Determine (caracterice) el núcleo y la imagen de ϕ. Es ϕ inyectiva? Es ϕ biyectiva?
29. Considere el espacio vectorial R3 [x, y, z] sobre R, formado por los polinomios de
grado ≤ 3 en las variables x, y, z. Considere las siguientes transformaciones:
4
∂
: R3 [x, y, z] −→ R3 [x, y, z]
∂x
∂
(b)
: R3 [x, y, z] −→ R3 [x, y, z]
∂y
∂2
: R3 [x, y, z] −→ R3 [x, y, z]
(c)
∂x∂y
∂2
∂2
∂2
(d)
+
+
: R3 [x, y, z] −→ R3 [x, y, z]
∂x2 ∂y 2 ∂z 2
(a)
En cada caso, determine si la función es o no lineal. En caso afirmativo, determine
dimensión del Kernel y de la Imagen.
30. Sea L : R2 [x] −→ R2 [x],
L(p(x)) = p(x − 1).
(a) Demuestre que es lineal.
2
(b) Determine [L]B
B1 ,
donde B1 = {1, x, x2 },
B2 = {1, x − 1, (x − 1)2 }
(c) Pruebe que L es un isomorfismo.
31. Sea T : R2 [x] −→ R3 ,
T (p(x)) = (p(−1), p(0), p(1)).
(a) Demuestre que es lineal.
(b) Determine [T ]C
B1 ,
donde B1 = {1, x, x2 },
y C es la base canónica.
(c) Pruebe que T es un isomorfismo.
(d) Determine T −1 y [T −1 ]C
B1
32. Encuentre la matriz cambio de base entre B1 y B2 :
(a) En R4 : B1 = {(1, 0, 0, 0), (1, 1, 0, 0), (1, 1, 1, 0), (1, 1, 1, 1)},
B2 = {0, 0, 0, 1) (0, 0, 1, 1), (0, 1, 1, 1), (1, 1, 1, 1)}
(b) En U ≤ R3 [x]: B1 = {1 − x, 1 + x2 , 1 − x3 },
B2 = {3 − x − 2x3 , 4 − 3x + x2 , 2 − 2x − x2 − x3 }
3 2
1 2
−2 1
(c) En V ≤ M2×2 (R): B1 =
,
,
,
2 3
1 5
2 1
1 0
1 6
8 9
B2 =
,
,
0 1
6 13
9 15
33. Sea L : R3 [x] −→ R2 [x] una transformación lineal tal que:
L(1) = x2 , L(1 + x) = x, L(1 + x + x2 ) = 1, L(1 + x + x2 + x3 ) = 0
(a) Determine L(p) para cualquier p ∈ R3 [x]
(b) Determine Ker(L) e Im(L).
(c) Encuentre [L] en las bases canónicas respectivas.
34. Sea L : R2 [x] −→ R4 una transformación lineal tal que:
L(1) = (1, 0, 2, −1), L(1 + x) = (2, 1, 0, −1), L(1 + x + x2 ) = (0, −1, 4, −1)
(a) Determine una base para Ker(L) y una para Im(L).
5
(b) Determine L(p) para cualquier p ∈ R2 [x]
(c) Sea B = {1, 1 + x, 1 + x + x2 } una base de R2 [x]. Determine la matriz L
de la base B a la base canónica de R4 y la matriz de L respecto a las bases
canónicas en ambos espacios.
35. Pruebe que los operadores lineales E11 , E12 , E21 , E22 : R2 → R2 , definidos por
E11 (x, y) = (x, 0), E12 (x, y) = (0, x), E21 (x, y) = (y, 0), E22 (x, y) = (0, y), forman
una base del espacio vectorial L(R2 ; R2 ). Pruebe que otra base de L(R2 ; R2 ) puede
ser dada por A(x, y) = (x + 3y, y), B(x, y) = (x, 0), C(x, y) = (x + y, x − y) y
I(x, y) = (x, y)
36. Sean P1 , . . . Pk : E → E operadores lineales tales que P1 + P2 + . . . + Pk = I donde
I denota el operador identidad y Pj ◦ Pi = 0 si i 6= j, pruebe que estos operadores
son proyecciones.
37. Sea {e1 , e2 , e3 } la base canónica de R3 y defina
f1 = e1 + e2 + e3 ,
f2 = e2 + e3 ,
f3 = e3
(a) Aplique el proceso de Gram-Schmidt a la base {f1 , f2 , f3 }.
(b) Determine qué se obtiene si se aplica Gram-Schmidt a la base {f3 , f2 , f1 }.
38. Sea V un espacio de dimensión finita con producto interior, definido sobre un
cuerpo K. Dado cualquier par de vectores u, v ∈ V prueba que se cumple
< u, v >= 0 ⇐⇒ kuk ≤ ku + αvk,
∀α ∈ K
39. Sea n ∈ N, ai , bi ∈ R, para i = 1, ..., n. Demuestre que
!2
!2
n
n
n
X
X
X
bi
ai b i ≤
iai
i
i=1
i=1
i=1
40. Sea V V Sea V un espacio de dimensión finita con producto interior, definido
sobre un cuerpo K y sea P ∈ L(V ) con las siguientes propiedades
(a) Dado cualquier vector v ∈ V , P (P (v)) = P (v), esto es P 2 = P .
(b) Dado cualquier vector u ∈ Ker(P ) y cualquier vector v ∈ Im(P ) se tiene<
u, v >= 0. Entonces P es una proyección ortogonal.
41. Considere el espacio R2 [x] provisto de la aplicación definida por:
< p, q >:= p(−1)q(−1) + p(0)q(0) + p(1)q(1),
∀p, q, ∈ R2 [x]
(a) Demuestre que < ·, · > es un producto interior sobre R2 [x].
(b) Pruebe que los vectores p(x) = 1 y q(x) = x son ortogonales con este p.i..
(c) Encuentre un tercer polinomio r tal que {p, q, r} sea una base ortogonal de
R2 [x] , y luego calcule las coordenadas de s(x) = 2x2 + 3x − 1 con respecto
a esta base.
6
42. Suponga que {e1 , ..., em } es un conjunto de vectores ortonormales de un espacio
finito dimensional V . Sea v ∈ V . Pruebe que:
(a) kvk2 ≤ | < v, e1 > |2 + | < v, e2 > |2 + · · · + | < v, em > |2
(b) kvk2 = | < v, e1 > |2 + · · · + | < v, em > |2 ⇔ v ∈< {e1 , ..., em } > .
43. Sea V = R4 , y sea U =< {(1, 1, 0, 0, ), (1, 1, 1, 2)} >≤ V . Encuentre ū ∈ U tal
que kū − (1, 2, 3, 4)k sea lo más pequeña posible.
44. Considere el espacio de las funciones cuadrado integrales en [−1, 1] y sea f (x) =
cos x. Encuentre p̄ ∈ R2 [x] tal que kp̄ − f k sea lo más pequeña posible.
45. Dado n ∈ N, considere el espacio vectorial real Rn [x] con el producto interior
definido por:
n+1
X
< p, q >=
p(j)q(j),
∀p, q ∈ Rn [x]
j=1
(a) Encuentre el valor de k ∈ R tal que p(x) = x + k y q(x) = x − k sean
P
m(m+1)(2m+1)
2
ortogonales. Recuerde que m
j=1 j =
6
(b) Para n = 3 considere los siguientes subespacios S = {p ∈ Rn [x] : p(2) +
p(3) = 0} y W = {p ∈ Rn [x] : p(−x) = −p(x)}. Encuentre S ⊥ y W ⊥ .
(c) Encuentre una base ortonormal para S, W, R2 [x] y R3 [x].
46. Consideremos C([a, b], R), el espacio vectorial de las fuciones continuas de [a, b]
en R. Compruebe que las siguientes son normas:
1/2
Z b
2
kf k2 =
f (t) dt
a
Z b
|f (t)|dt
kf k1 =
a
kf k∞ = max |f (t)|
t∈[a,b]
√
√
Demuestre ademas que kf k1 ≤ b − akf k2 y kf k2 ≤ b − akf k∞ .
47. Demuestre que
1
1
1
√ , √ cos nt, √ sin nt
n
n
2π
n=1,2,...
forman un conjunto ortonormal de C([0, 2π], R) con el producto interno
Z 2π
< f, g >=
f (t)g(t)dt.
0
48. Demuestre que < A, B >= tr(AB ∗ ) es producto interno de M n×n (C). Encuentre
la formula de la norma ||A||, inducida por este producto, en términos de los
elementos de A y luego pruebe que esta norma satisface
kABk ≤ kAkkBk
7
∀A, B ∈ M n×n (C).