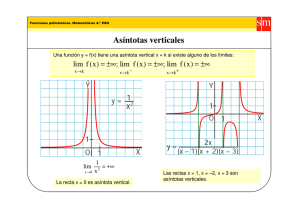
Tema 7 Límites y continuidad

Tema 7
Límites y continuidad
7.1
Definición de límite de una función
Sea f : I → R, I ⊂ R y sea a ∈ I un punto de acumulación de I, decimos
que f (x) tiene límite l ∈ R en el punto a
lim f (x) = l
x→a
si
∀ε > 0, ∃η > 0 : |x − a| < η ⇒ |f (x) − l| < ε
equivalente a decir que si
∀ε > 0, ∃η > 0 : x ∈ (a − η, a + η) ⇒ f (x) ∈ (l − ε, l + ε)
Ejercicio 7.1.1 ¿Será cierto?
lim
x→2
x2 − 4
=4
x−2
5
Podemos acotar la diferencia
¯
¯ x2 − 4
¯
¯
¯ x−2
¯
¯
− 4¯¯¯
=
¯
¯ x2
¯
¯
¯
¯
¯
¯
− 4 − 4x + 8 ¯¯ ¯¯ (x − 2)2 ¯¯
¯=¯
¯ = |x − 2|
¯
¯ x−2 ¯
x−2
∀ε > 0, ∃η = ε : |x − 2| < η ⇒
¯
¯ x2 − 4
¯
¯
¯ x−2
¯
¯
− 4¯¯¯
<ε
La dificultad de este ejercicio ya nos indica que la definición no sirve mucho
para demostrar si existe el límite o calcularlo.
Si usamos sucesiones, la definición anterior es equivalente a:
lim f (x) = l ⇔ [∀ (xn ) → a ⇒ (f (xn )) → l]
x→a
para toda sucesión (xn ) con límite a, la sucesión de las imágenes (f (xn ))
tiene por límite l. De hecho, esta definición es la que se usa para calcular un
límite. Así cuando nos piden calcular lim x2 + x + 1, cogemos una sucesión
x→2
que tiende a 2 y calculamos el límite de las imágenes
x → 2− 1 1, 9 1, 99 1, 999 · · ·
f (x) →? 3 6.5 6.95 6, 995 · · ·
y por eso decimos que lim x2 + x + 1 = 7.
x→2
En la práctica lo que se hace es sustituir directamente x por 2. Cuando
nos encontramos con expresiones del tipo 00 , 0 · ∞, etc, es decir, expresiones
que a priori no sabemos cuanto valen, decimos que hemos encontrado una
indeterminación. Estos problemas los estudiaremos más adelante .
Ejercicio 7.1.2 Demostrar la no existencia del siguiente límite
lim sen
x→0
Si usamos las sucesiones xn =
µ ¶
π
x
1
2
yn =
que convergen a cero:
1 + 4n
1 + 4n
(xn ) → 0, (yn ) → 0
tendríamos
f (xn ) = sen
f (yn ) = sen
Ã
Ã
π
1
1+4n
π
2
1+4n
!
!
= sen (π + 4nπ) = 0, ∀n
= sen
µ
¶
π
+ 2nπ = 1, ∀n
2
es decir (f (xn )) → 0 mientras que (f (yn )) → 1, no puede existir el límite ya
que el límite de una sucesión es único.
6
7.2
Propiedades de los límites
1. El límite de una función, si existe, es único.
2. Si existe x→a
lim f (x), existe un entorno del punto a donde f (x) está acotada.
3. Si en un entorno de a se cumple f (x) ≤ g(x) ≤ h(x) y
h(x) = l ⇒lim
g(x) = l
lim f (x) =lim
x→a
x→a
x→a
4. Operaciones con límites:
lim f (x) + s· x→a
lim g(x)
(a) x→a
lim [r · f (x) + s · g(x)] = r· x→a
(b) x→a
lim [f (x) · g(x)] =lim
f (x)· x→a
lim g(x)
x→a
(c) x→a
lim
lim f (x)
f (x)
= x→a
, si x→a
lim g(x) 6= 0
g(x)
lim
g(x)
x→a
lim f (x)
(d) x→a
lim bf (x) = bx→a
, si b > 0
∙
¸
lim f (x)
(e) x→a
lim ln [f (x)] = ln x→a
lim g(x)
(f) x→a
lim f (x)g(x) =lim
f (x)x→a
x→a
7.3
Límites laterales
Se llama límite por la izquierda al siguiente límite
lim f (x) =lim
f (x)
x→a
x→a−
x<a
o su equivalente usando sucesiones
lim f (x) = l ⇔ [∀ (xn ) → a, xn < a ⇒ (f (xn )) → l]
x→a−
Análogamente el límite por la derecha
f (x)
lim f (x) =lim
x→a
x→a+
x>a
lim f (x) = l ⇔ [∀ (xn ) → a, xn > a ⇒ (f (xn )) → l]
x→a+
Un resultado interesante para conocer la existencia o no de límites es: una
función tiene límite en un punto si y sólo si éxisten y coinciden los límites
laterales.
7
|x|
x→0 x
Calculamos los límites laterales
|x|
|x|
x
= lim
=lim
=1
lim+
x→0
x→0
x
x x→0
x
x>0
x>0
Ejercicio 7.3.1 Calcular lim
lim
x→0−
|x|
|x|
−x
= lim
=lim
= −1
x→0
x→0
x
x
x
x<0
x<0
y como no coinciden los límites laterales, el límite no existe.
7.4
Límites infinitos
Decimos que
lim f (x) = ∞ ⇔ ∀A > 0, ∃δ > 0 : |x − a| < δ ⇒ f (x) > A
x→a
Análogamente
lim f (x) = −∞ ⇔ ∀A > 0, ∃δ > 0 : |x − a| < δ ⇒ f (x) < −A
x→a
y todas sus variantes
lim f (x) = l ⇔ ∀ε > 0, ∃k > 0 : x > k ⇒ |f (x) − l| < ε
x→∞
lim f (x) = l ⇔ ∀ε > 0, ∃k > 0 : x < −k ⇒ |f (x) − l| < ε
x→−∞
lim f (x) = ∞ ⇔ ∀A > 0, ∃k > 0 : x > k ⇒ f (x) > A
x→∞
lim f (x) = −∞ ⇔ ∀A > 0, ∃k > 0 : x > k ⇒ f (x) < −A
x→∞
lim f (x) = ∞ ⇔ ∀A > 0, ∃k > 0 : x < −k ⇒ f (x) > A
x→−∞
lim f (x) = −∞ ⇔ ∀A > 0, ∃k > 0 : x < −k ⇒ f (x) < −A
x→−∞
1
2
x→0 x
Ejercicio 7.4.1 ¿Por qué decimos que lim
∀A > 0, ∃δ > 0 : |x − 0| < δ ⇒
7.5
= ∞?
1
1
> A, basta tomar δ = √
2
x
A
Indeterminaciones
Decíamos en el apartado 7.1, página 6, que cuando aparece 00 , 0 · ∞, . . .
tenemos una indeterminación. Atendiendo al tipo de indeterminación las
resolveremos de una forma u otra.
8
7.5.1
Indeterminación
k
0
con funciones racionales
Se calculan los límites laterales, si son iguales existe el límite y en caso
contrario no existe.
1
Por ejemplo, la función f (x) = x−1
presenta en x = 1 la indeterminación
1
, no tiene límite puesto que
0
lim−
x→1
7.5.2
1
= −∞
x−1
Indeterminación
0
0
lim+
x→1
1
= +∞
x−1
con funciones racionales
Desaparece factorizando numerador y denominador, y simplificando
lim
x→1
7.5.3
x3 − 1 0
(x − 1) (x2 + x + 1)
= =lim
=lim x2 + x + 1 = 3
x→1
x−1
0 x→1
x−1
Indeterminación
∞
∞
con funciones racionales
Desaparece dividiendo numerador y denominador por la máxima potencia
del denominador
lim
x→∞
7.5.4
4 + x1 − x12
4x2 + x − 1
∞
=4
=
=
lim
x2 − 1
∞ x→∞ 1 − x12
Límites de funciones irracionales
La indeterminación 00 ó ∞ − ∞ con radicales (de índice 2) desaparece multiplicando y dividiendo por la expresión radical conjugada
√
x−1
(x − 1) (1 + x)
0
√ = =lim
√
√ =
lim
x→1 1 −
x
0 x→1 (1 − x) (1 + x)
√
³
√ ´
(x − 1) (1 + x)
=lim
=lim − 1 + x = −2
x→1
x→1
(1 − x)
7.5.5
Funciones equivalentes
No lo vamos a demostrar pero debemos saber que
lim
x→0
sen x
tan x
=lim
=1
x→0
x
x
y que por eso se les llama funciones equivalentes. Usaremos este resultado en
la derivación de las funciones trigonométricas, en el apartado 8.4.4, página
21.
9
También conviene saber que
lim
x→0
ex − 1
=1
x
pues lo usaremos en el apartado 8.4.1 de la página 20.
7.6
Definición de función continua
Diremos que f (x) es continua en x = a cuando x→a
lim f (x) = f (a).
Si usamos la definición de límite quedará
∀ε > 0, ∃η > 0 : |x − a| < η ⇒ |f (x) − f (a)| < ε
∀x ∈ (a − η, a + η) ⇒ f (x) ∈ (f (a) − ε, f (a) + ε)
que se lee ”a incrementos pequeños de la variable independiente corresponden
incrementos pequeños de la variable dependiente” o más a lo bruto ”se pinta
la función sin levantar el lápiz del papel”.
Interpretación geométrica de la continuidad
La definición que se ha dado de continuidad implica tres condiciones:
1. ∃f (a)
2. ∃ x→a
lim f (x)
3. x→a
lim f (x) = f (a)
Si falla alguna de estas tres condiciones la función es discontinua.
10
⎧
⎪
⎨
2
x<1
1
x=1
⎩
x+2 x>1
Ejercicio 7.6.1 Estudiar la continuidad de f (x) = ⎪
Dos son las pistas que nos tienen que ayudar a buscar los puntos donde
la función es discontinua: donde no pueda calcular la función y donde pegue
un salto. En este ejemplo siempre podemos calcular la función en cualquier
punto, pero es posible que en x = 1 tengamos un salto. Si calculamos los
límites laterales
lim+ f (x) = 3
lim− f (x) = 2
x→1
x→1
y como no existe el límte deducimos que es discontinua.
Ejercicio 7.6.2 Estudiar la continuidad de f (x) =
(
x2 −1
x−1
3
x 6= 1
x=1
En todos los puntos distintos de x = 1 la función es continua, vemos qué
sucede en x = 1.
lim
x→1
x2 − 1
(x + 1) (x − 1)
=lim
=lim x + 1 = 2
x→1
x − 1 x→1
x−1
Como f (1) = 3 y el límite en ese punto es 2, la función es discontinua en
x = 1. Ahora bien, si hubieramos tomado f (1) = 2, la función sería continua
en toda la recta real, en este sentido decimos que la discontinuidad es evitable.
7.7
Propiedades de las funciones continuas
1. La suma de funciones continuas es otra función continua.
2. El producto de funciones continuas es otra función continua.
3. El cociente de funciones continuas es otra función continua siempre que
el denominador sea distinto de cero.
4. La composición de funciones continuas es otra función continua.
7.8
Teoremas de continuidad
Una función es continua en un intervalo abierto (a, b) si lo es en cada uno de
sus puntos.
Una función es continua en un intervalo cerrado [a, b] si lo es en (a, b) y
además es continua por la derecha en a y por la izquierda en b.
A partir de aquí I representa un intervalo.
11
7.8.1
Conservación del signo
f : I → R continua en x = a y f (a) 6= 0 ⇒existe un entorno del punto a
donde la función conserva el signo
7.8.2
Teorema de acotación
f : I → R continua en x = a ⇒existe un entorno del punto a donde la
función está acotada.
f : I → R continua en I, intervalo cerrado⇒la función está acotada en I.
7.8.3
Teorema de Weierstrass
f : I → R continua en I, intervalo cerrado⇒existen puntos del intervalo
I donde la función alcanza al supremo y al ínfimo, es decir, toda función
continua en un intervalo cerrado tiene máximo y mínimo absoluto.
Intuitivamente significa que la gráfica de la función debe tener un punto
más alto o igual que los demás y otro más bajo o igual que los restantes.
7.8.4
Teorema de Bolzano
Si f : [a, b] → R es continua y f (a) · f (b) < 0 ⇒ ∃c ∈ (a, b) : f (c) = 0
12
La interpretación geométrica de este teorema es muy sencilla: si la gráfica
se dibuja sin levantar el lápiz y tengo que ir de debajo del eje X hacia arriba
del eje X, o viceversa, a la fuerza tengo que atravesar el eje.
La principal aplicación de este teorema es asegurar la existencia de soluciones de una ecuación. Por ejemplo, demostrar que la ecuación
sen x + 1 − x = 0
tiene al menos una solución.
Si definimos la función f (x) = sen x + 1 − x, esta es una función continua
en cualquier intervalo, cumpliéndose además que f (0) = 1 > 0 y que f (π) =
1 − π < 0, con lo que ∃c ∈ (a, b) : f (c) = 0
7.8.5
Teorema del valor intermedio (para continuidad)
Si f : [a, b] → R es continua y f (a) ≤ l ≤ f (b) ⇒ ∃c ∈ [a, b] : f (c) = l
7.8.6
Lema de Darboux
Si f : [a, b] → R es continua entonces f toma todos los valores comprendidos
entre el máximo y el mínimo absoluto.
13
7.9
Ejercicios límites y continuidad
1. Calcular los límites
lim (x4 − x2 − x − 4) lim (x − 1)5
lim (−x2 + x + 15)
x→2
x→1
x→∞
x4 −1
2
x→1 x −1
(1+x)2 −1
x
x→0
x→∞
√
x+1−2
x−3
x→3
√
1− 1−x2
x
x→0
lim
lim
lim
x2 +2x+1
x→−1
x3 +3x2 +3x+1
lim
x→∞
√
x+1−x
lim
lim
x→0
sen 8x
4x
lim
x2 −6x+8
x2 −2
lim
lim
x→0
lim (−x3 + x2 )
x→−∞
lim
x→∞
(1+x)2 −1
x2
√
√ x+9−3
x→0 x+16−4
lim
1−cos x
x2
2. Calcular los límites laterales donde se indica
(a) f (x) =
(b) f (x) =
x−2
|x−2|
en x = 2
x sen x
|x|
en x = 0
3. Estudiar la continuidad de las funciones
(
x+1 x≥0
f (x) =
x−1 x<0
sen 2x
f (x) =
x
(
1
x<1
√ x
x+1 x≥1
x3 − 1
f (x) =
x−1
f (x) =
f (x) =
x2 −1
x3 +7x−8
4. Calcular el valor de a para que la función sea continua
f (x) =
(
x+1 x≤1
3 − ax2 x > 1
f (x) =
x3 + x2 + x + a
x−1
5. Demostrar que las ecuaciones tienen, por lo menos, una solución
(a) x3 − 3x + 1 = 0
(b) 3x − 2 = cos x
6. Demostrar que las ecuaciones π x = e y x = cos x tienen una solución
en (0, 1)
14