s - Uabc

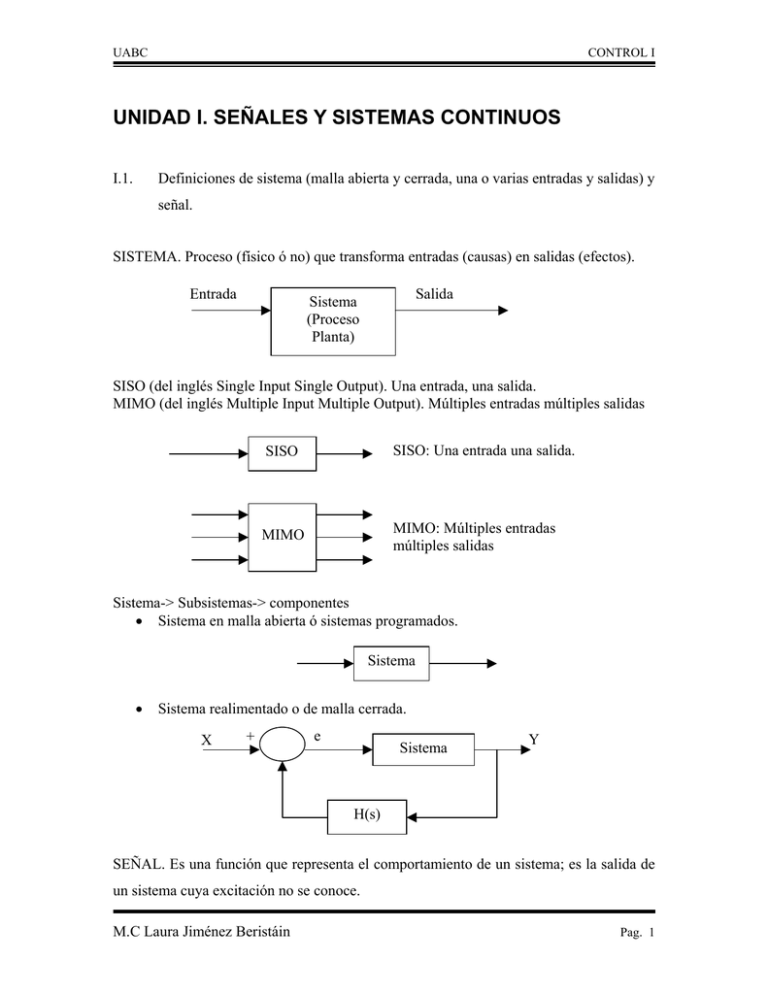
UABC
CONTROL I
UNIDAD I. SEÑALES Y SISTEMAS CONTINUOS
I.1.
Definiciones de sistema (malla abierta y cerrada, una o varias entradas y salidas) y
señal.
SISTEMA. Proceso (físico ó no) que transforma entradas (causas) en salidas (efectos).
Entrada
Salida
Sistema
(Proceso
Planta)
SISO (del inglés Single Input Single Output). Una entrada, una salida.
MIMO (del inglés Multiple Input Multiple Output). Múltiples entradas múltiples salidas
SISO
SISO: Una entrada una salida.
MIMO
MIMO: Múltiples entradas
múltiples salidas
Sistema-> Subsistemas-> componentes
• Sistema en malla abierta ó sistemas programados.
Sistema
•
Sistema realimentado o de malla cerrada.
X
+
e
Sistema
Y
H(s)
SEÑAL. Es una función que representa el comportamiento de un sistema; es la salida de
un sistema cuya excitación no se conoce.
M.C Laura Jiménez Beristáin
Pag. 1
UABC
CONTROL I
Sistema
I.2.
x(t)
Funciones singulares o generalizadas.
Son las derivadas e integraciones sucesivas del escalón unitario u0(t)
Escalón unitario. u(t)
1, t > 0
u (t ) = 
0, t < 0
u(t)
1
t
1, t ≤ 0
u (− t ) = 
0, t > 0
u(-t)
1
t
En general:
 A, t ≥ t 0
A u (t − t 0 ) = 
0, t < t 0
Au(t –t0)
A
t
t0
 A, t ≤ t 0
0, t > t 0
A u (t 0 − t ) = 
Au(t0-t)
A
t0
M.C Laura Jiménez Beristáin
t
Pag. 2
UABC
CONTROL I
DERIVADAS SUCESIVAS DEL ESCALÓN UNITARIO. Demostración del impulso
unitario. Sabemos que el escalón unitario u0(t) ≅ a una rampa con pendiente 1/∆
( m = 1 − 0 = 1 ) cuando lim ∆→0
∆−0
∆
∆ (t)
uo(t)
1
1
∆
≅
t
lim ∆ −> 0
t
Primera derivada (impulso unitario).
Derivando ∆(t), tenemos :
∆'(t)
1/∆
∆
t
Donde su área es (∆)1/∆=1. Si ∆→0 uo'(t)=∆ '(t)=δ(t) ,que es el impulso unitario o Delta
de Dirac.
∞, t 0 = 0
0, ∀t 0 ≠ 0
∞, t = 0
0, ∀t ≠ 0
δ (t ) = 
δ (t − t 0 ) = 
Aδ(t-to)
(1)
(A)
t
M.C Laura Jiménez Beristáin
to
t
Pag. 3
UABC
CONTROL I
Propiedades:
∫δ(t) dt= 1
∫f(t) δ(t) dt = f(o)
∫ f(t)δ(t-t )dt=f(t )
1.
2.
3.
o
o
Segunda derivada (doblete).
Para obtener la segunda derivada del escalón unitario uo”(t)=∆”(t)=δ’(t), como se vio
anteriormente, el impulso unitario δ(t), mostrado en la fig.3, se puede representar de la
siguiente forma :
∆ '(t)
∆'(t)
∆
1/∆
2∆
∆
t
∆
t
+
−1/∆
Derivando cada función nos queda:
∆ "(t)
∆"(t)
1/∆
2
∆
∆
2∆
t
∆
t
+
−1/∆
2
Cuando ∆ '(t) es derivada y ∆ '(t) --> 0.
M.C Laura Jiménez Beristáin
Pag. 4
UABC
CONTROL I
δ "(t)
2
1/∆
(1/∆)
∆
t
−(1/∆)
Tercera derivada (triplete).
Así mismo para obtener la tercera derivada del escalón unitario uo'''(t) = ∆'''(t) = δ ''(t),
se le conoce como triplete y se representa :
δ’’(t)
(1)
Triplete
t
(1)
INTEGRACIONES SUCESIVAS DE ESCALÓN UNITARIO
En general:
∫ L ∫ u 0 (t )dt =
t
t
0 0
0
∫
t
tk
u 0 (t ) , donde k=1,2, 3,...
k!
Cuando k=1
tu 0 (t )
Cuando k =1
Rampa Unitaria
t
M.C Laura Jiménez Beristáin
Pag. 5
UABC
CONTROL I
Cuando k=2
t2
u 0 (t )
2
Para k = 2
Parábola Unitaria
(1)
t
Ejemplos:
Problema I.1: Descomponer en funciones singulares a las siguientes funciones f(t) y g(t),
respectivamente:
f(t)
2
1
t
2
1.
f (t ) = tu 0 (t ) − (t − 2 )u o (t − 2 ) − u 0 (t − 2 )
g(t)
2
-1
1
t
2 2.5
2. g (t ) = 2u 0 (t ) − 3u 0 (t − 1) + u 0 (t − 2) + 4(t − 2)u 0 (t − 2) − 4(t − 2.5)u 0 (t − 2.5)
I.3.
Transformadas de Fourier y de Laplace.
Par transformado de Fourier:
X ( f ) = ∫ x(t ) e − jωt dt = F [x(t )]
∞
−∞
X (t ) = ∫ x( f ) e jωt df = F −1 [x( f )] =
∞
−∞
M.C Laura Jiménez Beristáin
1
2π
∞
ω
∫ x(ω )e dω
−∞
j t
rad/s, ω = 2πf
Pag. 6
UABC
CONTROL I
Obsérvese:
∞
Si f=0 x(0 ) = ∫ x(t )dt = Area bajo x(t)
−∞
∞
Si t=0 x(0 ) = ∫ x( f )df = Area bajo x(f)
−∞
Si x(t) = δ(t); Entonces la transformada de Fourier será:
F [δ (t )] = ∫ δ (t ) e − jωt dt = e − jωt
∞
−∞
t =0
=1
Es decir x(t)= δ(t)= F[δ(t)]= x(f) = 1
Expresión integral del impulso:
∞
∞
−∞
−∞
δ (t ) = ∫ 1e − jωt df ó también δ ( f ) = ∫ 1 e ± jωt dt
Ejemplo: Obtener la Transformada de Fourier de F [A cos ωs t ]
∞
A
 A ∞
F [ A cos ωs t ] = F  e jωst + e − jωst  =  ∫ e jωst ⋅ e − jωt dt + ∫ e − jωst ⋅ e − jωt dt 


−
∞
−
∞
2
 2
(
)
Empleando identidad de Euler
F [ A cos ωs t ] =
e jθ = cosθ + jsenθ
e − jθ = cosθ − jsenθ
e jθ + e − jθ = 2 cosθ
∞
A  ∞ − j (ω −ωs )t
A
+
e
dt
e − j (ω +ωs )t dt  = [δ ( f + fs ) + δ ( f − fs )]
∫
∫


−
∞
−
∞
 2
2
|X(f)|
(A/2)
-fs
(A/2)
fs
f
En general la transformada de Fourier de una señal periódica es:
∞
X ( f ) = ∑ a K δ ( f − Kfs )
−∞
Donde a K es el coeficiente de Fourier de un periodo:
Ejemplo Hallar la transformada de Fourier de un tren infinito de impulsos
M.C Laura Jiménez Beristáin
Pag. 7
UABC
CONTROL I
∞
X (t ) = ∑ δ (t − kT )
X(t)
−∞
(1)
t
-2T
T
2
T
−
2
1
ak =
T
∫ δ (t )e
x( f ) =
1 ∞
∑ δ ( f − kfs )
T −∞
− j 2π fs kt
dt =
-T
T
2T
1
T
Si x(t ) = x(t ) e −σt
∞
∞
−∞
−∞
∞
1
j 2π
x( f ) = ∫ x(t ) e − jσt ⋅ e − jωt dt = ∫ x(t ) e −(σ + jω ) t dt
como: σ + jω = s
x( f ) = ∫ x(t ) e − s t dt , x(t ) =
−∞
I.4.
∞
∫ x(s )e
−∞
st
ds . Par transformado de Laplace
Función y matriz de transferencia (FDT, MDT)
La función de transferencia de un sistema lineal e invariante en el tiempo (SLIT) se
define como la transformada de Laplace de la salida dividida entre la transformada de
Laplace en la entrada con condiciones iniciales nulas, o sea:
x(t)
h(t)
H(s)
(SLIT)
x(S)
H (s ) =
y(t)
y(s)
Y (s )
; C.I = 0
X (s )
Para el caso de linealidad
Ts[x1 (t ) + x 2 (t )] = Ts[x1 (t )] + Ts[x 2 (t )]
Invariancia
Ts[x(t − t 0 )] = y (t − t 0 )
M.C Laura Jiménez Beristáin
Pag. 8
UABC
CONTROL I
y(t)
x(t)
t
t
y(t-to)
x(t-to)
t0
t
t0
t
Si x(t) = δ(t) ⇒ X(s) = 1
∴ H(s) = Y(s)
L−1 [H (s )] = h(t ) = y (t ) , donde h(t)= Respuesta al impulso.
Para un sistema MIMO:
G11
X1(s)
+
Y1(s)
+
G12
G21
+
Y2(s)
+
X2(s)
G22
Y(s) = G(s) X(s)
Y1 (s ) G11
Y (s ) = G
 2   12
G21   X 1 (s )
G22   X 2 (s )
Donde: G(s), es la matriz de transferencia del sistema MIMO.
M.C Laura Jiménez Beristáin
Pag. 9
UABC
I.5.
CONTROL I
Convolución lineal y sus propiedades.
x(t)
y(t)
h(t)
SLIT
Integral de convolución: y (t ) = h(t ) * x(t ) ó y (t ) = ∫ h(τ )x(t − τ ) dτ
t
0
Nota: Los límites de la integración se aplica para sistemas causales y el símbolo *,
representa a la convolución lineal.
Sistema Causal. En un sistema causal su respuesta al impulso es h(t) = 0 ; t<0
δ(t)
h(t)
t
Sistema no causal. En un sistema no causal su respuesta al impulso es h(t) ≠ 0 para t<=0
δ(t)
t
Propiedades de la convolución (*)
h(t)
t
1. f * g = g * f
2. L[ f * g ] = F (s ) G (s )
3. f * δ = f
4. f * δ (t − t 0 ) = (t − t 0 )
d
( f * g ) = f& * g = g& * f
5.
dt
6. f * ( g1 + g 2 ) = f * g1 + f * g 2
Ejemplo: Obtener la convolución x1(t)*x2(t), si las funciones son:
M.C Laura Jiménez Beristáin
Pag. 10
UABC
CONTROL I
x1(t)
X2(t)
2
2
1
1
t
2
2
t
x1 (t ) = 2u 0 (t ) − u 0 (t − 1) − u 0 (t − 2 ) ,
x 2 (t ) = 2u 0 (t ) − 2u 0 (t − 2)
Sus respectivas transformada de la Laplace son:
1
2
X 1 (s ) = 2 − e − s + e − 2 s , X 2 (s ) = 1 − e − 2 s
s
s
Empleando la propiedad 2:
L[x1 * x 2 ] = X 1 (s ) X 2 (s )
2
X 1 (s ) X 2 (s ) = 2 2 − e − s − 3e − 2 s + e −3s + e − 4 s
s
Por lo tanto, el resultado de convolucionar a x1(t)*x2(t) es:
x1 (t ) * x 2 (t ) = 4tu 0 (t ) − 2(t − 1)u 0 (t − 1) − 6(t − 2)u 0 (t − 2) + 2(t − 3)u 0 (t − 3) + 2(t − 4)u 0 (t − 4)
[ (
)]
[
]
[
]
Otra forma de resolver la convolución es descomponiendo a x2(t) en funciones
singulares:
x2(t)
X'2(t)
2
2
1
2
2
-2
x 2 (t ) = 2u 0 (t ) − 2u 0 (t − 2)
Empleando la propiedad 5:
d
(x1 * x2 ) = x1 * x& 2 = x& 2 * x1
dt
4
x' 2 (t ) = 2δ (t ) − 2δ (t − 2 )
⇒
d
dt
[x 1 (t )* x 2 (t )]
t
1
2
3
4
-2
M.C Laura Jiménez Beristáin
Pag. 11
UABC
CONTROL I
Para obtener a x1(t) * x2(t) se realiza el proceso de integración en la gráfica anterior:
x1 (t )* x2 (t )
6
4
2
1
2
3
4
t
Sea el siguiente sistema:
uo(t)
y(t)
h(t)
H(s)
La respuesta al escalón del siguiente sistema es:
Y (s ) Y (s )
H (s ) =
=
= s Y (s )
1
X (s )
s
d
Antitransformando: h(t ) = y (t )
dt
Se demuestra que la derivada de la respuesta al escalón unitario es h(t).
En la reducción de sistemas conectados en paralelo o en serie se procede de la siguiente
forma:
h1 (n )
Paralelo
N
h2 (n )
h(n ) = ∑ hi (n )
i =1
hN (n )
Serie
h2 (n )
M.C Laura Jiménez Beristáin
...
hN (n )
N
h(n ) = Π hi (n )
i =1
Pag. 12
UABC
I.6.
CONTROL I
Fórmula canónica de la realimentación.
X
+
E
G
Y
H
E = X − HY K1
Y = GE
K2
Sustituyendo la ecuación 1 en la ecuación 2:
Y = G ( X − HY )
Y = GX − GHY
Y (1 + GH ) = GX
Y
G
=
... Sistema SISO.
Por lo tanto
X 1 + GH
El signo positivo de GH representa a la realimentación negativa.
Para el sistema MIMO
X
E
Y
G
H
Y
G
=
X I + GH
−1
Y = (I + GH ) GX
La realimentación negativa (características):
1. Linealiza
2. Aumenta la relación señal- ruido.
3. Desensitiviza con respecto a la variación de parámetros de la planta
4. Aumenta el ancho de Banda.
I.7.
El sistema de segundo orden.
Sistemas de Primer Orden:
1
Sea G (s ) =
y x(t ) = u 0 (t ) , obtener a y (t).
τs + 1
M.C Laura Jiménez Beristáin
Pag. 13
UABC
Y (s ) =
CONTROL I
1
A
B
= +
s (τs + 1) s τs + 1
A = Y (s ) ⋅ s
Y (s ) =
s =0
= 1 ; B = Y (s ) ⋅ (τs + 1)
s= −
1
= −τ
τ
τ
1
−
s τs + 1
y (t ) = u 0 (t ) − e
−
t
τ
u 0 (t )
t
−

τ

(
)
=
−
y
t
1
e
Por lo que su respuesta al escalón será:


1
Pendiente inicial =

u 0 (t )


τ
τ
Tiempo
τ
2τ
3τ
4τ
5τ
t
y(t)
0.632
0.865
0.95
0.982
0.993
t
1 −
d
Y su respuesta al impulso:
y (t ) = h(t ) = e τ u 0 (t )
τ
dt
Sistemas de 2do. Orden.
ωn
Y (s )
= 2
G (s ) =
X (s ) s + 2ζω n s + ω n 2
donde ; ζ= relación de amortiguamiento,
ω n = frecuencia natural.
2
Empleando la fórmula General para obtener las raíces de la ecuación característica:
2
s 2 + 2ζω n s + ω n = 0
M.C Laura Jiménez Beristáin
Pag. 14
UABC
s=
CONTROL I
− 2ζ ω n ± 4ζ 2ω n2 − 4ω n2
2
s = −ω n ζ ± jω n 1 − ζ 2 = −σ ± jω d
Ubicación de las raíces de la ecuación característica en el plano s:
jω
jω d
ωn
Plano s
− σ = −ςωn
σ
θ
− jω d
donde:
θ = sen −1 1 − ς 2 = cos −1 ς = tan −1
1−ς 2
ς
Se observa que cuando: ζ = 0; No amortiguado
0 < ζ < 1; Subamortiguado
ζ = 1; Críticamente amortiguada.
ζ > 1; Sobreamortiguado.
Si x(t ) = u 0 (t ) , su respuesta al escalón del sistema de segundo orden será:
Y (s ) =
ω n2
s (s 2 + 2ζω n s + ω n2 )
Antitransformando para cada caso:
M.C Laura Jiménez Beristáin
Pag. 15
UABC
CONTROL I
1.Caso no amortiguado ζ=0; c(t)=1-cos(ωnt)
2.Caso subamortiguado 0 < ζ < 1;
y (t ) = 1 −
e −ςω nt
1−ζ
2
(
sen ω n 1 − ζ 2 t + θ
)
o bien:
c(t ) = 1 − ae − ot sin( wd t + ϕ )
3.Caso críticamente amortiguado
M.C Laura Jiménez Beristáin
ζ = 1; c(t ) = 1 − e −σt [1 + ω n t ]
Pag. 16
UABC
CONTROL I
 e −σ 2t e −σ 1t 
4.Caso sobreamortiguado ζ > 1; c(t ) = 1 − b 
−

σ1 
 σ2
En la respuesta al escalón de un sistema subamortiguado se encuentran los siguientes
parámetros:
S te p R e s p o n s e
F rom : U (1)
1 .4
1 .2
0 .8
T o: Y(1)
Amplitude
1
0 .6
0 .4
0 .2
0
0
3
6
9
12
15
18
T im e ( s e c . )
Mp =e
Ta =
Tp =
−
3
ζω n
πζ
1−ζ 2
=
Máximo sobreimpulso o sobrepico
3
Tiempo de Asentamiento (±5%)
σ
π
=
π
ωd
ωn 1 − ζ
π −θ
π −θ
Tl =
=
2
ωd
ωn 1 − ζ
2
Tiempo pico
Tiempo de levantamiento o elevamiento
Ejercicio : Obtener Mp, ta, tp, y tl de G (s ) =
9
s + 2s + 9
2
1
3
Mp=0.33=33% , ta = 3 seg, tp= 1.11 seg, θ = 1.23 rad.=70.528o , tl= 0.676 seg
ωn2= 9, ωn = 3, 2ζωn = 2 , ζ =
M.C Laura Jiménez Beristáin
Pag. 17
UABC
I.8.
CONTROL I
Estabilidad de sistemas realimentados (Criterio de Routh y Lugar Geométrico
Positivo).
Un sistema de control es estable si a entradas acotadas proporciona salidas acotadas, o
sea:
x(t)
y(t)
h(t)
x(t) < M < ∞
Ó también
⇒ y(t)< N < ∞
∞
∫ h(t ) dt < ∞
−∞
La estabilidad se relaciona con la localización de los polos del polinomio característico
del sistema, es decir:
jω
H1 (s ) =
K1
s+a
jω
Estable
h1 (t ) = K1e − at
σ
-a
H 2 (s ) =
K1
s−a
Inestable
h2 (t ) = K 2 e at
a
σ
NOTA: Si las raíces están en el eje vertical; el sistema será críticamente estable.
Conclusión: Un sistema es estable si todos sus polos están en la parte izquierda del plano
complejo s.
•
Criterio de Hurwitz.
Una condición necesaria pero no suficiente para que un sistema sea estable, es que los
coeficientes de su polinomio característico sean todos del mismo signo y diferentes de
cero.
Ejemplos :
s+2
s − 2s 2 + s + 8
1
H 2 (s ) = 4
s + 3s 2 + s + 1
s −1
H 3 (s ) = 3
s + 2s 2 + s + 8
H 1 (s ) =
inestable
3
inestable. Falta s3 en el polinomio característico.
Se supone estable
M.C Laura Jiménez Beristáin
Pag. 18
UABC
•
CONTROL I
Criterio de Routh
El número de raíces en la parte derecha del plano complejo es igual al número de cambio
de signos en la primera columna del arreglo de Routh.
P(s ) = p n s n + p n −1 s n −1 + p n − 2 s n − 2 + L p 0
sn
s n −1
s n−2
L
s0
pn
p n −1
d1
L
c
p n−2
p n −3
d2
pn−4
p n −5
donde:
p p − p n p n −3
d1 = n −1 n − 2
p n −1
p p − p n p n −5
, etc.
d 2 = n −1 n − 4
p n −1
Ejemplo : Aplicar el criterio de Routh a P(s ) = s 3 + 2s 2 + s + 8 .
s3
s2
s1
s0
1 1
2 8
−3
8
Tiene 2 raíces en el semiplano derecho
LUGAR GEOMETRICO POSITIVO (LGP)
Es un representación gráfica de la posición de las raíces del sistema en malla cerrada al
variar K de 0 a infinito.
X
+
E
G
Y
K
q (s )
p(s )
Y (s )
G (s )
Q (s )
=
=
X (s ) 1 + KG (s ) P(s ) + KQ (s )
Sea G (s ) =
M.C Laura Jiménez Beristáin
Pag. 19
UABC
CONTROL I
El polinomio característico es: P(s ) + KQ (s ) = 0
P (s )
= −K
Q (s )
1
1
, ∠
= 180 o + n360 o
K =
G (s )
G (s )
Reglas para trazar el LGP
1. El LGP empieza en los polos para K = 0 y termina en los ceros cuando K → ∞ .
Si K= 0; tendremos p(s) el cual es un polo
Si K= ∞; tendremos q(s) el cual es un cero
2. Los puntos sobre el eje real que pertenecen al LGP tienen un número non de
singularidades (polos y ceros) a la derecha.
3. Si n es el grado del numerador y m es el grado del denominador, el LGP tiene
m-n asíntotas para K → ∞ a las rectas que forman ángulos con el eje real dadas
180 o (2 l + 1)
por θ =
; l = 0,1,2,3K m − n − 1 y se cruzan en un punto llamado
m−n
∑ polos − ∑ ceros .
centroide dado por σ 0 =
m−n
4. El ángulo de partida de un polo complejo es:
θ p = 180 o − ∑ angulos otros polos + ∑ angulos ceros
Y el ángulo de llegada a un cero complejo es:
θ a = 180 o + ∑ angulos polos + ∑ angulos otros ceros
(Los ángulos se miden en sentido antihorario)
5. Los puntos del LGP con raíces múltiples llamados puntos silla cumplen la
d
siguiente relación:
G (s ) s =s0 = 0 .
ds
6. El cruce del LGP con el eje imaginario se obtiene con el criterio de Routh de
1 + KG (s ) = 0 (polinomio característico)
1
7. Para un punto s=s0 sobre el LGP, el valor K esta dado por K =
.
G (s 0 )
Ejemplo 1: Trazar el LGP de G (s ) =
1
(s + 1)(s + 2)(s + 3)
Pasos 1 y 2:
Polos:
Ceros: (Ninguno)
s1 = -1,
s2 = -2,
s3 = -3
M.C Laura Jiménez Beristáin
Pag. 20
UABC
CONTROL I
2.5
2
1.5
1
Imag Axis
0.5
0
-0.5
-1
-1.5
-2
-2.5
-4
-3
-2
-1
Real Axis
0
1
2
Paso 3:
n = 0, m = 3 , m-n = 3 asíntotas a las rectas que forman ángulos con el eje real dado por:
180 o (2(0) + 1)
= 60 o
3
180 o (2(1) + 1)
θ1 =
= 180 o
3
o
180 (2(2 ) + 1)
θ2 =
= 300 o
3
Las asíntotas se cruzan en un punto llamado centroide:
−1− 2 − 3 − 0
σ0 =
= −2
3
Paso 4: Como no tenemos polos complejos nos brincamos punto 5.
d
Paso 5: Para determinar los puntos de ruptura, se aplica
G (s ) s =s0 = 0
ds
d
1
− (3s 2 + 12 s + 11)
d
G (s ) =
=
=0
ds s 3 + 6 s 2 + 11s + 6 (s 3 + 6 s 2 + 11s + 6 )2
ds
θ0 =
Se buscan las raíces del numerador para satisfacer a la condición.
3s 2 + 12s + 11 = 0
s1= -1.42 ; s2 = -2.58
Paso 6: El cruce del LGP con el eje imaginario se obtiene aplicando el criterio de Routh.
1 + KG (s ) = 0
1


3
2
1+ K 3
 = s + 6s + 11s + 6 + K = 0
2
 s + 6s + 11s + 6 
M.C Laura Jiménez Beristáin
Pag. 21
UABC
s3
s
2
s1
s0
CONTROL I
1
11
6
6+k
66 − (6 + k )
0
6
6+k
66-6-K=0, K= 60
6s2+66=0, s = ± j 11 , indica el cruce con el eje vertical.
Paso 7: Para un punto s 0 = −4 sobre el LGP, el valor de K está dado por: K =
1
G (s 0 )
Evaluando cuando s 0 = −4 , K = s 0 + 1 s 0 + 2 s 0 + 3 = (3)(2 )(1) , K = 6 estable
(
s + 2 )(s 2 + 4s + 8)
Ejemplo 2: Trazar el LGP de G (s ) =
(s + 3)(s 2 + 1)(s 2 + 2s + 5)
G (s ) =
(s + 2)(s + 2 + j 2)(s + 2 − j 2)
(s + 3)(s 2 + 1)(s + 1 + j 2)(s + 1 − j 2)
Pasos 1 y 2:
Polos:
s1 = -3,
s2 = +j,
s3 = -j,
s4 = -1+2j,
s5 = -1-2j,
Ceros: (Ninguno)
s1 = -2,
s2 = -2+2j,
s3 = -2-2j,
Paso 3:
n=3, m=5, m-n=2 asíntotas, l=0,1
M.C Laura Jiménez Beristáin
Pag. 22
UABC
CONTROL I
180 o (2(0) + 1)
= 90 o
2
o
180 (2(1) + 1)
θ1 =
= 270 o
2
−5+6
σ0 =
= 0.5
2
Paso 4: Para determinar los ángulos de partida de los polos complejos:
θ0 =
∑ ∠otros polos = 135 + 108.44 + 90 + 45 = 378.44
∑ ∠ceros = 75.96 + 63.44 + 0 = 139.4
θ = 180 − ∑ ∠otros polos + ∑ ∠ceros = 180 − 378.44
o
o
p
o
o
o
o
o
o
o
o
o
o
+ 139.4 o = −59.04 o
Para determinar los ángulos de llegada de los ceros complejos:
∑ ∠ polos = 180 + 153.44 + 123.69 + 104.03
∑ ∠otros ceros = 90 + 90 = 180
θ = 180 + ∑ ∠polos − ∑ ∠otros ceros = 180
o
o
o
a
o
o
o
+ 63.43o = 624.59 o
o
+ 624.59 o − 180 o = 624.59 o = 264.59 o
o
o
Paso 5,6,7: No son necesarios, se puede observar en el LGP que el sistema es inestable.
Polos:
s+2
s (s + 1)(s + 8)
Ceros:
s1 = 0,
s1 = -2
Ejemplo 3: Trazar el LGP de G (s ) =
Paso 1 y 2:
s2 = -1;
s3 = -8
M.C Laura Jiménez Beristáin
Pag. 23
UABC
CONTROL I
Paso 3:
n=1, m=3, m-n=2 asíntotas.
θ0 =
180 o
= 90 o , θ 1 = 270 o
2
σ0 =
0 −1− 8 + 2 − 7
=
= −3.5
2
2
Paso 4: No se aplica porque no hay polos complejos y conjugados.
Paso 5: Se determinan los puntos de ruptura:
(
)
d
s 3 + 9 s 2 + 8s − 3s 2 + 18s + 8 (s + 2 )
=0
G (s ) =
2
ds
s 3 + 9 s 2 + 8s
(
)
2s 3 + 15s 2 + 36 s + 16 = 0
s1 = -3.4654+j1.4304,
s2 = -3.4654-j1.4304,
s3 = -0.5692
Paso 6: Para determinar el cruce con el eje vertical: 1+KG=0
s 3 + 9 s 2 + 8s + Ks + 2 K = 0
s3
s2
s1
s0
72+7K=0, K = −
I.9.
1
9
72 + 9 K − 2 K
9
2K
8+ K
2K
0
72
∴No hay cruce con el eje imaginario ya que K es negativa.
7
Diagramas de Bode.
X(s)
Y(s)
G(s)
Haciendo s = jω
G(jω) = A(ω) + jB(ω), donde: A(ω) = Re G(jω) y B(ω) = Im G(jω).
Algunas de las trazas más comunes empleando la frecuencia son:
M.C Laura Jiménez Beristáin
Pag. 24
UABC
CONTROL I
B(ω )
G ( jω )
G ( jω )
ω1
ω1
ω2
ω2
ω
φ
A(ω )
Traza Polar o
Traza de Nyquist
φ
Diagrama de Bode
ω
Traza de Nychols
En los diagramas de Bode, se obtiene información de la variación de la magnitud y fase
con respecto a la frecuencia.
Si G(s) = G1(s) G2(s)…GN(s) entonces al hacer a s = jω :
G ( jω ) = G1 G2 K G N ∠φ1 ∠φ 2 K ∠φ N
Utilizando logaritmos para convertir a decibeles, los productos se convierten en sumas,
esto en el caso de la magnitud. Sin embargo en la fase se realiza una suma algebraica,
donde los productos se suman y en la división se restan.
El primer paso que debe realizarse es normalizar a los factores involucrados en la FDT,
por lo que los posibles factores que pueden presentarse son:
o Constante K
1
o Polos m y ceros s m en el origen
s
s
1
o Polos
y ceros 1 + reales
s
z
1+
p
1
o Polos
1+
2ς
ωn
s+
s2
y ceros 1 +
2ς
ωn
ω n2
s+
s2
ω n2
complejos
Ejercicio: Trazar el diagrama de Bode de las siguientes FDT’S
1.- G (s ) =
200s
s + 10s + 100
2
Se procede a normalizar a G(s): G (s ) =
200 s

1
s 

1001 + s +
100 
 10
K = 2, 20log2 = 6dB ganancia, ωn=10 rad/seg., ζ= 0.5
M.C Laura Jiménez Beristáin
2
2s
=
1+
s2
1
s+
10
(10)2
Pag. 25
UABC
CONTROL I
B ode Diagram s
From: U(1)
20
0
-10
-20
100
50
To: Y (1)
P hase (deg); M agnitude (dB )
10
0
-50
-100
10 -1
10 0
10 1
10 2
Frequency (rad/sec)
2.- G (s ) =
1000s (s + 6)
(s + 20)(s + 30)
s
s


10 s1 + 
1000 ∗ 6 s1 + 
 6
 6
Se normalizar a G(s): G (s ) =
=
s 
s  
s 
s 

20 ∗ 301 + 1 +  1 + 1 + 
 20  30   20  30 
K=10, 20log10 = 20dB
B ode Diagram s
From: U(1)
60
20
0
150
100
To: Y (1)
P has e (deg); M agnitude (dB )
40
50
0
10 -1
10 0
10 1
10 2
10 3
Frequency (rad/sec)
M.C Laura Jiménez Beristáin
Pag. 26
UABC
CONTROL I
3.- Dada la magnitud H
H
dB
obtener su FDT del siguiente diagrama de Bode .
dB
40
20
10 −1
10 0
101
10 2
10 3
s 
s 

101 + 1 +

10  10000 

−1 20
20dB ⇒ K = log
= 10, H (s ) =
2
20
s 
s 


1 +
1 +
 100  1000 
I.10. Representación de la función de transferencia (FDT).
1 −1 3 − 2
s + s
s+3
2
2
=
Ejemplo 1: H (s ) = 2
2 s + 8s + 5 1 + 4s −1 + 5 s − 2
2
Y (s )
Sabemos que H (s ) =
X (s )
Y (s ) Y (s ) U (s )
H (s ) =
=
∗
X (s ) U (s ) X (s )
1 −1 3 − 2 Y (s )
s + s =
2
2
U (s )
X(s)
 1 −1 3 − 2 
Y (s ) =  s + s U (s )
2

2
1
5
1 + 4s + s −2
2
−1
U (s )
=
X (s )
5 −2
s U (s )
2
5
U (s ) = X (s ) − 4s −1U (s ) − s − 2U (s )
2
X (s ) = U (s ) + 4s −1U (s ) +
M.C Laura Jiménez Beristáin
ω
10 4
2
1
2
U(s) s-1
s-1
3
2
-4
-5
2
Y(s)
Diagrama de lazo
-5/2
Pag. 27
UABC
CONTROL I
1 −1
s + s −2 + 2s −4
s + 2s + 4
2
Ejemplo 2: H (s ) = 4
=
2 s − 6 s 3 + 2 s 2 + 3s + 8 1 − 3s −1 + s − 2 + 3 s −3 + 4s − 4
2
Diagrama de Lazo.
1
2
3
2
1
U(s)
X(s)
s-1
s-1
s-1
s-1
Y(s)
2
3
-1
-3
2
-4
I.11.
Variables de estado, solución de las ecuación de estado, relación de la FDT con la
ecuación de estado.
Acciones básicas de control
n2 (t)
r(t)
u(t)
e(t)
+
n1(t)
Controlador
Planta
y(t)
-
Sensores
donde:
n1(t) = ruido de observación
n2(t) = ruido parámetros de la planta
r(t) = referencia o set point
u(t) = ley de control
En la ley de control en un controlador Proporcional-Integral-Derivativo se representa por:
t
d
u (t ) = K P e(t ) + K I ∫ e(t )dt + K D e(t )
0
dt
Análisis de sistemas de control en variables de estado.
En el Control Clásico se determina a u(t) con: Root Locus (LGP) o Respuesta a la
frecuencia.
M.C Laura Jiménez Beristáin
Pag. 28
UABC
CONTROL I
El Control Moderno inicia en 1960 con la introducción del concepto de espacio de
estados (state space).
Variables de estado: Son un conjunto mínimo de variables X1(t), X2(t)…,Xn(t) tal que
su conocimiento en t = to y la entrada para t≥t0, caracterizan el comportamiento del
sistema para t≥t0.
Ejemplo: Dado el siguiente sistema, representarlo en variables de estado.
Sistema
Planta
Proceso
u(t)
U(s)
y(t)
Y(s)
d3
d2
y
−
2
y − 6 y = 3u (t )
dt 3
dt 2
3 y ' ' '−2 y ' '−6 y = 3u
3
x1 = y
.
x2 = y
..
x3 = y
.
x&1 = y = x 2
.
..
.
...
x 2 = y = x3
x3 = y = u +
2
x3 + 2 x1
3
Diagrama de lazo
.
x = Ax + Bu
y = Cx
x& 3
 .  
 x. 1  0 1
 x 2  = 0 0
 .  
 x3  2 0
  
x3
X(s) s-1
U(s)

0   x1  0
1   x 2  + 0 u
2
  x3  1
3
2
3
x& 2
s-1
x2
s-1
x1
1
x&1 3
2
2
 x1 
y = [1 0 0]  x 2 
 x3 
En general, un sistema se puede representar como:
M.C Laura Jiménez Beristáin
Pag. 29
Y(s)
UABC
CONTROL I
A
U
∫
∑
B
C
x = Ax + Bu
y = Cx + Du
donde: x = Vector de estado
A = Matriz del sistema
B = Matriz de entrada
C = Matriz de salida
Y
x
x
.
∑
D
La representación anterior se generaliza para sistemas MIMO.
A un sistema coordenado n dimensional donde las coordenadas son las variables de
estado se le llama “espacio de estados”.
Solución de la ecuación de estado.
.
x = Ax + Bu
Aplicando la transformada de Laplace en ambos miembros:
sx(s ) − x(0) = Ax(s ) + Bu (s ) K ec.1
X (s )[sI − A] = X (0 ) + Bu (s )
X (s ) = (sI − A) X (0) + (sI − A) Bu (s )
Antitransformando:
−1
−1
x(t ) = L−1 (sI − A) X (0) + L−1 (sI − A) Bu (s )
−1
−1
[
]
[
]
x(t ) = e At x(0 ) + ∫ e A(t −τ ) Bu (τ )dτ
t
0
[
]
donde: Φ (t ) = e = L−1 (sI − A) . Matriz exponencial o de transición.
La inversa de la ecuación de transición Φ (− t ) = e − At cumple con la siguiente condición:
Φ (t )Φ (− t ) = e At e − At = e 0 = I
At
−1
Obtención de la función de transferencia dada la representación en variables de estados.
De la ecuación 1, se aplican las condiciones iniciales CI = 0 para obtener a su FDT:
sx(s ) = Ax(s ) + Bu (s ) K ec.2
y (s ) = Cx(s ) + Du (s ) K ec.3
De la ecuación 2;
−1
x(s ) = (sI − A) Bu (s )
K ec.4
Sustituyendo la ecuación 4 en la ecuación 3;
−1
y (s ) = C (sI − A) Bu (s ) + Du (s )
y (s )
−1
H (s ) =
= C (sI − A) B + D
u (s )
M.C Laura Jiménez Beristáin
Pag. 30
UABC
CONTROL I
Q (s )
sI − A
Donde los polos de H(s) son los eigenvalores de la matriz A.
En general. H (s ) =
Ejemplo: Obtener los valores de alfa para determinar el rango de estabilidad del siguiente
sistema.
 .   − 1 α   x  0 
1
 x. 1  = 

 +  u

 x 2  − 1 − 5  x 2  1
x 
y = [1 − 1]  1 
 x2 
1 0   − 1 α  s + 1 − α
sI − A = s 
=
−
= s 2 + 6s + 5 + α . Polinomio característico


s+5
1
0 1 − 1 − 5
s2
s1
s0
1
6
5 +α
5 +α
0
(30 + 6α) / 6 = 5 + α, 5 + α = 0
α = -5, el rango de variación de α es -5<α<∞ para que sea estable.
M.C Laura Jiménez Beristáin
Pag. 31