Document
Anuncio

Comunicaciones II
Tema 3
Transmisión digital PAM a través de canales AWGN limitados en banda
Javier Rodríguez Fonollosa y Margarita Cabrera Beán
Indice del Tema 3
Transmisión digital PAM a través de canales AWGN
limitados en banda
• 3.1 Autocorrelación y densidad espectral de potencia
– Introducción
– Cálculo de momentos de coeficientes del espacio de la señal
– Momentos para el caso L>1: notación matricial
– Ejemplos de cálculos de momentos con modulaciones PM
– Potencia media y densidad espectral de potencia
– Ejemplos de densidades espectrales para L=1
– Ejemplo de modulaciones con memoria
– Ejemplos de densidades espectrales para L=2
• 3.2 Interferencia inter-simbólica: ISI
– Introducción: Canal Ideal
– Caso de canal no ideal con L=1
09/10/2006
COM II
T3-2
1
Indice del Tema 3
Transmisión digital PAM a través de canales AWGN
limitados en banda
– Caso de canal no ideal con L>1
– Formulación del criterio MAP en presencia de ISI
• 3.3 Pulsos de Nyquist
– Introducción
– Diseño de pulsos para L=1
– Pulsos de coseno realzado
– Diseño de pulsos para L>1
• 3.4 Ecualización
– Introducción
– Ecualización Discreta: Forzador de ceros
– Ecualización Discreta: Criterio MSE
– Ejemplo de ecualización
• 3.5 Filtros terminales Óptimos
09/10/2006
T3-3
COM II
3.1 Autocorrelación y densidad espectral de potencia
Introducción
• En este tema se considerará estudiará el efecto de la limitación en
banda sobre las señales moduladas digitalmente. Para ello se estudiará
en primer lugar el ancho de banda requerido por estas modulaciones en
base a su densidad espectral de potencia.
• Se partirá de la definición de la señal modulada:
s (t ) =
+∞
∑s
n =−∞
m[ n ]
(t − nT ) =
+∞
+∞
L
L
∑ ∑ α [ n]ϕ (t − nT ) = ∑ ∑ α [ n]ϕ (t − nT )
n =−∞ l =1
ml
l
n =−∞ l =1
l
l
• Las las funciones que forman la base en el espacio de la señal son
deterministas de forma que el carácter aleatorio reside en qué símbolo,
de entre los M posibles, ha sido transmitido en cada periodo de
símbolo nT.
• Cada posible símbolo transmitido sm admite una representación en el
espacio de la señal mediante sus coeficientes α ml
• Estos coeficientes forman vectores aleatorios.
09/10/2006
COM II
T3-4
2
Cálculo de momentos de coeficientes del espacio de la señal
• Consideraremos que la secuencia de bits de entrada es estacionaria (su
función densidad de probabilidad no cambia con el tiempo) y que el
proceso de asignación de símbolos a partir de bits también lo es. De
esta forma los símbolos ( y por tanto el vector de sus coeficientes)
serán procesos discretos estacionarios.
• Los momentos de primer y segundo orden resultan:
μα [ n ] = E ⎣⎡α l [ n ]⎦⎤ = μα
l
l
Rαlα j [ n + k , n ] = E ⎡⎣α l [ n + k ]α j [ n ]⎤⎦ = Rαlα j [ k ]
• La función de covarianza se obtiene a partir de los anteriores como:
)(
(
)
Cαlα j [ k ] = E ⎡ α l [ n + k ] − μαl α j [ n ] − μα j ⎤
⎣
⎦
Cαlα j [ k ] = Rαlα j [ k ] − μαl μα j
09/10/2006
T3-5
COM II
Cálculo de momentos de coeficientes del espacio de la señal
(II)
• Cálculo de los momentos:
M
μα = E ⎡⎣α l [ n ]⎤⎦ = ∑ Pr {s m }α ml [ n ]
l
Rαlα j [ k ]
=
α l estacionarios
m =1
E ⎡⎣α l [ n + k ]α j [ n ]⎤⎦ =
∑ ∑ Pr {s
M
M
m[ n + k ]=1 m[ n ]=1
m[ n + k ]
, s m[ n ] }α ml [ n + k ]α mj [ n ]
• Cuando el mecanismo de asignación de bits a símbolos utilizado no
tiene memoria, los símbolos (y por tanto el vector de sus coeficientes)
son independientes entre si en instantes de tiempo distintos. De esta
forma:
Rαlα j [ k ] = E ⎡⎣α l [ n + k ]α j [ n ]⎤⎦ = E ⎡⎣α l [ n + k ]⎤⎦ E ⎡⎣α j [ n ]⎤⎦ = μαl μα j
; k≠0
Cαlα j [ k ] = Rαlα j [k ] − μαl μα j = 0 ; k ≠ 0
09/10/2006
COM II
T3-6
3
Cálculo de momentos de coeficientes del espacio de la señal
(III)
• Por tanto, en el caso sin memoria la covarianza de los símbolos resulta:
Cαlα j [ k ] = Rαlα j [ k ] − μαl μα j = ⎡ Rαlα j [0]δ [ k ] + μαl μα j (1 − δ [ k ]) ⎤ − μα l μα j =
⎣
⎦
(
)
= Rαl α j [0] − μαl μα j δ [ k ] = Cαl α j [ 0] δ [ k ]
09/10/2006
T3-7
COM II
Momentos para el caso L>1: notación matricial
• Cuando el espacio de la señal tiene dimensión L se define el vector de
medias (de dimensión L) y las matrices de correlación y covarianza (de
dimensión L × L
⎛ μα1 ⎞
⎜
⎟
μ = E [s m ] = ⎜
⎟
⎜ μα ⎟
⎝ L⎠
⎡ Rα1α1 [ k ]
Rα1αl [ k ] ⎤
⎢
⎥
T
R [ k ] = E ⎡⎣s m [n + k ]s m [n]⎤⎦ = ⎢
⎥
⎢ R [k ]
⎥
R
k
[
]
α
α
α
α
L L
⎣ L1
⎦
C [ k ] = E ⎡⎣s m [n + k ]sTm [n]⎤⎦ − μ [ n + k ] μ [ n ]
T
• En caso de modulaciones sin memoria en notación vectorial:
C [ k ] = ( R[0] − μμT ) δ [ k ] = C [ 0]δ [ k ]
09/10/2006
COM II
T3-8
4
Ejemplos de cálculos de momentos con modulaciones PM
• Ejemplos de modulaciones sin memoria con L=1: PAM
PAM:ϕ (t ) =
1
T
Π ( t −TT / 2 )
s1 = Eb =
– Modulaciones 2PAM
s 2 = − Eb = − d2
d
s2
l
L =1
Es = Eb = 14 d 2
α1
s1
μα = μα = E ⎣⎡α [ n ]⎦⎤
d
2
2
d d
⎛ d⎞
E [α ] = ∑ Pr {s m }α m = p ⎜ − ⎟ + (1 − p ) = (1 − 2 p)
Estacionario
2 2
⎝ 2⎠
m =1
=
2
2
d2
= Eb
Rαα [ 0] = E ⎡(α [ n ]) ⎤ = E ⎡⎣α 2 ⎤⎦ = ∑ Pr {s m }α 2 =
⎣
⎦ Estacionario
4
m =1
Cαα [ k ]
=
Sin memoria
Cαα [ 0] δ [ k ] = ( Rαα [ 0] − μα2 ) δ [ k ] =
09/10/2006
d2
(1 − (1 − 2 p)2 ) δ [ k ]
4
T3-9
COM II
Ejemplos de cálculos de momentos con modulaciones PM (II)
• Ejemplos de modulaciones sin memoria con L=1: PAM
PAM:ϕ (t ) =
1
T
Π ( t −TT / 2 )
– Modulaciones MPAM con símbolos equiprobables:
M
sm = ( 2 m −2M −1 ) d ; M = 2b ; Es = d 2 ∑ ( 2 m −21− M ) = M12−1 d 2
2
2
m =1
M
μα = E [α ] = ∑ Pr {s m }α m =
m =1
1
M
M
∑(
m =1
M
2 m − M −1
2
Rαα [ 0] = E ⎡⎣α 2 ⎤⎦ = ∑ Pr {s m }α 2 = Es =
m =1
Cαα [ k ] =
09/10/2006
M 2 −1
12
COM II
)d = 0
M 2 −1
12
d2
d 2δ [ k ]
T3-10
5
Ejemplos de cálculos de momentos con modulaciones PM
(III)
• Modulaciones sin memoria con L=2: 2PPM
2PPM:ϕ1 (t ) =
1
T /2
Π ( t −TT/ 2/ 4 ) ,ϕ2 (t ) =
y2
s2
Eb
d = 2 Eb
y1
Eb
Es = Eb = 12 d 2
1
T /2
Π ( t −T3T/ 2/ 4 ) ; L = 2
⎛ 0 ⎞
⎛ E ⎞
s1 = ⎜ b ⎟ ; s 2 = ⎜
⎜ E ⎟⎟
⎝ 0 ⎠
⎝ b⎠
s1
– Cálculo del vector media:
2
μ = E [s m ] = ∑ Pr {s m }s m =
m =1
09/10/2006
Eb ⎛ 1⎞
Eb
1 2
1 ⎛ Eb ⎞
sm = ⎜
1L
=
⎟=
∑
⎜
⎟
⎜
⎟
2 m =1
2 ⎝ Eb ⎠
2 ⎝ 1⎠
2
T3-11
COM II
Ejemplos de cálculos de momentos con modulaciones PM
(IV)
• Modulaciones sin memoria con L=2: 2PPM: Cálculo de la matriz de
covarianza
⎛ 0 ⎞
⎛ E ⎞
s1 = ⎜ b ⎟ ; s 2 = ⎜
⎜ E ⎟⎟
⎝ 0 ⎠
⎝ b⎠
μ=
1 2
1 ⎡⎛ E ⎞
s m sTm = ⎢⎜ b ⎟
∑
2 m =1
2 ⎢⎣⎝ 0 ⎠
E ⎛ 1 0 ⎞ Eb
IL
= b⎜
=
2 ⎝ 0 1 ⎟⎠ 2
R [ 0] = E ⎡⎣s m sTm ⎤⎦ =
C[0] = R[0] − μμT =
09/10/2006
COM II
(
Eb
Eb
2
1L
⎛ 0 ⎞
0 +⎜
0
⎜ E ⎟⎟
⎝ b ⎠
)
(
Eb
⎤
) ⎥⎥ =
⎦
Eb
E
I L − b 1L× L
2
4
T3-12
6
Potencia media y densidad espectral de potencia
• Empezaremos calculando la media estadística de la señal
transmitida:
⎡
+∞
L
μ s (t ) = E [ s(t ) ] = E ⎢ ∑
∑ α [ n ]ϕ
⎣ n =−∞ l =1
=
+∞
L
∑ ∑ E ⎡⎣α [ n]⎤⎦ ϕ
l
n =−∞ l =1
l
l
l
⎤
(t − nT ) ⎥ =
⎦
L
+∞
⎡
⎤
(t − nT ) = ∑ ⎢ μαl ∑ ϕ l (t − nT ) ⎥
l =1 ⎣
n =−∞
⎦
– La media es periódica de periodo T:
E [ s (t ) ] = E [ s (t + nT )]
el proceso s(t) es cicloestacionario en media
09/10/2006
T3-13
COM II
Potencia media y densidad espectral de potencia (II)
• A continuación se calcula la función de correlación de la señal
transmitida:
Rs (t + τ , t ) = E [ s (t + τ ) s (t ) ] =
⎡ +∞
E⎢ ∑
⎣ m =−∞
=
+∞
+∞
L
L
∑ α [ m]ϕ (t + τ − mT ) ∑ ∑ α [ n]ϕ
l
l
l =1
+∞
L
L
l =1
j =1
n =−∞
j =1
j
∑ ∑ ∑ ∑ Rα α [ m − n]ϕ (t + τ − mT )ϕ
m =−∞ n =−∞
l
l
j
j
j
⎤
(t − nT ) ⎥
⎦
(t − nT )
– Donde se ha tenido en cuenta que las coordenadas de los
símbolos son procesos discretos estacionarios. Tomando: k=m-n
resulta:
Rs (t + τ , t ) =
09/10/2006
+∞
L
+∞
L
∑ ∑ ∑ Rα α [ k ] ∑
k =−∞
l =1
j =1
l
j
n =−∞
COM II
ϕl (t + τ − (n + k )T )ϕ (t − nT )
j
T3-14
7
Potencia media y densidad espectral de potencia (III)
• Definiendo:
f (t ) =
+∞
∑ ϕ (t + τ − (n + k )T )ϕ
n =−∞
l
j
(t − nT ) = ϕl (t + τ − kT )ϕ j (t ) *
+∞
∑ δ (t − nT )
n =−∞
– Podemos observar que:
f (t ) = f (t − mT )
– Por tanto la función de autocorrelación también es periódica en t
con periodo T:
Rs (t + τ , t ) = Rs (t + mT + τ , t + mT )
– Lo que indica que la señal transmitida es cicloestacionaria en
correlación
09/10/2006
T3-15
COM II
Potencia media y densidad espectral de potencia (IV)
• Para proceder al cálculo de la densidad espectral, dado que s(t) es
cicloestacionario, utilizaremos el Teorema de Wiener-Khinchin [p.
179 Proakis-Salehi]. Como paso previo calculamos la media
temporal en un periodo de la función de autocorrelación:
1
1 +∞
Rˆ s (τ ) = ∫ Rs (t + τ , t )dt = ∑
TT
T k =−∞
L
L
l =1
j =1
∑ ∑ Rα α [ k ]∫ f (t )dt
l
j
T
• En el cálculo del promedio de la función f(t) se tendrá en cuenta que
se trata en un sumatorio infinito de integrales con periodos de
integración continuos y no solapados del mismo integrando:
∫
T
T
f (t )dt = ∫
+∞
∑ ϕ (t + τ − (n + k )T )ϕ
0 n =−∞
=
λ = t − nT
09/10/2006
l
+∞ (1− n )T
∑ ∫
n =−∞ − nT
j
(t − nT )dt =
ϕl (λ + τ − kT )ϕ (λ )d λ
COM II
j
T3-16
8
Potencia media y densidad espectral de potencia (V)
• Dado que el integrando en la expresión anterior no depende de n, se
obtiene:
∫
T
+∞
f (t )dt =
∫ ϕ (λ + τ − kT )ϕ
l
−∞
j
(λ ) d λ = Rϕlϕ j (τ − kT )
– Lo que nos permite expresar el promedio de la función de
correlación como:
1 +∞ L L
Rˆ s (τ ) = ∑ ∑∑ Rαlα j [ k ]Rϕlϕ j (τ − kT )
T k =−∞ l =1 j =1
– Puede observarse que la expresión resultante para la
autocorrelación promediada del proceso s(t), depende de las
correlaciones cruzadas entre las L secuencias de coordenadas
(procesos discretos) y de las correlaciones cruzadas entre las L
funciones de la base (señales deterministas de energía finita).
09/10/2006
T3-17
COM II
Potencia media y densidad espectral de potencia (VI)
• Una vez calculado el promedio de la función de correlación,
podemos calcular la potencia media:
T
1
1 +∞ L L
Ps = Rˆ s (0) = ∫ Rs (t , t )dt = ∑ ∑∑ Rαlα j [ k ]Rϕlϕ j [ − kT ] =
T0
T k =−∞ l =1 j =1
⎡
⎧l ≠ j ⎤
Es Eb
⎪
⎢
⎥ 1 L
R
kT
0
ó
−
=
[
]
⎨
ϕ
ϕ
⎢ l j
⎥ = T ∑ Rαlαl [ 0] = T = T
l =1
b
⎪
⎩k ≠ 0 ⎦⎥
⎣⎢
– En donde se ha utilizado:
M
M
L
Es = ∑ Pr {s m }Em = ∑ Pr {s m }∑ α ml 2 =
m =1
L
m =1
M
l =1
L
= ∑∑ Pr {s m }α ml 2 = ∑ Rαlαl [ 0]
l =1 m =1
09/10/2006
l =1
COM II
T3-18
9
Potencia media y densidad espectral de potencia (VII)
• El Teorema de Wiener-Khinchin establece que para un proceso
cicloestacionario la densidad espectral puede expresarse como la
Transformada de Fourier del promedio de la función de correlación:
+∞
Ss ( f ) =
∫
Rˆ s (τ )e − j 2π f τ dτ =
−∞
+∞
T
1
− j 2π f τ
∫−∞ T ∫0 Rs (t + τ , t )dt.e dτ
– Resultando:
+∞
Ss ( f ) =
+∞
L
L
1
Rα α [ k ]Rϕlϕ j (τ − kT )e − j 2π f τ dτ =
∑
∑∑
∫
T −∞ k =−∞ l =1 j =1 l j
∞
=
1 +∞ L L
∑ ∑∑ Rα α [ k ] ∫ Rϕlϕ j (τ − kT ) e− j 2π f τ dτ α =τ=− kT
T k =−∞ l =1 j =1 l j
−∞
=
1 +∞ L L
∑ ∑∑ Rα α [ k ]e− j 2π fkT ∫ Rϕlϕ j (α ) e− j 2π f α dα =
T k =−∞ l =1 j =1 l j
−∞
=
1 L L
∑∑ Sα α ( fT )Sϕlϕ j ( f )
T l =1 j =1 l j
∞
09/10/2006
T3-19
COM II
Potencia media y densidad espectral de potencia (VIII)
• Obteniendose la expresión:
Ss ( f ) =
1 L L
∑∑ Sϕ ϕ ( f ) Sαlα j ( fT )
T l =1 j =1 l j
– Las funciones de la base son deterministas:
Sϕlϕ j ( f ) = Φ l ( f )Φ*j ( f )
– Utilizando la expresión de las covarianzas de las secuencias de
coordenadas la densidad espectral resulta en la suma de dos
términos:
Deltas espectrales
Ss ( f ) =
1 +∞ L L
∑ ∑∑ Cα α [ k ] Φl ( f )Φ*j ( f ) exp ( − jk 2π fT ) +
T k =−∞ l =1 j =1 l j
+
09/10/2006
1
T2
L
+∞
L
∑∑ μα μα ∑ Φ (
l =1 j =1
l
COM II
j
k =−∞
l
k
T
)Φ*j ( Tk )δ ( f − Tk )
T3-20
10
Ejemplos de densidades espectrales para L=1
• Las expresiones calculadas anteriormente se simplifican en gran
medida en el caso L=1.
– La función de correlación de la señal transmitida resulta:
Rs (t + τ , t ) = E [ s (t + τ ) s (t ) ] =
=
+∞
+∞
∑ ∑ Rαα [ m − n]ϕ (t + τ − mT )ϕ (t − nT ) =
m =−∞ n =−∞
=
+∞
+∞
k =−∞
n =−∞
∑ Rαα [ k ] ∑ ϕ (t + τ − (n + k )T )ϕ (t − nT )
– Su correlación promediada:
1 +∞
Rˆ s (τ ) = ∑ Rαα [ k ] Rϕϕ (τ − kT )
T k =−∞
09/10/2006
T3-21
COM II
Ejemplos de densidades espectrales para L=1 (II)
– Realizando su Transformada de Fourier se obtiene la densidad
espectral de potencia:
Ss ( f ) =
1 +∞
2
Rα [ k ] Φ ( f ) exp ( − j 2π fkT )
∑
T k =−∞
– Expresada en función de la covarianza de los símbolos:
Ss ( f ) =
1 +∞
1
2
Cα [ k ] Φ ( f ) exp ( − j 2π fkT ) + 2 μα
∑
T k =−∞
T
09/10/2006
COM II
2
+∞
∑
k =−∞
Φ ( Tk ) δ ( f − Tk )
2
T3-22
11
Ejemplos de densidades espectrales para L=1 (III)
• Modulación 2PAM (bits equiprobables)
– Propiedades de la secuencia de coordenadas (Polar):
μα = 0 ; Rα [ k ] =
d2
4
δ [ k ] = Ebδ [ k ]
– Propiedades de la función base:
1
⎛ t −T / 2 ⎞
Π⎜
⎟
T ⎝ T ⎠
1 sen (π fT )
Φ( f ) =
exp ( − jπ fT ) = T sinc( fT ) exp ( − jπ fT )
πf
T
ϕ (t ) =
– En donde se ha definido:
sinc( x) =
09/10/2006
sen(π x)
πx
COM II
T3-23
Ejemplos de densidades espectrales para L=1 (IV)
• Modulación 2PAM (bits equiprobables)
– Su función de correlación promediada resulta:
E
1 +∞
Rˆ s (τ ) = ∑ Rαα [ k ] Rϕϕ (τ − kT ) = b Rϕϕ (τ )
T k =−∞
T
– Mientras que su densidad espectral:
S s ( f ) = Eb sinc2 ( fT ) = Eb sinc2 ( fTb )
09/10/2006
COM II
T3-24
12
Ejemplos de densidades espectrales para L=1 (V)
• Modulación 2PAM (bits equiprobables): Comparación con el caso
de utilizar pulsos con retorno a cero (RZ)
– En este caso su función base es:
ϕ RZ (t ) =
1
⎛ t −T / 4 ⎞
Π⎜
⎟ ; Φ RZ ( f ) = T / 2 sinc ( fT / 2 ) exp ( − jπ fT / 2 )
T /2 ⎝ T /2 ⎠
– Por lo que su densidad espectral resulta:
Ss ( f ) =
09/10/2006
Eb
sinc2 ( fTb / 2 )
2
T3-25
COM II
Ejemplos de densidades espectrales para L=1 (VI)
• Modulación 2PAM (bits equiprobables): Comparación entre NRZ y
RZ
1
0.9
Densidad espectral de potencia
0.8
NRZ
0.7
0.6
0.5
0.4
RZ
0.3
0.2
0.1
0
-4
09/10/2006
-3
-2
-1
0
fT II
COM
1
2
3
4
T3-26
13
Ejemplos de densidades espectrales para L=1 (VII)
• Modulación 2PAM Unipolar (bits equiprobables)
s1 = 2 Eb = d ; s 2 = 0 ; Es = Eb = 12 d 2
– Propiedades de la secuencia de coordenadas (Unipolar):
E
E
E
d
2
μα =
; Rα [ k ] = d4 δ [ k ] + μα2 = b δ [ k ] + b ; Cα [ k ] = b δ [ k ]
2
2
2
2
– Las función base pueden ser con o sin retorno a cero (NRZ, RZ):
ϕ NRZ (t ) =
ϕ RZ (t ) =
1
T
⎛ t −T / 2 ⎞
Π⎜
⎟ ; Φ NRZ ( f ) = T sinc( fT ) exp ( − jπ fT )
⎝ T ⎠
1
⎛ t −T / 4 ⎞
Π⎜
⎟ ; Φ RZ ( f ) = T / 2 sinc ( fT / 2 ) exp ( − jπ fT / 2 )
T /2 ⎝ T /2 ⎠
09/10/2006
T3-27
COM II
Ejemplos de densidades espectrales para L=1 (VIII)
• Modulación 2PAM Unipolar (bits equiprobables)
– Densidad espectral de potencia resulta:
NRZ : S s ( f ) =
Eb
2
sinc ( fT ) + T1
2
Eb 1 sen (π fT )
2 T
Tπ f
+∞
Eb
2
2
+∞
+ T12
Eb
2
∑
Tπ k /T
k =−∞
∑ sinc ( k ) δ ( f − ) =
2
k
T
k =−∞
2
sen (π k )
Eb
2
δ ( f − kr ) =
sinc 2 ( fT ) + T1
Eb
2
δ(f)
Delta
RZ : S s ( f ) =
Eb
4
(
T
Eb 1 sen π f 2
2 T
Tπ f
2
sinc 2 ( f
)
2
+ T12
+∞
Eb
2
+∞
T
2
∑
k =−∞
(
sen π k 12
)
2
T π k /T
2
) + T1 E4 ∑ sinc2 ( k2 ) δ ( f
b
k =−∞
δ ( f − Tk ) =
− Tk )
Secuencia de deltas (en el origen
y para valores impares de k)
09/10/2006
COM II
T3-28
14
Ejemplos de densidades espectrales para L=1 (IX)
• Modulación 2PAM Unipolar (bits equiprobables)
0.5
0.45
Densidad espectral de potencia
NRZ
0.4
0.35
0.3
0.25
0.2
RZ
0.15
0.1
0.05
0
-4
-3
-2
-1
0
1
2
3
4
fT II
COM
09/10/2006
T3-29
Ejemplos de modulaciones con memoria
PAM:ϕ (t ) = 1T Π ( t −TT / 2 )
• Modulaciones 2PAM Bipolar (L=1)
– Cuando el bit a transmitir es 0 entonces el símbolo también lo es.
Si el bit es 1 el símbolo es +d o -d de forma alternada (memoria):
2d
y1
s1 = 0 ; Pr {s1 } = 1/ 2
s 2 = d ; Pr {s 2 } = 1/ 4
s3
s1
s2
s3 = −d ; Pr {s3 } = 1/ 4
– Cálculo de la media
3
1
2
1
4
1
4
μα = ∑ Pr {s m }s m = 0 + d + (−d ) = 0
m =1
– Cálculo de la autocorrelación en el origen:
Rαα [ 0]
09/10/2006
=
α estacionarios
3
= ∑ Pr {s m }α m2 =
m =1
1 2 1 2 1 2 1 2
0 + d + d = d = Eb
2
4
4
2
COM II
T3-30
15
Ejemplos de modulaciones con memoria (II)
• Modulaciones 2PAM Bipolar (L=1)
– Cálculo de la autocorrelación de las coordenadas para k=1:
Rαα [1] = E ⎣⎡α [ n + 1]α [ n ]⎦⎤ =
3
∑
=
m[ n +1]=1
3
+
∑
m[ n +1] =1
+
m[ n +1]=1 m[ n ]=1
m[ n +1]
, s m[ n ] }α m [ n + 1]α m [ n ] =
Pr {s m[ n +1] , s 2[ n ] }α m [ n + 1]α 2 [ n ] +
m[ n +1] =1
09/10/2006
3
Pr {s m[ n +1] , s1[ n ] }α m [ n + 1]α1 [ n ] +
3
∑
∑ ∑ Pr {s
3
Pr {s m[ n +1] , s3[ n ] }α m [ n + 1]α 3 [ n ]
COM II
T3-31
Ejemplos de modulaciones con memoria (III)
• Desarrollando los sumatorios:
Rαα [1] =
= Pr {s1[ n +1] , s1[ n ] } 0 × 0 + Pr {s 2[ n +1] , s1[ n ] } d × 0 + Pr {s3[ n +1] , s1[ n ] } (− d ) × 0 +
+ Pr {s1[ n +1] , s 2[ n ] } 0 × d + Pr {s 2[ n +1] , s 2[ n ] } d × d + Pr {s3[ n +1] , s 2[ n ] } (− d ) × d +
+ Pr {s1[ n +1] , s3[ n ] } 0 × ( −d ) + Pr {s 2[ n +1] , s3[ n ] } d × (− d ) + Pr {s3[ n +1] , s3[ n ] } (− d ) × (− d ) =
= Pr {s3[ n +1] , s 2[ n ] } (−d 2 ) + Pr {s 2[ n +1] , s3[ n ] } (− d 2 ) =
• Cálculo de: Pr {s3[ n +1] , s 2[ n ] } , Pr {s 2[ n +1] , s3[ n ] }
Pr {s3[ n +1] , s 2[ n ] } = Pr {s 2[ n ] } Pr {s3[ n +1] | s 2[ n ] } =
1
11 1
=
Pr {b[n + 1] = 1} =
4
42 8
1
11 1
=
Pr {s 2[ n +1] , s3[ n ] } = Pr {s3[ n ] } Pr {s 2[ n +1] | s3[ n ] } = Pr {b[ n + 1] = 1} =
4
42 8
09/10/2006
COM II
T3-32
16
Ejemplos de modulaciones con memoria (IV)
• Resultando:
Rαα [1] = −
d2 d2
d2
1
−
=−
= − Eb
8
8
4
2
• Siguiendo un cálculo análogo se obtiene:
1
Rαα [ −1] = Rαα [1] = − Eb
2
• Puede demostrarse además:
Rαα [ k ] = 0 ;
09/10/2006
k >1
T3-33
COM II
Ejemplos de modulaciones con memoria (V)
• Densidad espectral de Modulaciones 2PAM Bipolar o AMI.
– Valores estadísticos de sus coordenadas:
⎧ d2 = Eb k = 0
⎪⎪ 2
μα = 0 ; Rαα [k ] = ⎨− d4 = − 12 Eb k = ±1
⎪
k >1
0
⎪⎩
2
– Utilizando la función base sin retorno a cero:
ϕ NRZ (t ) =
⎛ t −T / 2 ⎞
Π⎜
⎟ ; Φ NRZ ( f ) = T sinc( fT ) exp ( − jπ fT )
T ⎝ T ⎠
1
Ss ( f ) =
09/10/2006
1 +∞
2
Rα [ k ] Φ ( f ) exp ( − j 2π fkT )
∑
T k =−∞
COM II
T3-34
17
Ejemplos de modulaciones con memoria (VI)
• Densidad espectral de Modulaciones 2PAM Bipolar o AMI.
– Cálculo de la densidad espectral, utilizando la expresión de la
T3-22:
Ss ( f ) =
1 +∞
2
∑ Rα [ k ] Φ( f ) exp ( − j 2π fkT ) =
T k =−∞
1
1
⎞
⎛ 1
EbT sinc 2 ( fT ) ⎜ − exp ( − j 2π fT ) + 1 − exp ( j 2π fT ) ⎟
T
2
2
⎝
⎠
= Eb sinc 2 ( fT ) (1 − cos(2π fT ) ) = 2 Eb sinc 2 ( fT )sen 2 (π fT )
=
09/10/2006
T3-35
COM II
Ejemplos de modulaciones con memoria (VII)
• Densidad espectral de Modulaciones 2PAM Bipolar o AMI
1.4
S s ( f ) = 2 Eb sinc 2 ( fT ) sin 2 (π fT )
1.2
1
0.8
0.6
0.4
0.2
0
-4
09/10/2006
-3
-2
-1
0
COMfT
II
1
2
3
4
T3-36
18
Ejemplos de densidades espectrales para L=2
• Modulaciones sin memoria con L=2: 2PPM
ϕ1 (t ) =
1
T /2
Π ( t −TT/ 2/ 4 ) ; Φ1 ( f ) = T / 2 sinc( fT / 2) exp ( − jπ fT / 2 )
ϕ 2 (t ) =
1
T /2
Π ( t −T3T/ 2/ 4 ) ; Φ 2 ( f ) = T / 2 sinc( fT / 2) exp ( − jπ f 3T / 2 )
y2
s2
d = 2 Eb
Eb
Eb
⎛ 0
⎛ E ⎞
s1 = ⎜ b ⎟ ; s 2 = ⎜
⎜ E
⎝ 0 ⎠
⎝ b
Es = Eb = 12 d 2
y1
s1
⎞
⎟⎟
⎠
– Vimos:
μ=
Eb ⎛1⎞
Eb
=
1L
⎜
⎟
2 ⎝1⎠
2
C[0] = R[0] − μμT =
09/10/2006
Eb
E
I L − b 1L× L
2
4
T3-37
COM II
Ejemplos de densidades espectrales para L=2 (II)
• Modulaciones sin memoria con L=2: 2PPM
– La expresión general de la densidad espectral es:
Ss ( f ) =
1 +∞ L L
∑ ∑∑ Cα α [ k ] Φl ( f )Φ*j ( f ) exp ( − jk 2π fT ) +
T k =−∞ l =1 j =1 l j
+
1
T2
L
+∞
L
∑∑ μα μα ∑ Φ (
l =1 j =1
l
j
k =−∞
l
k
T
)Φ*j ( Tk )δ ( f − Tk )
– En el caso de modulaciones sin memoria resulta:
Ss ( f ) =
1 L L
1
Cαlα j [ 0] Φ l ( f )Φ*j ( f ) + 2
∑∑
T l =1 j =1
T
09/10/2006
L
+∞
L
∑∑ μα μα ∑ Φ (
COM II
l =1 j =1
l
j
k =−∞
l
k
T
)Φ*j ( Tk )δ ( f − Tk )
T3-38
19
Ejemplos de densidades espectrales para L=2 (III)
• Modulaciones sin memoria con L=2: 2PPM
– En este caso:
T
Φ1 ( f )Φ1* ( f ) = sinc 2 ( fT / 2)
2
T
*
Φ1 ( f )Φ 2 ( f ) = sinc 2 ( fT / 2) exp ( − jπ fT )
2
T
Φ 2 ( f )Φ*2 ( f ) = sinc 2 ( fT / 2)
2
T
Φ1 ( Tk )Φ*2 ( Tk ) = Φ 2 ( Tk )Φ1* ( Tk ) = sinc 2 (k / 2)(−1) k
2
Ss ( f ) =
1 L L
1
∑∑ Cα α [0] Φl ( f )Φ*j ( f ) + T 2
T l =1 j =1 l j
L
+∞
L
∑∑ μα μα ∑ Φ (
l =1 j =1
l
j
k =−∞
l
k
T
)Φ*j ( Tk )δ ( f − Tk ) =
= S sc ( f ) + S sδ ( f ) : Espectro continuo + deltas espectrales
09/10/2006
T3-39
COM II
Ejemplos de densidades espectrales para L=2 (IV)
• Cálculo del espectro continuo:
S sc ( f ) =
1 L L
∑∑ Cα α [0] Φl ( f )Φ*j ( f ) =
T l =1 j =1 l j
Eb T
sinc2 ( fT / 2) [1 − exp(− jπ fT ) + 1 − exp( jπ fT ) ] =
4T 2
E
= b sinc 2 ( fT / 2)sen 2 (π fT / 2)
2
=
• Cálculo de las deltas espectrales:
S sδ ( f ) =
L
+∞
L
∑∑ μα μα ∑ Φ (
l =1 j =1
l
j
k =−∞
l
k
T
)Φ*j ( Tk )δ ( f − Tk ) =
T
1 Eb ⎡ T
4 δ ( f ) + sinc 2 ( 12 )(1 + 1 − 1 − 1)δ ( f − Tk ) +
2
T 2 4 ⎢⎣ 2
1 Eb
=
δ(f)
T 2
COM II
=
09/10/2006
1
T2
⎤
⎥⎦
T3-40
20
Ejemplos de densidades espectrales para L=2 (V)
• Densidad espectral de Modulaciones 2PPM
0.35
0.3
Ss ( f ) =
Eb
1 Eb
δ(f)
sinc 2 ( fT / 2)sen 2 (π fT / 2) +
T 2
2
0.25
0.2
0.15
0.1
0.05
0
-4
-3
-2
-1
0
1
2
3
4
fT II
COM
09/10/2006
T3-41
3.2 Interferencia Inter-simbólica: ISI
Introducción: Canal Ideal
• Estructura del receptor óptimo MAP para canal ideal
y1 (t )
ϕ (T − t )
hc (t ) = δ (t )
y1 (tk )
1
y2 (tk )
⊕
s (t )
hc (t )
r (t )
Det.
MAP
ϕ (T − t )
sˆ [ k ]
2
y2 (t )
tk = kT + td
w(t )
yL (tk )
ϕ L (T − t )
r (t ) = s (t ) + w(t ) =
+∞
∑s
n =−∞
09/10/2006
m[ n ]
(t − nT ) + w(t ) =
y L (t )
+∞
L
∑ ∑ α [ n]ϕ (t − nT ) + w(t )
n =−∞ l =1
COM II
ml
l
T3-42
21
Introducción: Canal Ideal (II)
• A la salida de cada uno de los filtros adaptados a las funciones de la
base se tiene:
y j (t ) = ( s (t ) + w(t ) ) ∗ ϕ j (T − t ) =
=
+∞
+∞
L
∑ ∑ α [ n]ϕ (t − nT ) ∗ ϕ
ml
n =−∞ l =1
l
j
(T − t ) + w(t ) ∗ ϕ j (T − t ) =
L
∑ ∑ α [ n] Rϕ ϕ (t − (n + 1)T ) + β
n =−∞ l =1
ml
l
j
j
(t )
– En donde se ha utilizado:
ϕl (t − nT ) * ϕ j (T − t ) = ϕl (t ) * ϕ j (−t ) * δ (t − nT ) * δ (t − T ) =
= Rϕlϕ j (t ) * δ (t − (n + 1)T ) = Rϕlϕ j (t − (n + 1)T )
09/10/2006
T3-43
COM II
Introducción: Canal Ideal (III)
• Muestreando las salidas de los filtros adaptados en los instantes:
tk = (k + 1)T
y j (tk ) = y j [ k ] =
+∞
L
∑ ∑ α [ n] Rϕ ϕ ((k − n)T ) + β
n =−∞ l =1
ml
l
j
j
(tk ) = α mj [ k ] + β j [ k ]
– En donde se ha utilizado:
Rϕ jϕl (( k − n)T ) =
+∞
=
∫ϕ
−∞
j
⎧ Rϕl ϕl (nT ) = δ [n]
(( k − n)T + λ )ϕl (λ )d λ = δ [ j − l ]δ [ k − n ] ⇒ ⎨
⎩ Rϕ jϕl (nT ) = 0 ; j ≠ l
• En notación vectorial:
y [k ] = sm [k ] + n [k ]
09/10/2006
COM II
T3-44
22
Caso de canal no ideal con L=1
• En este caso, la señal recibida resulta:
r (t ) = s (t ) ∗ hc (t ) + w(t ) =
+∞
∑ α [ n]ϕ (t − nT ) ∗ h (t ) + w(t )
n =−∞
m1
1
c
• Mientras que la salida del filtro adaptado es:
y1 (t ) = ( s (t ) ∗ hc (t ) + w(t ) ) ∗ ϕ1 (T − t ) =
=
+∞
∑ α [ n]ϕ (t − nT ) ∗ ϕ (T − t ) ∗ h (t ) + w(t ) ∗ ϕ (T − t ) =
n =−∞
=
m1
1
1
1
c
+∞
+∞
∑ α [ n] Rϕ ϕ (t − (n + 1)T ) ∗ h (t ) + β (t ) = ∑ α [ n] p
n =−∞
m1
c
1 1
1
n =−∞
m1
11
(t − nT ) + β1 (t )
• Donde se ha definido:
plj (t ) = Rϕlϕ j (t − T ) ∗ hc (t )
09/10/2006
T3-45
COM II
Caso de canal no ideal con L=1 (II)
• Definiendo el instante de muestreo: tk = td + kT
y1 (tk ) =
+∞
∑ α [n] p
n =−∞
m1
11
(tk − nT ) + β1 (tk ) =
= α m1 [ k ] p11 (td ) +
+∞
∑ α [n] p
n =−∞
n≠k
m1
11
(td − (n − k )T ) + β1 (tk )
Intersymbol Interference (ISI)
Señal útil
Ruido
• Para canal causal de duración LcT la expresión anterior resulta:
y[k ] = y1 (tk ) =
k + Lc
∑
n = k − Lc
α m1 [ n ] p11 (td − (n − k )T ) + β1 (tk ) = α m1 [ k ] ∗ p11 [ k ] + β1 [ k ]
– Donde se ha definido:
p jl [k ]
09/10/2006
p jl (td + kT ) ; (para canal ideal td = T , p jl [k ] = δ [ j − l ]δ [k ])
COM II
T3-46
23
Caso de canal no ideal con L=1 (III)
ϕ1 (t ) =
• Ejemplos: Función base rectangular
⎛ t −T / 2 ⎞
Π⎜
⎟
T ⎝ T ⎠
1
1
0.9
0.8
0.7
Rϕ1ϕ1 (t ) =
0.6
Rϕ1ϕ1 (t ) 0.5
1 ⎛ t −T / 2 ⎞
⎛ −t − T / 2 ⎞
Π⎜
⎟*Π ⎜
⎟=
T ⎝ T ⎠
T
⎝
⎠
⎛t ⎞
= Λ⎜ ⎟
⎝T ⎠
0.4
0.3
0.2
0.1
0
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
t /T
09/10/2006
T3-47
COM II
Caso de canal no ideal con L=1 (IV)
hc (t ) = 2 exp(−2t / T ) u(t )
• Ejemplos: Canal exponencial
2
1.8
1.6
1.4
1.2
hc (t )
1
0.8
0.6
0.4
0.2
0
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
t /T
09/10/2006
COM II
T3-48
24
Caso de canal no ideal con L=1 (V)
• Ejemplos: Función base rectangular y canal exponencial
1
Rϕ1ϕ1 (t − T )
T
0.9
⎛ t −T / 2 ⎞
Π⎜
⎟
T ⎝ T ⎠
⎛t⎞
Rϕ1ϕ1 (t ) = Λ ⎜ ⎟
⎝T ⎠
ϕ1 (t ) =
0.8
0.7
0.6
0.5
1
⎛t⎞
p11 (t ) = p (t ) = Λ ⎜ ⎟
⎝T ⎠
p[k ] = p(td + kT ) = p (T + kT ) = δ [k ]
0.4
0.3
0.2
0.1
0
0
0.5
1
1.5
2
2.5
3
3.5
4
t /T
09/10/2006
T3-49
COM II
Caso de canal no ideal con L=1 (VI)
• Ejemplos: Función base rectangular y canal exponencial
p[1k ] = p (td + kT ) =
= p−1δ [k + 1] + pMAX δ [k ] + p1δ [k − 1] + p2δ [k − 2]
0.9
0.8
0.7
⎛ t −T / 2 ⎞
Π⎜
⎟
T ⎝ T ⎠
⎛t⎞
Rϕ1ϕ1 (t ) = Λ ⎜ ⎟
⎝T ⎠
ϕ1 (t ) =
1
0.6
hc (t ) = 2 exp(−2t / T ) u(t )
0.5
p(t ) = Rϕ1ϕ1 (t − T ) ∗ hc (t )
td
0.4
td + T
0.3
td − T
0.2
td + 2T
0.1
0
0
0.5
1
1.5
2
2.5
3
3.5
4
t /T
09/10/2006
COM II
T3-50
25
Caso de canal no ideal con L=1 (VII)
• Ejemplos: Función base rectangular y canal exponencial
– Canal discreto equivalente:
p[k ] = p−1δ [k + 1] + pMAX δ [ k ] + p1δ [k − 1] + p2δ [k − 2]
– Expresión de la señal recibida:
y[k ] = α m [ k ] ∗ p [ k ] + β [ k ] =
= p−1α m [k + 1] + pMAX α m [ k ] + p1α m [k − 1] + p2α m [k − 2] + β [ k ] =
= p−1 sm [k + 1] + pMAX sm [k ] + p1 sm [k − 1] + p2 sm [k − 2] + β [ k ]
– Receptor MAP?
09/10/2006
T3-51
COM II
Caso de canal no ideal con L=1 (VIII)
• Ejemplos: Canal exponencial invertido hc (t ) = 2 exp ( 2(t / T − 2) ) u(2 − t )
2
1.8
1.6
1.4
1.2
hc (t )
1
0.8
0.6
0.4
0.2
0
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
t /T
09/10/2006
COM II
T3-52
26
Caso de canal no ideal con L=1 (IX)
• Ejemplos: Función base rectangular y canal exponencial invertido
p[k ] = p(td + kT ) =
= p−2δ [k + 2] + p−1δ [k + 1] + pMAX δ [k ] + p1δ [k − 1]
⎛ t −T / 2 ⎞
Π⎜
⎟
⎝ T ⎠
⎛t⎞
Rϕ1ϕ1 (t ) = Λ ⎜ ⎟
⎝T ⎠
1
ϕ1 (t ) =
0.9
0.8
td
0.7
0.6
1
T
0.5
hc (t ) = 2 exp ( 2(t / T − 2) ) u(2 − t )
0.4
p (t ) = Rϕ1ϕ1 (t − T ) ∗ hc (t )
0.3
td − T
0.2
td + T
0.1
0
0
0.5
09/10/2006
1
1.5
2
2.5
3
3.5
4
t /T
td − 2T
T3-53
COM II
Caso de canal no ideal con L>1
• A la salida de cada uno de los filtros adaptados a las funciones de la
base se tiene:
y j (t ) = ( s (t ) ∗ hc (t ) + w(t ) ) ∗ ϕ j (T − t ) =
=
+∞
L
∑ ∑ α [ n]ϕ (t − nT ) ∗ ϕ
n =−∞ l =1
=
+∞
l
j
(T − t ) ∗ hc (t ) + w(t ) ∗ ϕ j (T − t ) =
L
∑ ∑ α [ n] Rϕ ϕ (t − (n + 1)T ) ∗ h (t ) + β
n =−∞ l =1
=
ml
+∞
ml
l
L
∑ ∑ α [ n] p
n =−∞ l =1
ml
lj
c
j
j
(t ) =
(t − nT ) + β j (t )
• Definiendo el instante de muestreo: tk = td + kT
L
y j (tk ) = ∑∑ α ml [ n ] plj (td − (k − n)T ) + β j (tk ) =
n
l =1
= α mj [ k ] p jj (td ) + ∑ α mj [ n ] p jj (td − (k − n)T ) + ∑
n≠ k
09/10/2006
Señal
útil
L
∑ α [n] p
n l =1;l ≠ j
ISI
COM II
ml
lj
ICI
(td − (k − n)T ) + β j (tk )
T3-54
Ruido
27
Caso de canal no ideal con L>1 (II)
• Utilizando notación discreta resulta
L
y j [ k ] = ∑∑ α ml [ n ] plj [ k − n ] + β j (tk )
n
l =1
p jl [k ] = p jl (td + kT )
– Donde
• De forma vectorial:
y [ k ] = ∑ P [ k − n ] s m [ n ] + n[k ] = P [ k ] ∗ s m [ k ] + n[k ]
n
– Donde
⎡ p11[k ]
P [k ] ⎢
⎢
⎢⎣ p1L [k ]
– Si el canal fuera ideal:
P [k ]
09/10/2006
pL1[k ] ⎤
⎥
⎥
pLL [k ]⎥⎦
Iδ [ k ] ⇒ y [ k ] = s m [ k ] + n[k ]
T3-55
COM II
Formulación del criterio MAP en presencia de ISI
• Vimos un ejemplo de canal con ISI tal que:
y[k ] = p−1 sm [k + 1] + pMAX sm [k ] + p1 sm [k − 1] + p2 sm [k − 2] + β [ k ]
– Supongamos que tan sólo está disponible una muestra, y[0]:
y[0] = p−1 sm [1] + pMAX sm [0] + p1 sm [ −1] + p2 sm [−2] + β [ k ]
– En ausencia de ISI, esta muestra contenía toda la información
disponible sobre el símbolo sm[0]. Ahora cada muestra tiene
contribución de más de un símbolo. Definiendo:
Sm [ sm [1], sm [0], sm [ −1], sm [−2]]
– El criterio MAP (con símbolos equiprobables) equivale a:
Sˆm = argmax f ( y[0] | Sm ) =
Sm
09/10/2006
argmax
sm [1], sm [0],sm [ −1], sm [ −2]
COM II
f ( y[0] | sm [1], sm [0], sm [−1], sm [−2])
T3-56
28
Formulación del criterio MAP en presencia de ISI (II)
• Sin embargo, condicionada al conocimiento de los símbolos
trasmitidos las muestras recibidas siguen siendo gaussianas de media
y varianza conocidas:
(
)= (
y[0] | sm [1], sm [0], sm [ −1], sm [−2] ∼ N p−1 sm [1] + pMAX sm [0] + p1 sm [−1] + p2 sm [−2],
(
= N x[0],
N0
2
1
π N0 )
1/ 2
(
exp − ( y[0]N− 0x[0])
2
)
N0
2
)=
• El criterio MAP puede aplicarse sin problemas, aunque el número de
combinaciones de símbolos a calcular crece exponencialmente con la
longitud de la ISI en símbolos.
• En general se dispondrán de múltiples muestras por lo que la
complejidad del problema aumenta, aunque puede hacerse depender
fundamentalmente de la longitud de la ISI [Proakis “Digital
Communications”, 4 ed., p. 251-254]
09/10/2006
COM II
T3-57
3.3 Pulsos de Nyquist
Introducción
• En esta sección se considera el diseño de funciones base (o pulsos a
la salida del filtro adaptado) que no generen ISI ni ICI al transmitirse
por canales limitados en banda. La limitación en banda de los pulsos
hace que no sean limitados en el tiempo. Se deberán aproximar por
pulsos limitados para que los filtros adaptados sean causales.
• Se considera inicialmente un canal ideal dentro de un ancho de
banda Bc que introduce exclusivamente un retardo
p jl (t ) = ϕ j (t ) ∗ ϕl (tϕ − t ) ∗ hc (t ) = Rϕ jϕl (t − tϕ ) ∗ δ (t − tc ) = Rϕ jϕl (t ) ∗ δ (t − td )
• La condición de ausencia de ISI e ICI se traduce en:
p jl (tk ) = p jl (td + kT ) = Rϕ jϕl (kT ) = δ [k ]δ [ j − l ]
• El retardo introducido en el filtro adaptado depende de la duración
efectiva del pulso. El retardo efectivo es:
td = tϕ + tc
09/10/2006
COM II
T3-58
29
Diseño de pulsos para L=1
• Se define en primer lugar la versión centrada en el origen del pulso a
la salida del filtro adaptado como:
pR (t ) = p (t + td ) = Rϕϕ (t )
• En el caso L=1 no existe ICI y la condición de diseño se simplifica a:
p[k ] = p (tk ) = p (td + kT ) = pR (kT ) = Rϕϕ (kT ) = δ [ k ]
Φ( f ) = 0 ;
f ≥ Bc
• La primera condición es equivalente a:
∞
∞
n =−∞
n =−∞
pR (t ) ∑ δ (t − nT ) = ∑ pR (nT )δ (t − nT ) =δ (t )
– Que tras realizar TF queda como:
PR ( f ) ∗
1 ∞ ⎛
n⎞ 1 ∞
n⎞
⎛
δ ⎜ f − ⎟ = ∑ PR ⎜ f − ⎟ =1
∑
T n=−∞ ⎝
T ⎠ T n=−∞ ⎝
T⎠
09/10/2006
COM II
T3-59
Diseño de pulsos para L=1 (II)
• El procedimiento a seguir para diseñar la función base es:
– Elección de PR(f) tal que
1 ∞
n⎞
⎛
PR ⎜ f − ⎟ =1
∑
T n =−∞ ⎝
T⎠
– Obtención de
Sϕϕ ( f ) = PR ( f )
– Obtención de
Φ ( f ) = Sϕϕ ( f )1/ 2 e jθ ( f ) ; θ ( f ) arbitrario
– Obtención de
09/10/2006
ϕ (t ) = F −1 [ Φ ( f )] = F −1 ⎡⎣ PR ( f )1/ 2 e jθ ( f ) ⎤⎦
COM II
T3-60
30
Diseño de pulsos para L=1(III)
• Ejemplo:
⎛t ⎞
PR ( f ) = T Π ( fT ) ⇒ pR (t ) = Rϕ (t ) = sinc ⎜ ⎟
⎝T ⎠
1
⎛t⎞
sinc ⎜ ⎟
ϕ (t ) = F −1 ⎣⎡ PR ( f )1/ 2 ⎦⎤ = F −1 ⎣⎡ T Π ( fT ) ⎦⎤ =
T
⎝T ⎠
1 ∞
n⎞
⎛
PR ⎜ f − ⎟ =1
∑
ϕ (t )
T n =−∞ ⎝
T⎠
1
1
0.8
0.8
0.6
0.4
0.6
0.2
0.4
0
0.2
-0.2
-0.4
-4
0
-3
-2
09/10/2006
-1
0
1
2
3
4
t /T
COM II
-3
-2
-1
0
1
2
3
T3-61
fT
Diseño de pulsos para L=1(IV)
• Principales problemas prácticos que asociados con la utilización de
esta función:
– Si se produce un pequeño error de sincronismo en los instantes
de muestreo se genera una ISI que decae tan sólo como 1/n
y1[k ] = y1 ( tk + Δt ) =
=
+∞
∑ α1 [ n]
n =−∞
+∞
∑ α [ n] sinc ( (k − n) + Δt / T ) + β (t
n =−∞
1
1
k
)
+∞
sen((k − n)π + Δtπ / T )
(−1)( k − n ) sen(Δtπ / T )
+ β1 (tk ) = ∑ α1 [ n ]
+ β1 (tk ) ≈
(k − n)π + Δtπ / T
( k − n)π + Δtπ / T
n =−∞
≈ α1 [ k ] +
+∞
∑
n =−∞ ; n ≠ k
α1 [ n ](−1)( k − n )
Δt
+ β1 (tk )
(k − n)T
– El diseño de los pulsos implica la implementación de filtros paso
bajo ideales
Φ ( f ) = T Π ( fT )
09/10/2006
COM II
T3-62
31
Pulsos de coseno realzado
• Además de la función paso bajo ideal, existen otras muchas
funciones limitadas en banda que cumplen la condición de ISI nula:
1 ∞
n⎞
⎛
∑ PR ⎜ f − T ⎟⎠ =1
T n =−∞ ⎝
• Las más utilizadas en la práctica son las denominadas coseno
realzado (raised cosine):
⎛t⎞
⎛ t ⎞ cos(2πβ t )
pRC (t ) = sinc ⎜ ⎟ pβ (t ) = sinc ⎜ ⎟
2
⎝T ⎠
⎝ T ⎠ 1 − ( 4β t )
– Pueden interpretarse como un modelado de la función sinc con
una función parametrizada por el parámetro β cuya transformada
de Fourier es:
⎛π f ⎞ ⎛ f ⎞
π
cos ⎜
F [ pβ (t )] = Pβ ( f ) =
⎟Π⎜
⎟
4β
⎝ 4β ⎠ ⎝ 2β ⎠
09/10/2006
T3-63
COM II
Pulsos de coseno realzado (II)
•La transformada de Fourier de las funciones coseno realzado admite
una expresión cerrada:
⎧
T
⎪
⎪
⎛ π ⎛
1
⎪
⎞⎞
+ β ⎟⎟
PRC ( f ) = T Π ( fT ) ∗ Pβ ( f ) = ⎨T cos 2 ⎜
⎜ f −
β
4
2
T
⎝
⎠⎠
⎝
⎪
⎪
0
⎪
⎩
de forma que su ancho de banda es:
1
1
BRC =
+β =
(1 + α )
2T
2T
1
−β
2T
1
1
−β < f <
+β
2T
2T
f <
1
+β < f
2T
en donde se ha definido el factor de roll-off o exceso de ancho de banda
normalizado α (que suele indicarse en tanto por ciento)
09/10/2006
COM II
T3-64
32
Pulsos de coseno realzado (III)
• El caso de factor de roll-off igual a cero se corresponde con el pulso
paso bajo ideal (con los problemas de implementación ya
comentados). Sin embargo a medida que el factor de roll-off
aumenta se consigue una característica frecuencial más suave y una
respuesta temporal que se atenúa como 1/t3.
• Para un factor de de roll-off del 100% los pulsos presentan las
siguientes características:
p100%
RC (t ) =
sen(π t / T ) cos(π t / T ) sinc(2t / T )
=
π t / T 1 − ( 2t / T )2 1 − ( 2t / T )2
⎛ π fT
100%
PRC
( f ) = T cos 2 ⎜
⎝ 2
09/10/2006
⎞ ⎛ f ⎞
⎟Π⎜
⎟
⎠ ⎝ 2/T ⎠
T3-65
COM II
Pulsos de coseno realzado (IV)
• Respuesta temporal de los pulsos de coseno realzado para α=0, 0.2,
0.4, 0.6, 0.8 y 1
1
0.8
0.6
pαRC (t )0.4
0.2
0
-0.2
-4
-3
-2
-1
0
1
2
3
4
t /T
09/10/2006
COM II
T3-66
33
Pulsos de coseno realzado (V)
• Respuesta frecuencial de los pulsos de coseno realzado para α=0,
0.2, 0.4, 0.6, 0.8 y 1
α
PRC
(f)
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
fT
09/10/2006
T3-67
COM II
Pulsos de coseno realzado (VI)
• La función base correspondiente a un pulso de coseno realzado se
obtiene mediante la expresión:
ϕ (t ) = F −1 [ Φ ( f ) ] = F −1 ⎡⎣ PR ( f )1/ 2 ⎤⎦
• Su expresión analítica en el dominio frecuencial es por tanto:
⎧
T 1/ 2
⎪
⎪
⎛ π ⎛
1
⎞⎞
1/ 2 ⎪ 1/ 2
Φ SRRC ( f ) = PRC ( f ) ⎨T cos ⎜
+ β ⎟⎟
⎜ f −
2T
⎠⎠
⎝ 4β ⎝
⎪
⎪
0
⎪
⎩
1
−β
2T
1
1
−β < f <
+β
2T
2T
f <
1
+β < f
2T
– Se denomina square root raised cosine
09/10/2006
COM II
T3-68
34
Pulsos de coseno realzado (VII)
• Su transformada de Fourier inversa admite una expresión analítica
cerrada:
sen (π t (1/ T − 2 β ) ) + 8β t cos (π t (1/ T + 2 β ) )
ϕ SRRC (t ) =
π tT −1/ 2 (1 − (8β t ) 2 )
La señal transmitida
tiene ISI aparente
1.4
1.2
1
0.8
ϕ SRRC (t )
0.6
0.4
0.2
0
-0.2
-4
-3
-2
-1
0
1
2
3
4
COM
II
t /T
09/10/2006
T3-69
Diseño de pulsos para L>1
• Se demostró que la condición de ausencia de ISI e ICI se podía
expresar como:
Rϕ jϕl (kT ) = δ [ k ]δ [ j − l ]
– Esta condición es equivalente a:
∞
∞
n =−∞
n =−∞
Rϕ jϕl (t ) ∑ δ (t − nT ) = ∑ Rϕ jϕl (nT )δ (t − nT ) =δ (t )δ [ j − l ]
– Tomando transformada de Fourier resulta:
Φ j ( f )Φ*l ( f ) ∗
09/10/2006
1 ∞ ⎛
n⎞ 1 ∞
n⎞ ⎛
n⎞
⎛
δ ⎜ f − ⎟ = ∑ Φ j ⎜ f − ⎟ Φ*l ⎜ f − ⎟ = δ [ j − l ]
∑
T n =−∞ ⎝
T ⎠ T n =−∞ ⎝
T⎠ ⎝
T⎠
COM II
T3-70
35
3.4 Ecualización
Introducción
• En ausencia de ISI la probabilidad de error resulta idéntica a la vista
en el Tema 2
y [ k ] = s m [ k ] + n[k ]
con la única diferencia que las funciones que forman la base no
tienen porqué están limitadas en el tiempo (por simplicidad en el
diseño del receptor MAP se suponían limitadas). Esta restricción no
es necesaria mientras se satisfaga el criterio:
•
1 ∞
n⎞ ⎛
n⎞
⎛
∑ Φ j ⎜ f − T ⎟⎠ Φ*l ⎜⎝ f − T ⎟⎠ = δ [ j − l ]
T n =−∞ ⎝
En la práctica, cierta ISI residual es inevitable y degrada las
prestaciones del receptor o complica su diseño. Para L=1:
y[k ] = sm [ k ] ∗ p [ k ] + β [ k ] = sm [ k ] p[0] + ∑ sm [ k − n ] p[ n] + β [ k ]
n≠0
• En esta sección consideraremos soluciones subóptimas que permiten
reducir la ISI y aplicar los receptores óptimos obtenidos suponiendo
que no existía ISI.
09/10/2006
T3-71
COM II
Introducción (II)
• Medidas de la distorsión introducida por la ISI:
y[k ] = sm [ k ] ∗ p [ k ] + β [ k ] = sm [ k ] p[0] + ∑ sm [ k − n ] p[ n] + β [ k ]
n≠0
– Degradación de la distancia mínima:
ISI
d min
= d min − 2 max
∑s
n≠0
m
p[n] ≥ d min − 2 max sm
∑ p[n]
n≠0
– Contribución de la ISI al ruido
⎡
⎤
2
σ ISI
= σ 2 + E ⎢ ∑ sm p[ n] ⎥ = σ 2 + Es ∑ p[ n]
2
⎣ n≠0
09/10/2006
⎦
COM II
2
n≠0
T3-72
36
Introducción (III)
• La ecualización se puede plantear siguiendo diferentes estrategias:
– Ecualización analógica:
ϕ (t ) ∗ hc (t ) ∗ hR (t ) = Rϕ (t − td )
α [k ]
ϕ (t )
y1 (t )
hR (t )
+
hc(t)
s(t)
r baudios
tk = kT + td
w(t)
– Filtros terminales óptimos analógicos:
hT (t ) ∗ hc (t ) ∗ hR (t ) = Rϕ (t − td ) y simultáneamente maximizar
α [k ]
hT (t )
hR (t )
+
hc(t)
p[0]
σ
y1 (t )
s(t)
r baudios
tk = kT + td
w(t)
COM II
09/10/2006
T3-73
Introducción (IV)
– Ecualización discreta:
p[k ] ∗ hQ [k ] ≈ δ [ k − k0 ]
α [k ]
ϕ (t )
ϕ (tϕ − t )
+
hc(t)
y1 (t )
s(t)
r baudios
tk = kT + td
yQ [ k ]
hQ [ k ]
w(t)
– Filtros terminales óptimos discretos:
hT [k ] ∗ p[k ] ∗ hR [ k ] = δ [k − k0 ] y simultáneamente maximizar
α [k ]
hT [ k ]
ϕ (t )
s(t)
r baudios
09/10/2006
+
hc(t)
ϕ (tϕ − t )
y1 (t )
tk = kT + td
p[0]
σ
hR [ k ]
yQ [ k ]
w(t)
COM II
T3-74
37
Introducción (V)
• Se considerará en primer lugar el problema de la ecualización discreta.
Para ello se supondrá que el ecualizador se implementa mediante in filtro
FIR del tipo:
LQ
LQ
l =0
l =0
hQ [k ] = ∑ h[l ]δ [k − l ] ; yQ [k ] = ∑ h[l ] y[ k − l ]
– Debe diseñarse los coeficientes y su orden.
• Se considerarán dos criterios:
– Forzador de ceros: Se diseña el filtro ecualizador para minimizar:
2
ε ZF = ∑ ( p[ k ] ∗ hQ [k ] − δ [k − k0 ])
k
El nivel de ruido no se controla
– Criterio MSE (Wiener): Se diseña el filtro ecualizador para
minimizar el error cuadrático medio entre la salida del ecualizador y
la secuencia de símbolos transmitida:
2
ε MSE = E ⎡⎢ yQ [k ] − sm [ k − k0 ] ⎤⎥
⎣
⎦
09/10/2006
COM II
T3-75
Ecualización Discreta: Forzador de ceros
• Se supone una duración de canal discreto equivalente p[k] de Lc+1
muestras y el objetivo es el diseño de un ecualizador discreto hQ[k] de
LQ+1 coeficientes.
• Puesto que la convolución entre ambas secuencias tiene una longitud
Lc+LQ+1 esta será la longitud del equivalente discreto tras la
LQ
ecualización:
p[k ] ∗ hQ [ k ] = ∑ hQ [n] p[k − n] = pQ′ [k ]
• En forma matricial:
n =0
⎛ p[0]
⎜ p[1]
⎜
⎜ p[2]
⎜
⎜ :
⎜ 0
⎝
09/10/2006
⎛ pQ′ [0] ⎞
⎞
⎟ ⎛ hQ [0] ⎞ ⎜
pQ′ [1] ⎟⎟
⎟ ⎜ hQ [1] ⎟ ⎜
⎟ = ⎜ p′ [2] ⎟
p[1] :
0 ⎟⎜
Q
⎟
⎟⎜ : ⎟ ⎜
:
:
:
: ⎟⎜
⎟ ⎜
⎟
h
L
[
]
Q
Q
⎠ ⎜ p′ [ L + L ] ⎟
0 : p [ Lc ] ⎟⎠ ⎝
Q ⎠
⎝ Q c
Ph = p′Q
:
0
p[0] :
0
0
COM II
T3-76
38
Ecualización Discreta: Forzador de ceros (II)
• El criterio utilizado implica un sistema sobredeterminado de Lc+LQ+1
ecuaciones con LQ+1 incógnitas. Se optará por la solución que
minimiza:
2
2
ε ZF = ∑ ( p[k ] ∗ hQ [k ] − δ [ k − k0 ]) = Ph − p Q
k
• Desarrollando la norma del vector:
ε FZ = ( Ph − pQ ) ( Ph − p Q ) = hT PT Ph − pQT Ph − hT PT p Q + p QT p Q
T
• Igualando el gradiente de dicha expresión con respecto a h a 0:
∇ ( ε FZ )h
09/10/2006
⎛ ∂ε FZ ⎞
⎜ ∂h [0] ⎟
⎜ Q
⎟
⎜ ∂ε FZ ⎟
⎜
⎟
= ⎜ ∂hQ [1] ⎟ = PT Ph − PT pQ = 0 LQ +1
⎜
⎟
:
⎜
⎟
⎜ ∂ε FZ ⎟
⎜ ∂h [ L COM
⎟
⎝ Q Q ] ⎠ II
T3-77
Ecualización Discreta: Forzador de ceros (III)
• Despejando el vector h resulta:
h ZF = ( PT P ) PT pQ = pinv ( P ) pQ
−1
pinv ( P )
P†
(P P)
T
−1
PT
– En donde se ha definido la función pseudoinversa de una matriz.
Cuando la matriz es invertible la pseudoinversa y la inversa
coinciden.
– Dado que el sistema es en general sobredeterminado, la ISI no se
cancela por completo. Sin embargo, como se verá en ejemplos se
reduce considerablemente.
• La utilización de este criterio tiene como principal inconveniente el
hecho de que el impacto de la ecualización sobre la potencia de ruido
no aparece en el criterio de diseño y por tanto no se controla.
09/10/2006
COM II
T3-78
39
Ecualización Discreta: Forzador de ceros (IV)
• Análisis del impacto del ecualizador en el ruido
β [k ]
β (t )
ϕ (tϕ − t )
w(t)
hQ [ k ]
t k = kT + t d
βQ [k ]
• Como vimos en el Tema 2, la componente de ruido a la salida del
filtro adaptado es gaussiana y por tanto también lo será a la salida del
ecualizador:
(
β [ k ] ∼ N 0, N2
0
)
LQ
βQ [ k ] = ∑ h [l ]β [ k − l ] ∼ N ( 0, σ Q2 )
l =0
09/10/2006
T3-79
COM II
Ecualización Discreta: Forzador de ceros (V)
• Además, desde el punto de vista de su dependencia temporal el ruido
a la salida del filtro adaptado es blanco, es decir:
Rβ [ k ] = E ⎡⎣ β [l + k ] β [l ]⎤⎦ =
– Demostración:
N0
2
δ [k ]
Rβ [ k ] = E ⎡⎣ β [l + k ] β [l ]⎤⎦ =
−∞
⎡ −∞
⎤
= E ⎢ ∫ w ( λ ) ϕ ( tϕ − ( tk + l − λ ) ) d λ ∫ w ( γ ) ϕ ( tϕ − ( tl − γ ) ) d γ ⎥ =
−∞
⎣ −∞
⎦
−∞
−∞
∫ ϕ ( tϕ − ( tk +l − λ ) ) ∫ E ⎡⎣ w ( λ ) w (γ )⎤⎦ ϕ ( tϕ − ( tl − γ ) ) d γ d λ =
−∞
−∞
−∞
N0
2
−∞
∫ ϕ ( tϕ − ( tk +l − λ ) ) ∫ δ ( λ − γ )ϕ ( tϕ − ( tl − γ ) ) d γ d λ =
−∞
−∞
−∞
N0
2
∫ ϕ ( tϕ − ( t
k +l
− λ ) ) ϕ ( tϕ − ( tl − λ ) ) d λ =
−∞
09/10/2006
N0
2
0
Rϕ ( tl − tk + l ) =COM
Rϕ ( − kT ) =
2 II
N
N0
2
δ [k ]
T3-80
40
Ecualización Discreta: Forzador de ceros (VI)
• Sin embargo, y debido al efecto del ecualizador, el ruido a la salida
del mismo deja de ser blanco. Su función de correlación se puede
calcular como:
RβQ [ k ] = E ⎡⎣ βQ [l + k ] β Q [l ]⎤⎦ =
LQ
⎡ LQ
⎤
E ⎢ ∑ h [ j ] β [ k + l − j ]∑ h [i ] β [l − i ]⎥ =
i =0
⎣ j =0
⎦
LQ
LQ
j =0
i =0
∑ h [ j ] ∑ h [i ] E ⎡⎣ β [ k + l − j ] β [l − i ]⎤⎦ =
LQ
LQ
LQ
LQ
j =0
i=0
j =0
i =0
∑ h [ j ] ∑ h [i ] Rβ [ k − j + i ] = ∑ h [ j ] ∑ h [i ]
LQ
N0
2
∑ h[ j] h[ j − k ] =
j =0
09/10/2006
N0
2
N0
2
δ [k − j + i] =
Rh [ − k ]
T3-81
COM II
Ecualización Discreta: Forzador de ceros (VII)
• La función de autocorrelación para k=0 nos proporciona el valor de la
potencia del ruido a la salida del ecualizador:
σ β2 = Rβ [ 0] =
Q
• Expresada en dB:
Q
LQ
N0
2
∑ ( h[ j ])
2
j =0
LQ
2
2⎞
⎛ σ βQ ⎞ = 10 log ⎛
⎜ σ β2 ⎟
10 ⎜ ∑ ( h[ j ] ) ⎟
⎝ ⎠ dB
⎝ j =0
⎠
• El efecto sobre el ruido depende del canal a ecualizar
09/10/2006
COM II
T3-82
41
Ecualización Discreta: Criterio MSE
• En este caso el criterio a minimizar actúa simultáneamente sobre la
ISI y el ruido al expresarse en forma de esperanza sobre el error
cuadrático a la salida del ecualizador con respecto a la señal deseada
(equivalente al filtro de Wiener)
2
⎡ LQ
⎤
2
ε MSE = E ⎢⎡ yQ [k ] − sm [k − k0 ] ⎥⎤ = E ⎢ ∑ h[ j ] y[ k − j ] − sm [k − k0 ] ⎥
⎣
⎦
⎢⎣ j =0
⎥⎦
• Al igual que se hizo en el caso del forzador de ceros, se iguala el
gradiente de la función a minimizar con respecto a la respuesta del
ecualizador a 0.
⎛ ∂ε MSE ⎞
⎜ ∂h[0] ⎟
⎜
⎟
⎜ ∂ε MSE ⎟
⎜
⎟
∇ ( ε MSE )h = ⎜ ∂h[1] ⎟ = 0 LQ +1
⎜ : ⎟
⎜ ∂ε
⎟
⎜ MSE ⎟
⎜ ∂h[ L ] ⎟
⎝ II Q ⎠
09/10/2006
COM
T3-83
Ecualización Discreta: Criterio MSE (II)
• Particularizando en cada una de sus componentes:
⎡
⎛ LQ
⎞⎤
∂ε MSE
= E ⎢ y[k − l ] ⎜ ∑ h[ j ] y[k − j ] − sm [k − k0 ] ⎟ ⎥ = 0
∂h[l ]
⎢⎣
⎝ j =0
⎠ ⎥⎦
Error ortogonal a los datos
• Equivalente a:
LQ
∑ h[ j ]E [ y[k − l ] y[k − j]] = E [ y[k − l ]s
m
j =0
LQ
∑ h[ j ]R [ j − l ] = E [ y[k − l ]s
j =0
y
m
[k − k0 ]] ⇒
[k − k0 ]]
– en donde se ha utilizado la propiedad de que la secuencia y[k] es
estacionaria en la autocorrelación (demostración?).
• A continuación supondremos que los símbolos tienen media nula y se
han codificado sin memoria:
Rs [k ] = σ s2δ [k ]
09/10/2006
COM II
T3-84
42
Ecualización Discreta: Criterio MSE (III)
• De esta forma se puede simplificar la expresión a la derecha de la
ecuación de diseño como:
E ⎡⎣ y [ k − l ] sm [ k − k0 ]⎤⎦ =
⎡ +∞
⎤
= E ⎢ ∑ sm [ n ] p [ k − l − n ]sm [ k − k0 ]⎥ + E ⎡⎣ β [ k − l ] sm [ k − k0 ]⎤⎦ =
⎣ n =−∞
⎦
=
+∞
∑
n =−∞
p [ k − l − n ]E ⎡⎣ sm [ n ] sm [ k − k0 ]⎤⎦ =
σ s2
+∞
∑ p [ k − l − n]R [ n − k + k ] =
s
n =−∞
+∞
∑ p [ k − l − n]δ [ n − k + k ] = σ p [ k
2
s
0
n =−∞
0
0
− l]
• De forma que el criterio MSE se simplifica a:
LQ
∑ h [ j ] R [ j − l ] = σ p [k
j =0
09/10/2006
2
s
y
0
− l]
T3-85
COM II
Ecualización Discreta: Criterio MSE (IV)
• Que en forma matricial queda como:
Ry [ −1]
⎛ Ry [0]
⎜ R [1]
Ry [0]
⎜ y
⎜ :
:
⎜
R
[
L
]
R
[
L
y
Q − 1]
⎝ y Q
Ry [− LQ ] ⎞⎛ h[0] ⎞
Ry [1 − LQ ] ⎟⎜ h[1] ⎟
⎟⎜
⎟ =σ2
sm
⎟⎜ : ⎟
:
⎟⎜
⎟
Ry [0] ⎠⎝ h[ LQ ] ⎠
⎛ p[k0 ] ⎞
⎜ p[k − 1] ⎟
0
⎟
⎜
⎟
⎜
:
⎜
⎟
p
[
k
L
]
−
0
Q ⎠
⎝
R y h = σ s2m p[ k0 ]
– En donde la matriz de correlación de y es cuadrada e invertible de
forma que:
h MSE = σ s2 R y −1p[k0 ]
09/10/2006
COM II
T3-86
43
Ecualización Discreta: Criterio MSE (V)
• En el caso de modulaciones sin memoria con símbolos de media
nula, la expresión de la matriz de correlación de y puede simplificarse
según:
Ry [ m ] = E ⎡⎣ y [ k + m ] y [ k ]⎤⎦ =
⎡⎛ +∞
⎞ ⎛ +∞
⎞⎤
E ⎢ ⎜ ∑ sm [ n ] p [ k + m − n ] + β [ k + m ] ⎟ ⎜ ∑ sm [ l ] p [ k − l ] + β [ k ] ⎟ ⎥ =
⎠ ⎝ l =−∞
⎠⎦
⎣⎝ n =−∞
+∞
+∞
∑ ∑ E ⎡⎣ s [ n] s [l ]⎤⎦ p [ k + m − n] p [ k − l ] +E ⎡⎣ β [ k + m] β [ k ]⎤⎦ =
m
n =−∞ l =−∞
σ s2
σ s2
09/10/2006
+∞
m
+∞
∑ ∑ δ [ n − l ]p [ k + m − n] p [ k − l ] +
n =−∞ l =−∞
+∞
∑ p [ k + m − n] p [ k − n] +
n =−∞
N0
2
N0
2
δ [ m] =
δ [ m ] = σ s2 R p [m] + N2 δ [ m ]
0
T3-87
COM II
Ecualización Discreta: Criterio MSE (VI)
• Que de forma vectorial resulta:
R y = σ s2 R p + R β = σ s2 R p +
R p [−1]
⎛ R p [0]
⎜
R p [1]
R p [0]
Rp = ⎜
⎜ :
:
⎜⎜
⎝ R p [ LQ ] R p [ LQ − 1]
N0
2
I
R p [− LQ ] ⎞
⎟
R p [1 − LQ ] ⎟
⎟
:
⎟
R p [0] ⎟⎠
• Debe recordarse que estos resultados se han obtenido exclusivamente
para símbolos codificados sin memoria y de media nula.
• La solución según el criterio MSE tiende a la del Forzador de ceros
cuando el ruido tiende a 0.
09/10/2006
COM II
T3-88
44
Ejemplo de ecualización
• Supongamos un canal equivalente discreto del tipo:
p [ k ] = 0.5147δ [ k ] + 0.7352δ [ k − 1] − 0.4411δ [ k − 2]
• Analizaremos las prestaciones del sistema sin ecualizar suponiendo
una modulación M-PAM:
2 M −2
M log 2 M
BER
⎛ d ISI
Q ⎜ min
⎜ 2σ
⎝ β
⎞
⎟⎟
⎠
Como disminución de la distancia mínima (modelado determinista
muy pesimista):
ISI
d min
= d min p[nmax ] − 2 max
d min p[nmax ] − 2d min
∑
n ≠ nmax
sm p[n] ≥ d min p[ nmax ] − 2 max sm
∑
p[ n]
n ≠ nmax
M −1
∑ p[n] = d min ( 0.7352 − 0.9558( M − 1) )
2 n ≠ nmax
Supone la posibilidad de distancia mínima cero!
09/10/2006
T3-89
COM II
Ejemplo de ecualización (II)
• Como aumento del ruido efectivo manteniendo la distancia mínima
⎡
2⎤
2
sm p[n] ⎥ = σ β2 + Es ∑ p[n] = σ β2 + 0.4595Es =
n ≠ nmax
⎣ n≠ nmax
⎦
N0
1
+ 0.4595Es = ( N 0 + 0.9189Eb log 2 M )
2
2
• Resulta una degradación respecto al sistema sin ISI ideal de:
2
σ ISI
= σ β2 + E ⎢
BER
2M −2
M log 2 M
∑
⎛ 0, 7352d min ⎞
Q⎜
⎟=
⎝ 2σ ISI
⎠
2M −2
M log 2 M
⎛
⎞
6 Eb log 2 M × (0, 7352) 2
Q⎜
⎟
⎜ ( M 2 − 1)( N 0 + 0.9189Eb log 2 M ) ⎟
⎝
⎠
En nuestro caso (M=2) :
N
σ β2 = 0 = 0.3Es = 0.3Eb
2
el ruido aumenta:
N 0 + 0.9189Eb log 2 M = (1 +
0.9189
) N 0 = 2.5315N 0
0.6
20 log(0.7352) -10 log(2.5315) = -6.7057dB
09/10/2006
COM II
T3-90
45
Ejemplo de ecualización (III)
• Diseño del forzador de ceros:
p [ k ] = 0.5147δ [ k ] + 0.7352δ [ k − 1] − 0.4411δ [ k − 2]
– Aplicando el criterio del forzador de ceros se plantea la siguiente
ecuación matricial:
0
0 ⎞
⎛ 0.5147
⎛0⎞
⎜ 0.7352 0.5147
⎟
0 ⎟ ⎛ h1 ⎞ ⎜⎜ 0 ⎟⎟
⎜
⎜ −0.4411 0.7352 0.5147 ⎟ ⎜ h2 ⎟ = ⎜ 1 ⎟
⎜
⎟⎜ ⎟ ⎜ ⎟
−0.4411 0.7352 ⎟ ⎜⎝ h3 ⎟⎠ ⎜ 0 ⎟
⎜ 0
⎜ 0
⎜0⎟
−0.4411⎟⎠
0
⎝
⎝ ⎠
– En donde se ha situado el máximo del pulso a la salida retrasado
una muestra con respecto al máximo a la entrada k0 = 2
09/10/2006
COM II
T3-91
Ejemplo de ecualización (IV)
• Aplicando la expresión calculada utilizando la pseudoinversa:
h ZF
0
0 ⎞⎛0⎞
⎛ 0.5147
⎜
0 ⎟⎟ ⎜⎜ 0 ⎟⎟ ⎛ -0.3934 ⎞
⎛ h1 ⎞
⎜ 0.7352 0.5147
= ⎜⎜ h2 ⎟⎟ = pinv ⎜ −0.4411 0.7352 0.5147 ⎟ ⎜ 1 ⎟ = ⎜ 0.7356 ⎟
⎟
⎜
⎟ ⎜ ⎟ ⎜⎜
⎜h ⎟
⎟
0.3856
−
0
0.4411
0.7352
0
⎝ 3⎠
⎝
⎠
⎜
⎟⎜ ⎟
⎜ 0
⎟
⎜
⎟
−
0
0.4411
0
⎝
⎠⎝ ⎠
• De forma que el pulso obtenido a la salida del ecualizador es:
pQ [k ] = p[k ] ∗ h[ k ] =
= -0.2024δ [ k ] + 0.0894δ [ k − 1] + 0.9128δ [ k − 2 ] + -0.0410δ [ k − 3] + -0.1701δ [ k − 4]
09/10/2006
COM II
T3-92
46
Ejemplo de ecualización (V)
• En incremento (o disminución en este caso) de potencia de ruido
debido al forzador de ceros es:
2
2
⎛ σ βQ ⎞ = 10 log ⎛ h 2 j ⎞ = 10 log(0.8445) = −0.7338dB
⎜ σ β2 ⎟
⎜ ∑ [ ]⎟
⎝ ⎠ dB
⎝ j =0
⎠
• Haciendo un modelado determinista de la ISI remanente
ZF
d min
= d min pQ [nmax ] − 2 max
d min pQ [ nmax ] − 2d min
∑
n ≠ nmax
sm pQ [n] ≥ d min pQ [ nmax ] − 2 max sm
∑
n ≠ nmax
pQ [n]
M −1
∑ pQ [n] = d min ( 0.9128 − 0.5029( M − 1) )
2 n ≠ nmax
Suponiendo modulación PAM con M=2 supone una pérdida de cómo
máximo 7 dB respecto al sistemas sin ISI:
BER
2M −2
M log 2 M
⎛ d ZF
Q ⎜ min
⎜ 2σ β
Q
⎝
09/10/2006
⎞
⎟=
⎟
⎠
2M −2
M log 2 M
⎛ (0.9128 − 0.5029)d ⎞
Q⎜
⎟
⎜ 2 0.8445σ
⎟
β
⎝
⎠
T3-93
COM II
Ejemplo de ecualización (VI)
• Haciendo un modelado aleatorio de la ISI:
⎡
2
σ ISI
= σ β2 + E ⎢
∑
⎣ n ≠ nmax
Q
2⎤
2
sm pQ [n] ⎥ = σ β2 + Es ∑ pQ [ n] = 0.8445σ β2 + 0.0796Es =
n ≠ nmax
⎦
N0
+ 0.0796Es
0.8445
2
Supondremos un valor para la potencia del ruido:
N0
2
= 0.3σ s2 = 0.3Es
N0
N
0.0796 N 0
)
+ 0.0796Es = (0.8445 +
= 1.1098 0
2
0.3
2
2
Resulta en una estimación de pérdidas de 1.25 dB frente al sistema
sin ISI:
0.8445
BER
09/10/2006
2M −2
M log 2 M
⎛ d ZF
Q ⎜ min
⎜ 2σ β
Q
⎝
⎞
⎟=
⎟
⎠
2M −2
M log 2 M
COM II
⎛ 0.9128d ⎞
Q⎜
⎟
⎜ 2 1.1098σ ⎟
β ⎠
⎝
T3-94
47
Ejemplo de ecualización (VII)
• Aplicando el criterio MSE para el diseño de un ecualizador FIR de 3
coeficientes, tomando también un retardo en el pulso de salida de una
muestra con respecto a la entrada, y suponiendo una modulación de
media 0 y sin memoria:
N
R y = σ s2 R p + R β = σ s2 R p + 20 I
⎛ 1.0000 0.0541 -0.2270 ⎞
R p = ⎜ 0.0541 1.0000 0.0541 ⎟
⎜
⎟
⎜ -0.2270 0.0541 1.0000 ⎟
⎝
⎠
N0
2
• Particularizando para
= 0.3σ s2 , k0 = 1
⎛ 1.3000 0.0541 -0.2270 ⎞ ⎛ h1 ⎞ ⎛ -0.4411⎞ ⎛ h1 ⎞ ⎛ -0.3072 ⎞
⎜ 0.0541 1.3000 0.0541 ⎟ ⎜ h ⎟ = ⎜ 0.7352 ⎟ ⇒ ⎜ h ⎟ = ⎜ 0.5651 ⎟
⎜
⎟⎜ 2 ⎟ ⎜
⎟ ⎜ 2⎟ ⎜
⎟
⎜ -0.2270 0.0541 1.3000 ⎟ ⎜ h ⎟ ⎜ 0.5147 ⎟ ⎜ h ⎟ ⎜ 0.3187 ⎟
⎝
⎠⎝ 3 ⎠ ⎝
⎠ ⎝ 3⎠ ⎝
⎠
09/10/2006
COM II
T3-95
Ejemplo de ecualización (VIII)
• Análisis de las prestaciones a la salida del ecualizador con el diseño
obtenido:
hQ [k ] = 0.3187δ [ k ] + 0.5651δ [ k − 1] − 0.3072δ [ k − 2]
pQ [k ] = p[ k ] ∗ hQ [k ] = −0.1581δ [k ] + 0.0650δ [k − 1] +
+0.7150δ [k − 2] − 0.0149δ [k − 3] − 0.1406δ [ k − 4]
Análisis de aumento (o disminución) de la potencia de ruido.
2
σ β2 = σ β2 ∑ hQ [ j ] = 0.5152σ β2
Q
⎛
⎜
⎝
σ β2Q
σ β2
2
j =0
2
⎞ = 10 log ⎛ h j 2 ⎞ = −2.8798 dB
⎟
10 ⎜ ∑ Q [ ] ⎟
⎠ dB
⎝ j =0
⎠
El ruido disminuye su potencia casi 3 dB con respecto a la entrada
del ecualizador
09/10/2006
COM II
T3-96
48
Ejemplo de ecualización (IX)
• Modelado del impacto de la ISI remanente. Suponiendo una
modulación M-PAM:
ISI − MMSE
2 M −2
M log 2 M
BER
⎛d
Q ⎜ min
⎜ 2σ
Q
⎝
⎞
⎟⎟
⎠
Como disminución de la distancia mínima (modelado determinista
muy pesimista):
∑
ISI − MMSE
d min
= d min pQ [nmax ] − 2 max
d min pQ [nmax ] − 2d min
n ≠ nmax
sm pQ [n] ≥ d min pQ [nmax ] − 2 max sm
∑
n ≠ nmax
pQ [n]
M −1
∑ pQ [n] = d min ( 0.7150 − 0.3786( M − 1) )
2 n ≠ nmax
La ISI sigue siendo importante
⎛ d MMSE ⎞
⎛ d min ( 0.7150 − 0.3786( M − 1) ) ⎞
min
2M −2
M −2
⎜
⎟
=
BER M2log
Q
Q
⎜
⎟
2 M
⎟
⎜ 2σ β ⎟ M log 2 M ⎜
2σ β 0.5152
Q ⎠
⎝
⎠
⎝
lo que representa una pérdida de 6,5 dB para M=2 respecto al caso
ideal sin ISI (7dB máximo el ZF)
09/10/2006
COM II
T3-97
Ejemplo de ecualización (X)
• Modelado del impacto de la ISI remanente. Como aumento de la
potencia de ruido:
BER
2 M −2
M log 2 M
⎛ d MMSE ⎞
Q ⎜ min ⎟
⎝ 2σ ISI ⎠
La distancia mínima se calcula como si no existiera ISI remanente:
MMSE
d min
= d min pQ [nmax ] = 0.7150d min
La ISI produce un incremente de ruido:
⎡
2⎤
2
sm pQ [ n] ⎥ = σ β2Q + Es ∑ pQ [n] =
n ≠ nmax
⎣ n ≠ nmax
⎦
2
0.5152σ β + 0.0492Es
2
= σ β2 + E ⎢
σ ISI
Q
∑
En nuestro caso:
0.0492 ⎞ 2
⎛
2
2
= ⎜ 0.5152 +
σ β2 = 0.3Es ⇒ σ ISI
⎟ σ β = 0.6793σ β
0.3 ⎠
⎝
09/10/2006
COM II
T3-98
49
Ejemplo de ecualización (XI)
• Resultando:
BER
2M −2
M log 2 M
⎛ d MMSE
Q ⎜ min
⎝ 2σ ISI
⎞
⎟=
⎠
2M −2
M log 2 M
⎛ 0.7150d
min
Q⎜
⎜ 2 0.6793σ
β
⎝
⎞
⎟
⎟
⎠
en una degradación con respecto al caso ideal sin ISI de -1,23 dB
20 log(0.7150) -10 log(0.6793) = −1.2347dB
frente a la degradación de 6,7 dB si no se utiliza el ecualizador y de
1,25dB con el forzador de ceros.
09/10/2006
T3-99
COM II
3.5 Filtros Terminales Optimos
• En este apartado consideraremos la posibilidad de diseñar la etapa de
transmisión de forma conjunta con la de recepción según el esquema
visto en la trasparencia T3-74.
α [k ]
hT [ k ]
ϕ (t )
+
hc(t)
s(t)
r baudios
ϕ (tϕ − t )
y1 (t )
tk = kT + td
hR [ k ]
yQ [ k ]
w(t)
hT [k ] ∗ p[k ] ∗ hR [k ] = δ [k − k0 ] y simultáneamente maximizar la SNR en recepción
• Este diseño implica conocimiento del canal por parte del transmisor y
receptor (en el caso de ecualización este conocimiento tan sólo es
necesario en el receptor)
09/10/2006
COM II
T3-100
50
Filtros Terminales Optimos (II)
• Formalmente el objetivo de diseño consiste calcular hT [k ], hR [ k ]
– Tal que se ecualice de forma perfecta el canal:
hT [ k ] ∗ p[k ] ∗ hR [k ] = δ [k − k0 ]
– Minimice la probabilidad de error (lo veremos para el caso MPAM)
M −2
BER M2log
Q 2σdβ
2M
( )
Q
– Manteniendo fijo el valor de la energía de bit Eb
• Como vimos para el caso del ecualizador forzador de ceros, la
potencia del ruido a la salida del ecualizador es:
σ β2 =
Q
N0
2
09/10/2006
LR
∑ ( h [ j ])
j =0
2
R
T3-101
COM II
Filtros Terminales Optimos (III)
• Cálculo de la energía por bit Eb
– La utilización de un filtro discreto en el transmisor modifica el
cálculo de la energía de símbolo trasmitida que ya no puede
calcularse directamente como la potencia de las coordenadas de
los símbolos. La expresión de la señal transmitida es:
s (t ) =
+∞
∑s
n =−∞
LT
m [ n] pT (t − nT ) ; pT (t ) = ∑ hT [ n]ϕ (t − nT )
n=0
– Como vimos al inicio de este tema, la correlación promediada de
la señal transmitida se puede expresar como:
1
1 +∞
Rˆ s (τ ) = ∫ Rs (t + τ , t )dt = ∑ Rα [m]R pT (τ − mT )
TT
T m =−∞
Es = Rˆ s (0)T =
09/10/2006
+∞
∑ Rα [m]R
m =−∞
COM II
pT
(mT )
T3-102
51
Filtros Terminales Optimos (IV)
– En el caso de M-PAM (modulación sin memoria de media nula)
se cumple:
2
Rα [ m ] = σ α2 δ [ m ] = M12−1 d 2δ [ m ]
y por tanto:
Eb =
1
log 2 M
Es =
1
log 2 M
LT
σ α2 R p (0) = 12Mlog−1M d 2 ∑ ( hT [n])
2
T
2
2
n=0
– despejando d:
d2 =
; d=
12 Eb log 2 M
( M −1)
2
LT
∑ ( hT [ n ])
2
12 Eb log 2 M
( M −1)
2
n=0
09/10/2006
LT
∑ ( hT [ n ])
2
n=0
T3-103
COM II
Ruido efectivo
Filtros Terminales Optimos (V)
• Sustituyendo en la expresión de BER:
⎛
⎛ d ⎞
2 M −2
2 M −2
BER M log2 M Q ⎜
Q⎜
⎟=
⎜ 2σ β ⎟ M log2 M ⎜⎜
Q ⎠
⎝
⎝
6 Eb log 2 M
( M 2 −1) N 0
LT
LR
∑ ( hT [ n ]) ∑ ( hR [ j ])
n =0
2
j =0
2
⎞
⎟
⎟
⎟
⎠
• Este expresión permite concluir que diseño de los filtros terminales
óptimos consiste en determinar los coeficientes que manteniendo ISI
nula minimicen la expresión:
LT
ε FT = ∑ ( hT [n])
2
n =0
LR
∑ ( h [ m])
m =0
2
R
• Este expresión sin embargo se puede minimizar considerando la
desigualdad de Cauchy-Schwartz:
LT
∑ ( hT [n])
n =0
09/10/2006
2
⎛ min{LR , LR }
⎞
2
( hR [m]) ≥ ⎜ ∑ hR [m]hT [m] ⎟
∑
m=0
⎝ m=0
⎠
LR
COM II
2
T3-104
52
Filtros Terminales Optimos (VI)
• Que expresada en el dominio frecuencial resulta:
+1/ 2
∫
H T ( f ) df
2
+1/ 2
∫
1
2π
−1/ 2
H R ( f ) df ≥
2
−1/ 2
+1/ 2
∫
2
H T ( f ) H R ( f ) df
−1/ 2
– Con igualdad para:
HT ( f ) = λ H R ( f )
• La condición de ISI nula es equivalente a:
hT [ k ] * p [ k ] * hR [ k ] = δ [ k − k0 ] ⇔ H T ( f ) P ( f ) H R ( f ) = e − j 2π fk0
• Imponiendo ambas condiciones resulta:
HT ( f ) =
λ
2
P( f )
09/10/2006
HR ( f ) =
2
;
1
λ P( f )
T3-105
COM II
Filtros Terminales Optimos (VII)
• Recordando que este diseño es que que satisfacía con igualdad la
desigualdad de Cauchy-Schwartz:
ε FTO =
+1/ 2
∫
2
H T ( f ) H R ( f ) df
2
+1/ 2
=
−1/ 2
∫
−1/ 2
1
P( f )
df
• De forma que la BER resultante es:
BER
09/10/2006
2M −2
M log 2 M
Q
( )=
d
2σ βQ
2M −2
M log 2 M
COM II
Q
(
6 Eb log 2 M
( M 2 −1) N 0 ε FTO
)
T3-106
53
Filtros Terminales Optimos (VIII)
• Procedimiento de diseño:
– Calcular:
P ( f ) = P ( f ) e j 2πφP ( f ) = ∑ p[k ]e− j 2π fk
k
– Expresar:
λ 1/ 2
HT ( f ) =
HR ( f ) =
1
λ P( f )
1/ 2
P( f )
e j 2πφR ( f ) =
1/ 2
e j 2πφT ( f )
1
λ P( f )
1/ 2
e
− j 2π ( k0 +φP ( f ) +φT ( f ) )
– Obtener las respuesta impulsional de los ecualizadores como la
aproximación FIR de:
1/ 2
hR [k ] ≈
∫
H R ( f )e j 2π fk df
1/ 2
; hT [k ] ≈
−1/ 2
09/10/2006
∫
H T ( f )e j 2π fk df
−1/ 2
COM II
T3-107
54
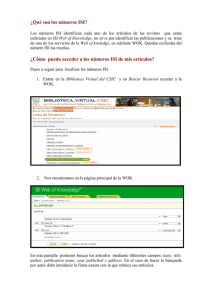




![caja capsulas dispensador de espumas isi [11620001].cdr](http://s2.studylib.es/store/data/005908580_1-6c0284c1c3fc2d86caf4c435b0f9667a-300x300.png)