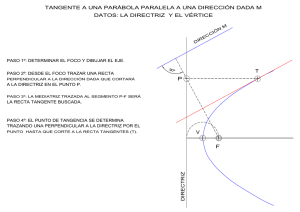
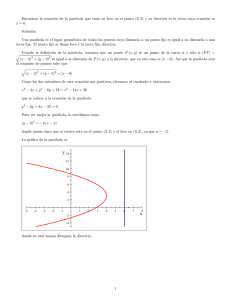
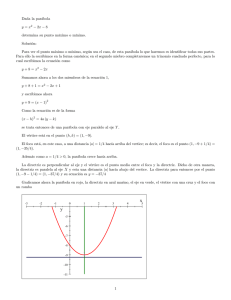
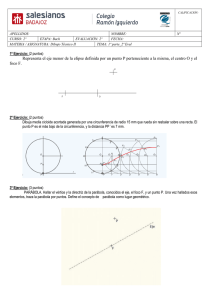
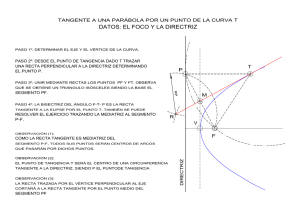
Tercer número

ISSN 0719-0077
diantes avanzados de carreras universitarias afines a
matemática, aunque también son bienvenidos artículos de tipo introductorio a temas más especializados.
Para ser considerados para publicación en el próximo
número, los artículos deben ser enviados al correo de
contacto antes del 30 de Marzo de 2012. Artículos
recibidos después de esta fecha serán considerados
para publicación en ediciones posteriores. Los artículos deben ser enviados en formato TEX, con el
correspondiente archivo PDF adjunto.
Equipo editorial:
Mark Ashbaugh
Departamento de Matemática, Universidad Missouri, Columbia, MO, EE.UU
Revista Joven Matemático, Número 3. Publicada de
forma electrónica el día 23 Enero del 2012. Próxima
edición: 30 de Marzo de 2012.
La revista cuenta con el patrocinio del Núcleo
Milenio “Teoría Matemática de Sistemas Magnéticos
Cuánticos y Clásicos”.
Contacto:
[email protected]
Suscripción:
Personas e instituciones interesadas en recibir copias
electrónicas de ediciones futuras pueden suscribirse
enviando un correo a la dirección de contacto,
indicando el nombre, ciudad, país, y afiliación en el
caso de estudiantes y profesores.
Información para autores:
Los editores invitan a alumnos y profesores a
enviar artículos para su publicación en esta revista,
previa revisión por parte del equipo editorial. Los
temas que pueden incluir los artículos son muy
variados, siendo los únicos requisitos el incluir
contenidos de índole matemática, y el que estén
escritos en lengua española. Estos pueden ser sobre
historia de las matemáticas, matemática aplicada,
física matemática, enseñanza de las matemáticas, y
cualquiera de los campos de las matemáticas puras.
El nivel de los artículos debe ser apto para estu-
Rafael Benguria
Departamento de Física, P. Universidad Católica de
Chile, Santiago, Chile
[email protected]
Sebastián García Sáenz
Departamento de Física, P. Universidad Católica de
Chile, Santiago, Chile
[email protected]
Felipe Garrido
Departamento de Física, P. Universidad Católica de
Chile, Santiago, Chile
[email protected]
Ariel Norambuena
Departamento de Física, P. Universidad Católica de
Chile, Santiago, Chile
[email protected]
Ricardo Repenning
Facultad de Ingeniería, P. Universidad Católica de
Chile, Santiago, Chile
[email protected]
Felipe Soto Arévalo
Facultad de Ingeniería, P. Universidad Católica de
Chile, Santiago, Chile
[email protected]
Francisco Vial
École Polytechnique, París, Francia
[email protected]
Artículos
Número 3 / 2011
Contenidos
El Teorema del círculo de Euler
2
La parábola
6
La paradoja de Banach Tarski
15
Sobre Desigualdades e Identidades Algebraicas
22
Funciones Continuas con Máximos Locales Densos
27
Problemas y Soluciones
34
Noticias
37
[email protected]
1
Artículos
Número 3 / 2011
EL Teorema del círculo de Euler
Gabriel Ramirez
Lycée Antoine de Saint-Exupéry, La Fase, Alliance Française
Introducción
Leonhard Euler, fue un respetado físico y matemático, tanto así que se le considera el más importante del
siglo XVIII y uno de los más importantes de todos los tiempos, todo ello gracias a sus importantes descubrimientos y avances en variadas áreas, como lo son, el cálculo, la teoría de grafos, la teoría de números y lógica.
Introdujo gran parte de la terminología y notación matemática moderna, particularmente en el área del análisis
matemático (por ejemplo, la función matemática). También se le conoce por sus aportes en los campos de la
mecánica, óptica y astronomía.
Su vida
Juventud
Euler nació el 15 de abril de 1707, en Basilea (Suiza), hijo de un pastor calvinista, Paul Euler. Poco
después de su nacimiento, su familia se traslado a Riehen, donde pasó su infancia. Su padre, era amigo de la
prestigiosa familia de matemáticos Bernoulli, entre los que destacaba Johann Bernoulli, que en ese momento
era considerado el mayor matemático europeo y quien ejercía una gran influencia sobre el joven Leonhard. La
educación formal de Euler comenzó a los 13 años cuando fue enviado a Basilea a vivir con su abuela, donde
se matriculó en la universidad de Basilea. A las 16 años recibió el título de maestro de filosofía. Por esos
tiempos, Euler recibía clases particulares de Johann Bernoulli todos los sábados por la tarde. Johann descubrió
rápidamente los talentos matemáticos de su nuevo pupilo.
San Petersburgo
Gracias a las buenas relaciones con los Bernoulli, Euler fue recomendado por Daniel Bernoulli para ocupar
una vacante libre en fisiología en la academia de ciencias de Rusia en San Petersburgo. Euler aceptó la oferta a
pesar de sus frustrados intentos de conseguir un puesto como profesor de física en la universidad de Basilea. Al
llegar a Rusia, Euler fue ascendido a un puesto en el departamento de matemáticas, donde trabajó con Daniel,
rápidamente aprendió ruso y se estableció para vivir en San Petersburgo.
[email protected]
2
Artículos
Número 3 / 2011
Berlín
A causa de los problemas políticos que estaban teniendo lugar en Rusia, Euler partió de San Petersburgo
en 1941, aceptando un cargo en la academia de Berlín ofrecido por Federico II Rey de Prusia. Vivió 25 años
en Berlín, donde escribió mas de 380 artículos y dos de sus principales obras: la Introductio in analysin infinitorum, un texto sobre las funciones matemáticas publicado en 1748, y la Institutiones calculi differentialis,
publicada en 1755 y que trataba sobre el cálculo diferencial. Además, se le ofrecía a Euler un puesto de tutor
de la princesa Anhalt-Dessau, sobrina de Federico II. Euler escribió más de 200 cartas dirigidas a la princesa
sobre varios temas de física y matemáticas, las cuales también muestran un aspecto de la personalidad de Euler
y su capacidad para enseñar y explicar ciencias a personas menos calificadas.
A pesar de todos sus avances y contribuciones hechas en Berlín, Euler se vio obligado a marcharse, principalmente a causa del conflicto que mantuvo con Federico II. Éste último, empezó a ver en Euler a una persona
poco sofisticada, en comparación con el grupo de filósofos que le rodeaban. Especialmente a causa de Voltaire,
quien era muy amigo del rey, y a diferencia de Euler, que era un hombre de carácter religioso y trabajador,
Voltaire era en cierto modo su contrario.
Tras la muerte de Catalina I de Rusia, quien era la principal colaboradora de la academia de Rusia, el poder
de la nobleza incrementó, y esta sospechaba de los científicos extranjeros como Euler, por lo que provocaron
una serie de dificultades para Euler y sus colegas. A pesar de esto, Euler logró seguir ascendiendo en la jerarquía
de la academia, convirtiéndose en profesor de física en 1931. Dos años más tarde pasó a ser Director del
departamento de matemáticas.
Retorno a Rusia
Finalmente la situación en Rusia había mejorado enormemente tras el ascenso de Catalina la grande. En
1766 Euler aceptó una invitación para volver a la academia de San Petersburgo, donde paso el resto de su vida.
El 18 de septiembre de 1783, Euler murió a causa de un accidente cerebrovascular.
Contribuciones Matemáticas
Euler realizó importantes aportes en todas las áreas de las matemáticas, destacándose entre ellas: geometría, cálculo, trigonometría, algebra, teoría de los números y muchas más. Esto muestra que ha sido uno de
los matemáticos más prolíficos de la historia. La labor de recopilar y publicar todos sus trabajos comenzó en
1911, lo cual concluyó en un total de 76 volúmenes publicados en toda su vida.
Notación Matemática
Euler introdujo y popularizó diversas notaciones matemáticas, probablemente la más importante fue la
introducción del concepto de función matemática, siendo el primero en escribir la famosa expresión f (x). Esta
nueva notación facilitó bastante la escritura y continua, hasta hoy en día, siendo la notación empleada por la
comunidad científica. También, introdujo la letra Σ como símbolo de los sumatorios y la letra i para hacer
referencia a la unidad imaginaria. Además popularizó el uso de la letra griega π, aunque no fue él quien utilizó
por primera vez este símbolo.
Número e
Euler definió la constante matemática conocida como número e como aquel número real tal que el valor
de su derivada en la función f (x) = ex en el punto x = 0 es exactamente 1.
[email protected]
3
Artículos
Número 3 / 2011
El número e es el único número real para el valor a para el cual se cumple que el valor de derivada de la
función f (x) = ax en el punto x = 0 es exactamente 1. En comparación se muestran las funciones 2x (línea
punteada) y 4x (línea discontinua), que no son tangentes a la línea de pendiente 1 (función x + 1, en rojo). La
función exponencial se muestra en color azul.
1.
La circunferencia de los nueve puntos
El nombre de la circunferencia de nueve puntos proviene del hecho que la circunferencia pasa por nueve
puntos notables, estos son: el punto medio de cada lado del triangulo, los pies de las alturas, los puntos medios
de los segmentos determinados por el ortocentro y los vértices del triangulo.
También se le conoce por círculo de Feuerbach, círculo de Euler, círculo de los seis puntos o círculo
medio-inscrito.
Historia
Generalmente se premia a Kart Feuerbach el descubrimiento de la circunferencia de los nueve puntos, pero
lo que el descubrió fue la circunferencia de 6 puntos. Anteriormente, Charles Brianchon y Jean-Victor Poncelet
habían demostrado su existencia.
Definición
Los segmentos que unen los vértices de un triángulo con el ortocentro H se denominan segmentos de Euler,
y sus puntos medios se llaman puntos de Euler, el triángulo que determinan estos puntos se llama triángulo de
Euler.
La circunferencia de los 9 puntos de un triángulo es la que pasa por los puntos medios de los lados (1, 2, 3),
por los pies de las alturas (4, 5, 6) y por los puntos medios (7, 8, 9) entre el ortocentro H y los vértices, como
se muestra en la siguiente figura
[email protected]
4
Artículos
Número 3 / 2011
El triángulo cuyos vértices son los puntos medios del triángulo 4ABC, se denomina triángulo medial.
La circunferencia de Feuerbach de un triángulo es homotética a la circunferencia circunscrita
El centro de la homotecia es el ortocentro del triángulo
La razón de la homotecia es 2
Teorema
Consideremos las alturas del triángulo 4ABC: AE, BG y CJ. El triángulo 4GEJ es el triángulo órtico
del triángulo 4ABC y el punto I es el ortocentro del triángulo 4ABC. Las alturas del triangulo 4ABC son
las bisectrices de los ángulos internos del triangulo 4GEJ. Los lados del triángulo 4ABC son las bisectrices
exteriores del triángulo 4GEJ. Las bisectrices del ángulo ]JGE cortan a la mediatriz del lado opuesto, EJ
en los puntos F y N que se hallan sobre la circunferencia circunscrita. Observemos que los triángulos 4ACJ y
4ACE son rectángulos teniendo ambos al lado AC como hipotenusa. Se sigue que los cuatro puntos A, C, E y
J son concíclicos y el centro de la circunferencia que los contiene se halla sobre la intersección de la hipotenusa
AC con la mediatriz del segmento EJ, esto es, el punto N . Se sigue que N es punto medio del segmento AC.
De modo semejante, los triángulos 4EIB y 4JIB son rectángulos compartiendo la hipotenusa IB. Por lo
tanto, los puntos E, I, J y B son concíclicos y el centro de la circunferencia que los contiene se halla sobre
la intersección de la hipotenusa IB con la mediatriz del segmento EJ, esto es el punto F . De igual modo, se
demuestra que los puntos M y P son los puntos medios de los lados AB y BC, respectivamente. De forma
análoga, se demuestra que los puntos D y H son puntos medios de los segmentos AI y CI, respectivamente.
[email protected]
5
Artículos
Número 3 / 2011
La parábola
José Lopez
Facultad de Matemáticas, PUC, Chile
Desde que en 1637 Descartes propusiera clasificar las curvas según la complejidad de las ecuaciones que
las representan, resulta natural considerar el estudio de las secciones cónicas, en cuanto se relacionan con las
ecuaciones de segundo grado. Sin embargo, las propiedades de estas curvas venían siendo extensamente investigadas por más de un milenio antes de la formulación del programa cartesiano. Esta circunstancia explica
que Galileo y Kepler hayan podido adquirir un conocimiento de ellas lo suficientemente profundo como para
reconocer que en los datos empíricos por ellos considerados subyacían parábolas y elipses. La posterior formulación de la dinámica constituyó, a su vez, un esfuerzo para dar cuenta de la intrigante aparición de las cónicas
en el mundo del movimiento natural; es decir, la intuición de ambos predecesores aportó las preguntas precisas
que Newton debió responder. La siguiente exposición, referida a la parábola, muestra la posibilidad de estudiar
las secciones cónicas desde el punto de vista de la geometría elemental, alejándose con ello, por cierto, del
enfoque que ha sido habitual desde Apolonio hasta Descartes y Fermat.
Definición A: Una parábola es el lugar geométrico de los centros de las circunferencias que pasan por un
punto dado (llamado foco de la parábola) y son tangentes a una recta dada (llamada directriz de la parábola).
De esta definición se deduce que los puntos de una parábola están a igual distancia del foco que de la directriz y, recíprocamente, todo punto equidistante del foco y de la directriz de una parábola es centro de una
circunferencia tangente a aquélla que pasa por éste. De este modo se demuestra que es equivalente a la anterior
la
Definición B: Una parábola es el lugar geométrico de los puntos que equidistan del foco y de la directriz.
Con esta última descripción resulta fácil comprobar que el punto medio del trazo perpendicular bajado desde
el foco a la directriz pertenece a la parábola. Dicho punto se denomina vértice de la parábola.
Las siguientes consideraciones están destinadas a determinar la forma de una parábola:
Proposición 1: Determinar la intersección de una parábola con una recta perpendicular a la directriz.
Análisis: Sea F el foco y δ la directriz; sea λ una recta perpendicular a
δ, que corta a ésta en Q y sea P un punto donde λ corta a la parábola.
Entonces, como P Q = P F , resulta que P está en la simetral del trazo
F Q.
[email protected]
6
Artículos
Número 3 / 2011
Basta, por lo tanto, intersecar1 la recta dada con la simetral del trazo que va desde el foco al punto de
intersección de la recta dada con la directriz.
Discusión: del análisis anterior se desprende que cualquier recta perpendicular a la directriz de una parábola corta a ésta en un punto y solamente en uno.
Las rectas que son perpendiculares a la directriz de una parábola se denominan diámetros de la parábola.
Proposición 2: Determinar la intersección de una parábola con una recta que pasa por el foco.
Análisis: Sea ahora λ una recta que pasa por el foco F , sea P un punto
en que λ corta a la parábola y sean G y Q respectivamente las proyecciones de estos puntos sobre la directriz. Entonces el triángulo F P Q
es isósceles y, por ende, los ángulos P F Q y P QF son iguales. Como,
por otra parte, las rectas P Q y F G son paralelas, el ángulo P QF es
también igual al ángulo QF G, por lo tanto, los ángulos P F Q y QF G
son iguales; esto es, F Q es bisectriz del ángulo GF P .
Construcción: Por lo anterior, basta bisectar el ángulo que la recta dada forma con la perpendicular a la
directriz trazada por el foco para encontrar la proyección del punto buscado sobre la directriz. Levantando allí
una perpendicular e intersecándola con la recta dada se encuentra el punto buscado.
Discusión: Como la recta dada forma dos ángulos con la perpendicular a λ por F , la bisectriz de cada uno
aporta una solución al problema. Por eso, toda recta que pasa por el foco de una parábola (excepto el diámetro)
corta a ésta exactamente en dos puntos.
Proposición 3: Determinar la intersección de una parábola con una recta cualquiera.
Análisis: Sea λ una recta cualquiera, pero que no sea un diámetro de la
parábola. Sea P un punto en que λ corta a dicha parábola. Entonces, la
circunferencia con centro en P que pasa por F es tangente a la directriz,
digamos, en T . Sea ρ la recta que pasa por F y es perpendicular a λ; ella
corta a la circunferencia en F y en el punto F 0 , simétrico de F respecto
a λ. Sea Q el punto donde ρ corta a la directriz (la corta, porque λ no es
un diámetro); entonces, como QT es tangente a la circunferencia y QF
y QF 0 son secantes, QT es media proporcional geométrica entre QF y
QF 0 .
Construcción: Se determina el punto F 0 , simétrico del foco F respecto a la recta dada. Se une F con F 0 y se
prolonga hasta cortar la directriz en un punto Q. Se determina la media geométrica entre QF y QF 0 y, con ese
radio, se traza circunferencia con centro en Q, la que corta a la directriz en T y T 0 . Las perpendiculares a la
directriz levantadas en estos puntos cortan a la recta dada en los puntos buscados.
1 Aunque es de uso habitual en Chile, la palabra “intersectar” no existe en el diccionario de la Real Academia Española. La palabra
correcta es “intersecar.”
[email protected]
7
Artículos
Número 3 / 2011
Discusión: La construcción anterior presupone que el punto F 0 está al mismo lado de la directriz en que está
el foco, puesto que de otro modo una circunferencia que pase por F y F 0 no podría ser tangente a la directriz
y, así, no habría intersección alguna de λ con la parábola. Por otra parte, si F 0 está, precisamente sobre la
directriz, el punto Q coincide con F 0 , de modo que QF 0 es nulo, lo mismo que su media geométrica con QF .
Así, T y T 0 coinciden en Q y, en realidad hay sólo un punto de intersección de λ con la parábola.
De la proposición anterior se deduce la importante
Proposición 4: Una recta que no es diámetro no tiene puntos en común con una parábola cuando el simétrico
del foco respecto a aquélla está separado de éste por la directriz; tiene dos puntos comunes con la parábola
cuando el simétrico del foco respecto a la recta está al mismo lado de la directriz en que está el foco y tiene
sólo un punto común cuando el simétrico del foco respecto a ella está en la directriz.
Aplicando, en particular, la Proposición 3 a una recta paralela a la directriz (de las que cortan a la parábola), se
observa que la recta F Q es la perpendicular a la directriz bajada desde el foco y que los puntos de intersección
resultan simétricos uno de otro respecto a dicha perpendicular, la que se denomina eje de la parábola, quedando
establecida la
Proposición 5: Toda parábola tiene un eje de simetría, constituído por la perpendicular a la directriz bajada
desde el foco.
Dada cualquiera de las rectas λ que cortan a la parábola en dos puntos P y P 0 , siendo Q el punto donde
la perpendicular bajada a λ desde el foco F corta a la directriz δ, resulta de la Proposición 3 que Q es el
punto medio del trazo T T 0 determinado por las proyecciones de P y P 0 sobre δ. Por ello, la perpendicular a
δ levantada en Q corta al trazo P P 0 (que es una cuerda de la parábola) en su punto medio M . Por otra parte,
si dos rectas son paralelas entre sí, las perpendiculares bajadas desde el foco a cada una de ellas se confunden
y determinan en la directriz un único punto Q. La perpendicular levantada en éste a la directriz contiene,
entonces, a los puntos medios de las cuerdas que eventualmente determinan las dos rectas en la parábola.
Queda así establecida la
Proposición 6: Los puntos medios de cuerdas paralelas se encuentran sobre un diámetro de la parábola.
En todo sistema de rectas paralelas que no sean diámetros hay exactamente una que corta a la parábola en
un solo punto (aquella que es simetral del trazo F Q de la construcción en la Proposición 3). Examinando los
simétricos del foco respecto a cada una, se comprueba que esta recta separa a las restantes paralelas en dos
clases: la de las que no cortan a la parábola y la de las que la cortan (en dos puntos). Así queda demostrada la
Proposición 7: Dada una recta que no sea diámetro y que tenga sólo un punto en común con la parábola, todos
los demás puntos de ésta se encuentran al mismo lado de la recta en que está el foco.
Las rectas que no son diámetros y tienen sólo un punto en común con la parábola se llaman tangentes a ésta; el
punto común, punto de tangencia. La proposición precedente muestra que la parábola no cruza ninguna de sus
tangentes. Las rectas que tienen dos puntos en común con la parábola se llaman secantes a ella.
La indagación de las propiedades de las tangentes se inicia enunciando la
Proposición 9: Una recta es tangente a una parábola si y sólo si el punto simétrico del foco respecto a ella se
encuentra sobre la directriz. (lo que resulta ser una consecuencia inmediata de la Proposición 4).
Proposición 10: Dados el foco y la directriz, trazar una tangente a la parábola.
[email protected]
8
Artículos
Número 3 / 2011
Análisis: cada punto de la directriz puede considerarse como el simétrico del foco respecto a una tangente.
Construcción: dado cualquier punto L en la directriz, una tangente a la
parábola es la simetral del trazo LF , siendo F el foco.
Esta construcción revela una propiedad de la tangente: si P es un punto
de la simetral de LF , resulta que LP = P F ; de modo que si LP es perpendicular a la directriz, P resulta ser un punto de la parábola y, como
está en la tangente, es el punto de tangencia; es decir, queda establecida
la
Proposición 11: El diámetro que pasa por el punto de tangencia corta a la directriz en el simétrico del
foco respecto a la tangente.
Tal diámetro se dice conjugado de la tangente y, considerando las paralelas a la tangente que son secantes de la
parábola, a la luz de la Proposición 6 resulta fácil demostrar la
Proposición 12: El diámetro conjugado a una tangente es el que contiene los puntos medios de las cuerdas
paralelas a ella.
Denominando radio focal de un punto de la parábola al trazo que lo une con el foco, resulta evidente la
Proposición 13:Toda tangente bisecta el ángulo formado por el radio focal del punto de tangencia con la
perpendicular bajada desde éste a la directriz.
Sea R el punto donde la tangente corta a la directriz. De las proposiciones precedentes se deduce que los
triángulos F P R y P LR son congruentes. Como este último es rectángulo en L, el ángulo P F R resulta ser
recto, con lo que queda demostrada la
Proposición 14: El segmento de una tangente limitado entre el punto de tangencia y la directriz se ve desde el
foco bajo ángulo recto.
Proposición 15: Dados el foco, la directriz y un punto de la parábola, trazar la tangente a ella en dicho punto.
Análisis: si P es un un punto de la parábola, L su proyección sobre la directriz y F es el foco, en virtud de lo
asegurado por la Proposición 13, la tangente a la parábola en P es la bisectriz del ángulo LP F .
Construcción: Se baja la perpendicular desde del punto dado a la directriz, se le une también con el foco y se
bisecta el ángulo asíformado. La bisectriz es la tangente pedida.
Discusión: Como L debe ser simétrico de F respecto a la tangente, ésta debe ser aquella de las bisectrices
que pasa entre F y L. De ello se deduce que hay una sola tangente a la parábola en P . Si el punto dado es el
vértice, el ángulo a bisectar resulta extendido y su bisectriz, es decir, la tangente en el vértice, resulta paralela
a la directriz.
Siendo V el vértice y A la proyección del foco en la directriz, como la proyección de F sobre la tangente es el
punto medio H del trazo LF y como AV = V F , resulta que HV es paralela a la directriz y, por lo tanto, es la
tangente a la parábola en el vértice. En consecuencia:
Proposición 16: La proyección del foco en una tangente está sobre la tangente a la parábola en su vértice.
[email protected]
9
Artículos
Número 3 / 2011
Afirmación que puede parafrasearse diciendo que, si un ángulo recto se mueve de modo que uno de sus lados
pasa siempre por un punto fijo, mientras su vértice se desliza por una recta fija, el otro lado se mueve teniendo
por envolvente una parábola.
Sea ahora N el punto donde la tangente corta al eje. La proposición 13 muestra que: ∠N P F = ∠N P L y,
como P L es paralela a F N , ∠N P L = ∠P N F , luego ∠N P F = ∠P N F y el triángulo N P F es isósceles.
Por lo tanto, queda establecida la
Proposición 17: La distancia desde el foco hasta el punto de intersección de una tangente con el eje es igual
a la distancia desde el foco hasta el punto de tangencia.
Proposición 18: Dados el foco, la directriz y un punto cualquiera, trazar por éste rectas tangentes a la parábola.
Análisis: sea λ una tangente que pasa por el punto P. Entonces el punto L, simétrico del foco F respecto a
λ se encuentra sobre la directriz δ y, como λ es la simetral del trazo F L, los puntos F y L equidistan de P .
Construcción: Se traza la circunferencia con centro en el punto dado P
y que pasa por el foco F . Se determina la intersección L de esta circunferencia con la directriz δ; la simetral λ del trazo F L es la tangente
pedida.
Discusión: Por el punto P pasarán tantas rectas tangentes a la parábola
como puntos haya de intersección entre la directriz y la circunferencia
con centro en P que pasa por el foco. Por eso, puede haber dos, una o
ninguna.
El punto P se dice exterior a la parábola si por él pasan dos rectas tangentes a ésta y se dice interior si por
él no pasan rectas tangentes a la parábola. El primer caso se da cuando la circunferencia con centro en P que
pasa por el foco corta a la directriz; el segundo, cuando no la corta. De la discusión anterior resulta claro que
por P pasa exactamente una tangente a la parábola cuando ése es un punto que pertenece a ella (porque es el
centro de una circunferencia que pasa por el foco y es tangente a la directriz). En este último caso, el punto de
tangencia es el mismo P .
Ahora bien, si P es un punto en una tangente, no puede ser interior, puesto que por él pasa, al menos, una
tangente, la cual, si P no es el punto de tangencia, no puede ser la única. En consecuencia, queda demostrada
la
Proposición 19: Los puntos de una tangente, con excepción del punto de tangencia, son puntos exteriores a la
parábola.
El estudio de la configuración de dos o más tangentes a una parábola se inicia con las siguientes observaciones:
Sean P y P 0 los puntos de tangencia de las dos tangentes trazadas a la
parábola desde un punto T . Es obvio que T equidista del foco y de los
simétricos L y L0 de éste respecto a ambas tangentes. Entonces, como L
y L0 están en la directriz y además, en virtud de la proposición 11, P L
y P 0 L0 son diámetros de la parábola, T equidista de estas dos rectas.
Por otra parte, en virtud de la proposición 13, el punto T está en las
bisectrices de los ángulos LP F y L0 P 0 F , luego también equidista de
los lados de ambos. Así, resulta demostrada la
[email protected]
10
Artículos
Número 3 / 2011
Proposición 20: El punto de intersección de dos tangente equidista de los radios focales de los puntos de
tangencia y de los diámetros conjugados de las tangentes.
Como esto dice que T equidista de los radios focales, se puede asegurar la
Proposición 21: La línea que une el foco con el punto de intersección de dos tangentes bisecta el ángulo
formado por los radios focales de los puntos de tangencia.
De la Proposición 20 se deduce también que el diámetro que pasa por T dimidia el trazo LL0 y, por lo tanto,
también dimidia P P 0 ; es decir,
Proposición 22: El diámetro trazado por el punto de intersección de dos tangentes dimidia la cuerda que une
los puntos de tangencia; es decir, es el diámetro conjugado de la tangente paralela a dicha cuerda.
Sean dos tangentes, con puntos de tangencia P 0 y P 00 , que se cortan en T ; sea una tercera tangente, con
punto de tangencia P , que corta a las dos anteriores en T 0 y T 00 respectivamente. Según la Proposición 21,
∠T 0 F P = ∠T 0 F P 0 y, de igual modo, ∠T 00 F P = ∠T 00 F P 00 , de modo que el ángulo T 0 F T 00 es la mitad del
ángulo P 0 F P 00 . De este modo queda asegurada la
Proposición 23: El segmento de una tangente móvil limitado entre dos tangentes fijas se ve desde el foco bajo
ángulo constante.
Este resultado puede hacerse más preciso notando que, si consideramos los diámetros que pasan por P 0 , T y P 00 , resulta que
cada uno de los dos ángulos en que el diámetro por T divide al
ángulo P 0 T P 00 es igual al ángulo alterno interno correspondiente
a la paralela respectiva. Pero la Proposición 13 asegura que cada tangente es bisectriz del ángulo formado por el diámetro con
el radio focal, de donde se deduce que el ángulo P 0 T P 00 equivale a la suma de los ángulos T P 0 F y F P 00 T . Pues bien, en el
cuadrilátero T P 0 F P 00 , la suma de los ángulos internos equivale
entonces a la suma del ángulo P 0 F P 00 con el doble del ángulo
P 0 T P 00 ; es decir, ∠P 0 F P 00 +2∠P 0 T P 00 = 4 rectos. Pero, como
el ángulo P 0 F P 00 es el doble del ángulo T 0 F T 00 , se deduce que
∠T 0 F T 00 + ∠P 0 T P 00 = 2 rectos, de modo que el cuadrilátero
T T 0 F T 00 es inscriptible.
De aquí resulta demostrada la
Proposición 24: La circunferencia circunscrita al triángulo formado por tres tangentes siempre pasa por el
foco.
Y resulta casi una paráfrasis de la anterior la afirmación: El lugar geométrico de los focos de las parábolas que
son tangentes a los tres lados de un triángulo es la circunferencia circunscrita a éste.
Se invita al lector a extender el estudio precedente a los otros dos géneros de cónicas, para lo cual es suficiente reemplazar, en la primera definición, “una recta dada” por “una circunferencia dada”. Resulta entonces
que la directriz es una circunferencia y el lugar geométrico corresponde a una elipse o una hipérbola según si
el foco está en el interior o en el exterior de la directriz, respectivamente.
[email protected]
11
Artículos
Número 3 / 2011
Ejercicios propuestos:
1. Diseñar diversos procedimientos para trazar parábolas, basados en la Definición B, en las Proposiciones 1 y
10 y en la paráfrasis de la Proposición 16.
2. Dados la directriz y dos puntos de una parábola, se pide determinar el foco. Discutir.
3. De una parábola se conocen el foco, la dirección del eje y una tangente. Se pide determinar la directriz, el
vértice y el punto de tangencia de la tangente dada.
4. Dados la directriz y el foco, se pide trazar una tangente que sea paralela a una recta dada. Discutir el caso en
que la recta dada sea el eje.
5. De una parábola se conocen una tangente, con su punto de tangencia, y la directriz. Se pide determinar el el
foco, el eje y el vértice.
6. De una parábola se conocen una tangente, con su punto de tangencia, y el eje. Se pide determinar el foco, la
directriz y el vértice.
7. Dados una tangente, con su punto de tangencia, y el foco, se pide determinar la directriz, el eje y el vértice.
8. Dados el foco, un punto de la parábola y la longitud de la tangente en éste (entre el punto de tangencia y el
eje), se pide determinar la directriz. Discutir.
9. Dados el eje, un punto de la parábola y la longitud de la tangente en éste (entre el punto de tangencia y el
eje), se pide determinar el foco y la directriz. Discutir.
10. Dados la directriz, un punto de la parábola y la longitud de la tangente en éste (entre el punto de tangencia
y el eje), se pide determinar el foco. Discutir.
11. Dados la directriz y los extremos de una cuerda paralela a ella, se pide determinar el foco y las tangentes
en dichos extremos. Discutir.
12. Dados la directriz y dos puntos cualesquiera de la parábola, se pide determinar las tangentes en ellos.
Discutir.
13. Dados el foco y dos puntos de la parábola, se pide determinar las tangentes en éstos. Discutir.
14. Dados la directriz, la distancia de ésta al foco y un punto P de la parábola, se pide determinar el foco y la
tangente en P . Discutir.
15. Dados el foco, la distancia de éste a la directriz y un punto de la parábola, se pide determinar la directriz y
la tangente en el punto dado. Discutir.
16. Dadas la tangente en el vértice, otra tangente y la distancia foco-directriz, se pide determinar la directriz y
el foco. Discutir.
17. Dadas la tangente en el vértice y otra tangente, esta última con su punto de tangencia, se pide determinar la
directriz y el foco.
18. Dados el foco y dos tangentes, se pide determinar la directriz y los puntos de tangencia.
[email protected]
12
Artículos
Número 3 / 2011
19. Dadas dos tangentes y la tangente en el vértice, se pide encontrar los puntos de tangencia.
20. Dados el vértice, la tangente en el vértice y otra tangente, se pide determinar el punto de tangencia de ésta.
21. Dados el foco, un punto P de la parábola y una tangente, se pide determinar la tangente en P .
22. Dadas la tangente en el vértice y otra tangente, esta última con su punto de tangencia, se pide determinar
los puntos de intersección de ambas tangentes con el eje, sin trazar éste.
23. Dados una tangente, con su punto de tangencia, la dirección del eje y otro punto P de la parábola, se pide
determinar la tangente en P .
24. Dadas dos tangentes y la tangente en el vértice, se pide determinar el foco y la directriz.
25. Dadas tres tangentes y la recta que une el punto de intersección de dos de ellas con el foco, se pide determinar los tres puntos de tangencia.
26. Dadas tres tangentes y la distancia de una de ellas al foco, se pide determinar los tres puntos de tangencia.
Discutir.
27. Dadas cuatro tangentes, se pide determinar el foco, la directriz y los puntos de tangencia. Discutir.
28. Dados el foco y la directriz, se pide trazar un triángulo de tangentes que sea semejante a un triángulo dado
y uno de cuyos lados corte al eje en un ángulo dado.
29. Dadas las directrices y el foco común de dos parábolas, se pide determinar la tangente común. Discutir.
30. Dados el foco y la directriz, se pide determinar la intersección de la parábola con la circunferencia con
centro en el foco tangente a la directriz, asícomo sus tangentes comunes.
31. Dado un triángulo isósceles, se pide determinar la parábola que es tangente a los dos lados iguales en los
extremos de la base.
32. Se denomina normal a una parábola en un punto P de ella a la recta que pasa por P y es perpendicular a la
tangente a la parábola allí. Demostrar que la normal a una parábola en P es bisectriz del ángulo formado por
el radio focal y el diámetro correspondientes a P .
33. Dado un triángulo isósceles, se pide determinar la parábola que es tangente a los dos lados iguales y cuyo
foco está en las simetrales de éstos.
34. Demostrar que el lugar geométrico de los centros de las circunferencias que son tangentes a una recta dada
y a una circunferencia dada es una parábola. Determinar su foco y su directriz.
35. Determinar una circunferencia que sea tangente a dos rectas dadas y a una circunferencia dada.
36. Demostrar que el foco de una parábola es punto interior de ella y que los puntos de la directriz son exteriores.
37. Demostrar que los puntos de una recta que no corta a la parábola son puntos exteriores a ella y que los
puntos de una cuerda, con excepción de los extremos, son interiores.
38. Demostrar que dos tangentes son ortogonales si y sólo si su punto de intersección está en la directriz y que
esto ocurre si y sólo si la cuerda que une los puntos de tangencia pasa por el foco.
[email protected]
13
Artículos
Número 3 / 2011
39. Sean p y q las longitudes de los segmentos en que el foco divide a una cuerda focal. Sea M el punto medio
de dicha cuerda. Demostrar que:
a) la media aritmética de p y q es la distancia de M a la directriz,
b) la media armónica de p y q es la distancia del foco a la directriz,
c) la media geométrica de p y q es la distancia desde el foco a la proyección H de M sobre la directriz,
d) la parábola dimidia el trazo M H,
e) el foco es la proyección de H sobre la cuerda y
f) la cuerda se ve desde H bajo ángulo recto.
40. Demostrar que el trazo que va desde el punto de intersección de dos tangentes hasta el punto medio de la
cuerda que une los puntos de tangencia es, a su vez, dimidiado por la parábola.
41. Demostrar que si desde el punto T se trazan dos tangentes a una parábola y se considera los trazos que unen
T con los puntos de tangencia,
a) los dos trazos se ven desde el foco bajo el mismo ángulo,
b) sus proyecciones sobre la directriz son iguales y
c) el ángulo que ellos forman tiene la misma bisectriz que el ángulo formado por el diámetro que pasa por T
con la recta que une a éste con el foco.
[email protected]
14
Artículos
Número 3 / 2011
La Paradoja de Banach Tarski
Ignacio Atal Chomali
École Polytechnique, París, Francia
Introducción
Teorema [Paradoja de Banach-Tarski] 1. Es posible cortar la bola cerrada de radio 1 de R3 en un número
finito de pedazos, y de conseguir, después de reordenarlos, dos veces la misma bola cerrada de radio 1.
Demostrar este resultado paradj́ico, y sobre todo entender como puede fabricarse una tal subdivisión de
la bola de radio 1 son los objetivos de este artículo, donde las ideas que existen detrás de cada demostración
son igual de interesantes que los teoremas demostrados. Demostraremos también una versión mas fuerte de
este teorema, también demostrada por Banach y Tarski. Hay que destacar que este resultado es consecuencia
directa del axioma de la elección, que permite pasar de conjuntos numerables a no numerables con una suerte
de “creación de materia”.
Es recomendable dibujar los conjuntos descritos para ver los fundamentos de las demostraciones.
1
1.1
Las Herramientas matemáticas
La equidescomponibilidad
Sean X un conjunto y G un grupo.
Definición [Operar sobre un conjunto] 1. Se dice que el grupo G opera sobre el conjunto X si existe una
aplicación G × X → X tal que la imagen de la pareja (g, x) ∈ G × X, que notaremos gx, verifica :
– ∀x ∈ X, 1G x = x
– ∀x ∈ X, ∀(g, g 0 ) ∈ G × G, (gg 0 )x = g(g 0 x)
Por ejemplo :
– El grupo de las rotaciones SO3 (R) opera sobre las partes de R3 ,
– Si H es un sub-grupo de G entonces H opera sobre G, y en particular G opera sobre sí mismo.
En lo que sigue G será un grupo que opera sobre el conjunto X, y el símbolo t denota la uniń disjunta.
Definición [Congruencia] 1. Sean A y B dos partes de X. Se dice que A es congruente a B con respecto al
grupo G si existe g ∈ G tal que A = gB ie. ∀a ∈ A, ∃b ∈ B, a = gb.
Definición [Equidescomponibilidad] 1. Sean A y B dos partes de X. Se dice que A y B son equidescomponibles (con respecto al grupo G), relación que notaremos A ∼ B, si existe una partición finita de A y de
B
n
n
G
G
A=
Ai , B =
Bi , tal que ∀i ∈ [1, n], ∃gi ∈ G , Ai = gi Bi .
i=1
i=1
Es decir que A y B son congruentes por partes.
Ejemplo 1. Ver el anexo.
Propriedad 1. La relación de equidescomponibilidad ∼ es una relación de equivalencia.
[email protected]
15
Artículos
Número 3 / 2011
Demostración : La reflexividad y la simetría son claras. Para demostrar la transitividad, hay que dividir los
conjuntos de la partición en partes más pequeñas :
Sean A, B, C subconjuntos de X tales que A ∼ B y B ∼ C. Entonces :
A=
n
G
Ai ,
i=1
B=
n
G
Bi ,
i=1
B=
m
G
Bi0 ,
C=
i=1
m
G
Ci ,
i=1
Con Ai = gi Bi , i = 1 . . . n, Bj0 = hj Cj , j = 1 . . . m. Si consideramos los conjuntos Aij = gi (Bi ∩ Bj0 ),
Cij = hj−1 (Bi ∩ Bj0 ) mostramos que A = ti,j Aij , y lo mismo para C, y para toda pareja (i, j) tenemos
Aij = gi hj Cij .
Propriedad 2. Sean A, B, C partes de X. Si A ∼ B y A ∩ C = ∅, B ∩ C = ∅, entonces (A ∪ C) ∼ (B ∪ C)
1.2
Conjuntos desdoblables
Definición [Conjunto desdoblable] 1. Sea A una parte de X. Se dice que A es desdoblable (respecto al grupo
G) si existen A1 y A2 tales que :
A = A1 t A2 ,
A ∼ A1 ,
A ∼ A2 ,
i.e. A ∼ {A, A}.
Podemos ver que el objetivo de la paradoja de Banach-Tarski es de demostrar que la bola de radio 1 de R3
es desdoblable con respecto al grupo de las isometrías de R3 . En ese caso, podremos cortar la bola de radio 1 en
dos pedazos tales que con cada uno, después de cortarlo en un número finito de pedazos y pegarlos, podamos
obtener la bola de radio 1.
Propriedad 3. Sean A y B dos partes de X tales que A sea desdoblable y A ∼ B. Entonces B es desdoblable.
Demostración : Por la transitividad de ∼, B ∼ A ∼ {A, A} ∼ {B, B}.
La existencia de conjuntos desdoblables no parece evidente, el objetivo de la segunda parte será exhibir
uno.
2
2.1
Grupos y conjuntos desdoblables
Un conjunto desdoblable : el grupo libre de dos generadores L2
Definición [Elementos independientes] 1. Sean a y b dos elementos del grupo G. Se dice que a y b son
independientes si toda palabra reducida (sin que a esté al lado de a−1 por ejemplo) no vacía hecha con las
letras a, a−1 , b, b−1 es distinta de 1G .
Nota 1. G no puede ser conmutativo. Por ejemplo en el grupo de las rotaciones del plano SO2 (R) no hay
elementos independientes.
Definición [Grupo Libre de dos generadores] 1. Si a y b son dos elementos independientes, llamamos grupo
libre de dos generadores, que notaremos L2 , el grupo engendrado por a y b.
Teorema 1. El grupo libre de dos generadores L2 es desdoblable con respecto a L2 .
Demostración : Primero, hay que destacar que aquí conjunto X de la Parte 1 es el grupo L2 , y que el grupo
G es también el grupo L2 que opera sobre sí mismo.
Para demostrar este resultado, proponemos una prueba “visual” utilizando el grafo de Cayley de L2 , presente
en el anexo, y que se basa en la idea del Hotel de Hilbert. Cada punto del grafo representa un elemento de L2 ,
donde el punto central representa 1G , y se construye de la siguiente manera :
[email protected]
16
Artículos
Número 3 / 2011
– Subir (resp. bajar) por el grafo quiere decir multiplicar a la izquierda por a (resp. a−1 ),
– Ir a la derecha (resp. izquierda) quiere decir multiplicar a la izquierda por b (resp. b−1 ).
Sea M (a) el conjunto que contiene los elementos de L2 cuya palabra representativa comienza con a, es decir
toda la rama superior del Grafo de Cayley. Multiplicar el conjunto M (a) a la izquierda por a−1 corresponde a
hacer bajar la rama superior del grafo un piso. Es decir :
a−1 M (a) = M (a) ∪ M (b) ∪ M (b−1 ) ∪ {1G },
entonces tenemos la conguencia
M (a) ∪ M (a−1 ) ∼ L2 porque a−1 M (a) ∪ M (a−1 ) = L2 ,
dado que basta con multiplicar M (a) a la izquierda por a−1 , y M (a) por 1G (ver el ejemplo del paralelogramo
en el anexo para visualizar la equidescomponibilidad). Del mismo modo mostramos que M (b) ∪ M (b−1 ) ∼
L2 .
Demostremos para terminar que M (a) ∼ M (a) ∪ {1G } .
Sea F (a) = {an , n = 1, 2, 3, . . .}, es decir la línea superior del Grafo de Cayley. Del mismo modo que antes,
basta con multiplicar este conjunto por a−1 a la izquierda para hacerlo bajar un piso.
a−1 F (a) = F (a) ∪ {1G }, luego M (a) ∪ {1g } = a−1 F (a) ∪ M (a) \ F (a) ,
entonces M (a) ∼ M (a) ∪ {1G } .
Entonces, como (M (a) ∪ {1G }) ∩ M (a−1 ) = ∅, utilizando la Propriedad 2, (M (a) ∪ {1G }) ∪ M (a−1 ) ∼ L2
por transitividad.
Así, podemos escribir que :
L2 = M (a) ∪ M (a−1 ) ∪ {1g } t M (b) ∪ M (b−1 )
con
M (a) ∪ {1G } ∪ M (a−1 ) ∼ L2 y M (b) ∪ M (b−1 ) ∼ L2 .
Lo que da el resultado : L2 es desdoblable.
Propriedad 4. L2 es numerable.
2.2
Pasar de un grupo desdoblable a un conjunto desdoblable
Definición [Operar libremente] 1. Sean G un grupo y X un conjunto. Se dice que G opera libremente sobre
X si
∀x ∈ X, ∀g ∈ G \ {1G }, gx 6= x
Es decir, si todo elemento de G distinto del elemento neutro no deja ningún punto fijo en X.
Teorema 2. Si G es un grupo desdoblable (con respecto a sí mismo) que opera libremente sobre el conjunto
X, entonces X es desdoblable (con respecto a G).
Demostración : La demostración se basa en un traslado de esctructura entre el grupo G y el conjunto X
que deja estable la congruencia, la reunión y la disjunción, y que deja entonces estable la equidecomponibilidad
y el carácter de desdoblable.
Sea R la relación de equivalencia sobre las partes de X tal que :
∀(x, y) ∈ X 2 ,
xRy
⇔
∃g ∈ G, x = gy
Las clases de equivalencia para R son las órbitas de X con respecto al grupo G, es decir tienen la forma Gx
donde x está en X.
Elijamos, gracias al axioma de la elección un sistema de representantes de estas órbitas que denotaremos M :
∃M,
[email protected]
∀x ∈ X,
∃y ∈ M,
Gx = Gy,
17
Artículos
∀(x, y) ∈ M × M,
Número 3 / 2011
Gx = Gy ⇒ x = y
De este modo, para toda parte A en G notemos
A∗ =
[
Ax
x∈M
La función que va de las partes de G a X que a A asocia A∗ conserva la congruencia y la reunión. Es decir que
si A = gB entonces A∗ = gB ∗ , y (A ∪ B)∗ = A∗ ∪ B ∗ .
Mostremos que la disjunción se conserva, es decir que si A ∩ B = ∅ entonces A∗ ∩ B ∗ = ∅. Aquí es necesario
el hecho que G opera libremente sobre X. Por el absurdo, sea x ∈ A∗ ∩ B ∗ , entonces
∃m1 ∈ M, a ∈ A,
∃m2 ∈ M, b ∈ B,
x = am1 = bm2
Lo que da que m1 = a−1 bm2 , entonces m1 ∈ Gm2 , entonces por construcción de M , m1 = m2 , y como
el único elemento de G que deja estable un elemento de X es el elemento neutro, tenemos que a = b, pero
A ∩ B = ∅, lo que da la contradicción.
Para terminar, G∗ = ∪x∈M Gx = X por construcción de M .
Directamente, si A ∼ B, entonces A∗ ∼ B ∗ , y entonces si A es desdoblable, A∗ es también desdoblable.
Más precisamente, si G es desdoblable con respecto a sí mismo, entonces G∗ = X es también desdoblable con
respecto a G.
Nota : En esta transferencia de estructura, si M no es numerable, permite pasar de un desdoblamiento
de un conjunto numerable (si G es numerable) al desdoblamiento de un conjunto no numerable (un conjunto
X no numerable tal que G opere libremente sobre X), he aquí la importancia del axioma de la elección en la
demostración.
3
Demostración de la Paradoja de Banach-Tarski
Ahora hay que poner todos estos resultados teóricos en práctica, en el caso del grupo de las isometrías de
R3 , y de la bola cerrada de radio 1 de R3 .
3.1
La Paradoja de Banach-Tarski-Hausdorff
Propriedad 5. El grupo de las rotaciones SO3 (R) tiene dos elementos independientes.
Demostración : Las rotaciones con un ángulo θ entre 0 y
grupo libre (es un cálculo sin mucho interés).
π
2
tal que cos θ =
1
3
con ejes x y z engendran un
Teorema 3 (Paradoja de Hausdorff-Banach-Tarski). Existe un conjunto numerable D en la esfera de radio
1 S2 tal que S2 \ D sea desdoblable con respecto a SO3 (R).
Demostración : Sea L2 el subgrupo de SO3 (R) engendrado por dos elementos libres de SO3 (R). L2 es
denumerable gracias a la Propriedad 4. Sólo hace falta encontrar un conjunto numerable D de S2 tal que L2
opere libremente sobre S2 \ D. Consideremos el conjunto D de la intersección entre los ejes de rotación de las
rotaciones (distintas del elemento neutro) de L2 y la esfera S2 . Claramente D es denumerable y L2 \ {Id} no
deja ningún elemento fijo en S2 \ D, lo que da el resultado que buscábamos usando el último teorema.
3.2
La Paradoja de la Esfera
Teorema 4 (La Paradoja de la Esfera). La esfera S2 es desdoblable.
[email protected]
18
Artículos
Número 3 / 2011
Demostración : Para esto, vamos a demostrar que S2 \ D ∼ S2 . Así, aplicando la Propriedad 3 y la
Paradoja de Banach-Tarski-Hausdorff tenemos directamente el resultado.
La idea de la demostración se basa en el principio del Hotel de Hilbert que consiste en “mover a la gente para
hacer cupo”. Mostremos primero que, en el plano complejo, notando C el círculo de radio 1 centrado en el
origen, tenemos que C ∼ C \ {1}. Sea r una rotación de centro O y de ángulo α tal que α
π sea irracional. En
ese caso,
∀n = 1, 2, 3, . . . , rn (1) 6= 1
S
Entonces, considerando el conjunto A = n≥0 rn (1), tenemos que :
r A = A \ {1}
entonces, C \ {1} = r(A) ∪ C \ A
Lo que da la relación de equidescomponibilidad C ∼ C \ {1}.
Ahora hay que hacer lo mismo, pero en dimensión 3 y con un conjunto numerable. Hay que encontrar una
rotación r tal que para todo entero natural n tengamos que rn (D) ∩ D = ∅.
Como D es denumerable, existe x0 en S2 \ D. Consideremos entonces d el eje (Ox), que no pasa por ningún
punto de D. Luego, consideremos rθ la rotación de ángulo θ y de eje d.
∀(x, y) ∈ D2 , n ∈ N ∪ {0}
Entonces,
Θ=
[
Θn,(x,y) = {θ ∈ R, rθn (x) = y} es denumerable.
[
Θn,(x,y)
es también denumerable
n∈N (x,y)∈D 2
Por lo tanto existe α ∈ R \ Θ. Así, la rotación rα es la rotación que buscábamos por construcción. Si consideramos
[
A=
rαn (D)
n∈N
podemos concluir la demostración igual que en el ejemplo anterior del plano complejo.
3.3
La Paradoja de Banach-Tarski (versión débil)
Teorema 5 (La Paradoja de Banach-Tarski (versión débil)). La bola cerrada de radio 1 de R3 es desdoblable.
Demostración : Mostremos primero que B(O, 1) \ {O} es desdoblable. Para eso, para todo conjunto A en
la esfera S2 consideremos
[
A∗ =
]0, 1]x
x∈A
∗
es decir, A es la reunión de los segmentos que unen los elementos de A al orígen O, privado de {O}. De
este modo, la función que a A le asocia A∗ es una transferencia de estructura que conserva la congruencia,
la reunión y la intersección
vacía, entonces conserva la equidescomponibilidad y el desdoblamiento. Como
(S2 )∗ = B(O, 1) \ {O} , entonces B(O, 1) \ {O} es desdoblable.
Mostremos ahora que B(O, 1) ∼ B(O, 1)\{O} . Para esto, consideremos x en B(O, 1)\{O}, y P un plano
que contiene
la recta (Ox). Luego, consideremos el círculo
C en P de centro O que contiene x. Ya vimos que
C \ {x} ∼ C. Entonces B(O, 1) ∼ B(O, 1) \ {x} , y haciendo una translación de O hacia x tenemos
claramente que B(O, 1) \ {x} ∼ B(O, 1) \ {O} . Tenemos así el resultado por transitividad.
Como B(O, 1) \ {O} es desdoblable, utilisando la Propriedad 3, B(O, 1) es desdoblable.
3.4
La Paradoja de Banach-Tarski (versión fuerte)
Teorema 6 (Paradoja de Banach-Tarski (versión fuerte)). Todas las partes acotadas de interior no vacío de
R3 son equidescomponibles entre ellas.
[email protected]
19
Artículos
Número 3 / 2011
Antes de demostrar este teorema hay que demostrar un par de resultados preliminares.
Teorema 7 (Cantor-Bernstein). Sean A y B dos partes de X. Si A es equidescomponible con una parte de
B, y B es equidescomponible con una parte de A, entonces A es equidescomponible con B.
Demostración : Para empezar, si A y B son dos partes de X tales que A ∼ B, entonces existe una bijección
g de A a B. Ya que, retomando las notaciones de la primera parte, definimos g de la manera siguiente : si x
está en Ai , g(x) = gi x.
Partiendo de esto, la demostración es la misma que para demostrar la versión clásica del teorema de CantorBernstein. Disponemos, gracias a lo que precede, de g una inyección de A en B, y h una inyección de B en A.
El argumento genealógico es el siguiente :
Sea y un elemento de B. Construimos la secuencia (yn ) que puede ser finita de la manera siguiente :
– y0 = y. Si y 6∈ Im(g) nos detenemos. Sino, ∃!x ∈ A tal que y = g(x).
– y1 = x. Si y 6∈ Im(h) nos detenemos. Y continuamos así.
Del mismo modo, para todo x en A construimos la secuencia (xn ). Consideremos los conjuntos siguientes :
– Ap = {x ∈ A, card((xn )) es par}, y del mismo modo Bp .
– Aimp = {x ∈ A, card((xn )) es impar}, y del mismo modo Bimp .
– A∞ = {x ∈ A, (xn ) es infinito}, y del mismo modo B∞ .
Tenemos entonces g(A∞ ) = B∞ , g(Ap ) = Bimp , h−1 (Aimp ) = Bp .
con
A = A∞ t Ap t Aimp ,
y lo mismo para B.
Esto nos da una relación de de equidescomponibilidad entre A y B, considerando las intersecciones de
A∞ , Ap , Aimp con los elementos de la partición (Ai )i para tener la congruencia por partes (ya que h y g no
son elementos de G).
Propriedad 6. Dos bolas cerradas de R3 de radio cualquiera son equidescomponibles.
Demostración : Usemos el teorema anterior. Si los radios de B1 et B2 son respectivamente r y R, r < R,
una parte de B1 es equidescomponible a una parte de B2 . Luego, considerando el conjunto de bolas de radio r,
{b1 , . . . , bn }, tales que su reunión cubra por completo la bola B2 . Sea, para i = 1 . . . n :
[ G
c i = bi ∩ B 2 \
bj
entonces B2 =
ci ,
j6=i
i
y cada uno de los ci es equidescomponible a una parte de bi . Entonces tenemos que B2 es esquidescomponible
a una parte de {b1 , . . . , bn }. Pero, iterando la Paradoja de Banach-Tarski, tenemor que {b1 , . . . , bn } ∼ B1 .
Por transitividad, B2 es equidescomponible a una parte de B1 . Aplicando el teorema de Cantor-Bernstein, tenemos el resultado.
Demostración de la Paradoja de Banach-Tarski : Sean C y D dos partes acotadas y de interior no vacío de
R3 , y b1 , B1 , b2 , B2 bolas cerradas tales que b1 ⊂ C ⊂ B1 y b2 ⊂ D ⊂ B2 . Usando la proposición anterior,
B1 ∼ b2 , y C es equidescomponible a una de B1 , entonces C es equidescomponible a una parte de b2 ⊂ D. La
simetría del problema nos da que D es equidescomponible a una parte de C. El teorema de Cantor-Bernstein
se aplica, lo que nos da el resultado.
Conclusión
Para demostrar la Paradoja de Banach-Tarski, primeramente tuvimos que introducir las nociones de equidescomponibilidad y de conjuntos desdoblables que traducen matemáticamente el enunciado, y que tienen propriedades
que simplifican las demostraciones. Con esas herramientas, y gracias a la existencia de elementos independientes en SO3 (R), podemos demostrar la existencia de un conjunto (un sub-grupo) desdoblable y numerable en
el grupo de las isometrías del espacio, isomorfo al grupo libre de dos generadores L2 . Luego, subdividiendo
[email protected]
20
Artículos
Número 3 / 2011
S2 en las órbitas deducidas de la acción de L2 , y eligiendo un sistema de representantes de esas órbitas (que es
claramente no numerable por numerabilidad de L2 ) usando el axioma de la elección podemos desdoblar casi
toda la esfera (la esfera privada de un conjunto numerable), podemos así “crear materia” no numerable. Así,
para demostrar que toda la esfera es desdoblable solo hace falta “crear materia” numerable, usando la idea del
Hotel de Hilbert.
Éstas son las ideas que son la base de esta paradoja que permite demostrar que no existe una medida que sea
finitamente aditiva, invariante por las isometrías, y definida en todas las partes acotadas de R3 .
Bibliografía
[1] Muller, J. “Le Paradoxe de Banach-Tarski”. Tesis presentada.
[2] Guinot, M. Le Paradoxe de Banach-Tarski. Aléas, 2002, 135 p.
[3] Choimet,D., Queffélec, H. “Les paradoxes de Hausdorff-Banach-Tarski” en Analyse Mathématique.
Grands théorèmes du vingtième siècle. Calvage et Mounet, 2009. p.139-170. (Tableau Noir).
[4] Wikipedia. “Le Graphe de Cayley” (actualizada el 04/09/2009) en el sitio wikipedia.org.
[5] Problema de la agregación interna francesa del 2005. “Emsembles paradoxaux”.
[email protected]
21
Artículos
Número 3 / 2011
Sobre desigualdades e identidades algebraicas
Andrés Navas
Universidad de Santiago de Chile, Santiago, Chile, [email protected].
La desigualdad clásica entre las media aritmética y geométrica, a saber,
√
x1 + x2 + · · · + xn
≥ n x1 x2 · · · xn ,
n
donde xi ≥ 0,
(1)
es tal vez la más hermosa de las desigualdades elementales. Por lo mismo, en la literatura existen muchos
tratamientos de ella con diversas demostraciones: vea por ejemplo la referencia [2] (vea también el Problema
1 del apéndice de esta Nota para una prueba al parecer novedosa). Nuestro propósito aquí no es rediscutir la
desigualdad desde una perspectiva clásica, sino presentar una aproximación puramente algebraica y no muy
ampliamente conocida basada en una identidad notable.
Primeramente, reemplazando cada xi por a2i , observamos que (1) es equivalente a que el polinomio
2n
2n
2 2
2
Pn (a1 , . . . , an ) := a2n
1 + a2 + · · · + an − na1 a2 · · · an
sólo asume valores no negativos. Ahora bien, una manera simple de mostrar que una expresión sólo toma valores no negativos consiste en reescribirla como suma de cuadrados. Motivado por una charla de Ricardo Baeza
el año pasado, me pregunté si el polinomio Pn puede ser escrito como suma de cuadrados de polinomios. Tras
obtener una respuesta afirmativa a esto, realicé una búsqueda en internet hasta constatar que “mi descubrimiento” correspondía a un teorema prácticamente olvidado del matemático alemán A. Hurwitz que data del año
1891 y que se resume en (la segunda de) las identidades
(a2(n−k) − b2(n−k) )(a2 − b2 ) = (a2 − b2 )2
n−k−1
X
a2j b2(n−k−j−1) ,
j=1
Pn (a1 , . . . , an ) =
n−1
X X 2(n−k)
1
2(n−k) 2
aσ(1) − aσ(2)
aσ(1) − a2σ(2) a2σ(3) a2σ(4) · · · a2σ(k+1) ,
2(n − 1)!
(2)
k=1 σ∈Sn
donde σ recorre el conjunto Sn de las n! permutaciones de {1, . . . , n} (vea el apéndice para una “prueba
guiada” de la segunda identidad). Observe que (2) también muestra que, en caso de igualdad en (1), todos los
términos a2i deben ser iguales. Como ejemplos ilustrativos de (2) tenemos la identidad evidente
P2 (a1 , a2 ) = a41 + a42 − 2a21 a22 = (a21 − a22 )2 ,
y el hecho que
2P3 (a1 , a2 , a3 ) = 2a61 + 2a62 + 2a63 − 6a21 a22 a23
coincide con
a21 (a21 −a22 )2 +a21 (a21 −a23 )2 +a21 (a22 −a23 )2 +a22 (a22 −a21 )2 +a22 (a22 −a23 )2 +a22 (a21 −a23 )2 +a23 (a23 −a21 )2 +a23 (a23 −a22 )2 +a23 (a21 −a22 )2
(alternativamente, se puede usar la identidad x3 + y 3 + z 3 − 3xyz = (x + y + z)(x2 + y 2 + z 2 − xy − yz − zx),
la cual lamentablemente carece de análogo en más variables). Para n = 4 obtenemos
P4 (a1 , a2 , a3 , a4 ) = a81 + a82 + a83 + a84 − 4a21 a22 a23 a24 = (a41 − a42 )2 + (a43 − a44 ) + 2(a21 a22 − a23 a24 )2 .
[email protected]
22
Artículos
Número 3 / 2011
Dejamos al lector la tarea de desarrollar (pacientemente) la identidad para n = 5 y para valores mayores de
n. Debemos señalar sin embargo que estas expresiones no siempre son optimales. En efecto, la expresión de
P2n arriba usa un número de cuadrados que es exponencial en n, pero existen reescrituras en las cuales el la
cantidad de cuadrado utilizados es lineal en n (vea referencia [5]).
Inmediatamente surge una pregunta: ¿puede siempre una desigualdad entre polinomios (a coeficientes
reales) ser reducida al hecho que cierta expresión polinomial puede ser reescrita como suma de cuadrados de
polinomios (a coeficientes reales)? Como vemos a seguir, diversos ejemplos apuntan en una dirección afirmativa.
Ejemplo 1. Todo polinomio en una variable que es no negativo sobre toda la recta puede ser escrito como suma
de cuadrados de polinomios: vea el Problema 3.
Ejemplo 2. La desigualdad de Cauchy-Schwarz
(a21 + · · · a2n )(b21 + · · · + b2n ) ≥ (a1 b1 + · · · an bn )2
puede ser inferida (junto con el caso de igualdad) de la identidad de Lagrange
X
(a21 + · · · a2n )(b21 + · · · + b2n ) − (a1 b1 + · · · an bn )2 =
(ai bj − aj bi )2 .
1≤i<j≤n
Ejemplo 3. Dados exponentes m1 ≥ m2 ≥ . . . ≥ mk y n1 ≥ n2 ≥ . . . ≥ nk , supongamos que las siguientes
relaciones se satisfacen:
m1 + · · · + mi ≥ n1 + · · · + ni
para todo 1 ≤ i < k,
m1 + · · · + mk = n1 + · · · + nk .
Entonces para toda k-upla de reales no negativos (x1 , . . . , xk ) se tiene la desigualdad de Muirhead
X mσ(1)
X nσ(1)
m
n
x1
· · · xk σ(k) ≥
x1
· · · xk σ(k) .
σ∈Sk
(3)
σ∈Sk
Por ejemplo, haciendo m1 = 1, m2 = . . . = mk = 0 y n1 = . . . = nk = 1/k, lo anterior se reduce a la
desigualdad entre las medias aritmética y geométrica.
Si los exponentes mi , ni son enteros no negativos, entonces es posible probar (vea el Problema 4) que el
polinomio correspondiente
X 2mσ(1)
X 2nσ(1)
2m
2n
P (a1 , . . . , ak ) =
a1
· · · ak σ(k) −
a1
· · · ak σ(k)
σ∈Sk
σ∈Sk
puede ser escrito como suma de cuadrados de polinomios.
Pese a la evidencia anterior, la respuesta a nuestra pregunta no siempre es afirmativa. Este hecho ya era
conocido por D. Hilbert, pero tal vez el ejemplo más simple que lo ilustra es el famoso polinomio de Motzkin
[4] (vea el Problema 5)
M (a, b) = 1 − 3a2 b2 + a2 b4 + a4 b2 .
Sin embargo, puede probarse que todo polinomio que asume sólo valores no negativos puede ser escrito como
suma de cuadrados de funciones racionales. Esto corresponde a un teorema profundo debido a E. Artin [1] que
responde al problema número 17 de la famosa lista de 20 problemas de Hilbert. A modo de ejemplo, para el
polinomio de Motzkin tenemos
M (a, b) =
a2 b2 (a2 + b2 + 1)(a2 + b2 − 2)2 + (a2 − b2 )2
.
(a2 + b2 )2
[email protected]
23
Artículos
Número 3 / 2011
No es nuestro propósito aquí el discutir las ideas de la demostración de Artin ni su inmensa influencia en
el desarrollo de la teoría de los cuerpos ordenados y las aplicaciones de la lógica matemática a ella. Lo que
quisiéramos es más bien invitar al lector a desarrollar los ejercicios/problemas del apéndice y, si estos logran
despertar su interés, permitirle acceder a esta bonita teoría a través de la breve bibliografía entregada al final.
Apéndice: algunos problemas relacionados.
Problema 1: Una demostración inductiva y aparentemente novedosa (aunque no la más simple) de la
desigualdad entre las medias aritmética y geométrica.
(i) Por la desigualdad para el caso de dos variables, para x, y, z no negativos tenemos
x + y ≥ 2x1/2 y 1/2 ,
y + z ≥ 2y 1/2 z 1/2 ,
z + x ≥ 2z 1/2 x1/2 .
Sumando y diviendo por 2 obtenemos
x + y + z ≥ x1/2 y 1/2 + y 1/2 z 1/2 + x1/2 z 1/2 .
Usando nuevamente la desigualdad para dos variables tenemos
x1/2 y 1/2 +y 1/2 z 1/2 ≥ 2x1/4 y 1/2 z 1/4 ,
y 1/2 z 1/2 +z 1/2 x1/2 ≥ 2x1/4 y 1/4 z 1/2 ,
z 1/2 x1/2 +x1/2 y 1/2 ≥ 2x1/2 y 1/4 z 1/4 ,
lo que tras sumar y dividir por 2 nos da
x + y + z ≥ x1/2 y 1/2 + y 1/2 z 1/2 + x1/2 z 1/2 ≥ x1/2 y 1/4 z 1/4 + x1/4 y 1/2 z 1/4 + x1/4 y 1/4 z 1/2 .
Repitiendo el proceso k veces, pruebe usando inducción que
x + y + z ≥ xmk y (1−mk )/2 z (1−mk )/2 + xmk y (1−mk )/2 z (1−mk )/2 + x(1−mk )/2 y (1−mk )/2 z mk ,
(4)
donde m1 = 0 y mk+1 = (1 − mk )/2. Usando esta relación de recurrencia pruebe (sin necesidad de calcular
explícitamente el valor de mk ) que mk converge al único punto fijo de la función m → (1 − m)/2, es decir, a
1/3. Pasando al límite la desigualdad (4), concluya que
x + y + z ≥ 3x1/3 y 1/3 z 1/3 .
(ii) Generalice el argumento anterior para probar que la desigualdad para n variables implica la de n + 1
variables para todo n ≥ 2.
Problema 2: La identidad de Hurwitz. Mediante argumentos de conteo, pruebe que el coeficiente del monomio
a2+2i
a22 · · · a2n−i en la expresión a derecha de (2) es igual a −n si i = 0, a 1 si i = n − 1, y a 0 en otro caso.
1
Concluya así la validez de la identidad de Hurwitz.
Problema 3: Polinomios no negativos de una variable. Sea P (x) un polinomio tal que para todo x ∈ R se
tiene P (x) ≥ 0.
(i) Pruebe que P es de grado par.
(ii) Pruebe que toda raíz real de P tiene multiplicidad par.
(iii) Usando (ii) y aplicando la identidad
x − (a + bi) x − (a − bi) = (x − a)2 + b2
a cada par de raíces complejas conjugadas de P , concluya que P puede ser escrito como suma de cuadrados de
binomios, monomios y reales positivos.
[email protected]
24
Artículos
Número 3 / 2011
Problema 4: La desigualdad de Muirhead y sumas de cuadrados. Suponga que los exponentes mi , ni
verifican las propiedades del Ejemplo 3 (lo cual denotaremos (mi ) (ni )) y existe i tal que mi 6= ni .
(i) Pruebe que si i (resp. j) es el menor (resp. mayor) índice para el cual los exponentes no coinciden, entonces
mi > ni (resp. mj < nj ).
(ii) Sean i, j índices tales que mi > ni , mj < nj , y ml = nl para todo i < l < j. Sea
2` = mín{mi − ni , nj − mj }.
Definamos m0r = mr si r 6= i, j y m0i = mi − `, m0j = mj + `. Pruebe que (m0i ) (ni ) y que el número
de entradas del vector (m0i ) que coinciden con las correspondientes de (ni ) supera en 1 al número de entradas
en común entre (mi ) y (ni ).
(iii) Defina `0 = mi − mj ≥ `. De la identidad
0
0
a2mi b2mj + b2mi a2mj − a2mi −2` b2mj +2` − b2mi −2` a2mj +2` = a2mj b2mj (a2` −2` − b2` −2` )(a2` − b2` ),
concluya que la expresión a izquierda puede ser escrita como suma de cuadrados de polinomios. Usando esto,
concluya que lo mismo vale para la diferencia
X
2mσ(1)
a1
2mσ(k)
· · · ak
σ∈Sk
−
X
2m0σ(1)
a1
2m0σ(k)
· · · ak
.
σ∈Sk
(iv) Usando (ii) y (iii) a lo más k veces, concluya que el polinomio
X 2mσ(1)
X 2nσ(1)
2m
2n
P (a1 , . . . , ak ) =
a1
· · · ak σ(k) −
a1
· · · ak σ(k)
σ∈Sk
σ∈Sk
puede ser escrito como suma de cuadrados de polinomios.
Problema 5: Sobre el polinomio de Motzkin.
(i) Usando la desigualdad entre las medias aritmética y geométrica (a 3 variables), pruebe que el polinomio
M (a, b) = 1 − 3a2 b2 + a2 b4 + a4 b2 no asume valores negativos.
(ii) Suponga que M puede escribirse como suma de cuadrados de polinomios Mi . Pruebe que cada Mi tiene
grado a lo más 3. Analizando coeficientes, pruebe que Mi es combinación
de 1, ab, a2 b, ab2 . Finalmente,
P lineal
2 2
2
obtenga una contradicción examinando el coeficiente de a b en M y i Mi .
Problema 6: Límites de sumas de cuadrados. Aplicando el teorema de aproximación de Stone-Weiertrass,
pruebe que toda función continua f : Rd → R que asume sólo valores no negativos puede ser aproximada
uniformemente sobre los compactos por cuadrados de polinomios.
Problema 7: Sobre la desigualdad de Minkowski. Para todo n ≥ 1 y toda familia de reales no negativos
x1 , . . . , xn , y1 , . . . , yn se tiene (vea referencia [2])
n
Y
! n1
(xi + yi )
≥
i=1
n
Y
! n1
xi
+
i=1
n
Y
! n1
yi
.
i=1
¿Puede el polinomio
P (a1 , . . . , an , b1 , . . . , bn ) =
n
Y
(a2n
i
i=1
+
b2n
i )
−
n
Y
i=1
a2i
+
n
Y
!n
b2i
i=1
ser escrito como suma de cuadrados de polinomios?
[email protected]
25
Artículos
Número 3 / 2011
Referencias
[1] E. A RTIN . Uber die Zerlegung definiter Funktionen in Quadrate. Abh. Math. Sem. Univ. Hamburg 5 (1927),
85-99.
[2] G. H. H ARDY, J. E. L ITTLEWOOD & G. P ÓLYA . Inequalities. Cambridge Mathematical Library (1934).
[3] D. H URWITZ . Über den Vergleich des arithmetischen und des geometrischen Mittels. Ver: Math. Werke, Basel,
E. BerkhÃd’user (1933), 505-507.
[4] T. S. M OTZKIN . The arithmetic-geometric inequality. 1967 Inequalities (Proc. Sympos. Wright-Patterson Air
Force Base, Ohio, 1965), 205-224.
[5] B. R EZNICK . A quantitative version of Hurwitz’ theorem on the arithmetic-geometric inequality. J. für die reine
und ang. Math. 377 (1987), 108-112.
[email protected]
26
Artículos
Número 3 / 2011
Funciones continuas con máximos locales densos
Godofredo Lommi
Facultad de Matemáticas, PUC, Chile, [email protected]
Resumen
En este artículo estudiaremos la clase de funciones continuas que poseen máximos estrictos locales en un
conjunto denso. Siguiendo el trabajo de Posey y Vaughan construiremos un ejemplo explícito de una función
que pertenece a dicha clase. Finalmente, siguiendo a Dorbot y Morayne, probaremos que el conjunto de
funciones con máximos densos es residual. Proponemos además algunos problemas para el lector.
1.
Introducción
Las funciones continuas son, en general, bastante menos regulares de lo que de lo que podría esperarse.
Un ejemplo clásico de lo anterior son las funciones continuas no diferenciables en ningún punto. Hasta antes
de 1850 la idea de que las funciones continuas eran diferenciables excepto, a lo más, en un número finito de
puntos, estaba absolutamente extendida. Por ejemplo, en el texto de Cálculo de J. L. Raabe, Die Differentialund Integralrechnung, publicado en 1839, la afirmación anterior aperece como Teorema. En 1861 Riemann
propuso la siguiente función
∞
X
sin(n2 x)
.
(1)
f (x) =
n2
n=1
Esta función es continua en toda la recta real, sin embargo no es diferenciable en ningún punto irracional (resultado que fue probado por Hardy en 1916). Sin embargo, existen infinitos puntos racionales donde la función es
diferenciable. Tras los trabajos de Bolzano, Hankel y varios otros, finalmente en 1872 Karl Weierstrass probó
que la función
∞
X
f (x) =
bn cos(an πx),
(2)
n=0
donde a ∈ N es impar, b ∈ (0, 1) y ab > 1 + 3π/2 es continua en toda la recta real y no es diferenciable en
ningún punto. Es interesante recalcar que la mayoría de los ejemplos de este tipo de funciones se construyen
utilizando series de funciones.
La situación es aún más sorprendente. Los ejemplos anteriores no son la excepción. Es posible demostrar que,
en un sentido preciso, la mayoría de las funciones continuas no son diferenciables en ningún punto.
Estas notas estan dedicadas a otra clase de funciones que han recibido mucho menos atención. A saber, funciones continuas tales que el conjunto de máximos locales estrictos (ver Definición 1.1) es denso en el dominio.
Para esta clase de funciones es posible obtener resultados análogos a los de las funciones continuas no diferenciables. En particular, es posible contruir ejemplos explícitos utilizando series de funciones (ver Sección 2) y
es posible probar que la mayoría de las funciones continuas satisface esta propiedad (ver Sección 3). Desarrollaremos estas ideas además de proponer algunos problemas. A continuación definiremos de un modo preciso
la clase de funciones que vamos a considerar.
[email protected]
27
Artículos
Número 3 / 2011
Definición 1.1. Diremos que una función f : R → R posee un máximo local estricto en x = c si existe > 0
tal que para todo x ∈ (c − , c + ) se tiene que f (c) > f (x) (análogamente podemos definir mínimo local
estricto).
Dada una función f : K ⊂ R → R definimos el conjunto de máximos locales estrictos de f por
M (f ) := {x ∈ R : x es un máximo local estricto para f } .
Schoenflies [5] en 1900 demostró que el conjunto de puntos máximos locales estrictos de una función continua
es a lo más numerable.
Teorema 1.1 (Schoenflies 1900). Sea f : R → R una función continua, entonces el conjunto M (f ) es a lo
más numerable.
Demostración. Consideremos el conjunto de intervalos abiertos con extremos racionales,
B := {(a, b) ⊂ R : a, b ∈ Q} .
El conjunto B es una base numerable de la topología usual en R. Para cada máximo local estricto x ∈ R de f
sea (ax , bx ) ∈ B un intervalo tal que si x ∈ (ax , bx ) y si y ∈ (ax , bx ) \ {x} entonces f (y) < f (x). El resultado
se obtiene notando que la correspondencia x 7→ (ax , bx ) es uno a uno.
No es difícil construir una función continua que posea máximos locales en un conjunto numerable.
n
o
1
1
Ejemplo 1. Consideremos la partición de [0, 1] dada por
,
:
n
∈
N
. En cada uno de estos intervalos
n+1 n
2n+1
definiremos la función f de modo que sea decreciente y lineal en el intervalo 2n(n+1)
, n1 y creciente y lineal
2n+1
1
2n+1
1
en n+1
. Notemos que x = 2n(n+1)
, 2n(n+1)
es el punto medio del intervalo n+1
, n1 . Sea f : [0, 1] → R
definida para todo n ∈ N por

2n + 1
2n + 1 1


2(n
+
1)x
−
si
x
∈
,



n
2n(n + 1) n
1
2n + 1
2n + 1
f (x) :=
(3)
si
x
∈
,
−2n
+



n+1
n + 1 2n(n + 1)


0
si x = 0
La función f es continua y en cada punto de la forma x = 1/n, con n ∈ N, posee un máximo local estricto. Es
decir
{1/n : n ∈ N} ⊂ M (f ).
(4)
Así, la función f posee máximos locales estrictos en un conjunto numerable.
Recordemos que un conjunto D ⊂ R es denso en R, si para todo número x ∈ R existe una sucesión (dn )n∈N
tal que para todo n ∈ N se tiene que dn ∈ D y lı́m dn = x. En virtud del ejemplo anterior cabe la siguiente
n→∞
pregunta:
¿Existe una función continua, f : R → R, tal que el conjunto de máximos locales estrictos sea un conjunto
denso en R?
La respuesta a esta pregunta es afirmativa. La existencia de dichas funciones fue establecida por Zalcwasser [7]
en 1927 y redescuebierta por Posey [3] en 1964. En estos dos trabajos se prueba la existencia de un modo no
constructivo.
[email protected]
28
Artículos
2.
Número 3 / 2011
Una función con máximos locales en los números racionales
En esta sección presentamos la construcción de un ejemplo de una función continua, f : R → R, que posse
un máximo local estricto en cada número racional. Recordemos que el conjunto de los números racionales es
denso en el conjunto de los números reales. Este ejemplo es debido a Posey y Vaughan [4] y fue obtenido en
1983. La construcción es similar a las construcciones clásicas de funciones continuas no diferenciables.
Sea Q := (qn )n∈N el conjuntos de los números racionales y g : R → R la función definida por
g(x) := 1 − mı́n {1, |x|} .
(5)
Notemos la función g es continua, tiene un máximo en x = 0 y es igual a cero para todo x ∈ R \ (−1, 1). En
el intervalo donde g no es nula, su gráfico es un triángulo isóceles. Consideremos ahora la función f : R → R
definida por
∞
X
f (x) :=
gn (x),
(6)
n=1
donde
gn (x) := An g
x − qn
wn
.
(7)
Los número reales positivos An y wn se especificarán más adelante. Notemos que si |x − rn | > wn entonces
gn (x) = 0. Además, la función gn posee un máximo en x = qn . Denotaremos por In := [qn − wn , qn + wn ]
el intervalo donde la función gn es positiva y lo llamaremos intervalo asociado a gn . Denotaremos por
fn (x) =
n
X
gj (x),
(8)
j=1
a la n−ésima suma parcial en la definición de la función f . Asumiremos las siguientes condiciones:
(a) La constante An es tal que 0 < An < 2−n
(b) Los extremos del intervalo In no son números racionales
(c) Si j < n entonces
1. tenemos que qn ∈
/ Ij y la constante wn se escoge de modo que In ∩ Ij = ∅, o bien
2. tenemos que qn ∈ Ij y la constante wn se escoge de modo que In esté estrictamente contenido
en la mitad del intervalo de Ij al que qn pertenece. Por ejemplo, si qj − wj < qn < qj entonces
qj − wj < qn − wn < qn + wn < qj .
Inductivamente escogemos las constantes An y wn de modo que se satisfagan las condiciones (a), (b) y (c). En
la segunda parte de la construcción algunas de estas constantes serán modificadas, pero seguirán satisfaciendo
las condiciones aquí establecidas.
Lema 2.1. La función f : R → R definida por f (x) =
∞
X
gn (x) es continua.
n=1
Demostración. En efecto, notemos que la serie de funciones
particular uniformemente convergente)
f (x) =
∞
X
n=1
gn (x) ≤
P∞
∞
X
n=1 gn (x)
es normalmente convergente (y en
2−n < ∞,
n=1
Por lo tanto la función f es continua. Este resultado sólo depende de las constantes {An }n∈N y no de la
elección de wn .
[email protected]
29
Artículos
Número 3 / 2011
En lo que sigue construiremos por inducción la sucesión de funciones fn . Recordemos que fn es la suma de
funciones gj que cuando no son nulas poseen un gráfico triangular. Sean A1 y w1 constantes satisfaciendo (a),
(b), (c) y por lo tanto definiendo f1 . Construiremos la función fn de modo tal que
(i) posee un máximo local estricto en qn ya que es lineal y creciente en (qn − wn , qn ) y al mismo tiempo
es lineal y decreciente en (qn , qn + wn )
(ii) si In ⊂ Ij entonces j < n y fn (qn ) < fj (qj )
Supongamos que la función fn−1 se ha definido satisfaciendo las condiciones (i) y (ii). Si In ∩ Ij = ∅ ∀
j ∈ {1, 2, . . . , n} entonces mantenemos la elección de An y wn obtenida en la primera parte de la construcción.
Caso contrario, sea h ∈ {1, 2, . . . , n−1} el mayor entero tal que rn ∈ Ih . En virtud de la condición c.2 tenemos
que In ⊂ (rh − wh , rh ) o In ⊂ (rh , rh + wh ). Por otra parte, como fh (rn − wn ) < fh (rh ) la constante An
puede escogerse de modo tal que fn (rn ) < fh (rh ). Ahora, si rh ∈ Ij para j < h entonces Ih ⊂ Ij y luego
por (ii) tenemos que fh (rh ) < fj (rj ), de donde fn (rn ) < fj (rj ) y por lo tanto se satisface (ii). Una vez fijado
An podemos escoger wn de modo que (i) se satisfaga. Para ello basta notar que como las pendientes máximas
y mínimas de gj son ±Aj /wj , si
n−1
X Aj
An
>
,
wn
wj
j=1
entonces se satisface (i). De este modo concluye la inducción.
Lema 2.2. La función f : R → R definida por f (x) =
∞
X
gn (x) posee un máximo local estricto en cada
n=1
punto racional.
Demostración. Sea x ∈ In \ {qn }, probaremos que f (x) < f (qn ). Si para todo j ∈ N tal que j > n se tiene
que x ∈
/ Ij entonces por (ii) tenemos que
f (x) = fn (x) < fn (qn ) ≤ f (qn ),
sea h ∈ {n + 1, n + 2, . . . } el menor índice mayor que n tal que x ∈ Ih . Si existe k > h tal que x ∈ Ik
entonces por (i) y (ii) tenemos que
f (x) = fk (x) < fk (qk ) < fn (qn ) ≤ f (qn ),
si no existe tal k ∈ N entonces
f (x) = lı́m fki (x),
i→∞
donde x ∈ Iki , con i ∈ N y ki > h. De este modo
fki (x) < fk−i (qki ) < fh (qh ) < fn (qn ),
y por lo tanto
f (x) ≤ fh (qh ) < fn (qn ) ≤ f (qn ),
De donde se obtiene el resultado.
Concluimos esta sección con dos problemas.
Problema 1. Construya, sin utilizar series de funciones, una función que posea máximos locales estrictos en
todos los números racionales. Es posible que para resolver este problema sea útil recordar el trabajo de Lui
Wen [6] quien en 2000 contruyó, sin utilizar series de funciones, una función continua que no es diferenciable
en ningún punto.
Problema 2. Sea A ⊂ [0, 1] un sub-conjunto numerable. Determine si existe una función diferenciable f :
[0, 1] → R tal que M (f ) = A.
[email protected]
30
Artículos
3.
Número 3 / 2011
La mayoría de las funciones posee máximos locales densos.
Denotaremos por C[0, 1] el conjunto de funciones continuas f : [0, 1] → R. Dotado con la siguiente
métrica
d(f, g) := sup {|f (x) − g(x)| : x ∈ [0, 1]} ,
(9)
el espacio de las funciones continuas definidas en el intervalo [0, 1] es un espacio métrico completo. Sea
D := {f ∈ C[0, 1] : M (f ) es un conjunto denso en [0, 1]} .
(10)
Esta sección esta dedicada a probar que el conjunto D es, en un sentido preciso, grande. Para determinar el
tamano de un sub-conjunto del espacio de las funciones continuas utilizaremos las siguientes nociones clásicas
de la teoría de Baire. Un sub-conjunto A ⊂ C[0, 1] es nunca denso si el interior de su clausura es vacío, es decir,
si todo conjunto abierto O ⊂ C[0, 1] contiene un sub-conjunto abierto O0 ⊂ O tal que O0 ⊂ C[0, 1] \ A. Dicho
de otro modo, el conjunto A no es denso en ningún sub-conjunto abierto de C[0, 1]. Diremos que un conjunto es
de primera categoría si puede escribirse como la unión numerable de conjuntos nunca densos. Un sub-conjunto
de C[0, 1] es residual si su complemento es un conjunto de primera categoría. Si A ⊂ C[0, 1] es un conjunto
residual entonces existe un conjunto O abierto y denso en C[0, 1] tal que O ⊂ A. Desde la perspectiva de la
topología los conjuntos residuales son grandes 1 . De otro modo, si A ⊂ C[0, 1] es un conjunto residual, una
función continua típica pertenece a A.
Vladimir Drobot y Michael Morayne [1] probaron en 1985 que la mayoría de las funciones continuas en
el intervalo unitario poseen un conjunto de máximos locales denso en [0, 1].
Teorema 3.1 (Dorbot y Morayne). El conjunto D es un subconjunto residual de C[0, 1].
Demostración. En primer lugar fijaremos notación. La letra I denotará siempre un sub-intervalo cerrado de
[0, 1], denotaremos por intI el interior de I y por |I| el largo del intervalo. Dado I ⊂ [0, 1] definimos el
siguiente conjunto
A(I) := {f ∈ C[0, 1] : existe x ∈ intI tal que f (x) > f (y) para todo y ∈ I \ {x}} .
Este es el conjunto de funciones continuas que están restringidas al intervalo I poseen un único máximo y éste
pertenece al interior del intervalo.
Lema 3.1. Si I ⊂ [0, 1] es un intervalo cerrado, entonces el conjunto A(I) es denso en C[0, 1].
Demostración. Sean f ∈ C[0, 1] y > 0. Denotemos por z := sup{f (y) : y ∈ I}. Sea J ⊂ I un intervalo
abierto no vacío tal que para todo x ∈ J se tiene que f (x) > z − . Definamos ahora una nueva función
g ∈ C[0, 1] del siguiente modo: en el punto medio de J la función g toma el valor z + ; en los dos extremos
de J la función g coincide con la función f ; en J el gráfico de g consta de dos líneas rectas que unen los tres
puntos descritos anteriormente; en I \ J la función g coincide con f . Notemos que
d(f, g) = sup{|f (x) − g(x)| : x ∈ J} = 2.
Por otra parte la función g es tal que posee un único máximo y este corresponde al punto medio del intervalo
J ⊂ I. Por lo tanto g ∈ A(I). Así, dada cualquier función continua f existe una función g ∈ A(I) a distancia
menor que 2 de la función f . Como es un número arbitarrio tenemos que el conjunto A(I) es denso en
C[0, 1].
Lema 3.2. Si I ⊂ [0, 1] es un intervalo cerrado, entonces el conjunto A(I) es la intersección numerable de
conjuntos abiertos.
1 Existen distintos puntos de vista para determinar si un conjunto es grande. Por ejemplo, en vez de considerar la prespectiva topológica
podemos utilizar nociones de teoría de la medida. Es posible que desde un punto de vista un conjunto sea grande mientra que de otro no lo
sea (ver el texto de Oxtoby [2] donde se tratan numerosos ejemplos de este tipo de situaciones.)
[email protected]
31
Artículos
Número 3 / 2011
Demostración. Para cada intervalo J ⊂ intI consideremos el siguiente conjunto
B(I, J) := {f ∈ C[0, 1] : sup{f (x) : x ∈ J} > sup{f (x) : x ∈ I \ intJ}} .
Notemos que el conjunto B(I, J) es abierto. En efecto, si f ∈ B(I, J), entonces la bola abierta de centro f y
radio
1
(sup{f (x) : x ∈ J} − sup{f (x) : x ∈ I \ intJ})
3
está contenida en B(I, J). Probaremos ahora que para cada intervalo cerrado I ⊂ [0, 1] tenemos que
A(I) =
∞ \
∪B(I, J) : J intervalo cerrado , J ⊂ intI, |J| <
i=1
1
i
.
(11)
T∞ Sea f ∈ i=1 ∪B(I, J) : J intervalo cerrado , J ⊂ intI, |J| < 1i . Es decir, para cada i ∈ N existe un intervalo cerrado Ji ⊂ intI tal que f ∈ B(I, Ji ) y |Ji | < 1/i. El conjunto ∩∞
i=1 Ji contiene todos los puntos donde
f alcanza su máximo en el intervalo I. En efecto, si f ∈ B(I, Ji ) entonces el máximo de f se alcanza en Ji y
no en I \ Ji . Como
lı́m |Ii | = 0,
i→∞
tenemos que ∩∞
i=1 Ji = {x}, es decir, consiste de un solo punto. Como para todo i ∈ N tenemos que Ji ∈ intI
podemos concluir que x ∈ intI y que f alcanza su máximo en el punto x y que si y ∈ I \ {x} entonces
f (x) > f (y). Luego f ∈ A(I). La inclusión opuesta es clara ya que si f ∈ A(I) basta considerar una sucesión
∞
de intervalos {Ji }∞
i=1 tales que el único máximo de f , que denotaremos por x, es tal que {x} = ∩i=1 Ji . Por lo
tanto la igualdad en la ecuación (11) es válida.
En virtud de los Lemas 3.1 y 3.2 tenemos que el conjunto A(I) es denso y es la intersección numerable de
conjuntos abiertos, es decir es un conjunto residual. El siguiente conjunto es, por lo tanto, residual
\
X=
{A(I) : I ⊂ [0, 1], los extremos de I son números racionales} .
(12)
Como X ⊂ D tenemos que el conjunto D es residual.
Dada una función f ∈ C[0, 1] definimos
m(f ) := {x ∈ R : x es un mínimo local estricto para f } .
(13)
Un argumento similar al de Schoenflies (Teorema 1.1) nos permite probar que este conjunto es a lo más numerable. Consideremos ahora el conjunto
E := {f ∈ C[0, 1] : m(f ) es un conjunto denso en [0, 1]} .
(14)
La demostración que acabamos de presentar permite probar que el conjunto E es residual y por lo tanto el
conjunto D ∩ E también los es. Concluimos esta nota con otro problema propuesto:
Problema 3. Escoja dos sub-conjuntos A, H ⊂ [0, 1] de modo que ambos sean densos en [0, 1] y tales que
A ∩ H = ∅. Construya una función f : [0, 1] → [0, 1] tal que M (f ) = A y m(f ) = H.
Referencias
[1] V. Drobot and M. Morayne Continuous Functions with a Dense Set of Proper Local Maxima. The American
Mathematical Monthly, Vol. 92, No. 3 (1985), pp. 209-211.
[2] J.C. Oxtoby, Measure and category. A survey of the analogies between topological and measure spaces. Second
edition. Graduate Texts in Mathematics, 2. Springer-Verlag, New York-Berlin, 1980. x+106 pp.
[email protected]
32
Artículos
Número 3 / 2011
[3] E.E. Posey, Proteus forms of wild and tame arcs. Duke Math. J. 31 (1964) 63–72.
[4] E. E. Posey and J. E. Vaughan Functions with a Proper Local Maximum in Each Interval The American Mathematical Monthly, Vol. 90, No. 4 (1983), pp. 281-282.
[5] A. Schoenflies, Die Entwickelung der Lehre von den Punktmannigfaltigkeiten, Bericht, erstattet der Deutschen
Mathematiker-Vereinigun (1900).
[6] L. Wen A Nowhere Differentiable Continuous Function. The American Mathematical Monthly, Vol. 107, No. 5
(2000), pp. 450–453.
[7] Z. Zalcwasser, Sur les fonctions de Kopcke Prace Mat. Fiz., 35 (1927-28) 57-99.
[email protected]
33
35
Problemas.
12. Propuesto por Mark Ashbaugh, University of Missouri, Columbia, MO. Calcule
∞
X
k=1
2k
.
22k+1 k k
1
Comentario. Al lector le podrı́a interesar ver los resultados de la sección 4 del artı́culo Transformadas de Laplace de Funciones
de Bessel: Funciones de Orden Cero, por M. Ashbaugh y S. Garcı́a Sáenz, publicado en el segundo número de Joven Matemático.
13. Propuesto por Mark Ashbaugh,
University of Missouri, Columbia, MO. La fórmula de Herón para el área A de un triángulo
p
de lados a, b, y c es A = s(s − a)(s − b)(s − c), donde s denota el semiperı́metro del triángulo, (a + b + c)/2.
(a) Encuentre una fórmula para A análoga a la fórmula de Herón pero basada en las longitudes de las medianas del triángulo.
(Asegúrese de dar las restricciones que las longitudes de las medianas deben obedecer de modo que correspondan a un
triángulo fı́sico.)
(b) Encuentre una fórmula para A análoga a la fórmula de Herón pero basada en las longitudes de las alturas del triángulo.
(Asegúrese de dar las restricciones que las longitudes de las alturas deben obedecer de modo que correspondan a un
triángulo fı́sico.)
(c) (∗) ¿Existe alguna fórmula similar para el área de un triángulo en términos de las longitudes de las bisectrices de sus
ángulos? (¿Qué restricciones, si es que las hay, deben satisfacer las bisectrices?)
14. Propuesto por Andrés Fielbaum, Universidad de Chile, Santiago, Chile. Sea A una matriz cuadrada de n × n de números
reales. Dé una condición necesaria y suficiente para que exista un grafo G = (V, E) dirigido con vértices, y una función de
costos (ce : e ∈ E) tal que Aij sea exactamente el costo de la ruta más barata entre i y j.
15. Propuesto por los editores. Calcule
lim n
n→∞
n Y
1−
k=1
1
1
+ 2
k 2k
.
16. Propuesto por los editores. Calcule
Y
(i2 − j 2 ).
0≤i<j≤n
Soluciones.
1. Sea f : [0, 1] → R una función diferenciable con derivada continua, tal que f (0) = f (1) = − 61 . Pruebe que
Z
1
2
(f 0 (x)) dx ≥ 2
1
Z
f (x) dx +
0
0
1
4
(Enunciado publicado originalmente en la revista Mathematics Magazine como problema 1852.)
Solución por Ariel Norambuena Zamorano, PUC, Santiago, Chile.
Sean g(x), h(x) ∈ C 1 (0, 1), definamos su producto interno como
Z
(g(x), h(x)) =
1
f (x)g(x) dx
0
36
si elegimos g(x) = f 0 (x) + λ y h(x) = x con λ ∈ R, usando la desigualdad de Cauchy-Schwarz
2
|(g(x), f (x))| ≤ kg(x)kkf (x)k
p
donde la norma está asociada al producto interno mediante kf (x)k = (f (x), f (x)), de esto modo obtenemos la desigualdad
1
Z
λ2 +
1
3
0
2
Z 1
λ
2
(f 0 (x)) dx ≥
+
xf 0 (x) dx
2
0
R1
R1
la integral del lado derecho se puede resolver integrando por partes, luego 0 xf 0 (x) dx = − 61 − 0 f (x) dx. Ası́, reordenando
las potencias de λ obtenemos una desigualdad para la función cuadrática p(λ)
2
p(λ) = λ + 12λ
1
+
6
1
Z
f (x) dx − 12
0
1
+
6
1
Z
2
Z
f (x) dx + 4
1
2
(f 0 (x)) dx ≥ 0
0
0
si p(λ) = λ2 + bλ + c ≥ 0, entonces el discriminante satisface ∆ = b2 − 4c < 0. Aplicando la condición ∆ < 0, después de
un poco de álgebra nos queda
Z
1
0
1
Z
2
(f (x)) dx ≥ 4
0
Z
f (x) dx + 12
0
0
1
2
1
f (x) dx +
3
R
2
R1
R1
1
ahora usamos la desigualdad ( 0 f (x) dx + α)2 ≥ 0 (α ∈ R) o equivalentemente 0 f (x) dx ≥ −α2 − 2α 0 f (x) dx,
de esta manera obtenemos una desigualdad un poco más general y que depende del parámetro α
Z
1
2
(f 0 (x)) dx ≥ 4 (1 − 6α)
1
Z
f (x) dx +
0
0
1
12
finalmente, se puede chequear que para el caso particular α =
Z
1
2
(f 0 (x)) dx ≥ 2
0
Z
1
− 12α2
3
recuperamos la desigualdad pedida, es decir
1
f (x) dx +
0
1
4
2. Solución al problema propuesto número 10. Sea A una matriz de n × n entradas reales aij , positiva definida, y sean λi ,
i = 1, . . . , n sus valores caracterı́sticos con repetición. Muestre que
n
Y
i=1
λi ≤
n
Y
aii .
i=1
Solución por los editores.
La desigualdad de Hadamard establece que, si M es una matriz cuadrada y ui son sus filas, entonces
| det(M )| ≤
n
Y
||ui ||.
i=1
Por otro lado tenemos que el determinante de una matriz es igual al producto de sus valores caracterı́sticos. Luego, como A es
positiva definida, existe una matriz R tal que A = R∗ R, donde R∗ denota el conjugado transpuesto de R. Sean ri las columnas
de R. Tenemos entonces que aii = [R∗ R]ii = (ri , ri ) = ||ri ||2 . Luego
n
Y
i=1
∗
2
λi = det(A) = det(R R) = (det(R)) ≤
n
Y
i=1
2
||ri || =
n
Y
i=1
aii .
37
3. Solución al problema propuesto número 11. Sean A, B dos matrices de n × n, positivas definidas. Muestre que
| det(AB)| ≤
1
(Tr(A)n + Tr(B)n )2
4n2n
Solución por los editores.
Como A, B son positivas definidas, por la desigualdad AM-GM tenemos que
det(AB) = det(A) det(B) ≤
1
(det(A) + det(B))2 .
4
Además, si λi , i = 1, . . . , n, son los valores caracterı́sticos de una matriz cuadrada M , entonces
n
1
λ1 + λ2 · · · + λn
= n Tr(M )n .
det(M ) = λ1 λ2 · · · λn ≤
n
n
De estos resultados se concluye inmediatamente la desigualdad.
Noticias
Número 3 / 2012
El destacado matemático argentino Luis Caffarelli obtuvo el martes 10 de
Enero el Premio Wolf en Matemáticas 2012.
El Premio Wolf es uno de los premios más prestigiosos en Ciencias y es otorgado anualmente desde 1978 en los
campos de Agricultura, Arte, Física, Matemáticas, Medicina y Química, El Profesor Caffarelli obtuvo su doctorado en matemáticas en la Universidad de Buenos Aires en 1971 bajo la supervisión de Calixto Calderón. Los
temas de investigación del Profesor Caffarelli incluyen el análisis no lineal, ecuaciones a derivadas parciales y
sus aplicaciones, cálculo de variaciones y optimización. El profesor Caffarelli ha obtenido numerosos premios
por su labor de investigación incluyendo el Premio Bôcher de la American Mathematical Society. Caffarelli
es el segundo matemático argentino en obtener este prestigioso premio. Con anterioridad éste fue otorgado al
Profesor Alberto Calderón (1920-1998) en 1989. El Profesor Caffarelli trabaja actualmente en el Departamento
de Matemáticas de la Universidad de Texas en Austin, TX, EE.UU.
[email protected]
37