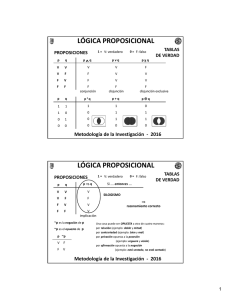
Módulo de Lógica Proposicional

UNIVERSIDAD NACIONAL DEL SANTA
FACULTAD DE CIENCIAS
Departamento de Matemática
Módulo de Lógica
Proposicional
(A)
p q
p

VV
V
VF
(B)
q
p q
(C)
p

(D)
q
pq
(E)
(F)
p / q p q
(G)
p q
F
F
V
F
V
V
V
F
V
F
V
F
F
FV
V
F
V
F
V
V
F
FF
F
V
F
F
V
V
V
q
Autor: Fidel Vera Obeso
Nuevo Chimbote, Perú
2013
Lógica Proposicional
Fidel Vera Obeso
PRÓLOGO
El estudio de la lógica nos beneficia en lo siguiente: desarrollar
habilidades para expresar ideas de manera clara y concisa, incrementar la
capacidad de definir los términos que utilizamos y aumentar la capacidad de
elaborar argumentos en forma rigurosa y de analizarlos críticamente. Pero
quizás el mayor beneficio es el reconocimiento de que la razón se puede aplicar
en todos los aspectos de las relaciones humanas.
Las instituciones democráticas requieren que los ciudadanos piensen por
sí mismos, que discutan libremente los problemas y que tomen decisiones con
base en la deliberación y la evaluación de evidencias. A través del estudio de
la lógica podemos adquirir no solamente práctica en el arte de razonar sino
también respeto por la razón, reforzando así y asegurando los valores de
nuestra sociedad.
En este módulo se abordan los siguientes temas: la lógica como ciencia;
definición, clases de proposiciones; operadores o conectivos lógicos; tautología,
contradicción y contingencia; equivalencia e implicación y las principales leyes
lógicas o tautologías notables.
Los objetivos específicos se logran siempre y cuando los grupos de ejercicios
se resuelvan con una eficacia del
80%,
en caso contrario deberán volver a
estudiar los cuadros correspondientes y resolver nuevamente los ejercicios
incorrectos o no resueltos. Resuelva los problemas propuestos del modo siguiente:
primero en forma individual, luego en forma grupal y por último preséntelos en un
grupo de un máximo de cinco (05) integrantes.
El Autor
i
Lógica Proposicional
Fidel Vera Obeso
ÍNDICE
PROLÓGO
OBJETIVOS
PRE-TEST
CONTENIDO
1.1.
LA LÓGICA COMO CIENCIA
CONCEPTUALIZACIÓN---------------------------------------------------------------------- 1
IMPORTANCIA------------------------------------------------------------------------------- 3
CUESTIONARIO----------------------------------------------------------------------------- 4
1.2.
PROPOSICIÓN. DEFINICIÓN Y CLASES------------------------------------------------- 5
EJERCICIOS---------------------------------------------------------------------------------11
1.3.
OPERADORES O CONECTORES LÓGICOS
NOTACIÓN, VALORES DE VERDAD Y LECTURA ---------------------------------------13
EJERCICIOS---------------------------------------------------------------------------------24
1.4.
TAUTOLOGÍA, CONTRADICCIÓN Y CONTINGENCIA----------------------------------27
EJERCICIOS---------------------------------------------------------------------------------30
1.5.
EQUIVALENCIA E IMPLICACIÓN---------------------------------------------------------31
EJERCICIOS---------------------------------------------------------------------------------35
1.6.
PRINCIPALES LEYES LÓGICAS O
TAUTOLÓGICAS NOTABLES---------------------------------------------------------------37
EJERCICIOS---------------------------------------------------------------------------------45
POST – TEST----------------------------------------------------------------------------------------BIBLIOGRAFÍA---------------------------------------------------------------------------------------48
ii
Lógica Proposicional
Fidel Vera Obeso
OBJETIVOS
OBJETIVO TERMINAL:
Identificar, formalizar y simplificar proposiciones.
OBJETIVOS ESPECÍFICOS:
1) Conceptualizar la lógica como ciencia y reconocer su importancia en el
avance científico.
2) Definir e identificar proposiciones.
3) Formalizar proposiciones usando variables proposicionales y los conectivos
lógicos, y determinar su valor de verdad.
4) Determinar cuando una proposición compuesta es una
tautología,
contradicción o contingencia.
5) Determinar
cuando
dos
proposiciones
compuestas
son
lógicamente
equivalentes y cuando una implica a la otra.
6) Enunciar, demostrar y aplicar las principales leyes lógicas o tautologías
notables.
iii
Lógica Proposicional
Fidel Vera Obeso
PRE - –
TEST
POST
TEST
Instrucción:
Resuelva el Post-Test de acuerdo a los requerimientos
dados.
01) De las siguientes expresiones:
(01) El ozono filtra los rayos ultravioletas
(02) C (n, k ) 
n!
, kn
k!(n  k )!
 1  i  i 2  1
(03)
(04) El aire contiene oxígeno e hidrógeno
(05) The earth rotates around the sun
No son proposiciones compuestas:
a) 1, 2, 3 y 5
b) 1, 2 y 3
c) 1 y 5
d) Sólo 1
e) 1 y 2
02) Si la proposición:
p  q)  r   (r  s) es verdadera
Hallar el valor de verdad de:
I.
p  q)  (r  s)
II.
 p  s)  r  w  p)
III. q  r  w  p  pq)
Son ciertas:
a) VVV
b) FVV
c) FFV
d) FFF
e) VFV
03) Determinar si la siguiente proposición es Tautológico, Contradictorio o
Contingente:

Como es hora laborable, se concluye que en el juzgado hay jueces y
testigos, dado que, si es hora laborable, en el juzgado hay jueces, y hay
testigos, si en el juzgado hay jueces.
04) Determinar cuáles de las siguientes proposiciones son equivalentes:
P = p   r  q)
Q = ( p  q)  r
R = q  (p  r)
iv
Lógica Proposicional
Fidel Vera Obeso
05) Se define el conector @ como:
p @ q   (p  q)  q   q q
Simplificar el esquema molecular:
  (p  q) @ (t  w) @ q  @ p
a) q
b) q
d) p
e) p  q
NOMBRE
:
FECHA
:
TIEMPO
: 1 HORA – 30 MINUTOS
c) p
v
Lógica Proposicional
Fidel Vera Obeso
OBJETIVO N° 01
ACTIVIDAD N° 01
Conceptualizar la lógica como
ciencia
y
importancia
reconocer
en
el
su
avance
científico.
Analice la siguiente información sobre
1.1.
LA LÓGICA COMO CIENCIA:
CONCEPTUALIZACIÓN:
Considerando que la lógica estudia tanto la estructura como el
contenido del pensamiento, conceptualmente afirmamos que “La
Lógica (en general) es la ciencia que estudia las leyes dialécticas y
lógico-formales, los métodos, los procedimientos, las propiedades y
las relaciones; sobre la base de las teorías del pensamiento”.
ESQUEMÁTICAMENTE:
LÓGICA (en general)
Principios
y/o leyes
- Identidad
- No contradicción.
- Tercio excluido
- Razón
suficiente.
- Unidad y lucha
de contrarios.
- Tránsito de
cantidad en
calidad.
- Negación de la
negación
Métodos
Formas
- Inducción
- Concepto
- Deducción
- Juicio
- Análisis
- Raciocinio
- Síntesis
Universidad Nacional del Santa
Base
-
Procedimientos
Propiedades
Definición
Clasificación
División
Explicación
Argumentación
Refutación
Demostración
Exposición
Investigación
- Espacio
1
- Tiempo
- Movimiento
- Cantidad
- Cualidad
Relaciones
-
Causa
Efecto
Necesidad
Casualidad
Posibilidad
Realidad
Singular,
particular,
universal.
Lógica Proposicional
Fidel Vera Obeso
LA LÓGICA Y LA CIENCIA:
Cuando el gran físico Albert Einstein inició sus investigaciones
sobre el micromundo, no lo hizo sobre la base de nada, sino que
tuvo que estudiar y someter a crítica las leyes y teorías de la física
clásica del macromundo. Es a partir de estas premisas que fue
estableciendo
deducciones,
inducciones
y
analogías
que
finalmente significan la creación de una nueva teoría: la teoría de
la relatividad. Sin embargo no fue suficiente que Einstein
conociese para sí, intersubjetivamente, sino que era necesario
que el mundo, la humanidad también lo conociese, de allí que
tuviese el autor que publicar, hacer público sus investigaciones.
Este ejemplo nos muestra que la ciencia, puede ser entendida
como proceso (investigación científica) y también como producto
(publicación o exposición de los resultados de la investigación
científica).
En ambos casos, la ciencia necesita de la lógica, sin ésta no
puede desenvolverse.
a) Como proceso la ciencia necesita de la lógica en tanto leyes,
procedimientos, métodos, propiedades y relaciones sobre la
base de las formas del pensamiento, para que el científico en
confrontación con la realidad, alcance la verdad objetiva.
Aquí el peso mayor recae en la lógica del contenido (condición
suficiente para la ciencia).
b) Como producto la ciencia en tanto teoría a exponerse,
publicarse,
necesita
de
la
lógica
para
organizarse,
sistematizarse, estructurarse, formalizarse a fin de poder
demostrar su validez o corrección lógico-formal: Aquí el peso
mayor recae en la lógica formal (condición necesaria para la
ciencia).
Universidad Nacional del Santa
2
Lógica Proposicional
Fidel Vera Obeso
IMPORTANCIA DE LA LÓGICA PARA EL AVANCE CIENTÍFICOTECNOLÓGICO:
 Permite en base al conocimiento ya obtenido y validado, deducir
nuevos conocimientos.
 En base a razonamientos inductivos (de lo particular a lo
general), podemos plantear hipótesis o predicciones científicas;
sin experimentación.
 Permite la formalización del lenguaje científico para la posterior
demostración
de
validez,
tornándose
preciso,
exacto,
convencional y universal.
 En tanto métodos lógicos son el puente entre los métodos de
investigación científica y los métodos de exposición científica.
 Es la base y hasta el momento la fundamentación de las
matemáticas (consideradas ciencias exactas), según la cual se
puede deducir de un conjunto de axiomas un conjunto de
teoremas. También se usa la inducción y analogía matemática.
 El desarrollo y el progreso de la lógica implican el desarrollo y el
progreso de las ciencias y la tecnología, por ejemplo los circuitos
lógicos son el fundamento de los circuitos eléctricos y de todo el
sistema de computación. Ahora, con las computadoras se
pueden hacer cálculos y predicciones sumamente complejos.
 Por sus aplicaciones a la matemática, a la lingüística, al análisis
del lenguaje natural, al análisis de los razonamientos filosóficos,
las aplicaciones al método científico, y en general, no hay campo
de la ciencia ni de la tecnología contemporánea donde la lógica
no sea utilizada. En este sentido, la lógica es la columna
vertebral de todos los acontecimientos en cuanto lo organiza
coherentemente.
 En la vida diaria hacemos uso de la lógica constantemente,
incluso para cruzar una pista, porque previamente razonamos:
“si viene un carro, no debo cruzar la pista. Viene un carro.
Luego, no debo cruzar la pista”, o cuando un campesino ve una
densa nube en el cielo infiere que va a llover, y así podemos
mencionar situaciones donde se usa la lógica indefinidamente.
Universidad Nacional del Santa
3
Lógica Proposicional
Fidel Vera Obeso
ACTIVIDAD N° 02
Resuelve a continuación el siguiente
CUESTIONARIO SOBRE LA LÓGICA COMO CIENCIA:
1) ¿Cómo se conceptualiza la lógica como ciencia? Haga un diagrama de
dicha conceptualización.
2) ¿Cómo se relaciona la lógica y la ciencia? Cite algunos ejemplos
prácticos.
3) Con ejemplos explique la importancia de la lógica en la vida diaria.
4) ¿Qué aplicaciones de la lógica podemos citar? Cite algunos ejemplos
prácticos.
5) ¿Por qué es necesaria la lógica para las ciencias?
Universidad Nacional del Santa
4
Lógica Proposicional
Fidel Vera Obeso
ACTIVIDAD N° 01
OBJETIVO N° 02
Definir
e
identificar
proposiciones.
Estudie la siguiente información sobre
1.2.
PROPOSICIÓN. DEFINICIÓN Y CLASES:
EL CONCEPTO:
Es una de las formas del reflejo del mundo en el pensar, mediante
el cual se entra en conocimiento de la esencia de los fenómenos y
procesos. En otras palabras, es el pensamiento. En otras
palabras, es el pensamiento elemental, la unidad lógica básica
que presenta al objeto o a una clase de objetos refiriéndose a sus
caracteres esenciales o indicando relación entre ellos.
Ejemplos:
 Carpeta
(designa un objeto real físico)
 Alegría
(designa un objeto real o psíquico)
 Número
(designa objeto abstracto).
 Perseverancia
(designa valor)
 Todos, algunos
(indican relación entre los anteriores)
Finalmente, un concepto no afirma ni niega nada, simplemente
indica algo ya sea objeto o entidad.
EL TÉRMINO:
Es la expresión, manifestación, explicitación lingüística del
concepto. Es decir, es la palabra o palabras con la cual se expresa
un conjunto. Así:
 El concepto estricto “cerebro” se expresa con un solo término
o palabra.
 El concepto estricto “ Universidad Nacional del Santa” se
expresa con varios términos o palabras.
Universidad Nacional del Santa
5
Lógica Proposicional
Fidel Vera Obeso
EL JUICIO:
Es una relación o conjunto de conceptos que se caracterizan
por construir una afirmación o aseveración de algo. Es una
forma, una estructura del pensamiento que objetivamente es
verdadero o falso.
LA ORACIÓN:
Convencionalmente, es una palabra o conjunto de palabras con
sentido o significado propio.
CLASIFICACIÓN DE LAS ORACIONES:
1) Declarativas o Aseverativas:
a) Informativas (Informan)
Ejm.: 2 + 3 = 5
b) Descriptivas (Describen)
Ejm.: La tierra gira alrededor del sol.
c) Explicativas (Explican)
Ejm.: El área de un cuadrado de 4 cm de lado es 16m2
porque para hallar el área de un cuadrado se
multiplica lado por lado.
2) Expresivas o no Aseverativas:
a) Exclamativas (Sentimientos, interjecciones)
Ejm.: ¡Viva el Perú!
b) Imperativas (Órdenes)
Ejm.: Silencio
c) Desiderativas (Deseos, súplicas)
Ejm.: Quiero viajar al Cuzco
d) Interrogativas (Preguntas)
Ejm.: ¿Qué hora es?
LA PROPOSICIÓN:
Es la expresión lingüística del juicio, de cuyo contenido o
significado se puede saber con certeza si es verdadero o falso
empíricamente y que generalmente se expresa como oración
declarativa. A nivel de pensamiento se llama juicio y a nivel de
lenguaje se llama proposición, por eso se dice que las
proposiciones son la envoltura material de los juicios.
Ejm.: Todo número par es divisible por dos.
Universidad Nacional del Santa
6
Lógica Proposicional
Fidel Vera Obeso
En síntesis, el proceso lógico puede esquematizarse del modo
siguiente:
PROPOSICIÓN
SE REFLEJA
JUICIO
OBJETO
A modo de resumen se da el siguiente cuadro para que pueda
identificar proposiciones.
Son proposiciones
No son proposiciones
 Las oraciones aseverativas.
 Los
 Las leyes científicas.
hechos
o
personajes
literarios.
 Los proverbios,
 Las fórmulas matemáticas.
 Las fórmulas y/o esquemas
modismos y
refranes.
 Creencias
lógicos.
 Los enunciados cerrados o
religiosas,
supersticiones y mitos.
 Las interrogantes.
definidos.
 Las órdenes.
 Las interjecciones.
 Los deseos, dudas y súplicas.
 Los abiertos o indefinidos.
Universidad Nacional del Santa
7
Lógica Proposicional
Fidel Vera Obeso
EJEMPLO 1
De
las
siguientes
oraciones,
identificar
las
que
son
proposiciones.
01) Cuando x > 3 entonces x2 > 9
02) Peter Drucker es autor de la obra “El Líder del Futuro”.
03) La traducción en inglés de “yo te amo” es “I love you”.
04) ¡Viva el Perú!
05) Dadme la vida o dadme la muerte.
06) ¡Chimbote! Alma mater de lucha y de inquietud.
07) ¿A qué hora termina el examen?
08) Todo triángulo es un polígono
09) Juega
un
papel
preponderante
en
el
desarrollo
y
conservación de los recursos.
10) El ADN es la molécula maestra de la célula.
11) El área del círculo es...
12) Es un método didáctico activo.
13) Del dicho al hecho hay mucho trecho.
14) Hoy tendré un mal día, se me cruzó un gato negro.
15) (a + b)2 = a2 + 2ab + b2.
Solución:
La característica fundamental de una proposición es verdadera o
falsa empíricamente. De acuerdo a esto:
Son proposiciones:
1, 2, 3, 8 y 10
15
(oraciones aseverativas)
(fórmula matemática)
No son proposiciones:
5y6
4
(figuras literarias)
(interjección)
Universidad Nacional del Santa
8
Lógica Proposicional
Fidel Vera Obeso
13
(refrán)
14
(superstición)
CLASES DE PROPOSICIONES:
Simples, atómicas o elementales: Aquellas que carecen de
conectores lógicos.
Compuestas, moleculares o coligativas: Aquellas que tienen uno
o más conectores lógicos.
EJEMPLO 2
De las siguientes proposiciones, identificar las proposiciones
simples y las proposiciones compuestas.
01) No existe la capa de ozono.
02) El SIDA y la TBC son enfermedades.
03) Los ofidios tienen extremidades o bien vértebras.
04) Los medios de comunicación son necesarios en la pedagogía.
05) i2 -1
06) Cero es un número par o impar.
07) La relación
es una función y representa
una circunferencia.
08) Si
09)
es un número irracional entonces es un número real.
si y sólo si x = h
10) Manipular la computadora y la impresora son ejemplos de
aprendizaje motor.
11) “Peruanicemos al Perú” es un tema crítico-científico-literario
de José María Arguedas.
12) Las palabras: mármol, carácter, baúl, tórax llevan tilde por
ser graves prosódicas.
13) Los metaloides son combinables con oxígeno para formar
anhídridos.
Universidad Nacional del Santa
9
Lógica Proposicional
Fidel Vera Obeso
14) En todo proceso redox existen uno o más elementos que se
oxidan.
15)
X + 6 = 4 si X = -2
Solución:
4 y 13 son proposiciones simples pues carecen de conectores
lógicos.
1 y 5 tienen la negación como conectivo. El símbolo matemático
“” “ diferente a” es equivalente a “no es igual a”.
2, 7, 10, 11 y 12 tienen la conjunción como conectivo.
3, 6 y 14 tienen la disyunción como conectivo.
8 y 15 tiene como conectivo el condicional.
9 tiene el bicondicional como conectivo.
Universidad Nacional del Santa
10
Lógica Proposicional
Fidel Vera Obeso
ACTIVIDAD N° 02
Resuelve a continuación la siguiente
EJERCICIOS SOBRE PROPOSICIÓN. DEFINICIÓN Y CLASES:
01) De las siguientes expresiones:
(1) Todo lo agradable es bueno
(2) ¡Viva el Perú carajo!
(3) Hay mujeres en la tierra
(4) Los alumnos de historia hicieron la tarea
(5) Entrégame mi libro de lógica.
No son proposiciones:
a) 2, 3 y 5
b) 2 y 5
c) 2, 4 y 5
d) N.A.
e) T.A.
02) De las siguientes expresiones:
(1) Solo sé que nada sé
(2) El calor dilata los cuerpos
(3) x + y = y + x
(4) Vargas Llosa es el mejor escritor del Perú
(5) Café es una palabra aguda.
No son proposiciones:
a) 1, 3 y 4
b) 1, 3 y 5
c) 3, 4 y 5
d) 1 y 3
03) De las siguientes expresiones:
(1) Los cuerpos caen por acción de la gravedad.
(2) La materia es energía concentrada.
Universidad Nacional del Santa
11
e) 1, 4 y 5
Lógica Proposicional
Fidel Vera Obeso
(3) El valor de  = 3.1416
(4) H2O es la fórmula del agua
(5) The sun is the center of our planetary system
Son proposiciones:
`
a) 1, 2, 4 y 5
b) 1, 2 , 3 y 4
c) 1,2 y 5
d) 1,2 y 3
e) Todas.
04) De las siguientes expresiones:
(1) El agua no se solidifica a 0°
(1) tg x = 1 cuando x=/4
(2) 2-1 = ½ no obstante
(3) x2 + y2 = 1; es la ecuación de una circunferencia
(4) 4 + 3  -3 -4
Son proposiciones compuestas:
a) 2, 3 y 4
b) 2, 3 y 5
c) 1,2 y 3
d) 1,2, 3 y 5
e) 1, 3 y 5
05) De las siguientes expresiones:
(01) El ozono filtra los rayos ultravioletas
(02)
(03)
(04) El aire contiene oxígeno e hidrógeno
(05) The earth rotates around the sun
No son proposiciones compuestas:
a) 1, 2, 3 y 5
b) 1, 2 y 3
c) 1 y 5
e) 1 y 2
Universidad Nacional del Santa
12
d) Sólo 1
Lógica Proposicional
Fidel Vera Obeso
ACTIVIDAD N° 01
OBJETIVO N° 03
Formalizar
proposiciones
usando
variables
proposicionales
y
los
conectivos
lógicos,
y
determinar su valor de verdad.
Analice la siguiente información sobre
1.3.
OPERADORES O CONECTIVOS LÓGICOS:
NOTACIÓN, VALORES DE VERDAD Y LECTURA:
Variables proposicionales:
- Del Lenguaje Objeto:
Las proposiciones simples se pueden denotar por medio de
letras minúsculas, generalmente, a partir de: p, r, s....
- Del Metalenguaje:
Son variables de mayor amplitud que las anteriores y sirven
para denotar proposiciones compuestas. Se usan las letras
mayúsculas, generalmente, a partir de: A,B,C, ...
Operadores o Conectivos Lógicos:
La Negación
Símbolo: ~
Esquema lógico
Lectura
~ p,
“no p”, “nunca p”,
“jamás p”, “tampoco p”
“es absurdo que p”
“es inadmisible que p”
“es falso que p”
“no acaece que p”
“es inconcebible que p”
“no es innegable que p”
“es imposible que p”
“carece de todo sentido que p”
“no ocurre que p”
“de ninguna forma se da p”
“no es verdad que p”
“es erróneo que p”
“es mentira que p”
“es incierto que p”
“nadie que sea p”
etc...
Universidad Nacional del Santa
13
Lógica Proposicional
Fidel Vera Obeso
La Disyunción Débil o Inclusiva
Símbolo:
v, +
Esquema lógico
p
Lectura
q, p + q
“p ó q”
“a menos que p, q”
“p ó también q”
“p ó de lo contrario q”
“p salvo que q”
“p a menos que q”
“p excepto que q”
“p ó en tal sentido q”
etc...
La Disyunción Débil o Exclusiva
Símbolo:
Esquema lógico
Lectura
“o p ó q”
“p no equivale a q”
“p no se define como q”
“ya sea p ya sea q”
“o bien p ó bien q”
“p es diferente a q”
“ya bien p ya bien q”
“p se contrapone a q”
“p excluye a q”
“p ó solamente q”
“p ó únicamente q”
El Operador de Nicond
Símbolo:
/
Esquema lógico P/q, ~p
Lectura
~q, ~ (p  q).
“no p ó no q”
“es falso que no p y no q”
La Conjunción
Símbolo:
Esquema lógico
Lectura
Universidad Nacional del Santa
, ., &
p  q, p.q , p&q
“p y q”
“p pero q”
“p aunque q”
“p sin embargo q”
“p incluso q”
“p así como q”
etc...
14
“p también q”
“p del mismo modo q”
“p de la misma forma q”
“p tal como q”
“p al igual que q”
“p no obstante q”
“p es compatible con q”
“no sólo p también q”
“siempre ambos p con q”
“tanto p como, cuanto q”
Lógica Proposicional
Fidel Vera Obeso
El operador de Sheffer
Símbolo:
Esquema lógico
Lectura

p  q, ~p~q, ~(pq)
“ni p ni q” “es falso que p ó q”
El Condicional
Símbolo:
Esquema lógico
Lectura

, 
p  q, p  q
“si p entonces q”
“cuando p así pues q”
“con tal de que p es obvio
que q”
“en virtud de que p es
evidente q”
“dado p por eso q”
“en cuanto p por tanto q”
“de p deviene q”
“de p deducimos q”
“p sólo si q”
En la condicional:
p

e s

“ya que p bien se ve que q”
“siempre que p por consiguiente q”
“como quien que p por lo cual q”
“en el caso de que p en tal sentido
q”
“toda vez que p en consecuencia q”
“en la medida que p de allí q”
“en el caso de p en este caso q”
“p impone q”
“p es condición suficiente para q”
etc...
q
e s
El Antecedente
La Hipótesis
La causa
El consecuente
La tesis
El efecto
La
Premisa
La Conclusión
Después de las siguientes palabras va el antecedente de una
condicional (INDICADORES DE PREMISAS):
puesto que
como es indicado por
dado que
la razón es que
a causa de
por las siguientes razones
porque
se puede inferir de
pues
se puede derivar de
se sigue de
se puede deducir de
como muestra
en vista de que
ya que
cuando
si
cada
vez
condición
que,
de
siempre
que,
es
que,
condición
necesaria para, es insuficiente para.
Universidad Nacional del Santa
15
a
Lógica Proposicional
Fidel Vera Obeso
En este caso el esquema lógico es:
Consecuente
Conclusión
Palabra
Indicador de premisa
Premisa
Antecedente
s
r
Este conectivo se llama REPLICADOR.
El Bicondicional
Símbolo:
, 
Esquema lógico
Lectura
p  q, p  q
“p sí y sólo si q”
“p es equivalente, equivale a q”
“p se define como q”
“p siempre que y sólo cuando q”
“p es lo mismo que q”
“p cada vez que y sólo si q”
“p es idéntico a q”
“p es equipolente a q”
etc....
“p es de la forma q”
“p es condición necesaria y
suficiente para q”.
EJEMPLO 1
Formalizar o simbolizar las siguientes proposiciones.
1) Estudias Lógica o Biología, pero no ambas a la vez.
(p

q)
 ~ (p  q)
(p  q)  ~ (p  q)  (p  q)  (p  q)
2) O bien los animales son vertebrados o bien invertebrados, pero

(p
p)
no es el caso que sean invertebrados a la vez vertebrados.


(p
p)
(p  p)   (p  p)
3) Un enunciado abierto no es una proposición a menos que
p

se le asignen valores a la variable.
q
p  q
Universidad Nacional del Santa
16

Lógica Proposicional
Fidel Vera Obeso
4) Una condición necesaria para que Rocío no sea premiada con un libro

p
es que estudie matemáticas y no apruebe el examen.

(q
r)
p  ( q  r)
5) Como es hora laborable, se concluye que en el juzgado hay
jueces y testigos, dado que, si es hora laborable, en el juzgado
hay jueces, y hay testigos si en el juzgado hay jueces.
Solución:
Sean:
p : hora laborable
q : hay jueces en el juzgado
r : hay testigos en el juzgado.

Simbolizando sólo las proposiciones simples:
Como p, se concluye que q y r, dado que, si
p, q, y r si q.

Simbolizando los operadores condicionales:
p  (q  r)

dado que (p  q)  (r si q)
Simbolizando los replicadores:
p  q  qr  p  qr
Universidad Nacional del Santa
17
Lógica Proposicional
Fidel Vera Obeso
VALORES VERITATIVOS DE LOS OPERADORES
O CONECTIVOS LÓGICOS
p
p
V
F
F
V
(A)
(B)
(C)
(D)
(E)
(F)
(G)
pq
pvq
pq
pq
pq
pq
VV
V
F
F
V
F
V
V
VF
V
F
V
F
V
F
F
FV
V
F
V
F
V
V
F
FF
F
V
F
F
V
V
V
pq pq

En el álgebra de Boole,

La parte sombreada es la regla de operación de cada operador

(A) y (B) son de valores de verdad opuestos
V es 1
F es 0
(D) y (E)

Sentido convencional de la verdad formal.
(A) es V  al menos p es 1 ó q es 0
(C) es V  p y q tienen valores de verdad desiguales
(E) es V  cuando menos p es 0 ó q es 0
(G) es V  p y q tienen valores de verdad iguales
etc.

Sentido convencional de la falsedad formal:
(D) es F  al menos p es 0 ó q es 0
(F) es F  p es 1 y q es 0
(G) es F  p y q tienen valores de verdad desiguales
(C) es F  p y q tienen valores de verdad iguales. etc.
Universidad Nacional del Santa
18
Lógica Proposicional

Fidel Vera Obeso
Se puede construir un mapa conceptual de los valores de
verdad de un operador, por ejemplo:
Mapa Conceptual de los Valores de Verdad de p q
V
entonces
F
p  q es
Si p es
V
F
entonces
V
p  q es
V
entonces
V
p  q es
Si p es
F
F
entonces
F
p  q es
EJEMPLO 2
Si la proposición q  r es falsa, el valor de verdad de las
siguientes proposiciones:
I.
r  (p  r)
II.
~ (q  r)
III.
(r  ~ q)  p
IV.
p  (q  r)
Son respectivamente:
(a) FVFV
(b) VVFV
c) VFVF
d) FFFV
e) FVVF
Solución:
Sabemos que:
qrF


VF
F
Luego:
I.
r  (p  r)  F
F  V
F
Universidad Nacional del Santa
19
q V
r  F
Lógica Proposicional
II.
Fidel Vera Obeso
 (q  r)  V
F
V
III.
( r  q)  p  V
( F  F)  p
F  p
cualquiera sea el valor de verdad de p
V
IV.
p  (q  r)  F
P F
F
cualquiera sea el valor de verdad de p
Respuesta (e)
EJEMPLO 3
Dadas las proposiciones:
q:“
es un número racional”
p y r cualquier proposición
además se sabe que:
~ (r  q)  (r  p)  es verdadera
Hallar el valor de verdad de:
I.
r  ( p   q)
II.
 ( r  (p  q)  (q  p)
III.
( r  p)  (q  p)
(a) VVV
(b) FFF
c) VFV
d) FVV
e) VVF
Solución:
Del dato, q  F, además
(r  q)  ( r  p)  F
V
(i)

r p F
F
(ii)
V F
Universidad Nacional del Santa
rqV
VF
20

p F
q F
r V
Lógica Proposicional
I.
Fidel Vera Obeso
r  (p  q)  V
V  (V  V)
V
V
V
II.
 (r  (p  q)  (q  p)  V
(V  F)
 (F  V)

F
F
V
III.
( r  p)  (q  p)  F
(V  V)  (F  F)
V 
F
F
Respuesta (c)
EJEMPLO 4
Si se sabe que:
r  s  t  (p  q)   r  t)  s qp)
es verdadera, hallar el valor de verdad de:
I.
p  q  r   ( t  p )  r
II.  (r  s)  t   (p  q)
III.  (p  q)  ( t   )
(a) VVV
(b) VFF
c) VFV
d) FVV
e) VVF
Solución:
Para que toda la proposición sea verdadera, cada una de las
expresiones entre llaves debe ser verdadera, o sea:
(i)
 r  s)  t   p  q)  V
(ii)
 r  t)  p  q  p)  V
V
Universidad Nacional del Santa
21
Lógica Proposicional
Fidel Vera Obeso
De (ii)
r  t)  s  q  p)  F

V

r  t)  s  V
V

F
s V
V
q  p)  F   (q  p)  F
 q  p V
De (i)  r  s)  t   p  q)  V

F

V
 r  s)  t  F
V
t F

F
Luego, evaluando los casos pedidos:
I.
p  q  r   ( t  p )  r  V
V  V   ( F  p )  V
V 
V V
 V
F
V
II.  (r  s)  t    (p  q)  F
 (V  V)  V    (V)
 (V  V   F
V
 F
F
Universidad Nacional del Santa
22
r V
Lógica Proposicional
Fidel Vera Obeso
IV.  (p  q)  ( t   s)  F
F
 ( F  F)
F

V
F
Respuesta (b)
Universidad Nacional del Santa
23
Lógica Proposicional
Fidel Vera Obeso
ACTIVIDAD N° 02
Resuelve a continuación los siguientes
EJERCICIOS SOBRE FORMALIZACIÓN DE PROPOSICIONES:
A. Formalizar o simbolizar las siguientes proposiciones:
1. No es cierto que 19 sea divisible por 9 ó por 19.
2. Einstein dice la verdad pues la teoría de la relatividad no es
exacta ni las leyes de la mecánica son absolutas.
3. En primavera soplan vientos fuertes o hace mucho frío, pero no
garúa, sin embargo es una bonita estación.
4. Las leyes de la mecánica son exactas, si Newton dice la verdad, y
sólo sí, el movimiento no es relativo.
5. 24 es un número par, o múltiplo de 6 y de 2, pero no es divisible
entre 10 ni entre 14.
6. Carlos es profesional sí y sólo sí, es graduado universitario.
Ocurre que Carlos es matemático. Por lo tanto, si Carlos es
matemático entonces es graduado universitario.
B. 7 La fórmula q  p se traduce como:
1) Hago deporte porque estoy sano.
2) Es necesario llorar para estar tranquilo.
3) Hago mis tareas al tener vacaciones.
4) Sólo si bailo, me divierto.
Son correctas:
a) 1, 2 y 3
b) 2, 3 y 4
Universidad Nacional del Santa
c) 3, 4 y 5
24
d) T.A.
e) N.A.
Lógica Proposicional
Fidel Vera Obeso
8 La fórmula  p  q   r   s, se traduce como:
1) No sólo la distancia es una magnitud del movimiento sino que
el tiempo también lo es igual que la velocidad y la aceleración
siempre y cuando se defina como cambio de un lugar a otro.
2) La distancia es una magnitud del movimiento del mismo modo
el tiempo y la velocidad por lo cual y según lo cual el
movimiento es el cambio de ubicación.
3) El tiempo, la velocidad y la aceleración son magnitudes del
movimiento, si el movimiento es cambio de espacio.
4) El avión aunque también el barco al igual que el bus son
medios de transporte cada vez que y sólo sí trasladan
pasajeros de un lugar a otro.
5) El perro, tanto como el gato lo mismo que el asno son
animales útiles para el hombre es equivalente a decir que son
domésticos.
Son correctas:
a) 1, 2 y 3
b) 2, 3 y 4
c) 3, 4 y 5
d) 2, 4 y 5
e) 1, 3 y 5
9. La fórmula q  p, se traduce como:
1) Si eres buen estudiante lógicamente serás buen profesional.
2) Ingresarás a la universidad porque eres buen estudiante.
3) De
ser
buen
estudiante
obviamente
ingresarás
a
universidad.
4) Ingresarás a la universidad si eres buen estudiante.
5) Crecen las plantas siempre que haya humedad en la tierra.
Son correctas:
a) 1, 2 y 3
b) 2, 3 y 4
c) 3, 4 y 5
e) 1, 3 y 5
Universidad Nacional del Santa
25
d) 2, 4 y 5
la
Lógica Proposicional
Fidel Vera Obeso
EJERCICIOS SOBRE VALORES VERITATIVOS:
C. 10. Si la proposición:
(p  q)  (p  r) es falsa,
Se afirma que:
I.
p  q es falsa
II.
r  q es verdadera
III.
q  p es verdadera
Son ciertas:
a) Sólo I
b) sólo II
c) Sólo I y III
d) Sólo II y III
11. Si la proposición:
(p  q)  (q  r) es falsa, luego:
I.
(p  q ) no es falsa
II.
(q  s) no es falsa
III.
(q  p) es verdad
Son ciertas:
a) Sólo I
b) Sólo II
d) Sólo II y III
e) I, II y III
c) Sólo I y III
12. Si la proposición:
p  q)  r   (r  s) es verdadera
Hallar el valor de verdad de:
I.
p  q)  (r  s)
II.
 p  s)  r  w  p)
III.
q  r  w  p  sq)
Son ciertas:
a) VVV
b) FVV
Universidad Nacional del Santa
c) FFV
26
d) FFF
e) VFV
Lógica Proposicional
Fidel Vera Obeso
ACTIVIDAD N° 01
OBJETIVO N° 04
Determinar
cuándo
una
proposición compuesta es
una tautología, contradicción
o contingencia.
Analice la siguiente información sobre
1.4.
TAUTOLOGÍA, CONTRADICCIÓN O CONTINGENCIA :
Una proposición molecular es una tautología si, como resultado
de su evaluación, los valores de verdad del operador de mayor
jerarquía son todos verdaderos. Si estos valores son todos falsos
es
una
contradicción.
Si
no
es
una tautología
ni
una
contradicción es una contingencia.
Para evaluar una proposición compuesta es necesario construir
su tabla de valores de verdad respetando la jerarquía de los
operadores de menor a mayor.
El total de valores de verdad por cada variable es 2n, donde “n” es
el número de variables proposicionales, combinándolos mitad V y
mitad F por cada columna, respectivamente.
EJEMPLO 1
Determinar, previa evaluación; si cada uno de los siguientes
esquemas
moleculares
es
una
tautología,
contradicción
contingencia.
1. p  q    r  q       p  q  q  r  
2.  p  q  r    r   (p  q  
3.  p  q  r )    (p  r   q 
Universidad Nacional del Santa
27
o
Lógica Proposicional
Fidel Vera Obeso
Solución:
1. n° de variables proposicionales: 3
Total de valores por cada variable: 23 = 8
p  q    r  q       p  q  q  r  
1
2
3
4
5
6
7
8
p q r
q
p 1
rq
3
2 4
23
6
57
1 1 1
0
1
1
0
0
1
0
1
1 1 0
0
1
0
1
1
0
1
1
1 0 1
1
0
0
1
0
1
0
1
1 0 0
1
0
0
1
0
1
0
1
0 1 1
0
0
1
0
0
1
0
1
0 1 0
0
0
0
1
0
1
0
1
0 0 1
1
1
0
1
1
0
1
1
0 0 0
1
1
0
1
1
0
1
1
El esquema molecular
Operador principal o
es una TAUTOLOGIA
de mayor jerarquía
2.
 p  q  r    r   (p  q  
1
2
3
4
5
6
7
8
9
p q r
p
1q
r
23
q
pv5
6
r7
48
1 1 1
0
0
1
1
0
1
0
0
0
1 1 0
0
0
1
1
0
1
0
0
0
1 0 1
0
0
1
1
1
1
0
0
0
1 0 0
0
0
1
1
1
1
0
0
0
0 1 1
1
1
0
0
0
0
1
1
0
0 1 0
1
1
1
1
0
0
1
0
0
0 0 1
1
0
1
1
1
1
0
0
0
0 0 0
1
0
1
1
1
1
0
0
0
El esquema molecular
Operador principal o
es una CONTRADICCIÓN
de mayor jerarquía
Universidad Nacional del Santa
28
Lógica Proposicional
Fidel Vera Obeso
3.
 p  q  r )    (p  r   q 
1
2
3
4
5
6
7
8
p q r
r
q1
p2
p
4r
q
56
37
1 1 1
0
0
1
0
1
0
0
0
1 1 0
1
1
1
0
0
0
1
1
1 0 1
0
1
1
0
1
1
1
1
1 0 0
1
1
1
0
0
1
0
0
0 1 1
0
0
0
1
1
0
0
0
0 1 0
1
1
1
1
1
0
0
0
0 0 1
0
1
1
1
1
1
1
1
0 0 0
1
1
1
1
1
1
1
1
El esquema molecular
Operador principal o
es una CONTINGENCIA
de mayor jerarquía
Universidad Nacional del Santa
29
Lógica Proposicional
Fidel Vera Obeso
ACTIVIDAD N° 02
Resuelve a continuación los siguientes
EJERCICIOS SOBRE EVALUACIÓN DE PROPOSICIONES
COMPUESTAS:
Determinar, previa evaluación, si cada uno de los siguientes esquemas
moleculares es una tautología, contradicción o contingencia.
1.   p  q   p  p  q    p  q
2. p   q  q  p     p     q    p  q 
3. p  q   q / p)   p  q)     p  q  p/ q)
4.  p  q)   r    q  r   p  p
5.  (p  q)  (q  p)   q  (p  r) 
6.
p  q   r  p    p  q  q  r)  
7.         p  q)  r   r  q  p    r  q  
8. Como es hora laborable, se concluye que en el juzgado hay jueces y
testigos, dado que, si es hora laborable, en el juzgado hay jueces, y
hay testigos, si en el juzgado hay jueces.
Universidad Nacional del Santa
30
Lógica Proposicional
Fidel Vera Obeso
OBJETIVO N° 05
ACTIVIDAD N° 01
Determinar cuándo dos
proposiciones compuestas
son lógicamente esquivalentes y cuando una implica
a la otra.
Analice la siguiente información sobre
1.5.
EQUIVALENCIA E IMPLICACIÓN:
Dos esquemas moleculares A y B son equivalentes si tienen los
mismos valores de verdad en su operador principal, o si unidos
por el bicondicional el resultado es una tautología. Es decir, A  B
si A  B es una tautología.
Un esquema molecular A implica a otro B si unidos por el
condicional, en ese orden, el resultado es una tautología. Es decir,
A implica a B si A  B es una Tautología;
B implica a A si B  A es una Tautología
EJEMPLO 1
Dados los siguientes esquemas moleculares:
A = p  q)  ( r  p
B = p
(r q)
C = q  ( r   p)
Determinar los que son equivalentes
Solución:
Universidad Nacional del Santa
31
Lógica Proposicional
Fidel Vera Obeso
A
p q r (pq)  (r p)
B
C
 p   r  q 
 q   r   p)
1 1 1
1
1
1
0
0
1
0
0
0
1
0
1
0
1 1 0
1
1
0
1
0
0
1
1
0
1
1
0
0
1 0 1
0
1
1
1
0
0
0
1
1
1
0
1
0
1 0 0
0
0
0
0
0
1
1
0
1
0
1
0
0
0 1 1
1
1
0
1
1
0
0
0
0
1
0
1
1
0 1 0
1
1
0
0
1
1
1
1
0
1
1
1
1
0 0 1
1
1
0
0
1
1
0
1
1
1
0
1
1
0 0 0
1
1
0
1
1
0
1
0
1
1
1
1
1
A y B tienen los mismos valores de verdad
en su operador de mayor jerarquía, por lo
tanto:
AC
EJEMPLO 2
Dados los siguientes esquemas moleculares:
A=p
q
B =  (p  r)
C=qp
D =  (q  r)
Determinar:
1) Si A implica a C
2) Si B es implicado por D
3) Si C implica a la disyunción de A, B y D
4) Si A entonces B está implicado por la negación de C.
Universidad Nacional del Santa
32
Lógica Proposicional
Fidel Vera Obeso
Solución:
1) A implica a C si A  C es una tautología verificando:
p
q
A
C
A  C
 (p   q)
qp
 p  q qp)
1
1
1
0
0
1
1
1
0
0
1
1
1
1
0
1
1
0
0
0
1
0
0
1
0
1
1
1
Por lo tanto, A implica a C
2)
p
es una tautología
B es implicado por D si D  B es una tautología verificando:
q
r
D
B
D  B
 (q   r)
 (p  r)
qr (pr)
1
1
1
1
0
0
0
1
0
1
1
0
0
1
1
0
1
1
1
0
1
0
1
0
0
1
1
1
0
0
0
1
1
0
1
1
0
1
1
1
0
0
0
1
0
0
1
0
0
1
1
1
0
1
0
0
1
0
1
0
0
1
1
0
0
0
0
1
1
1
0
1
Por lo tanto,
no es una tautología
B no es implicado por D
Universidad Nacional del Santa
33
es una contingencia
Lógica Proposicional
Fidel Vera Obeso
3) C implica a la disyunción de A, B y D si C  (ABD) es una
Tautología.
Verificando:
p
q
r
C
ABD
qp
pq(pr)  (qr
C(A  B  D)
1
1
1
1
1
1
0
1
1
1
1
0
1
1
1
0
0
1
1
0
1
1
0
0
0
0
0
1
0
0
1
0
0
0
0
0
0
1
1
0
0
1
0
1
1
0
1
0
0
0
1
1
0
1
0
0
1
1
1
1
0
0
0
0
0
0
1
1
1
1
0
1
Por lo tanto,
No es una tautología
C no implica a la disyunción
es una Contingencia
de A, B y D
4) A entonces B está implicado por la negación de C si
C  A  B) es una tautología. Verificando
C
p
q
r
A  B
 C  (A  B)
 (q p) pqpr) qppq pr)
1
1
1
0
1
1
0
0
0
1
1
1
0
0
1
1
0
0
0
1
1
0
1
0
1
0
1
1
0
1
1
0
0
0
1
0
1
1
0
1
0
1
1
1
0
0
1
1
0
1
0
1
0
1
0
0
1
1
1
1
0
0
1
0
1
1
0
0
0
1
0
0
0
0
1
1
0
1
1
1
Por lo tanto,
es una tautología
A entonces B está implicado
por la negación de C.
Universidad Nacional del Santa
34
Lógica Proposicional
Fidel Vera Obeso
ACTIVIDAD N° 02
Resuelve a continuación los siguientes
EJERCICIOS SOBRE EQUIVALENCIA E IMPLICACIÓN:
I.
En
cada
grupo
de
esquemas
moleculares
que
aparecen
a
continuación, determinar los que son equivalentes.
1.
P=p
 r  q)
Q = ( p  q)  r
R = q  (p  r)
2.
P = Si los fenómenos naturales se comportan según las leyes
de la mecánica de Newton, entonces Newton dice la
verdad; sin embargo, la Física clásica no es absoluta.
Q= Newton dice la verdad si la física clásica no es absoluta,
sí y sólo sí los fenómenos naturales no se comportan
según las leyes mecánicas de Newton.
R= Ni Newton dice la verdad ni la física clásica es absoluta,
o la física clásica no es absoluta a la vez que los
fenómenos naturales no se comportan según las leyes
mecánicas de Newton.
Universidad Nacional del Santa
35
Lógica Proposicional
II.
Fidel Vera Obeso
Dados los siguientes esquemas moleculares:
P = El estado es responsable de la economía del país sí y sólo sí
las leyes de la reforma económica no son aplicables a la
realidad.
Q = No se da el caso que las leyes de la reforma económica sean
aplicables a la realidad o el Estado sea responsable de la
economía del país.
R = Si los políticos dicen la
verdad, entonces, o el Estado es
responsable de la economía del país o las leyes de la reforma
económica non son aplicables a la realidad.
Determinar:
1) Si P implica a Q
2) Si R es implicado por Q
3) Si Q implica a R
4) Si R implica a la disyunción de P y Q
5) Si la conjunción de P y Q está implicada por R.
6) Si la bicondicional de P y Q está implicada por R.
7) Si la negación de Q está implicada por la disyunción de P
y R.
8) Si la negación de la conjunción de P y R implica a la
negación de Q.
Universidad Nacional del Santa
36
Lógica Proposicional
Fidel Vera Obeso
OBJETIVO N° 06
ACTIVIDAD N° 01
Enunciar,
demostrar
y
aplicar las principales leyes
lógicas
o
tautológicas
notables.
Analice la siguiente información sobre
1.6.
PRINCIPALES LEYES LÓGICAS O TAUTOLOGÍAS NOTABLES:
1) Identidad
(a) p  p  T
(b) p  p  p
2) No Contradicción:
 (p  p)  C  T
3) Tercio Excluido:
p  p  T
4) Idempotencia:
(a) p  p  p
(b) p  p  p
5) Conmutativa:
(a) p  q  q  p (b) p  q  q  p
6) Asociativa:
(a) p  (q  r)  (p  q) (b) p  (q  r)  (p  q)  r
7) Distributiva:
(a) p  ( q  r)  (p  q)  (p  r)
(b) p  ( q  r)  (p  q)  (p  r)
8) Doble Negación o Involución:
 (p)  p
Universidad Nacional del Santa
37
Lógica Proposicional
9)
Fidel Vera Obeso
Absorción:
(a) p  (p  q)  p
(b) p  (p  q)  p
(c) p  (p  q)  p  q
(d) p  (p  q)  p  q
10)
Morgan:
(a) (p  q)  p  q  p/q
(b) (p  q)  p  q  p  q
11)
Condicional:
(a) p  q  p  q
(b) (p  q)  p  q
12)
Disyunción Fuerte:
p  q  (p  q)   (p  q)  (p  q)  (q  p)
13)
Transposición:
(a) p  q  p  q
(b) (p  q)  q  p
14)
Transitiva:
(a) (p  q)  (q  r)  (p  r)
(b) (p  q)  (q  r)  (p  r)
15)
Elementos Neutros Respecto a  y 
(a) p  T  p
(b) p  T  T
(c) p  C  C
(d) p  C  p
Universidad Nacional del Santa
38
Lógica Proposicional
Fidel Vera Obeso
La demostración de las propiedades leyes lógicas a tautológicos
notables se realiza construyendo su tabla de valores veritativos.
En
los
siguientes
ejemplos
se
mostrará
algunas
de
las
aplicaciones de las principales leyes lógicas o tautologías
notables,
tales
como
equivalencia
de
proposiciones
simplificación de proposiciones complejas.
EJEMPLO 1:
Hallar la proposición equivalente a:
“No es el caso que, hace frío y no se congele”
(a) Hace frío o no congela
(b) No hace frío o congela
(c) No hace frío o no congela
(d) Hace frío o congela
(e) Hace frío y no congela
Solución:
Consideramos
p = hace frío
q = congela
Formalizando:
No es el caso que, p y no q
 (p  q)
Morgan
 p  q
cuya lectura es: “No hace frío o congela “. Respuesta (b)
EJEMPLO 2:
Hallar la proposición equivalente a:
“Hay que pagar 50 soles y servicio para ingresar al Club”
(a) No ingresar al club o pagar 50 soles, y ser socio.
(b) Pagar 50 soles o ser socio, y no ingresar al club.
Universidad Nacional del Santa
39
y
Lógica Proposicional
Fidel Vera Obeso
(c) Pagar 50 soles y ser socio, o no ingresar al club.
(d) Pagar 50 soles y no ser socio, y entrar al club.
(e) No es cierto que se pague 50 soles y ser socio, o ingrese al
club.
Solución:
Formalizando:
p = pagar 50 soles
q = ser socio
r = ingresar al club.
Hay que p y q para r.
 (p  q)  r
 (p  q) 
por condicional
r
Luego:
“No es cierto que se pague 50 soles y sea socio, o ingrese al club”.
Respuesta (c)
EJEMPLO 3:
Hallar la proposición equivalente a:
“17 es primo porque 17 es primo o 30 es par, y 30 es par”
(a) Si 17 es primo, entonces 30 no es par.
(b) Si 30 es par, entonces 17 no es primo.
(c) Si 17 no es primo, 30 no es par.
(d) 30 es par o 17 es primo.
(e) 17 es primo ya que 30 no es par.
Universidad Nacional del Santa
40
Lógica Proposicional
Fidel Vera Obeso
Solución :
Formalizando:
p = 17 es primo
q = 30 es par
(p  q)  q  p  q  p
Por absorción
“Si 30 es par, 17 es primo”
 q  p
Por condicional
“30 no es par o 17 es primo”
 p  q
Por transposición
“Si 17 no es primo, 30 no es par”
Respuesta (c)
EJEMPLO 4:
Simbolizar y luego simplificar la proposición:
“Viene a casa o se va de viaje, pero no viene; en
consecuencia se va de viaje”
(a) T
b) C
d) p  q
c) p
Solución:
Formalizando:
Sea
p = viene a casa
q = se va de viaje
p ó q, pero no p; en consecuencia q
 (p  q)  p  q
 (q  p)  q
Universidad Nacional del Santa
por absorción
41
e) p  q
Lógica Proposicional
Fidel Vera Obeso
  (q  p)  q
por condicional
 (q  p)  q
por Morgan
 p  (q  q)
asociativa
pT
tercio excluido
T
elemento neutro para 
Respuesta (a)
EJEMPLO 5:
Simbolizar y luego simplificar la proposición:
“Cuando obtenga mi título entonces ingreso a la carrera
magisterial, pero no ingreso a la carrera magisterial; luego no
obtuve mi título”
(a) p
b) p
c) p  q
d) C
e) T
Solución:
Formalizando:
Sea
p = obtengo mi título
q = ingreso a la carrera magisterial
Cuando p entonces q, pero no q; luego no p
 (p  q)  q  p
 (p  q)  q  p
Condicional
 p  q)  p
Absorción
 p  q)  p
Condicional
 (p  q)  p
Morgan
 q  (p  p)
Asociativa
q T
Tercio excluido
T
Elemento neutro para 
Respuesta (e)
Universidad Nacional del Santa
42
Lógica Proposicional
Fidel Vera Obeso
EJEMPLO 6:
Determinar los esquemas más simples equivalentes a:
(a)  (p  q)  q  p
(b)  (p  q)  p   (q  p)
(c)  p  (r)    (q ) (p  r) 
Solución:
(a)  (p  q)  q   p
  (p  q)  (q)  p
Condicional
  (p  q)  q  p
Involución
  (p  q)  q  p
Morgan
  (p  q)  q  p
Absorción
qp
Absorción
(b)  (p  q)  p  (q  p)
  (p  q)  p  (q  p)
Condicional
  (p  p)  q   (q  p)
Asociativa
  p  q   (q  p)
Idempotencia
  (p  q)  q    (p  q)  p 
Distributiva
 q  (q  p)
Absorción
q
Absorción
(c)  p  (r)   (q)  (p  r) 
  p  (r)   q  (p  r) 
Condicional
  p  (r)   q  (p)  (r) Morgan
  p  (r)  (r)  (q  p) Conmutativa y asociativa.
 r  q  p
Absorción
 (r  p)  q
Asociativa
  (r  p)  q
Morgan
 (r  p)  q
Condicional
Universidad Nacional del Santa
43
Lógica Proposicional
Fidel Vera Obeso
EJEMPLO 7:
Si definimos @ como:
p @ q  p  p  (q  t  r)   p
Simplificar:
 (p  q) @ (q  p)  @ (p  q)
a) p
b) p  q
c) p
d) q  p
e) p  q
Solución:
Por dato, tenemos:
p @ q  p  p  (q  t  r)   p
Por la condicional se obtiene
 p  p  (q  t  r)   p
Por absorción
p
Es decir
p@qp
Luego, la proposición molecular a simplificar:
 (p  q) @ (q  p)  @ (p  q)
Aplicando la definición @ dos veces
 (p  q) @ (q  p)
pq
pq
Respuesta (e)
Universidad Nacional del Santa
44
Lógica Proposicional
Fidel Vera Obeso
ACTIVIDAD N° 02
Resuelve a continuación los siguientes
EJERCICIOS SOBRE LAS PRINCIPALES LEYES LÓGICAS O
TAUTOLOGÍAS NOTABLES:
1. Hallar la proposición equivalente a:
“La conducta puede ser acción u omisión”
(a) La conducta no es acción ni omisión.
(b) La conducta es acción más no omisión.
(c)
La conducta no es acción no obstante es omisión.
(d) No es el caso que la conducta no sea acción ni omisión.
(e)
No es cierto que la conducta sea acción o no sea omisión.
2. Hallar la profesión equivalente a:
“Toma decisiones oportunas e inteligentes, pues es libre”
(a) Es libre o toma decisiones oportunas e inteligentes.
(b) No es libre, o toma decisiones oportunas e inteligentes.
(c)
Es libre y, toma decisiones oportunas como inteligentes.
(d) No es libre, ni toma decisiones oportunas e inteligentes.
(e)
No es libre y, no toma decisiones oportunas o inteligentes.
3. Hallar la proposición equivalente a:
“Tendrá el título universitario o sustenta su tesis”
(a) Sustenta su tesis o tiene el título universitario.
Universidad Nacional del Santa
45
Lógica Proposicional
Fidel Vera Obeso
(b) No es el caso que, sustente su tesis y tenga el título
universitario.
(c)
No es cierto que, sustente su tesis y no tenga el título
universitario.
(d) No tiene el título universitario, y sustenta su tesis.
(e)
No es verdad que no sustente su tesis o tenga el título
universitario.
4. Simbolizar y luego simplificar la proposición:
“Si el conocimiento es hipotético, se prueba; y si se prueba, entonces
es eficaz; luego, es eficaz cuando es hipotético”
a) r
b) p  r
c) T
d) C
e) (p  q)  r
5. Simbolizar y luego simplificar la proposición:
“Viene a casa o se va de viaje, pero no viene; en consecuencia se va
de viaje”
a) T
b) C
c) p
d) p  q
e) p  q
6. Simplificar el esquema:
p  (p  q)
a) p  q
b) q  p
d) q  p
e) p  q
c) p  q
7. Simplificar el esquema:
(p  q)   (r  p)  (q  p)
a) p  q
b) p  q
d) p
e) q
c) p  q
8. Simplificar:
(p  q)  (q  p)  (p  q)
a) p  q
b) p  q
d) p  q
e) q  p
Universidad Nacional del Santa
c) p  q
46
Lógica Proposicional
Fidel Vera Obeso
9. Simplificar:
 (p  q)  p  (q  p)  (p  q)
a) p  q
b) (p  q)
c) p  q
d) p  q
e) (p  q)
10.Se define el conector @ como:
p @ q   (p  q)  q   q  q
Simplificar el esquema molecular:
  (p  q) @ (t  w) @ q  @ p
a) q
b) q
d) p
e) p  q
Universidad Nacional del Santa
c) p
47
Lógica Proposicional
Fidel Vera Obeso
BIBLIOGRAFÍA
1.
BARKER, S. (1994). Elementos de Lógica. México: Libros Mc Graw Hill.
2.
COPI, I. & COHEN, C. (1996). Introducción a la Lógica. México: Editorial
Limusa.
3.
ROSALES, D. (1989). Introducción a la Lógica. Perú: Amaru Editores.
4.
SUPESS, P. (1985). Introducción a la Lógica Simbólica. México: CECSA.
5.
SUPESS, P. & HILL, SH. (1999). Primer Curso de Lógica Matemática.
España: Reverté Ediciones, S.A.
6.
TRELLES, O. & ROSALES, D. (2000). Introducción a la Lógica. Perú: Fondo
Editorial de la Pontificia Universidad Católica.
7.
VERA, F. (2003). Lógica Proposicional. Módulo de Autoaprendizaje. Perú:
Universidad Nacional del Santa.
8.
WHITESITT, J. (1986).
Álgebra Booleana y sus Aplicaciones. México:
CECSA.
Universidad Nacional del Santa
48