REPRESENTACIÓN DE FUNCIONES

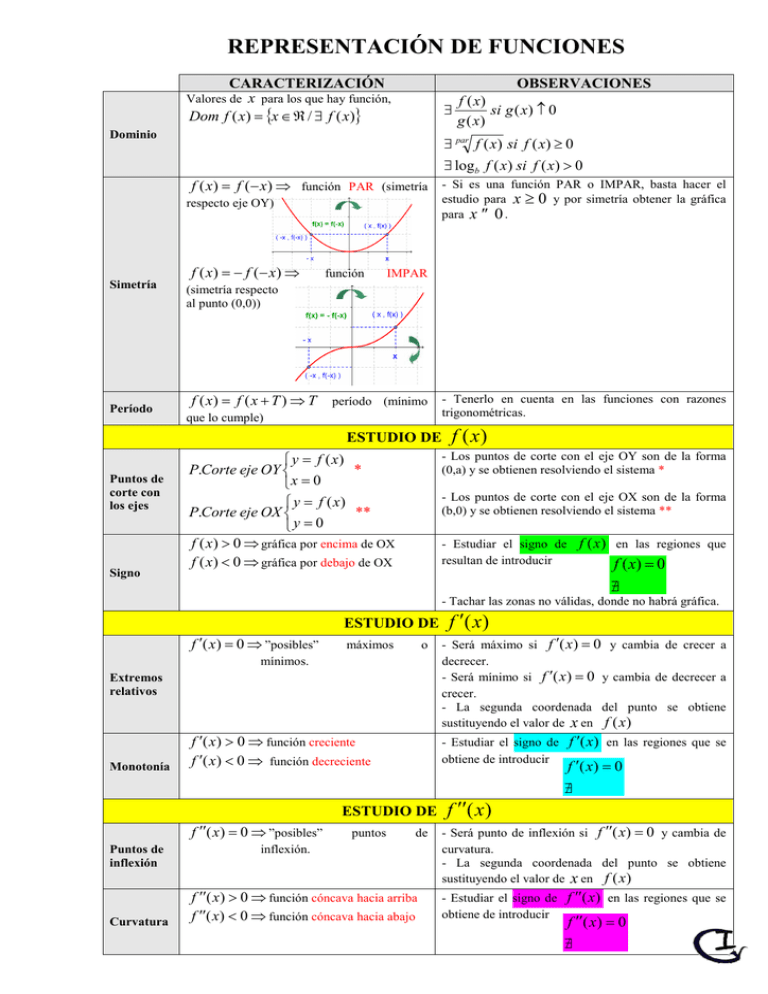
REPRESENTACIÓN DE FUNCIONES
CARACTERIZACIÓN
x para los que hay función,
Dom f ( x) = {x ∈ ℜ / ∃ f ( x)}
OBSERVACIONES
Valores de
∃
Dominio
f ( x)
si g ( x) ≠ 0
g ( x)
∃ par f ( x) si f ( x) ≥ 0
∃ logb f ( x) si f ( x) > 0
f ( x) = f (− x) ⇒ función PAR (simetría - Si es una función PAR o IMPAR, basta hacer el
estudio para
para x ≤ 0 .
respecto eje OY)
Simetría
Período
f ( x) = − f (− x) ⇒
función
Signo
y por simetría obtener la gráfica
IMPAR
(simetría respecto
al punto (0,0))
f ( x) = f ( x + T ) ⇒ T
período (mínimo
que lo cumple)
ESTUDIO DE
Puntos de
corte con
los ejes
x≥0
 y = f ( x)
P.Corte eje OY 
*
x = 0
 y = f ( x)
P.Corte eje OX 
**
y = 0
f (x) > 0 ⇒ gráfica por encima de OX
f (x) < 0 ⇒ gráfica por debajo de OX
- Tenerlo en cuenta en las funciones con razones
trigonométricas.
f ( x)
- Los puntos de corte con el eje OY son de la forma
(0,a) y se obtienen resolviendo el sistema *
- Los puntos de corte con el eje OX son de la forma
(b,0) y se obtienen resolviendo el sistema **
- Estudiar el signo de
resultan de introducir
f (x) en las regiones que
f ( x) = 0
∃/
- Tachar las zonas no válidas, donde no habrá gráfica.
ESTUDIO DE
f ′(x) = 0 ⇒ ”posibles”
máximos
o
mínimos.
Extremos
relativos
Monotonía
f ′(x) > 0 ⇒ función creciente
f ′(x) < 0 ⇒ función decreciente
f ′′( x) = 0 ⇒ ”posibles”
Curvatura
puntos
- Será máximo si f ′( x ) = 0 y cambia de crecer a
decrecer.
- Será mínimo si f ′( x ) = 0 y cambia de decrecer a
crecer.
- La segunda coordenada del punto se obtiene
sustituyendo el valor de x en f (x )
- Estudiar el signo de
obtiene de introducir
ESTUDIO DE
Puntos de
inflexión
f ′( x)
de
inflexión.
f ′′( x) > 0 ⇒ función cóncava hacia arriba
f ′′( x) < 0 ⇒ función cóncava hacia abajo
f ′′( x)
f ′(x) en las regiones que se
f ′( x) = 0
∃/
- Será punto de inflexión si f ′′( x) = 0 y cambia de
curvatura.
- La segunda coordenada del punto se obtiene
sustituyendo el valor de x en f (x )
- Estudiar el signo de
obtiene de introducir
f ′′( x) en las regiones que se
f ′′( x ) = 0
∃/
CARACTERIZACIÓN
ASÍNTOTAS
Se estudia el límite de la función en aquellos
valores que dan problemas de existencia.
OBSERVACIONES
- Si Dom f ( x) = ℜ , no hay A. Verticales.
- Representar los límites:
Si el Dom f ( x) = ℜ − {v} ,
lim f ( x) = ±∞
x→v +
Vertical
x = v
lim f ( x) = ±∞ 
x →v
−
lim f ( x) = +∞
x →v +
es la ecuación
de la asíntota
vertical.
lim f ( x) = − ∞
x →v −
- En funciones polinómicas,
No hay
f ( x) = P( x) :
P( x)
:
Q( x)
Si Q( x) = 0 ⇒ x = raíces de Q( x)
Hacer el límite de la función en +∞ y − ∞ .
lim f ( x) = h
x→+ ∞
lim
x→ − ∞
+


y=h
−
f ( x) = h 

es la ecuación
de la asíntota
horizontal.
- En funciones racionales,
f ( x) =
- Tiene A. Horizontal si
h ≠ ± ∞ . Puede que sólo
tenga por un lado o que no coincidan ambos límites y
por tanto tenga dos A.H.
- Representar los límites:
+
lim f (x) = h
x→+ ∞
lim f ( x) = h
−
x→ − ∞
Horizontal
- En funciones polinómicas, f ( x ) = P ( x ) :
No hay
P( x)
:
Q( x)
Si grado P( x) < grado Q( x) ⇒ y = 0
- En funciones racionales, f ( x ) =
Si grado P( x) = grado Q ( x) ⇒ y =
La ecuación es y = mx + n ,
m = lim
x→ ± ∞
Oblicua
f ( x)
≠ 0, ±∞
x
- Sólo se estudian donde no haya A.H.
- Representar la recta y hallar los puntos de corte de
(Si m=0, sería A.H.) dicha recta con la curva, para saber desde qué lado de
la recta hay que dibujar la gráfica.
n = lim ( f ( x) − mx) ≠ ±∞
x→ ± ∞
coef director P( x)
coef director Q( x)
- En funciones polinómicas, f ( x ) = P ( x ) :
No hay
- En funciones racionales, f ( x ) =
P( x)
:
Q( x)
 P( x) 
Si grado P ( x) = grado Q( x) + 1 ⇒ y = cociente 

 Q( x) 
Puntos de
la curva
TABLA DE VALORES
Sustituir el valor de x en f (x ) para hallar - Representar los puntos ( x , f (x ) ).
puntos de la curva.