mg w = yx ).

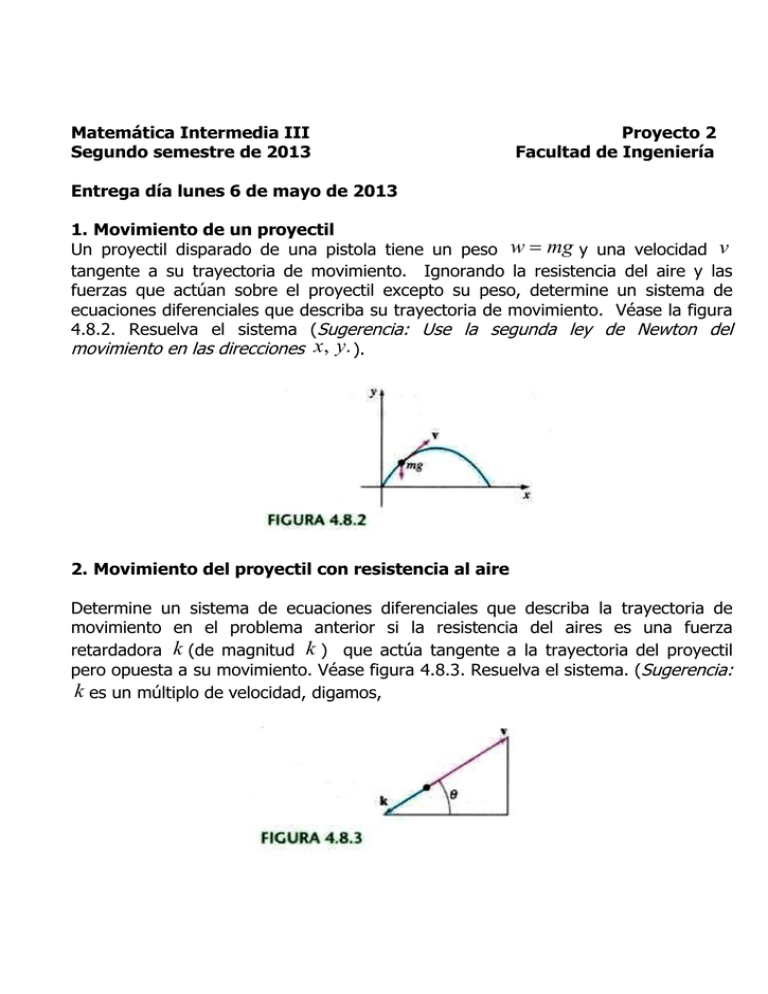
Matemática Intermedia III
Segundo semestre de 2013
Proyecto 2
Facultad de Ingeniería
Entrega día lunes 6 de mayo de 2013
1. Movimiento de un proyectil
Un proyectil disparado de una pistola tiene un peso w  mg y una velocidad v
tangente a su trayectoria de movimiento. Ignorando la resistencia del aire y las
fuerzas que actúan sobre el proyectil excepto su peso, determine un sistema de
ecuaciones diferenciales que describa su trayectoria de movimiento. Véase la figura
4.8.2. Resuelva el sistema (Sugerencia: Use la segunda ley de Newton del
movimiento en las direcciones x, y. ).
2. Movimiento del proyectil con resistencia al aire
Determine un sistema de ecuaciones diferenciales que describa la trayectoria de
movimiento en el problema anterior si la resistencia del aires es una fuerza
retardadora k (de magnitud k ) que actúa tangente a la trayectoria del proyectil
pero opuesta a su movimiento. Véase figura 4.8.3. Resuelva el sistema. (Sugerencia:
k es un múltiplo de velocidad, digamos,
3. Proyecto de cómputo
a) Lea el problema 8 de los ejercicios 3.3. (del libro de texto) En ese problema se
pidió demostrar que el sistema de ecuaciones diferenciales
dx1
1
  x1
dt
50
dx2
1
2

x1 
x2
dt
50
75
dx3
2
1

x2 
x3
dt
75
25
Es un modelo para las cantidades de sal en los tanques de mezclado conectados A,
B, y C que se muestran en la figura 3.3.7 (del libro de texto). Resuelva el sistema
sujeto a x1 (0)  15,
x2 (t )  10 y x3 (t )  5
b) Use un SAC para graficar x1 (t ), x2 (t ) y x3 (t ) en el mismo plano coordenado
(como en la figura a4.8.1) en el intervalo  0, 200  .
c) Debido a que se bombea agua pura hacia el tanque A, es lógico que en algún
momento la sal salga de los tres tanques. Utilice una aplicación de un SAC para
encontrar raíces para determinar el tiempo cuando la cantidad de sal en cada
recipiente sea menor o igual que o.5 libras en cada recipiente. ¿Cuándo son las
cantidades des sal x1 (t ),
que 0.5 libras.
x2 (t )
y
x3 (t ) simultáneamente menores o iguales
Referencias
a. Castillo Miguel. Instructivo para el uso de los Programas Scientific Notebook, Matemática
y Mathcad
b. Ecuaciones diferenciales con problemas con valores en la frontera (libro de texto del
Curso). Dennis G. Zill, Michael R. Cullen. CENGAGE Learning, septima edición.