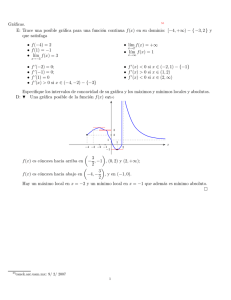
graficas maestria

Teorı́a de Gráficas
por Marı́a Luisa Pérez Seguı́
Introducción
Se presenta aquı́ el material correspondiente al curso de maestrı́a de Teorı́a de Gráficas,
el cual se imparte en el Posgrado Conjunto de Matemáticas UNAM-UMSNH. El material
del libro constituyó el 100 % del curso impartido el semestre de febrero-julio de 2013.
i
Índice
Introducción
I
1. Conceptos básicos
1
2. Cortes
8
3. Operaciones en gráficas
13
4. Grupo de automorfismos
15
5. Otras construcciones
20
6. Bloques
24
7. Gráficas eulerianas
27
8. Gráficas hamiltonianas
31
9. Planaridad
38
10.Gráfica dual
42
11.Género
47
12.Coloración
52
13.Teorı́a extrema de gráficas
66
14.Apareamientos
77
15.Digráficas
88
16.Redes y flujos
93
17.Conexidad
99
ii
1.
Conceptos básicos
Una gráfica (finita, simple) G consta de un conjunto (finito) V = V(G) cuyos elementos se llaman vértices, y de otro conjunto A = A(G) que consta de subconjuntos de dos
elementos de V llamados aristas. Escribimos G = (V, A). Si a = {u, v} ∈ A, escribimos
a = uv y decimos que u y v son extremos de a.
Por el momento sólo trabajaremos con este tipo de gráficas y dejaremos para después el
estudio de multigráficas en donde se permite que A sea multiconjunto (es decir, que entre
dos vértices haya más de una arista), de seudográficas en las que, además, se permite que
las aristas consten de un solo elemento de V (una arista ası́ se llama lazo), y de digráficas
(o multi/seudo digráficas) en las que las aristas son parejas ordenadas de vértices. En este
curso no trabajaremos con gráficas infinitas (aquéllas en las que el conjunto de vértices es
infinito).
En general se hace una representación geométrica de la gráfica poniendo un punto por
cada vértice y representando cada arista por una lı́nea entre los dos vértices que la determinan
(en el caso de digráficas se pone una flecha).
De aquı́ en adelante G denota una gráfica cualquiera con conjunto de vértices V y conjunto
de aristas A. Los vértices de G serán u, v, w, . . .. En estas notas el conjunto de los números
naturales es
N = {1, 2, 3, . . .}.
Para n ∈ N el conjunto [n] consta de los naturales del 1 al n.
El orden de G es |V|, su tamaño es |A| y si v es un vértice, el grado de v es el número δ(v)
de aristas que tienen como elemento a v. La vecindad de v es N (v) = {w ∈ V : vw ∈ A},
la vecindad cerrada de v es N (v) = N (v) ∪ {v} y, para un conjunto de vértices S, los
vecinos de S forman el conjunto N (S) = {u ∈ V : ∃ v ∈ S tal que uv ∈ A} (en el
que puede, o no, haber elementos de S). También tenemos ∆(G) = max{δ(v) : v ∈ V} y
δ(G) = min{δ(v) : v ∈ V}. La gráfica G es r-regular si ∆(G) = r = δ(G).
1.1 Proposición. La suma de los grados de los vértices de una gráfica es el doble del
número de aristas.
Demostración. Al sumar los grados de los vértices, cada arista se cuenta dos veces (una
por cada uno de sus extremos). ♦
1.2 Ejercicio. Probar que el número de personas en el mundo que tienen un número
impar de hermanos es par.
1.3 Ejercicio. Sea G una gráfica regular. Si G tiene 26 aristas, ¿cuántos vértices puede
tener?
1
1.4 Ejercicio. Se quiere diseñar una competencia con n participantes en la que cada
uno compita exactamente con otros k. Probar que una competencia tal puede diseñarse si y
sólo si nk es par y n ≥ k + 1.
Si a = uv ∈ A, decimos que u y v son adyacentes y que a es incidente a u y a v. Si
dos aristas tienen exactamente un vértice en común decimos que son adyacentes.
La matriz de adyacencias de G es una matriz de 0’s y 1’s y tamaño |V| × |V|, con
renglones y columnas etiquetadas con los elementos de V, y en la que en la entrada (u, v)
(denotada por Auv ) hay un 1 si, y sólo si, uv ∈ A. La matriz de incidencias de G es una
matriz de 0’s y 1’s y tamaño |V| × |A|, con renglones etiquetados con los elementos de V,
columnas etiquetadas con los elementos de A, y en la que en la entrada Aua = 1 si, y sólo
si, u ∈ a.
1.5 Observación. La matriz de adyacencias es simétrica y tiene ceros en la diagonal; la
de incidencias tiene exactamente dos 1’s en cada columna.
Dados u, v ∈ V, un camino C de u a v (o uv-camino) es una sucesión de vértices
alternados con aristas C = (u = v0 , a1 , v1 , a2 , . . . , an , vn = v) tal que para cada i = 1, . . . , n,
la arista ai es incidente a (los vértices distintos) vi−1 y vi . También escribimos C = (u =
v0 , v1 , . . . , vn = v) o C = (a1 , . . . , an ). La porción del camino de vi a vj (para i < j) se denota
por (vi , C, vj ). El camino (vn , . . . , v0 ) se denota por C −1 . El camino es cerrado si v0 = vn ;
si no, se dice que es abierto. El camino es trayectoria si no repite vértices, es paseo si no
repite aristas y es ciclo si no se repiten aristas y los únicos vértices que se repiten son el
primero y el último (v0 = vn ). En estas notas llamamos longitud del camino, l(C), a n (el
número de aristas).
1.6 Ejercicio. Probar que si A es la matriz de adyacencias de G y k es natural, entonces
Akuv es el número de caminos de longitud k de u a v.
1.7 Proposición. Todo uv-camino C contiene una uv-trayectoria.
Demostración. Inducción sobre la longitud del camino. Es claro para l(C) ∈ {0, 1}. Sea C
camino de longitud n > 1 y supongamos que C no es trayectoria. Sea i < j tal que vi = vj ;
entonces C 0 = (v0 , . . . , vi , vj+1 , . . . , vn ) tiene longitud menor que n ası́ que aplica la hipótesis
de inducción. ♦
Una gráfica es conexa si dados cualesquiera dos vértices u y v existe un uv-camino (o
uv-trayectoria). En caso contrario se dice que la gráfica es disconexa.
1.8 Proposición. Todo camino cerrado C de longitud impar contiene un ciclo.
Demostración. Inducción sobre l(C). Si l(C) = 3 entonces C es ciclo (pues cada arista
consta de vértices distintos). Supongamos que l(C) = n > 3 impar y que C = (v0 , v1 , . . . , vn )
no es ciclo. Entonces C repite algún vértice: vi = vj para ciertas i 6= j con i > 0 y alguna de
2
las dos porciones que forman C, (v0 , v1 , . . . , vi , vj+1 , . . . vn ) o (vi , vi+1 , . . . vj ), tiene longitud
impar menor que n, ası́ que ahı́ aplica la hipótesis de inducción. ♦
1.9 Ejercicio. Determinar cuándo es posible afirmar que un camino cerrado de longitud
par contiene un ciclo.
Dos gráficas G1 = (V1 , A1 ) y G2 = (V2 , A2 ) son isomorfas si existe una biyección f :
V1 → V2 tal que uv ∈ A1 si, y sólo si, f (u)f (v) ∈ A2 . Cuando dos gráficas son isomorfas,
las consideramos iguales; ası́ por ejemplo podemos hablar de la gráfica que consta de un solo
vértice. Es claro que dos gráficas isomorfas comparten las mismas propiedades, por ejemplo
de conexidad o del grado de los vértices (más aún un isomorfismo debe mandar un vértice
a otro del mismo grado). Denotamos por Tn la trayectoria de longitud n y por Cn al ciclo de
longitud n.
Decimos que una gráfica H es subgráfica de G (o que está contenida en G) si el
conjunto de vértices y de aristas de H son subconjuntos del conjunto de vértices y del de
aristas de G, respectivamente (o si hay un isomorfismo entre H y una subgráfica de G).
Una componente conexa de G es una subgráfica conexa maximal (es decir, ella es conexa,
pero cualquier otra subgráfica que la contenga propiamente es disconexa). La componente
conexa de un vértice v es la subgráfica conexa maximal que lo contiene.
1.10 Ejemplo. Hay 6 gráficas conexas no isomorfas con 4 vértices. Son las siguientes 6:
•........................•.........................•..........................•..
•.......
•
....
...
......................................................
•
•
•
•
...................................
.. ...
... ...
... .....
..
...
.
.
..
.............................
•
•
•..............................•........
•.........................................•...........
•......................................................•...........
•
•
•..................................•.......
...
....
...
...
...
.............................
•
...
.. ...
... .........
....
.. ......
.
................................
•
... ....... ..
... .............. ..
.. .... .... ..
♦
1.11 Ejercicio. Dar un ejemplo de dos gráficas conexas no isomorfas en las que los
grados de los vértices sean los mismos.
1.12 Ejercicio. ¿Cuál es el máximo número de aristas que puede tener una gráfica no
conexa con n vértices? (Sugerencia: Recordar que 2r = 1 + 2 + · · · + (r − 1).)
La gráfica completa con n vértices es aquélla en la que por cada par de vértices hay
una arista que los une (es decir, tiene n2 aristas); denotamos esta gráfica por Kn . Si G es
una gráfica con n vértices, la podemos considerar como subgráfica de Kn y el complemento
G de G es la subgráfica de Kn formada por los mismos vértices de G pero en el que las aristas
son aquellas aristas de Kn que no son aristas de G.
3
•......
•
...
...
..
...
...
...
...
...
....
.
•
K1
K2
•
...
... ....
... .....
..
...
.
.
...
...
...
...
...
..
...
.
...
..
.
...
..
.
...
..
...
.
...
..
.
...
.
.
.
.....................................................................
•
•
K3
•.....................................................................................•..........
... ....
... ........
.....
.....
...
...
..... .........
...
..
..... .....
...
.........
...
...
.
.
.
.
.
.
...
.
.
...
... .......
.
.
.
...
.
.....
.
...
.
.
.
.
...
.
.
..... ....
..
..... ...
... ........
..... ..
............
..............................................................
•
•
K4
•
............
..... ..........
...... ... ... ......
...... .... .... ...........
...
......
......
.
.
.
.
.
.
.....
..
.....
..
.................................................................................................
...
... .......
.
..... .
.
.
.
.
.
.
... ...... ..
... ........... ....
.......
...
.
.
...
........
...
...
........
... .... ................... .... ...
... ... ........ ........ ... ...
...... ... ..
... .. ........
.... . .
.............
..................................................
•
•
•
•
K5
La subgráfica inducida por un subconjunto V 0 del conjunto de vértices es (V 0 , A0 ),
donde si u, v ∈ V 0 y uv ∈ A entonces uv ∈ A0 . Una subgráfica generadora es aquélla que
tiene todos los vértices de G.
En demostraciones por inducción, muchas veces conviene considerar las gráficas obtenidas
de la original al quitar un vértice o una arista. Si v ∈ V, la subgráfica de G que tiene por
conjunto de vértices a V \ {v} y por conjunto de aristas a A \ {a ∈ A : v ∈ a} se denota
por G − v. Si a ∈ A, la subgráfica (V, A \ {a}) de G se denota por G − a. También, si u y v
son vértices de G no adyacentes, la gráfica G + uv tiene por conjunto de vértices a V y por
conjunto de aristas a A∪{uv}. Análogamente podemos considerar G −S para S subconjunto
del conjunto de aristas o vértices.
1.13 Proposición. Si G es una gráfica entonces ella o su complemento es conexa.
Demostración. Primera forma. Supongamos que G no es conexa. Probaremos que cualesquiera dos vértices están conectados en G. Tomemos u, v ∈ V distintos. Si u y v están en
diferente componente conexa de G, entonces hay una arista entre ellos en G. Si u y v están en
la misma componente conexa de G, sea w un vértice en otra componente (que existe porque
estamos suponiendo que G no es conexa. Entonces, en G hay una arista de u a w y también
de v a w y, por tanto, (u, w, v) es una uv-trayectoria en G.
Segunda forma. Procedemos por inducción sobre el orden n de G. Para n = 1 el resultado
es obvio. Supongamos entonces que n ≥ 2. En Kn pintemos las aristas de G de verde y las
aristas de G de rojo. Si un vértice u tiene todas sus aristas de un mismo color, entonces u
está unido con todos los demás vértices en la gráfica de ese color, ası́ que el resultado es
cierto. Supongamos entonces que u tiene aristas de cada uno de los dos colores. Por hipótesis
de inducción, en Kn − u, alguna de las dos subgráficas resultantes G − u o G − u es conexa.
Pero a u le llegan aristas de ambos colores ası́ que está unido con las dos gráficas y, en
consecuencia, G o G es conexa. ♦
1.14 Ejercicio. Encontrar una gráfica G en la que ambas G y G sean conexas.
1.15 Ejercicio. Probar que sólo hay dos gráficas 4-regulares de orden 7. ¿Cuántas gráficas 6-regulares hay de orden 9?
Una gráfica conexa sin ciclos se llama árbol. Un bosque es una gráfica cuyas componentes conexas son árboles. Un vértice de grado 1 es una hoja.
4
1.16 Lema. Un árbol con dos o más vértices tiene al menos dos hojas.
Demostración. Una trayectoria maximal tiene sus extremos de grado 1. ♦
1.17 Proposición. Una gráfica conexa con n vértices es árbol si, y sólo si, tiene n − 1
aristas.
Demostración. (⇒) Inducción sobre n. Si n = 1, el número de aristas es 0 = n − 1.
Supongamos n ≥ 1. Sea u vértice de grado 1. Entonces G − u es árbol con n − 1 vértices,
por tanto, por hipótesis de inducción, tiene n − 2 aristas, ası́ que el árbol que tenı́amos tiene
n − 1 aristas.
(⇐) Supongamos que la gráfica tiene k ≥ 1 ciclos y quitemos una arista de un ciclo
(la gráfica permanece conexa); repitamos esto hasta eliminar todos los ciclos; obtenemos un
árbol con n vértices y n − 1 − k < n − 1 aristas, lo cual es una contradicción. ♦
1.18 Ejercicio. Probar que las siguientes tres propiedades son equivalentes para una
gráfica conexa G:
(a) G es árbol.
(b) Si a G se le quita una arista cualquiera, la gráfica resultante es disconexa.
(c) Entre cualesquiera dos vértices hay exactamente una trayectoria.
1.19 Ejercicio. En cada uno de los casos siguientes explicar por qué no se puede construir una gráfica G con las condiciones indicadas.
(a) Que los grados de los vértices sean (7, 4, 4, 3, 3, 2, 1).
(b) Que los grados de los vértices sean (7, 4, 4, 4, 3, 3, 2, 1, 1).
(c) Que sea árbol y los grados de los vértices estén dados por la sucesión (6, 5, 4, 2, 2, 1, 1, 1).
1.20 Ejemplo. Hay 6 árboles no isomorfos con 6 vértices. Son los siguientes 6:
•...............•.................•.................•.................•.................•...
•.......
.
•...............•....................•.................•.................•...
•.......
.
•...............•.................•....................•.................•...
•.......
.
•...............•.........................•.................•...
..
•....
•.......
.
•...............•......................•....................•...
..
•....
•.......
.
•..................•..............................•..
.. ..
•.... •...
♦
1.21 Ejercicio. Probar que toda gráfica G tiene una trayectoria de longitud δ(G), y que
si δ(G) ≥ 2, entonces tiene un ciclo de longitud al menos δ(G) + 1.
1.22 Ejercicio. Sea n ≥ 2 un entero y sea g1 ≥ g2 ≥ · · · ≥ gn una sucesión de naturales
tales que g1 + g2 + · · · + gn = 2(n − 1). Probar que existe un árbol G con n vértices cuyos
grados son los gi .
5
1.23 Ejercicio. Probar que toda gráfica conexa tiene árbol generador.
1.24 Ejercicio. Sea G un árbol con ∆(G) = k ≥ 1 y sea ni el número de vértices de
grado i, para i ∈ [k]. Probar que
n1 = 2 + n3 + 2n4 + 3n5 + · · · + (k − 2)nk .
1.25 Ejercicio. Probar que si δ(G) ≥ k entonces G tiene como subgráfica a todo árbol
con k + 1 vértices.
Decimos que G es bipartita si V se puede partir en dos conjuntos (ajenos) U y W, no
vacı́os, de manera que todo elemento de A tiene un extremo en U y otro en W. Para m y n naturales la gráfica completa bipartita, Km,n , consta de m+n vértices u1 , . . . , um , w1 , w2 , . . . , wn
y las mn aristas ui wj con i ∈ [m] y j ∈ [n]. Análogamente se define gráfica s-partita, y
la gráfica s-partita completa, Kn1 ,...,ns , es aquélla con ni vértices en el i-ésimo conjunto
de una partición de su conjunto de vértices, y en la que hay una arista entre cada par de
vértices de cualesquiera dos subconjuntos diferentes de la partición.
1.26 Ejercicio. Describir las matrices de adyacencia de gráficas bipartitas.
1.27 Proposición. Una gráfica es bipartita si, y sólo si, no tiene ciclos de longitud
impar.
Demostración. (⇒) Coloreemos los vértices de uno de los conjuntos de rojo y el del otro
de azul. En cualquier ciclo los vértices están coloreados alternadamente, ası́ que no puede
haber ciclos de longitud impar.
(⇐) Sin pérdida de generalidad G es conexa. Supongamos que no tiene ningún ciclo de
longitud impar. Tomemos un vértice cualquiera v y pintémoslo de azul. Ahora pintemos
todos los vértices unidos a v de rojo; posteriormente pintemos todos los vértices unidos a
éstos de azul, etc. El que no haya ciclos impares nos dice que si un vértice ya está pintado
de un color no trataremos de pintarlo del color contrario. La coloración nos da la partición
buscada. ♦
1.28 Proposición. Sea G una gráfica con n vértices y m aristas. Si m >
G tiene un triángulo (ciclo de longitud 3).
n 2
2
entonces
Demostración. Supongamos que no y sea u un vértice de grado maximal k. Como no hay
ciclos de longitud 3, dentro de N (u) no hay aristas. Tenemos que V \ N (v) tiene n − k − 1
elementos y cada uno de ellos tiene grado a lo más k (pues k se eligió como grado maximal).
2
Entonces m ≤ k + k(n − k − 1) = k(n − k) ≤ n2 , lo cual es una contradicción. ♦
Sea G conexa. Si u, v ∈ V, entonces su distancia es:
d(u, v) = min{l(T ) : T es uv−trayectoria}.
(Para gráficas no conexas podrı́a definirse d(u, v) = |V| cuando u y v pertenecen a diferente
6
componente conexa.)
1.29 Observación. Sea G una gráfica conexa. Entonces d : V × V → R es una métrica.
Dado u ∈ V su excentricidad es
e(u) = max{d(u, v) : v ∈ V};
El diámetro de G es
D(G) = max{d(u, v) : u, v ∈ V}.
El centro de G, Z(G), consta de los vértices con menor excentricidad, es decir,
Z(G) = {u ∈ V : e(u) ≤ e(v) ∀v ∈ V}.
1.30 Ejemplo. El diámetro de la siguiente gráfica es 4; junto a cada vértice se ha escrito
su excentricidad; su centro consta del único vértice con excentricidad 2.
4
•
3
•
3
•
4
•
•
3
•
2
•
3
.....................................................
.....
..
.....
..........
...
.....
..... .........
....
...
.....
.....
.....
...
...
.....
.....
.....
.
.
.
...
.
.
...
.....
.....
...
.
.
.
.
.
.
.
...
.
.
.....
.....
...
...
.
.
.
.
.
.
...
.
.
.....
.....
...
...
.
.
.
.
.
.
...
.
.
.....
...
.....
...
.
.
.
.
.
.
.
.
.
...
.....
..... ..
...
.
.
.
.
.
.
.
.
.
...
.....
..... ..
...
.
.
.
.
.
.
.
.
.
.
.............................................................................................................................................................................................................
•
4
1.31 Ejemplo. Si v ∈ Kn entonces e(v) = 1; D(Kn ) = 1 y Z(Kn ) = V(Kn ).
1.32 Observación. Si e(u) = k entonces k es el menor natural con el cual se tiene que
{v ∈ V : d(u, v) ≤ k} es todo V.
1.33 Lema. Si G es árbol con al menos tres vértices y H es el conjunto de hojas de G
entonces Z(G) = Z(G − H).
Demostración. Es claro que si v ∈ V no es hoja, entonces eG (v) = eG−H (v) − 1 pues la
distancia máxima de v a otros vértices se alcanza en una hoja. Entonces la excentricidad
mı́nima en ambas gráficas se alcanza en el mismo conjunto de vértices. ♦
1.34 Proposición. Si G es árbol, entonces |Z(G)| consta de un solo vértice o de dos
vértices adyacentes.
Demostración. Hacemos inducción sobre el número de vértices y aplicamos el lema anterior. ♦
7
2.
Cortes
Decimos que v es vértice de corte si G − v tiene más componentes conexas que G.
Decimos que a es puente si G − a tiene más componentes conexas que G.
•..............................
•
•..............................
..
.........
....... ....
.......
.......
...
...
.......
.......
.
.
.
...
...
.
.
.
.......
.
...
...
.......
.......
....... .............
...
...
.
.
............
...
...
.
.
.
.
.
.
.
.
.......
...
...
.....
.
.
.
.
.
.
.
.
.
.
.......
...
...
.....
.
.
.
.
.
.
.
.
.
.
.......
...
...
.....
.
.
.
.
.
.
.
.
.
.
.......
...
....
....... ....
... .............
..........
..
......
v
•
•
•
..
.........
....... ....
.......
.......
...
...
.......
.......
.
.
.
...
...
.
.
.
.......
..
...
...
.......
.......
.......
.......
.
...
...
.
.
.
.
.
.
......................................................
...
...
.
.
.
.
.
.
.
.
.......
...
...
.....
.
.
.
.
.
.
.
.
.
.
.......
...
...
.....
.
.
.
.
.
.
.
.
.
.
.......
...
...
.....
.
.
.
.
.
.
.
.
.
.
.
.......
.
...
....
....... ....
... .............
.........
.
......
•
a
•
•
•
•
2.1 Observación. Una gráfica puede no tener arista de corte aun cuando tenga vértices
de corte.
2.2 Proposición. Si G conexa tiene al menos tres vértices y un puente uv entonces u o
v es vértice de corte.
Demostración. Sea w ∈ V \ {u, v} y supongamos que w está en la misma componente
conexa que v en G − uv. Entonces toda uw-trayectoria en G pasa por v ası́ que u y w están
en distintas componentes de G − v, de donde v es vértice de corte. ♦
2.3 Observación. Si a es arista de corte, entonces G − a tiene una componente más que
G exactamente. Si v es vértice de corte, entonces G − v puede tener dos o más componentes
que G.
...
•...............
..•
.....
.....
.....
.
.....
....
.....
.....
..... .........
..........
.
........
..... .........
.....
.....
.....
.....
.....
.....
.
.
.
.
.....
...
.
.
.....
.
.
..
.....
•
•
•
Un bloque es una gráfica conexa, con al menos tres vértices y sin vértices de corte.
2.4 Ejemplo. Si n ≥ 3 entonces Kn y Cn son bloques.
2.5 Proposición. Las siguientes propiedades son equivalentes para una gráfica conexa
G con al menos tres vértices.
(a) G es bloque.
(b) Dados u 6= v vértices existe un ciclo que pasa por u y v.
(c) Dados u vértice y a arista existe un ciclo que pasa por u y a.
(d) Dados a 6= e aristas existe un ciclo que pasa por a y e.
(e) Dados u 6= v vértices y a arista existe una uv-trayectoria que pasa por a.
(f) Dados u, v, w vértices existe una uw-trayectoria que pasa por v.
8
(g) Dados u, v, w vértices existe una uw-trayectoria que no pasa por v.
Demostración. (a) ⇒ (b) Observemos que no hay vértices de grado 1 pues si δ(v) = 1 y
w ∈ N (v), entonces w es de corte. Sea u ∈ V y sea
X = {v ∈ V : ∃ C ciclo tal que u, v ∈ C}.
Veremos que X = V. Sea v ∈ N (u) y sea w ∈ N (v) \ {u}. Sea T uw-trayectoria en G − v
(existe pues v no corta G). Entonces (u, T, w, v, u) es ciclo y ası́ v ∈ X, de donde tenemos
que X 6= ∅ y que N (u) ⊂ X. Supongamos que X 6= V y sea w ∈
/ X que tiene un vecino
x ∈ X. Sea C ciclo que contiene a u y a x. Como x no es de corte, existe T wu-trayectoria
en G − x. Sea y el primer vértice de T en C. Entonces (x, w, T, y, C, u, C, x) es un ciclo que
contiene a u y a w, lo cual es una contradicción, de donde X = V.
(b) ⇒ (c) Sea a = vw.
Caso (1). Si u = w, usando (b) construyamos un ciclo C que pase por u y v. Si a ∈ C,
ya acabamos. Si no, entonces tomemos T , una de las dos vu-trayectorias determinadas por
C. Ası́ (u, a, v, T, u) es el ciclo buscado.
Caso (2). u ∈
/ a. Sea Cv ciclo que contenga a u y a v, y sea Cw ciclo que contiene a u y a
w. Si alguno de esos ciclos contiene a a ya acabamos y también si Cv pasa por w (o si Cw pasa
por v). Si no, sea Tw una de las dos wu-trayectorias determinadas por Cw . Sea z el primer
vértice de Tw en Cv (posiblemente z = u). Sin pérdida de generalidad, Cv pasa primero por
z que por v (empezando desde u). El ciclo buscado es (u, Cv , z, Tw−1 , w, a, v, Cv , u).
(c) ⇒ (d) Sean a = u1 u2 y e = v1 v2 .
Caso (1). Si a y e son adyacentes, digamos u2 = v1 , tomamos ciclo que contenga a a y a
v1 . Si este ciclo contiene a e, ya acabamos; si no, en el ciclo sustituimos la trayectoria T de
v1 a v2 que no contiene a a en el ciclo por e obteniendo un ciclo por a y e.
Caso (2). a y e no adyacentes. Sea C1 ciclo que contiene a u1 y a e; digamos C1 =
(u1 , T1 , v1 , v2 , S1 , u1 ), y sea C2 ciclo que contiene a u2 y a e, digamos C2 = (u2 , T2 , v1 , v2 , S2 , u2 ).
Si alguno de estos ciclos contiene al otro vértice de a entonces ya acabamos. Supongamos
que no. Sea z el primer vértice de T2 en C1 . Sin pérdida de generalidad, z ∈ T1 . El ciclo
buscado es (u1 , u2 , T2 , z, T1 , v1 , v2 , S1 , u1 ).
(d) ⇒ (e) Si alguno de u o v pertenece a a o si u y v son adyacentes, entonces es claro.
Supongamos que no. Sean u0 adyacente a u y v 0 adyacente a v. Tomemos un ciclo Cu que contenga a a y a uu0 , y un ciclo Cv que contenga a a y a vv 0 . Si u ∈ Cv o v ∈ Cu entonces ya acabamos ası́ que supongamos que no. Sea a = ww0 . Supongamos que Cu = (u, u0 , Tu , w, w0 , Su , u)
y que Cv = (v, v 0 , Tv , w, w0 , Sv , v) (posiblemente v y v 0 están invertidos en el ciclo, pero no es
relevante en lo que sigue). Sea z el primer vértice en Tv ∩ Cu (posiblemente z = u0 o z = w).
Sin pérdida de generalidad, z ∈ Tu . La trayectoria buscada es (v, v 0 , Tv , z, Tu , w, w0 , Su , u).
9
(e) ⇒ (f) Sea v 0 adyacente a v y tomemos uw-trayectoria que pase por vv 0 .
(f) ⇒ (g) Tomemos uv-trayectoria T que pase por w. Entonces la porción de esta trayectoria de u a w, (u, T, w), es uw-trayectoria que no pasa por v.
(g) ⇒ (a) Sea v ∈ V. Veamos que G − v es conexa. Sean u, w ∈ V \ {v}. Por hipótesis,
hay uw-trayectoria que no pasa por v, ası́ que esa trayectoria está en G − v. ♦
2.6 Observación. Sea G un bloque. Dados u, v y a no necesariamente existe ciclo que
pasa por a y contiene a u y a v.
u•...........................................•.....
...
..
..
..
...
...
...
...
...
...
...
...
...
.
...
..
.
...
.
.
.
.
............................................................................................
...
..
...
..
.
.
...
...
...
.
...
...
...
...
...
..
...
..
.
.
...
................................................
a
•
•
•
•v
2.7 Corolario. Si G es gráfica con al menos tres vértices, entonces G es bloque si, y sólo
si, dados u, v existen uv-trayectorias T1 y T2 que sólo tienen en común a u y a v. ♦
2.8 Ejercicio. ¿Es cierto que si G es bloque y T1 es una uv-trayectoria entonces existe
T2 uv-trayectoria tal que V(T1 ) ∩ V(T2 ) = {u, v}?
2.9 Proposición. Sea G gráfica con al menos tres vértices. Si cualesquiera dos vértices
u 6= v son tales que δ(u) + δ(v) ≥ |V| entonces G es bloque.
Demostración. Sean u, v ∈ V distintos. Por (b) de 2.5, basta probar que existe un ciclo
que contiene a u y a v.
Caso (1). u y v no adyacentes, Entonces N (u) y N (v) están contenidos en V \ {u, v} y
|N (u)| + |N (v)| = δ(u) + δ(v) ≥ |V|,
10
ası́ que N (u) y N (v) tienen al menos dos elementos w1 , w2 en común, de donde (u, w1 , v, w2 , u)
es un ciclo que contiene a u y a v.
Caso (2). u y v adyacentes. Sea w ∈ V \ {u, v}.
Caso (2a). Si w es adyacente a ambos, entonces los tres forman un triángulo.
Caso (2b). w es sólo adyacente a uno de ellos, digamos, a v. Por el caso (1), tomemos cuadrado (ciclo de longitud 4) (u, w1 , w, w2 , u); sin pérdida de generalidad, w1 6= v y entonces
el ciclo buscado es (u, w1 , w, v, u).
Caso (2c). w no es adyacente ni a u ni a v. Sin pérdida de generalidad podemos suponer
que no existe ningún vértice adyacente a ambos (pues estarı́amos en el caso (2a)). Por
el caso (1) y nuestra suposición podemos tomar vértices distintos w1 , w2 , w3 , w4 tales que
(u, w1 , w, w2 , u) y (v, w3 , w, w4 , v) sean cuadrados. Sin pérdida de generalidad w1 6= w4 . El
ciclo buscado es (u, w1 , w, w4 , v, u). ♦
u
•
u
•
v
•
v
•
..............................................................................................
. .
... ........
.. ...
... ........
... .....
.....
..
.
...
...
.....
.
..
...
.
.
.
.....
...
..
.....
...
...
..
.....
..
.
...
.
.
.....
.
..
.
...
.
.
.
.
.....
.
...
.
..
.
.
.
.
...
...
..
..
.
.
...
.
..
..
...
..
.
.
.
...
..
..
..
.
.
.
...
.
.
.
.
.
.
.
.
.
.
.
.
.......
.
.
.....
.
.
......
.......
.
.
.. ...
.
.
......
.
.
.
. ...
.....
......
.
.
.
.
.
.
.
.
......
...
......
.......
.... ....
.......
......
... ...
.......
......
.......
......
... ...
.......
.
......
.
.
.
.
.
.
.
.
.
...... .... .........
...... .... .......
.............
..........................................................................................
... ........
..
... ........
...
.....
..
..
.
.....
..
.
..
.
.
.....
.....
...
...
.....
...
...
.....
..
.....
...
..
.....
.
..
.
.
..
...
...
..
...
...
...
..
..
...
..
..
.
.
.
.
.
.
.......
...
....
......
......
...
...
......
... ....
......
. ..
......
.
......
.... ....
......
......
... ...
......
...... .... ....
...... ....
.......
w2•
w1•
w1•
•
w
caso (2b)
w2• •w3
•
w4
•
w
(2c)
2.10 Ejercicio. Probar que si todos los vértices tienen grado par, entonces G no tiene
puentes.
2.11 Ejercicio. Probar que toda gráfica no trivial tiene, al menos, dos vértices que no
son de corte.
2.12 Ejercicio. El cuello de una gráfica es la mı́nima longitud de sus ciclos. Probar que
si G tiene diámetro 2 y cuello 5, entonces es regular. Probar que si G es r-regular, entonces
el orden de G es r2 + 1 y dar ejemplo para r = 2 y r = 3.
2.13 Ejercicio. Un conjunto de 1990 personas se divide en subconjuntos ajenos entre
sı́ de tal manera que:
(a) Ninguna persona conoce a todas las demás del conjunto en el que ella está.
(b) Entre cualesquiera tres personas de un conjunto existen siempre al menos dos que no
se conocen entre sı́.
(c) Para cualesquiera dos personas en un subconjunto que no se conozcan entre sı́ existe
exactamente una persona en el mismo subconjunto que las conoce a ambas.
11
Probar que dentro de cada subconjunto cada persona tiene el mismo número de conocidos
y determinar el máximo número de subconjuntos posible. (Se entiende que si A conoce a B
entonces B conoce a A y que cada persona se conoce a sı́ misma.)
2.14 Ejercicio. Un conjunto de personas es tal que cada uno tiene al menos un amigo
dentro del conjunto y si dos personas del conjunto tienen el mismo número de amigos (dentro
del conjunto), entonces esas dos personas no tienen amigos en común (dentro del conjunto).
Probar que alguna persona tiene exactamente un amigo dentro del conjunto.
2.15 Ejercicio. En una sesión de entrenamiento de ajedrez cada participante ganó a lo
más k puntos repartidos de la siguiente manera: En cada juego el ganador obtuvo un punto,
el perdedor 0 y, en caso de empate, cada jugador obtuvo 12 punto. Probar que
(a) Hubo un participante que jugó a lo más 2k juegos.
(b) Los jugadores pueden acomodarse en 2k + 1 cuartos (o menos) de manera que ningún
par de jugadores de un mismo cuarto hayan jugado entre sı́.
12
3.
Operaciones en gráficas
Sean G y H gráficas. A partir de ellas construimos las siguientes gráficas:
La unión, G ∪ H, con vértices V(G) ] V(H) y aristas A(G) ∪ A(H). (Aquı́ el sı́mbolo ]
significa unión ajena.)
La suma, G + H, con vértices V(G) ] V(H) y aristas
A(G) ∪ A(H) ∪ {gh : g ∈ V(G), h ∈ V(H)}.
El producto cuadro, G H, con vértices V(G) × V(H) y aristas
{(g, h)(g 0 , h0 ) : (g = g 0 y hh0 ∈ A(H)) o (h = h0 y gg 0 ∈ A(G)}.
Se puede pensar que en cada nivel (vértice en G) hay una copia de H y, recı́procamente, en
cada vértice de H hay una copia de G.
El producto tache, G × H, con vértices V(G) × V(H) y aristas
{(g, h)(g 0 , h0 ) : gg 0 ∈ A(G)) y hh0 ∈ A(H)}.
La composición o producto lexicográfico, G[H], con vértices V(G) × V(H) y aristas
{(g, h)(g 0 , h0 ) : (g = g 0 y hh0 ∈ A(H)) o gg 0 ∈ A(G)}.
3.1 Ejemplo. Dibujemos las gráficas recién definidas cuando G = T1 y H = K3 :
•.......
•......
...
...
..
...
...
...
..
...
..
...
...
.
....
....
...
...
...
...
...
...
•
•
•
T1 ∪ T2
•
.......
..........
....... ..
..... .... ....
.
.
.
.
.
..... .. ..
..... .. ...
.
..... ....
.
.....
.....
..
.....
.
.
.
.
.
.......................................................
..
... ....
.
.
.
.... ........ ....
.
..
... ........... ......... .....
...
... .... ............
..
... ... ....... .......
..... ....
... ..........
..... ..
.............
.. .
......................................................
•
•
•
•
T1 + T2
•...........................................•.........
•...............
•
•
•
•
...
..
...
...
...
..
...
...
...
...
..............................................
...
...
...
...
...
...
...
...
...
...
...
...
....
...
............................................
•
•
•
T1 T2
.
.....
.....
.....
.....
..... ........
........
..... .....
..... .........
.....
.....
.....
.....
.
.
.
.
.......
.....
.....
.....
.....
.....
.
.....
.
.
.
..... ......
........
..... .....
..... .........
.....
.....
.....
.....
.
.
.
.
..
..
•
•
T1 × T2
•..............................................................................•............
... ... .....
.. . .
... ... ...... ......... ... ...
... ... ........... ... ...
... ........ ........
..
... ........... .......... ....
.. ...... ... ... ...... ..
.................................................................
..
.
..
..... ........ .... ..... ........ ....
... ........... .......... ...
... .... ............ .... ...
... ... ....... ....... .... ...
..... ... ..
... ..........
....... ...
.............
...
.........................................................
•
•
•
•
T1 [T2 ]
•....................................................................•.......................................................................•..........
... .....
. .
. . .
..... ......... ... ......... ......... ...
...
..
..
........
..
...
.
.
..
........
...
..... ......... .... ......... ......... ....
.
.
.
.
..... ..
..... .. .....
... .....
.
.
.
.
.
.
.
.
.
... ....
.. .
.. ..
..........................................................................................................
•
•
T2 [T1 ]
•
3.2 Proposición. G H es conexa si, y sólo si, G y H lo son.
Demostración. (⇐) Sean (g, h), (g 0 , h0 ) vértices en G H. Sean T = (g = g0 , g1 , . . . , gk =
g 0 ) y S = (h = h0 , h1 , . . . , hl = h0 ) trayectorias en G y en H, respectivamente. Entonces una
(g, h)(g 0 , h0 )-trayectoria es
((g, h) = (g0 , h), (g1 , h), . . . , (gk , h) = (g 0 , h) = (g 0 , h0 ), (g 0 , h1 ), . . . , (g 0 , hl ) = (g 0 , h0 )).
13
(⇒) Probemos que G es conexa. Sean g, g 0 vértices en G y sea h ∈ V(H). Tomemos una
trayectoria T de (g, h) a (g 0 , h). Tomando la primera coordenada de T obtenemos un camino
(no necesariamente trayectoria) de g a g 0 en G. ♦
El cubo de dimensión n, Qn , está definido recursivamente por Q1 = K2 y, para n ≥ 2,
Qn = Qn−1 K2 .
•
•......
....
...
..
...
...
...
...
..
•
Q1
•......................................................•.......
•
...
....
...
...
...
...
...
...
...
...
...
...
...
...
.
.......................................................
•
•
.............................................................
......
.... ..
..... ..
..... ...
..... ...
..... ....
.....
.
.
.....
.
...
....
.
.....
....
.
.
.
.
.
...
.
.
.
.....................................................
...
..
...
..
...
...
...
...
...
...
...
...
..
...
...
...
.......................................................
..
.
.
..
.
.
.
...
.
.
.
.
.
.
.
.
.
...
...
.
.
...
.
.
.
.
.
.
.
.
..
..
.... .........
.... .........
... .......
.. .....
............................................................
•
•
•
•
Q2
•
•
Q3
3.3 Observación. Qn es (isomorfo a) la gráfica que tiene por vértices a {(x1 , x2 , . . . , xn ) :
xi ∈ {0, 1}} y por aristas a las parejas de vértices que difieren exactamente en una coordenada.
3.4 Ejercicio. Probar que si G y H tienen al menos dos vértices cada una entonces
G H es bipartita si, y sólo si, G y H lo son.
3.5 Ejercicio. Probar que si G y H tienen al menos dos vértices cada una entonces
G × H es bipartita si, y sólo si, G o H lo son.
3.6 Corolario. Para toda n, Qn es bipartita. ♦
14
4.
Grupo de automorfismos
Sean G y H gráficas. Un homomorfismo de G en H es una función λ : V(G) → V(H)
tal que si uv ∈ A(G) entonces λ(u)λ(v) ∈ A(H).
4.1 Ejemplo. (a) Sean C6 = (v1 , v2 , v3 , v4 , v5 , v6 , v1 ) y C3 = (w1 , w2 , w3 , w1 ). Para cada
i ∈ [6] sea r(i) el residuo de i módulo 3. Entonces la función λ : V(C6 ) → V(C3 ) dada por
λ(vi ) = wr(i) es homomorfismo.
(b) Sea ho ∈ V(H). La inclusión de G en G H dada por v 7→ (v, h0 ) es homomorfismo.
(c) La proyección de G H en G no es homomorfismo (pues un vértice no es adyacente
a sı́ mismo).
(d) La proyección de G × H en G es homomorfismo.
4.2 Nota. Algunos autores consideran como homomorfismo a una función λ : V(G) →
V(H) tal que si uv ∈ A(G) entonces λ(u)λ(v) ∈ A(H) o λ(u) = λ(v) (por ejemplo, la
proyección de G H en G). Para nosotros, una función de este tipo es homomorfismo que
pega.
4.3 Observación. Un isomorfismo es un homomorfismo biyectivo tal que la función
inversa también es homomorfismo.
Una inmersión o encaje de una gráfica H en una gráfica G es un homomorfismo inyectivo
de H en G. Un automorfismo es un isomorfismo de una gráfica en sı́ misma. El conjunto
de automorfismos de G en G se denota por Aut(G).
4.4 Observación. Aut(G) con la composición de funciones es grupo.
4.5 Ejemplo. (a) Aut(Tn ) = Z2 .
(b) Aut(Kn ) = Sn , el grupo de permutaciones de [n].
(c) Aut(Cn ) = Dn , el grupo diédrico de orden 2n.
4.6 Nota. Es posible probar que todo grupo es grupo de automorfismos de una gráfica.
A continuación veremos la idea de la construcción.
4.7 Ejemplo. La siguiente gráfica tiene grupo de automorfismos Z3 .
15
•
.....
..
.......
......
.....
.......
.. .....
.
.
.
.
.
.
.
.......
.
...
..
...
.......
...
.......
.......
...
... ............
.......
....... ....
..........
.......
......
....
.......
.
.
.
...
.
.......
...
...
.......
..
.......
...
......
.......
...
...
.......
....... .....
... ............
........
.......
.
.
.
...
..
...
...
...
...
...
..
...
...
.
.
.
.........................................................................................................
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
.
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
Recordemos que una acción (por la izquierda) de un grupo Λ en un conjunto X es una
función Λ × X → X, (λ, x) 7→ λ · x, que satisface que para x ∈ X, λ, µ ∈ Λ, 1λ · x = x y
(λµ) · x = λ · (µ · x). En general se omite el sı́mbolo · y el paréntesis pues, debido a la última
propiedad, no hay confusión.
De manera natural se tiene una acción de Aut(G) (o de cualquier subgrupo de Aut(G))
en V y en A.
Decimos que la acción de un subgrupo Λ de Aut(G) en G es transitiva en vértices
si para todo par de vértices (u, v) existe λ ∈ Λ tal que λ(u) = v. Análogamente definimos
acción transitiva en aristas. La acción es libre en vértices si el único automorfismo que
fija todos los vértices es la identidad.
4.8 Ejemplo. La gráfica de Petersen, P, consta de 10 vértices, y cada vértice tiene
grado 3. La dibujamos aquı́ abajo. Veremos que en esta gráfica la acción del grupo de
automorfismos es transitiva en vértices y en aristas.
1....
.......
...•
...... .. .....
..... .. ......
......
..
...
......
.....
...
......
......
......
......
...
......
.....
.
.
.
.
.
.
......
.
....
.
.
.
.
......
.
.
..
....
......
.
.
.
.
.
.
......
....
....
.
.
.
.
.
.
......
. ....
....
.
......
.
.
.
.
.
. ...
......
...
.
.
.
.
.
.
.
.
..........
...
..
..........
... ............
.
.
...
.
......... ....
.
.
.........
.
.
.
.
...
.
.
.
.
..............................................................................................
..
...
.
.
.
.
.
......
...
..
...
.
...
..
.
.
.
......
.
.
.
.
... ......
...
...... ...
... .......
...
........
...
....
...
...
.......
... .......
...... ...
...
...
..
.. .................. ....
...
.
.
.
.....
...
...
...
..... ........... ....
...
...
...... ...
... ......
...
..
.. ......
...... ..
...
........
..
...........
.
.
.
.
...
...
...
...
...
...
...
...
..
...
...
...
..
...
...
... ....
... .....
... ..
... ...
. .
.......................................................................................................
•6
5•
10
•
9•
•
7
•2
8•
•
4
•
3
La acción en vértices es clara pues las potencias de la rotación ρ = (1 2 3 4 5)(6 7 8 9 10)
mandan a 1 en cualquiera de 2, 3, 4 o 5 y a 6 en cualquiera de 7, 8, 9 o 10, y la permutación
siguiente σ intercambia 1 y 6:
16
6
•
..........
..... .. .....
..... .... ...........
......
......
..
.....
......
.
.
.
...
.
......
......
...
......
.....
.
.
.
......
.
.
.
.
.
......
....
.
.
.
.
.
.
......
..
....
.
.
.
.
......
.
.
.....
....
......
.
.
.
.
.
.
......
. ...
....
.
.
.
.
.
.
......
..
.. .....
...............
.
.....
...
..
...........
... ............
.
.
...
......... ....
.........
.
.
.
...
.
.
.
.
.
.
.
...........................................................................................
.
...
.
.
.
.
.
.
.
.
.
......
...
..
...
..
......
... ..........
...
...
...... ....
... .......
...
...
.........
....
..
...
.
..
.........
.
.............
.
.
.
...
.
.
.
...... ....... ...
...
...
..
...
....
...
...
...... ........... ....
...
...
..
...... ...
.. .....
...
.. ..........
...... ..
..
.
.
.
.
.
........
...
......
...
...
...
....
...
...
...
...
...
...
...
...
...
...
...
...
..
.
.
.
... ..
... ....
... ..
... ....
.......................................................................................................
•1
9•
4
•
2•
•
3
•8
5•
•
7
•
10
Para ver que la acción es transitiva en aristas observamos que la arista a con extremos 1 y
2 puede ir en cualquier arista del pentágono exterior aplicando ρ (y análogamente cualquier
arista del pentágono interior va en otra del pentágono interior); para mandar a en una arista
del pentágono interior basta aplicar σ; finalmente, la permutación τ siguiente manda a en
una arista que une el pentágono exterior con el interior.
1.....
......
...•
...... .. ......
...... .. .....
......
..
....
......
...
......
......
......
...
......
.....
.
.
.
......
.
.
.
.
.
......
....
.
.
.
.
.
.
......
.
....
.
.
.
.
......
.
.
....
....
......
.
.
.
.
.
.
......
. ....
....
.
.
.
.
......
.
.
. ...
....
.
.
.....
.
.
.
.
...
............
.
.
......
.
.
... ............
...
......... ....
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.........
...
....................................................................................................
..
...
......
.
..
..
.
.
.
.
.
.
.
...
.
.
.
.
......
...
..
..
...
...... ....
... ..........
..
........
...
.
.
.
.
.
.
.
..
...
........
...........
...
...
..... ..
...
... ................... ....
...
..
...
...
.......
...
..
.. .......... .......... ....
...
.
.
...... ...
...
...
... ........
........
...
......
...
.........
...
...
..
...
...
...
..
...
.
.
.
.
.
...
...
..
...
...
...
...
... ...
... .....
... ..
... ...
.
......................................................................................................
•2
6•
8
•
7•
•
10
•5
3•
•
4
•
9
4.9 Ejercicio. Probar que el grupo de automorfismos de la gráfica de Petersen es S5 .
(Sugerencia: Considerar la gráfica de Petersen que tiene por conjunto de vértices a los biciclos
de S5 en el que (a b)(c d) es arista si, y sólo si, {a, b} ∩ {c, d} = ∅.)
4.10 Ejercicio. Encontrar una gráfica G tal que la acción de Aut(G) sea
(a) transitiva en vértices pero no en aristas.
(b) transitiva en aristas pero no en vértices.
Sea Λ un grupo (finito) y sea L un conjunto de generadores de Λ cerrado bajo inversos.
La gráfica de Cayley de Λ con respecto a L, Cay(ΛL ), tiene por vértices a los elementos
de Λ, y una arista de u a v si, y sólo si, existe λ ∈ L tal que v = uλ. Observemos que, por
pedir que L sea cerrado bajo inversos, esta definición es correcta.
4.11 Ejemplo. Sea Λ = D3 = {1, r, r2 , s, rs, r2 s}, donde r = (1 2 3) (rotación) y
s = (1 2), cuyo orden es 2. Sea L = {r, r2 , s}. Entonces Cay(ΛL )) es:
17
r
•
........
..... .. .....
..... ... ......
..... .... .........
.
.
.
.
.....
..
.....
.....
.....
.....
.....
...
.....
.....
.....
...
.....
.....
.....
.
.
.
.
.
..
.
.
............................................................................................................
...
...
...
....
....
...
...
...
...
...
...
...
....
....
...
...
..
...
......................................................................................................
.
.....
.
.
.
.....
....
.
....
.
.
.
.....
....
.....
....
.....
.....
.....
.....
...
.....
.....
.
.....
.....
..... .... .........
..... .. .....
..... .. .....
..........
1•
• r2
s•
•r 2 s
•
rs
4.12 Observación. Cay(ΛL ) es conexa y, si L tiene k elementos, Cay(ΛL ) es k-regular.
4.13 Proposición. Dado un grupo Λ y un conjunto de generadores L de Λ cerrado bajo
inversos, Λ es subgrupo del grupo de automorfismos de G := Cay(ΛL ).
Demostración. Sea λ ∈ Λ. Definimos fλ : V(G) → V(G) por fλ (v) = λv. Es claro que fλ
es una función biyectiva. Veamos que define un homomorfismo de gráficas:
v1 v2 ∈ A ⇔ ∃ µ ∈ L tal que v2 = v1 µ ⇔ ∃ µ ∈ L tal que λv2 = λv1 µ ⇔ (λv1 )(λv2 ) ∈ A.
Es claro que la asignación f : λ 7→ fλ es una función inyectiva de Λ en Aut(G), ası́ que
sólo falta ver que fλ es homomorfismo de grupos, pero esto también es claro pues para toda
λ ∈ Λ, fλ1 λ2 (v) = λ1 λ2 v = fλ1 ◦ fλ2 (v). ♦
4.14 Ejemplo. Supongamos que queremos encontrar una gráfica cuyo conjunto de automorfismos sea Q4 = {±1, ±i, ±j, ±k}, el grupo de los cuaternios. Tomemos L = {±i, ±j}.
La gráfica de Cayley es:
1
.........
.•
......................
.
.
.
.. . . .
... .. .. ...
..... .. .. .....
..... .. ..... .........
.....
..... ....
...
.....
.....
.
...
.
.
..
.....
...
..
.....
.....
..
.....
...
.
.....
.
.
.
.
.
.....
...
.
...
.
.
.
.
.
.
.....
...
...
.
.
.
.
.....
.
.
.
. ............................ ....
.....
....
.
.
.
.
.
.
.
.
.
.....
....... ...... ...... ................
...
.
.
.
.
.
.
.
.
.
....
.
.
.
.
.
.
.
.
..... ... ............
...
....... ... .......
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.......... .........
..... ..
. .......
... ...............
.
.......... .....
.
.
.
.
.
.
.
.
........
..............
.......
...................
.
.
.
.
.
.
.
.
.
.
.
.............
.......
..
.........
..... ...........
.......
.........
..............
..... ...........
..... ..
.......... .........
. ...
..........
.....
..... .... ...................
.
.
.
.
.
.......... ..... .........
.
.
.....
.......... .... ....... ..................
....
.....
..................... ....................
.....
.....
.
.....
... .......
.....
..
.....
.....
...
.....
..
.
.....
.
.
.
.
.
.
...
..
.....
.....
.....
...
...
....
.....
...
...
.....
.....
..
...
.....
.....
.. .........
..... .....
.
..... .. ... .....
..... ... .. .....
..... .. .. .....
....... .......
...............
.
−1
•
i •
−i •
•−j
•j
•
k
•
−k
En esta gráfica, reflejar con respecto al eje que pasa por 1 y k, y rotar son automorfismos,
ası́ que D4 está contenido en el grupo de automorfismos; también es automorfismo la función
que manda x en −x, lo cual nos produce, combinando con D4 , otros 8 automorfismos. Para
obtener Q4 se deberı́an romper algunos automorfismos como se hizo al construir la gráfica
que tenı́a por grupo de automorfismos Z3 .
18
4.15 Ejercicio. Determinar Aut(Km,n ) para m 6= n. ¿Qué pasa si m = n?
4.16 Ejercicio. Encontrar una gráfica cuyo grupo de automorfismos sea Z3 × Z3
4.17 Ejercicio. (∗) Encontrar un grupo Λ y un conjunto de generadores L de Λ tal que
que Cay(ΛL ) = Kn .
4.18 Ejercicio. Encontrar un grupo Λ (y un conjunto de generadores L de Λ) tal que
que Cay(ΛL ) = Cn .
4.19 Proposición. Sea G una gráfica conexa. Existe un subgrupo Λ de Aut(G) que
actúa libre y transitivamente en los vértices de G si, y sólo si, G es gráfica de Cayley de Λ.
Demostración. (⇒) Como Λ actúa transitivamente en vértices, tenemos que G es regular,
digamos de grado k. Tenemos que encontrar el conjunto L de k generadores de Λ que nos determinan la gráfica. Escojamos un vértice u para corresponder al neutro de Λ, y supongamos
que N (u) = {v1 , . . . , vk }. Para cada i ∈ [k] sea gi el único elemento de Λ tal que gi (u) = vi .
Entonces L = {g1 , . . . , gk } y cada vértice vi corresponde al elemento del grupo gi . Ahora, sea
w un vértice de G y sea λ ∈ Λ tal que λ(u) = w; entonces w representa al elemento λ del
grupo. Como λ es un automorfismo de G, manda a los vecinos de u en los vecinos de w, es
decir, N (w) = {λ(v1 ), . . . , λ(vk )} = {λg1 , . . . , λgk } = {wg1 , . . . , wgk }.
(⇐) Es claro que Λ actúa libre y transitivamente en Cay(ΛL ). ♦
4.20 Ejemplo. En la siguiente gráfica, el grupo de automorfismos D6 actúa transitivamente en vértices pero la acción no es libre; sin embargo, Z6 ≤ D6 sı́ actúa libre y
transitivamente en los vértices, ası́ que la gráfica es de Cayley (el conjunto de generadores
que la define es L = {g, g 3 , g 5 } donde g es la rotación (1 2 3 4 5 6)).
•
........
...... .. ......
...... .... ...........
......
......
...
......
......
.
.
...
.
.
.
......
...
......
......
......
......
.
.
.
.
.
.
.
..
.
...........
.
.
........
...
....... ....
.
.....
.
.
.... .............
.
...
.....
.
.......
.
.
.
.
.
...
.
.
.......
..
....
....... .... .............
...
.............
...
...
...
................
.
.
.
.
.
...
.
...
..... ... ...........
.
.
.
.
.
...
.
.......
..
..
.......
....
... ..............
....... ....
...
.............
.........
...
......
.
.
.
......
....
.
.
.
....
.
.
......
......
......
...
......
......
.
......
......
...... .... ...........
...... .. ......
............
•
•
•
•
•
19
5.
Otras construcciones
La k-ésima potencia de G es la gráfica G k que tiene el mismo conjunto de vértices de
G y tal que uv ∈ A(G k ) si, y sólo si, 0 < d(u, v) ≤ k.
5.1 Ejemplo. Si G = T4 , entonces G 2 es:
•.........................................•..........................................•..............................................•.............................................•..........................................•........
...
...
... ....
... ....
...
...
...
...
... .....
... .....
...
...
...
...
...
...
...
...
.....
.....
.....
.....
....
......
...... .........
...... .........
...... .........
.
.
.
.
.
.
.......
..
..
..
.......................................................................................................................................................
5.2 Ejercicio. Hay 2n + 1 perros. Al principio cada perro tiene exactamente n amigos
entre los demás perros. Cada dı́a cada perro se convierte en amigo de los amigos de sus
amigos. Probar que debe llegar un dı́a en el que todos sean amigos entre sı́.
5.3 Ejercicio. (∗) Probar que si G tiene al menos tres vértices y es conexa, entonces G 2
es bloque.
La gráfica de lı́neas L(G) de G tiene por conjunto de vértices a A(G) y
ab ∈ A(L(G)) ⇔ |a ∩ b| = 1.
5.4 Ejemplo. (a) L(Tn ) = Tn−1 .
(b) L(Cn ) = Cn .
(c) L(K4 ) = K6 − (las tres diagonales).
(d) L(K1,3 ) = C3 .
(e)
2
•
1
•
4
1 ........................................................................ 2
...
•......
..•
..... ...
.... ..
•
.
.......
..... ...
..... ..
..... ...
.
.
.
.
.
..
.....
.....
....
...
.....
...
.....
.............................................................
...
.....
...
.....
...
.....
.....
....
.....
..... ....
..... ..
..... ...
......
.
...
. .
.... ...
...
..
.....
...
.....
...
...
.....
.
.
.
...
.
...
...
.
.
.
...
.
...
...
.
.
.
...
.
...
...
.
.
.
...
...
.
...
.
.
...
.
...
.
...
.
.
...
.
...
.
...
.
...
.
.
...
.
... ........
...
.. ......
..
..............................................................................
3
•
•
4
G
L(G)
•
3
5.5 Observación. Cada vértice v de G induce en L(G) la gráfica completa entre las
aristas incidentes a v.
20
5.6 Proposición.
|A(L(G))| =
1 X 2
δ (v) − |A(G)|.
2
v∈V(G)
Demostración. Por 5.5,
X δ(v)
X δ(v)(δ(v) − 1)
1 X 2
1 X
|A(L(G))| =
=
=
δ (v) −
δ(v). ♦
2
2
2
2
v∈V(G)
v∈V(G)
v∈V(G)
v∈V(G)
5.7 Proposición. Si a1 , a2 , . . . , ar ∈ V(L(G)) forman gráfica completa Kr con r ≥ 4,
entonces existe v ∈ V(G) tal que v ∈ ai para toda i.
Demostración. Si dos aristas de G son vértices adyacentes en L(G) entonces tienen vértice
común de G. Entonces tres aristas adyacentes podrı́an tener la forma uv, vw y wv con u, v, w
distintos pero entonces una cuarta arista no podrı́a ser adyacente a estas tres. ♦
5.8 Ejercicio. (∗) Probar que si G es conexa y L(G) ≈ G entonces G es ciclo.
5.9 Ejercicio. Probar que si L(G) es r-regular con r ≥ 3 impar, entonces G es bipartita.
Para cada r par, dar un ejemplo que pruebe que el resultado es falso.
Probaremos que las gráficas de lı́neas determinan a las gráficas salvo en el caso de K1,3 y
C3 (que tienen por gráfica de lı́neas a C3 ). Necesitamos verios lemas.
5.10 Lema. Supongamos que G es conexa, que tiene al menos 5 vértices y que L =
L(G) ≈ L(H) con isomorfismo λ. Si un triángulo T de L proviene de un K1,3 de G, entonces
la imagen de λ del triángulo proviene de un K1,3 de H.
Demostración. Supongamos que T está producido por u ∈ V(G) y tres vecinos v1 , v2 y v3
(o sea, T = (uv1 , uv2 , uv3 , uv1 )).
Caso (1). Si δ(u) = 3, por ser G conexa y con al menos 5 vértices, tomemos w 6= u tal
que w sea vecino de algún vi . Entonces en L, el vértice vi w es adyacente a exactamente uno
de T .
Caso (2). Si δ(u) > 3 y w es otro vecino de u distinto de los vi , entonces el vértice uw es
adyacente a los tres de T .
v1
v1
w
•.......................................•..
•......
uv
v
w
uv1
uw
1
1
w
....
....
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
.
.
...
...
......
. ...
.................................................................•
•
......•
.•
.
.
.
.
.
.
..•
.
.
.
.
...
.
.
..... ...
.
.. ....
... .....
.
.....
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
.
.
.
...
...
. ..........
..
..
..
........
........
.....
.
.
.
.
.
.
u....•.............
u
.
.
.
.
.
.
.
.
.
.
.
.
...
... .......
..........................................
..........................................
........
.
.
.
.
.
.
.
.
.
•
.
.
.
.
.
.
.
.
.
.
.
.
...
..
..
.......
..
..... .........
... .......
..
...
...
....... ...
....
....
..
...
.....
.....
.....
....
.
.
.
.
.....
....
•
v2
.....
.....
.....
.....
.....
.....
.....
.
•
v3
...
.
...
...
...
...
...
...
...
...
.
.
...
...
.
..........................................................................
•
uv2
...
.....
.....
.....
....
.
.
.
.
.....
....
•
uv3
•
v2
Caso (1)
.....
.....
.....
.....
.....
.....
.....
.
•
v3
...
.
....
...
...
...
......
...
...
...
.......
... ...
... .......
... ...
... ...........
.
.
... ..
..........
................................................................................
•
uv2
Caso (2)
21
•
uv3
En cualquier caso existen vértices en L adyacentes a un número impar de vértices de T .
Por otro lado, si T estuviera inducido por un triángulo de H, (r, s, t, r), un vecino x de
alguno a estos vértices, digamos a r, producirı́a un vértice rx en L adyacente a exactamente
dos de T . ♦
r
•
x
•
.........................................................
... ...
... .....
...
...
.
.
...
.
...
...
...
...
...
...
.
.
...
..
.
...
.
..
...
.
.
...
..
.
.
...
..
.
.
...........................................................................
•
s
rs
•
..
................................................
..
•
t
xr
•
...........................................................
.
... ...
... .....
...
...
...
..
.
.
...
..
..
.
.
.
.
.
...
..
...
...
...
...
...
...
...
..
...
...
..
...
.
.
.
.
.
... ..
.
... ..
...
..
...
.............................................................................
•
rt
•
st
5.11 Lema. Sean G y H conexas con al menos 5 vértices. Supongamos que L(G) ≈ L(H)
con isomorfismo λ. Dado u ∈ V(G) existe un único r ∈ V(H) tal que para toda a arista en
G incidente a u se tiene que λ(a) es incidente a r.
Demostración. Caso (1). δ(u) = d ≥ 4. Entonces u con sus aristas induce un Kd y
aplicamos 5.7.
Caso (2). δ(u) = 3. Aplicamos 5.10.
Caso (3). δ(u) = 2. Entonces en L(G) las dos aristas incidentes a u forman una arista la
cual debe venir de dos aristas adyacentes en H, y el vértice al cual son incidentes no puede
tener grado mayor, por lo anterior.
Caso (4). δ(u) = 1. sea rs la arista de H que induce a λ(a); queremos probar que alguno
de r o s tiene grado 1. Sea v el otro extremo de a.
Caso (4a). δ(v) = 1. Entonces L(G) consta de un solo punto y el resultado es claro.
Caso (4b). δ(v) = 2. Si w es el otro vértice adyacente a v entonces λ(a) intersecta a
exactamente una arista de L(G), por lo tanto uno de los extremos de la arista de H que
induce λ(a) tiene grado 1.
Caso (4c). δ(v) = 3. Aplicamos lema anterior.
Caso (4d). δ(v) ≥ 4. Sea N (v) = {u = w1 , w2 , . . . , wd }. Las aristas vwi inducen en L(G)
un Kn , uno de cuyos vértices es a. Por 5.7 existe un vértice de H que pertenece a todas las
aristas; ese vértice es s, digamos, y entonces el vértice r tal que rs = λ(a) tiene grado 1. ♦
5.12 Ejercicio. Probar que las gráficas conexas de orden a lo más 4, salvo K1,3 y C3 ,
inducen todas gráficas de lı́neas diferentes (y diferentes de C3 ).
5.13 Teorema. Sean G y H conexas distintas de K1,3 y de C3 . Entonces G ≈ H si, y sólo
si L(G) ≈ L(H).
22
Demostración. Sólo tenemos que probar la implicación (⇐). Por 5.12, basta considerar
gráficas con 5 o más vértices. Usamos 5.11 para definir V(G) → V(H). Es claro que esta
asignación es biyectiva y preserva adyacencias. ♦
Queremos ahora determinar las gráficas que son gráficas de lı́neas de otras. Recordemos
que cada subgráfica completa Kr en una gráfica de lı́neas proviene de un vértice de grado r
y viceversa. Analicemos el ejemplo siguiente.
5.14 Ejemplo. La siguiente gráfica L es gráfica de lı́neas de G.
7
...
•...... 7
...
...
...
...
...
7.....
...
...
.
.
.
.
...
.
.
.
•
.
... .... .......
.
.
.
.
...
.
.
.
.... ... ........
.
.
.
.
...
.
...
.....
.
...
.
.
.
16
589
.
.
...
.
.
6 ..................................................................................8.............................................. 9
6
8 ........
.
..
.
...................................................•
....................................................•
.................................................................................................................
.
•................. ..... ...........•. ............
•
•
.. .........
.
.
.
..
.
.....
.....
. ...........
.
... ...
.
.......
.
.
.
.
.
.
.
.
...
.
.
...
.
.......
.....
.....
.....9
.
.
... ...
.....
.
... ..... .. .....
.
.......
.
.
.
.
.
.
.
.
.
.
.
.
...
.
.
.
.
.......
.....
.....
..... ... ....
39
.....
.......
.
.
.
.4678
...
...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.......
.
...
.
.
.
.
.
.
.
.......
.....
.....
..... .. ....
..... .....
.
...
.
.
.
.......
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.....
.....
........
....
.......
...
.
.
.
.
.
....
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
•
.
.
.
.
.
.
.....•
.
.
.
.....
.....
...
1
5
....
.
.
.
... .......
... .......
. 4
.
.
.
.
.
.......
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.....
.....
.....
.....
.
.
.
....
....
.
.
...
.
.
.
.
.... ........
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..... ..
..... ..
.....
.
.
... 5 ....... ...
.....
.....
... ......
.
.
.
.
.
.
.
4
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
..... ..
..... ..
.. ..
..
..
...
....................................................................
•...................................................................•............................................................•........
•....................................................•............... 3
3
2
1
2
124
235
L
partición en completas
G
5.15 Teorema. Una gráfica conexa H es gráfica de lı́neas de otra gráfica si, y sólo si,
existen subgráficas completas H1 , . . . , Hk de H ajenas en aristas, cuya unión es H y tales
que cada vértice de H pertenece a exactamente dos Hi .
Demostración. (⇒) Sea L la gráfica de lı́neas de G. Todo vértice u de G induce una gráfica
completa Lu de L. Si a es una arista de L entonces existen u, w1 , w2 vértices en G tales que
a = {uw1 , uw2 } para ciertos w1 , w2 adyacentes a u en G. Esto nos dice que la unión de las
Lu es todo L y que si u 6= v, entonces A(Lu ) ∩ A(Lv ) = ∅; ası́ tenemos la partición de L en
aristas buscada.
(⇐) Dada la partición H1 , . . . , Hk de las aristas de H definamos G como sigue: Sus
vértices son los elementos de la partición y los vértices de las Hi que sólo pertenecen a un
elemento de la partición. Las aristas están formadas por las parejas (distintas) de éstos que
tienen exactamente un elemento en común. La conclusión es clara. ♦
23
6.
Bloques
Un bloque de una gráfica G es una subgráfica máxima con la propiedad de ser conexa
y no tener vértices de corte (aunque tenga 3 o menos vértices). La gráfica de bloques de
G, B(G), tiene por vértices a los bloques de G, y B1 B2 es arista si, y sólo si, B1 ∩ B2 6= ∅.
6.1 Ejemplo. (a) Si G es bloque (por ejemplo, si G es un ciclo), entonces B(G) es K1 .
(b) B(Tn ) = Tn−1 .
(c) B(K1,n ) = Kn .
(d) Si G es la gráfica del dibujo, entonces los bloques son: {1, 2, 3, 4, 5, 6, 7, 8, 9}, {7, 13},
{10, 12}, {11, 12} y {12, 13, 14}.
10
•
2
•
11
•
...
....
...
...
............
...
...
..... .. .....
..
..... ... .........
...
.
.....
.....
..
.
.
.
.
.
.
.
.
.
.
.....
...
....
.....
... .....
....
.....
.....
... ..
...
.....
.....
......
.
.....
...........
..........................................................................................................................................................................
... ...............
... ...
... .......
.
.
..
.
.
.... .........
.
.
..........
.
.
.
.....
...
... ...
...
.
.
..........
.
.
.
.
.
.... .........
....
.
.
.
...
.....
..........
.
...
...
.
.
.
.
.....
.
.
.
.
.
...
.
.
...
.
.
.
.....
.
.
.....
...
...
......
.
.
.
.
.
.
.
.
.
.
...
.
.
.
.
.
......
..... .. ....
.....
...
.
...
.
.
.
......
..... .. .....
.....
.
...
.
.
...
.
......
............
..... .......
.
.
.
.
.
...
.
.
.
.
.........
........
...
......
...
....
...
..... .....
..... .....
......
...
...
... ...........
..... ........
..... ........
.....
.....
.....
.....
...
...
... ........
.....
.....
.....
.....
.
.
.
.
.
.
.
.
.
...
.
.
.
.
.....
.
.
.....
....
.....
.....
..... ....
... .........
..........
.....
.....
..... ..
..........
... .......
..... .........
..... .. ....................
. ....
.
. .
.
.....................................................................................................................................................................
4
•
1•
•
3
9
•
•
5
•
6
•
8
•
7
•
12
•
14
•
13
10 12
11 12
•..............................................................•......
...
...
...
...
...
...
...
..
...
.
...
..
..
...
... .....
... ..
... ..
.
.................................................................................................................................................
•
123456789
7 13
•
•
12 13 14
B(G)
G
6.2 Observación. Toda arista de G pertenece exactamente a un bloque.
6.3 Lema. Si H es una subgráfica conexa de G sin vértices de corte, u, v ∈ V(H) y T es
una uv-trayectoria en G, entonces la subgráfica H ∪ T de G no tiene vértices de corte.
Demostración. Sea w ∈ H ∪ T . Analizando los distintos casos para w es fácil ver que no
es de corte. ♦
6.4 Proposición. Dos bloques de una gráfica G se intersectan en a lo más un vértice y
éste es de corte.
Demostración. Supongamos que u, v ∈ B1 ∩ B2 con u 6= v, y sea w ∈ B1 \ B2 . Como B1
es bloque, existe uv-trayectoria T en B1 que pasa por w; por 6.3, B2 ∪ T no tiene puntos
de corte, pero esto es una contradicción a la maximalidad de B2 . Ahora supongamos que
{w} = B1 ∩ B2 y veamos que w es de corte. Tomemos u ∈ B1 y v ∈ B2 . Si w no fuera
de corte entonces habrı́a uv-trayectoria T en G − w; tomemos una vw-trayectoria S en B2 ,
y del camino (T, S) extraigamos una trayectoria T 0 de u a w. Entonces B1 ∪ T 0 contiene
propiamente a B1 y, otra vez por 6.3, esto es una contradicción. ♦
24
6.5 Proposición. Una gráfica conexa H es una gráfica de bloques si, y sólo si, cada
bloque de H es gráfica completa.
Demostración. (⇒) Veamos que todo bloque de B(G) es gráfica completa. Probaremos
que los bloques de B(G) provienen de los bloques que se intersectan en un mismo punto. Sea
Λ un bloque de B(G). Sean B y C dos vértices distintos de Λ (es decir, B y C son bloques
de G). Queremos probar que BC es arista en Λ, es decir, que B ∩ C 6= ∅. Si B o C tiene
menos de 3 elementos, entonces es arista ası́ que el resultado es claro. Entonces supongamos
que B y C son bloques (como gráficas) y que no se intersectan. Como Λ es bloque, hay un
ciclo que contiene a B y a C, digamos (B = B1 , B2 , . . . , Br = C, Br+1 , . . . , Bs = B) y en
el cual B y C no están juntos. Para cada i sea vi el único vértice de G en la intersección
de Bi con Bi+1 y recordemos que vi es de corte. Observemos que es posible que algunos de
estos vi sean iguales (ver la ilustración abajo) y, como estamos suponiendo que B y C no se
intersectan, entonces no todos son iguales. Eliminemos algunos bloques (y los vi que definen)
de manera que no haya vi consecutivos que coincidan. En los bloques que hayan sobrado se
pueden construir trayectorias de un vértice de corte al siguiente (que no se intersectan con
las trayectorias dentro de otros bloques, salvo, tal vez, en los vértices de corte) y nótese que,
como dos bloques cualesquiera se intersectan en a lo más un punto, no es posible que sean
iguales dos vértices vi y vi+2 . Se tendrá entonces un camino cerrado en G, de longitud mayor
o igual a 3, en el que no hay aristas consecutivas en sentido inverso. Entonces es claro que
este camino contiene un ciclo, el cual induce una trayectoria que empieza y termina en un
mismo bloque, lo cual, por 6.3, es imposible.
(⇐) Ahora supongamos que en la gráfica H todo bloque es gráfica completa y veamos
cómo encontrar una gráfica G cuya gráfica de bloques sea H. Hacemos inducción sobre el
número de gráficas completas de H. Si sólo hay una, Kr , entonces H = B(Kr,1 ). Supongamos
que hay t ≥ 2 gráficas completas y sea U un vértice de corte tal que manera que al quitarlo
alguna de las componentes conexas conste de una sola gráfica completa (esto es posible tomando una trayectoria máximal entre vértices de corte y considerando uno de los extremos);
digamos entonces que la gráfica completa unida a U es isomorfa a Kr . Sea H0 la gráfica que
25
se obtiene de quitar esta gráfica completa (sin quitar U ) de H y, por hipótesis de inducción
tomemos G 0 tal que B(G 0 ) = H0 . Modifiquemos G 0 como sigue para obtener la gráfica buscada: En el bloque de G 0 que representa a U en H0 tomemos una arista vw y sustituyámosla
por dos aristas xv y xw con x un vértice nuevo (es decir, “partamos” la arista poniendo un
vértice x intermedio); luego agreguemos r − 2 vértices y pongamos una arista de cada uno
de éstos a x (por ser H conexa, r ≥ 2). La nueva gráfica G cumple que B(G) = H. ♦
La gráfica de bloques y cortes BC(G) de G tiene por vértices a los bloques de G y a
los vértices de corte de G. Las aristas son de la forma {u, B} donde u es vértice de corte de
G y B es bloque de G que contiene a u.
6.6 Ejemplo. En la siguiente ilustración vemos como BC(G) rompe los ciclos de B(G).
•.....................
E
•
•
..
...
...
... .....
.....
...
...
.....
...
...
.....
...
.....
...
.....
...
...
.....
...
...
.
.....
...
.
...
.
.....
...
.
..
.
.
.
....................................................................................................................................................................
. ...
.
...
.
.
.
.
.
...
. ...
.
.
...
.
.
.
.
...
....
...
...
....
.....
...
...
.....
...
...
..
.....
...
...
.....
...
.
...
.
.
.
.
.
...
...
.
...
.
.
.
.
...
.
.
.
... .......
.
...
.
..
.
...
.
.
.............
.
.....................................................
•
A
E
•
1
B
•
D
2
A
•
•
C
•
•
E
•.......
....
...........
..... .. ...
..... .... ....
.
.
.
.
...
.... ...
...
.....
...
.....
...
...
..
.....
...
..
.....
.
.
.
.
.
.
...
.
...
.
.
.
.
...
.
.
.
...
.
.
...
.
.
.
.
.
.
........................................................................................................................................
...
.
..
.
.
.
...
.
...
.
.
.
.
.
.
...
....
...
...
.....
...
.....
...
...
..
.....
...
..
.....
.
.
.
.
.
.
... .. .....
... .. .....
... .. ......
... .........
.......
•
B
•
....
...
..
...
..
.......................................................................................................
..
...
...
...
...
...
...
A
•
D
•
B
•
•
1
2
D
•
•
C
•
C
B(G)
G
•
BC(G)
6.7 Observación. De la demostración de 6.5 tenemos que no puede haber ciclos en
BC(G), ası́ que esta gráfica es un árbol.
6.8 Ejercicio. De las siguientes gráficas, determinar cuáles son gráficas de lı́neas y cuáles
son gráficas de bloques (y, en dado caso, encontrar una gráfica de la cual provengan).
.......
•.....................
•......
•...........................................................•........
....•
..... ..
. .
...
.
..... .....
... ........
....
... ....
•
•...........................................................................•...........
...
..............
.....
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
.
...
...
..... .....
.
.
..
...
...
... .... ........
.......
.....
...........................•
...........................•
.........................•
.........
...
..... ....
.
.
......
.
.
.
•
•
...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... .......
.
.
.....
... ..
... .....
.....
.....•
.
.
.
. ...
...
.
...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..... ...
.
.
.
.
... .......
.
..... .
.....
....
... .......
.
.
. ...
...
...
.
.
.
..... ...
.
.
.
.
.....
.
.
.
.
.
.
.
.
.
.
.
...
.
•
.....
..... .
.....
...
. ....
....
.
...
.
...
. ...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
.
.
.
.
.
.
...
.
...
......
..........
.
.
.
....
. ....................•
....
.....
...
...
....
... ..............................................
.........................•
...
•......................................•........................................•..................................•....
..•
....
...
... ....
... ......• ................. •
...
....
.....
.....
..
.. ..
.
.....
... .....
.....
...
.....
... .....
..
... ......
...
.
. ...
...................................................................
•
•
... ..
..
... ..
...
.....
...
....................................................
•
•
. ...
......
... ..... .........
....................
...........
.. ....
.. .....
.. .....
.......
•
•
..... ...
..... ..
..... ..
.....
•
...
.....
.....
.....
.
.
.
.
....
.....
.....
.....
.....
.
.
.
.
..
•
•
26
7.
Gráficas eulerianas
El problema de los puentes de Köninsberg describe 4 trozos de tierra A, B, C y D,
separados por un rı́o pero unidos por algunos puentes, como se muestra en el esquema. Se
pregunta si es posible pasar de pedazos de tierra a otros usando cada puente exactamente
una vez.
Un paseo euleriano en una multigráfica (sin lazos) es un paseo que pasa por todas las
aristas de G. Una multigráfica es euleriana si tiene paseo euleriano cerrado.
El problema de Köninsberg se traduce a buscar un paseo euleriano en la multigráfica
siguiente:
Sin embargo no es posible encontrar tal paseo por lo que veremos a continuación. De
hecho, el siguiente teorema nos da una respuesta completa sobre qué gráficas son eulerianas.
7.1 Teorema. Las siguientes son propiedades equivalentes para una multigráfica conexa
G.
(a) G es euleriana.
(b) Todo vértice de G tiene grado par.
(c) A(G) admite una partición en ciclos (posiblemente de longitud 2).
27
Demostración. (a) ⇒ (b) Es claro, porque cada vez que se pasa por un vértice se usan
dos aristas.
(b) ⇒ (c) Hacemos inducción sobre el tamaño |A| de G. Si |A| = 2, entonces se tiene
una arista doble uv, ası́ que el paseo es (u, v, u). Podemos construir un ciclo de la gráfica
empezando en un vértice y recorriendo aristas sin repetir hasta que se repita un vértice:
(v1 , v2 , . . . , vi , . . . , vj = vi ) (esto es posible porque cada vez que se entra a un vértice, se
puede salir ya que cada vértice tiene grado par); éste nos determina un ciclo (vi , . . . , vj = vi )
y, al retirar sus aristas de la gráfica se quitan dos aristas a cada vértice. Si G es ese ciclo, ya
terminamos, si no entonces queda una gráfica (posiblemente disconexa) con menos aristas,
en la que en cada componente cada vértice tiene grado par ası́ que aplicamos la hipótesis de
inducción.
(c) ⇒ (a) Ahora hacemos inducción sobre k, donde k es el número de ciclos en que se
parte G. Si k = 1, entonces es claro. Supongamos que k > 1 y sea C uno de los ciclos de
la partición. Sea C = (u0 = u1 , u2 , . . . , us = u0 ). Consideremos G 0 = G − A(C). La misma
partición de G nos da partición de cada componente de G 0 en menos de k ciclos, ası́ que
cada componente es euleriana. Para cada componente Gi (i = 1, 2, . . . , r) sea Pi un paseo
euleriano en Gi y sea ij el menor ı́ndice tal que Pj intersecta a C en uij . Sin pérdida de
generalidad supongamos que i1 ≤ i2 ≤ · · · ≤ ir . Construimos el paseo euleriano en G:
(u0 , . . . , ui1 , P1 , ui1 , . . . , ui2 , P2 , ui2 , . . . , Pr , uir , . . . , us = u0 ).
7.2 Corolario. Una multigráfica G tiene paseo euleriano abierto si, y sólo si, tiene exactamente dos vértices de grado impar.
Demostración. Agregamos arista entre esos vértices y, usando 7.1, construimos un paseo
empezando en una de esas aristas; después retiramos del paseo la arista agregada. ♦
7.3 Observación. De la demostración del teorema es claro que el paseo puede empezar
en cualquier arista si todos los vértices tienen grado par y en, el otro caso, en cualquier arista
de cualquier vértice de grado impar.
28
En el lema y la proposición siguientes se habla de gráficas, no de multigráficas.
7.4 Lema. Si G es una gráfica conexa que tiene exactamente dos vértices u y v de grado
impar, entonces entre u y v hay un número impar de paseos que no repiten a v.
Demostración. Hacemos inducción sobre el número de aristas. Si |A| = 2 entonces G = T2 ,
de donde sólo hay un paseo. Supongamos que |A| ≥ 3 y sea w un vértice adyacente a u.
Tenemos los siguientes casos:
Caso (1). δ(u) = 1. En este caso, si w = v entonces sólo hay un paseo, y si w 6= v entonces
aplicamos hipótesis de inducción a G − u (ahora es w el que tiene grado impar).
Caso (2). δ(u) ≥ 2. Para cada w ∈ N (u) \ {v} se tiene que en G − u los únicos vértices de
grado impar son v y w. Además G − u es conexa porque en G existe un uv-paseo euleriano
(que empieza con uw). Por hipótesis de inducción hay un número impar de wv-paseos. Los
paseos de u a v se obtienen todos empezando con cualquier arista de u a un vértice vecino,
ası́ que son una cantidad impar de impares lo cual da un total impar de uv-paseos. ♦
7.5 Proposición. Una gráfica conexa es euleriana si, y sólo si, cada arista pertenece a
un número impar de ciclos.
Demostración. (⇒) Sea a = uv. Por 7.4 hay un número impar de uv-paseos que no repiten
a v. Ahora veamos que hay un número par de estos paseos que no son trayectorias; para ello,
observemos que podemos aparearlos como sigue: en cada paseo que repite vértices tomemos
el primer vértice que repite e invirtamos el orden de todos los vértices intermedios (ver el
esquema).
(⇐) Veamos que todo vértice tiene grado par. Sea u ∈ V y sean a1 , a2 , . . . , ak sus aristas.
Sea mi el número (impar) de ciclosPque contienen a ai . Por otro lado sea m el número de
ciclos que contienen a u. Entonces i mi = 2m (pues cada ciclo usa dos de las aristas de u)
y esto sólo es posible si k es par. ♦
7.6 Nota. Una multigráfica dirigida y conexa es euleriana (es decir, hay paseo dirigido
que usa cada arista) si, y sólo si, en cada vértice el número de aristas que entran es el mismo
29
que el que salen. Esto es equivalente a que el conjunto de aristas admita una partición en
ciclos dirigidos. La misma demostración sirve.
7.7 Ejercicio. ¿Es cierto que si una multigráfica es euleriana entonces cada arista pertenece a un número impar de ciclos?
7.8 Ejercicio. Sea G conexa con n vértices de los cuales 2k tienen grado impar. Probar
que A(G) se puede partir en k paseos ajenos en aristas.
7.9 Ejercicio. Probar que si G es conexa de tamaño par y tiene exactamente 4 vértices
de grado impar, entonces A(G) se puede partir en dos paseos de longitud par.
7.10 Ejercicio. Probar que si G es conexa entonces es euleriana si, y sólo si, para todo
S ⊂ V(G) no vacı́o el número de aristas entre S y V(G) \ S es par.
7.11 Ejercicio. (a) Sea G una gráfica regular en la que los vértices tienen grado 4.
Probar que es posible colorear las aristas de G de manera que a cada vértice lleguen dos
aristas azules y dos rojas.
(b) Probar que si en G todos los vértices tienen grado 6, entonces no necesariamente es
cierto que se puedan pintar de manera que a cada vértice lleguen tres aristas azules y tres
rojas.
Un camino euleriano en una gráfica conexa es un camino cerrado de longitud mı́nima
que pasa por todas las aristas de la gráfica.
7.12 Proposición. Sea G una gráfica conexa con m aristas; sea C un camino euleriano
y sea l su longitud. Entonces
m ≤ l ≤ 2m.
Demostración. La primera desigualdad es por definición. Si en G convertimos cada arista
de G en dos aristas, entonces la multigráfica es euleriana y tiene 2m aristas, de donde es
claro que l ≤ 2m. ♦
7.13 Observación. Ambas igualdades son posibles en 7.12 . Para lograr la cota m
tomemos Cm . En cualquier árbol se alcanza la otra cota.
7.14 Nota. El problema del cartero chino es el siguiente: Dada una gráfica G, encontrar el camino euleriano de menor longitud.
La idea de la solución de este problema es como sigue: Se localizan los vértices de grado
impar y se aparean para poner una arista entre cada pareja de manera de poder construir
un paseo euleriano en la nueva gráfica y que el camino que ellas definan sea lo más corto
posible. Para esto se localizan los vértices de grado impar; con ellos se construye una gráfica
30
completa y se define una función de peso de las aristas de esta gráfica completa, es decir,
a cada arista se le asigna el valor de la distancia que tienen los vértices en la gráfica G. En
esta nueva gráfica se aparean los vértices de manera que la suma de los pesos que aparezcan
en esas aristas sea mı́nimo. (Hay algoritmos polinomiales que hacen esto.) Se muestra un
ejemplo a continuación.
u1 .............................................
•.....
•.....
.....
•
•
•
•u
2
•
u3
u4
u
• 1
•
................................................
.....
.
.....
...
...
..
.....
.
..
.
.
...
.... ....
.
...
...
.
.
.
...
.
... ....
.
.
.
...
.....
.. ..
...
... .........
...
... ..
... ......
..
... ...
..........
..
.
.
.... .....
.....
.................................................
.. ..
...
...
.....
...
...
...
...
....
...
...
.....
...
...
.
..
.....
.
.
...
.
...
.....
.
........
.
.
.
.
....
...
...
.......
...
.......
..
... .........
...
.......
...
... ......
.
.......
...... ....
.. ....
...
........................................................................
......
•
•
u1 ...............................................
•..... .
•.....
..... ..
6
2
•
2
u
• 4
3
y
•
z
•
................................................
.....
.
.....
...
...
..
.....
.
..
.
.
...
.... .... ...
.
...
...
.
.
.
...
.
... .... ...
.
.
.
...
.....
.. ..
...
...
... .........
...
... ..
...
... ......
..
... ...
..........
..
...
.
.
.... .....
........ .... .... .... .... .... .... .... .... .................................................
...
.. ..
...
...
.....
...
...
...
...
...
....
...
...
.....
...
...
...
.
..
.....
.
.
...
.....
... ....
.
........
.
.
.
.
....
...
.
.......
...
. ..
.......
..
... .........
....... ... ....
...
... ......
....... .. ..
...... ..
.. ....
...
..........................................................................
......
.....
..... ...
... ... ...
... .... .....
.
.
...
..
.....
...
...
...
...
...
...
...
...
...
...
...
.
...
.
..
...
...
.
.
...
...
..
.
.
...
..
..
.
...
.
.
...
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
..... ...........
..
.
.
.
.
.
...
.
.
.
.......
.....
..
.
...
.
.
.
.
.
.
.
.
.
.
.
.......
.
..
.....
.
.
.
.
.
.
.
.
.
.
.
.
....... .....
.. ............
.
.
.
.
.
.
....... ....
.............
..........
.
.
. ..
.
...........................................................................................................................................
•x
5
•
•
u2
u3
1
mı́nimo apareamiento
u1 ∼ u3 , u2 ∼ u4
•
•u
2
u4
•
•
•
•
u3
u1 u3 → u1 xu3
u2 u4 → u2 yzu4
Observamos que en el ejemplo, un paseo euleriano define en la gráfica original un camino
de longitud de 13+2+3 (pues 13 era el número original de aristas, y los pesos correspondientes
que se agregan son 2 y 3).
7.15 Ejercicio. Determinar la longitud de un camino euleriano en la siguiente gráfica.
•
•
...............................................................................
......... ......
...
...... .. ............
...
...... ..
......
...
...... ....
......
.
.
.
.
.
......
...
.
....
.
.
.
.
.
.
.
.
.
......
...
....
..
.
.
.
.
.
.
.
.
...
.
.
......
....
.
.
.
.
.
.
.
.
.
...
.
.
......
....
.
.
.
.
.
.
.
..
.
.
.
.
......
.
....
.
.
.
.
.
.
.
.
.
.
...... ....
.
....
.
.
.
.
.
.
.
.
.
.
.
.......................................................
...................................................................................................................
...
...
....
.
.
.....
...
.....
...
...
...
...
...
...
....
...
....
...
...
...
...
...
...
...
...
...
..........................................................................................................
.....
..
.....
.....
.....
.....
...
.....
...
.....
.....
....
.....
...
.....
..
.....
..... ....
..... ..
..... ..
.....
•
•
•
•
•
•
•
•
•
7.16 Ejercicio. Sea G una gráfica en la que para cada vértice v se tiene que δ(v) es
congruente con 0 o −1 módulo 4. Probar que es posible partir A de G en dos conjuntos
A y B (con A ∪ B = A y A ∩ B = ∅) de tal manera que para todo v ∈ V se tenga
|δG−A (v) − δG−B (v)| ≤ 1.
8.
Gráficas hamiltonianas
Ası́ como hablamos de caminos eulerianos, los cuales usan todas las aristas, podemos
considerar caminos hamiltonianos; son aquéllos que usan todos los vértices. Ası́ habla31
mos de ciclo hamiltoniano o de trayectoria hamiltoniana. Una gráfica G es gráfica
hamiltoniana si tiene ciclo hamiltoniano.
8.1 Ejemplo. Para n ≥ 3, Kn y Cn son hamiltonianas.
No existe respuesta completa sobre la existencia de ciclos hamiltonianos en una gráfica
(es un problema NP-completo). El siguiente es un criterio que podemos usar para determinar
que ciertas gráficas no son hamiltonianas. Dada una gráfica G denotamos por k(G) al número
de componentes conexas de G.
8.2 Proposición. Si G es hamiltoniana, entonces para todo S ⊂ V no vacı́o se tiene que
k(G − S) ≤ |S|.
Demostración. Si C es un ciclo hamiltoniano en G entonces k(G − S) ≤ k(C − S) ≤ |S|. ♦
El recı́proco de 8.2 es falso como veremos en el siguiente ejemplo.
8.3 Ejemplo. La gráfica de Petersen, P, no es hamiltoniana, pero al quitar cualquier
conjunto de vértices S el número de componentes conexas de P − S, k(P − S), es a lo más
|S|.
Para ver que no es hamiltoniana, usando la notación de 4.8, podemos suponer que,
si lo fuera, entonces el ciclo usarı́a la trayectoria (5, 1, 2). Observemos que el ciclo usarı́a
exactamente dos aristas en cada vértice, por lo tanto, no podrı́a usarse la arista {1, 6} por
lo que alrededor de 6 se usarı́an las aristas {6, 9} y {6, 8}. Tenemos dos casos:
Caso (1). Se usa la arista {2, 7}. En este caso no se usa la arista {2, 3} por lo que debe
usarse {3, 8} y también {3, 4}. Ahora vemos que no puede usarse {9, 4} porque se formarı́a
el ciclo (9, 4, 3, 8, 6, 9), ni tampoco puede usarse {9, 7} porque esto forzarı́a a usar la arista
{4, 5} lo cual dejarı́a a 10 fuera del ciclo.
Caso (2). Se usa la arista {2, 3}. En este caso no se usa la arista {2, 7} por lo que deben
usarse {10, 7} y {7, 9}. Ahora vemos que no puede usarse {9, 4} por lo que deben usarse
{4, 3} y {4, 5}; aquı́ ya se forma el ciclo (1, 2, 3, 4, 5, 1), lo cual es una contradicción.
32
1
•
1
•
............
........................
............ .. .....................
............
.............
............
...............
.
.
.
.
....
.
.
.
............
............
.
............
...............
............
.
.
.
.
.
.
.
............
.
.........
.
.
.
.
.
............
.
.
.
.
......
.........
.
............
.
.
.
.
.
.
.
.
.
.
.
...........
...................
.........
.
.
.
.
.
.
.
.
.
.
...........
......... ............
.........
.
............
.
.
.
.
.
.
.
.
.
...
...........
........... ..................
..............
.
.......
............ ............
...
.
....................
.
.
............
................... .
.
.
..........
.
.
.
.
.
.
.
.
.
.
...
.............. .................... ........ ...................... .........................
..
..
.
............
..
.......
...
............ ......
...... ................
.. .....
............ .
...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
..
......................
..
............. .....
............
..........
...........
...
.
........
. ..
............
..
...
...... ....................
.
........... ........
.
.. ........
...
...............
.
................
..
.......
............
...
..........
.
.........
...
.
...
.
.
.
........
..
........ ...
..
.........
......... ..
... ...
.. .
...................................................................................................................................................................................................
..........
......................
........... .. .....................
...........
.............
..............
............
.
.
.
.
.
...
..
............
............
..
............
.............
.
............
.
.
.
.
............
...........
.
.
.
.
.
.
.
............
...
...........
.
.
.
............
.
.
.
.
.
....................
...........
............
.
.
.
.
.
.
.
.
............
......... ............
...........
.
.
.
.
............
.
.
.
.
......... ................
...........
.
.........
.
.
.
.
.
.
.
........
......... ............
.
.............
.
.
.
.
.
.
.
....... .....
............
..... .............
.
..............
.
.
........
.
..........
.
.
.
.
.
.........................................................................................................................................................................
.........
..........
...
.............
..........
.........
.........
.........
............ ..................
.........
...... ............
.......
.. .........
........................
..........
..........
.
.
.
.
.
.
.........
.
..............
...........
..................
.........
......... ........
............
................... ................
.........
..........
........
.......
.........
.............
............
..........
...... ................
........... ...................
.
..........
.
.
.
.
.. ............
..
.........
.........
........................
.................
..........
..................
..........
......
.........
.........
.......
..
.........
...
..........
.
.
.
.
.
........
...
....
.........
...
.. .............
......... ..
...
.............
. .......
..................................................................................................................................................
•6
5•
10
•
•
7
9•
•6
•2
5•
•
7
9•
8•
•
4
10
•
•
3
8•
•
4
caso (1)
•2
•
3
caso (2)
Ahora tomemos S ⊂ V. Si |S| ≥ 5, entonces sobran a lo más 5 vértices por lo que es claro
que k(P − S) ≤ |S|. Observemos también que si |S| ≤ 2 entonces P − S es conexa, de donde
también k(P − S) ≤ |S|. Si |S| = 3, como cada vértice tiene grado 3, se quitan a lo más
3 · 3 = 9 aristas, de donde sobran al menos 15 − 9 = 6 aristas en una gráfica de 7 vértices.
Si P − S tuviera 4 o más componentes conexas, las posibilidades de distribución de los
vértices en ellas serı́an (1, 1, 1, 1, 1, 1, 1), (1, 1, 1, 1, 1, 2), (1, 1, 1, 2, 2), (1, 2, 2, 2) y (1, 1, 2, 3),
y en ninguna de ellas se tendrı́an 6 aristas. Análogamente, si |S| = 4 entonces a lo más se
quitarı́an 12 aristas por lo que sobrarı́an por lo menos 3 aristas con 6 vértices; si hubiera
al menos 5 componentes los números de vértices de ellas sólo podrı́an ser (1, 1, 1, 1, 1, 1),
(1, 1, 1, 1, 2), ası́ que tampoco podrı́an formarse 3 aristas.
8.4 Teorema. (Teorema de Ore.) Si G es una gráfica con n ≥ 3 vértices en la que
para cada par de vértices u y w no adyacentes se tiene que δ(u) + δ(w) ≥ n, entonces G es
hamiltoniana.
Demostración. Supongamos que G no tiene ciclo hamiltoniano y agreguemos todas las
aristas que podamos sin que se forme un ciclo hamiltoniano. En la nueva gráfica la condición
de que la suma de grados de vértices no adyacentes es mayor o igual que n se satisface ası́ que
podemos suponer que la misma G es tal que al agregarle cualquier arista se forma un ciclo
hamiltoniano. Sean u y w dos vértices entre los cuales no hay arista (existen porque en Kn
hay ciclo hamiltoniano). Como al agregar la arista uw se formarı́a un ciclo hamiltoniano,
eso quiere decir que hay una trayectoria hamiltoniana (u = v1 , . . . , vn = w). Ahora, como
δ(u) + δ(w) ≥ n, existe un ı́ndice i tal que uvi+1 y vi w son ambas aristas puesto que, en
caso contrario, consideremos la función f : N (w) → V \ N (u) dada por f (vi ) = vi+1 que es
inyectiva, y tenemos que N (u) ∩ Im(f ) = ∅ y que u ∈
/ N (u) ∪ Im(f ), de donde
δ(u) + δ(w) = |N (u)| + |N (w)| = |N (u)| + |Im(f )| ≤ n − 1,
lo cual es una contradicción. Tomemos entonces un ı́ndice i tal que uvi+1 ∈ A y vi w ∈ A e
invertamos la porción de la trayectoria de vi+1 a w para obtener el ciclo:
(u = v1 , v2 , . . . , vi , w = vn , vn−1 , . . . , vi+1 , v1 = u),
33
de donde tenemos una contradicción. ♦
Podemos debilitar un poco la hipótesis del teorema de Ore para tener trayectoria hamiltoniana, como vemos en el siguiente corolario.
8.5 Corolario. Si G es una gráfica con n ≥ 3 vértices en la que para cada par de
vértices no adyacentes u y v se tiene que δ(u) + δ(v) ≥ n − 1, entonces G tiene trayectoria
hamiltoniana.
Demostración. Agreguemos a G un vértice w y pongamos una arista de w a todos los
vértices de G para obtener la gráfica G 0 . En esta gráfica se satisfacen las condiciones del
teorema de Ore pues si u y v son vértices no adyacentes en G 0 entonces u, v ∈ V y
δG 0 (u) + δG 0 (v) = δG (u) + 1 + n ≥ n + 1,
La construcción de un ciclo hamiltoniano en G 0 nos da una trayectoria hamiltoniana en G. ♦
8.6 Ejercicio. A una comida van a asistir n ≥ 3 embajadores. Cada uno de ellos es
amigo de al menos n2 embajadores. Probar que se pueden sentar en una mesa redonda de
manera que cada embajador esté al lado de dos de sus amigos.
8.7 Ejercicio. Determinar si las siguientes gráficas (gráficas de los sólidos platónicos)
son hamiltonianas o no.
34
Decimos que G es hamiltonianamente conexa si entre cualquier pareja de vértices hay
una trayectoria hamiltoniana.
8.8 Proposición. Si G es hamiltonianamente conexa entonces G es hamiltoniana.
Demostración. Tomemos uv ∈ A y consideremos una uv-trayectoria hamiltoniana T ;
entonces (vu, T ) es ciclo hamiltoniano. ♦
El recı́proco de 8.8 es falso pues si n ≥ 4 entonces Cn es hamiltoniana pero no hamiltonianamente conexa.
8.9 Nota. Se puede probar que si G tiene al menos cuatro vértices y en G se tiene
que δ(u) + δ(v) ≥ |V| + 1 para cada pareja de vértices no adyacentes u y v, entonces G es
hamiltonianamente conexa.
8.10 Ejercicio. Probar que el octaedro es hamiltonianamente conexo.
Un camino hamiltoniano en una gráfica conexa es un camino cerrado de longitud
mı́nima que pasa por todos los vértices de la gráfica.
8.11 Nota. El problema del agente viajero es el siguiente: Dada una gráfica G,
encontrar el camino hamiltoniano de menor longitud.
Al igual que en el problema del cartero chino, el rango de longitudes de un camino hamiltoniano va de |V| (por ejemplo, en el caso de un ciclo) a 2|V| (en el caso de un árbol). Podrı́a
aplicarse la misma idea de la solución del problema del cartero chino: agregar aristas hasta
que se forme gráfica completa, y a cada arista ponerle como peso la distancia en G entre los
vértices correspondientes. El problema se reduce entonces a encontrar un ciclo hamiltoniano
de peso mı́nimo en la gráfica completa. Sin embargo, a diferencia del problema del cartero
chino, aquı́ se complica demasiado y no se tiene algoritmo polinomial para resolverlo (de
hecho, es un problema NP-duro). A continuación damos un ejemplo de cómo aplicar la solución propuesta para encontrar un camino hamiltoniano de longitud 8 (en una gráfica con
6 vértices).
35
8.12 Ejercicio. Sea Gm,n la gráfica cuyos vértices son los cuadros de un tablero rectangular de ajedrez de m × n con una arista entre dos vértices si, y sólo si, los cuadros
correspondientes se pueden alcanzar con un salto de caballo. Probar que G4,4 y G5,5 no son
hamiltonianas.
8.13 Ejercicio. Sea n ≥ 2. Probar que el n-cubo Qn es hamiltoniano pero no hamiltonianamente conexo.
8.14 Ejercicio. Probar que si G y H son hamiltonianas entonces también lo es G H.
8.15 Ejercicio. Para cada n ≥ 3 encontrar una gráfica con n vértices que no tenga
trayectoria hamiltoniana pero en la que cada par de vértices no adyacentes tengan suma de
grados mayor o igual que n − 2.
8.16 Ejercicio. Decir cuál es el error en la siguiente “demostración” del problema de
los embajadores 8.6: “Procedemos por inducción sobre n. Para n = 3 es cierto pues n2 = 23 ,
ası́ que cada embajador debe tener al menos dos amigos y la gráfica de amistades es un
triángulo. Consideremos ahora el caso de n embajadores con n ≥ 4; usando la hipótesis de
inducción sentemos a n − 1 de los embajadores en mesa redonda y sea E el embajador que
36
falta por sentarse. Como él tiene al menos n2 amigos hay dos embajadores sentados juntos
que son amigos de E y entonces él se puede sentar entre ellos.”
8.17 Ejercicio. Probar que la gráfica de Tutte dibujada aquı́ abajo no es hamiltoniana. (Sugerencia: Probar que la subgráfica definida por el triángulo con vértices u, v, w y su
“interior”no tiene vw-trayectoria hamiltoniana.)
8.18 Ejercicio. En una fiesta ningún hombre bailó con todas las mujeres, pero cada
mujer bailó con al menos un hombre. Probar que hay dos parejas (m, h) y (m0 , h0 ) tales que
m y h bailaron entre sı́, m0 y h0 bailaron entre sı́, pero m no bailó con h0 ni tampoco lo
hicieron m0 y h. (Sugerencia: Considerar una matriz que represente el problema poniendo 1
en el lugar (i, j) si el i-ésimo hombre bailó con la j-ésima mujer y 0 si no. Tomar un renglón
i con máximo número de 10 s.)
8.19 Ejercicio. En un conjunto de personas cada uno tiene a lo más tres enemigos
dentro del mismo conjunto. Probar que se pueden separar en dos subconjuntos de manera
que cada persona en un subconjunto tenga a lo más un enemigo dentro de ese subconjunto.
8.20 Ejercicio. Probar que G + K1 es hamiltoniana si, y sólo si, G es trayectoria.
8.21 Ejercicio. Hay un tesoro en cada cubo de 1 × 1 × 1 de los 343 que forman un cubo
de 7 × 7 × 7. Un duende se encuentra en el cubo central; en cada momento puede pasar de
un cubo a cualquier otro que comparta un cuadrado con el cubo donde está. Resulta que si
regresa a un cubo por el que ya pasó, entonces un monstruo le quita todos los tesoros que
ha obtenido hasta el momento. Las salidas están en las 8 esquinas del cubo. ¿Es posible que
salga del cubo con todos los 343 tesoros?
37
9.
Planaridad
Decimos que G es una (multi)gráfica plana si V ∪ A es un subconjunto del plano en el
que los elementos de V son puntos, cada arista es un arco (es decir, conjunto homeomorfo al
intervalo [0, 1]) entre los vértices que la forman (o lazo en caso de seudográficas, cuando la
arista consta de un solo vértice) y dos aristas sólo pueden intersectarse cuando tienen vértice
en común y, en ese caso, sólo se intersectan en dicho(s) vértice(s).
Una (multi/seudo) gráfica G es aplanable si es isomorfa a una (multi/seudo) gráfica
plana; en otras palabras, si existe una inmersión de G en el plano.
9.1 Ejemplo. Son aplanables Cn , los árboles y las gráficas de los sólidos platónicos (ver
8.7).
9.2 Ejercicio. Probar que K2,n es aplanable.
9.3 Observación. Una (multi/seudo) gráfica es aplanable si, y sólo si, admite una inmersión en la esfera.
Si G es plana entonces las componentes conexas de R2 \ G se llaman caras de G.
En lo que sigue, denotamos por V , A y C a los números de vértices, aristas y caras,
respectivamente, de una (multi/seudo) gráfica plana G.
9.4 Teorema. (Fórmula de Euler.) Si G es conexa, entonces
V − A + C = 2.
Demostración. Inducción sobre A. Por ser la gráfica conexa, el menor número de aristas
que puede tener es A = V − 1, cuando G es un árbol. En este caso sólo hay una cara, de
donde se satisface trivialmente la fórmula. Ahora tomemos una gráfica G con A aristas, donde
A ≥ V . Entonces G tiene ciclos; sea a una arista perteneciente a un ciclo y consideremos la
gráfica G 0 obtenida de quitar a a G. Observemos que al quitar la arista a, alguna cara se une
con otra (todo esto, incluso si a es lazo o arista múltiple), de manera que
V 0 = V,
A0 = A − 1,
C 0 = C − 1,
donde V 0 , A0 y C 0 son, respectivamente, los números de vértices, de aristas y de caras de
G 0 , y ası́, usando la hipótesis de inducción, es claro que la fórmula se satisface también para
G. ♦
9.5 Corolario. El número de caras de una (multi/seudo) gráfica aplanable conexa no
depende de la inmersión. ♦
38
9.6 Ejercicio. (∗) Usar la fórmula de Euler para determinar el número de regiones en
que n rectas en posición general dividen al plano.
9.7 Observación. Toda cara de una gráfica (simple) plana conexa con V ≥ 4 tiene al
menos 3 aristas.
9.8 Proposición. Si G tiene al menos 3 vértices y es gráfica aplanable máxima (es decir,
al agregar una arista ya no es aplanable) entonces todas sus caras son triángulos.
Demostración. Consideremos una inmersión de G en el plano, y supongamos que alguna cara tiene más de 3 lados; entonces se puede agregar una arista entre dos vértices no
consecutivos de esa cara y la gráfica sigue siendo plana, lo cual es una contradicción. ♦
9.9 Proposición. Si G es gráfica aplanable con V ≥ 3 vértices y A aristas entonces
A ≤ 3V − 6.
Demostración. Construyamos G 0 a partir de G agregando aristas de manera que G 0 sea
plana máxima (y conexa). Si V 0 , A0 y C 0 son los números de vértices, aristas y caras de G 0 ,
0
respectivamente; entonces 3C2 = A0 (pues cada cara tiene tres aristas y cada arista pertenece
a dos caras), de donde C 0 = 32 A0 ; sustituyendo en la fórmula de Euler tenemos
2
1
2 = V 0 − A0 + A0 = V 0 − A0 .
3
3
Pero V = V 0 y A ≤ A0 , de donde
1
1
V − A ≥ V 0 − A0 = 2,
3
3
y de aquı́ tenemos el resultado buscado. ♦
9.10 Corolario. K5 no es aplanable.
Demostración. Si fuera aplanable cumplirı́a que A ≤ 3V − 6, pero 3V − 6 = 3 · 5 − 6 =
9 < 10 = A. ♦
9.11 Observación. Si H es subgráfica de una gráfica aplanable, entonces H es aplanable.
9.12 Corolario. Kn no es aplanable para n ≥ 5. ♦
9.13 Ejercicio. Probar que K3,3 no es aplanable.
9.14 Corolario. Si G es aplanable entonces tiene al menos un vértice de grado menor o
igual que 5.
39
Demostración. Si todos tuvieran grado mayor o igual que 6, entonces 2A =
de donde A ≥ 3V > 3V − 6. ♦
P
v
δ(v) ≥ 6V,
Como acabamos de ver, K5 y K3,3 no son aplanables ni lo es ninguna gráfica que contenga
alguna de ellas como subgráfica. Una especie de recı́proco de este resultado es cierto, sólo
que hay que interpretar lo de “contenga” de otra manera, por ejemplo, es claro que si a K5
le agregamos un vértice enmedio de una arista, la nueva gráfica tampoco será aplanable a
pesar de no contener a K5 ni a K3,3 . Veamos los conceptos apropiados que nos llevan a la
buena interpretación de contención en este caso.
Dada una arista a = uv en G, la gráfica obtenida mediante contracción de a es la gráfica
G/a, cuyos vértices son
V(G/a) = (V((¸G)) \ {u, v}) ∪ {w},
para cierto w ∈
/ V, y las aristas son
A(G/a) = (A(G) \ {xu, xv : x ∈ V}) ∪ {xw : xu o xv ∈ A}.
u
•
a
v
•
...........................................................
........
... ...........
...... ..
......
...... ....
...
......
......
.
.
.
.
...
...
.
......
....
.
.
......
.
.
.
.
...
.
..
.
..........
.
.
.
.
.....
......
......
......
....
....
......
.
......
.
.
.
.
.
.
.
.
......
...
...... ....
.... ...........
...... ..
.
...............................................................
•
•
•
•
•
u
•
.................................................................
...... ..
... ...........
...... ...
......
......
...
...
......
......
.
.
.
.
......
.
....
....
....
.
......
.
.
.
.
..
.
.
.
........
.
.
.
.
.....
......
..
..
......
......
.
.
.
.
....
.
.
......
.
.
.
.
.
.
.
.
.
.
......
.. ...........
...... ....
.
. .
...... ..
...............................................................
•
a
•
•
w
•
..
...............................................................
..
.......
......................
........ .... .... .................
.
.........
.........
.. ....
........
.........
.
.
.
.
.
.
.
.
.
...
.........
....
..
.........
...
.........
...
............
.
.
.
.
......
......
...
..
......
......
.
...
.
......
.
......
.
.
.
.
.
.
.
...
..
......
...... ....
... ............
...... ...
................................................................
•
•
•
•
..
..............................................................
..
•
v
•
.........
...... .. .......
...... ... ..............
............................
.......
......
...
.......
.......
.....
......
.
.
.
.
.
....... ........
....
....
....... .
......
...
..
....
...........
.
.
.
.
.
.
.
.
.
.
......
..... ......
.
.
..
...
......
.
.
.
.
.
......
.
......
....
.....
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
......
.....................
...... .... ..............
...... .. .......
.......
•
w
•
•
•
Un menor de una gráfica G es una gráfica isomorfa a una gráfica H que se obtiene de
G a partir una cantidad finita de sucesivas aplicaciones de las siguientes tres operaciones:
contracción de aristas, eliminación de vértices y eliminación de aristas; equivalentemente, H
es menor de G si es isomorfa a una gráfica que se obtiene de una subgráfica de G mediante
contracción de aristas.
9.15 Observación. Si G es aplanable y G 0 es menor de G entonces G 0 es aplanable.
Enunciamos a continuación el teorema que determina completamente las gráficas aplanables. No daremos demostración.
9.16 Teorema. Teorema de Kuratowsky. Una gráfica es aplanable si, y sólo si, no
contiene ningún menor isomorfo a K5 o a K3,3 . ♦
9.17 Corolario. La gráfica de Petersen no es aplanable.
Demostración. Al contraer las aristas a, b, c, d, e se obtiene K5 . ♦
40
•
a
•
..........
..... .. .....
..... .... ...........
......
......
..
.....
......
.
.
.
...
.
......
......
...
......
.....
.
.
.
......
.
.
.
.
.
......
....
.
.
.
.
.
.
......
..
....
.
.
.
.
......
.
.
.....
....
......
.
.
.
.
.
.
......
. ...
....
.
.
.
.
.
.
......
..
.. .....
...............
.
.....
...
..
...........
... ............
.
.
...
......... ....
.........
.
.
.
...
.
.
.
.
.
.
.
...........................................................................................
.
...
.
.
.
.
.
.
.
.
.
......
...
..
...
..
......
... ..........
...
...
...... ....
... .......
...
...
.........
....
..
...
.
..
.........
.
.............
.
.
.
...
.
.
.
...... ....... ...
...
...
..
...
....
...
...
...... ........... ....
...
...
..
...... ...
.. .....
...
.. ..........
...... ..
..
.
.
.
.
.
........
...
......
...
...
...
....
...
...
...
...
...
...
...
...
...
...
...
...
..
.
.
.
... ..
... ....
... ..
... ....
.......................................................................................................
• e
•
d
•
• b
•
•
c
•
•
9.18 Ejercicio. Probar que si una gráfica G con 11 vértices es aplanable, entonces su
complemento no lo es.
9.19 Ejercicio. Sea G una gráfica plana tal que δ(G) = 5 y ∆(G) = 8. Probar que si G
tiene exactamente tres vértices de grado 8 y siete de grado 7 entonces G tiene al menos 25
vértices de grado 5.
41
10.
Gráfica dual
Veremos en esta sección otras aplicaciones de la fórmula de Euler para gráficas planas.
La gráfica dual de una (multi/seudo) gráfica plana conexa G es (multi/seudo) gráfica
G construida a través de G poniendo un vértice por cada cara de G y tal que dos vértices de
G ∗ están unidos mediante una arista si, y sólo si, las caras correspondientes en G comparten
arista.
∗
10.1 Observación. (a) Como vimos en la figura, aun cuando G sea simple, G ∗ no necesariamente lo es.
(b) G ∗ también es aplanable porque por cada cara de G sólo hay un vértice y por cada
arista de G hay exactamente una arista de G ∗ , ası́ que, dentro de cada cara, las aristas se
pueden dibujar de manera que no haya intersección (salvo en el vértice que representa la
cara).
42
Más formalmente: En cada arista a escojamos un punto interior Pa . Sea c una cara y sea
c∗ un punto de ella. Bastará probar que dentro de c se pueden trazar arcos Γa de c∗ a los Pa
cuyo único punto en común sea c∗ . Haremos inducción sobre el número de arcos necesarios
(cada arista contenida en la cara necesita que se construyan dos arcos) y usaremos que los
abiertos conexos de R2 son arcoconexos. Sea B una bola alrededor de c∗ cuya cerradura B
esté contenida en c y digamos que tiene radio r. Sea B 0 la bola con centro c∗ y radio 2r . Veamos
la construcción general de los arcos que usaremos más abajo en la inducción. Tomemos una
arista a de c y un consideremos una media bola Ba alrededor de Pa cuya cerradura no
intersecte a ninguna otra arista, ni a ningún arco ya construido, ni a B; llamemos ra al radio
de Ba y consideremos una bola Ba0 de centro Pa y radio r2a . Sean Q0a ∈ B \ B 0 y Ra0 ∈ Ba \ Ba0 .
Dentro de c \ (B 0 ∪ Ba0 ) construyamos un arco Λ0a de Q0a a Ra0 . Sea Qa el último punto de Λ0a en
la frontera de B y sea Ra el primer punto Λ0a en la frontera de B. El arco buscado Γa se obtiene
al unir el radio de B que va de c∗ a Qa con Γa y el radio de Ba que va de Ra a Pa . Tenemos
ası́ que Γa \ {Pa } está totalmente contenido en c. Ahora, sean a1 , a2 , . . . , ak las aristas de
c, escribiendo dos veces aquellas aristas cuyo interior queda dentro de c, y supongamos que
para cierta l < k y cada i ∈ [l−1] se tienen construidos arcos Γai de c∗ a Pai cuyo único punto
en común es c∗ . Construyamos Γal con el mismo procedimiento descrito arriba al tomar una
media bola Bai alrededor de Pai de tal manera que su cerradura no intersecte a ninguna otra
arista, ni a B, ni a las Ba anteriores, ni a ningún arco ya construido; en el caso de las aristas
cuyo interior queda dentro de c deben tomarse medias bolas de distintos lados.
(c) La gráfica dual de G ∗ es G.
(d) La gráfica dual depende de la inmersión. Por ejemplo, las dos gráficas G1 y G2 dibujadas abajo son isomorfas, pero observemos que las dimensiones de las caras de G1 son
(5, 5, 4, 3), mientras que las de G2 son (6, 4, 3, 3), lo cual hace que en G1∗ no haya vértice de
grado 6, mientras que en G2 sı́ lo hay.
43
Como primera aplicación de lo anterior probaremos que los únicos poliedros regulares son
los platónicos.
Se puede abstraer la definición de poliedro de diversas maneras. Nos interesa aquı́ analizarlos como gráficas y considerar algunas propiedades básicas, las cuales mencionamos aquı́:
Son gráficas conexas, planas (más bien las consideramos dentro de la esfera), cada cara
está definida por un ciclo de longitud al menos 3 y cada vértice tiene grado al menos 3. A
una gráfica que cumple estas propiedades le llamamos poliédrica.
10.2 Observación. La gráfica dual de una gráfica poliédrica también es poliédrica.
10.3 Ejercicio. Probar que si G es poliédrica entonces A ≤ 3C − 6 y existe una cara
con a lo más 5 aristas.
10.4 Teorema. Los únicos poliedros regulares son los platónicos.
Demostración. Supongamos que G es una gráfica poliédrica regular en la que el grado de
cada vértice es g y el número de aristas de cada cara es l. Sea V el número de vértices, A
el número de aristas y C el número de caras de G. Por la definición de gráfica poliédrica
tenemos que
g, l ∈ {3, 4, 5}.
Además,
A=
Vg
Cl
=
.
2
2
Consideremos los distintos casos para g:
∗ Si g = 3, entonces 3V2 = A = Cl
, de donde V = Cl
y en la fórmula de Euler Cl
− Cl
+C =
2
3
3
2
2 y, por tanto, C(6 − l) = 12. Para l = 3 se tiene C = 4, A = 6 y V = 4; éste es el caso del
tetraedro. Para l = 4 se tiene C = 6, A = 12 y V = 8; éste es el caso del cubo. Para l = 5
se tiene C = 12, A = 30 y V = 20; éste es el caso del dodecaedro.
∗ Si g = 4, entonces 4V2 = A = Cl
, de donde V = Cl
, y en la fórmula de Euler Cl
− Cl
+C =
2
4
4
2
2, ası́ que C(4 − l) = 8. Aquı́ la única posibilidad es l = 3, y entonces C = 8, A = 12 y
V = 6; éste es el caso del octaedro.
, de donde V = Cl
, y en la fórmula de Euler Cl
− Cl
+C =
∗ Si g = 5, entonces 5V2 = A = Cl
2
5
5
2
2, y tenemos C(10 − 3l) = 20. Aquı́ la única posibilidad es l = 3, y entonces C = 20, A = 30
44
y V = 12; éste es el caso del icosaedro. ♦
Ahora consideraremos otra aplicación importante: la coloración de mapas. El problema
consiste en lo siguiente: Dado un mapa (de paı́ses), ¿cuántos colores bastan para colorear
cada paı́s de manera que si dos paı́ses comparten una frontera entonces su color es distinto?
El problema traducido a gráficas es el siguiente: Dada una gráfica plana en la que no hay
vértices de grado 1, ¿cuántos colores bastan para pintar sus caras de manera que caras
adyacentes tengan distinto color? Se ha demostrado, mediante el uso de la computadora,
que 4 colores bastan. Nosotros lo probaremos aquı́ para 5 colores. Consideraremos el caso
dual (coloración de vértices es decir, función del conjunto de vértices en un conjunto cuyos
elementos se llaman colores), recordando que los lazos en la gráfica dual de una gráfica se
producen cuando un vértice de la gráfica original tiene grado 1. Decimos que una coloración
de vértices es buena o propia si vértices adyacentes tienen distinto color.
10.5 Proposición. Sea G una gráfica plana sin lazos. Entonces existe una buena coloración con 5 colores para los vértices de G.
Demostración. Sin pérdida de generalidad podemos suponer que la gráfica es conexa.
También es claro que podemos suponer que no hay aristas múltiples. Supongamos entonces
que G es una gráfica simple conexa. Procedemos por inducción sobre V . Si V = 1 no hay
nada que probar. Supongamos que V > 1 y que el resultado es cierto para gráficas con menos
de V vértices. Si la gráfica no es poliédrica, por ser simple y conexa debe de tener un vértice
de grado menor que 3; si la gráfica es poliédrica entonces, tiene un vértice de grado menor
o igual que 5; en cualquier caso, sea v un vértice de grado menor o igual que 5 y usemos la
hipótesis de inducción para colorear los vértices de G − v con 5 colores de manera que no
haya vértices adyacentes con el mismo color. Es claro que si alguno de los 5 colores no se
usó en los vértices adyacentes a v, entonces podemos pintar v con uno de ellos, obteniendo
ası́ la buena coloración buscada para G. Veamos que existe una coloración para los vértices
de G − v en la que en los vértices adyacentes a v no se usan los 5 colores. Supongamos que no
y sean v1 , v2 , . . . , v5 los vértices adyacentes a v, escritos en orden de las manecillas del reloj;
sea i el color usado para vi . Por nuestra suposición, el color 3 no puede usarse para v1 (pues
v3 lo usa); eso quiere decir que v1 está unido a algún otro vértice ya pintado con el color 3,
pero análogamente, ese otro vértice no puede cambiarse de color al 1 por estar unido a otro
con el número 3 y ası́ sucesivamente; la única posibilidad de que no pueda intercambiarse el
color 1 por el 3 en toda la gráfica sin cambiar también el color de v3 es que se forme una
trayectoria de v1 a v3 en G − v en que los vértices vayan alternando los colores 1 y 3. Esto
mismo puede hacerse con los vértices v2 y v4 ; sin embargo esto produce dos trayectorias que
se intersectan; como la gráfica es plana, la intersección es un vértice común a los caminos,
lo cual es un absurdo.
45
1
•
3
•
.... .... .... .... .... .... .... ....
....
....
....
....
....
....
....
•1
2
....
....
..
. .... .... .... .... .... .... ...........
.
. ...
. ...
.
.
.
.. ...
....
.
.
...
.
.
.
..
.
.
.
...
.
...
....
...
......
....
...
...
...
...
...
...
...
...
.
...
....
..
..
...
...
..
.
...
..
.
....
.
...
.
.
...
.
.
.
.
...
......
...
...
......
.
.
.
...
.
..
.
...
....
.
.
...
.
.
.
....
.
.
.
...
...
.
.........
.
.
.......
...
......
.......
...
......
.
...
.
.
.......
.
.
...
.......
.
.
.
...
.
.
.
.
.
.......
....... .... ...........
...
.............
.
.
...
.. ...............
.
.
.
.
.
.
..........
.
.
..........
....
...
..........
....
..
.
.
.
.
.
.
.
..........
....
..........
...
........... ....
...
...
...
.
...
...
...
....
....
....
...
.
....
3•
v1 •
1
v2
•
2
•
v
v5 • 5
•
4
3•
v3
4
•
v4
•4
•2
♦
10.6 Ejercicio. Explicar por qué no puede continuarse la demostración de 10.5 para
que, una vez cambiado el color de v3 por el color 1, continuar con un argumento similar para
intentar cambiar el color de v5 por el de v3 (o el de v4 por el de v2 ), y entonces concluir que
4 colores son suficientes.
10.7 Ejercicio. Encontrar una gráfica plana sin lazos cuyos vértices no tengan una
buena coloración con 3 colores.
10.8 Ejercicio. Determinar si la gráfica de Heawood dibujada aquı́ abajo es aplanable.
10.9 Ejercicio. Sea G una gráfica poliédrica. Probar que son equivalentes el que sus
caras puedan bien colorearse con dos colores y el que todos los vértices tengan grado par.
10.10 Ejercicio. Sea G una gráfica plana conexa tal que su dual G ∗ no tiene lazos ni
aristas múltiples. Demostrar que G y G ∗ tienen el mismo número de árboles generadores.
46
11.
Género
Las superficies compactas orientables sin frontera son la esfera S2 y las obtenidas de S2
al agregarle asas. El número de asas es el género de la superficie.
El género de una gráfica G, γ(G), es el menor género de una superficie en el cual G puede
encajarse sin cruces. Por ejemplo, el género de las gráficas aplanables es 0.
11.1 Proposición. Toda gráfica tiene género y éste es menor o igual que el número de
aristas de la gráfica.
Demostración. Ponemos los vértices en la esfera y un asa por cada arista. ♦
11.2 Proposición. γ(K5 ) = γ(K6 ) = γ(K7 ) = 1 y γ(K3,3 ) = γ(K3,4 ) = γ(K4,4 ) = 1.
Demostración. Basta ver que podemos encajar K7 y K4,4 en el toro. El esquema de la
izquierda muestra cómo puede encajarse K7 en el toro y el de la derecha muestra un encaje
de K4,4 en el toro. ♦
...
.
... .. ......
......
...
.......
......
...... ....
...
... ....
......
...... .. ..............
...
...
... ...
................
......
...
...
........
......
... ...
.
.
.
.
.
.
.
.
.
...
.
.
.
.
......
...
..... ..............
.
.
.
......
.
..... ....
.
...
.
... .......
.....
...... ....
.
.
.
... ....
.
.
.
...
.
......
...... ..
.
...
...
...
.
...... ... ..............
.
.
...
.
......
...
...............
...
.
.
....
.
...... ....
...
...
................
.
.
.
.
...
.
.
.
.
.
.
.........
...
...
.... ... ........
.
.
.
.
.
.......
.
.
.
.
...
... ........
...
... ....... ....
.......
......
....
...
...
... ......... .... .............
......
...
...
...
........ ........
......
...
...
...
......
...
...................
.
.
.
.
.
.
....
.
.
.
.
.
.
.
...
.
......
... ......
...
...
...
.
.
.
................
...
... ........
.
......
...
...
.
.
......
.
.
.
.
...
.
.
.
...
.
.
...... ...
...
......
.... ....
.
.
.
...
.
.
.
.
.
...
.
.
.
.
...
......
........ .......
...
.
.
.
.
.
.
...
....
.
.
......
...
...
..............
......
...
..
....... .... ........... ....
...
......
.......
... ...... ..
...
...
...... ....
.......
.
.
.
.
.
.
...... ...
.
.
.
.
......
...
...
.
.
...
...... .. ...........
...
...
... .........
...
...............
...
...
.
... .........
...
......................
...
.
.
......
.
.
.
.
...
.
.
...
...
......
... ........
.....
.
.
.
.
.
...
...... .....
.
.
......
...
... ....
.....
.
...... ..
.
.
.
.
.
.
.
.
...
......
...
... ...
...... .. .........
......
...
...............
.
...
... ...
......
..
...
...
......
... ...
............
...
......
....... ................
.. ..
...
......
.......
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
.
.
...
......
...... ..... ....
...
....
......
.
.
.
...
... .............
.
... ...
.
...............................................................................................................................................................................................................
•
C
•
•
P
Q
R
•A
C•
B
•D
B•
C
•
•
X
S
•
A•
A
•
B
R
•
......................................................................................................................................................................................................
.
..
.
.
..
... . ..
..........
...
..... ... ...
...
.....
...
..... .. ..
..
..... .. .....
...
..... ... ..
...
...
.... ....
..
...
...
..... .... ....
.
.
.
.
.
.
.
.
.
.
.
.
...
...
...
.
...
.
... .... ...
.
.
.
.
.
.
...
.
.
.
.
.
.
.
.
...
...
. ..
...
...
.
.
..
....
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
...
.
.
...
.
.
...
.
...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... ..... .........
... ...
.
.
..
..
....
.
.
.
.
.
.
.
.
.
.
.
... ... ........
.
... ....
..
.
.
.
..
.
.
.
...
.
.
.
.
.
... .... .......
.
.
... ...
.
..
.
... ..
...
...............
...
... .......
...
.....
...
...
.........
... ... .....
.. .... ........
..
..
...
.
...
.
.
. ... .....
.
.
.....
.
.
.
.
.
.
.
...
.. ....
.
. ... .......
..
.
.
.
.
.
.
.
.
...
.
.
. ....
.. ............
.
.
...
.
.
...
.
.
.
.. ...
..
............
...
...
...
...
........
...
...
....
...
...
.......
..
...
...
...
...
.............
...
.
.
.
.
....
... .....
...
.
.
..
........ ...
.
.
.
.
.
... ....
...
.
.
.. ... ...
.
.
.
.
.
.
.
... ....
...
....
... ... ...
..
.
.
.
.
...
......
...
.
.
... .... ...
..
.
.
.
.
.
.
.
.
.
......
.
.
.
.
............
.... ...
.
.
.
.
.
.
.
.
.
... ....
.
....
.
.
.
...... ...
..
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... ....
.
.
.
. .
.
....
..... .. ..
...
... ....
...
...
...
.....
..... ... ....
...
...
...
...
...
.....
...
..... ..
...
..
...
..
.....
...
..... ....
...
....
....
...
.. .....
..
..
.
.....
.
.
.
.
.
.
.
.
.
.
.
...
...
.
.
.
.
.
...
.
..
..
.
...
...
...
...
.....
...
... ... ......
...
..
.. .........
.. .... .........
...
.
..
...
...
.
.
.
.
. ... ......
.
... ... .....
..
.
.
.
.
...
...
.
.
... .. .....
..
...............
...
.
...
..
.
.
..........
.
.............................................................................................................................................................................................
•
A
Q
•
P
•
Q R
X•..............................................................P
X
................................................................................................................................•
...
......
...
... .
...
...... .......
......
....... ....
..
..
. .. .....
.
.......
•B
•
P
•
X
•
Q
•
R
•
S
Un encaje de una gráfica en una superficie es de 2-celdas si todas las caras son homeo-
47
morfas (topológicamente) a discos.
El siguiente teorema generaliza la fórmula de Euler.
11.3 Teorema. Sea G una (seudo/multi) gráfica conexa con un encaje de 2-celdas en
una superficie compacta orientable sin frontera de género g. Entonces
V − A + C = 2 − 2g.
Demostración. Hacemos inducción sobre g. La base de inducción es g = 0 y nos lo da
la fórmula de Euler. Sea G con un encaje de 2-celdas en una superficie compacta orientable
sin frontera S de género g ≥ 1. Modificaremos G “cortando” un asa de S para poder aplicar
inducción. Tomemos una curva cerrada (homeomorfa a un cı́rculo) C alrededor de un asa
α de manera que S no contenga ningún vértice de G y que corte cada arista de G en un
conjunto finito de puntos (posiblemente vacı́o). Sea k el número total de intersecciones de C
con las aristas de G; observemos que, como el encaje es de 2-celdas, forzosamene k ≥ 1. Ahora
cortamos la superficie S a través de C poniendo aristas de cada lado del corte (siguiendo
el corte) y vértices por cada intersección de C con una arista. También ponemos una cara
alrededor de cada corte.
Obtenemos una gráfica G 0 con V 0 = V + 2k vértices, A0 = A + 3k aristas y C 0 = C + k + 2
caras que, por hipótesis de inducción, satisface
V 0 − A0 + C 0 = 2 − 2(g − 1),
y ası́
V − A + C = (V 0 − 2k) − (A0 − 3k) + (C 0 − k − 2) = 2 − 2g. ♦
11.4 Nota. El conjunto de gráficas que admiten encaje en una superficie compacta
orientable sin frontera de género g es cerrada bajo menores; en particular, si H es menor de
G entonces γ(H) ≤ γ(G). Para cada género hay una lista finita de gráficas prohibidas. Para
el toro son varios cientos.
11.5 Nota. Sea G una gráfica conexa de género g. Entonces todo encaje de G en una
superficie compacta orientable sin frontera de género g es de 2-celdas. La idea de la demostración es que si en una cara aparecen asas entonces se pueden quitar.
48
11.6 Corolario. γ(K8 ) > 1.
Demostración. Como K5 está contenida en K8 sabemos que K8 ≥ 1. Supongamos que
γ(K
8 ) = 1 y tomemos un encaje (de 2-celdas) de K8 en el toro. Entonces C = A − V =
8
− 8 = 20. Como cada cara tiene al menos 3 aristas, tenemos que 3C ≤ 2A, de donde
2
60 ≤ 58, lo cual es absurdo. ♦
Si una gráfica tiene género g y existe una inmersión de 2-celdas en una superficie entonces
la superficie no necesariamente tiene género g como vemos en el siguiente ejemplo.
11.7 Ejemplo. La siguiente es una inmersión de K4 de 2-celdas en el toro (y, por tanto,
podemos verificar que satisface V − A + C = 0 pues V = 4, A = 6 y C = 2).
A
...................................................................................................................................
...
...
....
...
...
...
...
..
...
...
..
.
...
.
...
...
...
...
.
...
..
...
.
...
..
.
...
...
..
.
...
...
......................................................
...
...
...
. ..........
.
.
...
.
.......
...
...
.
.
.
.
.
.
.
....... ....
...
...
.
.
.
.
.
.
.
..
...
.........
.
.
.........
.
.
...
...
... ..........
....
...
...
.......
.......
....
...
...
....... ....
.
...
.
...
....... ..
...
................................................
...
...
..
...
.
..
....
...
.
..
....
...
.
..
...
...
.
.
.
.
...
...
...
...
...
.
..
...
..
.
........................................................................................................................................
•
B
•
•
B
•
A
En este caso, aunque las caras son 2-celdas, la orilla de una de ellas no es un cı́rculo.
Para ver la forma que tiene, hagamos cortes como se indica en la figura siguiente y notemos que la orilla es el octágono (1, 2, 4, 1, 3, 4, 2, 3, 1) en el que aparecen las aristas {1, 3} y
{2, 4} repetidas; al pegarlas sobran las aristas {1, 2}, {2, 3}, {3, 4} y {4, 1} sobre las cuales
está pegada la otra cara.
2•................
... ...........
.......
...
.......
.......
...
.......
..
....
...
... ..............
.......
...
..
.......
.......
...
................................................
.
...
.
..
.
.
.
.
...
.
...
.
.
...
..
..
...
.
.
..
..
.
.
.
...
...
...
...
...
..
..
...
...
...
.
.
.
.
.
.
... .... .... .... .... .... .... .... .... ....... .... .... .... .... .... .... .... .... .... .... .... .... .... .... .... .... .... .......
...
...
...
...
...
...
..
...
..
..
..
..
..
...
.
.
.
.
.
.
.
...
...
...
...
..
...
...
...
...
...
...
.......................................................
.....
...
...
... ............
...
...
...
.......
...
...
...
.
.......
...
...
...
....... ..
...
.........
.
.
...
.
.
......
.......
....
...
..
....
.
.
.
.
. ..........
.
....
.
...
...
.
.
.
.
.
.
....
.......
.
...
.
.
....
.
.
.
.
.
...
.
.
.
.
....... ....
.... ...
.
.
.
.
.
.
.
.
.
.
..............................................
.....
...
.
.
.
.
..
...
.
.
..
...
...
...
..
.
...
...
.
..
.
...
.
..
.
..
...
.... .... .... .... .... .... .... .... .... ...... .... .... .... .... .... .... .... .... ...
B
3• m
X
b1
B
b2
X
a1
1
n
•
2
•4
3•
k
•
X
b1
A
k
•1
B
a2
A
•3
l
a1
m
l
a1
b2
a2
A
4
•
b2
•
4
X
11.8 Nota. No existe algoritmo que determine el género de una gráfica. Es un problema
49
NP-completo. Se puede probar que
γ(Kn ) = d(n − 3)(n − 4)/12e ,
γ(Km,n ) = d(m − 2)(n − 2)/4e ,
γ(Qn ) = (n − 4)2n−3 + 1, n ≥ 3.
11.9 Proposición. Sea G conexa con V vértices y A aristas. Entonces
γ(G) ≥ 1 +
A V
− .
6
2
Demostración. Tomemos un encaje de G en una superficie de género γ(G) y digamos que
tiene C caras. Por 11.8 el encaje es de 2-celdas ası́ que V − A + C = 2 − 2γ(G). Pero cada
cara tiene al menos tres aristas ası́ que C ≤ 2A
; sustituyendo tenemos
3
2 − 2γ(G) = V − A + C ≤ V − A +
A
2A
=v−
3
3
y de aquı́ ya tenemos el resultado. ♦
El número de cruce, ν(G), de una gráfica G es el menor número de intersecciones de
aristas entre todos los encajes de G en la esfera. Aquı́ hay que suponer varias cosas:
(a) Aristas adyacentes no se cruzan.
(b) Dos aristas cualesquiera se cruzan a lo más en un punto.
(c) Ninguna arista se cruza a sı́ misma.
(d) Por cada punto de la esfera pasan a lo más dos aristas.
(e) Ningún vértice está en el interior de una arista.
11.10 Ejemplo. Es fácil ver que ν(K5 ) = ν(K3,3 ) = 1.
11.11 Proposición. ν(G) ≥ γ(G).
Demostración. Cada vez que haya un cruce se puede poner un asa en una de las aristas
que se cruzan. ♦
Es posible la desigualdad estricta en 11.11 como vemos en el siguiente ejemplo.
11.12 Ejemplo. ν(K6 ) = 3.
Demostración. El siguiente dibujo demuestra que ν(K6 ) ≤ 3.
50
Para ver la otra desigualdad supongamos que tenemos un dibujo de K6 en la esfera con
ν(K6 ) cruces. Ponemos un vértice en cada cruce y entonces tenemos una gráfica plana. Sea
G la gráfica resultante. Esta gráfica es plana y conexa ası́ que cumple cumple A ≤ 3V − 6,
pero V = 6 + ν(K6 ) y A = 15 + 2ν(K6 ), ası́ que
15 + ν(K6 ) ≤ 3(6 + ν(K6 )) − 6 = 12 + 3ν(K6 ),
de donde ν(K6 ) ≥ 3. ♦
11.13 Nota. Calcular el número de cruces de una gráfica es problema NP-completo.
11.14 Nota. Se prueba que
ν(Kn ) ≤
1
bn/2c b(n − 1)/2c b(n − 2)/2c b(n − 3)/2c .
4
11.15 Ejercicio. Encontrar un encaje sin cruces de Q4 en el toro.
11.16 Ejercicio. Probar que para n ≥ 4,
γ(Kn ) ≥ d(n − 3)(n − 4)/12e
y que para para m, n ≥ 2,
γ(Km,n ) ≥ d(n − 2)(m − 2)/4e .
11.17 Ejercicio. Determinar γ(P) y ν(P) donde P es la gráfica de Petersen.
11.18 Ejercicio. Probar que ν(K7 ) ≤ 9.
11.19 Ejercicio. ¿Es cierto que si G no es plana pero tiene una arista a tal que G − a
es plana entonces ν(G) = 1?
11.20 Ejercicio. Determinar ν(K2,2,2 ).
11.21 Ejercicio. Probar que para todo g ∈ N existe una gráfica G tal que γ(G) = g.
51
12.
Coloración
Recordemos que una coloración para G es una función c : V(G) → I donde I es un
conjunto de colores y que decimos que la coloración es buena o propia si vértices adyacentes
tienen distinto color. El número cromático de G, χ(G), es el menor número de colores para
el cual existe una buena coloración para G. Dada una coloración propia para los vértices de
G llamamos clase cromática a todos los vértices de un mismo color.
12.1 Ejemplo. (a) χ(Kn ) = n,
(b) χ(G) = 2, si G es árbol con al menos dos vértices
(c) χ(G) = 2, si, y sólo si, G es bipartita con al menos una arista.
(d) χ(C2k+1 ) = 3,
(e) χ(G) = 1 si, y sólo si, G no tiene aristas.
(f) χ(P) = 3 para P la gráfica de Petersen.
1
............
...•
..... .... ..........
.
.
.
.
.
.
.
......
......
......
....
......
......
...
.....
......
......
...
......
.....
.
.
.
......
.
.
.
.
......
....
.
.
.
.
.
.
......
...
....
.
.
.
.
......
.
.
. ....
....
......
.
.
.
.
.
.
......
. ...
...
.
.
.
.
.
.
.
.....
. ....
...............
.
.
.......
...
.
... ............
.
......... ...
.
.
.
.
.
...
.........
.....
...
.
.
.
.
.
.
.
.
.
.
.
.
.
...
.
.
.
......................................................................................
...
......
.
...
...
....
...
......
..
... ..........
..
...
...... ....
..
... .......
.
........
...
.
....
...
...
........
........
...
... ........... .......... ....
...
...
....
..
.
..
...
..
..
............... .....
.
.
.
.
.
.
.
.
...
...... ..
..
...... ...
...
... ........
...
........
...
..........
...
....
..
......
...
...
..
...
...
.
.
.
.
.
.
...
...
...
...
...
...
...
... ...
... .....
... ...
... ...
.
........................................................................................................
•3
2•
3
•
2•
•
1
•2
2•
•
1
•
3
12.2 Proposición. Si c es una coloración de G con χ(G) colores entonces dados i, j
colores distintos existe una pareja de vértices adyacentes tales que uno tiene color i y el otro
tiene color j.
Demostración. Si no, entonces todos los vértices de color j podrı́an repintarse con color
i y la coloración seguirı́a siendo buena. ♦
12.3 Observación. G es s-partita si, y sólo si, χ(G) ≤ s.
12.4 Observación. El número cromático de G es el máximo de los números cromáticos
de sus componentes conexas y también el máximo de los números cromáticos de sus bloques.
12.5 Proposición. χ(G) ≤ ∆(G) + 1.
52
Demostración. Inducción sobre el número de vértices. Para |V| = 1 no hay nada que
probar. Sea u un vértice cualquiera y, usando la hipótesis de inducción, pintemos los vértices
de G − u con ∆(G) + 1 colores. El vértice u tiene a lo más ∆(G) vecinos ası́ que es posible
usar un color para pintarlo. ♦
Veremos que las gráficas completas y los ciclos impares son los únicos en los que se necesita
la igualdad en 12.5; en los demás casos basta con ∆ colores. Para probar eso necesitamos el
siguiente lema.
12.6 Lema. Si G es gráfica con al menos 4 vértices y existen dos vértices u y v tales que
d(u, v) = 2 y tales que G − u − v es conexa, entonces χ(G) = ∆(G).
Demostración. Sea w1 un vértice adyacente a u y a v. Numeremos el resto de los vértices
w2 , w3 , . . . , wn−2 de manera que, para cada i > 2, wi es adyacente a algún wj con j < i
(esto es posible dada la conexidad de G − u − v). Digamos que los colores disponibles son
1, 2, . . . , ∆(G). Pintemos a u y a v con el color 1 y después pintemos los vértices de uno
en uno empezando por el último en el orden de la numeración usando siempre el primer
color con el cual la coloración sea buena; observemos que hasta llegar a w2 sólo se usan
∆(G) − 1 colores puesto que cada vértice es adyacente a a lo más ∆(G) − 1 otros vértices
con numeración mayor (y, por tanto, ya pintados). Entonces w1 puede pintarse con el color
∆(G) y la coloración es buena. ♦
12.7 Teorema. Teorema de Brooks. Si G es conexa, no trivial y distinta de C2n+1 y
de Kn , entonces χ(G) ≤ ∆(G).
Demostración. Quitemos vértices de G lo más posible mientras el número cromático no
disminuya. Obtenemos entonces una subgráfica H tal que χ(H) = χ(G) y para todo v vértice
de H se tiene que χ(H − v) < χ((H). Observemos que H es un bloque de G porque si tuviera
dos o más bloques podrı́amos retirar todavı́a vértices sin disminuir el número cromático (por
12.4). Analicemos distintos casos para H.
Caso (1). Si H = C2n+1 entonces χ(G) = χ(H) = 3 ≤ ∆(G) puesto que, por hipótesis,
G 6= C2n+1 , ası́ que por lo menos hay otra arista que sale de algún vértice de H.
Caso (2). Análogo al caso anterior tenemos que si H = Kn entonces χ(G) = χ(H) = n ≤
∆(G).
Caso (3). Si todos los vértices de H son de grado 2 o |V(H)| − 1 entonces, por ser H
bloque, no puede tener sólo un vértice de grado |V(H)| − 1 (pues serı́a un triángulo y ya
cubrimos este caso); ası́ H es ciclo de longitud par o Kn−2,1,1 y, en cualquiera de estos casos
tenemos que χ(G) = χ(H) ≤ 3 ≤ ∆(G).
Por lo anterior, supongamos que H es bloque, no es completa, no es ciclo y no tiene
vértices de grado |V(H)| − 1. Por lo tanto, además, |V(H)| ≥ 4. Tomemos v vértice de grado
distinto de 2 y de |V(H)| − 1.
Caso (4). Si H − v es bloque entonces tomemos w vértice a distancia 2 de v y usemos
53
12.6.
Caso (5). Si H−v no es bloque tomemos dos bloques extremos B1 y B2 de H−v (es decir,
B1 y B2 sólo tienen un vértice de corte de H−v cada uno o, en otras palabras, corresponden a
hojas en la gráfica de bloques y cortes). Como H sı́ es bloque, existen elementos w1 , w2 ∈ N (v)
no vértices de corte de H − v y tales que w1 ∈ V(B1 ) y w2 ∈ V(B2 ). Ası́ d(w1 , w2 ) = 2 y,
puesto que δ(v) ≥ 3, H − w1 − w2 es conexa. Aplicamos 12.6. ♦
A continuación veremos más cotas para χ(G).
12.8 Lema. Si G es tal que χ(G−v) < χ(G) para todo v vértice entonces χ(G) ≤ δ(G)+1.
Demostración. Suponiendo que δ(G) < χ(G) − 1 tomemos un vértice v de grado δ(G);
podemos bien-pintar los vértices de G − v con χ(G) − 1 colores, pero entonces, como v tiene
menos de χ(G) − 1 vecinos, lo podemos bien-colorear con alguno de los χ(G) − 1 colores, lo
cual es una contradicción. ♦
12.9 Proposición. Sea f una función que asigna a cada gráfica un número real y que
cumple:
(a) f (G) ≥ δ(G) para toda G y
(b) f (H) ≤ f (G) para toda G y toda subgráfica inducida H de G.
Entonces χ(G) ≤ f (G) + 1.
Demostración. Sea H0 una subgráfica inducida de G tal que χ(H0 ) = χ(G) y χ(H0 − v) <
χ(H0 ) para todo v vértice de H0 . Por 12.8 tenemos que δ(H0 ) ≥ χ(H0 ) − 1, de donde
χ(G) = χ(H0 ) ≤ δ(H0 ) + 1 ≤ f (H0 ) + 1 ≤ f (G) + 1. ♦
Ejemplos de funciones que cumplen 12.9 son ∆, |V|, |A|, la función l que calcula la
longitud máxima de trayectorias de las gráficas (por 1.21 sabemos que δ(G) ≤ l(G)).
12.10 Corolario. χ(G) ≤ min{∆(G) + 1, |V(G)| + 1, |A(G)| + 1, l(G) + 1}. ♦
12.11 Corolario. χ(G) ≤ d + 1 donde d es el máximo de los δ(H) tomado sobre todas
las subgráficas inducidas H de G.
Demostración. Sea f la función definida por f (G) = d. Entonces δ(G) ≤ f (G) porque G es
subgráfica inducida de ella misma. Si H es una subgráfica inducida de G entonces cualquier
subgráfica inducida de H también lo es de G ası́ que el máximo para H se toma en un
subconjunto del de G y, por tanto, f (H) ≤ f (G). ♦
12.12 Proposición. Sea G una gráfica con n ≥ 3 vértices y sea G su complemento.
Entonces√
(a) 2 n ≤ χ(G) + χ(G) ≤ n + 1 y
(b) n ≤ χ(G)χ(G) ≤
(n+1)2
.
4
54
Demostración. Probemos primero que n ≤ χ(G)χ(G). Sabemos que χ(Kn ) = n, ası́ que
basta ver que podemos colorear Kn con χ(G)χ(G) colores. Sea c una buena coloración para G
y sea c una buena coloración para G. Dado un vértice v lo coloreamos con el color (c(v), c(v)).
Ahora probemos que χ(G)+χ(G) ≤ n+1. Sea H subgráfica de G con δ(H) = m maximal
y sea J subgráfica de G con δ(J) = k maximal. Sabemos que χ(G) ≤ m+1 y que χ(G) ≤ k+1.
Bastará ver que m + 1 + k + 1 ≤ n + 1, es decir, que m + k ≤ n − 1. Supongamos que no,
o sea que m + k > n − 1. Como δ(H) = m y δ(J) = k tenemos que |V(H)| ≥ m + 1 y
|V(J)| ≥ k + 1 y entonces V(H) ∩ V(J) 6= ∅. Tomemos v en esta intersección. Entonces
δH (v) ≥ m y δJ (v) ≥ k, y de aquı́ m ≤ δG (v) ≤ n − k − 1, de donde m + k ≤ n − 1, contrario
a nuestra suposición.
√
Para ver que 2 n ≤ χ(G) + χ(G) usamos que n ≤ χ(G)χ(G) y la desigualdad entre
media aritmética y media geométrica.
Finalmente, para ver que χ(G)χ(G) ≤ (n + 1)2 /4 usamos que χ(G) + χ(G) ≤ n + 1 y,
otra vez, usamos la desigualdad entre media geométrica y media aritmética. ♦
Un clan de una gráfica es una subgráfica completa maximal. El número de clan de G,
ω(G), es el orden máximo de un clan de G.
12.13 Observación. χ(G) ≥ ω(G) y es posible la desigualdad estricta (por ejemplo, en
un ciclo impar).
12.14 Nota. Se prueba que dados dos naturales a ≤ b existe gráfica G con χ(G) = a y
ω(G) = b.
12.15 Ejemplo. La siguiente gráfica G tiene χ(G) = 4 y ω(G) = 2.
u1
..................
.........•
.
. ...
.
.
.
.
... . ... .....
... ......
..... ..
... .......
..... ...
......
...
..... ....
......
...
......
......
...
.....
...
.
.
.
.
.
.
......
...
.
....
.
.
.
......
.
.
.
.. .......................... ....
......
....
.
.
.
.
.
.
...............
...
..
............
...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... .............. ...........
.
... ..................... ....
.
.
.
.............. .....
.
.
.
.
.
.
...
.. .....
..
................
.
.
.
.
.....................
.
...
..
....
...
......
.
.
.....
...
.......
....
.....
...
....
... ....
... ..
.
.
..............
.
.
.
.
.
.
.
.
.
..........
... ....
..
.
... ...
...... ....
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.......... .. ..........
... ...
...
.
.. .
.............
... .... ....
... ..... ....
... ..
...
.
... ...
... ...
... ..
... .....
...
......
...
.....
...
...
.
...
..
.
.
.
.
.
...
....
..
.
..
...
.......
.
.
.
.
.
.
.
.
...
.
...
..
.. ..
...
... ..
...
...
..
.. ...... .....
... ..... ....
... ....
... ....
......
......
.........
... ..
... ...
........
.
.........
.
.
.
.
... ...
.
.
.
.
..................
... ..
... ..
... ...
...... ...............
... ...
.........
.........
... ...
... ...
........
.........
..... .................
......... .......
.
.
.
...........................................................................................................
v1
•
u5 •
v5 •
v4•
• u2
v
2
•
•
w
•v
3
•
u4
•
u3
Demostración. Es claro que ω(G) = 2. También es claro que χ(G) ≥ 3 pues contiene
un pentágono. Supongamos que χ(G) ≥ 3 y sea 1 el color de w. Entonces los vi tienen
color 2 o 3 y no pueden tener todos el mismo color pues eso forzarı́a a que el pentágono
(u1 , u2 , u3 , uu .u5 , u1 ) usara sólo dos colores. Tenemos esencialmente 3 casos para la coloración
de los vi . En las siguientes figuras analizamos cómo deberı́a completarse la coloración en cada
55
caso, y en todos vemos que algún vértice no puede colorearse.
1
...........
..•
............
..•
.......... ...............
.
.
.
......... .........
.
.
. ....
.... .
...... ... ... .....
... ......
.... .
... ......
..... ...
......
...
..... ....
......
...
......
......
...
.....
...
.
.
.
.
.
.
......
...
...
..
.
.
.
.
......
.
.
.
. ............................... ....
....
......
.
.
.
.
.
.
...............
...
...........
.
....
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... ............... ..........
..
... ..................... ...
.
.
.............. ......
.
.
.
.
.
. ...
...
...........
....
...
.....................
.
.
...
.
.
......
.
.....
.
.
.
.
...
..
.......
.....
.....
..
... ....
............
... ....
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
... ...
. ...
..
. ...............
......
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.......... .. ..........
... ...
...
. .
.
.........
... .... ...
... ..... ....
... ..
...
... ....
.
... ....
... ...
...
... .....
......
...
....
...
.
.
...
..
.
.
.
.
.
.
.
...
.
.....
...
..
......
.
.
.
.
.
.
.
.
.
.
.
..
...
.
. .
...
... ..... ....
...
... ..... .....
...
... ..
... ...
...
...
...
...
.....
........
... ...
... ....
.........
.
........
.
.
.
.
.
.
... ..
.
.
.
.
.
.
.
.
.
......... ........
... ..
... ...
... ...
.......................
... ...
.........
.........
... ..
... ...
........
.........
..... ................
......... ........
.
.
.
.
.
.
.......................................................................................................
... ......
... .
... .......
..... ..
......
...... ..
...
......
...... .....
...
.....
......
.
.
...
.
.
.
.
......
..
..
....
.
.
.
.
......
.
.
. .................... .....
....
.
......
.
.
.
.
.
............... .. .................
..
.
....
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.................... ...........
... .........................
.
.
.
.............. .....
.
.
.
.
.
...
... .......
....
................
...
.....................
.
.
...
..
.
.
.
.
.......
.
.....
...
.
... ...
...
.....
...
.....
........
... ..
... ....
.
.
.
.
.
.
.
.
.
.
.
..
... ....
..... ...
. ...............
... ....
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.......... .. .........
...
... ...
.
.
.................
... ..... ....
... .... ....
... ...
... ..
......
...
..
... ..
... .....
... ....
...
...
.....
...
...
.
.
.
...
..
.
.
.
.
...
...
..
.
..
...
.......
.
.
.
.
.
.
.
.
.
...
.
...
... ...
...
...
... ...
...
...
... ..... ....
.. ...... .....
..
...
.....
..
... ....
.......
.
... ....
.........
... ..
........
.
.
.
.
.........
.
... ..
.
.
.
... ..
...................
... ..
... ..
.... ....
... ...
... ...
......... .................
... ...
.........
.
.........
......... ........
..... ................
.
.
.
................................................................................................................
2
•
•
3•
•
2
•
?
•
1
•2
?
•
...
..............
........ .........
...... .. ..... ...........
..... ....
... ......
.
.
.
.
......
...
.... ....
......
.....
...
......
..
......
...
......
...
.....
.
.
...
.
.
.
.
......
.
....
.
.
.
.
.
......
.
.
.
.
.
.
.
.
.
...................... ... ...........................
....
..
.
.
.
.
.
.
.
.
...................... ...........
.... ..........................
.
.
.
.
.
.............. .....
.
...
...
.
......................
.
.
.................
.
.
.
.
.
.
.
...
.
.........
...
.
.
.
.
.
....
......
.
...
...
.....
...
...
.......
... ..
....
.
... ....
.
..............
.
... ....
...... ....
.
.
.
..
.
. ...........
.
.
... ...
.
.
.
.
.
.
.
.
.
.......... . ..............
...
.. .
... ....
..
.................
... ..... ....
... .... ....
..
.
... ...
... ..
...
... ...
... ..
...
... ....
...
... .....
.
..
.
.
.
.
.
.
.
.
.
.
...
...
..
.
..
.
..
.
.
.
.
.
...
.
.
.
.........
...
.
... ...
...
...
...
...
.. ..
... ..... ....
...
..
.. ..... .....
... ...
...
......
..
... ....
........
... ....
... ...
......
.
.
.
.
.
.
.
.
.
.
.
.
.
.........
... .
... ..
......................
... ...
... ...
...... ..............
... ...
... ..
........
.........
.. ..
... ...
.........
.........
......... ........
...... .................
..............................................................................................................
2
•
•3
•
•
2
3•
•2
•
1
•
3
•
1
•
2
•
1•
•
2
•
?
2•
•
3
•
1
•
•
1
•3
•
•
2
•
La siguiente es una buena coloración con 4 colores:
1
............
..•
......... .........
...... .. ... .....
... ......
..
..... ...
... .......
..... ..
......
...
...... .....
......
...
.....
.
......
.
.
.
...
.
.
......
.
....
.
.
...
.
.
.
.
......
..
.
....
.
.
.
.
......
.
.
.
.
.
.
.
.
.
.
.
......... ... ........................
...
.
.
.
.
......
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..................
...
..
.... ...........................
.
.
.
.
.
.
... ..................................
.
......................
.
.
.
.
.
.
...........
.
.
.
.
.
.
..
.
...
........
.
.
.
....
.
.
......
...
...
.
.
.....
.
.......
...
.
... ..
.....
.
... ....
.
.
.
.
................
.. ....
...... ....
.
.
.
.
..........
.
.
.
... ...
.
.
.
.
.
.
.
.
.
.
.......... .. ..............
...
.. .
... ....
..
................
... ..... ....
... .... ....
...
.
... ...
... ..
...
... ...
... ..
...
... ....
...
... .....
.
..
.
.
.
.
.
.
.
.
.
.
...
...
.
..
..
.....
.
.
.
...
.
.
.........
.
.
...
..
.
...
...
...
... ..
.. ..
...
...
... .... .....
.. ..... ....
..
.. ...
... ...
... ....
... ....
........
... ...
......
... ...
.
.
.
.
.
.
.
.
.
.
.
.
.
.........
.
... ..
... ..
..... ............
... ...
... ...
.......................
... ..
... ...
........
.........
... ...
.........
..
.........
..... .................
......... ........
..............................................................................................................
1
•
2•
2•
•
3
•3
•
4
•3
•
2
•
2
•
3
♦
La construcción usada en 12.15 se puede imitar para obtener gráficas sin triángulos y con
un número cromático especificado, como veremos en la siguiente proposición.
12.16 Proposición. Para toda k ≥ 2 existe una gráfica con ω(G) = 2 y χ(G) = k.
Demostración. Hacemos inducción sobre k. Para k = 2 tomamos T1 o C4 ; para k = 3
tomamos C5 ; para k = 4 tenemos el ejemplo anterior. Sea k ≥ 5 y supongamos que G 0 cumple
con que ω(G 0 ) = 2 y χ(G 0 ) = k − 1. Sean u1 , u2 , . . . , un los vértices de G 0 . Construyamos G
con vértices u1 , u2 , . . . , un , v1 , v2 , . . . , vn , w y aristas definidas por:
ui uj ∈ A(G) ⇔ ui uj ∈ A(G 0 ),
N (w) = {v1 , v2 , . . . , vn } y
vi uj ∈ A(G) ⇔ ui uj ∈ A(G 0 ).
Es fácil convencerse que ω(G) = 2. Tomemos una buena coloración c de G 0 con los k − 1
colores {1, 2, . . . , k−1} y extendamos ésta a G poniendo c(w) = k y para cada i, c(vi ) = c(ui ).
Es claro que ésta es una buena coloración para G.
56
Ahora supongamos que c es una coloración propia para G con colores en [k − 1]. A partir
de c construyamos una coloración propia c0 de G0 en [k − 2]. Sin pérdida de generalidad,
c(w) = k − 1 y entonces para toda i, c(vi ) 6= k − 1. Definamos
c(ui ), si c(ui ) 6= k − 1,
0
c (ui ) =
c(vi ), si c(ui ) = k − 1.
Veamos que es buena coloración. Supongamos que ui uj ∈ A(G 0 ) y que c0 (ui ) = c0 (uj );
entonces ui uj ∈ A(G) ası́ es que no es posible que c(ui ) = c(uj ) y entonces exactamente uno
de c(ui ) es k − 1. Supongamos que c(ui ) 6= k − 1 y que c(uj ) = k − 1; entonces c0 (uj ) = c(vj ),
pero esto también es imposible porque ui vj ∈ A(G). ♦
El número cromático de una superficie S, χ(S), es el menor número de colores
necesario para pintar cualquier gráfica que tenga inmersión en S. Como vimos en la sección
10, el número cromático de la esfera es 4. El teorema de Heawood establece que el número
cromático de una superficie Sg de género g es
√
7 + 1 + 48g
.
χ(Sg ) =
2
Probaremos a continuación este resultado para g = 1.
12.17 Teorema. Teorema de Heawood. El número cromático del toro T es 7.
Demostración. Como el género de K7 es 1, entonces χ(T ) ≥ χ(K7 ) = 7. Por otro lado,
tomemos una gráfica G que tenga un encaje en el toro y sea H una subgráfica de G tal que
δ(H) = d sea maximal. Bastará probar que d ≤ 6 pues entonces, usando 12.11, tendremos
χ(G) ≤ d + 1 = 7. Sea V = |V(H)| y sea A = |A(H)|. Tenemos que γ(H) ≤ γ(G) ≤ 1, de
donde, por 11.9, 1 ≥ 1 + A6 − V2 y ası́ A ≤ 3V . Entonces
X
Vd≤
δH (v) = 2A ≤ 6V
v∈V(H)
y obtenemos d ≤ 6, como querı́amos. ♦
Para t ∈ N ∪ {0} y G gráfica con los vértices numerados, el polinomio cromático, fG (t)
cuenta el número de coloraciones propias de G con t colores.
12.18 Ejemplo. (a) Si t < χ(G) entonces fG (t) = 0 y χ(G) = min{t : fG (t) 6= 0}.
t!
(b) Si t ≥ n entonces fKn (t) = nt n! = (t−n)!
.
(c) Si t ≥ 2 y n ≥ 1 entonces fTn (t) = t(t − 1)n .
(d) Si G es árbol con A aristas, entonces fG (t) = t(t − 1)A .
(e) Si G tiene n vértices y no tiene aristas entonces fG (t) = tn .
57
La siguiente proposición nos permite calcular los valores del polinomio cromático recursivamente (reduciendo a gráficas con menos aristas), haciendo notar que al contraer una arista
es posible que queden aristas múltiples pero éstas se pueden eliminar pues no se afecta la
cuenta de la coloración.
12.19 Proposición. Si a ∈ A(G) entonces
fG (t) = fG−a (t) − fG/a (t).
Demostración. fG−a (t) cuenta las coloraciones de los vértices de G en las que todos los
vértices están bien coloreados salvo, tal vez, los vértices que forman a, ası́ que hay que restar
las coloraciones con los vértices de a del mismo color y éstas son fG/a (t). ♦
También es útil la versión de 12.19 siguiente.
12.20 Corolario. Si a ∈ A(G) y H es subgráfica de G entonces
fH (t) = fH+a (t) + f(H+a)/a (t). ♦
12.21 Ejemplo. Sea G la gráfica del dibujo con a la arista marcada.
.....
•..............................
......•
....... ....
.......
.......
...
...
.......
.......
...
...
.......
.......
...
...
.......
.......
....... ..............
...
...
.
...........
...
...
.
.
.
.
.
.
.
.
.......
...
...
.....
.
.
.
.
.
.
.
.
.
.
.......
...
...
.....
.
.
.
.
.
.
.
.
.
.
.......
...
...
.....
.
.
.
.
.
.
.
.
.
.
.......
..
...
....
.
.
.
.
.
.
.
.
.
.
.
.
... .......
....... ....
.....
.....
•
•
a
•
Usamos 12.19 para reducir el cálculo de fG (t) al de árboles:
fG (t) = fG−a (t) − fG/a (t) = (fK1,4 (t) − fK1,3 (t)) − (fK1,3 (t) − fT2 (t)).
12.22 Ejemplo. Ahora usamos 12.20 para reducir el cálculo de un polinomio cromático
al polinomio cromático de gráficas completas. Sea G = K5 − 2K2 la gráfica que se obtiene de
quitar dos aristas no adyacentes a y b a K5 . En varios pasos eliminamos aristas múltiples:
fK5 −2K2 (t) = fK5 −b (t) + f(K5 −b)/a (t)
= (fK5 (t) + fK5 /b (t)) + fK4 −b (t)
= (fK5 (t) + fK4 (t)) + (fK4 (t) + fK3 (t)).
12.23 Observación. Si G1 , G2 , . . . , Gk son las componentes conexas de G entonces
Y
fG (t) =
fGi (t).
i
58
12.24 Proposición. Para toda G, fG (t) es un polinomio en t.
Demostración. El resultado es claro haciendo inducción sobre |A|. ♦
12.25 Proposición. Sea G una gráfica con n vértices, m aristas y k componentes. Entonces el polinomio fG (t) cumple:
(a) Su grado es n.
(b) El coeficiente principal es 1.
(c) Si G es conexa, entonces los coeficientes de fG (t) alternan los signos.
(d) Si G es conexa, entonces el coeficiente del término lineal es distinto de 0.
(e) El término constante es 0.
(f) La potencia de t con menor coeficiente distinto de 0 es tk .
(g) Si m > 0 entonces la suma de los coeficientes es 0.
(h) El coeficiente de tn−1 es −m.
Demostración. (a), (b), (c) y (d). Para (a) y (b), por 12.23 podemos suponer que G es
conexa. Hacemos inducción sobre m. Para m = n − 1 tenemos un árbol y ya sabemos que
fG (t) = t(t − 1)n−1 . Supongamos que m ≥ n y sea a una arista de G en un ciclo. Por 12.19,
fG (t) = fG−a (t) − fG/a (t). Como G − a tiene n vértices, G/a tiene n − 1 vértices y ambas son
conexas con m − 1 aristas; al aplicar la hipótesis de inducción tenemos el resultado.
(e) El término constante es fG (0).
(f) Esto es consecuencia de (d), (e) y de 12.23.
(g) La suma de los coeficientes es fG (1) y este valor es 0 si hay por lo menos una arista.
(h) Hacemos inducción sobre m. Si m = 0 entonces fG (t) = tn . Supongamos que m > 0.
Por 12.19, fG (t) = fG−a (t) − fG/a (t). Aplicamos hipótesis de inducción, (a) y (b), y tenemos
fG−a (t) = tn − (m − 1)tn−1 + . . . y fG/a (t) = tn−1 + . . ., ası́ que fG (t) = tn − (m)tn−1 + . . .. ♦
12.26 Corolario. Una gráfica G con n vértices es un árbol si, y sólo si fG (t) = t(t −
1) . ♦
n−1
Una coloración de aristas de G es una función c : A(G) → C, donde C es un conjunto
de colores. La coloración es propia si aristas adyacentes tienen distinto color. El ı́ndice
cromático o número cromático por aristas de G, χ1 (G), es el menor número de colores
con los cuales se puede dar una coloración propia de aristas.
59
12.27 Ejemplo. (a) χ1 (C2n ) = 2.
(b) χ1 (C2n+1 ) = 3.
(c) χ1 (Tn ) = 2 para n ≥ 2.
(d) χ1 (Km,n ) = max{m, n}. (Para ver esto, digamos que m ≤ n, que los colores son
1, 2, . . . , m y que los vértices de la parte que tiene m vértices son u1 , u2 , . . . , um y los otros
son v1 , v2 , . . . , vn ; coloreamos la arista ui vj con el color (i−1)+(j −1), donde esta numeración
se reduce módulo n.)
12.28 Observación. χ1 (G) ≥ ∆(G).
12.29 Observación. χ(L(G)) = χ1 (G).
12.30 Teorema. Teorema de Vizing. χ1 (G) ≤ ∆(G) + 1.
Demostración. Supongamos falso el resultado y tomemos gráfica G con número mı́nimo
de aristas tal que χ1 (G) ≥ ∆(G) + 2. Sea u un vértice de grado ∆ = ∆(G) y sea a = uv arista
de G. Por construcción de G, como ∆(G − a) ≤ ∆, coloreemos las aristas de G − a con ∆ + 1
colores. En esta coloración, digamos que las aristas de w0 = v no usan el color c0 . Observemos
que alguna arista de u debe usar ese color, pues de lo contrario podrı́amos colorear a con c0
obteniendo una buena coloración en aristas para G con ∆ + 1 colores. Digamos que la arista
uw1 usa el color c0 pero que ninguna arista de w1 usa el color c1 . Otra vez, seguro hay otra
arista de u que usa c1 , si no, se podrı́a cambiar el color de uw1 a que fuera c1 y pintar a
con c0 . Continuamos ası́ mientras podamos considerar vértices distintos v = w0 , w1 , . . . , wk
adyacentes a u de tal manera que para cada 1 ≤ j ≤ k la arista uwj es de color cj−1 , un
color (distinto de los anteriores) no usado por ninguna arista incidente a wj−1 y un color ck ,
no usado por ninguna arista de uwk , es distinto de los demás ci .
60
Observemos que k < ∆ − 1, pues si k = ∆ − 1 (es decir, ya se consideraron todos los
vértices adyacentes a u y todos los colores ci son distintos) entonces se podrı́a dar a la arista
uv el color c0 y repintar cada arista uwi con el color ci , lo cual darı́a una buena coloración
en aristas para G lo cual es contrario a lo que estamos suponiendo.
Entonces tenemos que ck = ci para cierta i < k. Tomemos un color c no usado por
ninguna de las aristas incidentes a u y observemos que alguna de las aristas de wi usa el
color c pues si no se podrı́a repintar uwi+1 con c y esto nos evitarı́a repeticiones. De la misma
manera, alguna de las aristas de wk usa el color c.
61
Sea T una trayectoria de longitud máxima que empieza en wk y que alterna los colores c
y ci , y sea x su extremo final. Observemos los distintos casos para x, notando que x 6= wi+1
pues uwi+1 tiene color ci , ası́ que más bien el extremo final de T serı́a u.
Caso (1). Si x 6= u y x 6= wi entonces podemos intercambiar los colores de la trayectoria
(c por ci y viceversa), logrando que wk no use c, que sigue siendo un color no usado por
ninguna arista incidente a u y ya vimos que eso no es posible.
Caso (2). Supongamos x = u. Observemos que el penúltimo vértice de T es wi+1 y que
la arista uwi+1 tiene el color ci . En este caso logramos una buena coloración para las aristas
de G intercambiando los colores de T , dando a uwj el color cj para cada j < i + 1, a uwi+1
el color c y a cada wj , con j > i + 1, el color que ya tenı́a. Ası́ tenemos que este caso es
imposible.
62
Caso (3). Finalmente supongamos que x = wi . En este caso, la última arista de T es de
color c. También en este caso intercambianos los colores de T , damos a uv el color c0 , a uwi
el color c, a uwj el color cj para cada j < i y a cada wj , con j > i, el color que ya tenı́a. Esto
produce una buena coloración para las aristas de G contradiciendo nuestra suposición. ♦
Una gráfica G es de tipo I si χ1 (G) = ∆(G); es de tipo II si χ1 (G) = ∆(G)+1. Determinar
si una determinada gráfica es de tipo I o de tipo II es problema NP-completo.
63
12.31 Proposición. K2n+1 es de tipo II.
Demostración. Supongamos que χ1 (K2n+1 ) = ∆(K2n+1 ) = 2n. Entonces cada vértice
tiene exactamente una arista de cada color, pero esto es imposible porque entonces en la
gráfica de cualquiera de los colores la suma de los grados de los vértices es 2n + 1, ası́ que
este número no puede ser el doble de aristas de ese color. ♦
Más adelante veremos que K2n es de tipo I.
Una coloración propia de vértices y aristas para G es una función de A(G) ∪ V(G)
en un conjunto de colores tal que vértices adyacentes, aristas adyacentes y aristas incidentes
a vértices tienen distinto color. Al mı́nimo número de colores necesario se le llama número
cromático total y se le denota por χ2 (G).
12.32 Observación. χ2 (G) ≥ ∆(G) + 1.
12.33 Ejemplo. (a) χ2 (K3 ) = 3.
(b) χ2 (C4 ) = 4.
(c) χ2 (Cn ) = 3 si n es múltiplo de 3 y es 4 si no.
12.34 Ejercicio. Probar que fCn (t) = (t − 1)n + (−1)n (t − 1).
12.35 Ejercicio. Encontrar una gráfica G con 15 vértices tal que χ(G) = 4 y ω(G) = 2.
12.36 Ejercicio. En cada inciso encontrar una gráfica con n ≥ 5 vértices que cumpla el
enunciado del inciso:
√
(a) χ(G) + χ(G) = 2 n.
(b) χ(G)χ(G) = n.
(c) χ(G)χ(G) =
(n+1)2
.
4
12.37 Ejercicio. Probar que si G es regular y χ(G) + χ(G) = n + 1, con n = |V(G)|,
entonces G es Kn , Kn o C5 .
12.38 Ejercicio. Determinar el número cromático y el ı́ndice cromático de cada uno de
los sólidos platónicos.
12.39 Ejercicio. Probar que toda gráfica regular no vacı́a de orden impar es de tipo II.
12.40 Ejercicio. Probar que toda gráfica regular cúbica (es decir, 3-regular) hamiltoniana es de tipo I.
64
12.41 Ejercicio. Probar que si G es cúbica y tiene al menos un puente, entonces su
ı́ndice cromático es 4.
12.42 Ejercicio. Hay doce duendes viviendo en el bosque, cada uno de ellos en su propia
casa que puede ser azul o roja. En el i-ésimo mes del año, el i-ésimo duende visita a sus amigos
y si encuentra que la mayorı́a de ellos tiene su casa de diferente color a la suya, entonces se
les une y cambia de color su casa. Probar que llegará un momento (tal vez después de varios
años) en que ningún duende tenga que volver a repintar su casa. (La amistad de los duendes
es mutua y no cambia a través del tiempo.)
12.43 Ejercicio. Sea G una gráfica con a lo más r ciclos impares. Probar que χ(G) ≤
r + 2.
12.44 Ejercicio. Sea G la gráfica cuyos vértices son los enteros del 2 al 100 y dos vértices
son adyacentes si, y sólo si, tienen un factor común y no coinciden en el dı́gito de las unidades.
Determinar el número cromático de G. ¿Es G conexa?
65
13.
Teorı́a extrema de gráficas
Analizaremos ahora el siguiente problema:
¿Cuántos vértices n o cuántas aristas m se necesitan para poder asegurar que una gráfica G con n vértices o m aristas tenga determinada
propiedad?
Ya hemos visto varias propiedades de este estilo, como recordamos en el siguiente ejemplo.
13.1 Ejemplo. (a) De 1.17 sabemos que si G tiene al menos n aristas, entonces existe
un ciclo en G.
2
(b) De 1.28 tenemos que una gráfica con m > n2 aristas seguro tiene un triángulo.
(c) De 9.9 sabemos que si m > 3n − 6 entonces la gráfica no es plana.
(d) De 1.12 sabemos que si m > n−1
entonces G debe ser conexa.
2
Empezaremos generalizando 13.1(b). Ahı́ se tiene una cota justa: el máximo número de
aristas que puede tener una gráfica sin triángulos se alcanza en la gráfica bipartita en la que
las cardinalidades de los conjuntos de la partición difieren a lo más en 1:
K b n c ,d n e .
2
2
El contenido de la proposición que demostraremos habla de gráficas multipartitas. Decimos
que una gráfica multipartita es casi regular si cualesquiera dos subconjuntos de la partición
tienen cardinalidad con diferencia de 1 a lo más. Denotamos por T (n, s) la gráfica s-partita
completa casi regular con n vértices; su número de aristas, t(n, s), se llama número de
Turán.
13.2 Observación. (a) Si n = sq + r, con q y r enteros tales que 0 ≤ r < s, entonces
en la partición en conjuntos de vértices de T (n, s) hay s − r conjuntos con q vértices y r
conjuntos con q + 1 vértices, y de aquı́ que
n
q
q+1
t(n, s) =
− (s − r)
−r
.
2
2
2
(b) Si G es s-partita completa entonces ω(G) = s pero que si se le agrega una arista a
entonces ω(G + a) = s + 1.
13.3 Teorema. Teorema de Turán. Sean n ≥ 2 y s ≥ 1 naturales con n > s.
(a) El máximo número de aristas m que puede tener una gráfica con n vértices que no
contenga Ks+1 como subgráfica es t(n, s).
(b) Si G tiene orden n y tamaño maximal sin subgráficas isomorfas a Ks+1 , entonces G es
T (n, s).
66
Demostración. Probemos, por inducción sobre s que si ω(G) ≤ s y G tiene n vértices y
m aristas entonces existe una gráfica s-partita G 0 con n vértices y tal que |A(G 0 )| ≥ m.
Para s = 1 se tiene que G no tiene aristas ası́ que tomamos G 0 = G, que es 1-partita.
Sea s ≥ 1. Sin pérdida de generalidad supongamos que G tiene tamaño maximal m entre
todas las gráficas de orden n que no tienen un clan de orden s + 1. Sea u un vértice de G de
grado máximo ∆ y sea H la gráfica inducida por N (u). Entonces ω(H) ≤ s − 1 (pues si H
tuviera un clan con s vértices entonces u junto con ese clan serı́a un clan de orden s + 1). Por
hipótesis de inducción existe una gráfica s-partita H0 de orden ∆ tal que |A(H0 )| ≥ |A(H)|.
Sea G 0 = Kn−∆ + H 0 (es decir, agregamos a H 0 el número de vértices que le faltan para llegar
a n y ponemos todas las aristas posibles de esos vértices a los vértices de H0 ). Entonces G 0
es (s + 1)-partita y
|A(G0 )| = |A(H)| + |V(H)|(n − ∆) ≥ |A(G)|,
donde la última desigualdad es porque en la construcción de G 0 se sustituyeron los vértices
de G fuera de H por la misma cantidad de vértices pero poniendo a cada uno de esos vértices
grado mayor o igual al que tenı́an los que se quitaron.
Ahora, por 13.2 sabemos existe una gráfica s-partita con n vértices, t(n, s) aristas y
número de clan s (a saber, T (n, s)) ası́ que, por lo que acabamos de probar, existe una
gráfica s-partita G que tiene número de aristas mayor o igual que t(n, s), y tal que ω(G) = s
pero si se le agrega una arista a entonces ω(G + a) > s. Por último supongamos que las
cantidades de elementos de dos de los s conjuntos que determinan la s-partición de V(G)
difieren en más de un elemento; digamos que uno tiene k vértices y otro k − l, con l ≥ 2,
entonces el número de aristas entre ellos (cuya cuenta no afecta
el resto de la cuenta de
2k−l
·
. De aquı́ concluimos
las aristas) es k(k − l) que sabemos que es menor que 2k−l
2
2
entonces que G es T (n, s). ♦
13.4 Ejemplo. (a) t(4, 2) = 2 · 2 = 4 y la gráfica con 4 vértices y máximo número de
aristas que no tiene triángulo es T (4, 2) = C4 .
(b) La gráfica con 6 vértices y máximo número de aristas que no contiene a K4 es el
octaedro (en otras palabras, K6 − a − b − c donde a, b, c son aristas no adyacentes dos a dos)
pues aquı́ n = 6, s = 3, q = 2, r = 0 y t(6, 3) = 62 − 22 3 = 12.
13.5 Ejercicio. Probar que si G tiene n vértices y la suma de grados de dos vértices
es mayor o igual que n + 2, entonces G tiene ciclo de longitud 4. Probar también que no se
puede debilitar la hipótesis a que la suma de grados sea mayor o igual que n + 1.
Los siguientes resultados son parte de la llamada Teorı́a de Ramsey. La pregunta
general es:
Dadas dos gráficas G1 y G2 , ¿existe un natural mı́nimo r(G1 , G2 ) con el
que se que se pueda asegurar que dada una gráfica con r(G1 , G2 ) vérti67
ces ella contiene como subgráfica a G1 o su complemento G contiene
como subgráfica a G2 ?
La versión coloreada del mismo problema es:
Dadas dos gráficas G1 y G2 cómo debe ser n para que se pueda asegurar
que si se colorean las aristas de la gráfica completa Kn usando los
colores rojo y azul se pueda asegurar que la gráfica roja contiene a G1
como subgráfica o la gráfica azul contiene a G2 como subgráfica.
Empecemos analizando un ejemplo simple de esto.
13.6 Proposición. En cualquier grupo de 6 personas forzosamente hay 3 que se conocen
todas entre sı́ o tres que no se conocen entre sı́, pero existen grupos de 5 personas en las que
no hay tres que se conozcan entre sı́ ni tampoco tres que no se conozcan entre sı́.
Demostración. El problema equivale a probar que si en K6 algunas aristas se pintan de
rojo y el resto se pintan de azul entonces forzosamente habrá un triángulo cuyas aristas son
del mismo color, pero que esto no pasa en K5 . Fijémonos en uno de los vértices de K6 ; de
ahı́ salen 5 aristas ası́ que hay al menos tres del mismo color.
•
.......
... ..........
... .... .............
...
...
.......
.
.
.......
...
.
.......
...
...
.......
...
...
.......
...
.
.
.
.
.......
...
..
.
.......
.
.
....... .... ....
......
..
.
.
.
.
.
.
.
... ....
..
..
.
.
.... .... ............
.
.
.
...
.... .... .......
..
.
.
.
.
.
.
.......
..
...
.
.
.
.
.
.... .... .... ...
..
...
.... .... .... ....
....
... .... .... ....
... ... ....
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
... ....
.............. .... .... .
•
•
•
Si entre los extremos de éstas hay una lı́nea de ese mismo color, tenemos el triángulo buscado;
si no, entonces las tres son del otro color y ése es el triángulo que querı́amos.
Para ver que el resultado es falso en K5 consideremos la siguiente coloración de sus aristas
•
...........
....... ........
...... .. . ......
...... ... ... ...........
.
.
.
.
......
. ..
......
......
.
...
.....
..
......
......
......
...
......
...
......
.....
.
.
.
...
.
.
.
.
........... .... .... .... .... ........... .... .... ..... .... .... .... .... .............
...
...... .
.
.. ..
... ... ..
. .. ...
.
.
.
.
.
.
.
.
..
... .. ..
....
.. . ...
...
...
... . ....
....
..
..
...
..
.. ....
...... ....
.
.
...
.
.
...
..
.... ... ....
...
...
..
...
..
... ....
...... .
... ...
.... ... ....
.
... ...
.... ... ....
... . .... ....
.... . ..
..... ....
...........................................................................
•
•
•
•
en la que no hay triángulo de ninguno de los dos colores. ♦
Consideremos ahora un problema más general que el del ejemplo:
¿Cómo debe ser n para que si pintamos las aristas de la gráfica completa de n vértices con rojo y azul se pueda asegurar que se forma una
68
gráfica completa de k vértices roja o una gráfica completa de l vértices
azul?
De la siguiente proposición inductiva tenemos que un tal n siempre existe. Al menor de
ellos se le denota por r(k, l). Observemos que 13.6 demuestra que r(3, 3) = 6.
Antes de demostrar la existencia de r(k, l) hagamos un ejemplo para ilustrar que el papel
de los colores no es simétrico.
13.7 Ejemplo. La figura siguiente, en la que sólo se pusieron las aristas de color rojo,
prueba que se pueden colorear las aristas de K8 de rojo y azul de manera que no haya ningún
triángulo rojo ni ningún K4 azul.
............................
..........
.......... •
...
..........
..........
..........
...
......
.•
•
..........
.
...
..... ..
.
..... ...
... .....
..
.
...
.....
.
..
.....
.....
...
...
..
.....
.....
...
.
...
.....
.....
...
..... .... ........
...
...
..... .. .....
..
.
....... .....
..
..
.
.
.
.....................................................................................................................
...
... ... .......
.
..
.
.
.
...
..
... ... .......
.
.
.
.
.
...
.
.....
...
.....
...
...
....
.....
.....
...
.....
...
...
.....
... .........
...
..... ....
... ......
.
.
.
.
.
.
.
.......
........
..
....
..........
..........
..........
.......... .... ...................
.................
•
•
•
•
•
♦
En el ejemplo necesariamente hay triángulo azul pues r(3, 3) = 6. El ejemplo prueba
además que r(3, 4) > 8.
13.8 Proposición. Dados k, l naturales, r(k, l) existe y se tiene que
r(k, l) ≤ r(k − 1, l) + r(k, l − 1).
Demostración. La demostración de la existencia se basa en probar la desigualdad del
enunciado y hacer un razonamiento recursivo. Convengamos en que r(1, l) = 1 = r(k, 1).
Observemos también que r(2, k) = k (y que r(l, 2) = l). Ahora probaremos que
r(k, l) ≤ r(k − 1, l) + r(k, l − 1),
para k, l ≥ 2. Es claro que la fórmula es válida para k = 2 o l = 2. Para ver que también es
válida en general, sean k, l ≥ 3 y supongamos que r(k − 1, l) y r(k, l − 1) existen. Probaremos
que una gráfica con r(k −1, l)+r(k, l−1) vértices tiene un Kk rojo o un Kl azul. Para esto sea
u un vértice cualquiera; este vértice tiene grado r(k − 1, l) + r(k, l − 1) − 1; entonces tiene al
menos r(k−1, l) aristas rojas o r(k, l−1) aristas azules (si no, para el número r de aristas rojas
y a el de azules se tendrı́a que el número de aristas r +a ≤ (r(k −1, l)−1)+(r(k, l −1)−1) =
r(k − 1, l) + r(k, l − 1) − 2, lo cual es una contradicción). Sin pérdida de generalidad hay al
menos r(k − 1, l) aristas rojas. Los extremos de éstas forman una gráfica completa que tiene
un Kk−1 con todas las aristas rojas o un Kl con todas las aristas azules; en el primer caso, al
agregar u se tiene un Kk con todas las aristas rojas; en el segundo ya se tiene el Kl buscado
con todas las aristas azules. ♦
El número obtenido en la fórmula de la proposición anterior puede ser estrictamente
69
menor. En efecto, según la fórmula
r(3, 4) ≤ r(2, 4) + r(3, 3) = 4 + 6 = 10;
sin embargo, veamos que r(3, 4) = 9.
13.9 Proposición. r(3, 4) = 9.
Demostración. De 13.7 ya sabemos que r(3, 4) > 8. Supongamos que tenemos pintadas
las aristas de K9 con rojo o azul y que no hay un K3 rojo ni un K4 azul. De cada vértice
salen 8 aristas exactamente; afirmamos que 3 de ellas son rojas y 5 son azules. Supongamos
que algún vértice v no tiene tres aristas rojas; entonces tendrı́a al menos 6 aristas azules y
en los otros extremos de esas aristas habrı́a un K6 , ası́ que se formarı́a ahı́ un triángulo rojo
o uno azul; por nuestra suposición deberı́a ser azul, pero entonces, con v se formarı́a un K4
azul, lo cual es una contradicción. Análogamente, si algún vértice no tuviera 5 aristas azules
(al menos) entonces tendrı́a 4 aristas rojas, como estamos suponiendo que no hay triángulo
rojo, entre los otros extremos todas las aristas serı́an azules, pero entonces eso serı́a un K4
azul, lo cual es también una contradicción. La única posibilidad es, como dijimos arriba,
que en cada vértice haya 3 aristas rojas y 5 azules; sin embargo esto también es un absurdo
.♦
porque son 9 vértices, y el número de aristas rojas serı́a 9×3
2
En la proposición anterior realmente sólo se usó que r(2, 4) y r(3, 3) son pares ası́ que
podemos generalizar al siguiente corolario.
13.10 Corolario. Si r(k − 1, l) y r(k, l − 1) son pares entonces la desigualdad de 13.8
es estricta. ♦
El cálculo de los r(k, l) ha resultado ser muy difı́cil y sólo se conocen los siguientes valores
(para k ≤ l):
k/l 1 2 3 4 5 6 7 8 9
1 1 1 1 1 1 1 1 1 1
2
2 3 4 5 6 7 8 9
3
6 9 14 18 23 28 36
4
18 25
Veamos algunas cotas para r(k, l).
13.11 Proposición. Para k, l ≥ 2, se tiene que r(k, l) ≤
k+l−2
k−1
.
Demostración. Hagamos inducción sobre
k + l. El caso k + l = 4 es claro pues la única
2
posibilidad es k = l = 2, r(k, l) = 2 = 1 . Tomemos k y l con k + l > 4. Usamos 13.8, la
hipótesis de inducción y la fórmula de Pascal para obtener
k+l−3
k+l−3
k+l−2
r(k, l) ≤ r(k − 1, l) + r(k, l − 1) ≤
+
=
,
k−2
k−1
k−1
70
como querı́amos. ♦
Ahora encontraremos una cota superior para cuando k = l.
k
13.12 Proposición. Para todo k ≥ 3 se tiene que r(k, k) > 2 2 .
k
Demostración. Queremos probar que si n ≤ 2 2 entonces existe una coloración (con dos
colores) para las aristas de Kn de manera que ninguna subgráfica de k vértices es monocromática.
Sea Ω el conjunto de todas coloraciones para Kn en las que las aristas están coloreadas
n
con dos colores (ası́ |Ω| = 2( 2 ) ). Analizaremos el número de elementos del conjunto de
coloraciones que producen alguna Kk monocromática para ver que no es todo Ω, y esto
terminará la prueba.
Dado S subconjunto de [n] con k elementos sea XS el subconjunto de Ω que consta de
las coloraciones monocromáticas para las subgráficas con vértices en S. Entonces
n
k
|XS | = 2 · 2( 2 )−(2)
pues hay dos gráficas monocromáticas con los vértices en S y las n2 S− k2 aristas restantes
pueden estar coloreadas con cualquiera de los dos colores. Sea X = S XS . Entonces
|X| ≤
X
S
n
|XS | = 2
·
k
n
n
nk 2( 2 )
2( 2 )
≤2
.
k
k! 2 k22−k
2(2)
k
Ahora, por hipótesis, n ≤ 2 2 ası́ que, sustituyendo, tenemos
|X| ≤
2
k+2
2
k!
n
2( 2 ) .
k+2
Por último, como k ≥ 3, es fácil probar por inducción que 2 2 < k! de donde obtenemos
n
que |X| < 2( 2 ) y esto nos dice que X no puede ser todo Ω, como querı́amos probar. ♦
13.13 Ejercicio. Sean m, n ≥ 2. Si n2 < 2m entonces es posible construir una matriz de
n × n formada por 00 s y 10 s y que no tenga ninguna submatriz (es decir, matriz obtenida de
quitar algunas columnas y algunos renglones de la matriz) de tamaño m × m formada sólo
por 00 s o sólo por 10 s. (Nótese que esto es equivalente a probar que se pueden colorear las
aristas de Kn,n con dos colores de manera que no se forme ninguna subgráfica monocromática
Km,m .)
13.14 Ejercicio. Probar que para k ≥ 2, se tiene que r(k, k) ≤ 4k−1 .
Un conjunto de vértices S es independiente si para cualesquiera u, v ∈ S se tiene que
u y v no son adyacentes. El número de independencia de G, denotado por α(G), es el
número máximo de vértices independientes de G.
71
13.15 Ejemplo. (a) α(Kn ) = 1.
(b) α(C2n ) = α(C2n+1 ) = n.
(c) α(P) = 4 pues los vértices marcados con 2, 5, 8 y 9 en la figura forman un conjunto
independiente y no es posible encontrar 5 vértices independientes pues 3 de ellos estarı́an en
el mismo pentágono: (1, 2, 3, 4, 5, 1) o (6, 8, 10, 7, 9, 6).
1
............
...•
..... .... ..........
.
.
.
.
.
.
.
......
.
......
......
....
.....
......
...
.....
......
......
...
......
.....
.
.
......
.
.
.
.
.
......
....
.
.
.
.
.
.
......
...
....
.
.
.
......
.
.
.
. ....
......
....
.
.
.
.
.
.
......
. ...
....
.
.
.
.
.....
.
.
. ....
..............
.
.
.......
...
.
... ............
......... ....
.
.
.
.
.
.
...
.........
...
.
......
.
.
.
.
.
.
.
.
.
.
.
...
.
.
.
.
.......................................................................................
...
.
......
...
...
...
...
..
......
... ..........
..
...
...... ....
..
... ......
.
...
........
.
......
...
.......
...
.......
...
...
... ........... ........... ....
...
..
.
..
..
...
..
.. ................... ....
.
.
.
.
...... ...
...
..
...... ..
... ........
...
...
.........
...
...
..........
.....
..
.....
...
...
..
...
...
.
.
.
.
.
.
...
...
...
...
...
...
...
... ...
... .....
... ...
... ...
.
........................................................................................................
•6
5•
10
•
•
7
9•
•2
8•
•
4
•
3
13.16 Lema. χ(G) ≤ |V(G)| − α(G) + 1.
Demostración. Se puede obtener una coloración propia para los vértices de G dando a
todos los vértices de un conjunto independiente máximo el mismo color (y un color diferente
a cada uno de los restantes). ♦
13.17 Lema. |V(G)| ≤ α(G)χ(G).
Demostración. Sea k = χ(G) y sean C1 , C2 , . . . , Ck las clases cromáticas de G definidas
por una buena coloración. Observemos que cada Ci es un conjunto independiente ası́ que
para toda i se tiene que |Ci | ≤ α(G). Entonces
X
|V(G)| =
|Ci | ≤ kα(G). ♦
i
13.18 Observación. α(G) = ω(G).
Recordemos los dos resultados siguientes, los cuales usaremos en la demostración de la
siguiente proposición, además de los lemas anteriores:
1.25 dice que si δ(G) ≥ k entonces G tiene como subgráfica a todo árbol con k +1 vértices.
12.8 dice que si G es tal que χ(G −v) < χ(G) para todo v vértice entonces δ(G) ≥ χ(G)−1.
13.19 Proposición. Si G es árbol con k vértices entonces el menor número n = r(G, Kl )
con el que se puede asegurar que si se pintan las aristas de Kn usando los colores rojo y azul
entonces se puede garantizar que la gráfica roja contiene a G o la gráfica azul contiene a Kl
72
es
r(G, Kl ) = 1 + (k − 1)(l − 1).
Demostración. Tomemos la gráfica completa H con n = 1 + (k − 1)(l − 1) vértices y sus
aristas coloreadas con alguno de los colores rojo o azul. Llamemos Hr a la gráfica que tiene
los mismos vértices de H pero sus aristas son las que se pintaron de rojo en H. De manera
análoga consideramos Ha (que es la gráfica complementaria de Hr ). Supongamos que Ha
no contiene a Kl . Probaremos que Hr tiene grado mı́nimo mayor o igual que k − 1 y esto
concluirá la demostración gracias a 1.25.
Tenemos que ω(Ha ) ≤ l − 1. Por 13.18 α(Hr ) ≤ l − 1. Ahora, por 13.17
1 + (k − 1)(l − 1) ≤ α(Hr )χ(Hr ) ≤ (l − 1)χ(Hr ),
de donde
1
+ (k − 1) ≤ χ(Hr ),
l−1
ası́ que χ(Hr ) ≥ k. Sea Hr∗ subgráfica inducida de Hr tal que χ(Hr∗ ) = χ(Hr ) pero χ(Hr∗ −
v) < χ(Hr ) para todo vértice v. Entonces, usando 12.8 tenemos que δ(Hr∗ ) ≥ χ(Hr∗ ) − 1 =
χ(Hr ) − 1 ≥ k − 1 y de aquı́ que, por 1.25, Hr∗ contiene a G, pero Hr∗ es subgráfica de Hr ,
ası́ que Hr también contiene a G.
Por último veamos que existe una coloración de las aristas de la gráfica completa con
(k − 1)(l − 1) vértices en la que la gráfica roja no contiene a G y la gráfica azul no contiene
a Kl . Sea n0 = (k − 1)(l − 1). En Kn0 escojamos l − 1 copias ajenas de Kk−1 y pintemos las
aristas dentro de cada una de esas copias de rojo; pintemos el resto de las aristas de Kn0 de
azul. Como en la gráfica roja cada componente tiene k − 1 vértices, la gráfica roja no puede
contener un árbol con k vértices. Además el número de independencia de la gráfica roja es
l − 1 ası́ que la gráfica azul (que es complementaria de la roja) tiene número de clan l − 1,
es decir, no contiene a Kl . ♦
Hemos visto que hay distintas interpretaciones y aplicaciones de la Teorı́a de Ramsey.
Hemos buscado subgráficas completas de un determinado color o gráficas monocromáticas
iguales a una gráfica especı́fica. Incluso puede hacerse un juego en el que haya una gráfica
dibujada y cada persona tenga un lápiz de un color determinado y que en su turno coloree
con su lápiz una arista de la gráfica; la primera persona que obtenga la gráfica buscada
con su color gana. También uno puede buscar condiciones mı́nimas de la gráfica inicial para
asegurar que en algún momento alguno de los jugadores debe obtener la gráfica buscada.
Otras generalizaciones son las siguientes:
Generalización 1: t colores. Se habla de los números r(k1 , k2 , . . . , kt ).
13.20 Proposición. r(3, 3, 3) ≤ 17.
Demostración. Tomamos una gráfica completa con 17 vértices en que las aristas están
pintadas usando los colores rojo, azul y verde. Nos fijamos en un vértice u. Como a él llegan
73
16 aristas y 5 × 3 = 15 < 16, uno de los colores, digamos el rojo, aparece (al menos) en 6
aristas. Los otros extremos de esas aristas forman un K6 ; si alguna de las aristas entre ellos
es roja, ya encontramos el triángulo buscado; si no, entonces el K6 está pintado con sólo dos
colores y po 13.6 hay triángulo verde o azul. ♦
13.21 Proposición.
r(3, 3, . . . , 3) ≤ nt ,
| {z }
t
donde nt está definido por
nt = 1 +
t!
t!
t!
t!
+ + + ··· + .
0! 1! 2!
t!
Demostración. La demostración es semejante a la de la proposición anterior. Procedemos
2!
+ 1!
+ 2!
= 1 + 2 + 2 + 1 = 6, ası́ que el
por inducción sobre t. Tenemos que n2 = 1 + 2!
0!
2!
resultado es válido para t = 2. Supongamos que es cierto para cierta t ≥ 2 y tomemos una
gráfica completa con nt+1 vértices. Tenemos que
(t + 1)! (t + 1)! (t + 1)!
(t + 1)!
+
+
+ ··· +
0!
1!
2!
(t + 1)!
= 1 + (t + 1)(nt − 1) + 1 = 2 + (t + 1)(nt − 1).
nt+1 = 1 +
Tomemos un vértice u cualquiera; su grado es nt+1 − 1 = 1 + (t + 1)(nt − 1), ası́ que, por
el Principio de las Casillas, hay nt aristas del mismo color, digamos rojo. Los extremos de
ellas forman un Knt . Si una de las aristas en este Knt es roja, entonces con u se forma un
triángulo rojo; si todas son de los otros t colores entonces, por hipótesis de inducción, hay
un triángulo de un solo color y esto termina la prueba. ♦
13.22 Observación. Con la notación de 13.21 calculamos los siguientes valores para nt :
n2
n3
n4
n5
n6
= 6,
= 17,
= 66,
= 327,
= 1958.
Generalización 2: Colorear s-adas de vértices en lugar de parejas (aristas). Hasta ahora
hemos estado asignando colores a las aristas de las gráficas. Notemos que el conjunto de
aristas de una gráfica completa es A = {a ⊂ V : |a| = 2}. Una coloración de este tipo con
t colores c1 , c2 , . . . , ct es una función A → {c1 , c2 , . . . , ct }. Entonces una coloración de todas
las s-adas de vértices es una función M → {c1 , c2 , . . . , ct }, donde M = {S ⊂ V : |S| = s}.
74
Como antes, podemos considerar rs (k1 , k2 , . . . , kt ). Por ejemplo se demuestra la existencia
de r3 (k, l), el menor entero para el cual si se colorean con rojo y azul todas las ternas de
un conjunto V de r3 (k, l) elementos, se puede asegurar que hay un subconjunto de V de
k elementos en el que todas las ternas tienen color rojo, o hay un subconjunto de V de l
elementos en el que todas las ternas tienen color azul.
Veamos una aplicación de esto. Para entender mejor el contenido de la proposición que
probaremos, ilustremos primero con un ejemplo.
13.23 Ejemplo. Si se tiene un conjunto de 5 puntos en el plano (no tres alineados)
entonces 4 de ellos forman un cuadrilátero convexo. Además 5 es el menor número con esta
propiedad.
Demostración. En efecto, con 4 puntos es posible que no se forme un cuadrilátero convexo,
como se muestra en el siguiente dibujo.
•
•
•
•
Sin embargo con 5 puntos forzosamente hay 4 que forman un cuadrilátero convexo. Para ver
esto consideremos la envolvente convexa de los puntos (el menor convexo que contiene a
los puntos). Es claro que si la envolvente convexa es un cuadrilátero o un pentágono, entonces
no hay nada que demostrar. Consideremos entonces el caso en que la envolvente convexa es
un triángulo y tracemos una recta por los puntos que están en el interior del triángulo. Esta
recta divide al plano en dos semiplanos y en uno de ellos quedan dos vértices del triángulo;
esos dos vértices junto con los interiores forman el cuadrilátero convexo buscado.
•
...
........
... ....... .........
.....
... ... ....
.....
.....
..... ....
.....
.
.....
.
.
.....
.. ... ...
.....
... .......
.....
.....
....
...
.....
.
.
.
.....
...
.
.....
.
.
...
.....
..
...
.....
.....
...
..............
.....
. ..............
..
.....
.............
...
.
.
...
.
.
.............
.
.
.
.
.
.
.
.
.. .....
....... .... .... .... .... .... ...... .... .... .... .... .... .... .... ....................................
..
...
...
•
•
•
•
♦
En la notación de la proposición siguiente, el ejemplo probó que ES(4) = 5.
13.24 Proposición. Teorema de Erdös-Szekeres. Existe un entero menor ES(n) tal
que si se tiene un conjunto de ES(n) puntos en el plano (no tres alineados) entonces n de
ellos forman un n-ágono convexo.
Demostración. Veremos que si se tienen r3 (n, n) puntos en el plano, forzosamente n de
ellos forman un n-ágono convexo (ası́, ES(n) ≤ r3 (n, n)). En efecto, dado el conjunto con
r3 (n, n) puntos no tres alineados numerémoslos del 1 al r3 (n, n) al azar y coloreemos de rojo
75
una terna si su numeración en orden creciente lleva el sentido de las manecillas del reloj, y
de azul si lleva el sentido contrario. Por ser r3 (n, n) puntos, podemos asegurar que hay n con
la propiedad de que todas las ternas son del mismo color, digamos rojo. Esos n puntos deben
formar un n-ágono convexo pues el que el n-ágono que forman no fuera convexo querrı́a decir
que 4 de los puntos tienen numeración m1 < m2 < m3 < m4 , pero uno quedarı́a en el interior
del triángulo formado por los otros tres; en cualquier caso, habrı́a un triángulo azul:
m1
....
.•
........
........... .
.... .
.................. ..
.................. ...
..
...................
..................................
.
...
.
.
..........................
...
..............................................
.
.
...
...................................................... ....
.
..
.......................
.
.
.
.
.
.
.... ...
...................
.... .
....................
.
.
.
....... .... .... .... .... .... .... .... .... ...........
• m4
•
m3
•
m2
m1
•.....
.. .
. ... ..
.. ... ...
... .. ...
..
...
...
.
...
.
...
.
...
...
...
........
...
...
.....................
... ......................................................................... ...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...............................................................................
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..................................................................................
m3
•
•
m4
•
m2
m1
•...........
... ...........
....
.. ......................
... ..............................
......................
...
................................
............................
...
............................
...
....................................................
.
.
.
.
...................
.
....
.
......................
.
.
.. .... ..
...............
.........
.......
..... .... .... .... .... .... .... .... .... ...........
m2•
•
m4
•
m3
m2
..........
.•
......... .
........... ..
........... ..
................ ...
.
..................
...................................
...
.
.................
...
.............................................
.
.
.
...
...................................................... ....
.
..
.....................
.
.
.
.
.
.
.... ...
.....................
.... .
..................
.
.
....... .... .... .... .... .... .... .... .... ...........
• m1
•
m4
•
m3
♦
13.25 Ejercicio. En un salón de clase hay 66 alumnos de 4 paı́ses. Demostrar que
forzosamente uno de los alumnos tiene número de lista la suma de dos números de lista (posiblemente iguales) de compatriotas suyos. (Sugerencia: Recordar una cota para R(3, 3, 3, 3).)
13.26 Ejercicio. En un cı́rculo con centro O hay 21 puntos P1 , P2 , . . . , P21 . Probar que
existen al menos 100 parejas (i, j) (con i 6= j) tales que ∠Pi OPj ≤ 120o . (Sugerencia:
Considerar la gráfica con un vértice representando a cada Pi y poner una arista de Pi a Pj
si, y sólo si, ∠Pi OPj > 120o .)
13.27 Ejercicio. Probar que si en un grupo de 14 personas de cada tres hay dos que se
conocen entre sı́, entonces debe haber 5 personas que se conocen todas entre sı́.
13.28 Ejercicio. Sean S un conjunto con n elementos, y A1 , A2 , . . . , An subconjuntos
distintos de S. Probar que existe un elemento x ∈ S tal que son distintos entre sı́ todos los
conjuntos
A1 − {x}, A2 − {x}, . . . , An − {x}.
(Sugerencia: Suponer falso el resultado. Considerar la gráfica cuyos vértices son los Ai . Para
cada x ∈ S, escoger Ai 6= Aj tal que Ai − {x} = Aj − {x} (si hay varios, escoger sólo un par)
y poner una arista entre Ai y Aj .)
13.29 Ejercicio. Sea G una gráfica con 12 vértices y 40 aristas. ¿Cuáles de las siguientes
afirmaciones son verdaderas?
(a) G tiene un triángulo.
(b) G tiene un cuadrado.
(c) G tiene un K4 .
76
14.
Apareamientos
Un apareamiento es un subconjunto del conjunto de aristas de tal manera que cualesquiera dos aristas del subconjunto sean ajenas. El apareamiento es perfecto si todo vértice
pertenece a alguna arista del apareamiento, es máximo si ningún otro apareamiento tiene
más aristas y es maximal si ningún otro apareamiento lo contiene propiamente.
14.1 Observación. Se tienen las siguientes implicaciones no reversibles:
perfecto ⇒ máximo ⇒ maximal.
perfecto
máximo no perfecto
maximal no máximo
Recordemos que la diferencia simétrica de dos conjuntos X y Y es
X4Y = (X ∪ Y ) \ (X ∩ Y ) = (X \ (X ∩ Y )) ∪ (Y \ (X ∩ Y )) = (X \ Y ) ∪ (Y \ X).
14.2 Lema. Sean M1 y M2 apareamientos de G y sea H la subgráfica generadora de G
que tiene por aristas a M1 4M2 . Entonces las posibilidades para las componentes conexas de
H son: vértices aislados, ciclos pares y trayectorias.
Demostración. En H todo vértice tiene grado menor o igual que 2. Si en una componente
todos los vértices son de grado 2 entonces es ciclo y, como dos aristas consecutivas no pueden
pertenecer al mismo apareamiento, entonces se alternan y el ciclo es de longitud par. ♦
Dado un apareamiento M y una trayectoria T en G decimos que T es M -alternante si
para cada dos aristas consecutivas de T se tiene que exactamente una de ellas está en M ;
decimos que T es M -aumentante si es M -alternante y los dos vértices extremos de T no
pertenecen a ninguna arista de M .
14.3 Observación. Si T es trayectoria M -aumentante entonces l(T ) es impar, y si
l(T ) = 1 entonces la única arista de T no pertenece a M y los extremos de esa arista no son
vértices de aristas de M .
14.4 Proposición. Un apareamiento M es máximo si, y sólo si, G no tiene trayectorias
M -aumentantes.
77
Demostración. (⇒) Supongamos que M es apareamiento máximo que tiene una trayectoria M -aumentante T = (u0 , u1 , . . . , u2k+1 ) (cierta k ≥ 1). Definimos
M 0 = (M \ {u1 u2 , u2 u3 , . . . , u2k−1 u2k }) ∪ {u0 u1 , u1 u2 , . . . , u2k u2k+1 }.
Entonces M 0 también es apareamiento pero |M 0 | > |M | y esto prueba que no puede existir
T.
(⇐) Ahora supongamos que no hay trayectorias M -aumentantes pero que M no es máximo. Sea M ∗ apareamiento máximo y sea H la subgráfica generadora de G con aristas M 4M ∗ .
Las componentes conexas de H son trayectorias M -alternantes (posiblemente de longitud 0)
o ciclos pares. Pero |M ∗ \ M | > |M \ M ∗ | ası́ que M 4M ∗ tiene más elementos de M ∗ que
de M , de donde alguna trayectoria tiene longitud impar y es M -aumentante, contra nuestra
suposición. ♦
Si M es apareamiento en G y u ∈ V decimos que u es M -saturado si existe a ∈ M tal
que u ∈ a.
14.5 Teorema. Teorema de Hall. Sea G gráfica bipartita con partición (U, V ). Entonces existe un apareamiento que satura todo vértice de U si, y sólo si, para todo S ⊂ U
se tiene que |N (S)| ≥ |S|.
Demostración. Sólo hay que probar la implicación (⇐). Probaremos que todo apareamiento máximo satura todo U . Sea M apareamiento máximo y supongamos que u ∈ U no
es M -saturado. Sea
X = {w ∈ V(G) : ∃ uw−trayectoria M −alternante}.
Sean U1 = U ∩ X y V1 = V ∩ X. Tomando S = U1 , que es no vacı́o porque u ∈ U1 , vemos que
V1 6= ∅. Veamos ahora que todos los elementos de V1 son M -saturados. En efecto, si v ∈ V1 y
T = (u = w0 , w1 , w2 , . . . , wk = v) es uv-trayectoria M -alternante, entonces, l(T ) = k es impar
y la arista wk−1 v no está en M , de donde, como u no es M -saturado y M es máximo, por
14.4, T no puede ser M -aumentante lo que implica que v pertenece a alguna arista de M ,
ası́ que existe wk+1 ∈ U1 tal que vwk+1 ∈ M .
78
Tenemos entonces que M induce un apareamiento en la subgráfica de G inducida por
U1 ∪ V1 que satura a V1 y no satura a u, de donde |V1 | < |U1 |. Sin embargo esto contradice
la hipótesis tomando S = U1 puesto que N (U1 ) ⊂ V1 . ♦
14.6 Corolario. En una fábrica hay ciertas labores U que deben asignarse. Se cuenta
con cierto personal V y cada uno de sus miembros es capaz de realizar algunas de las labores.
Es posible cubrir todos los puestos si, y sólo si, para cada conjunto de labores existe al menos
el mismo número de personas capaces de realizar esas labores. ♦
Un sistema de representantes para una familia de k conjuntos S1 , S2 , . . . , Sk es un
conjunto {v1 , v2 , . . . vk } tal que para cada i, vi ∈ Si y vi 6= vj si i 6= j.
14.7 Corolario. La familia de conjuntos S1 , S2 , . . . , Sk tiene sistema de representantes
si, y sólo si, para toda j ≤ k la unión de cualesquiera j de los conjuntos tiene al menos j
elementos.
Demostración.
Construimos la gráfica bipartita G = (U, V ) con U = {S1 , S2 , . . . , Sk },
S
V = i Si y Sx ∈ A(G) si, y sólo si, x ∈ S. ♦
14.8 Nota. A continuación describimos un algoritmo para construir un apareamiento
que satura U en una gráfica bipartita con bipartición de vértices (U, V ) (en caso de que
exista).
Paso (1). Empezamos con un apareamiento arbitrario M (posiblemente vacı́o). Vamos al
paso (2).
Paso (2). Si M satura U , terminamos. Si no, sea u ∈ U no M -saturado. Hacemos S = {u}
y P = ∅. Vamos al paso (3).
Paso (3). Si N (S) ⊂ P , entonces no existe apareamiento y terminamos. Si N (S) * P ,
tomamos v ∈ N (S) \ P . Vamos al paso (4).
Paso (4). Si v es M -saturado, tomamos u0 ∈ U tal que u0 v ∈ M . Agregamos u0 a S y v a P ,
y vamos al paso (3). Si v no es M -saturado, tomamos T una uv-trayectoria M -aumentante,
cambiamos M por M 4A(T ) y vamos al paso (2).
Veremos que el algoritmo descrito produce apareamiento en caso de existir. Antes veamos
un ejemplo para ilustrar el algoritmo.
14.9 Ejemplo. Vamos a aplicar 14.8 en la siguiente gráfica.
79
(1). Sea M = {u1 v1 }.
(2). Sean S = {u3 }, P = ∅.
(3). Tenemos N (S) = {v1 , v3 }. Tomemos v1 ∈ N (S) \ P .
(4). v1 es M -saturado pues u1 v1 ∈ M . Agregamos u1 a S: S = {u1 , u3 } y v1 a P : P = {v1 }.
(3). Tenemos N (S) = {v1 , v2 , v3 , v4 }. Sea v3 ∈ N (S) \ P .
(4). v3 no es M -saturado. Tomamos T = (u3 , v3 ) trayectoria M -aumentante. Ahora cambiamos M por M 4A(T ): M = {u1 v1 , u3 v3 }.
(2). Tomamos S = {u2 }, P = ∅.
80
(3). Tenemos N (S) = {v2 , v4 }. Tomamos v2 ∈ N (S) \ P .
(4). v2 no es M -saturado. Tomamos T = (u2 , v2 ) trayectoria M - aumentante. Ahora
hacemos M = {u1 v1 , u2 v2 , u3 v3 }.
(2). Sean S = {u4 }, P = ∅.
(3). Tenemos N (S) = {v3 }. Tomamos v3 ∈ N (S) \ P .
(4). v3 es M -saturado pues u3 v3 ∈ M . Agregamos u3 a S: S = {u3 , u4 } y agregamos v3 a
P : P = {v3 }.
(3). Tomamos v1 ∈ N (S) \ P .
(4). v1 es M -saturado pues u1 v1 ∈ M . Agregamos u1 a S: S = {u1 , u3 , u4 } y agregamos
v1 a P : P = {v1 , v3 }.
81
(3). Sea v4 ∈ N (S) \ P .
(4). v4 no es M -saturado. Tomamos T = (v4 , u1 , v1 , u3 , v3 , u4 ) trayectoria M -aumentante.
Finalmente cambiamos M por M 4A(T ): M = {u1 v2 , u2 v4 , u3 v1 , u4 v3 } y éste es el apareamiento buscado. ♦
Ahora veamos por qué funciona el algortitmo. Notamos primero que siempre |P | = |S|−1,
ası́ que, por 14.5, en caso de existir apareamiento, debe haber un elemento en N (S) \ P .
Supongamos que en determinado paso se tiene un elemento u = u0 ∈ U no saturado, y se
construyen S = {u1 , u2 , . . . , uk }∪{u0 } y P = {v1 , v2 , . . . , vk } siguiendo el algoritmo, es decir,
de manera que para cada i ∈ [k], vi ∈ N ({uj : j < i}) y ui vi ∈ M , y supongamos también que
v = vk+1 ∈ N (S) \ P es no saturado. Queremos ver que hay una trayectoria M -aumentante
que empieza en u y termina en v. En efecto, empezando por v = vk+1 construyamos una
trayectoria maximal T = (v, ui1 , vi1 , ui2 , vi2 , . . . , uir ) de manera que i1 > i2 > · · · > ir (esto
es posible dada la elección de cada vi ∈ N ({uj : j < i})); la maximalidad nos dice que debe
terminar en u0 , como querı́amos y, dado que tanto u como v eran no saturados, se tiene que
T es M -aumentante.
82
Finalmente, como el procedimiento aumenta aristas, debe llegar a construir un apareamiento que satura a U .
El teorema de Hall nos habla de apareamientos en gráficas bipartitas. Consideraremos
ahora el problema más general de determinar la existencia de apareamientos en gráficas
generales.
14.10 Teorema. Teorema de Tutte. Una gráfica G tiene apareamiento perfecto si, y
sólo si, para cada S ⊂ V(G) el número k0 (G − S) de componentes de G − S con número
impar de vértices es a lo más |S|.
Demostración. (⇒) Sea S ⊂ V(G) y sea M apareamiento perfecto. Como hay apareamiento perfecto, |V(G)| es par. Si C es una componente con un número impar de elementos,
entonces algún elemento C tiene a su vecino por M en S. Para cada componente conexa C
de orden impar escogemos un elemento vC ∈ S tal que su pareja según M esté en C. La
asignación C 7→ vC es una función inyectiva del conjunto de componentes conexas de orden
impar de G − S en S.
(⇐) Haciendo S = ∅ vemos que no hay componentes de orden impar; en particular,
V(G) es par y todo vértice pertenece a al menos una arista. Entonces para cada S ⊂ V(G),
los números |S| y k0 (G − S) son de la misma paridad pues S tiene una cantidad impar de
elementos si, y sólo si, el complemento de S, V(G − S) (que es la suma de los números de
elementos de las componentes de G − S), también tiene cantidad impar de elementos, lo cual
es equivalente a que el número de componentes de G − S con número impar de elementos
sea impar.
Vamos a hacer inducción sobre n = |V(G)|. Para n = 2, como todo vértice pertenece a
alguna arista tenemos que G = K2 , que tiene apareamiento perfecto. Supongamos entonces
que n > 2.
Caso (1). Supongamos que para toda S ⊂ V(G) se tiene que k0 (G − S) < |S|. Entonces
k0 (G − S) ≤ |S| − 2. Sea uv ∈ A(G) y sea G 0 = G − u − v. Veremos que podemos completar
el apareamiento de u con v a un apareamiento de G. Para esto, queremos aplicar la hipótesis
de inducción ası́ que bastará probar que para todo S 0 ⊂ V(G 0 ) se tiene que k0 (G 0 − S 0 ) ≤ |S 0 |;
83
supongamos que para cierta S 0 pasa lo contrario y sea S = S 0 ∪ {u, v}; entonces k0 (G − S) =
k0 (G 0 − S 0 ) > |S 0 | = |S| − 2, contrario a nuestra suposición.
Caso (2). Existe S ⊂ V(G) tal que k0 (G − S) = |S|. Tomemos S de cardinalidad máxima
con esta propiedad; digamos |S| = k. Observemos que la maximalidad de S nos dice que
G − S no tiene componentes de orden par, pues si una componente C fuera de orden par se le
podrı́a quitar un elemento y agregárselo a S, lo cual incrementarı́a un elemento a S, quedando
las demás componentes sin afectar y descomponiendo C en exactamente dos componentes
(pues el número de componentes de orden impar no puede exceder el número de elementos
del nuevo S, por hipótesis).
Ahora, si v ∈ S entonces no es posible que N (v) ⊂ S porque si éste fuera el caso entonces
k0 (G − (S ∪ {v}) = k0 (G − S) + 1 > |S ∪ {v}|.
Ahora veamos que si S 0 ⊂ S y |S 0 | = j ≥ 1 entonces hay al menos j componentes
impares distintas en las que los elementos de S 0 tienen vecinos. Supongamos lo contrario y
sean C1 , C2 , . . . , Ci componentes impares de G − S tales que N (S 0 ) ⊂ C1 ∪ C2 ∪ · · · ∪ Ci
con i < j. Sea S ∗ = S \ S 0 , el cual tiene k − j elementos y las k − i componentes en las
que los elementos de S 0 no tienen vecinos son también componentes de G − S ∗ , de donde
k0 (G − S ∗ ) ≥ k − i > k − j = |S ∗ |, lo cual es una contradicción.
Usando 14.7 tomamos un elemento xv ∈ Cv tal que vxv es arista de G y apareamos v con
xv . Ahora ya sólo falta probar que si C es componente de G − S y x ∈ V(C) es vecino de
algún elemento de S, entonces dentro de cada C −x hay apareamiento, para lo cual basta ver
que cumple la hipótesis del teorema, pues entonces la hipótesis de inducción puede aplicarse.
Tomemos R ⊂ V(C − x); queremos ver que el número de componentes impares de C − x − R
es a lo más |R|. Supongamos que no: k0 (C − x − R) > |R|; entonces k0 (C − x − R) ≥ |R| + 2
(pues recordemos que k0 (C − x − R) y |R| tienen la misma paridad). En este caso se tiene
k0 (G − (S ∪ R)) ≥ k − 1 + k0 (C − x − R) − 1 ≥ k − 1 + |R| + 2 − 1 = k + |R| = |S ∪ R|,
lo cual es una contradicción por maximalidad de S; esto termina la prueba. ♦
14.11 Corolario. Toda gráfica cúbica sin puentes tiene apareamiento perfecto.
84
Demostración. Supongamos que G es gráfica cúbica sin puentes. Tomemos ∅ =
6 S ⊂ V(G)
y C componente conexa de orden impar de G − S. Sea m el número de aristas de C a S.
Veamos que m ≥ 3. En efecto, primero observemos que m es impar porque si fuera par, en
la gráfica C habrı́a un número impar de vértices de grado impar (ya que la gráfica es cúbica
y C tiene orden impar); además no puede haber una sola arista de C a S pues ésa serı́a
puente.
Entonces tenemos que 3k0 (G − S) ≤ M , donde M es el número de aristas de S a G − S.
Por otro lado, M ≤ 3|S| pues cada elemento de S tiene grado 3; ası́ k0 (G − S) ≤ |S|. ♦
Un factor en G es una subgráfica generadora de G. Un r-factor es un factor r-regular .
Si H es gráfica, un H-factor es un factor isomorfo a H. Una factorización es una colección
de factores F1 , F2 , . . . , Ft tal que la (A(F1 ), A(F2 ), . . . , A(Ft )) es una partición de A(G); la
factorización es r-factorización si los factores son r-regulares y es H-factorización si los
factores son isomorfos a H.
14.12 Ejemplo. (a) Un 1-factor es un apareamiento perfecto.
(b) Un ciclo hamiltoniano es un 2-factor.
(c) En K6 dos triángulos ajenos forman un 2-factor.
(d) K2k+1 tiene 2-factorización. Se muestra en la figura uno de los 2-factores (para k = 4);
para conseguir los demás, rotamos.
14.13 Proposición. Si G es bipartita r-regular entonces tiene 1-factorización.
Demostración. Hacemos inducción sobre r. Para r = 1, la misma gráfica es 1-factor. Sea
G = (U, V ) r-regular con r ≥ 2. Queremos usar el teorema de Hall 14.5, ası́ que tomemos
S ⊂ U . El número de aristas que salen de S es |S|r, pero todas esas aristas llegan a N (S) y
el número total de aristas que llegan a N (S) es |N (S)|r, ası́ que |S|r ≤ |N (S)|r, de donde
|S| ≤ |N (S)|, como querı́amos. Tenemos un 1-factor F . Aplicamos hipótesis de inducción a
G − A(F ), que es (r − 1)-regular. ♦
14.14 Ejercicio. Demostrar, con un diseño constructivo, que dado un número par 2n
de equipos de volibol es posible organizar un torneo de manera que en cada ronda haya n
juegos y después de 2n − 1 rondas cada equipo haya competido exactamente una vez con
cada uno de los demás. (En otras palabras, K2n es 1-factorizable.)
85
14.15 Proposición. Kn es de tipo I para n par.
Demostración. Tenemos que 14.14 nos dice que Kn es 1-factorizable para n par. Cada
1-factor determina una clase cromática en una buena coloración de aristas. ♦
14.16 Ejercicio. Probar que la gráfica de Petersen no es 1-factorizable.
14.17 Ejercicio. Usar el algoritmo descrito en 14.8 empezando con M = {u1 v1 , u3 v3 , u4 v4 }
para encontrar un apareamiento en la siguiente gráfica.
14.18 Ejercicio. Probar que si G es cúbica y todos los puentes de G están contenidos
en una trayectoria, entonces G tiene apareamiento perfecto.
14.19 Ejercicio. Determinar si la siguiente gráfica tiene apareamiento perfecto.
14.20 Ejercicio. Determinar si la siguiente gráfica tiene 1-factorización.
86
14.21 Ejercicio. Probar que el n-cubo es 1-factorizable y que es k-factorizable si, y sólo
si, k | n.
14.22 Ejercicio. En un torneo cada participante debe competir exactamente una vez
contra cada uno de los demás. Hay 2n participantes y ya se jugaron dos rondas. Probar
que todavı́a se pueden partir los equipos en dos grupos de n jugadores de manera que los
participantes de un mismo grupo no hayan competido todavı́a entre ellos.
14.23 Ejercicio. Sea M una matriz de 0’s y 1’s tal que en cada renglón y en cada
columna hay exactamente dos 1’s. Probar que M es suma de dos matrices de permutación.
87
15.
Digráficas
En esta sección consideraremos digráficas D; a las aristas dirigidas les llamaremos arcos
y denotaremos al conjunto de arcos por A. Escribimos uv = (u, v) para los elementos de A.
Un arco a = uv es simétrico si también a−1 = vu ∈ A. Una digráfica es simétrica si todos
sus arcos son simétricos. La digráfica es transitiva si
{uv, vw} ⊂ A ⇒ uw ∈ A.
La gráfica subyacente de una digráfica D se obtiene de D tomando el mismo conjunto
de vértices, convirtiendo arcos en aristas y eliminando aristas múltiples. Un uv-camino
dirigido (resp. paseo dirigido , trayectoria dirigida, ciclo dirigido) es un camino
→
−
C = C = (u = v0 , v1 , . . . , vt = v) (resp. paseo, trayectoria, ciclo) de la gráfica subyacente tal
que vi−1 vi ∈ A para toda i.
15.1 Nota. Al igual que en gráficas, se puede probar que todo uv-camino dirigido contiene una trayectoria dirigida (tomando uv-camino de longitud mı́nima).
Una digráfica es débilmente conexa si la gráfica subyacente es conexa; es unilateralmente conexa si dados u y v vértices existe una uv-trayectoria dirigida o una vu-trayectoria
dirigida; es fuertemente conexa si dados u y v vértices existe una uv-trayectoria dirigida.
15.2 Observación. Tenemos las siguientes implicaciones no reversibles:
fuertemente conexa ⇒ unilateralemente conexa ⇒ débilmente conexa.
15.3 Proposición. D es unilateralmente conexa si, y sólo si, existe un camino dirigido
que pasa por todos los vértices.
Demostración. (⇐) es clara. Para (⇒) tomamos camino C = (u0 , u1 , . . . , ut ) que use el
mayor número posible de vértices y suponemos que algún vértice v queda fuera de C. Por
maximalidad de C, no hay camino dirigido de v a u0 , ası́ que hay camino dirigido C0 de u0 a
v. Si hubiera camino dirigido C1 de v a u1 entonces (u0 , C0 , v, C1 , u1 , C) serı́a camino dirigido
que pasa por más vértices que C, ası́ que el camino C1 va de u1 a v. Ası́ continuamos hasta
ver que hay camino dirigido Ct de ut a v, pero esto también es una contradicción porque
entonces (C, Ct ) serı́a camino de longitud mayor. En conclusión, no existe v fuera de C. ♦
15.4 Corolario. D es fuertemente conexa si, y sólo si, existe un camino dirigido cerrado
que pasa por todos los vértices.
Demostración. (⇐) es clara. Tomemos camino dirigido C que pase por todos los vértices;
digamos que empieza en u y termina en v. Como la digráfica es fuertemente conexa, existe
C 0 camino dirigido de v a u. Entonces (C, c0 ) es el camino cerrado buscado. ♦
De manera análoga a las gráficas, se consideran componentes fuertemente conexas.
88
15.5 Observación. La componentes fuertemente conexas inducen una partición en el
conjunto de vértices.
Dado u ∈ V(D) su ingrado, δ − (u), es el número de arcos que tienen a u como extremo
final; su exgrado, δ + (u), es el número de arcos que inician en u. Ası́, N + (u) es el conjunto
de exvecinos de u, es decir, los v ∈ V tales que uv es arco. Análogamente hablamos del
conjunto N − (u) de invecinos de u. Decimos que v es fuente si δ − (v) = 0; es pozo si
δ + (v) = 0.
15.6 Observación.
P
−
v δ (v) =
P
v
δ + (v).
Decimos que D es acı́clica si no tiene ciclos dirigidos.
15.7 Observación. Si D es acı́clica entonces D tiene fuentes y pozos.
Una orientación para una gráfica G es una digráfica D sin aristas simétricas que tiene
por gráfica subyacente a G.
15.8 Proposición. Una gráfica G admite orientación fuertemente conexa si, y sólo si, G
es conexa y no tiene puentes.
Demostración. (⇒) Es claro que G es conexa. Consideremos una orientación fuerte para
G y sea a ∈ A(G). Tomemos w1 y w2 vértices distintos en G − a; queremos ver que existe
→
−
un camino en G de w1 a w2 que no usa a. Tomemos trayectorias dirigidas T1 de w1 a w2 , y
→
−
→
− →
−
T2 de w2 a w1 en la gráfica orientada. Si alguna de T1 o T2 no usa a entonces, ya acabamos.
Como la gráfica no tiene aristas múltiples, si ambas trayectorias usan a, entonces la usan en
el mismo sentido, digamos a = (u, v). Sean
→
−
T1 = (w1 = u0 , u1 , . . . , us−1 , u, v, us , . . . , uk , w2 ) y
→
−
T2 = (w2 = v0 , v1 , . . . , vt−1 , u, v, vt , . . . , vl , w1 ).
Entonces construimos el w1 w2 -camino (no dirigido)
(w1 , u1 , . . . , us−1 , u, vt−1 , . . . v1 , w2 ).
89
(⇐) Tomemos H subgráfica inducida de G con orden máximo que admite una orientación
fuerte. Si H 6= G tomemos una arista uv con u ∈ V(H) y v ∈ V(G) \ V(H). Como a = uv no
es puente, existe trayectoria T de v a H en G − a tal que V(T ) ∩ V(H) es un solo vértice w.
Ahora orientamos la arista a de u a v y las aristas T en el sentido de v hacia w, obteniendo
una gráfica orientada fuertemente conexa que contiene a H propiamente, lo cual es una
contradicción. ♦
15.9 Ejercicio. Dar un ejemplo de una gráfica conexa con vértice de corte que tiene
orientación fuerte.
15.10 Proposición. Un árbol tiene orientación unilateral si, y sólo si, es trayectoria.
Demostración. (⇐) es obvio.
(⇒) Queremos ver que todo vértice tiene grado a lo más 2. Supongamos que un vértice u
tiene al menos tres vecinos. Si δ + (u) ≥ 2 y si uv1 y uv2 son arcos entonces no hay trayectoria
dirigida de v1 a v2 ni de v2 a v1 pues cualquier trayectoria debe pasar por u. Lo mismo ocurre
si δ − (u) ≥ 2. ♦
15.11 Proposición. G conexa tiene orientación unilateral si, y sólo si, todos los puentes
están en una misma trayectoria.
Demostración. Sea P el conjunto de puentes de G y sean C1 , . . . , Ct las componentes
conexas de G − P . Definimos una gráfica GP con V(Gp ) = {C1 , . . . , Ct } y con Ci Cj ∈ A(Gp )
si, y sólo si existen vi ∈ V(Ci ) y vj ∈ V(Cj ) tales que vi vj ∈ P . Es claro que GP es acı́clica.
Para concluir la demostración bastará ver que G es conexa y admite orientación unilateral
si, y sólo si, GP es trayectoria.
La implicación (⇒) es clara porque una orientación unilateral en G induce orientación
unilateral en GP .
Veamos (⇐): Es claro que el que GP sea conexa implica que G es conexa. Como GP
es acı́clica y estamos suponiendo que es conexa, entonces es árbol; pero además estamos
suponiendo que admite orientación unilateral ası́ que, por 15.10, es una trayectoria orientada.
También sabemos que cada Ci es conexa sin puentes, de donde, por 15.8, la podemos orientar
fuertemente. Al juntar todas las orientaciones de las Ci y de GP obtenemos la orientación
unilateral para G. ♦
Un torneo es una digráfica completa sin arcos simétricos.
15.12 Lema. Si D es un torneo no acı́clico, entonces D tiene un triángulo dirigido.
Demostración. Tomemos un ciclo dirigido de longitud mı́nima l y supongamos que l > 3.
Entonces cualquier diagonal induce un ciclo de longitud menor. ♦
90
15.13 Proposición. Un torneo D es acı́clico si, y sólo si, es transitivo.
Demostración. (⇒) Sean uv y vw arcos en D; como no hay ciclos dirigidos, la orientación
de la arista de u a w es uw y esto prueba que es transitivo.
(⇐) Supongamos que D tiene un ciclo dirigido. Por 15.12 tiene un triángulo, (u, v, w, u),
pero entonces, por ser transitivo, uw es arco, lo cual no es posible porque no hay arcos
simétricos. ♦
Si v es vértice de un torneo, le llamamos marcador de v a δ + (v).
15.14 Proposición. Un torneo D es transitivo si, y sólo si, la sucesión de marcadores
es (0, 1, 2, . . . , n − 1), donde |V(D)| = n.
Demostración. (⇒) Podrı́amos hacer la demostración en forma simple por inducción
usando 15.13 y 15.7; sin embargo procedamos de otra manera, para variar: Supongamos
falso el resultado. Entonces algún marcador se repite, digamos, δ + (u) = δ + (v). Supongamos,
sin pérdida de generalidad que el arco entre u y v va de u a v. Por ser el torneo transitivo,
para todo vw arco, se tiene que uv también es arco, lo cual produce una contradicción porque
entonces δ + (u) > δ + (v).
(⇐) Hacemos inducción sobre n, siendo trivial el caso n = 1. Tomamos un vértice u de
exgrado n − 1. Observemos que al quitar u de D en la nueva digráfica D − u los exgrados
son los mismos, ası́ que podemos aplicar hipótesis de inducción y obtenems el resultado. ♦
15.15 Ejercicio. Probar que sólo existe un torneo acı́clico con n vértices, salvo isomorfismo.
15.16 Ejercicio. En un torneo de tenis cada dos jugadores jugaron una vez exactamente.
No hubo empates. Cuando el torneo terminó, cada uno de los jugadores hizo una lista en la
que escribió el nombre de los jugadores a los que él le ganó y el de los jugadores a los que
le ganó alguien a quien él le ganó. Probar que algún jugador puso a todos los demás en su
lista. Reescribir el enunciado de este ejercico en términos de gráficas.
15.17 Ejercicio. En un torneo de basquetbol hay 2k equipos, cada pareja de equipos
compitió exactamente una vez y no hubo empates. Probar que se puede hacer una lista con
k + 1 equipos en la que cada uno le ganó a todos los que le siguen en la lista. Reescribir el
enunciado de este ejercico en términos de gráficas.
91
15.18 Ejercicio. Probar que en cualquier digráfica acı́clica con n vértices es posible
numerar los vértices del 1 al n de manera que para cada arista que empiece en un vértice
con número i y termine en un vértice con número j, se tenga que i < j.
15.19 Ejercicio. Demostrar que en cualquier ciudad es posible darle un sentido a cada
una de las calles de manera que cualquiera que salga de su casa en carro nunca pueda regresar
a ella (a menos que cometa una infracción).
15.20 Ejercicio. Probar que todo torneo tiene trayectoria hamiltoniana (dirigida) y
que si tiene al menos 3 vértices y es fuertemente conexo, entonces tiene ciclo hamiltoniano
(dirigido).
92
16.
Redes y flujos
En esta sección, D denota una digráfica con una fuente distinguida s y un pozo distinguido
t que cuenta con una función de capacidad c : A(D) → R. A (D, s, t, c) le llamamos red.
Consideraremos aquı́ sólo capacidades con valores racionales no negativos.
Un flujo en (D, s, t, c) es una función f : A(D) → R que cumple:
(a) Ley de Kirchoff: Para todo u ∈ V \ {s, t},
X
X
f (uv) =
f (vu).
v∈N − (u)
v∈N + (u)
(b) Para todo uv ∈ A(D),
0 ≤ f (uv) ≤ c(uv).
Por ejemplo, podemos pensar que la red está formada por tuberı́as (o carreteras, o cables,
etc.) con determinada capacidad de conducción en cierto sentido, y se quiere encontrar cuál
es el flujo máximo que puede conducirse de s a t a través de ellas. Nótese que la ley de
Kirchoff pide que de cada vértice, salvo de la fuente y del pozo, salga exactamente lo mismo
que entra.
16.1 Ejemplo. En la figura, con números más pequeños se muestra la capacidad de
cada arco y con números más grandes los valores de un flujo.
Dado f flujo y un conjunto de vértices U , denotamos por f + (U ) lo que “sale” de U y
f − (U ) lo que “entra” a U , es decir,
X
f + (U ) =
f (uv)
u∈U, v ∈U
/
f − (U ) =
X
v ∈U,
/ u∈U
93
f (vu)
El flujo total de U es f (U ) = f + (U ) − f − (U ). El valor del flujo es |f | = f + (s). Observemos
que |f | representa lo que puede transportarse de s a t mediante el flujo f . En el ejemplo,
|f | = 2, cantidad que puede transportarse de s a t al juntar lo que llevan las trayectorias
(s, u, y, x, t) y (s, v, z, y, x, t) (cada una lleva 1 de flujo y juntas llevan 2).
El problema que queremos tratar es: Problema del flujo máximo: Dada una red
(D, s, t, c), encontrar un flujo máximo, es decir, un flujo con valor máximo.
Un corte en la red es una colección de vértices S tal que s ∈ S y t ∈
/ S. La capacidad
del corte es
X
c(S) =
c(uv).
u∈S, v ∈S
/
En el ejemplo, si S = {s, v, z, y}, entonces c(S) = c(su)+c(zt)+c(yx)+c(yt) = 4+5+2+4 =
15; si S = {s, u, v} entonces c(S) = c(uy) + c(vz) = 1 + 2 = 3.
16.2 Proposición. Dado f flujo y S corte en la red (G, s, t, c), se tiene que |f | = f (S).
Demostración. Veamos primero que
f (S) = f + (S) − f − (S) =
X
(f + (u) − f − (u)).
u∈S
En efecto, si xy es arista en G tenemos las siguientes posibilidades:
Si x ∈
/ S, y ∈
/ S, entonces no contribuyen en ningún lado de la igualdad.
Si x ∈ S, y ∈ S, entonces en el lado izquierdo de la igualdad no contribuyen, y en el lado
derecho contribuyen dos veces, una positiva y otra negativa.
Si x ∈ S, y ∈
/ S, entonces contribuyen una vez en forma positiva en ambos lados de la
igualdad.
Si x ∈
/ S, y ∈ S, entonces contribuyen una vez en forma negativa en ambos lados de la
igualdad.
Ahora observemos el lado dereho de la igualdad recién probada: Para cada u ∈ S \ {s}
se tiene que f + (u) − f − (u) = 0 y f + (s) − f − (s) = f + (s) = |f | y ası́ queda probada la
proposición. ♦
16.3 Corolario. |f | = f + (s) = f − (t).
Demostración. Tenemos que el valor del flujo es el valor de cualquier corte; en particular
pueden tomarse los cortes S1 = {s} y S2 = V(G) \ {t}, ası́ que
f + (s) = f (S1 ) = |f | = f (S2 ) = f − (t). ♦
16.4 Corolario. El valor de cualquier flujo f está acotado superiormente por la capacidad de cualquier corte S.
94
Demostración. Tenemos
|f | = f + (S) − f − (S) ≤ f + (S) ≤ c(S). ♦
Veremos que el valor máximo de entre todos los flujos coincide con la capacidad mı́nima
de los cortes. Haremos la demostración de esto en el siguiente teorema a través del algoritmo
de Ford-Fulkerson.
16.5 Teorema. Teorema del flujo máximo/corte mı́nimo. El valor máximo que
puede alcanzar un flujo es igual a la mı́nima capacidad que puede tener un corte.
Demostración. Haremos la demostración mediante el siguiente algoritmo:
Sea (G, s, t, c) una red. Tomamos un flujo inicial (que puede ser uno con todos los valores
0).
Paso (1). Ponemos R = {s} y S = ∅.
Paso (2). Si R = S vamos al paso (3). Si no, tomamos u ∈ R \ S y agregamos a R todos
los vértices v ∈ N + (u) tales que f (uv) < c(uv) y también todos los vértices w ∈ N − (u)
tales que f (wu) > 0. Agregamos u a S. Repetimos este paso hasta lograr R = S.
Paso (3). Si t ∈
/ R, terminamos. Si t ∈ R, tomamos st-trayectoria (no dirigida) T = (s =
w0 , w1 , . . . , wk = t) de tal manera que cada wi haya sido agregada a R en algún paso en que
se tenı́a f (wi−1 wi ) < c(wi−1 wi ) o f (wi wi−1 ) > 0. Para a = wi−1 wi consideramos si wi fue
agregado porque c(a) − f (a) > 0 o porque a−1 es arco con f (a−1 ) > 0; definimos
c(a) − f (a), en el caso (1),
d(a) =
f (a−1 ),
en el caso (2).
Tomamos m = min{d(a) : a ∈ T } y definimos el flujo f 0 por

si a ∈
/ T,
 f (a),
0
si a ∈ T,
f (a) = f (a) + m,

f (a) − m, si a−1 ∈ T.
Regresamos al paso (1) con el flujo f 0 . ♦
Antes de hacer la observación que nos permitirá concluir que el algoritmo anterior encuentra un flujo máximo con su respectivo corte de mı́nima capacidad, ilustremos tomando
el flujo del ejemplo 16.1.
16.6 Ejemplo. Tomemos el flujo inicial y la red de 16.1.
95
R = {s},
↓ s f (su) < c(su) y f (sv) < c(sv)
R = {s, u, v},
↓u
R = {s, u, v},
↓ v f (yv) > 0
R = {s, u, v, y},
↓ y f (zy) > 0 y f (yt) < c(yt)
R = {s, u, v, y, z, t},
↓ t f (xt) > 0
R = {s, u, v, y, z, t, x},
↓x
R = {s, u, v, y, z, t, x},
↓z
R = {s, u, v, y, z, t, x},
S = ∅,
S = {s},
S = {s, u},
S = {s, u, v},
S = {s, u, v, y},
S = {s, u, v, y, t},
S = {s, u, v, y, t, x},
S = {s, u, v, y, t, x, z}.
Tomamos la trayectoria (no dirigida) T = (s, v, y, t) y tenemos que m = 1 de donde
obtenemos el flujo:
96
Volvemos a empezar y ahora tenemos:
R = {s},
↓ s f (su) < c(su) y f (sv) < c(sv)
R = {s, u, v},
↓u
R = {s, u, v},
↓v
R = {s, u, v},
S = ∅,
S = {s},
S = {s, u},
S = {s, u, v}.
El flujo obtenido tiene valor 3, que es igual a la capacidad del corte correspondiente
S = {s, u, v}, lo cual implica que el flujo es máximo y el corte es mı́nimo, por 16.4.
16.7 Observación. Notamos lo siguiente (lo cual concluye la demostración de 16.5):
(a) Cada vez que se logra construir un flujo nuevo usando el algoritmo, el nuevo flujo
tiene valor mayor que el anterior y está acotado por la capacidad de la red, ası́ que, si ésta
tiene valores enteros, el algoritmo termina y el flujo obtenido tiene valores enteros.
(b) Al terminar se tiene un flujo f y un corte S tal que cualquier arista a que sale
de S tiene f (a) = c(a), y cualquier arista a que entra a S tiene f (a) = 0. De esta manera,
f (S) = c(S), por lo cual f tiene valor máximo (por 16.2), y S es corte con capacidad mı́nima.
(c) Si c toma valores racionales, entonces puede sustituirse por valores enteros multiplicando por el mı́nimo común múltiplo M de los denominadores, trabajar el algoritmo y, al
final, dividir los valores obtenidos del flujo máximo por M .
(d) Si c tomara valores reales, es posible que este algoritmo no terminara. Hay otros
algoritmos que sı́ terminan en ese caso (de manera que el resultado también es cierto para
capacidades reales).
(e) Si se permite que c tome valores negativos, es posible modificar las capacidades sumando constantes (de manera que se equilibre la capacidad de entrada con la capacidad de salida
en cada vértice) y trabajar el algoritmo. Al encontrar el flujo máximo deben modificarse los
valores del flujo restando lo apropiado.
(f) Si se tiene una gráfica (no dirigida) G con vértices distinguidos s y t y con una función
de peso w : A → R y se pide encontrar un flujo de s a t que use las aristas en cualquier
sentido, se trata de encontrar una trayectoria de peso máximo. Para esto se puede convertir
cada arista no incidente a s ni a t por un arco simétrico; se busca entonces una trayectoria
de s a t de peso máximo.
16.8 Ejercicio. Seguir el algoritmo de Ford-Fulkerson en la siguiente red para encontrar
97
un flujo máximo y su correspondiente corte mı́nimo. Empezar con el flujo trivial.
16.9 Ejercicio. Probar la implicación (⇐) del teorema de Hall (ver 14.5) usando el
teorema del flujo máximo/corte mı́nimo (ver 16.5).
98
17.
Conexidad
La conexidad de G, κ(G), es el mı́nimo número de vértices que se deben eliminar para
que G se desconecte o se vuelva trivial. La conexidad lineal de G, λ(G) es el mı́nimo número
de aristas que deben quitarse para que G se desconecte.
17.1 Observación. (a) κ(G) = 0 ⇔ λ(G) = 0 ⇔ G es disconexa.
(b) κ(G) = 1 si, y sólo si G es conexa y tiene vértice de corte o es K2 .
(c) λ(G) = 1 si, y sólo si G es conexa y tiene puente.
17.2 Ejemplo. (a) κ(Cn ) = 2 = λ(Cn ) para toda n ≥ 3.
(b) κ(Kn ) = n − 1 = λ(Kn ) para toda n ≥ 3.
17.3 Proposición. κ(G) ≤ λ(G) ≤ δ(G) para toda gráfica G.
Demostración. Sea v de grado δ(G); entonces al quitar las aristas de v aislamos v, por lo
tanto λ(G) ≤ δ(G).
Probemos que κ(G) ≤ λ(G). La desigualdad se cumple si G es completa o es disconexa.
Supongamos que G es conexa y no completa. Consideremos un conjunto E de λ(G) aristas
que desconecte G. Observemos que G − E tiene exactamente dos componentes conexas (por
2.1); sean éstas H1 y H2 . Sea |V(G)| = n.
Caso (1). Todos los vértices de H1 son adyacentes a todos los vértices de H2 . Entonces
|E| ≥ n − 1. Como G no es completa, entonces alguna de las componentes tiene dos vértices
no adyacentes; supongamos, sin pérdida de generalidad, que u, v son vértices no adyacentes
de H1 . Entonces X = V(G) − {u, v} es un conjunto de n − 2 vértices que separa G y, por lo
tanto, κ(G) ≤ |V| − 2 < |E| = λ(G).
Caso (2). Sean u ∈ H1 y v ∈ H2 no adyacentes. Definamos la función f : E → V(G)
x,
si a = ux
f (a) =
a ∩ V(H1 ), si u ∈
/a
Sea X la imagen de f . Entonces X no contiene a u ni a v y, como X contiene a un vértice
por cada arista de E, se tiene que X separa a u de v (cualquier uv-trayectoria usa alguna
arista de E). Tenemos entonces κ(G) ≤ |X| ≤ |E| = λ(G). ♦
Consideraremos ahora los tamaños de conjuntos de vértices o de aristas que separan a
dos vértices dados. Usaremos 16.5 en su demostración.
17.4 Teorema. Teorema de Menger para aristas. Sean u y v dos vértices en una
gráfica (no dirigida) G. Entonces el menor número de aristas necesarias para separar u de v
(es decir, de manera que al quitar las aristas, u y v queden en componentes conexas distintas)
99
es igual al máximo número de uv-trayectorias ajenas en aristas.
Demostración. Convirtamos G en una red (D, s, t, c) poniendo s = u, t = v y, por cada
arista xy de G que no contenga a s ni a t, dos arcos: xy y yx; pongamos también un arco sx
por cada arista sx y un arco yt por cada arista yt. Definamos la función de capacidad con
valor 1 para todo arco de D. Un flujo máximo f determina |f | trayectorias ajenas en aristas
de s a t; las aristas que salen de cualquier corte con capacidad mı́nima separan s de t. ♦
17.5 Ejercicio. Demostrar el Teorema de Menger para vértices. Sean s y t dos
vértices no adyacentes en una gráfica (no dirigida) G. Entonces el menor número de vértices
necesarios para separar s de t (es decir, de manera que al quitar esos vértices, s y t queden
en componentes conexas distintas) es igual al máximo número de st-trayectorias internamente ajenas en vértices (es decir, trayectorias cuyos únicos vértices en común son s y
t). (Sugerencia: Construir una digráfica D0 a partir de G como sigue: Sustituir cada vértice
u distinto de s o de t por dos vértices u− y u+ ; poner un arco u− u+ por cada u, arcos su−
por cada arista su de G, arcos u+ t por cada arista ut de G, y arcos u+ v − por cada arista uv
de G.)
17.6 Ejercicio. Probar que si una gráfica con n ≥ 2k vértices es k-conexa, (es decir,
κ(G) ≥ k) entonces para todo par de subconjuntos ajenos de vértices U y V , con |U | = |V | =
k, existen k trayectorias ajenas de U a V .
100
Índice alfabético
(D, s, t, c), 90
(V, A), 1
(a1 , a2 , . . . , an ), 2
(u, C, v), 2
(u = v0 , a1 , v1 , a2 , . . . , an , vn = v), 2
(u = v0 , v1 , . . . , vn = v), 2
A, 36
Aua , 2
Auv , 2
Aut(G), 14
C, 36
C −1 , 2
Cay(ΛL ), 16
D(G), 6
ES(n), 72
T (n, s), 63
V , 36
X4Y , 74
Z(G), 6
[n], 1
∆(G), 1
α(G), 68
A(G), 1
B(G), 23
BC(G), 25
Cn , 3
D, 85
G + H, 12
G + uv, 4
G, H, . . ., 1
G − S, 4
G − a, 4
G − v, 4
G/a, 38
G[H], 12
G H, 12
G ∪ H, 12
G × H, 12
G ∗ , 40
G k , 19
Kn , 3
Km,n , 5
Kn1 ,...,ns , 5
L(G), 19
N (S), 1
N (v), 1
N + (u), 86
N − (u), 86
P, 15
Qn , 12
V(G), 1
χ(G), 50
χ(S), 55
χ1 (G), 57
χ2 (G), 61
δ(G), 1
δ(v), 1
δ + (u), 86
δ − (u), 86
γ(G), 45
κ(G), 96
λ(G), 96
ν(G), 48
ω(G), 53
G, 3
N (v), 1
→
−
C , 85
a−1 , 85
c(S), 91
d(u, v), 6
e(u), 6
f (U ), 91
f + (U ), 90
f − (U ), 90
fG , 55
k-conexa, 97
r(G1 , G2 ), 64
r(k, l), 66
101
r(k1 , k2 , . . . , kt ), 70
r3 (k, l), 71
t(n, s), 63
u, v, w, . . ., 1
uv, 1
Tn , 3
acción, 15
libre en vértices, 15
transitiva en aristas, 15
transitiva en vértices, 15
adyacentes (aristas), 2
adyacentes (vértices), 2
agente viajero (problema del), 33
apareamiento, 74
máximo, 74
maximal, 74
perfecto, 74
saturado, 75
arbol, 4
arco, 85
simétrico, 85
arista, 1
incidente a vértice, 2
automorfismo, 14
bloque, 8
bloque (de gráfica), 23
bloques (gráfica de), 23
bloques y cortes (gráfica de), 25
bosque, 4
Brooks (teorema de), 51
camino, 2
abierto, 2
cerrado, 2
dirigido, 85
euleriano, 29
hamiltoniano, 30, 33
capacidad de un corte, 91
cara (de gráfica), 36
cartero chino (problema del), 29
Cayley (gráfica de), 16
centro, 6
ciclo, 2
dirigido, 85
hamiltoniano, 30
clan, 53
clase cromática, 50
coloración
buena de vértices, 43
de aristas, 57
de mapas, 43
de vértices, 43
propia de aristas, 57
propia de vértices, 43
propia de vértices y aristas, 61
complemento (de gráfica), 3
componente conexa de gráfica, 3
componente conexa de vértice, 3
componente de digráfica, 85
fuertemente conexa, 85
composición de gráficas, 12
conexidad de una gráfica, 96
conexidad lineal de gráfica, 96
contracción de arista, 38
corte de una red, 91
cuadrado, 10
cubo, 33
cubo de dimensión n, 12
cuello, 11
diámetro, 6
diferencia simétrica, 74
digráfica, 1
acı́clica, 86
débilmente conexa, 85
fuertemente conexa, 85
simétrica, 85
torneo, 87
transitiva, 85
unilateralmente conexa, 85
distancia entre vértices, 6
dodecaedro, 33
dual de una gráfica, 40
encaje, 14
102
de 2-celdas, 45
envolvente convexa, 72
Erdös-Szekeres (teorema de), 72
Euler (fórmula de), 36
excentricidad, 6
exgrado de un vértice, 86
extremo de una arista, 1
exvecinos de un vértice, 86
regular, 1
simple, 1
gráfica subyacente de una digráfica, 85
grado de vértice, 1
factor
regular, 82
factor de una gráfica, 82
factorización de una gráfica, 82
regular, 82
flujo, 90
total de un conjunto, 91
flujo máximo (problema del), 91
flujo máximo/corte mı́nimo (teorema del), 92
Ford-Fulkerson (algoritmo de), 92
fuente, 86
función de capacidad, 90
género
de una gráfica, 45
de una superficie, 45
gráfica, 1
s-partita, 5
s-partita completa, 5
aplanable, 36
bipartita, 5
cúbica, 61
completa, 3
completa bipartita, 5
conexa, 2
contenida en, 3
disconexa, 2
euleriana, 26
finita, 1
hamiltoniana, 30
hamiltonianamente conexa, 33
multipartita casi regular, 63
plana, 36
poliédrica, 42
Hall (teorema de), 75
Heawood (gráfica de), 44
Heawood (teorema de), 55
hoja, 4
homomorfismo, 14
que pega, 14
icosaedro, 33
independiente (conjunto de vértices), 68
indice cromático, 57
ingrado de un vértice, 86
inmersión, 14
invecinos de un vértice, 86
isomorfas (gráficas), 2
Köninsberg (problema de los puentes), 26
Kirkoff (ley de), 90
Kuratowsky (teorema de), 38
lı́neas (gráfica de), 19
lazo, 1
longitud de un camino, 2
marcador de un vértice, 88
matriz de adyacencias, 2
matriz de incidencias, 2
Menger (teorema de aristas para), 96
Menger (teorema de vértices para), 97
menor de una gráfica, 38
multigráfica, 1
número
de clan, 53
de cruce, 48
de independencia, 68
de Turán, 63
número cromático, 50
de una superficie, 55
por aristas, 57
total, 61
103
octaedro, 33
orden de una gráfica, 1
Ore (teorema de), 32
orientación para una gráfica, 86
paseo, 2
dirigido, 85
euleriano, 26
Petersen (gráfica de), 15
polinomio cromático, 55
potencia de una gráfica, 19
pozo, 86
producto cuadro de gráficas, 12
producto lexicográfico de gráficas, 12
producto tache de gráficas, 12
puente, 8
vértice, 1
de corte, 8
valor de flujo, 91
vecindad, 1
cerrada, 1
vecino, 1
Vizing (teorema de), 58
Ramsey (teorı́a de), 64
red, 90
sólidos platónicos, 32
seudográfica, 1
sistema de representantes, 76
subgráfica, 3
generadora, 3
inducida, 3
suma de gráficas, 12
tamaño de una gráfica, 1
tetraedro, 33
tipo I, 60
tipo II, 60
trayectoria, 2
alternante, 74
aumentante, 74
dirigida, 85
hamiltoniana, 30
trayectorias
internamente ajenas en vértices, 97
triángulo, 6
Turán (teorema de), 63
Tutte (gráfica de), 35
Tutte (teorema de), 80
unión de gráficas, 12
104